转子动力学课件第1次课 共27页PPT资料

转子动力学是固体力学的一个分支。

本文主要研究转子支承系统在旋转状态下的振动，平衡和稳定性，特别是在接近或超过临界转速的情况下转子的横向振动。

转子是涡轮机，电动机和其他旋转机械的主要旋转部件。

200多年来，工程和科学界一直关注转子振动。

w.j.m. 1869年英格兰的兰金（Rankin）和1889年法国的拉瓦尔（c.g.p.de Laval）对挠性轴的测试是研究此问题的先驱。

随着现代工业的发展，高速细长转子逐渐出现。

由于它们通常在柔性状态下工作，因此它们的振动和稳定性变得越来越重要。

转子动力学的主要研究内容如下：①临界速度由于制造误差，转子每个微小部分的质心与旋转轴略有偏离。

当转子旋转时，由上述偏差引起的离心力将使转子产生横向振动。

在某些速度（称为临界速度）下，这种振动似乎非常强烈。

为了确保机器不会在工作速度范围内产生共振，临界速度应适当偏离工作速度，例如大于10％。

临界速度与转子的弹性和质量分布有关。

对于具有有限集总质量的离散旋转系统，临界速度的数量等于集总质量的数量；对于具有连续质量分布的弹性旋转系统，临界速度是无限的。

传递矩阵法是计算大型转子支撑系统临界转速的最常用数值方法。

要点是：首先，将转子分成几个部分，每个部分左右两端的四个部分参数（挠度，挠度角，弯矩和剪切力）之间的关系可以通过传递来描述。

该部分的矩阵。

以此方式，可以获得系统的左端和右端的横截面参数之间的总传递矩阵。

然后，根据边界条件和自然振动中非零解的条件，通过试错法求出各阶的临界速度，得到相应的振动模式。

②通过临界速度的状态通常，转子以可变速度通过临界速度，因此通过临界速度的状态是不稳定的。

与以临界速度旋转时的静止状态不同，有两个方面：一是振幅的最大值小于静止状态的振幅，速度越大，振幅的最大值越小。

另一个是振幅的最大值不会在像静止状态那样的临界速度下出现。

在不稳定状态下，频率转换干扰力作用在转子上，这使分析变得困难。

为了解决这种问题，在数值计算或非线性振动理论中必须使用渐近法或级数展开法。

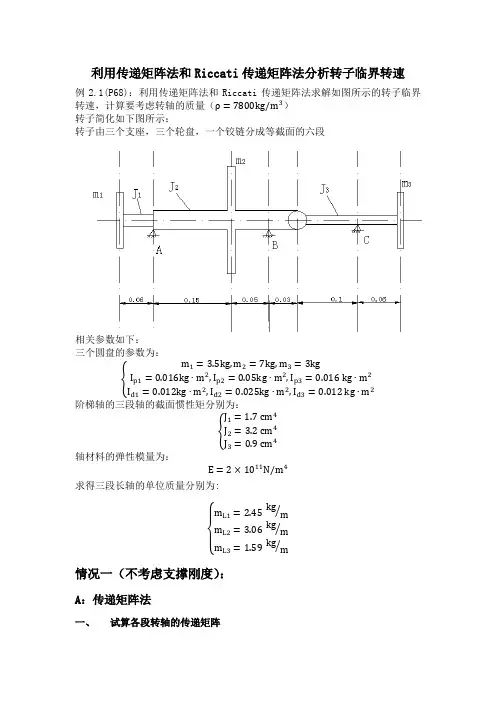
利用传递矩阵法和Riccati 传递矩阵法分析转子临界转速 例2.1(P68)：利用传递矩阵法和Riccati 传递矩阵法求解如图所示的转子临界转速，计算要考虑转轴的质量（ρ=7800kg/m 3）转子简化如下图所示：转子由三个支座，三个轮盘，一个铰链分成等截面的六段相关参数如下：三个圆盘的参数为：{m 1=3.5kg,m 2=7kg,m 3=3kgI p1=0.016kg ∙m 2,I p2=0.05kg ∙m 2,I p3=0.016 kg ∙m 2I d1=0.012kg ∙m 2,I d2=0.025kg ∙m 2,I d3=0.012 kg ∙m 2阶梯轴的三段轴的截面惯性矩分别为：{J 1=1.7 cm 4J 2=3.2 cm 4J 3=0.9 cm 4轴材料的弹性模量为：E =2×1011N/m 4求得三段长轴的单位质量分别为:{ m L1=2.45 kg m ⁄m L2=3.06 kg m ⁄m L3=1.59 kg m ⁄ 情况一（不考虑支撑刚度）：A ：传递矩阵法一、 试算各段转轴的传递矩阵取试算转速p=ω=1500 rad s⁄ ; 则各轴段的传递矩阵分别为：第1段{l=0.06 mJ=1.7×10−8 m4 m L1=2.45 kg m⁄p=1500rad/s ; H1=[10.060.058415.29e−7 1.06e−81.77e−5 5.29e−79.92e31983.31e59.92e31 0.060.0584 1]第2段{l=0.15 mJ=3.2×10−8 m4 m L2=3.06 kg m⁄p=1500rad/s ; H2=[10.150.60611.76e−68.79e−82.35e−5 1.76e−67.76e4 3.88e31.04e67.76e41 0.150.606 1]第3段{l=0.05 mJ=3.2×10−8 m4 m L2=3.06 kg m⁄p=1500rad/s ; H3=[10.050.022411.95e−7 3.26e−97.81e−6 1.95e−78.61e31433.44e58.61e31 0.050.0224 1]第4段{l=0.03 mJ=3.2×10−8 m4 m L2=3.06 kg m⁄p=1500rad/s ; H4=[10.034.84e−317.03e−87.03e−104.69e−67.03e−83.10e331.02.07e53.10e31 0.034.84e−3 1]第5段{l=0.1 mJ=0.9×10−8 m4 m L3=1.59 kg m⁄p=1500rad/s ; H5=[10.10.33112.78e−69.26e−85.57e−5 2.78e−61.79e45963.58e5 1.79e41 0.10.331 1]第6段{l=0.06 mJ=0.9×10−8 m4 m L3=1.59 kg m⁄p=1500rad/s ; H6=[10.060.071611.00e−62.00e−83.33e−5 1.00e−66.44e31292.15e5 6.44e31 0.060.0716 1]此6段传递矩阵均采用MATLAB编程求解，MATLAB的源文件为zhouduan.m二、采用传递矩阵法进行各段轴的状态参数的传递初始参数列阵为：[X01θ01M01 Q01]=[X01θ01−(1−ωPI pI d)I d p2θ01m1p2X01]令X01=1，则初始矩阵可化为：[1θ019000θ017.875e6]以初始矩阵乘第一轴段的传递矩阵，则可得第一段轴的终端状态参数：[X k1θk1M k1 Q k1]=[1.08+0.065θ014.23+1.16θ014.825e5+9.206e3θ018.21e6+1.045e3θ01]根据X k1=0可计算得：θ01=−16.739；则，可得支座A后第2段的起始端参数阵为：[X02θ02M02 Q02]=[−15.1853.28e58.038e6−R A]其中，R A为刚性支座的反作用力；用第2段的传递矩阵乘此矩阵，可得第2段终端参数：[X k2θk2M k2Q k2]=[−1.003−8.79e(−8)∗R A6.353−1.76e(−6)∗R A1.488e6−0.15∗R A7.241e6−1.023R A]用中间圆盘的传递矩阵乘第2段终端参数阵，即可得第3段起始端参数：[X03θ03M03 Q03]=[−1.003−8.79e(−8)∗R A6.353−1.76e(−6)∗R A1.85e6−0.249∗R A−8.556e6−2.408∗R A]用第3段传递矩阵乘其始端参数矩阵，得其终端参数：[X k3θk3M k3Q k3]=[−0.353−2.32e(−7)∗R A19.08−4.184e(−6)∗R A1.41e6−0.371∗R A−8.81e6−2.459∗R A]则，根据X k3=0可得：R A=−1.518e6;则，可得支座B后第4段的起始端参数阵为：[X04θ04M04 Q04]=[25.431.974e6−5.075e6−R B]同上，用此段轴的传递函数乘其起始端的状态参数，可得：[X k4θk4M k4 Q k4]=[0.898−7.03e(−10)∗R B34.33−7.03e(−8)∗R B1.822e6−3e(−2)∗R B−4.987e6−R B]则，根据M k4=0可得：R B=6.075e7;则，可得第5段的起始参数矩阵：[X05θ05M05 Q05]=[0.85530.055+θ5−6.574e7]其中，θ5为铰链处的转角。