圆柱的表面积测试题
- 格式:docx
- 大小:31.87 KB
- 文档页数:8

圆柱的表面积和体积练习测试卷一.选择题(共5小题)1.用一张长6.28cm,宽1dm的长方形铁皮,围成一个圆柱体,这个圆柱的侧面积是()A.31.4cm2B.3.14 m2C.12.56cm2 D.62.8cm22.一个底面积是20cm2的圆柱,斜着截去了一段后,剩下的图形如图.截后剩下的图形的体积是()cm3.A.140B.180C.220D.3603.压路机的前轮转动一周所压过的路面面积是指()A.前轮的表面积B.前轮的侧面积C.前轮的底面积4.在长12厘米,宽10厘米,高8厘米的长方体中切出一个体积最大的圆柱,这个圆柱的体积是()立方厘米.A.1130.4B.602.88C.628D.904.325.一个圆柱的底面直径扩大到原来的2倍,高缩小到原来的,圆柱的侧面积()A.扩大到原来的2倍B.缩小到原来的C.不变D.扩大到原来的3倍二.填空题(共10小题)6.一根长20分米的圆柱形圆木,锯成两段后表面积增加了4平方分米,它原来的体积是立方分米.7.一个长4cm,宽3cm的长方形,以一条边为轴旋转一周,得到一个,侧面积是cm2,体积最大是cm3.8.如图,把一个底面半径为4cm的圆柱,拼成一个近似的长方体,长方体的表面积比圆柱增加了40cm2,圆柱的高是cm,体积是cm3.9.李叔叔家新买了一台空调,外观为圆柱体,底面半径30厘米,高约2米,这台空调所占空间为立方米,若需要一个防尘罩,至少需要布平方米.10.一个圆柱体,底面积是3dm2,高是15cm,它的体积是dm3.11.一个正方体棱长之和是36厘米,把它挖去一个最大的圆柱体,圆柱体的体积是立方厘米.12.把一个圆柱的侧面展开是一个正方形,这个圆柱的底面直径是4厘米,圆柱的高是厘米.(ð取3.14)13.一根长1米的圆柱形木棒,锯成3段后,表面积增加了64平方分米,这根木棒的体积是.14.如图,一个内直径是6cm的瓶里装满矿泉水,小兰喝了一些后,这时瓶里水的高度是12cm,把瓶盖拧紧后倒置放平,无水部分高8cm.小兰喝了ml水;这个瓶子的容积是ml.15.一个高20cm的圆柱,沿着底面直径切成两个半圆柱,表面积增加360cm2,这个圆柱的底面直径是cm.三.判断题(共5小题)16.两个圆柱的侧面积相等,它们的高一定相等.(判断对错)17.圆柱的表面积等于底面积乘高.(判断对错)18.圆柱的侧面展开是正方形时,这个圆柱的高和它的底面周长相等.(判断对错)19.压路机滚筒滚动一周能压多少路面是求滚筒的侧面积.(判断对错)20.做一个铁皮烟囱需要多少铁皮,就是求烟囱的表面积.(判断对错)四.计算题(共2小题)21.计算下面圆柱的表面积和体积.22.如图,阴影部分的材料正好可以做成一个圆柱,求这个圆柱的体积.五.应用题(共5小题)23.一种无盖的消防桶是圆柱形.底面半径是10cm,高40cm.现在要在桶的外侧面和外底面涂上油漆.(1)涂油漆的面积是多少平方厘米?(2)这个消防桶的容积是多少立方厘米?(桶的厚度忽略不计).24.一种圆柱形的铁皮通风管长4米,横截面的直径是3分米,要做20节这样的通风管,至少需要多少平方分米的铁皮?25.100个无盖油桶的外表面要刷油添,每平方米需油漆0.5kg.每个油桶的底面直径是40cm,高是60cm.刷这100个无盖油桶需多少千克油漆?26.一个圆柱形水桶,从里面量底面直径是2.6米,深2米,这个水桶能装多少吨花水?(每立方米水重1吨)(最后结果保留一位小数)27.一个盛有水的圆柱形容器的底面直径是10厘米,水深12厘米,放入一块石头,从容器中溢出50毫升水,这个容器的高是22厘米,石头的体积是多少?圆柱的表面积和体积练习测试卷参考答案与试题解析一.选择题(共5小题)1.用一张长6.28cm,宽1dm的长方形铁皮,围成一个圆柱体,这个圆柱的侧面积是()A.31.4cm2B.3.14 m2C.12.56cm2 D.62.8cm2【解答】解:1dm=10cm6.28×10=62.8(平方厘米)答:这个圆柱的侧面积是62.8平方厘米.故选:D.【点评】此类题解答的关键是理解圆柱侧面积的计算方法,然后根据计算公式代入数据解答即可.2.一个底面积是20cm2的圆柱,斜着截去了一段后,剩下的图形如图.截后剩下的图形的体积是()cm3.A.140B.180C.220D.360【解答】解:20×(7+11)÷2=20×18÷2=180(立方厘米)答:节后剩下的图形的体积是180立方厘米.故选:B.【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式.3.压路机的前轮转动一周所压过的路面面积是指()A.前轮的表面积B.前轮的侧面积C.前轮的底面积【解答】解:压路机的前轮转动一周所压过的路面面积是指前轮的侧面积.故选:B.【点评】压路机的前轮的形状是圆柱,这个圆柱是侧躺在地面,转动一周,所压过的面正好是圆柱的侧面.4.在长12厘米,宽10厘米,高8厘米的长方体中切出一个体积最大的圆柱,这个圆柱的体积是()立方厘米.A.1130.4B.602.88C.628D.904.32【解答】解:以10厘米为底面直径,高是8厘米;3.14×(10÷2)2×8=3.14×25×8=78.5×8=628(立方厘米答:这个圆柱体的体积是628立方厘米.故选:C.【点评】解答此题的关键是,如何将一个长方体削成一个最大的圆柱,并找出它们之间的联系,再根据相应的公式解决问题.5.一个圆柱的底面直径扩大到原来的2倍,高缩小到原来的,圆柱的侧面积()A.扩大到原来的2倍B.缩小到原来的C.不变D.扩大到原来的3倍【解答】解:根据圆的周长公式:C=ðd,因为圆周率一定,所以圆的周长和直径成正比例,因此,一个圆柱的底面直径扩大到原来的2倍,也就是圆柱的底面周长扩大2倍,高缩小到原来的,所以圆柱的侧面积不变.故选:C.【点评】此题考查的目的是理解掌握圆柱的侧面积公式及应用,以及因数与积的变化规律及应用.二.填空题(共10小题)6.一根长20分米的圆柱形圆木,锯成两段后表面积增加了4平方分米,它原来的体积是40立方分米.【解答】解:4÷2×20=2×20=40(立方分米)答:它用来的体积是40立方分米.故答案为:40.【点评】此题考查的目的是理解掌握圆柱表面积的意义,以及圆柱体积公式的灵活运用,关键是熟记公式.7.一个长4cm,宽3cm的长方形,以一条边为轴旋转一周,得到一个圆柱,侧面积是75.36cm2,体积最大是150.72cm3.【解答】解:(1)以4厘米的边为轴旋转一周得到的圆柱的底面半径是3厘米,高是4厘米;2×3.14×3×4=18.84×4=75.36(平方厘米);3.14×32×4=3.14×9×4=28.26×4=113.04(立方厘米);(2)以3厘米的边为轴旋转一周得到的圆柱的底面半径是4厘米,高是3厘米;2×3.14×4×3=25.12×3=75.36(平方厘米);3.14×42×3=3.14×16×3=50.24×3=150.72(立方厘米);150.72>113.04;答:得到一个圆柱,侧面积是75.36平方厘米,体积最大是150.72立方厘米.故答案为:圆柱、75.36、150.72.【点评】此题考查的目的是理解掌握圆柱的特征,以及圆柱的侧面积公式、体积公式的灵活运用,关键是熟记公式.8.如图,把一个底面半径为4cm的圆柱,拼成一个近似的长方体,长方体的表面积比圆柱增加了40cm2,圆柱的高是5cm,体积是251.2cm3.【解答】解:40÷2÷4=5(厘米)3.14×42×5=3.14×16×5=50.24×5=251.2(立方厘米)答:圆柱的高是5厘米,体积是251.2立方厘米.故答案为:5、251.2.【点评】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用,以及圆柱体积公式的灵活运用,关键是熟记公式.9.李叔叔家新买了一台空调,外观为圆柱体,底面半径30厘米,高约2米,这台空调所占空间为0.5652立方米,若需要一个防尘罩,至少需要布 4.0506平方米.【解答】解:30厘米=0.3米3.14×0.32×2=3.14×0.09×2=0.5652(立方米)3.14×0.3×2×2+3.14×0.32=3.14×1.2+3.14×0.09=3.14×1.29=4.0506(平方米)答:这台空调所占空间为0.5652立方米,至少需要布4.0506平方米.故答案为:0.5652;4.0506.【点评】解答此题主要分清所求物体的形状,转化为求有关圆柱体表面积的问题,把实际问题转化为数学问题,再运用圆柱的表面积公式和体积公式解决问题.10.一个圆柱体,底面积是3dm2,高是15cm,它的体积是 4.5dm3.【解答】解:15厘米=1.5分米答:它的体积是4.5立方分米.故答案为:4.5.【点评】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式,注意:底面积与高单位的对应.11.一个正方体棱长之和是36厘米,把它挖去一个最大的圆柱体,圆柱体的体积是21.195立方厘米.【解答】解:36÷12=3(厘米)3.14×(3÷2)2×3=3.14×2.25×3=7.065×3=21.195(立方厘米)答:圆柱的体积是21.195立方厘米.故答案为:21.195.【点评】此题主要考查正方体的棱长总和公式、圆柱的体积搜狗的灵活运用,关键是熟记公式.12.把一个圆柱的侧面展开是一个正方形,这个圆柱的底面直径是4厘米,圆柱的高是12.56厘米.(ð取3.14)【解答】解:3.14×4=12.56(厘米)答:圆柱的高是12.56厘米.故答案为:12.56.【点评】解答此题的关键是根据侧面展开图是一个正方形,明确圆柱的高与底面周长相等.13.一根长1米的圆柱形木棒,锯成3段后,表面积增加了64平方分米,这根木棒的体积是160立方分米.【解答】解:1米=10分米64÷4×10=16×10=160(立方分米)答:这根木棒的体积是160立方分米.【点评】抓住圆柱的切割特点和增加的表面积,先求出圆柱的底面积是解决此类问题的关键.14.如图,一个内直径是6cm的瓶里装满矿泉水,小兰喝了一些后,这时瓶里水的高度是12cm,把瓶盖拧紧后倒置放平,无水部分高8cm.小兰喝了226.08ml水;这个瓶子的容积是565.2ml.【解答】解:3.14×(6÷2)2×8=3.14×9×8=28.26×8=226.08(立方厘米)3.14×(6÷2)2×(12+8)=3.14×9×20=28.26×20=565.2(立方厘米)226.08立方厘米=226.08毫升565.2立方厘米=565.2毫升答:小红喝了226.08毫升,这个瓶子的容积是565.2毫升.故答案为:226.08、565.2.【点评】此题主要考查圆柱的容积(体积)公式在实际生活中的应用,关键是熟记公式,注意:体积单位与容积单位之间的换算.15.一个高20cm的圆柱,沿着底面直径切成两个半圆柱,表面积增加360cm2,这个圆柱的底面直径是9cm.【解答】解:360÷2÷20=180÷20=9(厘米)答:这这个圆柱的底面直径是9厘米.故答案为:9.【点评】此题主要考查圆柱的表面积公式、体积公式的灵活运用,关键是熟记公式,重点是明确:表面积增加的360平方厘米是两个截面的面积,每个截面的长等于圆柱的高,宽等于圆柱的直径.三.判断题(共5小题)16.两个圆柱的侧面积相等,它们的高一定相等.×(判断对错)【解答】解:侧面积相等的两个圆柱,它们的底面周长和高不一定相等.如侧面积是6.28,即底面周长×高=6.28,因为3.14×2=6.28,6.28×1=6.28,所以它们的底面周长和高不一定相等.原题说法错误.故答案为:×.【点评】本题考查了圆柱的侧面积公式的应用和积一定,一个数越大另一个数就越小的规律.17.圆柱的表面积等于底面积乘高.×(判断对错)【解答】解:圆柱的表面积=侧面积+底面积×2,因此,圆柱的表面积等于底面积乘高.这种说法是错误的.故答案为:×.【点评】此题考查的目的是理解掌握圆柱表面积的意义,以及圆柱的表面积公式.18.圆柱的侧面展开是正方形时,这个圆柱的高和它的底面周长相等.√(判断对错)【解答】解:如果圆柱的侧面展开是一个正方形,那么这个圆柱的底面周长和高相等.所以题干说法正确.故答案为:√.【点评】此题考查的目的是理解掌握圆柱侧面展开图的特征.19.压路机滚筒滚动一周能压多少路面是求滚筒的侧面积.√(判断对错)【解答】解:因为压路机的滚筒是一个圆柱,所以压路机滚筒滚动一周能压多少路面是求滚筒的侧面积.因此,压路机滚筒滚动一周能压多少路面是求滚筒的侧面积.这种说法是正确的.故答案为:√.【点评】此题考查的目的是理解掌握圆柱的特征,以及圆柱侧面积的意义.20.做一个铁皮烟囱需要多少铁皮,就是求烟囱的表面积.×(判断对错)【解答】解:因为,烟囱是通风的,是没有上下两个底的所以,做一个铁皮烟囱需要多少铁皮,就是求烟囱的侧面积,题干的说法是错误的.故答案为:×.【点评】此题主要考查了圆柱体的侧面积的意义,及在生活中的实际应用.四.计算题(共2小题)21.计算下面圆柱的表面积和体积.【解答】解:侧面积:3.14×8×10=251.2(平方厘米)表面积:251.2+3.14×(8÷2)2×2=251.2+3.14×16×2=251.2+100.48=351.68(平方厘米)体积:3.14×(8÷2)2×10=3.14×16×10=502.4(立方厘米);答:表面积是351.68平方厘米,体积是502.4立方厘米.【点评】此题主要考查圆柱的侧面积、表面积、体积的计算,直接根据它们的计算公式,把数据代入公式解答即可.22.如图,阴影部分的材料正好可以做成一个圆柱,求这个圆柱的体积.【解答】解:设圆柱的底面直径为x分米,3.14x+x=16.564.14x=16.56x=4.3.14×(4÷2)2×(4×2)=3.14×4×8=12.56×8=100.48(立方分米),答:这个圆柱的体积是100.48立方分米.【点评】此题主要考查圆的周长公式、圆柱的体积公式的灵活运用,关键是熟记公式.五.应用题(共5小题)23.一种无盖的消防桶是圆柱形.底面半径是10cm,高40cm.现在要在桶的外侧面和外底面涂上油漆.(1)涂油漆的面积是多少平方厘米?(2)这个消防桶的容积是多少立方厘米?(桶的厚度忽略不计).【解答】解:(1)3.14×102+3.14×10×2×40=3.14×100+3.14×800=3.14×900=2826(平方厘米)答:涂油漆的面积是2826平方厘米;(2)3.14×102×40=3.14×100×40=12560(立方厘米)答:这个消防桶的容积是12560立方厘米.【点评】解答此题主要分清所求物体的形状,转化为求有关圆柱体表面积的问题,把实际问题转化为数学问题,再运用圆柱的表面积公式和体积公式解决问题.24.一种圆柱形的铁皮通风管长4米,横截面的直径是3分米,要做20节这样的通风管,至少需要多少平方分米的铁皮?【解答】解:4米=40分米3.14×3×40×20=3.14×2400=7536(平方分米)答:至少需要7536平方分米的铁皮.【点评】此题考查了圆柱的侧面积公式的计算应用,此类问题要结合生活实际进行解答.25.100个无盖油桶的外表面要刷油添,每平方米需油漆0.5kg.每个油桶的底面直径是40cm,高是60cm.刷这100个无盖油桶需多少千克油漆?【解答】解:侧面积=底面周长×高=3.14×40×60=7536(平方厘米)底面积S=ðr2=3.14×(40÷2)2=1256(平方厘米)表面积=侧面积+底面积=7536+1256=8792(平方厘米)=0.8792(平方米)0.8792×0.5×100=43.96(千克)答:需要43.96千克油漆.【点评】在物体表面刷漆的问题,都是求物体的表面积,搞清物体的形状和面数解答即可.26.一个圆柱形水桶,从里面量底面直径是2.6米,深2米,这个水桶能装多少吨花水?(每立方米水重1吨)(最后结果保留一位小数)【解答】解:2.6÷2=1.3(米)3.14×1.32×2=3.14×3.38=10.6032(立方米)10.6032×1≈10.6(吨)答:这个水桶大约能装10.6吨水.【点评】从里面量圆柱的底面直径和高,根据V=Sh算出来的是圆柱的容积.27.一个盛有水的圆柱形容器的底面直径是10厘米,水深12厘米,放入一块石头,从容器中溢出50毫升水,这个容器的高是22厘米,石头的体积是多少?【解答】解:50毫升=50立方厘米3.14×(10÷2)2×(22﹣12)+50=3.14×25×10+50=78.5×10+50=785+50=835(立方厘米)答:石头的体积是835立方厘米.【点评】此题主要考查圆柱的容积(体积)公式的灵活运用,关键是熟记公式,注意:容积单位与体积单位之间的换算.。

六年级下册数学圆柱的表面积试题一、选择题。
1.做一个无盖的原型笔筒,求至少需要多少材料,就是求圆柱的()。
A.底面积B.侧面积C.表面积D.侧面积和一个底面积2.一个援助的侧面积是100.24cm2,底面周长是6.28cm,它的高是()。
A.4cmB.8cmC.16cmD.32cm3.一个圆柱形铁桶的底面半径是4cm,高是25cm。
这个圆柱形铁桶直立放置时的占地面积是()dm2。
A.62.8B. 50.24C. 25.124.同一个圆柱,如图,从正面和右侧面看到的图形()A.不相同B.相同C.无法确定5.用一张长60cm,宽40cm的长方形纸,以两种不同的方法各围成一个圆柱,那么围成的圆柱()。
A. 高一定相等B.侧面积一定相等C. 侧面积和高都相等D. 侧面积和体积都相等6.一个圆柱的侧面展开图恰好是一个正方形,这个圆柱的高是底面直径的()。
A. π倍B. 2π倍C. 4π倍二、填一填1.如果把圆柱的侧面沿高展开,就得到一个长方形,这个长方形的长等于圆柱的(),宽等于圆柱的(),长方形的面积=长×宽,所以圆柱的侧面积=()×(),用字母表示是()。
2.一个长3cm、宽2cm的长方形,分别以长和宽为轴旋转一周,可得到一个(),它的底面半径分别是()和(),高是()和(),侧面积是()和()。
3.一个圆柱的底面半径是1dm,高是5dm,侧面积是(),表面积是()。
4.用一张边长5cm的正方形纸围成一个圆柱(接头不计),这个圆柱的底面周长是(),高是(),侧面积是()。
5.在解决实际使用的面料问题时,通常实际使用的面料要比计算的结果()(“多”或“少”)一些,所以,这类问题往往用()取近似数。
三、求圆柱的侧面积。
1.底面周长是12.56cm,高是8cm。
2.底面直径是6cm,高是10cm。
3.底面半径是3dm,高是5dm。
四、解决问题。
1.用长方形纸刚好围成一个底面半径是1cm的圆柱(接头不计),这个圆2.一个圆柱形的蓄水池,底面直径是10m,深2m。

北师大版六年级下册数学《圆柱的表面积》练习题圆柱的表面积测试题一、填空题。
1.圆柱的侧面积加上底面积,就是圆柱的表面积。
2.把圆柱体的侧面沿着它的高展开,得到一个长方形,这个长方形的长等于圆柱的周长,宽等于圆柱的高;也可以得到一个正方形,这时圆柱的直径和高相等。
3.计算做一个圆柱形的茶叶筒要用多少铁皮,要计算圆柱的表面积。
4.计算做一个圆柱形的烟囱要用多少铁皮,要计算圆柱的侧面积。
5.计算做一个没有盖的圆柱形水桶要用多少铁皮,要计算圆柱的侧面积。
6.一个圆柱,它的高是8厘米,侧面积是200.96平方厘米,它的底面积是25平方厘米。
7.2.6米=260厘米,48分米=0.48米,7.5平方分米=750平方厘米,9300平方厘米=0.93平方米。
8.把一个圆柱体的侧面展开后,正好得到一个边长为15.7厘米的正方形,圆柱体的高是15.7厘米。
9.将一根长5米的圆柱形木料锯成2段小圆柱体,表面积增加60平方分米。
这根木料的底面面积是50平方分米。
10.把一个底面积是15.7平方厘米的圆柱,切成两个同样大小的圆柱,表面积增加了31.4平方厘米。
11.一个圆柱的底面半径和高都是2米,它的侧面积是8π平方米,表面积是12π平方米。
12.一个圆柱体的底面半径是3厘米,将它锯成两个圆柱体后表面积增加3π平方厘米。
13.一个圆柱体底面周长是12.56分米,高是10厘米,它的侧面积是125.6平方厘米,表面积是251.2平方厘米。
14.把一个底面直径和高都是2分米的圆柱,切拼成一个近似的长方体,这个长方体底面的长约是3.14分米,宽约是4分米,底面积约是12.56平方分米,体积约是12.56立方分米.15.一个圆柱体的侧面积是12.56平方厘米,底面半径是2厘米,它的高是5厘米。
16.把一张长8分米,宽5分米的白纸,围成一个圆柱形纸筒,这个纸筒的侧面积是40平方分米.二、判断题1.两个圆柱体的侧面积相等,它们的底面积一定也相等。

求圆柱的表面积的练习题
圆柱的表面积=侧面积+底面面积×2
练习题:
1、计算下面各圆柱的表面积。
①C=9.42厘米,h=5厘米。
②d=8米,h=3米。
③r=2分米,h=6分米。
2、填空。
①用一张长5厘米、宽8厘米的长方形纸围成一个圆柱体,这个圆柱体的侧面积是()平方厘米。
②做一节底面直径是10厘米、长95厘米的圆柱体通风管,至少用一张长()厘米宽()厘米的长方形铁皮。
3、一个圆柱,底面周长是94.2厘米,高是25厘米,求它的侧面积。
4、一个圆柱,底面直径是2分米,高是45分米,求它的表面积。
5、砌一个圆柱形沼气池,底面直径是4米,深是2米。
在池的周围与底面抹上水泥,抹水泥部分的面积是多少平方米?
答:抹水泥的面积是37.68平方米
6、一个圆柱体的侧面展开是个边长9.42厘米的正方形,这个圆柱体的表面积是多少平方厘米?(得数保留两位小数)
答:这个圆柱体的表面积是102.86平方厘米。
7、一个圆柱体的侧面积是226.08平方厘米,底面半径4厘米,它的高是多少?
答:它的高是9厘米。
8、一个圆柱的高是15厘米,底面半径是5厘米,它的表面积是多少?
9、一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做这个水桶要用铁皮多少平方厘米?(得数保留整百平方厘米)
10、一个圆柱,底面的直径是0.5米,高是1.8米,求它的侧面积.(得数保留两位小数)。

圆柱的表面积练习题答案圆柱是一种常见的几何图形,它具有特殊的形状和特点。
在计算圆柱的表面积时,我们需要考虑其底面积和侧面积。
下面是一些圆柱表面积的练习题及其答案。
练习题1:已知一个圆柱的高度为8cm,底面半径为4cm,求其表面积。
解答:首先,我们需要计算圆柱的底面积和侧面积,然后将它们相加得到表面积。
底面积= π * r^2 = 3.14 * 4^2 = 3.14 * 16 ≈ 50.24(平方厘米)侧面积 = 周长 * 高度= 2 * π * r * h = 2 * 3.14 * 4 * 8 = 3.14 * 32 ≈ 100.48(平方厘米)表面积 = 底面积 + 侧面积 = 50.24 + 100.48 = 150.72(平方厘米)因此,该圆柱的表面积约为150.72平方厘米。
练习题2:一个圆柱的高度为12cm,表面积为180π平方厘米,求其底面半径。
解答:我们已知该圆柱的表面积,可以利用这一信息来求解底面半径。
表面积 = 底面积 + 侧面积已知表面积为180π平方厘米,将其代入公式中:180π = π * r^2 + 2π * r * h由于高度已知为12cm,将其代入公式中:180π = π * r^2 + 2π * r * 12化简公式:180 = r^2 + 24r移项并整理:r^2 + 24r - 180 = 0我们可以将上述二次方程进行因式分解或者使用求根公式求解出r 的值。
通过解方程,得到底面半径r ≈ 6cm 或r ≈ -30cm,由于半径不可能为负值,所以底面半径约为6cm。
练习题3:一个圆柱的底面积为20π平方厘米,侧面积为60π平方厘米,求其高度和底面半径。
解答:我们已知该圆柱的底面积和侧面积,可以通过这些信息来求解其高度和底面半径。
底面积= π * r^2 = 20π解方程,得到底面半径r ≈ 2.83cm侧面积 = 周长 * 高度= 2 * π * r * h = 60π解方程,得到高度h ≈ 5cm因此,该圆柱的底面半径约为2.83cm,高度约为5cm。
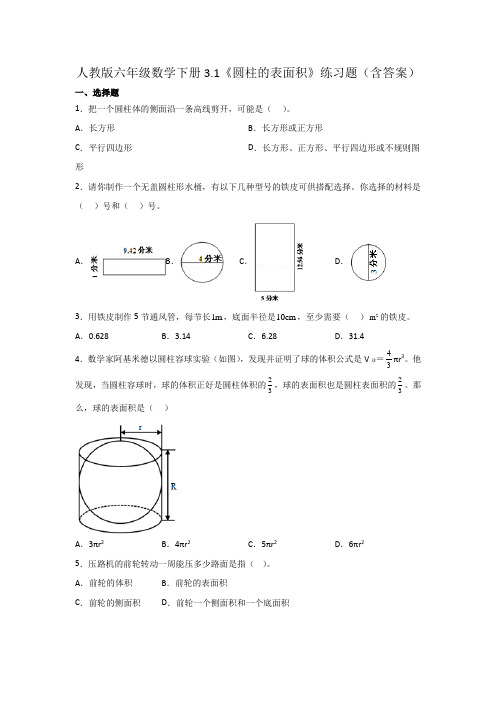
人教版六年级数学下册3.1《圆柱的表面积》练习题(含答案)一、选择题1.把一个圆柱体的侧面沿一条高线剪开,可能是()。
A.长方形B.长方形或正方形C.平行四边形D.长方形、正方形、平行四边形或不规则图形2.请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。
你选择的材料是()号和()号。
A.B.C.D.3.用铁皮制作5节通风管,每节长1m,底面半径是10cm,至少需要()2m的铁皮。
A.0.628 B.3.14 C.6.28 D.31.44.数学家阿基米德以圆柱容球实验(如图),发现并证明了球的体积公式是V球=43πr3。
他发现,当圆柱容球时,球的体积正好是圆柱体积的23,球的表面积也是圆柱表面积的23。
那么,球的表面积是()A.3πr2B.4πr2C.5πr2D.6πr2 5.压路机的前轮转动一周能压多少路面是指()。
A.前轮的体积B.前轮的表面积C.前轮的侧面积D.前轮一个侧面积和一个底面积二、填空题6.700平方厘米=( )平方分米20000公顷=( )平方千米5平方米=( )平方分米 2.04千克=( )克3小时15分=( )小时9080平方米=( )公顷320立方厘米=( )立方分米7.相邻两个面积单位间的进率是( ),相邻两个体积单位间的进率是( ).8.一个长方体水箱从里面量底面积是25cm2,水深1.6m,这个水箱能装水( )立方米。
9.一个圆柱的侧面积是188.4平方米,高是1米,它的底面直径是( )米。
10.把一个长4米的长方体木料切成两段,表面积增加了100平方分米,这根木料的体积是( )立方分米。
三、判断题11.两个圆柱的底面周长相等,它们的侧面积也相等。
( )12.圆柱的侧面展开图只能是长方形或正方形。
( )13.两个圆柱的底面积相等,那么它们的侧面积也一定相等。
( )14.压路机滚筒在地面上滚动一周所压路面面积正好是压路机滚筒的侧面积。
( ) 15.棱长是1 m的正方体可以切成1000个棱长是1 cm 的小正方体.( )四、连线题16.小兔拔萝卜.(连一连)五、解决问题17.一个无盖的圆柱形铁皮水桶,底面直径是30厘米,高是45厘米,做一个这样的水桶要用多少平方厘米铁皮?18.一个圆柱形铁皮水桶(无盖),高20dm,底面半径是2dm,做这个水桶需要用多少平方分米的铁皮?(接头处不计)19.建一个圆形池塘,池底直径是20米,深度是5米。
圆柱的表面积练习题习题精选(一)填空1、把圆柱体的侧面展开,得到一个(),它的()等于圆柱底面周长,()等于圆柱的高.2、一个圆柱体,底面周长是94.2厘米,高是25厘米,它的侧面积是()平方厘米.3、一个圆柱体,底面半径是2厘米,高是6厘米,它的侧面积是()平方厘米.4、一个圆柱体的侧面积是12.56平方厘米,底面半径是2分米,它的高是()厘米.5、把一张长8分米,宽5分米的白纸,围成一个圆柱形纸筒,这个纸筒的侧面积是()平方分米.6、把一张边长为5.5厘米的正方形白纸,围成一个圆柱形纸筒,这个纸筒的侧面积是()平方分米.判断1、圆柱的侧面展开后一定是长方形.()2、6立方厘米比5平方厘米显然要大.()3、一个物体上、下两个面是相等的圆面,那么,它一定是圆柱形物体.()4、把两张相同的长方形纸,分别卷成两个形状不同的圆柱筒,并装上两个底面,那么制的圆柱的高、侧面积、表面积一定相等.()求下面各圆柱体的侧面积.1、底面周长是6分米,高是3.5分米.2、底面直径是2.5分米,高是4分米.3、底面半径是3厘米,高是15厘米.习题精选(二)一、填表二、判断1、圆柱体的表面积=底面积×2+底面积×高.()2、圆柱体的表面积一定比它的侧面积大.()3、圆柱体的高越长,它的侧面积就越大.()三、选择题1、做一个无盖的圆柱体的水桶,需要的铁皮的面积是().①侧面积+一个底面积②侧面积+两个底面积③(侧面积+底面积)×22、一个圆柱的底面直径是10厘米,高是4分米,它的侧面积是()平方厘米.①400②12.56③125.6④12563、圆柱的底面直径扩大2倍,高缩小到原来的,圆柱的侧面积是().①扩大2倍②缩小2倍③不变1、 2.6米 = ()厘米 48分米 =()米7.5平方分米 = ()平方厘米9300平方厘米 = ()平方米2、填空:(1)圆柱的()面积加上()的面积,就是圆柱的表面积。
圆柱的表面积练习题答案一、选择题1. 圆柱的表面积由哪几部分组成?A. 底面积和侧面积B. 顶面积和底面积C. 顶面积和侧面积D. 底面积、顶面积和侧面积2. 若圆柱的底面半径为r,高为h,则圆柱的侧面积公式为:A. πr²B. 2πrhC. πrhD. 2πr²3. 圆柱的底面积公式为:A. πr²B. 2πrhC. πrhD. 2πr²4. 圆柱的总表面积公式为:A. 2πr² + 2πrhB. πr² + 2πrhC. 2πr² + πrhD. πr² + πrh5. 若圆柱的底面半径为3厘米,高为5厘米,其表面积为:A. 150π平方厘米B. 90π平方厘米C. 75π平方厘米D. 60π平方厘米二、填空题6. 圆柱的侧面积等于底面周长乘以________。
7. 圆柱的底面积等于π乘以底面半径的________。
8. 圆柱的总表面积等于底面积的________加上侧面积。
9. 若圆柱的底面半径为4厘米,高为6厘米,则其表面积为________π平方厘米。
10. 圆柱的表面积公式可表示为S=________+2πrh。
三、计算题11. 已知圆柱的底面半径为2厘米,高为10厘米,求圆柱的表面积。
12. 一个圆柱形油桶,底面直径为40厘米,高为60厘米,求油桶的表面积。
13. 一个圆柱形烟囱,底面半径为0.5米,高为15米,求烟囱的表面积。
四、应用题14. 一个圆柱形的储水罐,底面直径为3米,高为5米。
如果需要在储水罐的侧面和顶面刷漆,求需要刷漆的总面积。
15. 一个圆柱形的通风管道,底面半径为0.3米,高为10米。
如果需要在管道的侧面安装保温材料,求需要保温材料的面积。
五、综合题16. 一个圆柱形的玻璃瓶,底面半径为5厘米,高为15厘米。
如果需要在玻璃瓶的侧面和顶面贴上装饰纸,求需要装饰纸的总面积。
17. 一个圆柱形的柱子,底面直径为80厘米,高为3米。
圆柱表面积的计算练习题一、选择题1. 圆柱的表面积是指()。
A. 侧面积B. 侧面积与底面积之和C. 底面积的两倍D. 侧面积的两倍2. 一个圆柱的底面半径为r,高为h,则其表面积为()。
A. 2πr^2B. 2πrhC. 2πr^2 + 2πrhD. πr^2 + πrh3. 圆柱的侧面积是底面积的()倍。
A. 2B. πC. hD. 2π二、填空题1. 圆柱的表面积公式是:S = ________。
2. 一个圆柱的底面半径为5cm,高为10cm,则其侧面积为______cm²。
3. 一个圆柱的底面积为25πcm²,高为10cm,则其表面积为______cm²。
三、计算题1. 已知圆柱的底面直径为10cm,高为20cm,求圆柱的表面积。
2. 已知圆柱的底面半径为8cm,侧面积为100πcm²,求圆柱的高。
3. 已知圆柱的底面积为36πcm²,表面积为150πcm²,求圆柱的高。
4. 计算下列圆柱的表面积:(1)底面半径为3cm,高为7cm;(2)底面半径为4cm,高为6cm;(3)底面半径为5cm,高为8cm。
5. 一个圆柱的底面半径为4cm,高为9cm,求其表面积。
四、应用题1. 制作一个无盖的圆柱形铁皮水桶,底面直径为40cm,高为60cm,求所需铁皮的面积。
2. 一个圆柱形油桶,底面半径为30cm,高为80cm,求油桶的表面积。
3. 计算一个底面半径为10cm,高为15cm的圆柱形烟囱的表面积。
4. 一个圆柱形茶叶罐,底面直径为10cm,高为20cm,求茶叶罐的表面积。
5. 有一根底面直径为20cm,高为50cm的圆柱形钢材,求其表面积。
五、判断题1. 圆柱的表面积等于两个底面积加上一个侧面积。
()2. 圆柱的侧面积与底面积成正比。
()3. 如果圆柱的底面半径和高都增加一倍,那么圆柱的表面积也会增加一倍。
()4. 圆柱的表面积与其底面半径的平方成正比。
圆柱表面积练习题------------------------------------------作者------------------------------------------日期圆柱表面积练习题1. 把一个底面半径6分米,高1米的圆柱切成3个小圆柱,表面积增加了多少?【解】切成3段后增加了4个底面积。
S底=rrπ=6×6×3.14=113.04(平方分米)增加的表面积=4S底=4×113.04=452.16(平方分米)答:表面积增加了452.16平方分米。
2. 工人叔叔把一根高1米的圆柱形木料,沿与底面平行的方向锯成两段,这时表面积比原来增加了25.12平方分米,求这根料的底面半径是多少?【解】增加的表面积是2个底面积,圆柱底面积=25.12÷2=12.56(平方分米)根据S=rrπ知rr=S/π=12.56÷3.14=4r=2(分米)答:这根料的底面半径是2分米。
3. 一圆柱底面直径是4米,高是6米,沿着底面直径把圆柱切成两半,求这个圆柱的表面积增加多少?【解】增加两2个以直径和高形成的矩形。
矩形面积=4×6=24(平方分米)增加的表面积=矩形面积×2=24×2=48(平方分米)答:这个圆柱的表面积增加48平方分米。
4. 把一棱长10厘米的正方形木块,削成一个最大的圆柱体,这个圆柱体的表面积是多少?【解】圆柱体的高和底面直径等于正方体棱长10厘米。
圆柱体侧面积=高×周长=10×10×3.14=314(平方厘米)圆柱体底面积=(10÷2)×(10÷2)×3.14=78.5(平方厘米)圆柱体表面积=侧面积+底面积×2=314+78.5×2=471(平方厘米)答:这个圆柱体的表面积是471平方厘米。
5. 一个圆柱体的表面积是1884平方厘米,底面半径是10厘米,它的高是多少?【解】先求出底面积,从表面积中减去两个底面积,剩下的面积是侧面积,由此求出圆柱体的高。
1、下面物体中,( )的形状是圆柱。 6、一个圆柱的侧面展开以后正好是一个正方形,那么圆柱的高等于 7.压路机滚筒滚动一周能压多少路面是求滚筒的( A 、表面积 B 、侧面积 C 、体积 &一个棱长4分米的正方体木块削成一个最大的圆柱体,圆柱体的
体积是( )立方分米。
、选一选。(将正确答案的序号填在括号里, 每小题 2分)
A. 1 -—」 © 9 □ 16
16 7
杯中的饮料最多
5、一个圆柱有( )条
高。
3、下面( )图形是圆柱的展开图。
(单位: cm)
4、下面( 、三 D 、无数条
它的底面( )。
A .半径 B. 直径 C. 周长 D. 面积
B 、 C 、
D 、
C. 9, 圆柱体的底面半径扩大 3 倍,高不变 ,体积扩大( ) A 、 3 倍 B 、 9 倍 C 、 6 倍 10, 求长方体 , 正方体 , 圆柱体的体积共同的公式是( ) A、V= abh B、V= a3 C、V= Sh 二、填空(每空 3 分) 1、将一张长 12.56 厘米,宽 9.42 厘米的长方形纸卷成一个圆柱体, 圆柱体的体积是( )立方厘米。 2、一个圆柱体的侧面展开后,正好得到一个边长 25.12 厘米的正方 形,圆柱体的高是( )厘米。 3、有一个圆柱形罐头盒,高是 1 分米,底面周长 6.28 分米,盒的侧 面商标纸的面积最大是( )平方分米,这个盒至少要用( ) 平方分米的铁皮。 4、用一张长 4.5 分米,宽 1.2 分米的长方形铁皮制成一个圆柱,这 个圆柱的侧面积最多是( )平方分米。(接口处不计) 三、判断(每小题 2 分) 1、圆柱的体积一般比它的表面积大。( ) 2、底面积相等的两个圆柱,体积也相等。( ) 3、两个圆柱的体积相等那么它们的表面积也相等。( ) 4,圆柱体的侧面积等于底面积乘 高。 ( ) 5、圆柱两底面之间的距离处处相等。 ( ) 四、计算题。 计算下列圆柱的表面积和体积。( 16 分) (1)底面半径是 5分米,高 20 厘米。 (2)底面的周长是 12.56分米,高 3分米
A、50.24 B、100.48 C 、 64 五、解决问题。
1、压路机的滚筒是一个圆柱形,它的宽是 1、5 米,滚筒横截面的半 径
是 0、6 米,以每分钟滚动 5周计算,这台压路机每小时可压路多少 米?每小时压路的面积是多少平方米? (8 分)
2、一个会议大厅有 6 根同样的圆柱形木柱,每根高 4 米,底面周长 1.5 米,如果每千克油漆可以漆 4.5 平方米,漆这些木柱需要多少千 克?( 8 分) 3. 一个圆柱形水池,底面直径 20米,深 2 米,在它的侧面和底部 抹上水泥, (1) 抹水泥部分的面积是多少平方米?( 4 分)
(2) 水池内最多可储存多少吨水? (每立方米水重 1 吨)(4分)
4、 一个圆柱形容器的底面直径是 20 厘米,水深 18 厘米,把一块 铁放入这个容器后,水深 23 厘米,这块铁的体积是多少立方厘 米? ( 7 分) 5、把一根长 4 米的圆柱形的钢材截成相等的两段以后,表面积增加 了 0.28 平方分米,如果每立方分米钢材重 7.8 千克,这根钢材重多 少千克?( 8 分) 内容结构特点 本章是在学生对一元一次方程已有认识的基础上,从一个篮球联赛中的问题入手, 引导学生直接用x和y表示两个未知数,并进一步表示问题中的两个等量关系,得到两 个相关的二元一次方程,由此得到二元一次方程(组)的概念,然后,研究用代入消元法 和加减消元法解二元一次方程组,并用此解决实际问题。
2 •本章知识结构图
3 •教材的地位及作用
本章是在研究一元一次方程的基础上,以实际问题为背景对一次方程及其解法的探 索,是数学建模思想在数学中的具体应用,其中的消元思想是解方程的基本思想,它对 研究高等数学具有重要作用。
4 .教学重点和教学难点
教学重点:以方程组为工具分析问题、解决含有多个未知数的问题 教学难点:以方程组为工具分析问题、解决含有多个未知数的问题 5.教学目标
(1)以含有多个未知数的实际问题为背景,经历 分析数量关系,设未知数,列方 程组,解方程组和检验结果”的过程,体会方程组是刻画现实世界中含有多个未知数的问 题的数学模型.
(2) 了解二元一次方程及其相关概念, 能设两个未知数并列方程组表示实际问题中 的两种相关的等量关系.
— 冥 元 际 — ------- ► 衣T
75 程 加彼(启元】法
进一歩探 宛利用二 无一次方 程组诗析 解袂实际
消元黒憩 (3) 了解解二元方程组的基本目标 (使方程组逐步转化为 x=a ,的形式),体会消 元”思想,掌握解二元一次方程组的代入法和加减法,能根据二元一次方程组的具体形式 选择适当的解法.
(4) 通过探究实际问题,进一步认识利用二元一次方程组解决问题的基本过程(见 下图),体会数学的应用价值,提高分析问题、解决问题的能力.
6 .教学建议
(1) 注意在对方程已有认识的基础上发展,做好从一元到多元的转化
本章从一个篮球联赛中的胜负场数问题开始讨论,其中含有两个未知数.在此之前 学生已经学习过一元一次方程的内容,用代数方法解决上述问题有两种不同方法:一种 方法是设一个未知数为 ,并用含有 的式子表示另一个未知数,根据问题中的等量关系 列出一元一次方程;另一种方法是直接设两个未知数 和,根据问题中的等量关系列出 两个二元一次方程,由它们组成方程组.比较这两种方法,可以发现,第一种方法的难 点在于 列”第二种方法的难点在于 解”由于列一元一次方程时要综合考虑问题中的各 等量关系,因此有一定难度,但是学生已经熟悉一元一次方程的解法;列二元一次方程 组时可以分别考虑两个等量关系,分别列出两个方程,一般说这比将这个问题列成一个 一元一次方程容易,但是由于方程中出现两个未知数,因此如何解方程组成为新问题.用 方程组是新方法,这种方法对于解含有多个未知数的问题很有效,并且它的优越性会随 着问题中未知数个数的增加体现得更明显.二元一次方程组是方程组中最基本的类型, 通过学习它可以了解一般的一次方程组,提高对多元问题的认识.本章学习中,应注意 所学内容与前面有关内容的联系与区别,明确本章内容的特点,做好从 一元”向多元”的 转化.
(2) 关注实际问题情景,体现数学建模思想
现实中存在大量问题涉及多个未知数,其中许多问题中的数量关系是一次(也称线 性)的,这为学习二元一次方程组”提供了大量的现实素材.在本章教科书中,实际问题 情境贯穿于全章,对方程组解法的讨论也是在解决实际问题的过程中进行的, 列方程组 在本章中占有突出地位•在本章的教学和学习中,要充分注意二元一次方程组的现实背 景,通过大量丰富的实际问题,反映出方程组来自实际又服务于实际,加强对方程组是 解决现实问题的一种重要数学模型的认识. 本章明确提出方程组是解决含有多个未知数 问题的重要数学工具”,并在多处体现方程组在解决实际问题中的工具作用,实际上这就 是在渗透建立模型的思想.
设未知数、列方程组是本章中用数学模型表示和解决实际问题的关键步骤,而正确 地理解问题情境,分析其中的多种等量关系是设未知数、列方程组的基础•在本章的教 学和学习中,可以从多种角度思考,借助图形、表格、式子等进行分析,寻找等量关系, 检验方程的合理性•教师还可以结合实际情况选择更贴近学生生活的各种问题,引导学 生用二元一次方程组分析解决它们.
(3) 重视解多元方程组中的消元思想
本章所涉及的数学思想方法主要包括两个:一个是由实际问题抽象为方程组这个过 程中蕴涵的符号化、模型化的思想,这已在上面进行了讨论;另一个是解方程组的过程 中蕴涵的消元化归思想, 它在解方程组中具有指导作用. 解二元一次方程组的各个步骤, 都是为最终使方程组变形为 x=a ,的形式而实施的,即在保持各方程的左右两边相等关 系的前提之下,使 未知”逐步转化为 已知”•解多元方程组的基本策略是 消元”,即逐步 减少未知数的个数,以至使方程组化归为一元方程,先解出一个未知数,然后逐步解出 其他未知数.代入法和加减法都是消元解方程组的方法, 只是具体消元的手法有所不同.
在本章的教学和学习中,不能仅仅着眼于具体题目的具体解题过程,而应不断加深 对以上思想方法的领会,从整体上认识问题的本质.
(4) 加强学习的主动性和探究性
设计本章教科书的内容和结构时,比较注意加强学习的主动性和探究性•本章内容 涉及许多实际问题,多彩的问题情境容易激起学生对数学的兴趣•在本章的教学中,应 注意引导学生从身边的问题研究起,主动收集寻找 现实的、有意义的、富有挑战性的 ” 问题作为学习材料,并更多地进行数学活动和互相交流,在主动学习、探究学习的过程 中获得知识,培养能力.