2014年数学建模养猪问题
- 格式:pdf
- 大小:250.14 KB
- 文档页数:19

生猪养殖场的经营管理策略成宝娟【摘要】以2014年高教社杯全国大学生数学建模竞赛C题为背景,针对生猪养殖场的经营管理问题,要求利用自己的种猪自行繁衍,提供最佳经营管理策略,求出生猪养殖场的最大利润.从合理化的角度对养猪过程进行分析,建立线性规划模型,结合所收集的数据给出最佳经营管理策略,使养猪利润最大化.【期刊名称】《温州职业技术学院学报》【年(卷),期】2015(015)002【总页数】6页(P65-70)【关键词】生猪养殖;盈亏平衡点;母猪;存栏数;极值点【作者】成宝娟【作者单位】咸宁职业技术学院工学院,湖北咸宁437100【正文语种】中文【中图分类】O242.1;F326.3DOI:10.13669/ki.33-1276/z.2015.0392014年高教社杯全国大学生数学建模竞赛C题“生猪养殖场的经营管理”给出了养猪的一般过程,已知生猪养殖场最多存栏数为10 000头,要求利用自己的种猪进行繁育,建立数学模型并回答以下问题:(1)不出售猪苗时,要达到或超过盈亏平衡点,每头母猪每年平均产仔量要达到多少?(2)求使得该养殖场养殖规模达到饱和时,小猪选为种猪的比例和母猪的存栏数。
(3)假设已知三年内生猪价格变化的预测曲线,请根据价格预测确定该养殖场的最佳经营管理策略,计算这三年内的平均年利润,并给出在此策略下的母猪及肉猪存栏数曲线。
2.1 模型假设条件将每年的时间分割成两个周期,即一个周期为半年;刚出生的母猪半年后可以进行配种,母猪的生育期为4年,共生育8胎;种猪在出生4年半后失去生育能力,被无害化处理;养殖场经过4年半的养殖后,已经处于近似稳定状态;假设无害化处理每头猪补贴80元;成年种母猪失去生育能力后全部进行无害化处理;养殖场存栏数最多为10 000头。
本文主要研究4年半后养殖场的经营状况,即从第10个周期开始,因而模型中i的取值范围为:i=10,11,12,…2.2 符号说明注:本文是在2 0 1 4年高教社杯全国大学生数学建模竞赛荣获国家级二等奖的基础上改编而成,竟赛指导老师为成宝娟。
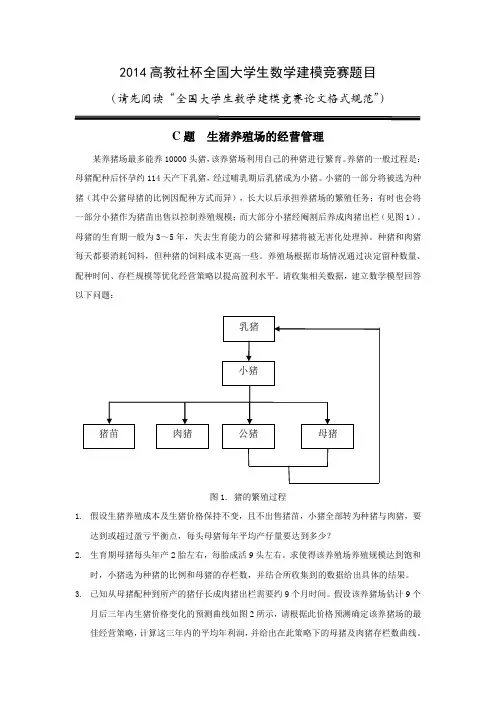
2014高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)
C题生猪养殖场的经营管理
某养猪场最多能养10000头猪,该养猪场利用自己的种猪进行繁育。
养猪的一般过程是:母猪配种后怀孕约114天产下乳猪,经过哺乳期后乳猪成为小猪。
小猪的一部分将被选为种猪(其中公猪母猪的比例因配种方式而异),长大以后承担养猪场的繁殖任务;有时也会将一部分小猪作为猪苗出售以控制养殖规模;而大部分小猪经阉割后养成肉猪出栏(见图1)。
母猪的生育期一般为3~5年,失去生育能力的公猪和母猪将被无害化处理掉。
种猪和肉猪每天都要消耗饲料,但种猪的饲料成本更高一些。
养殖场根据市场情况通过决定留种数量、配种时间、存栏规模等优化经营策略以提高盈利水平。
请收集相关数据,建立数学模型回答以下问题:
图1. 猪的繁殖过程
1.假设生猪养殖成本及生猪价格保持不变,且不出售猪苗,小猪全部转为种猪与肉猪,要
达到或超过盈亏平衡点,每头母猪每年平均产仔量要达到多少?
2.生育期母猪每头年产2胎左右,每胎成活9头左右。
求使得该养殖场养殖规模达到饱和
时,小猪选为种猪的比例和母猪的存栏数,并结合所收集到的数据给出具体的结果。
3.已知从母猪配种到所产的猪仔长成肉猪出栏需要约9个月时间。
假设该养猪场估计9个
月后三年内生猪价格变化的预测曲线如图2所示,请根据此价格预测确定该养猪场的最佳经营策略,计算这三年内的平均年利润,并给出在此策略下的母猪及肉猪存栏数曲线。
横坐标说明:以开始预测时为第一年,D2表示第二年,依次类推。


数学建模论文肥猪的最优销售时机摘要:人们通过对猪的饲养和销售,总希望获阿得最大收益。
因此建立与此相关的数学模型来求解最大收益与最优销售时间就有着重要的实际意义。
对于收入局部,由于市场价格受多种不确定因素的影响且变化较大,我们假设价格保持不变,所以收入正比于猪的体重;猪的体重与时间的关系可以用Gompertz模型来模拟。
对于本钱局部,认为由饲料本钱和猪仔价格组成。
通过对饲料消耗量和体重的实际数据的分析,发现线性拟合的效果较理想,由此利用该关系确定饲料的消耗。
至此问题转化为建立猪的生长模型和饲料消耗模型。
对于最优化模型,我们从两个方面进展了考虑,一是总利润的最大值,二是日均利润最大值。
通过以上分析,较好地解决了肥猪最优销售时机问题,对养殖户有一定参考意义。
通过以上分析,较好地解决了肥猪最优销售时机问题,对养殖户有一定参考意义。
肥猪的最优销售时机关键词:数学建模;肥猪最优销售时机;饲料消耗模型;Gompertz模型问题的表示与分析:一般从事猪的饲养和销售总希望获得利润,因此饲养某种猪是否获利,怎样获得最大利润,是饲养者必须考虑的问题。
如果把饲养技术水平,猪的性质等因素看成不变的,且不考虑市场的需求变化,那么影响获利大小的一个主要因素是如何选择猪的售出时机,即何时把猪卖出获利最大。
也许有人认为,猪养的越大,售出后获利愈大,其实不然,因为随着猪的生长,单位时间消耗的饲养费用也就愈多,但同时其体重的增长速度却不断下降,所以饲养时间过长是不合算的。
考虑某个品种猪的最优销售时机的数学模型。
要求猪的最优销售时机,目标是寻求最大利润的取得,由此实际上需要找出收入和支出分别是什么,受什么影响。
为了简化问题,我们只考虑一头猪的利润,并且做了一系列的理想化的假设,比如生猪价格固定等,所以收入与猪的体重成正比,而本钱如此由固定本钱〔如猪仔价格,防疫费用〕和变化本钱〔主要是饲料的消耗〕组成,最终问题转化成建立猪的生长模型和饲料消耗模型。

数学建模公选课结课作业
2014128112 石子涛
一.例题
一饲养场每天投入5元资金用于饲料、设备、人力,估计可使一头80公斤重的生猪每天增加2公斤。
目前生猪出售的市场价格为每公斤8元,但是预测每天会降低0.1元,问该场应该什么时候出售这样的生猪可以获得最大利润。
解:设在第t天出售这样的生猪(初始重80公斤的猪)可以获得的利润为z元。
每头猪投入:5t元产出:(8-0.1t)(80+2t)元
利润:Z = 5t +(8-0.1t)(80+2t)=-0.2 t^2 + 13t +640 =-0.2(t^2-65t+4225/4)+3405/4 当t=32或t=33时,Zmax=851.25(元)
因此,应该在第32天过后卖出这样的生猪,可以获得最大利润。
二.建议
一. 课堂建议
1. 教师在课堂上可以多和学生互动,因为这个公选课是以普及数学建模为目的,所以
可以适当考虑减少课程的内容。
课堂上可以把学生分为若干个小组,每个小组组员坐一起,给出题目后教师先启发下,再让小组讨论,然后选代表说出小组讨论结果,对于表现突出的小组予以给予平时成绩加分的奖励。
2. 课堂上可以不仅仅是教师讲授,还可以邀请参加过数学建模竞赛的同学参与讲授
3. 可以适当布置课后作业,让学生们课后思考,然后下节课来了,小组讨论并说出构
思和解题过程
二.校园普及建议
1.数学建模学会多与各个学院学生会或各大社团组织展开交流活动
2.可以时常举办一些小讲座,吸引同学们去听
3.每年的进行学院间的数学建模竞赛,优胜者予以奖励
4.为每届的数学建模获奖者举行颁奖典礼。



养猪SWINE PRODUCTION2018第4期中国养猪科学中的经典数学模型张伟力,张晓东(安徽农业大学,安徽合肥230036)中图分类号:S828文献标志码:A文章编号:1002-1957(2018)04-0001-03摘要文章对中国养猪科学中的经典数学模型作了通俗介绍。
以《三国演义》矩阵和循环小数为典型例证演示了经典数学模型的科学性、趣味性及实际生产应用价值。
关键词中国养猪;数学模型;《三国演义》;循环小数;实践应用Classical Mathematics Moldeling of Swine Science in ChinaZHANG Weili,ZHANG Xiaodong(Anhui Agricultural University,Hefei230036,China)Abstract Some classical mathematics modeling of swine science in China was illustrated popularly.The array of The Three Kingdoms and the recurring decimal were illustrated to show its value as regard to scientific na-ture,interests and practical usage.Key words Chinese swine production;mathematics modeling;The Three Kingdoms;recurring decimal;practicalusage现代养猪育种中由指数选择公式发展到数学模型组合已经成为习以为常的技术手法。
数学模型的组成形式与运算方法在趋向精细化的同时也变得越来越复杂,对于育种场家的使用条件要求也越来越苛刻。
其实在养猪育种中对于中小型育种场来说,经典实用的传统数学模型具有更大的灵活性和准确性。

2021高教社杯全国大学生数学建模比赛C题评阅要点[说明]本要点仅供参考, 各赛区评阅组应根据对题目的理解及学生的解答, 自主地进行评阅。
本题要求根据生猪预测价格, 建立大型生猪养殖场的经营管理模型, 从而求出较合理的经营管理策略。
本题目主要考察学生对一个涉及因素较多且随时间动态变化的实际问题的建模功底, 以及根据这个模型作出合理决策的功底。
问题1. 最小平均产仔量问题本问题关键是建立收支平衡方程, 然后根据此方程求出每头母猪每年平均产仔量与各种成本参数以及生猪价格参数之间的关系, 有明确的最终关系表达式为佳。
评阅时需注意有无遗漏收入或成本因素的情形。
本问不要求给出具体数值结果。
问题2. 最大规模平衡态问题本问题主要是根据养殖场规模, 计算小猪转化为母猪的比例, 使达到最大养殖规模且保持动态平衡。
在求数值结果时, 需要对母猪生育年限作出具体约定, 从而结果有一定的变化范围, 小猪转化为母猪的比例应当在0. 8%~2%之间较为合理, 母猪存栏数在1000头左右问题3. 经营管理模型及策略问题本问题要求在已知9个月后预测价格条件下, 寻求养殖场较合理的经营管理策略, 这是本题的核心问题。
应有明确的优化策略。
母猪存栏数以及育龄母猪配种率直接影响大约9个月后的生猪存栏数, 从而影响利润率, 所以这是本问题要考虑的关键因素。
在利用题目所给的生猪价格预测曲线时, 预测区间取为9个月较为切合实际。
并且, 预测价格与实际价格之间肯定存在一定的偏差, 加入在建模时能够将这种偏差纳入策略挑选考虑, 则更佳。
评阅时应考察各种成本参数取值是否在合理范围内, 以及猪苗出售价格是否合理。
在参数合理取值的条件下, 平均年利润的合理范围大约为: 400万~700万, 过低则优化不足, 过高应检查假定及参数取值是否过于脱离实际。
解决本问题的方法之一是: 建立分时段的母猪、小猪及肉猪数量之间的递推关系式, 然后通过仿真比较不同策略下的利润率, 寻求较合理的经营管理策略。

生猪养殖问题之浅谈作者:童宁江来源:《科技视界》2015年第02期【摘要】本文针对生猪养殖问题,进行合理的基本假设,进行必要的符号说明,寻找猪的繁殖规律,建立数学模型。
【关键词】生猪养殖;繁殖规律;数学建模;递推公式1 问题重述某养猪场最多能养10000头猪,该养猪场利用自己的种猪进行繁育。
养猪的一般过程是:母猪配种后怀孕约114天产下乳猪,经过哺乳期后乳猪成为小猪。
小猪的一部分将被选为种猪(其中公猪母猪的比例因配种方式而异),长大以后承担养猪场的繁殖任务;有时也会将一部分小猪作为猪苗出售以控制养殖规模;而大部分小猪经阉割后养成肉猪出栏。
母猪的生育期一般为3~5年,失去生育能力的公猪和母猪将被无害化处理掉。
种猪和肉猪每天都要消耗饲料,但种猪的饲料成本更高一些。
养殖场根据市场情况通过决定留种数量、配种时间、存栏规模等优化经营策略以提高盈利水平。
请收集相关数据,建立数学模型回答以下问题[1-2]:假设生猪养殖成本及生猪价格保持不变,且不出售猪苗,小猪全部转为种猪与肉猪,要达到或超过盈亏平衡点,每头母猪每年平均产仔量要达到多少?2 基本假设有充足的流动资金。
每头小猪的饲养成本一样。
成年公种猪的营养需要与生育期母猪相近。
每头生育期母猪的饲养成本一样。
每头成年公种猪的饲养成本一样。
猪养殖成本及生猪价格保持不变。
不出售猪苗,小猪全部转为种猪与肉猪。
成活的小猪的公母比值为1。
小母种猪与小母猪的比值不变。
小公种猪与小公猪的比值不变。
最初的母猪已同时怀孕。
后来的母猪也可同时怀孕。
肉猪可以立马全部卖出。
每头肉猪的体重一样。
每头肉猪的售价一样。
失去生育能力的种猪的无害化处理费可忽略不计。
种猪不可转为肉猪。
母猪生育期限为3年。
小母猪的受孕时间延迟与初始母猪受孕时间相同。
母猪每半年受孕一次。
3 符号说明每头母猪每年平均产仔为2y头,公母比例为1:1。
每头生育期母猪养殖平均每月成本为c1元/月。
每头成年公种猪养殖平均每月成本也为c1元/月。

2014 年全国大学生数学建模试题分析--生猪养殖场的经营管理 谢艳云 蔡文良 / 重庆水利电力职业技术学院 【摘 要】借鉴养殖场的生猪养殖技术和经营管理策略,解决了 2014 年全国数学建模大赛 C 题生猪 养猪场的经营管理问题。
在小猪全部转为种猪与肉猪的条件下,计算达到或超过盈亏平衡点母猪每年的平 均产仔量;假定母猪的年产量,预算养殖场规模达到 1 万头时母猪、公猪、肉猪的存栏数;根据给出的 3 年价格曲线的走势图,决定经营策略,并计算这三年内的平均年利润。
【关键词】生猪养殖;盈亏平衡点;存栏数 1 问题提出 2014 年全国数学建模大赛 C 题生猪养猪场的经营管理中要求根据小猪全部转为种猪与肉猪, 要达到或 超过盈亏平衡点, 求得每头母猪每年平均产仔量; 并根据初步拟定每头母猪年产两胎, 每胎成活 9 头左右, 该养殖场规模达到饱和(1 万头)时,确定小猪选为种猪的比例及母猪的最终存栏数;最后给出三年生猪 价格预测曲线从而确定肉猪的出栏数,得到最佳的经营策略。
本文根据相关资料,给定数据,计算得到达 到盈亏平衡点时的母猪每年平均产仔量;进一步讨论养殖规模达到饱和时的存栏数;并根据价格曲线的走 势分析经营策略。
2 问题分析及模型结果 2.1 求每头母猪每年平均产仔量 根据市场价格出售种猪和肉猪, 当达到一定的数量才能盈利, 但母猪年产量有限, 假设最优化条件下, 母猪达到一个产仔量,如果能求出种猪和肉猪分配的最优比例,就能找出模型最优设计。
在建模之前,必 须考虑种猪和肉猪的饲养成本,种猪第一次达到繁殖所需时间,种猪繁殖周期,肉猪到出栏时所需时间。
假设不考虑购买第一批次的种猪成本。
设 C(x):全年盈利额度,k:预留种猪所占小猪比例,r:平均每头母猪的年产仔量,T1:繁殖周期(繁 殖周期=妊娠天数+哺乳天数+配种天数=114+35+10=159) ,G:市场商品猪平均体重(均为 100kg) ,P:市场 肉猪销售价格 14 元/kg(参考猪肉价格网,网址为 /) ,T0:种猪断奶后至繁 殖期(一般为三个月),C1:种猪每年饲养的费用(3000 元/头/年) ,C2:肉猪每年饲养的费用(700 元/头/ 年) ,设 x 为种母猪头数,且种母猪:种公猪为 1:25,因此种公猪头数为错误!未找到引用源。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):所属学院(请填写完整的全名):参赛队员(打印并签名) :1.2.3.日期: 2010 年 5 月 29 日评阅编号(教师评阅时填写):生猪价格问题摘要本文主要就生猪价格下跌原因以及如何制定合理的生猪价格定价策略问题采用线性回归和对数线性模型以及统计学知识对其进行分析。
问题一,采用线性回归法,对猪肉价格的发展趋势进行短期预测。
首先通过对2009年12月到2010年5月我国猪肉价格分析得出,猪肉价格在短期内呈线性下降趋势,得到线性方程^t S a bt =+,然后用根据这个线性方程拟合该时间序列上的猪肉变化趋势,再与实际的变化曲线进行比较,说明此方法的可行性,并对2010年6月的猪肉价格进行预测。
问题二,首先根据猪的不同重量,将猪分为三个成长阶段:5Kg ~25Kg 为幼年期;25Kg ~90Kg 为成长期;90Kg ~110Kg 为成年期。
由于猪的体重从5到110公斤呈正态分布,可以算出这三个阶段的猪的数量比为6:988:6。
然后根据猪场收入与成本建立猪场盈亏平衡点等式模型362%100n X G m ⨯⨯⨯=⨯生。
可以得到猪粮比约为6:1,即该养猪场的盈亏平衡点,从而得问题四出定价策略的数学模型中的猪粮比参数s 。
接着对2009年12月到2010年5月的猪肉价格和猪料价格进行统计,分别求出他们之间的猪料比值。
生猪养殖的经营管理模型分析与建立作者:田茹会来源:《现代农业科技》2015年第01期摘要根据某养猪场2009年与2014年实际养殖情况,主要分析和解决了关于生猪养殖经营管理的3个问题,即运用不等式解决种猪与肉猪的比例关系问题,进而得到盈亏平衡时,母猪的平均产仔量;运用一、二胎饱和思想,建立数学模型,求得选种率与母猪的存栏量;通过得到的数据,由价格随时间的变化曲线图,得到经营策略,并运用MATLAB软件,求得母猪的存栏数与肉猪的存栏数曲线图。
关键词生猪养殖;经营管理;存栏数;选种比率;MATLAB中图分类号 S828;F326.3 文献标识码 A 文章编号 1007-5739(2015)01-0270-02Abstract According to actual breeding of a pig farm in 2009 and 2014,three problems about pig breeding management were analyzed and solved.Inequation was used to calculate the proportion of breeding pigs and pork pigs,and could get the sow litter size,according to the first and the second off-spring quantity reach saturation,mathematical modeling was built to calculate the seed selection ratio and sow breeding stock,operating strategy were got based the data and the price time graph,sow breeding stock and pork pig breeding stock graph were obtained by using MATLAB.Key words pigs feeding;management;stock;selection ratio;MATLAB某养猪场最大饲养量为1万头,该养猪场利用本场的种猪进行繁育。
饲养场养殖类型的选择摘要随着国家近几年对养殖业重视程度的提高,补贴力度的不断加大,很大程度上刺激了养殖企业的飞速发展。
但对于中国养殖业来说,目前急需解决两个问题:一是科学养殖,二是可持续发展,但存在的问题是如何科学养殖。
许多企业在养殖类型的选择上犹豫不决,对到底养殖哪类畜种能获得更大利润存在疑问。
本文通过层次分析法,从理论上解决养殖类型的选择问题,为养殖企业选择养殖类型提供一个参考,以增加企业效益。
【关键字】 层次分析法 养殖类型选择一、模型假设:1.养殖厂占地面积相同;2.排除主观因素,即不受个人喜好等因素的影响。
二、建立模型:层次结构图:目标层:准则层:方案层:三、模型求解1.构造成对比较阵①准则层对目标层的成对比较阵每次取准则层的两个因素i C 、j C ,用ij C 表示i C 和j C 对目标层O 的影响之比,全部比较结果可用成对比较矩阵:115315315516361131611531451351313131613111514361A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦则:最大特征根为 6.5550λ=,特征向量w=(0.0808,0.3297,0.0561,0.1825, 0.0384,0.3125)T 。
一致性指标CI =λ−66−1=0.1110,查表得当n=6时,随机一致性指标RI=1.24。
所以,一致性比率CR =CIRI =0.0895<0.1,A 的不一致程度在容许范围之内,通过一致性检验,可用其特征向量作为权向量。
②方案层对准则层的成对比较阵:在养殖类型的选择问题中,已经得到了第2层(准则层)对第1层(目标层)的权向量,记作(2)(0.0808,0.3297,0.0561,0.1825,0.0384,0.3125)w T =。
用同样的方法构造第3层(方案层)对第2层(准则层)的每一个准则的成对比较阵,分别设为123456B B B B B B 、、、、、,则:111215521165318151611B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 21131312312231213212131B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 3112317212113121177571B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 4111525127512161217161B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 51171271286121512111B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 6113135311631161516161B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦这里矩阵(k 1,)k B =…6中的元素(k)ij b 是方案i P 与j P 对准则k C 的优越性的比较尺度。
利用数学模型求解生猪的最佳销售时机问题
于红
【期刊名称】《安徽农业科学》
【年(卷),期】2009(037)014
【摘要】数学建模是联系数学与实际问题的桥梁,是数学在各个领域广泛应用的媒介,是数学科学技术转化的主要途径.而农业上对于数学建模的应用也很多,主要介绍了利用数学建模求解生猪的最佳销售时机问题,把实际问题转化为高等数学中的一阶非齐次线性微分方程的解法问题.
【总页数】2页(P6653-6654)
【作者】于红
【作者单位】唐山职业技术学院,河北唐山,063000
【正文语种】中文
【中图分类】F302.5
【相关文献】
1.抓住变革销售的最佳时机 [J], 天明
2.猪的最佳销售时机研究 [J], 叶扩会;尹国成
3.抓住变革销售的最佳时机! [J], 天月
4.水产品最佳销售时机的选择 [J], 封琦;袁圣;唐晟凯
5.企业要债的最佳时机——销售旺季 [J], 姚岸埂
因版权原因,仅展示原文概要,查看原文内容请购买。
基于数学建模的生猪养殖场经营管理分析刘有新;丛松;孔孟;郭前程【期刊名称】《芜湖职业技术学院学报》【年(卷),期】2015(17)2【摘要】The mathematical model and the optimal management strategy were set up for pig farms for the purpose of its better profitability. Firstly, we established the profit function of pig farms by using income function, and then we got yearly average bearing amount of 14 to 16 by use of the break-even point principle. Secondly, in consideration of livability of suckling pigs, piglets and hogs, with the method of artificial insemination, we could estimate their respective amount and further that the rate of piglets chosen as breeding pigs was 1.45%, and livestock of sows was 928. Thirdly, we divided 928 sows into 16 groups and set up an income optimization model for each group. Without regard to the government subsides, the average annual profit calculated through MATLAB is¥2.2 million. When the price of live pigs is lower than the breeding cost, we will dispose pig breeds nine month before so that only 879 sows and 7215 hogs will be on hand at least.%我们为生猪养殖场的经营管理建立了数学规划模型,给出优化经营策略,以提高养殖场的盈利水平。