二次函数的图像和性质同步练习

30.2 二次函数的图像和性质第1课时 二次函数y=ax 2的图像和性质1.填空： （1）y ＝x 2的图像是 ；开口向 ；对称轴是 ；顶点坐标是；（2）在抛物线y ＝x 2的对称轴左侧y 随x 的减小而 ；而在对称轴的右侧是y 随着x 的增大而；此时函数y ＝x 2当x ＝ 时的值最是 .（3）y ＝-x 2的图像是；开口向；对称轴是；顶点坐标是；（4）在抛物线y ＝-x 2的对称轴左侧y 随x 的减小而 ；而在对称轴的右侧是y 随着x 的增大而；此时函数y ＝-x 2当x ＝时的值最是.2.假设点A 〔3，m 〕是抛物线y=－x 2上一点，那么m= ．3.假设点A 〔-5，y 1〕、B 〔2，y 2〕都在y=2x 2上，那么1y ____2y 〔填“>〞或“<〞〕4.如图，⊙O 的半径为2．C 1是函数y=x 2的图像，C 2是函数y=﹣x 2的图像，那么阴影局部的面积是 _________ ．5.函数2ax y =〔a ≠0〕的图像与a 的符号有关的是〔 〕A ．对称轴B ．顶点坐标C ．开口方向D ．开口大小 6.在同一坐标系中，抛物线y ＝4x 2,y ＝41x 2,y ＝-41 x 2的共同特点是( ) A.关于y 轴对称，抛物线开口向上;B.关于y 轴对称，y 随x 的增大而增大 B.关于y 轴对称，y 随x 的增大而减小;D.关于y 轴对称，抛物线顶点在原点. 7.原点是抛物线2)3(x m y +=的最高点，那么m 的范围是 ( )A ． 1-<mB ． 3-<mC ． 2->mD ． 3->m8.二次函数y=ax 2与一次函数y=ax ＋a 在同一坐标系中的图像大致为〔 〕9.二次函数2y ax 的图像经过点A(-1，1) ① 求这个二次函数的关系式； ② 求当x =2时的函数y 的值．10.直线y=－2x ＋3与抛物线y=ax 2相交于A 、B 两点，且A 点坐标为〔－3，m 〕． 〔1〕求a 、m 的值；〔2〕求抛物线的表达式及其对称轴和顶点坐标；〔3〕x 取何值时，二次函数y=ax 2中的y 随x 的增大而减小；〔4〕求A 、B 两点及二次函数y=ax 2的顶点构成的三角形的面积第3课时 二次函数y=ax 2+bx+c 的图像和性质1．已知二次函数y=ax 2﹣2x+2（a ＞0），那么它的图像一定不经过（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．二次函数y=ax 2+bx+c （a≠0）的大致图像如图，关于该二次函数，下列说法错误的是（ ）函数有最小值B．对称轴是直线x=A．C．当x＜，y随x的增大而减小D．当﹣1＜x＜2时，y＞03．如图，平面直角坐标系中，点M是直线y=2与x轴之间的一个动点，且点M 是抛物线y=x2+bx+c的顶点，则方程x2+bx+c=1的解的个数是（）A．0或2 B．0或1 C．1或2 D．0，1或24．如果抛物线y=x2+（m﹣1）x﹣m+2的对称轴是y轴，那么m的值是_________．5．二次函数y=x2﹣4x﹣5的图像的对称轴是直线_________．6．若抛物线y=2x2﹣mx﹣m的对称轴是直线x=2，则m=_________．7．已知抛物线y=x2﹣x﹣1．（1）求抛物线y=x2﹣x﹣1的顶点坐标、对称轴；（2）抛物线y=x2﹣x﹣1与x轴的交点为（m，0），求代数式m2+的值．8．如图，已知抛物线y=x2﹣x﹣6，与x轴交于点A和B，点A在点B的左边，与y轴的交点为C．（1）用配方法求该抛物线的顶点坐标；（2）求sin∠OCB的值；（3）若点P（m，m）在该抛物线上，求m的值．9．若二次函数y=a1x2+b1x+c1的图像记为C1，其顶点为A，二次函数y=a2x2+b2x+c2的图像记为C2，其顶点为B，且满足点A在C2上，点B在C1上，则称这两个二次函数互为“伴侣二次函数”．（1）一个二次函数的“伴侣二次函数”有_________个；（2）①求二次函数y=x2+3x+2与x轴的交点；②求以上述交点为顶点的二次函数y=x2+3x+2的“伴侣二次函数”．（3）试探究a1与a2满足的数量关系．10．已知二次函数y=﹣x2+2x+3图像的对称轴为直线．（1）请求出该函数图像的对称轴；（2）在坐标系内作出该函数的图像；（3）有一条直线过点P（1，5），若该直线与二次函数y=﹣x2+2x+3只有一个交点，请求出所有满足条件的直线的关系式．。

二次函数的图象和性质单元同步测试题（01）一．选择题（共10小题）1．把抛物线y＝5x2向左平移2个单位，再向上平移3个单位，得到的抛物线是（）A．y＝5（x﹣2）2+3B．y＝5（x+2）2﹣3C．y＝5（x+2）2+3D．y＝5（x﹣2）2﹣32．对于抛物线y＝﹣2（x﹣1）2+3，下列判断正确的是（）A．抛物线的开口向上B．抛物线的顶点坐标是（﹣1，3）C．对称轴为直线x＝1D．当x＝3时，y＞03．二次函数y＝4ax2+4bx+1与一次函数y＝2ax+b在同一平面直角坐标系中的图象可能是（）A．B．C．D．4．如图是四个二次函数的图象，则a、b、c、d的大小关系为（）A．d＜c＜a＜b B．d＜c＜b＜a C．c＜d＜a＜b D．c＜d＜b＜a5．抛物线y＝x2﹣4与y轴的交点坐标是（）A．（0，﹣4）B．（﹣4，0）C．（2，0）D．（0，2）6．函数y＝ax2﹣a与y＝ax﹣a（a≠0）在同一坐标系中的图象可能是（）A．B．C．D．7．将抛物线y＝3x2﹣2先向右平移3个单位长度，再向下平移2个单位长度得到的新抛物线解析式为（）A．y＝3（x+3）2﹣4B．y＝3（x﹣3）2C．y＝3（x﹣3）2﹣4D．y＝3（x+3）28．已知y=(m+1)x m2+1+2x−3是二次函数，则m的值为（）A．0B．1C．﹣1D．1或﹣19．已知二次函数y＝x2﹣2x﹣3的自变量x1，x2，x3对应的函数值分别为y1，y2，y3.当﹣1＜x1＜0，1＜x2＜2，x3＞3时，y1，y2，y3三者之间的大小关系是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y1＜y2D．y2＜y3＜y1 10．二次函数y＝ax2+bx+c的图象如图所示，以下结论正确的个数为（）①abc＜0；②c+2a＜0；③9a﹣3b+c＝0；④am2﹣a+bm+b＞0（m为任意实数）A．1个B．2个C．3个D．4个二．填空题（共2小题）11．将抛物线y＝﹣2（x+2）2向右平移3个单位长度，再向下平移4个单位长度得到的抛物线的函数解析式为．12．点A（2，y1），B（a，y2）在二次函数y＝x2﹣2x+3的图象上．若y1＜y2，写出一个符合条件的a的值．三．解答题（共3小题）13．如图，已知二次函数y＝ax2+bx+c（a≠0）的顶点是（1，4），且图象过点A（3，0），与y轴交于点B．（1）求二次函数y＝ax2+bx+c的解析式；（2）求直线AB的解析式；（3）在直线AB上方的抛物线上是否存在一点C，使得S△ABC＝3，如果存在，请求出C 点的坐标，如果不存在，请说明理由．14．已知一个抛物线经过点（3，0），（﹣1，0）和（2，﹣6）．（1）求这个二次函数的解析式；（2）求这个二次函数图象的顶点坐标和对称轴．15．如图，已知抛物线y＝ax2+bx+5与x轴交于A（﹣1，0），B（5，0）两点（点A在点B 的左侧），与y轴交于点C．（1）求抛物线的解析式；（2）点D是第一象限内抛物线上的一个动点（与点C，B不重合），过点D作DF⊥x轴于点F，交直线BC于点E，连接BD，直线BC能否把△BDF分成面积之比为2：3的两部分？若能，请求出点D的坐标；若不能，请说明理由．（3）若M为抛物线对称轴上一动点，使得△MBC为直角三角形，请直接写出点M的坐标．。

人教版数学九级上册《22.1.2二次函数的图y=ax2图像和性质》同步练习一．选择题（共12小题）1．在同一平面直角坐标系中，函数y=ax+b与y=bx2+ax的图象可能是（）A．B．C．D．2．在下列二次函数中，其图象对称轴为x=﹣2的是（）A．y=（x+2）2﹣3 B．y=2x2﹣2 C．y=﹣2x2﹣2 D．y=2（x﹣2）2 3．已知二次函数y=ax2+bx+c的图象如图所示，那么这个函数的顶点坐标是（）A．（1，﹣）B．（1，）C．（1，﹣）D．（1，﹣）4．对于二次函数y=（x﹣2）2+3的图象，下列说法正确的是（）A．开口向下B．对称轴是直线x=﹣2C．顶点坐标是（2，3）D．与x轴有两个交点5．抛物线y=x2﹣2x+m2+2（m是常数）的顶点在（）A．第一象限B．第二象限C．x轴的正半轴上D．x轴的负半轴上6．从﹣4，﹣2，0，1，2，34这七个数中，随机抽取一个数记为a，若数a使关于x的分式方程+=﹣2有正整数解，又使函数y=x2﹣（2a﹣7）x+1的顶点在第三象限，那么这七个数中所有满足条件a的个数为（）A．2 B．3 C．4 D．57．已知，平面直角坐标系中，直线y1=x+3与抛物线y2=﹣+2x的图象如图，点P是y2上的一个动点，则点P到直线y1的最短距离为（）A．B．C．D．8．已知函数y=2mx2+（1﹣4m）x+2m﹣1，下列结论错误的是（）A．当m=0时，y随x的增大而增大B．当m=时，函数图象的顶点坐标是（，﹣）C．当m=﹣1时，若x＜，则y随x的增大而减小D．无论m取何值，函数图象都经过同一个点9．二次函数y=﹣x2+（12﹣m）x+12，时，当x＞2时，y随x的增大而减小；当x＜2时，y随x的增大而增大，则m的值为（）A．6 B．8 C．10 D．1210．已知y=ax2+bx+c（其中a，b，c为常数，且a≠0），乐老师在用描点法画其的图象时，列出如下表格，根据该表格，下列判断中不正确的是（）x …﹣1 0 1 2 …y …﹣2 2.5 4 2.5 …A．a＜0B．一元二次方程ax2+bx+c﹣5=0没有实数根C．当x=3时y=﹣2D．一元二次方程ax2+bx+c=0有一根比3大11．已知函数y=mx2+nx﹣3，且2m﹣n=1，若不论m取何正数时，函数值y 都随自变量x的增大而减小，则满足条件的x的取值范围是（）A．﹣4≤x≤﹣2 B．C．1＜x≤3 D．3≤x≤512．定义运算“※”为：a※b=，如：1※（﹣2）=﹣1×（﹣2）2=﹣4．则函数y=2※x的图象大致是（）A．B．C．D．二．填空题（共5小题）13．抛物线y=x2+4的对称轴是．14．若抛物线y=（a﹣2）x2的开口向上，则a的取值范围是．15．二次函数y=﹣x2﹣2x图象x轴上方的部分沿x轴翻折到x轴下方，图象的其余部分保持不变，翻折后的图象与原图象x轴下方的部分组成一个“M”形状的新图象，若直线y=x+b与该新图象有两个公共点，则b的取值范围为．16．如图，抛物线y=ax2+1与y轴交于点A，过点A与x轴平行的直线交抛物线y=4x2于点B、C，则线段BC的长为．三．解答题（共5小题）17．画函数y=的图象．18．已知二次函数y=ax2（a≠0）与一次函数y=kx﹣2的图象相交于A、B两点，如图所示，其中A（﹣1，﹣1），求△OAB的面积．19．如图，A点是抛物线y=ax2上第一象限内的点，A点坐标为（3，6），AB ⊥y轴与抛物线y=ax2的另一交点为B点．（1）求a的值和B点坐标；（2）在x轴上有一点C，C点坐标为（5，0），请求出△AOC的面积．20．如图，抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B．（1）求抛物线的解析式；（2）求△AOB的面积；（3）若点P（m，﹣m）（m≠0）为抛物线上一点，求与P关于抛物线对称轴对称的点Q的坐标．（注：抛物线y=ax2+bx+c的对称轴是x=﹣）21．小东根据学习函数的经验，对函数y=图象与性质进行了探究，下面是小东的探究过程，请补充完整，并解决相关问题：（1）函数y=的自变量x的取值范围是；（2）如表是y与x的几组对应值．x …﹣2 ﹣1 ﹣0 1 2 3 4 …y … 2 4 2 m …表中m的值为；（3）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出函数y=的大致图象；（4）结合函数图象，请写出函数y=的一条性质：（5）解决问题：如果函数y=与直线y=a的交点有2个，那么a的取值范围是．参考答案一．选择题1．A．2．A．3．A．4．C．5．A．6．A．7．B．8．C．9．B．10．D．11．A．12．C．二．填空题13．y轴；14．a＞215．0＜b＜1或b＜﹣16．1．三．解答题17．解：列表：描点、连线：18．解：∵一次函数y=kx﹣2的图象相过点A（﹣1，﹣1），∴﹣1=﹣k﹣2，解得k=﹣1，∴一次函数表达式为y=﹣x﹣2，∴令x=0，得y=﹣2，∴G（0，﹣2），∵y=ax2过点A（﹣1，﹣1），∴﹣1=a×1，解得a=﹣1，∴二次函数表达式为y=﹣x2，由一次函数与二次函数联立可得，解得，，∴S△OAB=OG•|A的横坐标|+OG•点B的横坐标=×2×1+×2×2=1+2=3．19．解：（1）把A点（3，6）代入抛物线y=ax2，解得a=，则B点坐标为（﹣3，6）；（2）S△AOC=OC•y A=×5×6=15．20．解：（1）设二次函数的解析式为y=a（x﹣2）2+1，将点O（0，0）的坐标代入得：4a+1=0，解得a=﹣．所以二次函数的解析式为y=﹣（x﹣2）2+1；（2）∵抛物线y=﹣（x﹣2）2+1的对称轴为直线x=2，且经过原点O（0，0），∴与x轴的另一个交点B的坐标为（4，0），∴△AOB的面积=×4×1=2；（3）∵点P（m，﹣m）（m≠0）为抛物线y=﹣（x﹣2）2+1上一点，∴﹣m=﹣（m﹣2）2+1，解得m1=0（舍去），m2=8，∴P点坐标为（8，﹣8），∵抛物线对称轴为直线x=2，∴P关于抛物线对称轴对称的点Q的坐标为（﹣4，﹣8）．21．解：（1）函数y=的自变量x的取值范围是：全体实数，故答案为：全体实数；（2）把x=4代入y=得，y==，∴m=，故答案为：；（3）如图所示，（4）①图象位于一二象限，②当x=1时，函数由值最大4，③当x＜1时，y随x的增大而增大，④当x＞1时，y随x的增大而减小，⑤图象与x轴没有交点．故答案为：①图象位于一二象限，②当x=1时，函数由值最大4，③当x＜1时，y随x的增大而增大，④当x＞1时，y随x的增大而减小，⑤图象与x轴没有交点．（5）由图象，得0＜a＜4．故答案为：0＜a＜4．第11页共11页。

二次函数y=a （x-h)2+k(a ≠0)的图象与性质—巩固练习（基础）【巩固练习】一、选择题1.抛物线2(2)3y x =-+-的顶点坐标是（ ）A ．(2，-3)B ．(-2，3)C ．(2，3)D ．(-2，-3)2.函数y=21x 2+2x+1写成y=a(x －h)2+k 的形式是（ ） A.y=21(x －1)2+2 B.y=21(x －1)2+21 C.y=21(x －1)2－3 D.y=21(x+2)2－13．抛物线y=21x 2向左平移3个单位，再向下平移2个单位后，所得的抛物线表达式是( )A.y=21(x+3)2－2B.y=21(x －3)2+2C.y=21(x －3)2－2D.y=21(x+3)2+24．把二次函数122--=x x y 配方成顶点式为（ ）A ．2)1(-=x yB ． 2)1(2--=x yC ．1)1(2++=x y D ．2)1(2-+=x y5．由二次函数22(3)1y x =-+，可知（ ）A ．其图象的开口向下B ．其图象的对称轴为直线3x =-C ．其最小值为1D ．当3x <时，y 随x 的增大而增大 6．（2020•泰安）在同一坐标系中，一次函数y=﹣mx+n 2与二次函数y=x 2+m 的图象可能是（ ）.A. B. C. D.二、填空题7. （2020•怀化）二次函数y=x 2+2x 的顶点坐标为，对称轴是直线．8．已知抛物线y=－2(x+1)2－3，如果y 随x 的增大而减小，那么x 的取值范围是______. 9．抛物线y=－3(2x 2－1)的开口方向是_____，对称轴是_____. 10．顶点为（－2，－5）且过点（1，－14）的抛物线的解析式为．11．将抛物线22y x x =-向上平移3个单位，再向右平移4个单位得到的抛物线是_______．12．抛物线22(2)6y x =--的顶点为C ，已知3y kx =-+的图象经过点C ，则这个一次函数的图象与两坐标轴所围成的三角形面积为________． 三、解答题13．已知抛物线的顶点（-1，-2），且图象经过（1，10），求抛物线的解析式． 14. 已知抛物线212y x =-向上平移2个单位长度，再向右平移1个单位长度得到 抛物线2()y a x h k =-+；（1）求出a ，h ，k 的值；（2）在同一直角坐标系中，画出2()y a x h k =-+与212y x =-的图象； （3）观察2()y a x h k =-+的图象，当x ________时，y 随x 的增大而增大；当x ________时，函数y 有最________值，最________值是y =________； （4）观察2()y a x h k =-+的图象，你能说出对于一切x 的值，函数y 的取值范围吗？ 15．（2020•珠海）已知抛物线y=ax 2+bx+3的对称轴是直线x=1． （1）求证：2a+b=0；（2）若关于x 的方程ax 2+bx ﹣8=0的一个根为4，求方程的另一个根． 【答案与解析】 一、选择题 1.【答案】D ；【解析】由顶点式可求顶点，由20x +=得2x =-，此时，3y =-． 2.【答案】D ；【解析】通过配方即可得到结论. 3.【答案】A ； 【解析】抛物线y=21x 2向左平移3个单位得到y=21(x+3)2，再向下平移2个单位后， 所得的抛物线表达式是y=21(x+3)2－2.4.【答案】B ；【解析】通过配方即可得到结论. 5.【答案】C ；【解析】可画草图进行判断. 6.【答案】D ；【解析】解：A 、由直线与y 轴的交点在y 轴的负半轴上可知，n 2＜0，错误；B 、由抛物线与y 轴的交点在y 轴的正半轴上可知，m ＞0，由直线可知，﹣m ＞0，错误；C 、由抛物线y 轴的交点在y 轴的负半轴上可知，m ＜0，由直线可知，﹣m ＜0，错误；D 、由抛物线y 轴的交点在y 轴的负半轴上可知，m ＜0，由直线可知，﹣m ＞0，正确， 故选D ．二、填空题 7．【答案】（﹣1，﹣1）； x=﹣1； 【解析】∵y=x 2+2x=（x+1）2﹣1，∴二次函数y=x 2+4x 的顶点坐标是：（﹣1，﹣1），对称轴是直线x=﹣1．8．【答案】x ≥－1；【解析】由解析式可得抛物线的开口向下，对称轴是x=-1，对称轴的右边是y 随x 的增大而减小，故x ≥－1.9．【答案】向下，y 轴； 10．【答案】249y x x =---；【解析】设2(2)5y a x =+-过点（1，－14）得1a =-，所以22(2)549y x x x =-+-=---.11．【答案】21027y x x =-+；【解析】先化一般式为顶点式，再根据平移规律求解. 12．【答案】 1； 【解析】C(2，-6)，可求932y x =-+与x 轴交于2(,0)3，与y 轴交于(0，3)，∴123123S =⨯⨯=. 三、解答题13.【答案与解析】∵ 抛物线的顶点为（-1，-2），∴ 设其解析式为2(1)2y a x =+-，又图象经过点（1，10），∴1042a =-，∴3a =， ∴ 解析式为23(1)2y x =+-． 14.【答案与解析】（1）由212y x =-向上平移2个单位，再向右平移1个单位所得到的抛物线是21(1)22y x =--+． ∴12a =-，1h =，2k =． （2）函数21(1)22y x =--+与212y x =-的图象如图所示．（3）观察2()y a x h k =-+的图象，当1x <时，y 随x 的增大而增大；当1x =时，函数y 有最大值，最大值是2y =． （4）由图象知，对于一切x 的值，总有函数值2y ≤． 15.【答案与解析】（1）证明：∵对称轴是直线x=1=﹣，∴2a+b=0；（2）解：∵ax 2+bx ﹣8=0的一个根为4，∴16a+4b ﹣8=0， ∵2a+b=0， ∴b=﹣2a ，∴16a ﹣8a ﹣8=0， 解得：a=1，则b=﹣2，∴ax 2+bx ﹣8=0为：x 2﹣2x ﹣8=0， 则（x ﹣4）（x+2）=0， 解得：x 1=4，x 2=﹣2，故方程的另一个根为：﹣2．《圆》全章复习与巩固—巩固练习（提高）【巩固练习】一、选择题1．如图所示，AB 、AC 为⊙O 的切线，B 和C 是切点，延长OB 到D ，使BD ＝OB ，连接AD ．如果∠DAC ＝78°，那么∠ADO 等于( )．A ．70°B ．64°C ．62°D ．51°2．在半径为27m 的圆形广场中心点O 的上空安装了一个照明光源S ，S 射向地面的光束呈圆锥形，其轴截面SAB 的顶角为120°(如图所示)，则光源离地面的垂直高度SO 为( )． A ．54m B ．63m C ．93m D ．183m第1题图 第2题图 第3题图 第4题图3．设计一个商标图案，如图所示，在矩形ABCD 中，AB=2BC ，且AB=8cm ，以A 为圆心、AD 的长为半径作半圆，则商标图案(阴影部分)的面积等于( ).A.(4π+8)cm 2B.(4π+16)cm 2C.(3π+8)cm 2D.(3π+16)cm 24．如图，的半径为5，弦的长为8，点在线段(包括端点)上移动，则的取值范围是( ). A. B. C. D. 5.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何?”用数学语言可表示为：如图所示，CD 为⊙O 的直径，弦AB ⊥CD 于E ，CE=1寸，AB=10寸，则直径CD 的长为( )A ．12.5寸B ．13寸C ．25寸D ．26寸 6．（2020•贵港）如图，已知P 是⊙O 外一点，Q 是⊙O 上的动点，线段PQ 的中点为M ，连接OP ，OM ．若⊙O 的半径为2，OP=4，则线段OM 的最小值是（ ）A ．0B ．1C ．2D ．37．一条弦的两个端点把圆周分成4:5两部分，则该弦所对的圆周角为( )． A ．80° B ．100° C ．80°或100° D ．160°或200°8．如图所示，AB 、AC 与⊙O 分别相切于B 、C 两点，∠A ＝50°，点P 是圆上异于B 、C 的一动点，则∠BPC的度数是( )．A ．65°B ．115°C ．65°或115°D ．130°或50° 二、填空题 9．如下左图，是的内接三角形，，点P 在上移动(点P 不与点A 、C 重合)，则的变化范围是__________.第9题图 第10题图10．如图所示，EB 、EC 是⊙O 是两条切线，B 、C 是切点，A 、D 是⊙O 上两点，如果∠E=46°，∠DCF=32°，那么∠A 的度数是________________. 11．已知⊙O 1与⊙O 2的半径1r 、2r 分别是方程2680x x -+= 的两实根，若⊙O 1与⊙O 2的圆心距d =5．则⊙O 1与⊙O 2的位置关系是____ .12．（2020•巴彦淖尔）如图，AB 为⊙O 的直径，AB=AC ，BC 交⊙O 于点D ，AC 交⊙O 于点E ，∠BAC=45°，给出以下五个结论：①∠EBC=22.5°；②BD=DC ；③AE=2EC ；④劣弧是劣弧的2倍；⑤AE=BC ，其中正确的序号是．13.两个圆内切，其中一个圆的半径为5，两圆的圆心距为2，则另一个圆的半径是_______________.14.已知正方形ABCD外接圆的直径为2a，截去四个角成一正八边形，则这个正八边形EFGHIJLK的边长为________，面积为________．15．如图(1)(2)…(m)是边长均大于2的三角形、四边形、……、凸n边形，分别以它们的各顶点为圆心，以l为半径画弧与两邻边相交，得到3条弧，4条弧，……(1)图(1)中3条弧的弧长的和为________，图(2)中4条弧的弧长的和为________；(2)求图(m)中n条弧的弧长的和为________(用n表示)．16．如图所示，蒙古包可以近似地看做由圆锥和圆柱组成，如果想用毛毡搭建20个底面积为9πm2，高为3.5m，外围高4 m的蒙古包，至少要________m2的毛毡．三、解答题17.如图，⊙O是△ABC的外接圆，FH是⊙O的切线，切点为F，FH∥BC，连结AF交BC于E，∠ABC的平分线BD交AF于D，连结BF．（1）证明：AF平分∠BAC；（2）证明：BF＝FD.18.（2020•南京）如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．（1）求证：∠A=∠AEB；（2）连接OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形．19．如图，相交两圆的公共弦长为120cm，它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.20.问题背景：课外学习小组在一次学习研讨中，得到了如下两个命题：①如图(1)，在正△ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON＝60°，则BM＝CN；②如图(2)，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON＝90°，则BM＝CN．然后运用类似的思想提出了如下命题：③如图(3)，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON＝108°，则BM＝CN．任务要求：(1)请你从①②③三个命题中选择一个进行证明；(2)请你继续完成下面的探索；①在正n(n≥3)边形ABCDEF…中，M、N分别是CD、DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM＝CN成立(不要求证明)；②如图(4)，在正五边形ABCDE中，M、N分别是DE、AE上的点，BM与CN相交于点O，∠BON＝108°时，试问结论BM＝CN是否成立．若成立，请给予证明；若不成立，请说明理由．【答案与解析】一、选择题1．【答案】B；【解析】由AB为⊙O的切线，则AB⊥OD．又BD＝OB，则AB垂直平分OD，AO＝AD，∠DAB＝∠BAO．由AB、AC为⊙O的切线，则∠CAO＝∠BAO＝∠DAB．所以，∠DAB＝∠DAC＝26°．∠ADO＝90°-26°＝64°．本题涉及切线性质定理、切线长定理、垂直平分线的性质、等腰三角形的性质等．2．【答案】C；【解析】圆锥的高、底面半径与母线组成直角三角形．由题意，SO⊥AB于O，∴∠SOA＝∠SOB＝90°．又SA＝SB，∠ASB＝120°，∴∠SAB＝∠SBA＝180120302=°-?°，设SO＝x m，则AS＝2x m．∵ AO＝27，由勾股定理，得(2x)2-x2＝272，解得93x=(m)．3．【答案】A.；【解析】对图中阴影部分进行分析，可看做扇形、矩形、三角形的面积和差关系.∵矩形ABCD中，AB=2BC，AB=8cm，∴ AD=BC=4cm，∠DAF=90°，，，又AF=AD=4cm，∴，∴.4.【答案】A；【解析】OM最长是半径5；最短是OM⊥AB时，此时OM=3，故选A.5．【答案】D；【解析】因为直径CD垂直于弦AB，所以可通过连接OA(或OB)，求出半径即可.根据“垂直于弦的直径平分弦，并且平分弦所对的两条弧”，知(寸)，在Rt△AOE中，，即，解得OA=13，进而求得CD=26(寸).故选D.6．【答案】B.【解析】设OP与⊙O交于点N，连结MN，OQ，如图，∵OP=4，ON=2，∴N是OP的中点，∵M为PQ的中点，∴MN为△POQ的中位线，∴MN=OQ=×2=1，∴点M在以N为圆心，1为半径的圆上，当点M在ON上时，OM最小，最小值为1，∴线段OM的最小值为1．故选B．7．【答案】C；【解析】圆周角的顶点在劣弧上时，圆周角为5136010092⨯⨯=°°；圆周角的顶点在优弧上时，圆周角为413608092⨯⨯=°°．注意分情况讨论．8．【答案】C；【解析】连接OC、OB，则∠BOC＝360°-90°-90°-50°＝130°．点P在优弧上时，∠BPC＝12∠BOC＝65°；点P在劣弧上时，∠BPC＝180°-65°＝115°．主要应用了切线的性质定理、圆周角定理和多边形内角和定理．二、填空题 9．【答案】； 10．【答案】99°；【解析】由EB=EC ，∠E=46°知，∠ECB= 67°，从而∠BCD=180°-67°-32°=81°， 在⊙O 中，∠BCD 与∠A 互补，所以∠A=180°-81°=99°. 11．【答案】相交；【解析】求出方程2680x x -+= 的两实根1r 、2r 分别是4、2，则1r -2r <d <1r +2r ,所以两圆相交.12.【答案】①②④；【解析】连接AD ，AB 是直径，则AD ⊥BC ，又∵△ABC 是等腰三角形，故点D 是BC 的中点，即BD=CD ，故②正确； ∵AD 是∠BAC 的平分线，由圆周角定理知，∠EBC=∠DAC=∠BAC=22.5°，故①正确；∵∠ABE=90°﹣∠EBC ﹣∠BAD=45°=2∠CAD ，故④正确； ∵∠EBC=22.5°，2EC ≠BE ，AE=BE ，∴AE ≠2CE ，③不正确； ∵AE=BE ，BE 是直角边，BC 是斜边，肯定不等，故⑤错误． 综上所述，正确的结论是：①②④．13.【答案】7或3；【解析】两圆有三种位置关系：相交、相切(外切、内切)和相离(外离、内含).两圆内切时，圆心距，题中一圆半径为5，而d=2，所以有，解得r=7或r=3，即另一圆半径为7或3.14.【答案】(21)a ； 2(222)a ；【解析】正方形ABCD 外接圆的直径就是它的对角线，由此求得正方形边长为a ．如图所示，设正八边形的边长为x ．在Rt △AEL 中，LE ＝x ，AE ＝AL ＝22x ，∴222x x a ⨯+=，21)x a =， 即正八边形的边长为(21)a ．222224[(21)](222)AEL S S S a x a a a =-=-=-=△正方形正八边形．15.【答案】(1)π； 2π； (2)(n-2)π；【解析】∵ n 边形内角和为(n-2)180°，前n 条弧的弧长的和为(2)1801(2)3602n n -=-个以某定点为圆心，以1为半径的圆周长，∴ n 条弧的弧长的和为121(2)(2)2n n ππ⨯⨯-=-．本题还有其他解法，比如：设各个扇形的圆心角依次为1α，2α，…，n α， 则12(2)180n n ααα+++=-…°，∴ n 条弧长的和为1212111()180180180180n n απαπαππααα⨯+⨯++⨯=+++……(2)180(2)180n n ππ=-⨯=-．16.【答案】720π；【解析】∵ S ＝πr 2，∴ 9π＝πr 2，∴ r ＝3．∴ h 1＝4，∴2215l h r =+=，∴223523 3.5152136S S S rl rh πππππππ=+=+=⨯⨯+⨯⨯=+=锥柱，2036720S ππ=⨯=总．所求面积包括圆锥的侧面积和圆柱的侧面积，不包括底面积．三、解答题17.【答案与解析】（1）连结OF∵FH 是⊙O 的切线 ∴OF⊥FH ∵FH∥BC ， ∴OF 垂直平分BC∴BF FC =∴AF 平分∠BAC .（2）由（1）及题设条件可知∠1=∠2，∠4=∠3，∠5=∠2 ∴∠1+∠4=∠2+∠3 ∴∠1+∠4=∠5+∠3 ∠FDB =∠FBD ∴BF =FD.18．【答案与解析】 证明：（1）∵四边形ABCD 是⊙O 的内接四边形， ∴∠A+∠BCD=180°， ∵∠DCE+∠BCD=180°， ∴∠A=∠DCE ， ∵DC=DE ，∴∠DCE=∠AEB ， ∴∠A=∠AEB ；（2）∵∠A=∠AEB ， ∴△ABE 是等腰三角形， ∵EO ⊥CD ， ∴CF=DF ，∴EO 是CD 的垂直平分线， ∴ED=EC ， ∵DC=DE ， ∴DC=DE=EC ，∴△DCE 是等边三角形， ∴∠AEB=60°，∴△ABE 是等边三角形． 19.【答案与解析】A BCDEO 12345A BCD EO 12解：∵公共弦AB＝120.20. 【答案与解析】(1)如选命题①．证明：在图(1)中，∵∠BON＝60°，∴∠1+∠2＝60°．∵∠3+∠2＝60°，∴∠1＝∠3．又∵ BC＝CA，∠BCM＝∠CAN＝60°，∴△BCM≌△CAN，∴ BM＝CM．如选命题②．证明：在图(2)中，∵∠BON＝90°，∴∠1+∠2＝90°．∵∠3+∠2＝90°，∴∠1＝∠3．又∵ BC＝CD，∠BCM＝∠CDN＝90°，∴△BCM≌△CDN，∴ BM＝CN．如选命题③．证明：在图(3)中，∵∠BON＝108°，∴∠1+∠2＝108°．∵∠2+∠3＝108°，∴∠1＝∠3．又∵ BC＝CD，∠BCM＝∠CDN＝108°，∴△BCM≌△CDN，∴ BM＝CN．(2)①答：当∠BON＝(2)180nn°时结论BM＝CN成立．②答：当∠BON＝108°时．BM＝CN还成立．证明：如图(4)，连接BD、CE在△BCD和△CDE中，∵ BC＝CD，∠BCD＝∠CDE＝108°，CD＝DE，∴△BCD≌△CDE．∴ BD＝CE，∠BDC＝∠CED，∠DBC＝∠ECD．∵∠CDE＝∠DEN＝108°，∴∠BDM＝∠CEM．∵∠OBC+∠OCB＝108°，∠OCB+∠OCD＝108°．∴∠MBC＝∠NCD．又∵∠DBC＝∠ECD＝36°，∴∠DBM＝∠ECM．∴△BDM≌△CEN，∴ BM＝CN．。

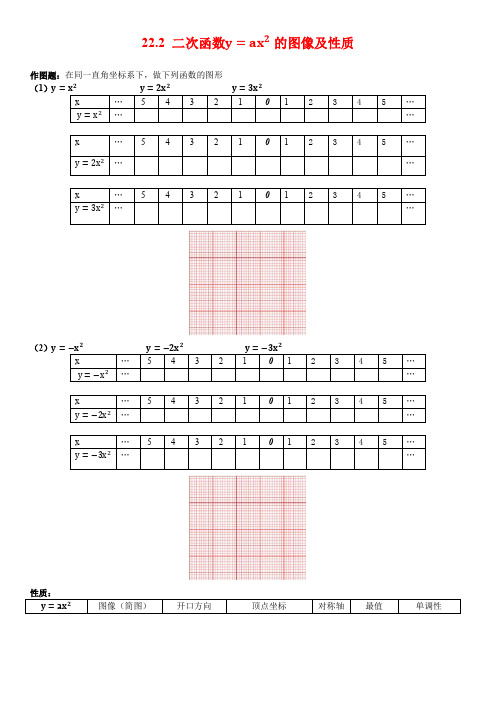
22.2 二次函数y=ax2的图像及性质作图题：在同一直角坐标系下，做下列函数的图形（1）y=222（2）y=222一、选择题本大题共小题1.关于y =13x 2，y =x 2，y =3x 2，的图象，下列说法中不正确的是（ ）A.顶点相同B.对称轴相同C.图象形状相同D.最低点相同 2.抛物线y =ax 2过点（1，-1），则a 的值为（ ） A.1 B.-1 C.12 D.-123.二次函数y =x 2的图象的开口方向是（ ）A.向上B.向下C.向左D.向右 4.抛物线y =-2x 2开口方向是（ ） A.向上 B.向下 C.向左 D.向右5.下列函数中，当x ＞0时，y 的值随x 的值增大而增大的是（ ） A.y =-x 2 B.y =x -1 C.y =-x +1 D.y =1x6.下列个函数图象中当x 时，y 随x 的增而减小的是（ ）A. B. C. D.7.已知抛物线y =ax 2（a ＞0）过A （-2，y 1）、B （1，y 2）两点，则下列关系式一定正确的是（ ） A.y 1＞0＞y 2 B.y 2＞0＞y 1 C.y 1＞y 2＞0 D.y 2＞y 1＞0 8.如图，函数y =-2x 2 的图象是（ ）A.①B.②C.③D.④9.抛物线y =10x 2的顶点坐标是（ ）A.（1，10）B.（0，10）C.（0，0）D.（5，5）10.若二次函数y =ax 2的图象经过点P （-2，4），则该图象必经过点（ ） A.（4，-2） B.（-4，2） C.（-2，-4） D.（2，4）11.在抛物线y =-x 2上，当y ＜0时，x 的取值范围应为（ ） A.x ＞0 B.x ＜0 C.x ≠0 D.x ≥012.两条抛物线y =x 2与y =-x 2在同一坐标系内，下列说法中不正确的是（ ） A.顶点相同 B.对称轴相同 C.开口方向相反 D.都有最小值二、填空题(本大题共8小题)13.抛物线y =-3x 2的对称轴是____________，当x ____________时，抛物线上的点都在x 轴的下方． 14.二次函数y =ax 2（a ＞0）的图象经过点（1，y 1）、（2，y 2），则y 1 ______ y 2（填“＞”或“＜”）．x2的图象如图所示，点A0位于坐标原点，点A1，A2，A3，…，A2011在y 15.二次函数y=23x2位于第一象限的图象上，若△A0B1A1，△A1B2A2，轴的正半轴上，点B1，B2，B3，…，B2011在二次函数y=23△A2B3A3，…，△A2010B2011A2011都为等边三角形，则△A2010B2011A2011的边长=____________．16.函数y=ax2（a＞0）中，当x＜0时，y随x的增大而______ ．17.二次函数y=3x2的图象开口______ ，对称轴是______ ，顶点坐标是______ ，图象有最______ 点，x ______ 时，y随x的增大而增大，x ______ 时，y随x的增大而减小．18.若二次函数y=m x m2−m的图象开口向下，则______ ．19.若点A（x1，8），B（x2，8），（x1≠x2）均在抛物线y=ax2上，则当x=x1+x2时，y的值是______ ．x2的顶点坐标是______ ，对称轴是______ ．20.二次函数y=18三、解答题(本大题共1小题，共8.0分)21.已知二次函数y=ax2（a≠0）与一次函数y=kx-2的图象相交于A、B两点，如图所示，其中A（-1，-1），求△OAB的面积．【答案】1.C2.B3.A4.B5.B6.B7.C8.C9.C 10.D 11.C 12.D 13.x =0(或y 轴);≠0 14.＜ 15.2011 16.减小17.向上；y 轴；（0，0）；低；＞0；＜0 18.m =-1 19.020.（0，0）；y 轴21.解：∵一次函数y =kx -2的图象相过点A （-1，-1）， ∴-1=-k -2，解得k =-1，∴一次函数表达式为y =-x -2， ∴令x =0，得y =-2， ∴G （0，-2），∵y =ax 2过点A （-1，-1）， ∴-1=a ×1，解得a =-1，∴二次函数表达式为y =-x 2， 由一次函数与二次函数联立可得y =−x2y =−x −2解得 y1=−1x 1=−1， y 2=−4x 2=2 ∴S △OAB =12OG•|A 的横坐标|+12OG•点B 的横坐标=12×2×1+12×2×2=1+2=3．。

5.2《二次函数的图像和性质》同步练习卷一．选择题1．在同一坐标系中，一次函数y＝ax+2与二次函数y＝x2+a的图象可能是（）A．B．C．D．2．当ab＞0时，y＝ax2与y＝ax+b的图象大致是（）A．B．C．D．3．在同一平面直角坐标系中，函数y＝ax2+bx与y＝bx+a的图象可能是（）A．B．C．D．4．如果抛物线y＝x2﹣6x+c﹣2的顶点到x轴的距离是3，那么c的值等于（）A．8B．14C．8或14D．﹣8或﹣145．已知两点A（﹣5，y1），B（3，y2）均在抛物线y＝ax2+bx+c（a≠0）上，点C（x0，y0）是该抛物线的顶点．若y1＞y2≥y0，则x0的取值范围是（）A．x0＞﹣5B．x0＞﹣1C．﹣5＜x0＜﹣1D．﹣2＜x0＜36．已知二次函数y＝ax2+bx+c（a＜0）的图象如图，当﹣5≤x≤0时，下列说法正确的是（）A．有最小值﹣5、最大值0B．有最小值﹣3、最大值6C．有最小值0、最大值6D．有最小值2、最大值67．把抛物线y＝﹣2x2向上平移1个单位，再向右平移1个单位，得到的抛物线是（）A．y＝﹣2（x+1）2+1B．y＝﹣2（x﹣1）2+1C．y＝﹣2（x﹣1）2﹣1D．y＝﹣2（x+1）2﹣18．对于二次函数y＝﹣（x﹣1）2+2的图象与性质，下列说法正确的是（）A．对称轴是直线x＝1，最小值是2B．对称轴是直线x＝1，最大值是2C．对称轴是直线x＝﹣1，最小值是2D．对称轴是直线x＝﹣1，最大值是29．下列对二次函数y＝x2﹣x的图象的描述，正确的是（）A．开口向下B．对称轴是y轴C．经过原点D．在对称轴右侧部分是下降的10．已知二次函数y＝x2﹣2mx（m为常数），当﹣1≤x≤2时，函数值y的最小值为﹣2，则m的值是（）A．B．C．或D．或11．将二次函数y＝x2﹣4x+a的图象向左平移1个单位，再向上平移1个单位．若得到的函数图象与直线y＝2有两个交点，则a的取值范围是（）A．a＞3B．a＜3C．a＞5D．a＜512．抛物线y＝（x﹣1）2+2的顶点坐标是（）A．（﹣1，2）B．（﹣1，﹣2）C．（1，﹣2）D．（1，2）13．如图，一次函数y1＝x与二次函数y2＝ax2+bx+c图象相交于P、Q两点，则函数y＝ax2+（b﹣1）x+c的图象可能是（）A．B．C．D．14．在同一平面直角坐标系中，若抛物线y＝x2+（2m﹣1）x+2m﹣4与y＝x2﹣（3m+n）x+n 关于y轴对称，则符合条件的m，n的值为（）A．m＝，n＝﹣B．m＝5，n＝﹣6C．m＝﹣1，n＝6D．m＝1，n＝﹣215．若二次函数y＝|a|x2+bx+c的图象经过A（m，n）、B（0，y1）、C（3﹣m，n）、D（，y2）、E（2，y3），则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y2＜y1D．y2＜y3＜y1 16．当a﹣1≤x≤a时，函数y＝x2﹣2x+1的最小值为1，则a的值为（）A．1B．2C．1或2D．0或317．如图，已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc ＞0；②b﹣a＞c；③4a+2b+c＞0；④3a＞﹣c；⑤a+b＞m（am+b）（m≠1的实数）．其中正确结论的有（）A．①②③B．②③⑤C．②③④D．③④⑤18．如图是抛物线y1＝ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x 轴的一个交点B（4，0），直线y2＝mx+n（m≠0）与抛物线交于A，B两点，下列结论：①2a+b＝0；②abc＞0；③方程ax2+bx+c＝3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y2＜y1，其中正确的是（）A．①②③B．①③④C．①③⑤D．②④⑤二．填空题19．已知抛物线y＝ax2+bx+c的部分图象如图所示，若y＞0，则x的取值范围是．20．如图，抛物线y＝﹣x2+2x+3与y轴交于点C，点D（0，1），点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为．21．已知点A（x1，y1）、B（x2，y2）在二次函数y＝（x﹣1）2+1的图象上，若x1＞x2＞1，则y1y2（填“＞”、“＜”或“＝”）．22．如图，对称轴平行于y轴的抛物线与x轴交于（1，0），（3，0）两点，则它的对称轴为．23．二次函数y＝﹣（x﹣6）2+8的最大值是．24．将抛物线y＝2（x﹣1）2+2向左平移3个单位，再向下平移4个单位，那么得到的抛物线的表达式为．25．如图，已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x＝1．下列结论：①abc＞0；②4a+2b+c＞0；③4ac﹣b2＜﹣4a；④＜a＜；⑤b＞c．其中正确结论有（填写所有正确结论的序号）．三．解答题26．如图，已知二次函数y＝x2+ax+3的图象经过点P（﹣2，3）．（1）求a的值和图象的顶点坐标．（2）点Q（m，n）在该二次函数图象上．①当m＝2时，求n的值；②若点Q到y轴的距离小于2，请根据图象直接写出n的取值范围．27．用描点法作出函数y＝﹣x2+2x的图象．28．已知抛物线y＝ax2+3经过点A（﹣2，﹣13）．（1）求a的值．（2）若点P（m，﹣22）在此抛物线上，求点P的坐标．29．如图，二次函数y＝（x﹣3）2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点，已知一次函数y＝kx+b的图象经过该二次函数图象上的点A（1，0）及点B．（1）求二次函数与一次函数的解析式；（2）抛物线上是否存在一点P，使S△ABP＝S△ABC？若存在，请求出点P的坐标，若不存在，请说明理由．30．如图，平面直角坐标系中，抛物线y＝﹣x2+4x+m﹣4（m为常数）与y轴的交点为C，M（3，0）与N（0，﹣2）分别是x轴、y轴上的点（1）当m＝1时，求抛物线顶点坐标．（2）若3≤x≤3+m时，函数y＝﹣x2+4x+m﹣4有最小值﹣7，求m的值．（3）若抛物线与线段MN有公共点，直接写出m的取值范围是．31．已知函数y＝（m+2）x2+kx+n．（1）若此函数为一次函数；①m，k，n的取值范围；②当﹣2≤x≤1时，0≤y≤3，求此函数关系式；③当﹣2≤x≤3时，求此函数的最大值和最小值（用含k，n的代数式表示）；（2）若m＝﹣1，n＝2，当﹣2≤x≤2时，此函数有最小值﹣4，求实数k的值．参考答案一．选择题1．解：当a＜0时，二次函数顶点在y轴负半轴，一次函数经过一、二、四象限；当a＞0时，二次函数顶点在y轴正半轴，一次函数经过一、二、三象限．故选：C．2．解：根据题意，ab＞0，即a、b同号，当a＞0时，b＞0，y＝ax2与开口向上，过原点，y＝ax+b过一、二、三象限；此时，没有选项符合，当a＜0时，b＜0，y＝ax2与开口向下，过原点，y＝ax+b过二、三、四象限；此时，D选项符合，故选：D．3．解：A、对于直线y＝bx+a来说，由图象可以判断，a＞0，b＞0；而对于抛物线y＝ax2+bx 来说，对称轴x＝﹣＜0，应在y轴的左侧，故不合题意，图形错误．B、对于直线y＝bx+a来说，由图象可以判断，a＜0，b＜0；而对于抛物线y＝ax2+bx来说，图象应开口向下，故不合题意，图形错误．C、对于直线y＝bx+a来说，由图象可以判断，a＜0，b＞0；而对于抛物线y＝ax2+bx来说，图象开口向下，对称轴x＝﹣位于y轴的右侧，故符合题意，D、对于直线y＝bx+a来说，由图象可以判断，a＞0，b＞0；而对于抛物线y＝ax2+bx来说，图象开口向下，a＜0，故不合题意，图形错误．故选：C．4．解：根据题意＝±3，解得c＝8或14．故选：C．5．解：∵点C（x0，y0）是抛物线的顶点，y1＞y2≥y0，∴抛物线有最小值，函数图象开口向上，∴a＞0；∴25a﹣5b+c＞9a+3b+c，∴＜1，∴﹣＞﹣1，∴x0＞﹣1∴x0的取值范围是x0＞﹣1．故选：B．6．解：由二次函数的图象可知，∵﹣5≤x≤0，∴当x＝﹣2时函数有最大值，y最大＝6；当x＝﹣5时函数值最小，y最小＝﹣3．故选：B．7．解：∵函数y＝﹣2x2的顶点为（0，0），∴向上平移1个单位，再向右平移1个单位的顶点为（1，1），∴将函数y＝﹣2x2的图象向上平移1个单位，再向右平移1个单位，得到抛物线的解析式为y＝﹣2（x﹣1）2+1，故选：B．8．解：由抛物线的解析式：y＝﹣（x﹣1）2+2，可知：对称轴x＝1，开口方向向下，所以有最大值y＝2，故选：B．9．解：A、∵a＝1＞0，∴抛物线开口向上，选项A不正确；B、∵﹣＝，∴抛物线的对称轴为直线x＝，选项B不正确；C、当x＝0时，y＝x2﹣x＝0，∴抛物线经过原点，选项C正确；D、∵a＞0，抛物线的对称轴为直线x＝，∴当x＞时，y随x值的增大而增大，选项D不正确．故选：C．10．解：y＝x2﹣2mx＝（x﹣m）2﹣m2，①若m＜﹣1，当x＝﹣1时，y＝1+2m＝﹣2，解得：m＝﹣；②若m＞2，当x＝2时，y＝4﹣4m＝﹣2，解得：m＝＜2（舍）；③若﹣1≤m≤2，当x＝m时，y＝﹣m2＝﹣2，解得：m＝或m＝﹣＜﹣1（舍），∴m的值为﹣或，故选：D．11．解：∵y＝x2﹣4x+a＝（x﹣2）2﹣4+a，∴将二次函数y＝x2﹣4x+a的图象向左平移1个单位，再向上平移1个单位，得到的函数解析式为y＝（x﹣2+1）2﹣4+a+1，即y＝x2﹣2x+a﹣2，将y＝2代入，得2＝x2﹣2x+a﹣2，即x2﹣2x+a﹣4＝0，由题意，得△＝4﹣4（a﹣4）＞0，解得a＜5．故选：D．12．解：∵顶点式y＝a（x﹣h）2+k，顶点坐标是（h，k），∴抛物线y＝（x﹣1）2+2的顶点坐标是（1，2）．故选：D．13．解：点P在抛物线上，设点P（x，ax2+bx+c），又因点P在直线y＝x上，∴x＝ax2+bx+c，∴ax2+（b﹣1）x+c＝0；由图象可知一次函数y＝x与二次函数y＝ax2+bx+c交于第一象限的P、Q两点，∴方程ax2+（b﹣1）x+c＝0有两个正实数根．∴函数y＝ax2+（b﹣1）x+c与x轴有两个交点，又∵﹣＞0，a＞0∴﹣＝﹣+＞0∴函数y＝ax2+（b﹣1）x+c的对称轴x＝﹣＞0，∴A符合条件，故选：A．14．解：∵抛物线y＝x2+（2m﹣1）x+2m﹣4与y＝x2﹣（3m+n）x+n关于y轴对称，∴，解之得，∴则符合条件的m，n的值为m＝1，n＝﹣2，故选：D．15．解：∵经过A（m，n）、C（3﹣m，n），∴二次函数的对称轴x＝，∵B（0，y1）、D（，y2）、E（2，y3）与对称轴的距离B最远，D最近，∵|a|＞0，∴y1＞y3＞y2；故选：D．16．解：当y＝1时，有x2﹣2x+1＝1，解得：x1＝0，x2＝2．∵当a﹣1≤x≤a时，函数有最小值1，∴a﹣1＝2或a＝0，∴a＝3或a＝0，故选：D．17．解：①∵对称轴在y轴的右侧，∴ab＜0，由图象可知：c＞0，∴abc＜0，故①不正确；②当x＝﹣1时，y＝a﹣b+c＜0，∴b﹣a＞c，故②正确；③由对称知，当x＝2时，函数值大于0，即y＝4a+2b+c＞0，故③正确；④∵x＝﹣＝1，∴b＝﹣2a，∵a﹣b+c＜0，∴a+2a+c＜0，3a＜﹣c，故④不正确；⑤当x＝1时，y的值最大．此时，y＝a+b+c，而当x＝m时，y＝am2+bm+c，所以a+b+c＞am2+bm+c（m≠1），故a+b＞am2+bm，即a+b＞m（am+b），故⑤正确．故②③⑤正确．故选：B．18．解：∵抛物线的顶点坐标A（1，3），∴抛物线的对称轴为直线x＝﹣＝1，∴2a+b＝0，所以①正确；∵抛物线开口向下，∴a＜0，∴b＝﹣2a＞0，∵抛物线与y轴的交点在x轴上方，∴c＞0，∴abc＜0，所以②错误；∵抛物线的顶点坐标A（1，3），∴x＝1时，二次函数有最大值，∴方程ax2+bx+c＝3有两个相等的实数根，所以③正确；∵抛物线与x轴的一个交点为（4，0）而抛物线的对称轴为直线x＝1，∴抛物线与x轴的另一个交点为（﹣2，0），所以④错误；∵抛物线y1＝ax2+bx+c与直线y2＝mx+n（m≠0）交于A（1，3），B点（4，0）∴当1＜x＜4时，y2＜y1，所以⑤正确．故选：C．二．填空题19．解：已知抛物线与x轴的一个交点是（﹣1，0），对称轴为x＝1，根据对称性，抛物线与x轴的另一交点为（3，0），观察图象，当y＞0时，﹣1＜x＜3．20．解：∵△PCD是以CD为底的等腰三角形，∴点P在线段CD的垂直平分线上，如图，过P作PE⊥y轴于点E，则E为线段CD的中点，∵抛物线y＝﹣x2+2x+3与y轴交于点C，∴C（0，3），且D（0，1），∴E点坐标为（0，2），∴P点纵坐标为2，在y＝﹣x2+2x+3中，令y＝2，可得﹣x2+2x+3＝2，解得x＝1±，∴P点坐标为（1+，2）或（1﹣，2），故答案为：（1+，2）或（1﹣，2）．21．解：∵a＝1＞0，∴二次函数的图象开口向上，由二次函数y＝（x﹣1）2+1可知，其对称轴为x＝1，∵x1＞x2＞1，∴两点均在对称轴的右侧，∵此函数图象开口向上，∴在对称轴的右侧y随x的增大而增大，∵x1＞x2＞1，∴y1＞y2．故答案为：＞．22．解：∵点（1，0），（3，0）的纵坐标相同，∴这两点一定关于对称轴对称，∴对称轴是：x＝＝2．故答案为：直线x＝2．23．解：∵a＝﹣1＜0，∴y有最大值，当x＝6时，y有最大值8．故答案为8．24．解：抛物线y＝2（x﹣1）2+2向左平移3个单位，再向下平移4个单位得到y＝2（x﹣1+3）2+2﹣4＝2（x+2）2﹣2．故得到抛物线的解析式为y＝2（x+2）2﹣2．故答案为：y＝2（x+2）2﹣2．25．解：①∵函数开口方向向上，∴a＞0；∵对称轴在y轴右侧∴ab异号，∵抛物线与y轴交点在y轴负半轴，∴c＜0，∴abc＞0，故①正确；②∵图象与x轴交于点A（﹣1，0），对称轴为直线x＝1，∴图象与x轴的另一个交点为（3，0），∴当x＝2时，y＜0，∴4a+2b+c＜0，故②错误；③∵二次函数y＝ax2+bx+c的图象与y轴的交点在（0，﹣1）的下方，对称轴在y轴右侧，a＞0，∴最小值：＜﹣1，∵a＞0，∴4ac﹣b2＜﹣4a；∴③正确；④∵图象与y轴的交点B在（0，﹣2）和（0，﹣1）之间，∴﹣2＜c＜﹣1∴﹣2＜﹣3a＜﹣1，∴＞a＞；故④正确⑤∵a＞0，∴b﹣c＞0，即b＞c；故⑤正确．综上所述，正确的有①③④⑤，故答案为：①③④⑤．三．解答题26．解：（1）把点P（﹣2，3）代入y＝x2+ax+3中，∴a＝2，∴y＝x2+2x+3＝（x+1）2+2，∴顶点坐标为（﹣1，2）；（2）①当m＝2时，n＝11，②点Q到y轴的距离小于2，∴|m|＜2，∴﹣2＜m＜2，∴2≤n＜11；27．解：列表x…﹣10123…y…﹣3010﹣3…描点、连线画出函数图象如图：28．解：（1）将点A（﹣2，﹣13）．代入y＝ax2+3，得﹣13＝4a+3，解得a＝﹣4，∴抛物线的函数解析式为y＝﹣4x2+3，（2）∵点P（m，﹣22）在此抛物线上，∴﹣22＝﹣4m2+3，解得m＝±，∴点P的坐标为（，﹣22）或（﹣，﹣22）．29．解：（1）将点A（1，0）代入y＝（x﹣3）2+m得（1﹣3）2+m＝0，解得m＝﹣4．所以二次函数解析式为y＝（x﹣3）2﹣4，即y＝x2﹣6x+5；当x＝0时，y＝9﹣4＝5，所以C点坐标为（0，5），由于C和B关于对称轴对称，而抛物线的对称轴为直线x＝3，所以B点坐标为（6，5），将A（1，0）、B（6，5）代入y＝kx+b得，，解得：．所以一次函数解析式为y＝x﹣1；（2）假设存在点P，设点P（a，a2﹣6a+5），∵S△ABP＝S△ABC，∵，如图1，当点P在直线AB的下方时，过点P作PE∥y轴交直线AB于点E，∴＝15，∴E（a，a﹣1）∴PE＝﹣a2+7a﹣6，∴，∴a2﹣7a+12＝0解得：a1＝4，a2＝3，∴P1（3，﹣4），P2（4，﹣3），如图2，当点P在直线AB的上方时，过点P作PF∥y轴交直线AB于F，同理可得S△P AB＝S△PF A﹣S△PFB＝＝15，∴，解得a＝0（舍去），a＝7，∴P3（7，12）．综合以上可得P点坐标为（3，﹣4）或（4，﹣3）或（7，12）．30．解：（1）当m＝1时，y＝﹣x2+4x﹣3＝﹣（x﹣2）2+1，∴顶点坐标为（2，1）；（2）由抛物线y＝﹣x2+4x+m﹣4（m为常数）可知：开口向上，函数的对称轴为直线x ＝2，∴当3≤x≤3+m时，y随x的增大而减小，∴当x＝m+3时，y有最小值﹣7，∴﹣（m+3）2+4（m+3）+m﹣4＝﹣7，解得m1＝2，m2＝﹣3（舍去），∴m＝2；（3）∵M（3，0），N（0，﹣2），∴直线MN的解析式为y＝x﹣2，∵抛物线与线段MN有公共点，则方程﹣x2+4x+m﹣4＝x﹣2，即x2﹣x﹣m+2＝0中△≥0，且m﹣4≤﹣2，∴（﹣）2﹣4（﹣m+2）≥0，解得﹣≤m≤2，故答案为﹣≤m≤2．31．解：（1）①m＝﹣2，k≠0，n为任意实数；②当k＞0时，y随x的增大而增大，直线经过（﹣2，0）（1，3），函数关系式为：y＝x+2当k＜0时，y随x的增大而减小，直线经过（﹣2，3）（1，0），函数关系式为：y＝﹣x+1③当k＞0时，x＝﹣2，y有最小值为﹣2k+nx＝3时，y有最大值为3k+n当k＜0时，x＝﹣2，y有最大值为﹣2k+nx＝3时，y有最小值为3k+n（2）若m＝﹣1，n＝2时，二次函数为y＝x2+kx+2对称轴为x＝﹣，当﹣≤﹣2，即k≥4时，把x＝﹣2，y＝﹣4代入关系式得：k＝5当﹣2＜﹣＜2，即﹣4＜k＜4时，把x＝﹣，y＝﹣4代入关系式得：k＝±2（不合题意）当﹣≥2，即k≤﹣4时，把x＝2，y＝﹣4代入关系式得：k＝﹣5．所以实数k的值为±5．。

初中数学华东师范大学九年级下册第二十六章26.2.1. 二次函数y=ax2的图象与性质随堂练习一、单选题1．给出下列四个函数：①y＝﹣x；②y＝x；③y＝x2，x＜0时，y随x的增大而减小的函数有（ ）A．1个B．2个C．3个D．4个2．下列关于抛物线y=（x+2）2+6的说法，正确的是（ ）A．抛物线开口向下B．抛物线的顶点坐标为（2，6）C．抛物线的对称轴是直线x=6D．抛物线经过点（0，10）3．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，那么下列判断正确的是（ ）A．b＞0，c＞0B．b＞0，c＜0C．b＜0，c＞0D．b＜0，c＜0．4．已知抛物线C的解析式为y=ax2+bx+c，则下列说法中错误的是（ ）A．a确定抛物线的形状与开口方向B．若将抛物线C沿y轴平移，则a，b的值不变C．若将抛物线C沿x轴平移，则a的值不变D．若将抛物线C沿直线l：y=x+2平移，则a、b、c的值全变5．下列各点中，在二次函数y=-x2的图象上的是（ ）A．B．C．D．6．与抛物线y=―12x2+3x―5的形状大小开口方向相同，只有位置不同的抛物线是（ ）A．y=―14x 2+32x―52B．y=―12x2―7x+8C．y=12x2+6x+10D．y=―x2+3x―57．如图，二次函数y=a x2+bx的图象经过点A，B，C，则判断正确是（ ）A．a>0,b>0B．a<0,b<0C．a>0, b<0D．a<0, b>08．已知物体下落高度h关于下落时间t的函数关系式h＝1gt2，则此函数的图象为（ ）2A．B．C．D．二、填空题9．若抛物线y=a x2+bx+c（a≠0）的示意图如图所示，则a 0，ba 0，ca 0（填“ >”，“＝”或“ <”）．10．若点A（1，n）在二次函数的图象上，则点A关于抛物线对称轴的对称点的坐标是 ，这两点间的线段被对称轴 ．11．二次函数y=x2的图象开口方向是 （填“向上”或“向下”）.12．写出一个开口向上，顶点是坐标原点的二次函数的解析式： .13．当a>0时，二次函数y=a x2―2x―1的图象开口向 14．如果抛物线y=（m﹣1）x2的开口向上，那么m的取值范围是 ．三、解答题15．已知抛物线y＝ax2+bx+c的大致图象如图所示，试确定a，b，c，b2－4ac及a+b+c 的符号．16．由于x2≥0，所以x2有最小值0，从而x2+1有最小值1．据此请求出（1）x2﹣2的最小值；（2）x2﹣4x+1的最小值；（3）﹣x2+3x+2有最大值还是最小值呢？请你求出这个最大或最小值来．17．在平面直角坐标系中，反比例函数与二次函数y＝k(x2＋x－1)的图象交于点A(1，k)和点B(－1，－k)．(1)当k＝－2时，求反比例函数的解析式；(2)要使反比例函数与二次函数都是y随着x的增大而增大，求k应满足的条件以及x的取值范围．(3)设二次函数的图象的顶点为Q，当△ABQ是以AB为斜边的直角三角形时，求k的值．参考答案与试题解析1．B2．D3．D4．D5．A6．B7．A8．A9．＞；＜；＜10．；垂直平分11．向上12．y=2x213．上14．m＞115．解：∵抛物线开口向上，∴a＞0．∵抛物线与y轴的交点在y轴的负半轴上，∴C＜0．又∵对称轴在y轴左侧，∴ab＞0．∵a＞0，∴b＞0．∵抛物线与x轴有两个交点，∴△＝b2－4ac＞0．∵当x=1时，y＞0，∴a＋b＋c＞0．16．解：（1）x2﹣2的最小值为﹣2；（2）x2﹣4x+1=（x﹣2）2﹣3，所以x2﹣4x+1的最小值为﹣3；（3）﹣x2+3x+2=﹣（x﹣32）2+174，所以﹣x2+3x+2有最大值，最大值为174．17．解：(1)因为k＝－2，所以A(1，－2)，设反比例函数为y＝k1x ，因为点A在函数的图象上，所以－2＝k11，解得k1＝－2，反比例函数解析式为y＝－2x.(2)由y ＝k(x 2＋x －1)＝k x +－54k ，得抛物线对称轴为直线x ＝－12，当k>0时，反比例函数不存在y 随着x 的增大而增大的取值范围，所以k<0，此时，当x<0或x>0时，反比例函数值y 随着x 的增大而增大；当x≤－12时，二次函数值y 随着x 的增大而增大，所以自变量x 的取值范围是x≤－12.(3)由题(2)得点Q 的坐标为（-12，-54k ），因为AQ ⊥BQ ，点O 是AB 的中点，所以OQ ＝12AB ＝OA ，得14＋2516k 2＝12＋k 2，解得k ＝±233.。

2.3二次函数y=ax2的图象和性质同步练习 1．在同一直角坐标系中作出函数y＝x2，y＝2x2和y＝3x2的图象，然后根据图象填空：

抛物线y＝x2的顶点坐标是( )，对称轴是________，开口向________； 抛物线y＝2x2的顶点坐标是( )，对称轴是________，开口向________； 抛物线y＝3x2的顶点坐标是( )，对称轴是________，开口向________． 可以发现，抛物线y＝x2，y＝2x2，y＝3x2的开口大小由二次项系数决定，二次项系数的绝对值越大，抛物线的开口越________． 2．在同一直角坐标系中作出函数y＝－x2，y＝－2x2和y＝－3x2的图象，然后根据图象填空： 抛物线y＝－x2的顶点坐标是( )，对称轴是________，开口向________； 抛物线y＝－2x2的顶点坐标是( )，对称轴是________，开口向________； 抛物线y＝－3x2的顶点坐标是( )，对称轴是________，开口向________． 可以发现，抛物线y＝－x2，y＝－2x2，y＝－3x2的开口大小由二次项系数决定，二次项系数的绝对值越大，抛物线的开口越________．

3．(1)抛物线 y＝ax2的开口方向和开口大小由________决定，当a________0时，抛物线的开口向上；当a________0时，抛物线的开口向下； (2)抛物线y＝ax2的顶点坐标是( )，当a________0时，它是抛物线的最低点，即当x＝________时，函数取得最小值为________；当a________0时，它是抛物线的最高点，即当x＝________时，函数取得最大值为________；

(3)抛物线y＝ax2的对称轴是________． 4．在同一直角坐标系中作出函数y＝－x2，y＝－x2＋2，y＝－x2－3的图象，然后根据图象填空： 抛物线y＝－x2的顶点坐标是( )，对称轴是________，开口向________； 抛物线y＝－x2＋2的顶点坐标是( )，对称轴是________，开口向________； 抛物线y＝－x2－3的顶点坐标是( )，对称轴是________，开口向________． 可以发现，抛物线 y＝－x2＋2，y＝－x2－3与抛物线 y＝－x2的形状、开口大小相同，只是抛物线的顶点位置发生了变化．把抛物线y＝－x2沿y轴向________平移________个单位即可得到抛物线 y＝－x2＋2；把抛物线y＝－x2沿y轴向________平移________个单位即可得到抛物线y＝－x2－3．

课题 26.1 二次函数（2）练习九年级 备课人：洪双桥 审核： 审批： 班级：____________ 姓名：____________ 使用时间：2012年12月10日 目标知识点：会用描点法画出二次函数2ax y =的图象，概括出图象的特点 及函数的性质⒈抛物线y=ax 2与y=2x 2形状相同，则a= 。

⒉已知函数y=ax 2当x=1时y=3，则a= , 对称轴是 ，顶点是 , 抛物线的开口 ，在对称轴的左侧，y 随x 增大而 ，当x= 时，函数y 有最 值，是 .⒊已知二次函数y=-x 2 ①; 235y x =②; y=15x 2③; y=-4x 2④; 2910y x =-⑤; y=4x 2⑥ ;(1)其中开口向上的有 (填题号)；(2)其中开口向下且开口最大的是________(填题号)； (3)当自变量由小到大变化时，函数值先逐渐变大，然后渐变小的有______(填题号).⒋已知函数y=ax 2的图象过点1(,2)2,则此图象上纵坐标为12时的点的坐标为 .⒌若抛物线y=ax 2经过点P ( l ，-2 )，则它也经过 （ ）A. P 1(-1，-2 )B. P 2(-l, 2 )C.P 3( l, 2)D.P 4(2, 1)⒍已知a≠0,b<0，一次函数是y=ax+b ，二次函数是y=ax 2，则下面图中，可以成立的是（ ）⒎已知42)2(-++=k k x k y 是二次函数，且当0x <时，y随x 的增大而增大．（1）求k 的值；（2）求顶点坐标和对称轴．8．底面是边长为x 的正方形，高为0．5cm 的长方体的体积为ycm 3．（1）求y 与x 之间的函数关系式；（2）画出函数的图象；（3）根据图象，求出y=8 cm3时底面边长x的值；（4）根据图象，求出x取何值时，y≥4．5 cm3．9．二次函数2axy=与直线3y交于点P（1，b）．=x2-（1）求a、b的值；（2）写出二次函数的关系式，并指出x取何值时，该函数的y随x的增大而减小．10.一个函数的图象是以原点为顶点，y轴为对称轴的抛物线，且过M（-2，2）．（1）求出这个函数的关系式并画出函数图象；（2）写出抛物线上与点M关于y轴对称的点N的坐标，并求出⊿MON的面积．。