- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 x k
xk,
2
k 0, 1, 2, 3,...
原点处为波腹
波腹处的振幅为原来波振幅的2倍。
波节的位置: | cos 2 x | 0
2 x (2k 1)
2
x (2k 1) , k 0, 1, 2, 3,... 4
相邻波腹间的距离为:x k 1
xk
(k
1)
2
k
2
2
相邻波节间的距离为:x k 1
频率相同、振动方向相同、有恒定位相差的两 列波(或多列波)相遇时,在介质中某些位置质点 的振动始终加强,另一些位置振动始终削弱,而其它 位置,振动的强弱介乎二者之间,保持不变。这种 现象为干涉现象。
能产生干涉现象的波称为相干波。
满足相干条件的波源称为相干波源。
2 干涉加强、减弱条件
设有两列相干波在空间某点P相遇,两波在该
xk
[2(k
1) 1]
4
(2k
1)
4
2
波节
波腹
2 42
四 驻波的相位
y 2Acos 2 x cost
考查波节两边质点振动的相位
y
O
x
x =λ/4
• 波节两侧的质点振动相位相反。位移同时达到反向 最大或最小。速度方向相反。
• 两个相邻波节之间的质点振动相位相同。 位移同时 达到最大或最小。速度方向相同。
tg
A1
sin
1
2
r1
A2
sin
2
2
r2
A1
cos
1
2
r1
A2
cos
2
2
r2
A A12 A22 2A1A2 cos
(2
1 )
2 (r2ຫໍສະໝຸດ r1)波的强度与振幅间满足下列关系:I 1 2uA2
2
则合振动的强度为:
I I1 I2 2 I1I2 cos
对空间不同的位置,位相差∆φ 不随时间变化, 因而合强度在空间形成稳定的分布,形成干涉现象。
点引起的分振动分别为:
y1
A1
cos(t
1
2
r1 )
r1
y2
A2
cos(t
2
2
r2
)
1, 2: 波源的初相位.
S1
A1, A2 : 波源在P点引起振动的振幅。
P
r2
S2
在 P 点的振动(同方向同频率振动的合成)可表示为:
y y1 y2 Acos(t )
y y1 y2 Acos(t )
驻波不传播能量。
驻波中,波节不参加振动,因而没有振动状态或相 位的传播,也没有能量的传播,所以称为驻波。
驻波是分段振动现象 ,它是媒质的一种特殊的运动 状态,此时媒质处于稳定态。
驻波是分段振动现象
圆驻波
A A12 A22 2A1A2 cos , I I1 I2 2 I1I2 cos
a.波场的振幅
(2
1 )
2
(r2
r1)
当∆φ=±2kπ, (k=0,1,2,3…)时,合振幅最大
A Amax A1 A2
I Imax I1 I2 2 I1I2
干涉相长
当∆φ=±(2k+1)π, (k=0,1,2,3…)时, 合振幅最小
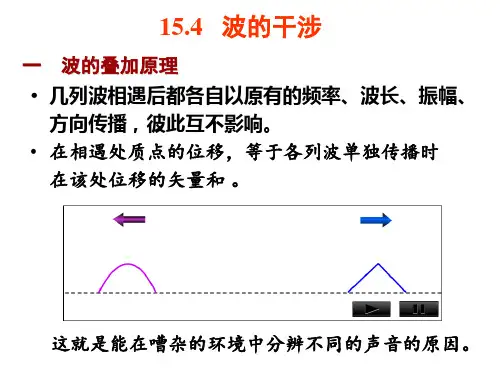
15.4 波的干涉
一 波的叠加原理 • 几列波相遇后都各自以原有的频率、波长、振幅、
方向传播,彼此互不影响。 • 在相遇处质点的位移,等于各列波单独传播时
在该处位移的矢量和 。
这就是能在嘈杂的环境中分辨不同的声音的原因。
二 波的干涉 1 波的干涉现象 ——波动所独有的现象 一般地说,振幅、频率、相位等都不相同的几 列波在某一点叠加时,情形是很复杂的。
在波节处, 势能最大. [sin(.)最大=>x=(2k+1)*λ/4 ↔ 波节]
势能集中在波节。
• 各质点回到平衡位置时,动能不为零, 势能为零.
在波腹处, 动能最大. [cos(.)最大=>x=k*λ/2 ↔ 波腹]
动能集中在波腹。
能量从波腹传到波节,又从波节传到波腹,往复 循环,能量不被传播。
当一列波遇到障碍时产 生的反射波与入射波叠 加也会产生驻波.
特点
媒质中各质点都作稳定的振动, 波形并没有移动.
二 驻波方程
cos cos 2cos cos
2
2
设有两列相干波,初相位均为0.
y1
A cos(t
2
x
)
y2
A cos(t
2
x
)
则两波相遇处的合振动为
y
y1
y2
A cos(t
2
x
)
Acos(t
2
x
)
特点:
2Acos 2 x cost ——驻波方程
1. 各点都在作简谐振动,振动的频率相同,等于原
来波的频率。
2. 各点振幅随位置x作周期性变化,与时间无关。
三 波腹与波节
y 2Acos 2 x cost
振幅最大的点称为波腹,振幅为零的点称为波节。
波腹的位置: | cos 2 x | 1
A Amin | A1 A2 |
干涉相消
I Imin I1 I2 2 I1I2
一般情况下,合振幅的大小介于二者之间。
b.波源初相相同时
(2
1)
2
(r2
r1)
若两相干波源初位相相同,即φ1= φ2 此时相干条件简化为:
δ = r2-r1 ----波程差
k, k 0,1, 2,3,...
• 波节质点不参加振动。 • 驻波不传播振动状态或相位.
五 驻波的能量
y 2Acos 2 x cost
设介质密度为ρ, 取体积为dV 的质(元)点,其动能和
势能为:
k dV 2
Ek
1 2
k
2
A
cos
2 x
2
sin2 t
Ep
1 2
k
2 A sin
2 x
2
cos2 t
• 各个质点位移最大时, 动能为零, 势能不为零.
(2k 1) , k 0,1, 2,3,...
2
干涉相长 干涉相消
初相相同的两个相干波源, 在两列波叠加的区域内:
当波程差为波长的整数倍时,相干相长,波强最大;
当波程差为半波长的奇数倍时, 相干相消,波强最小.
15.5 驻波
一 驻波的形成 两列振幅相等的相干波在同一直线上沿相反方
向传播时,在它们迭加的区域内形成的一种特殊的 波,称为驻波。