2019-2020学年四川省阆中中学高二4月月考数学(理)试题(解析版)
- 格式:doc
- 大小:2.82 MB
- 文档页数:18


四川省南充市阆中中学2018-2019学年高二数学3月月考试题理(含解析)一、选择题(本大题共12个小题)1.设是椭圆上的点.若是椭圆的两个焦点,则等于( )A. 4B. 5C. 8D. 10【答案】D【解析】【分析】由椭圆定义知=2a,即可得到结果.【详解】解:椭圆中,∵a5,P是椭圆上的点,是椭圆的两个焦点,∴由椭圆定义知=2a=10.故选:D.【点睛】本题考查椭圆的定义的应用,是基础题,解题时要熟练掌握椭圆的简单性质.2.已知=(2,-3,1),则下列向量中与平行的是()A。
(1,1,1) B。
(-4,6,-2) C. (2,-3,5) D。
(-2,-3,5)【答案】B【解析】【分析】利用向量共线定理即可得出.【详解】解:若(﹣4,6,﹣2),则2(2,﹣3,1)=﹣2,所以∥.故选:B.【点睛】本题考查空间向量共线的充要条件,熟练掌握向量共线定理是解题的关键.3.已知命题;命题若,则.下列命题为真命题的是()A。
B. C. D.【答案】B【解析】【分析】分别判断出p,q的真假,从而判断复合命题的真假即可【详解】由时成立知p是真命题,由可知q是假命题,所以是真命题,故选:B.【点睛】“”,“”“”等形式命题真假的判断步骤:(1)确定命题的构成形式;(2)判断其中命题的真假;(3)确定“”,“”“”等形式命题的真假。
4。
已知向量a=(1,1,0),b=(-1,0,2),且k a+b与2a-b互相垂直,则k的值是( )A. 1B. C。
D.【答案】D【解析】试题分析:由的坐标可得,,两向量互相垂直则,即,解得.考点:两向量垂直坐标满足的条件.5.若焦点在轴上的椭圆的离心率为,则()A. B. C. D。
【答案】B【解析】分析:根据题意,由椭圆的标准方程分析可得a,b的值,进而由椭圆离心率公式,解可得m的值,即可得答案.详解:根据题意,椭圆的焦点在x轴上,则,则,离心率为,则有,解得.故选:B.点睛:本题考查椭圆的几何性质,注意由椭圆的焦点位置,分析椭圆的方程的形式。
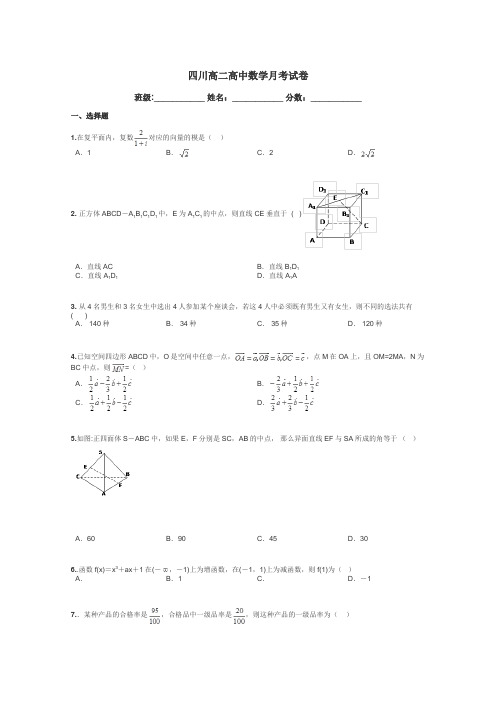
四川高二高中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.在复平面内,复数对应的向量的模是( )A .1B .C .2D .2. 正方体ABCD -A 1B 1C 1D 1中,E 为A 1C 1的中点,则直线CE 垂直于 ( )A .直线ACB .直线B 1D 1C .直线A 1D 1 D .直线A 1A3. 从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有( )A . 140种B . 34种C . 35种D . 120种4.已知空间四边形ABCD 中,O 是空间中任意一点,,点M 在OA 上,且OM=2MA ,N 为BC 中点,则=( )A .B .C .D .5.如图:正四面体S -ABC 中,如果E ,F 分别是SC ,AB 的中点, 那么异面直线EF 与SA 所成的角等于 ( )A .60°B .90°C .45°D .306..函数f(x)=x 3+ax +1在(-,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( ) A . B .1 C . D .-17..某种产品的合格率是,合格品中一级品率是,则这种产品的一级品率为( )A.B.C.D.8.已知函数f(x)=x2(ax+b)在x=2时有极值(其中a,b∈R),其图象在点(1,f(1))处的切线与直线3x+y=0平行,则函数f(x)的单调减区间为()A.(-∞,0)B.(0,2)C.(2,+∞)D.(-∞,+∞)9.某校高三年级举行一次演讲赛共有10位同学参赛,其中一班有3位,二班有2位,其它班有5位,若采用抽签的方式确定他们的演讲顺序,则一班3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学没有被排在一起的概率为()A.B.C.D.10.下列关于函数f(x)=(2x-x2)e x的判断①f(x)>0的解集是{x|0<x<2};②f(-)是极小值,f()是极大值;③f(x)没有最小值,也没有最大值.其中正确的是()A.①③B.①②③C.②D.①②11.正三棱柱的棱长都为2,为的中点,则与面GEF成角的正弦值是()A.B.C.D.12..已知f(x),g(x)都是定义在R上的函数,f(x)=a x×g(x),(a>0且a¹1), ,在有穷数列{}(n=1,2,¼,10)中,任取正整数k(1£k£10),则数列{}前k项和大于的概率是( )A.B.C.D.二、填空题1.设随机变量X等可能地取1,2,3,…,n,若,则=.2..若f(x)=x3+3ax2+3(a+2)x+1没有极值,则a的取值范围为 .3.,则= 。


四川省南充市阆中中学2018-2019学年高二数学3月月考试题 理(总分:150分 时间:120分钟)一、选择题(本大题共12个小题,每小题5分,共60分) 1.设是椭圆上的点.若是椭圆的两个焦点,则等于( )A .4B .5C .8D .102.已知a =(2,-3,1),则下列向量中与a 平行的是( )A .(1,1,1)B .(-4,6,-2)C .(2,-3,5)D .(-2,-3,5)3.已知命题;命题若,则.下列命题为真命题的是( ) A. B. C. D.4.已知向量a =(1,1,0),b =(-1,0,2),且k a +b 与2a -b 互相垂直,则k 的值是( ) A .1 B.15 C.35 D.755.若焦点在轴上的椭圆的离心率为,则( )A .B .C .D . 6.设p: , q: ,则p 是q 的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 7.双曲线的离心率为,则其渐近线方程为 A .B .C .D .8.以下命题为假命题的是( )A. “若m >0,则方程x 2+x -m =0有实数根”的逆命题B. “面积相等的三角形全等”的否命题C. “若xy =1,则x ,y 互为倒数”的逆命题D. “若A∪B=B ,则A ⊆B”的逆否命题9.. 一个动圆的圆心在抛物线上,且该动圆与直线l:x=-1相切,则这个动圆必过一个定点的坐标是A .B .C .D .10. 椭圆上一点与两焦点组成一个直角三角形,则点到轴的距离是( )A B C D 或11.已知抛物线的焦点为,是准线上的一点,是直线与的一个交点,若,则A. B. C. D.12. 已知椭圆上有一点,它关于原点的对称点为,点为椭圆的右焦点,且满足,设,且,则该椭圆的离心率的取值范围为()A.B.C.D.二、填空题:(本大题共4小题,每小题5分)13.已知a=(1,-2,1),a+b=(-1,2,-1),则b等于________.14.命题“若,则”的逆否命题是__________15.已知抛物线的准线经过椭圆的焦点,则.16.已知是双曲线的右焦点,是左支上一点,,当周长最小时,该三角形的面积为.三、解答题(本大题共6个小题,共70分)17.(本题满分10分)求符合下列条件的曲线的标准方程。

四川省南充市阆中中学2018-2019学年高二数学3月月考试题 理(总分:150分 时间:120分钟)一、选择题(本大题共12个小题,每小题5分,共60分)1.设p 是椭圆2211625x y +=上的点.若12F F ,是椭圆的两个焦点,则12PF PF +等于( )A .4B .5C .8D .102.已知a =(2,-3,1),则下列向量中与a 平行的是( )A .(1,1,1)B .(-4,6,-2)C .(2,-3,5)D .(-2,-3,5)3.已知命题2:,10p x R x x ∃∈-+≥;命题:q 若22a b <,则a b <.下列命题为真命题的是( )A. p q ∧B. p q ⌝∧C. p q ⌝∧D. p q ⌝⌝∧4.已知向量a =(1,1,0),b =(-1,0,2),且k a +b 与2a -b 互相垂直,则k 的值是( )A .1 B.15 C.35 D.755.若焦点在x 轴上的椭圆2212x y m +=的离心率为12,则m =( )A B .32C .83 D .236.设p: 0log 2≤x , q: 22≤x ,则p 是q 的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.双曲线2222:1(0,0)x y C a b a b-=>>A .y =B .y =C .2y x =±D .2y x =± 8.以下命题为假命题的是( )A. “若m >0,则方程x 2+x -m =0有实数根”的逆命题B. “面积相等的三角形全等”的否命题C. “若xy =1,则x ,y 互为倒数”的逆命题D. “若A ∪B =B ,则A ⊆B ”的逆否命题9.. 一个动圆的圆心在抛物线x y 42=上,且该动圆与直线l:x=-1相切,则这个动圆必过一个定点的坐标是A .(0,2)B .(2,0)C .(0,1)D .(1,0)10. 椭圆221259x y +=上一点P 与两焦点12,F F 组成一个直角三角形,则点P 到x 轴的距离是( )A165 B 94 C 95 D 95或9411.已知抛物线2:8C y x =的焦点为F ,P 是准线l 上的一点,Q 是直线PF 与C 的一个交点,若4FP FQ =,则||QF = A .72 B .52C .3D .2 12. 已知椭圆()222210x y a b a b +=>>上有一点A ,它关于原点的对称点为B ,点F 为椭圆的右焦点,且满足AF BF ⊥,设ABF α∠=,且ππ,126α⎡⎤∈⎢⎥⎣⎦,则该椭圆的离心率e 的取值范围为( )A .⎣⎦B .⎣⎦C .⎦D .⎦ 二、填空题:(本大题共4小题,每小题5分)13.已知a =(1,-2,1),a +b =(-1,2,-1),则b 等于________.14.命题“若,则”的逆否命题是__________15.已知抛物线24y x =-的准线经过椭圆2221(0)4x y b b+=>的焦点,则b = .16.已知2F 是双曲线22:18y C x -=的右焦点,P 是C 左支上一点,(0A ,当2APF ∆周长最小时,该三角形的面积为 .三、解答题(本大题共6个小题,共70分)17.(本题满分10分)求符合下列条件的曲线的标准方程。
四川省南充市阆中中学2018—2019学年高二数学6月月考试题 理(总分:150分 时间:120分钟)一、选择题(本大题共12个小题,每小题5分,共60分)1。
设集合,,则( ) A. B 。
C. D 。
2。
设,是虚数单位,则的虚部为( ) A 。
1B. -1C. 3D. -33。
曲线在点(1,1)处的切线方程为=( ) A .-4 B .—3 C .4D .34.将函数的图象上所有的点向右平移个单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得图象的解析式为( )A 。
B 。
C 。
D 。
5.在等差数列中,,是方程的两根,则数列的前11项和等于( ) A 。
66B 。
132 C. —66 D 。
-1326.从10名高三年级优秀学生中挑选3人担任校长助理,则甲、乙至少有1人入选,而丙没有入选的概说为( )A. B. C 。
D.7.某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条{}1,2,3A ={|10}B x x =->A B ⋂={}1,2{}2,3{}1,3{}1,2,33iz i+=iz 21y a x b x =+-,y x b a =-则sin 6y x π⎛⎫=- ⎪⎝⎭4π5s in 212y x π⎛⎫=- ⎪⎝⎭sin 212x y π⎛⎫=+ ⎪⎝⎭5sin 212x y π⎛⎫=- ⎪⎝⎭5sin 224x y π⎛⎫=- ⎪⎝⎭{}n a 3a 9a 224120x x ++={}n a 241715712049307虚线互相垂直且相等,则该几何体的体积是( )A 。
B 。
C 。
D. 328。
若,,,满足,,,则( )A 。
B 。
C.D.9。
宋元时期数学名着《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思 想的一个程序框图,若输入的,分别为5,2,则输出的( )A. 5B 。
2019-2020学年四川省阆中中学高二下学期第二次月考数学(理)试题一、单选题1.已知集合{},xA y y e x R ==∈,[]2,3B =-,则AB =( )A .()0,2B .(]0,3C .[]2,3-D .[]2,3【答案】B【解析】求得集合A ,利用交集的定义可求得集合A B .【详解】{}(),0,x A y y e x R ==∈=+∞,[]2,3B =-,因此,(]0,3A B =.故选:B. 【点睛】本题考查交集的计算,同时也考查了指数函数值域的求解,考查计算能力,属于基础题. 2.已知i 为虚数单位,复数52i -的共轭复数为( ) A .2i + B .2i -C .2i --D .2i -【答案】B【解析】利用复数的除法可将复数52i -表示为一般形式,利用共轭复数的定义可得出结果. 【详解】()()()5252222i i i i i ⨯--==----+--,因此,复数52i -的共轭复数为2i -+. 故选:B. 【点睛】本题考查共轭复数的计算,解答的关键就是利用复数的除法运算将复数表示为一般形式,考查计算能力,属于基础题.3.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:由表中数据,求得线性回归方程4y x a =-+,则a =( ) A .100 B .104C .106D .108【答案】C【解析】计算出x 和y 的值,再将样本的中心点(),x y 代入回归直线方程,可求得实数a 的值.【详解】由表格中的数据可得4567896.56x +++++==,908483807568806y +++++==,所以,回归直线过点()6.5,80,则有4 6.580a -⨯+=,解得106a =. 故选:C. 【点睛】本题考查利用回归直线过样本的中心点求参数,考查计算能力,属于基础题. 4.已知()~,X B n p ,且()2E X =,()43D X =,则n =( ) A .5 B .6C .7D .8【答案】B【解析】∵~(,)X B n p ,∴()2E X =,4()3D X =,∴2np =,且4(1)3np p -=,解得613n p =⎧⎪⎨=⎪⎩,∴6n =,故选B .5.已知α满足1cos 23πα⎛⎫+=- ⎪⎝⎭,则cos2=α( ) A .79B .712C .79-D .718-【答案】A【解析】由题意结合诱导公式可得1sin 3α=,再由余弦的二倍角公式即可得解. 【详解】由题意1cos sin 23ααπ⎛⎫+=-=- ⎪⎝⎭,所以1sin 3α=,所以2217cos 212sin 1239αα⎛⎫=-=-⨯= ⎪⎝⎭.故选:A. 【点睛】本题考查了三角函数诱导公式与三角恒等变换的应用,考查了运算求解能力,属于基础题.6.方程()22420x y x y ----=表示的曲线的大致形状是(图中实线部分)( )A .B .C .D .【答案】B【解析】依题意可知,方程表示的曲线为直线20x y --=或双曲线22144x y -=位于直线20x y --=的下方的图象,由此得解. 【详解】依题意可知,20x y --=或224020x y x y ⎧--=⎨--≥⎩,而2240x y --=表示双曲线22144x y -=,且满足在直线20x y --=的下方,结合选项可知,只有选项B 符合题意. 故选:B 【点睛】本题考查的是曲线与方程,考查了数形结合思想,解题的关键是要注意当2240x y --=时必须满足20x y --≥,属于基础题.7.设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为A .2a πB .273a πC .2113a π D .25a π【答案】B【解析】【详解】试题分析:根据题意条件可知三棱柱是棱长都为a 的正三棱柱,上下底面中心连线的中点就是球心, 如图:则其外接球的半径为222722sin 6012o a a R a ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭球的表面积为22774123a S a ππ=⨯=球;故选B .8.对于R 上可导的任意函数()f x ,若满足10'()xf x -≤,则必有( ) A .(0)(2)2(1)f f f +> B .(0)(2)2(1)f f f +≤ C .(0)(2)2(1)f f f +< D .(0)(2)2(1)f f f +≥【答案】A【解析】试题分析:由题意1x <时,'()0f x <,()f x 递减,1x >时,'()0f x >,()f x 递增,因此(0)(1)f f >,(2)(1)f f >,所以(0)(2)2(1)f f f +>.故选A . 【考点】导数与函数的单调性.9.已知椭圆2222:1(0)x y C a b a b+=>>的左焦点为F ,直线3y x =与椭圆C 相交于A ,B 两点,且AF BF ⊥,则椭圆C 的离心率为( )A .212- B .21-C .312- D .31-【答案】D【解析】可解得点A 、B 坐标,由AF BF ⊥,得0AF BF =,把222b a c =-代入该式整理后两边同除以4a ,得e 的方程,解出即可,注意e 的取值范围 【详解】解:由222213x y a b y x⎧+=⎪⎨⎪=⎩,消y 可得得22222(3)a b x a b +=,解得223x a b =±+,分别代入2233ab y a b =±+,22(3A a b ∴+,223)3ab a b +,22(3B a b -+,223)3ab a b -+,∴22(3AF c a b=++,223)3ab a b+,22(3BF c a b=-+,223)3ab a b-+,AF BF ⊥∴2222222223033a b a b AF BF c a b a b=--=++,2222243a b c a b∴=+,(*) 把222b a c =-代入(*)式并整理得22422244()a c c a a c -=-, 两边同除以4a 并整理得42840e e -+=,解得2423e =- 31e ∴=-,故选:D . 【点睛】本题考查椭圆的简单性质、直线与椭圆的位置关系,考查学生的运算能力,属中档题. 10.已知实数a ,b ,c ,d 成等比数列,且对函数y=ln (x+2)﹣x ,当x=b 时取到极大值c ,则ad 等于( ) A .-1 B .0C .1D .2【答案】A【解析】本题考查函数的极值、等比数列相关知识. 对已知函数求导,,令,注意到,解得,故,,从而113P ABC -的顶点都在球O 的球面上,PA ⊥平面ABC ,2PA =,120ABC ∠=︒,则球O 的体积的最小值为( )A .73B .73C .19193D .76193【答案】B【解析】根据余弦定理计算b 的最小值,从而得出外接圆半径的最小值,进而求得外接球半径的最小值,最后得出结论. 【详解】设,,AB c BC a AC b ===1=33P ABC ABCV SPA -=⋅,2PA =331sin12022ABCSac ∴==︒ 6ac ∴=,由余弦定理可得:222222cos1202318b a c ac a c ac ac ac ac =+-︒=++≥+== ,当且仅当a c =时,等号成立, 此时min 32b =,设ABC 外接圆的半径为r ,则=2sin120br ︒,min 3263r ∴== 如图,设1O 为ABC 外接圆的圆心,D 为PA 的中点,R 为球的半径, 连接11,,,,O A O O OA OD PO , 易知112PAOO ==,2222117R r OO r =+=+≥, ∴球的体积342873O V R π=≥.故选:B.【点睛】本题考查了棱锥与球的位置关系,正余弦定理解三角形,球的体积,考查了空间想象能力和计算能力. 12.若函数()()()()()1cos sin cos sin 3sin cos 412f x x x x x a x x a x =-++-+-在,02π⎡⎤-⎢⎥⎣⎦上单调递增,则实数a 的取值范围为( ) A .1,17⎡⎤⎢⎥⎣⎦B .11,7⎡⎤-⎢⎥⎣⎦C .[)1,1,7⎛⎤-∞-+∞ ⎥⎝⎦D .[)1,+∞ 【答案】D【解析】化简函数的解析式,求出函数的导数,通过函数的单调性,转化为不等式恒成立,构造函数列出不等式组求解即可. 【详解】 解:函数1()(cos sin )(cos sin )3(sin cos )(41)2f x x x x x a x x a x =-++-+- 1cos 23(sin cos )(41)2x a x x a x =+-+- 2()sin 23(cos sin )41(cos sin )3(cos sin )40f x x a x x a x x a x x a ∴=-+++-=-++++',对[,0]2x π∈-恒成立.cos sin 2)4x x x π+=+,∴当[,0]2x π∈-时,1cos sin 1x -+.令2()34(11)g t t at a t =-++-,欲使()0g t 恒成立,只需(1)0(1)0g g -⎧⎨⎩,即2(1)3(1)4011340a a a a a ⎧--+⨯-+⇒⎨-++⎩. 故选:D . 【点睛】本题考查函数的导数判断函数的单调性的应用,函数恒成立条件的应用,考查转化思想以及计算能力.二、填空题13.在6(1)x x +的展开式中,含3x 项的系数是________. 【答案】15【解析】求出6(1)x +的2x 项的系数即可. 【详解】6(1)x x +的展开式中,含3x 项的系数即为6(1)x +的2x 项的系数,也即2615C =.故答案为:15. 【点睛】本题主要考查利用二项展开式的通项公式求指定项的系数,属基础题.14.已知两个单位向量1e 、2e 的夹角为60,向量1232m e e =-,则|m =_____.【解析】利用平面向量数量积的运算律和定义计算出2m 的值,进而可求得m 的值.【详解】根据题意,两个单位向量1e 、2e 的夹角为60,则121211cos601122e e e e ⋅=⋅=⨯⨯=, 1232m e e =-,则()222221211221329124131272m m e e e e e e ==-=-⋅+=-⨯=,因此,7m =.. 【点睛】本题考查向量数量积的计算,涉及向量模的计算,属于基础题.15.已知:p 函数()4xy a =-在R 上单调递减,:12q m a m +≤≤,若p 是q 的必要不充分条件, 则实数m 的取值范围为__________. 【答案】(),1-∞ 【解析】【详解】当p 为真时,4a 5<<.记集合A {}|4a 5a =<<,{}B |12a m a m =+≤≤.若p 是q 的必要不充分条件, 则B A?≠⊂ ①当12m m +>,即1m <时,B A φ≠=⊂; ②当1m ≥时,B A?≠⊂等价于11425m m m ≥⎧⎪+>⎨⎪<⎩,解得m ∅∈. 综上所述,实数m 的取值范围为(),1-∞ 故答案为(),1-∞ 16.已知函数()ln x axf x x-=,若有且仅有一个整数k ,使()()20f k f k ⎡⎤->⎣⎦,则实数a 的取值范围是__________.【答案】11ln 21ln 3123a -≤<- 【解析】因ln ()xf x a x=-,故由题设问题转化为“有且仅有一个整数k 使得()1f k >或()0f k <”。
阆中中学校2019年秋高2018级期中教学质量检测数学试题(理科)一、单选题(每小题5分,共60分)1.过点(1,2)-,且斜率为2的直线方程是( )A. 240x y -+=B. 20x y +=C. 250x y -+=D. 230x y +-= 【答案】A 【详解】因直线过点(1,2)-,且斜率为2,所以该直线方程为22(1)y x -=+,即240x y -+=.故选A2.已知圆()221x a y -+=与圆()221x y b +-=外切,则( ). A. 224a b += B. 222a b += C. 221a b += D. 228a b += 【答案】A【详解】因为两圆相外切,故圆心距为半径之和, ()()220011a b -+-=+即224a b +=,故选A.3.已知圆22:240C x y x y +-+=,则通过原点且与圆C 相切的直线方程为( ). A. 2y x =- B. 12y x =- C. 12y x = D. 2y x =【答案】C【详解】因为22:240C x y x y +-+=,故()1,2C -,所以2OC k =-,所以切线的斜率为12,故切线方程为12y x =,选C.4.已知直线10ax by ++=与直线4350x y ++=平行,且10ax by ++=在y 轴上的截距为13,则+a b 的值为( ) A. 7- B. 1-C. 1D. 7【答案】A详解:因为直线10ax by ++=与直线4350x y ++=平行, 所以43b a =,又直线10ax by ++=在y 轴上的截距为13, 所以1103b +=,解得3b =-,所以4a =-,所以7a b +=-,故选A.5.已知实数,x y 满足2050370x y x y x y -≤⎧⎪+-≤⎨⎪+-≥⎩,则z x y =-+的最大值是( )A. 53-B. 1-C. 3D. 5【答案】C【详解】由题意,作出线性约束条件表示的可行域,如图所示, 表示三角形ABC 阴影部分区域(含边界),设直线0:l y x =,平移直线0l 时,目标函数取得最大值,又由50370x y x y +-=⎧⎨+-=⎩,解得()1,4A ,此时目标函数z x y =-+的最大值为max 143z =-+=. 故选C.6.点(,2,1)P x 到点(1,1,2),(2,1,1)Q R 的距离相等,则x 的值为( ) A.12B. 1C.32D. 2【答案】B 【解析】试题分析:根据题意,结合空间中两点的距离公式可知,点(,2,1)P x 到点(1,1,2),(2,1,1)Q R 的距离相等,则有22(1)11(2)101PQ PR x x x =⇔-++=-++⇔=则可知x 的值为1,选B.7.如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a ,b 分别为2,8,则输出的a 等于()A. 4B. 0C. 2D. 14 【答案】C【详解】由题a=2,b=8:a b ¹且a b <,则b=8-2=6;此时a=2,b=6: a b ¹且a b <,则b=6-2=4;此时a=2,b=4:a b ¹且a b <,则b=4-2=2;此时a=2,b=2:a=b ,输出a=2,故选C.8.在圆22x y 2x 6y 0+--=内,过点()E 0,1的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为()A. 52B. 102C. 152D. 202【答案】B详解:圆22260x y x y +--=变形为22(1)(3)10x y -+-=。
2019-2020学年四川省阆中中学高二4月月考数学(理)试题一、单选题1.抛物线28y x =-的焦点坐标是() A .()0,2- B .()2,0-C .10,32⎛⎫- ⎪⎝⎭D .1,032⎛⎫-⎪⎝⎭【答案】C【解析】先将抛物线方程化为标准方程,进而可得出焦点坐标. 【详解】因为28y x =-可化为218=-x y , 所以128=-p ,且焦点在y 轴负半轴, 因此焦点坐标为10,32⎛⎫- ⎪⎝⎭故选C 【点睛】本题主要考查由抛物线的方程求焦点问题,熟记抛物线的标准方程即可,属于基础题型.2.已知方程22112x y m m -=+-表示双曲线,则m 的取值范围是( )A .1m >-B .2m >C .1m <-或2m >D .12m -<<【答案】C【解析】双曲线的焦点可能在x 轴,也可能在y 轴上,分别写出两种情况下的双曲线的标准方程,22112x y m m -=+-或22121y x m m -=---,可得10,20,m m +>⎧⎨->⎩或20,10,m m ->⎧⎨-->⎩,解不等式可得答案. 【详解】当双曲线的焦点在x 轴上,双曲线方程22112x y m m -=+-,则10,20,m m +>⎧⎨->⎩解得:2m >; 当双曲线的焦点在y 轴上,双曲线方程22112x y m m -=+-22121y x m m ⇔-=---,所以20,10,m m ->⎧⎨-->⎩解得:1m <-;故选:C. 【点睛】本题考查双曲线标准方程,求解的关键在于双曲线方程标准形式的认识.3.若双曲线22221x y a b-=的离心率2e =,则其渐近线方程为( )A .2y x =±B .2y x =±C .y =D .2y x =±【答案】C【解析】通过双曲线的离心率,推出a 、b 关系,然后直接求出双曲线的渐近线方程. 【详解】解:由双曲线的离心率2e =,可知2c a =,又222+=a b c ,所以b =,所以双曲线22221x y a b-=的渐近线方程为:b y x a =±=.故选:C . 【点睛】本题考查双曲线的基本性质,渐近线方程的求法,考查计算能力,属于基础题.410=的化简结果为( )A .2212516x y += B .2212516y x +=C .221259x y +=D .221259y x +=【答案】D【解析】根据题意得到给出的曲线方程的几何意义,是动点(),x y 到两定点的距离之和等于定值,符合椭圆定义,然后计算出相应的,,a b c 得到结果. 【详解】10=,所以其几何意义是动点(),x y 到点()0,4-和点()0,4的距离之和等于10,符合椭圆的定义. 点()0,4-和点()0,4是椭圆的两个焦点.因此可得椭圆标准方程()222210y x a b a b+=>>,其中210a =,所以5a =4c =,所以3b ==所以曲线方程的化简结果为221259y x +=.故选D 项. 【点睛】本题考查曲线方程的几何意义,椭圆的定义,求椭圆标准方程,属于简单题.5.若双曲线22221x y a b-=的离心率为43,且过点(,则该双曲线的实轴长为( )A .4B .C .D .6【答案】D【解析】利用双曲线的离心率与双曲线经过的点,列出方程求出a ,即可得到结果. 【详解】解:双曲线22221x y a b-=的离心率为43,且过点(,可得43c a =,221871a b-=,222c a b =+,解得3a =,所以26a =. 故选:D . 【点睛】本题考查双曲线的简单性质的应用,属于基础题.6.(2016新课标全国Ⅱ理科)已知F 1,F 2是双曲线E :22221x y a b-=的左,右焦点,点M 在E 上,M F 1与x 轴垂直,sin 2113MF F ∠= ,则E 的离心率为A B .32C D .2【答案】A【解析】试题分析:由已知可得,故选A.【考点】1、双曲线及其方程;2、双曲线的离心率.【方法点晴】本题考查双曲线及其方程、双曲线的离心率.,涉及方程思想、数形结合思想和转化化归思想,考查逻辑思维能力、等价转化能力、运算求解能力,综合性较强,属于较难题型. 由已知可得,利用双曲线的定义和双曲线的通径公式,可以降低计算量,提高解题速度.7.已知向量(,3,4),(6,,12)a x b y ==r r,且//a b r r,则x y +的值为( ) A .11 B .6C .7D .15【答案】A【解析】利用向量共线定理即可求出. 【详解】Q 向量(,3,4),(6,,12)a x b y ==r r ,且//a b r r ,∴存在实数λ使得b a λ=r r,63124x y λλλ=⎧⎪∴=⎨⎪=⎩, 解得29x y =⎧⎨=⎩,11x y ∴+=.故选:A . 【点睛】本题追要考查是向量共线定理的应用,考查了计算能力,及空间向量的应用,是基础题. 8.在平行六面体1111ABCD A B C D -中,M 为11A C 与11B D 的交点,若,AB a AD b ==u u u r r u u u r r ,1AA c =u u u r r ,则与BM u u u u r相等的向量是( )A .1122a b c ++r r rB .1122a b c --+r r rC .1122a b c -+r r rD .1122-++r r ra b c 【答案】D【解析】根据空间向量的线性运算,用,,a b c r r r 作基底表示BM u u u u r即可得解.【详解】根据空间向量的线性运算可知11BM BB B M =+u u u u r u u u r u u u u r11112AA B D =+u u u r u u u u r()1111112AA B A A D =++u u u r u u u u r u u u u r()112AA AB AD =+-+u u u r u u u r u u u r因为,AB a AD b ==u u u r r u u u r r ,1AA c =u u ur r ,则()112AA AB AD +-+u u u r u u u r u u u r1122a b c =-++r r r即1122BM a b c =-++u u u u r r r r ,故选:D. 【点睛】本题考查了空间向量的线性运算,用基底表示向量,属于基础题.9.已知ABCD 为平行四边形,且(413)(251)(375)A B C --,,,,,,,,,则顶点D 的坐标( )A .7412⎛⎫- ⎪⎝⎭,, B .(241),, C .(2141)-,, D .(5133)-,, 【答案】D【解析】设出D 的坐标,利用AB DC =u u u r u u u r列方程,由此求得D 的坐标. 【详解】设(),,D a b c ,由于四边形ABCD 是平行四边形,所以AB DC =u u u r u u u r,即()()2,6,23,7,5a b c ---=----,即236725ab c -=-⎧⎪-=-⎨⎪-=--⎩,解得5,13,3a b c ===-,即()5,13,3D -,故选D.【点睛】本小题主要考查空间向量的坐标运算,考查空间向量相等的条件,属于基础题.10.O 为空间任意一点,,,A B C 三点不共线,若OP uuu v =111326OA OB OC ++u u uv u u u v u u u v ,则,,,A B C P 四点A .一定不共面B .不一定共面C .一定共面D .无法判断【答案】C【解析】点P 在平面ABC 内,O 是平面ABC 外的任意一点,则OP xOA yOB zOC =++u u u v u u u v u u u v u u u v且1x y z ++=.利用此推论可直接证明一定共面.【详解】因为OP uuu v =111326OA OB OC ++u u u v u u u v u u u v ,且1111326++=,所以,,,A B C P 四点共面.【点睛】四点共面问题,在空间向量中经常涉及,要熟练掌握共面向量定理.11.O 为坐标原点,F 为抛物线2:4C y x =的焦点,P 为C 上一点,若4PF =,则POF V 的面积为A. BC .2D .3【答案】B【解析】由抛物线的标准方程24y x =可得抛物线的焦点坐标和准线方程,设出(,)P x y ,由PF =4以及抛物线的定义列式可得(1)4x --=,即3x =,再代入抛物线方程可得点P 的纵坐标,再由三角形的面积公式1||2S y OF =可得. 【详解】由24y x =可得抛物线的焦点F (1,0),准线方程为1x =-,如图:过点P 作准线1x =- 的垂线,垂足为M ,根据抛物线的定义可知PM =PF =4,设(,)P x y ,则(1)4x --=,解得3x =,将3x = 代入24y x =可得23y =±, 所以△POF 的面积为1||2y OF ⋅=123132⨯⨯=. 故选B .【点睛】本题考查了抛物线的几何性质,定义以及三角形的面积公式,关键是①利用抛物线的定义求P 点的坐标;②利用OF 为三角形的底,点P 的纵坐标的绝对值为高计算三角形的面积.属中档题.12.如图,正方体ABCD -A 1B 1C 1D 1的棱长为2,E 是棱AB 的中点,F 是侧面AA 1D 1D 内一点,若EF ∥平面BB 1D 1D ,则EF 长度的范围为()A .2,3]B .[2,5]C .2,6]D .2,7]【答案】C【解析】过F 作1//FG DD ,交AD 于点G ,交11A D 于H ,根据线面垂直关系和勾股定理可知222EF AE AF =+;由,//EF FG 平面11BDD B 可证得面面平行关系,利用面面平行性质可证得G 为AD 中点,从而得到AF 最小值为,F G 重合,最大值为,F H 重合,计算可得结果. 【详解】过F 作1//FG DD ,交AD 于点G ,交11A D 于H ,则FG ⊥底面ABCD2222222221EF EG FG AE AG FG AE AF AF ∴=+=++=+=+//EF Q 平面11BDD B ,//FG 平面11BDD B ,EF FG F ⋂=∴平面//EFG 平面11BDD B ,又GE Ì平面EFG //GE ∴平面11BDD B又平面ABCD I 平面11BDD B BD =,GE Ì平面ABCD //GE BD ∴E Q 为AB 中点 G ∴为AD 中点,则H 为11A D 中点即F 在线段GH 上min 1AF AG ∴==,max 145AF AH ==+=min 112EF ∴=+max 156EF +=则线段EF 长度的取值范围为:2,6⎡⎣本题正确选项:C 【点睛】本题考查立体几何中线段长度取值范围的求解,关键是能够确定动点的具体位置,从而找到临界状态;本题涉及到立体几何中线面平行的性质、面面平行的判定与性质等定理的应用.二、填空题13.已知抛物线22(0)y px p =>的过焦点的弦为AB ,且9AB =, 6A B x x +=,则p =_____________.【答案】3【解析】由题意知|AB |=A B x x ++p ,即p =|AB |−(A B x x +)=9−6=3. 故答案为3.14.设正方体1111ABCD A B C D -的棱长为2,则点1D 到平面1A BD 的距离是_______.【答案】233【解析】如图建立空间直角坐标系,利用向量法求点1D 到平面1A BD 的距离. 【详解】如图建立空间直角坐标系,则1(0,0,2)D ,1(2,0,2)A ,(0,0,0)D ,2,20B (,),∴11(2,0,0)=u u u u r D A ,1(2,0,2)DA =u u u u r ,(2,2,0)DB u u u r=, 设平面1A BD 的一个法向量为(,,)n x y z =r,1220220n DA x z n DB x y ⎧⋅=+=⎨⋅=+=⎩u u uu v r u u u v r,令1x =,则(1,1,1)n =--r, ∴点1D 到平面1A BD 的距离11||23||3D A n d n ⋅===u u u u r rr . 23. 【点睛】本题主要考查点到平面的距离的求法,意在考查学生对这些知识的理解掌握水平.15.已知()3,2,3a =--v,()1,1,1b x =--v ,且a v 与b v 的夹角为钝角,则x 的取值范围是__________.【答案】552,,33⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭U【解析】由题意可知0a b ⋅<r r 且a r 与b r不共线,由此可得出实数x 的取值范围.【详解】由题意可知0a b ⋅<r r 且a r 与b r不共线,则()()312131240a b x x ⋅=⨯--⨯--⨯=--<r r,解得2x >-.若a r 与b r 共线,则111323x --==--,得53x =,a r Q 与b r 不共线,则53x ≠,因此,实数x 取值范围是552,,33⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭U .故答案为:552,,33⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭U . 【点睛】本题考查利用空间向量的夹角为钝角求参数的取值范围,一般转化为两向量数量积为负,且两向量不共线,结合空间向量的坐标运算得出不等式组求解,考查运算求解能力,属于中等题.16.设E ,F 分别是正方体ABCD ﹣A 1B 1C 1D 1的棱DC 上两点,且AB =2,EF =1,给出下列四个命题:①三棱锥D 1﹣B 1EF 的体积为定值; ②异面直线D 1B 1与EF 所成的角为45°; ③D 1B 1⊥平面B 1EF ;④直线D 1B 1与平面B 1EF 所成的角为60°. 其中正确的命题为_____. 【答案】①②【解析】①根据题意画出图形,结合图形求出三棱锥D 1﹣B 1EF 的体积为定值; ②求得异面直线D 1B 1与EF 所成的角为45°; ③判断D 1B 1与平面B 1EF 不垂直;④直线D 1B 1与平面B 1EF 所成的角不一定是为60°. 【详解】由题意,如图所示,三棱锥D 1﹣B 1EF 的体积为11111122213323D EF V S B C ∆=⋅=⨯⨯⨯⨯=为定值,①正确;EF ∥D 1C 1,∠B 1D 1C 1是异面直线D 1B 1与EF 所成的角,为45°,②正确; D 1B 1与EF 不垂直,由此知D 1B 1与平面B 1EF 不垂直,③错误;直线D 1B 1与平面B 1EF 所成的角不一定是为60°,④错误. 综上,正确的命题序号是①②. 故答案为:①②.【点睛】本题主要考查了空间中的直线与平面之间的位置关系应用问题,其中解答中熟记线面位置关系的判定与性质定理,以及几何体的体积的计算公式是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.三、解答题17.已知空间三点()()()2,0,2,1,1,2,3,0,4A B C ---,设,a AB b AC ==r u u u r r u u u r.(1)求a r 和b r的夹角θ的余弦值;(2)若向量()(),2k ka b a b -+r r r r互相垂直,求k 的值.【答案】(1)10;(2)52k =-或2【解析】(1)结合空间向量夹角的余弦公式求解即可;(2)分别结合向量的坐标公式表示出()(),2k ka b a b -+r r r r ,由()()20ka b a b k +-=⋅r r r r即可求解 【详解】(1)由题可知()()1,1,0,1,0,2a AB b AC ====-r u u u r r u u u r,则10cos 25a b a b θ⋅-===⋅⋅r r r r(2)由()()()()220ka b a b k b b k a ka +⊥+-⇔-⋅=r r r r r r r r,()()()1,1,01,0,21,,2ka b k k k +=+-=-r r, ()()()1,1,021,0,222,,4a b k k k k =--=+--r r则()()()()221280ka b a k k b k k -=+⋅-⋅++-=r r r r ,即()()2520k k +⋅-=,解得125,22k k =-= 【点睛】本题考查空间向量的夹角求法,由两向量垂直求参数,属于基础题18.如图,在正方体1111ABCD A B C D -中,点E 为AB 的中点,F 为1D C 的中点.(1)证明://EF 平面11ADD A ;(2)若2AE =,求二面角D EF C --的余弦值. 【答案】(1)证明见解析(2)19【解析】(1)以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,()4,0,2EF =-u u u r ,平面11ADD A 的法向量()10,1,0n u r =,10EF n ⋅=u u u r u r,得到证明.(2)计算平面DEF 的法向量()1,2,2n =-r ,平面CEF 的法向量()1,2,2m =u r,计算夹角得到答案. 【详解】(1)以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系, 设4AB =,则()4,2,0E ,()0,2,2F ,()4,0,2EF =-u u u r ,平面11ADD A 的法向量()10,1,0n u r=,∵10EF n ⋅=u u u r u r,EF ⊄平面11ADD A ,∴//EF 平面11ADD A .(2)2AE =,()0,0,0D ,()4,2,0E ,()0,2,2F ,()0,4,0C ,()4,2,0DE =u u u r ,()0,2,2DF =u u u r ,()4,2,0CE =-u u u r ,()0,2,2CF =-u u u r, 设平面DEF 的法向量(),,n x y z =r,则420220n DE x y n DF y z ⎧⋅=+=⎨⋅=+=⎩u u u v v u u u v v ,取1x =,得()1,2,2n =-r , 设平面CEF 的法向量(),,m a b c =u r,则420220m CE a b m CF b c ⎧⋅=-=⎨⋅=-+=⎩u u u v v u u u v v ,取得1a =,得()1,2,2m =u r , 设二面角D EF C --的平面角为θ,则二面角D EF C --的余弦值为11cos 339m n m n θ⋅===⨯⋅u r rur r . 、【点睛】本题考查了线面平行,二面角,意在考查学生的计算能力和空间想象能力. 19.在如图所示的四棱锥P ABCD -中,已知PA ⊥平面ABCD ,//ABDC ,90DAB ︒∠=,1PA AD DC ===,2AB =,M 为PB 的中点.(1)求异面直线PB 与AC 所成角的余弦值; (2)求直线MC 与平面PAC 所成角的余弦值; 【答案】(1)105;(2)155【解析】(1)利用向量的几何运算计算()=2PB AC PA AB AC PA AC AB AC ⋅=+⋅=⋅+⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r,利用公式cos ,PB P PB AC PB ACC ⋅=⋅u u u r u u u r u u u u u u r r u u u ru u u r 可求异面直线PB 与AC 所成角的余弦值;(2)取PC 中点N ,则可得MCN ∠为直线MC 与平面PAC 所成角,从而可求直线MC 与平面PAC 所成角的余弦值.【详解】解:(1)由图可知()PB AC PA AB AC PA AC AB AC ⋅=+⋅=⋅+⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r,PA ⊥Q 平面ABCD ,又AC ⊂平面ABCD ,PA AC ∴⊥,即0PA AC ⋅=u u u r u u u r, 又()212AB AC AB AD DC AB AD AB DC ⋅=⋅+=⋅+⋅=⨯=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r,2PB AC ∴⋅=u u u r u u u r,222210cos ,51211P PB PC B AC PB AC ∴===⨯+⋅⋅+u u u r u u u r u u u r u u u u u u r u r u ur ,所以异面直线PB 与AC 所成角的余弦值为105; (2)取PC 中点N ,则//BC MN ,22222AC BC AB +=+=Q ,AC BC ∴⊥,又PA ⊥Q 平面ABCD ,又BC ⊂平面ABCD ,PA BC ∴⊥,BC ∴⊥平面PAC ,则MN ⊥平面PAC ,所以MCN ∠为直线MC 与平面PAC 所成角,2112+1==2222131+5222NC PC MC PB ====Q15cos NC MCN MC ∴∠==.【点睛】本题考查异面直线所成的角以及线面角的求解,难度不大.20.已知直线():400l x y m m -+=>与抛物线()2:20C y px p =>交于A ,B 两点,已知弦AB 的中点的纵坐标为2. (1)求p ;(2)直线():4l y m x '=-与抛物线C 交于M ,N 两点,求MN 的取值范围. 【答案】(1)8p =(2)()32,+∞ 【解析】(1)联立l 与C 的方程,得出122y y +即可 (2)联立l '与C 的方程得出M ,N 两点的横坐标之和,然后用m 表示出MN ,运用函数的知识求出范围即可 【详解】解:(1)设()11,A x y ,()22,B x y , 联立l 与C 的方程得220y py pm -+=, 则12224y y p+==, 即8p =.(2)直线l '经过C 的焦点(4,0),设()33,M x y ,()11,N x y ,则31MN x x p =++.联立()2416y m x y x⎧=-⎨=⎩,得()2222816160m x m x m -++=,则342168x x m+=+. 因为()2864640p pm m --=->,且0m >,所以01m <<. 所以342161632MN x x p m =++=+>. 从而MN 的取值范围为()32,+∞. 【点睛】要注意31MN x x p =++,比用弦长公式求MN 计算量要小些.21.已知椭圆()2222:10x y C a b a b +=>>的离心率为2,1F ,2F分别是椭圆的左、右焦点,直线l 过点2F 与椭圆交于A 、B 两点,且1F AB V的周长为 (1)求椭圆C 的标准方程;(2)是否存在直线l 使1F AB V 的面积为43?若存在,求出直线l 的方程;若不存在,请说明理由.【答案】(1)2212x y += (2)存在,直线l 的方程为1y x =-或1y x =-+.【解析】(1)根据离心率公式、椭圆定义,结合椭圆性质,解方程组即可求出椭圆方程; (2)分两种情况讨论,当斜率不存在时,其面积为1F AB S =△存在时,可设出直线方程,代入椭圆方程可得()2222120k y ky k ++-=,结合韦达定理代入三角形面积公式()1121212121122F AB S F F y y F F y y =⨯⨯+=⨯⨯-△,即可得解. 【详解】解:(1)由题意得2224,c e a a a b c ⎧==⎪⎪⎪=⎨⎪-=⎪⎪⎩∴1,1,a b c ⎧=⎪=⎨⎪=⎩ 故椭圆C 的标准方程为2212x y +=.(2)存在直线l 满足题意,由(1)知右焦点()21,0F ,当直线l的斜率不存在时,此时1,2A ⎛⎫ ⎪ ⎪⎝⎭,1,2B ⎛- ⎝⎭,AB =11211222F AB S F F AB =⨯⨯=⨯=△,不符合题意,故设直线的方程为()1y k x =-,设()11,A x y ,()22,B x y ,联立方程组()221,1,2y k x x y ⎧=-⎪⎨+=⎪⎩消去x 得()2222120k y ky k ++-=. ∵>0∆,∴122212k y y k -+=+,212212k y y k-=+,∴()() ()222221212122222422244121212k kk ky y y y y yk k k+--⎛⎫-=+-=-⋅=⎪++⎝⎭+,∴()11212121212111422223F ABS F F y y F F y y y y=⨯⨯+=⨯⨯-=⨯⨯-=△,∴()()222242216912k kk+=+,∴4220k k+-=,∴21k=或2-(舍去),∴1k=±,故直线l的方程为1y x=-或1y x=-+.【点睛】本题考查了利用椭圆定义、性质、离心率求椭圆方程,主要考查韦达定理在直线和圆锥曲线中的应用,考查了转化思想和较高的计算能力,属于较难题.22.如图,在长方体1111ABCD A B C D-中,11AD AA==,2AB=,点E在棱AB上移动.(1)证明:11D E A D⊥;(2)AE等于何值时,二面角1D EC D--的大小为4π.【答案】(1)见解析(2)23【解析】试题分析:第一问利用长方体的特殊性,建立相应的坐标系,应用向量的数量积等于零来得出向量垂直,从而得证两直线垂直,第二问县设出AE的长,从而利用空间向量求得二面角的大小,从而得出关于AE长度所满足的等量关系式,从而求得结果.试题解析:(1)在如图所示的空间直角坐标系中,11(1,0,1),(0,0,0),(0,0,1)A D D,设(1,,0)([0,2])E y y∈则11(1,,1),(1,0,1)D E y DA=-=u u u u r u u u u r,所以11D E DA⋅=u u u u r u u u u r,所以11D E A D⊥;(2)设(,,)n u v w=r为平面1D CE的一个法向量,由110{0n CD n D E ⋅=⋅=u u u u r r u u u u r r ,得20{0v w u yv w -+=+-=,所以(2){2u y vw v =-= 因为二面角1D EC D --的大小为4π,所以cos4π=== 又[0,2]y ∈,所以2y =即当2AE =1D EC D --的大小为4π. 【考点】线线垂直,二面角.。