人口规模预测方法

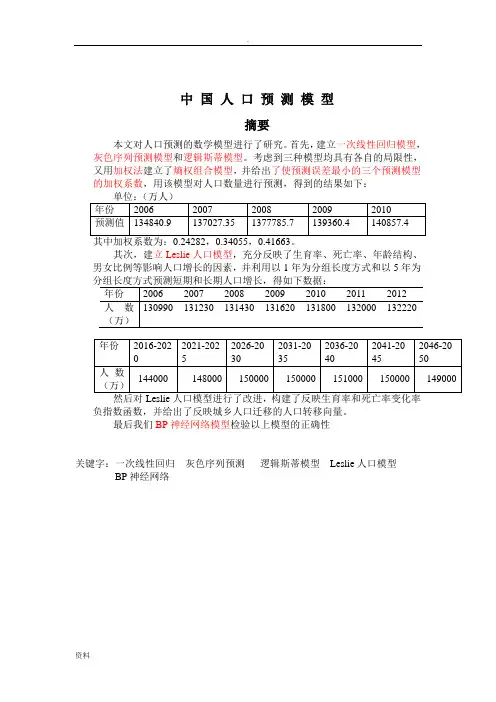
中 国 人 口 预 测 模 型摘要本文对人口预测的数学模型进行了研究。

首先，建立一次线性回归模型，灰色序列预测模型和逻辑斯蒂模型。

考虑到三种模型均具有各自的局限性，又用加权法建立了熵权组合模型，并给出了使预测误差最小的三个预测模型的加权系数，用该模型对人口数量进行预测，得到的结果如下：其次，建立Leslie 人口模型，充分反映了生育率、死亡率、年龄结构、男女比例等影响人口增长的因素，并利用以1年为分组长度方式和以5年为负指数函数，并给出了反映城乡人口迁移的人口转移向量。

最后我们BP 神经网络模型检验以上模型的正确性关键字：一次线性回归 灰色序列预测 逻辑斯蒂模型 Leslie 人口模型BP 神经网络一、问题重述1. 背景人口增长预测是随着社会经济发展而提出来的。

由于人类社会生产力水平低，生产发展缓慢，人口变动和增长也不明显，生产自给自足或进行简单的以货易货，因而对未来人口发展变化的研究并不重要，根本不用进行人口增长预测。

而当今社会，经济发展迅速，生产力达到空前水平，这时的生产不仅为了满足个人需求，还要面向社会的需求，所以必须了解供求关系的未来趋势。

而人口增长预测是对未来进行预测的各环节中的一个重要方面。

准确地预测未来人口的发展趋势，制定合理的人口规划和人口布局方案具有重大的理论意义和实用意义。

2. 问题人口增长预测有短期、中期、长期预测之分，而各个国家和地区要根据实际情况进行短期、中期、长期的人口预测。

例如，中国人口预期寿命约为70岁左右，因此，长期人口预测最好预测到70年以后，中期40—50年，短期可以是5年、10年或20年。

根据2007年初发布的《国家人口发展战略研究报告》（附录一）及《中国人口年鉴》收集的数据（附录二），再结合中国的国情特点，如老龄化进程加速，人口性别比升高，乡村人口城镇化等因素，建立合理的关于中国人口增长的数学模型，并利用此模型对中国人口增长的中短期和长期趋势做出预测，同时指出此模型的合理性和局限性。

【园区百问】第97问：如何确定园区的人口规模和居住用地规模?问题提出编制园区规划方案，人口规模预测和产业规模预测同等重要。

然而，园区的人口规模预测涉及多方面因素，如何预测园区的人口规模，又如何确定园区的居住用地规模？这是让规划人员颇为头痛的问题。

解决方案园区的人口规模和居住用地规模是两个相互作用、相互影响的指标。

人口规模需要居住用地规模支撑，居住用地规模反过来会影响人口规模。

在规划研究实践中，通常的做法是根据园区的产业定位及发展战略需要先预测人口规模，再以人口规模为重要的指标预测居住用地规模。

人口规模预测和一般城镇规划相比，产业园区的人口规模预测难度较大。

究其原因有几方面：01不同产业对人力资源需求不同，劳动密集型产业需要较多的劳动力，相反，资本密集型或知识密集型产业需要较少的劳动力。

02大部分园区建设前都是一片空地，人迹稀少，参考基础数据意义不大，因此很难用机械增长的方式预测人口规模。

03园区区位交通条件不同将对人口规模预测影响很大，如靠近城市的园区，人们工作在园区但生活在城市，园区的常住人口就不多；相反，远离城市的园区，其常住人口规模就会大很多。

04园区的发展对人口规模的影响同时作用于两个相反的动力：一个是随着工业企业资金与技术含量提高，职工密度将降低；另一个是随着土地集约使用程度的提高，职工密度可能增加。

园区的人口发展到底是持续增长抑或逐步下降，取决于两者的合力。

尽管准确预测园区人口规模的难度较大，但在规划实践中，参考国内外园区的发展经验，我们通常综合运用以下几种预测方法，并经过综合考虑其他因素，最终确定园区的人口规模。

现以铁岭某园区的下：规划实践举例如方法一：按人均建设用地进行测算规划按人均建设用地120～150m2/人指标计算，以规划面积为28.14 km2测算，规划区人口规模约为18.8万～23.5万人。

方法二：按工业用地进行测算考虑到该园区产业多属于劳动密集型，故规划按每公顷工业用地职工120～140人测算，以规划工业用地1193.91公顷计算，需要职工人数为14.3万～16.7万人。

摘要：对苍南县“十二五”期间人口增长规模进行预测，认识全县人口的发展变化规律，对于制定本县社会和经济发展规划，促进国民经济发展、科学治县具有十分重要的现实意义。

文章运用综合增长率法和趋势外推法进行预测分析，趋势外推法采用线性回归模型和乘幂回归模型进行预测，回归分析采用PASW软件，得到苍南县“十二五”期间各年度的户籍人口总数、外来流动人口和外出流动人口总数。

关键词：综合增长率法；趋势外推法；人口增长；预测一、苍南县人口现状苍南县是浙江省第一人口大县，根据苍南县公安部门、计生部门统计数据显示，2009年苍南县总人口为132.21万人，其中户籍人口127.59万人，外来流动人口约12.67万人，外出流动人口约8.05万人（见表1）。

二、苍南县“十二五”期间人口增长规模预测对总人口规模的预测从三个部分来进行：户籍人口、外来流动人口、外出流动人口。

外来流动人口指外省、市、县流入到苍南县居住半年以上的人口，外出流动人口指本县流出到其他省、市、县居住半年以上的人口。

本次预测采用综合增长率法和趋势外推法对苍南县人口增长规模进行综合预测。

（一）户籍人口预测1、综合增长率法这种方法主要是参考历年自然增长率及机械增长率，确定预测期内的年平均综合增长率，然后再根据相应的公式预测出目标年末的人口规模。

根据苍南县历年统计数据算得，2004-2009年间苍南县人口的年均增长率为7.47‰，以自然增长为主；机械增长2007年以前呈现流出态势，近两年呈现流入态势，2008-2009年均增长率为1.71‰。

综合考虑未来五年国家人口政策的稳定性以及苍南县目前的人口自然增长率，推断“十二五”期间苍南县人口自然增长率将略有下降；同时，随着苍南县经济的发展和新城区的建设，未来苍南县的机械人口增长将有所提高。

公式：P=P0×（1+α+β）N①其中：P为规划期末人口数；P0为基准年人口数，本预测方法采用2009年人口数127.59万；α为人口自然增长率，2011-2012年取7‰，2013-2015年取6.5‰；β为人口机械增长率，取2‰；N为规划年限。

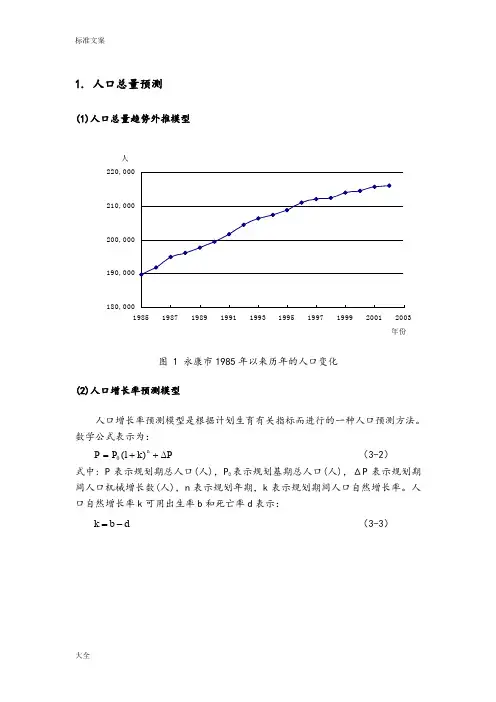
1. 人口总量预测(1)人口总量趋势外推模型图 1 永康市1985年以来历年的人口变化(2)人口增长率预测模型人口增长率预测模型是根据计划生育有关指标而进行的一种人口预测方法。

数学公式表示为：+1(=)+P n∆kPP（3-2）0式中: P表示规划期总人口(人)，P表示规划基期总人口(人)，ΔP表示规划期间人口机械增长数(人)，n表示规划年期，k表示规划期间人口自然增长率。

人口自然增长率k可用出生率b和死亡率d表示：=（3-3）k-db图 2 永康市1989年以来历年的人口出生率、死亡率和自然增长率图 3 永康市1989年以来历年的户籍人口迁移数量(3)人口离散预测模型人口离散预测模型也即人口差分方程预测模型，又称“宋健模型”，是我国自行提出的比较成功的人口发展预测模型，能较好的运用人口普查资料对未来人口进行预测。

该模型是根据分年龄的人口结构递推公式进行预测，模型的数学表达如下：1,...,2,1,0)()()](1[)1()()()()()](1[)(100021-=+⋅-=+⋅⋅⋅⋅-=+∑m i t f t X t t X t X t k t h t t t X i i i i r r i i i μβμ （3-6）式中：X 0(t)为t 年代0岁出生婴儿数，X i (t)为t 年代之年龄组人口数，μ00(t)为t 年出生婴儿当年死亡率，β(t)为妇女总和生育率，即社会人中平均意义下一个妇女在整个育龄时期的生育总数（r 2，r 1即为生育年龄的上下限），h i (t)为生育模式，反映某一地区某一个育龄妇女生育状态分布，k i (t)为t 年代之年龄组女性性别比，μi (t)为t 年代之年龄组人口死亡率，f i (t)为t 年代之年龄组净迁移数。

在模型的具体应用中，课题组工作的重点是如何确定公式3-6中的各种参数。

①第五次人口普查资料中的数据是2000年11月1日的数据，而规划所需的数据是年末的数据，课题组将普查的户籍人口分龄人口数按比例修正到2000年底的统计人口总数作为X i (t)；②从普查资料来看45岁以下的性别比比较稳定，为了简化模型，t 年代之年龄组女性性别比k i (t)用常量 k 表示，即采用普查资料中的45岁以下的男女性别比=104.85(女性=100)推算，故k= 0.488326；③根据普查资料，妇女总和生育率取2000年的数据β(t)= 0.8795；④模型中出生婴儿当年死亡率μ00(t)假定与2000年出生婴儿当年死亡率的80%，即采用μ00=3.88‰。

城市人口预测方法人口预测就是指以人口现状为基础,对未来人口的发展趋势提出合理的控制要求与假定条件,即参数条件来获得对未来人口数据提出预报的技术或方法。

城市人口预测就是城市总体规划的首要工作,它既就是城市规划的目标,又就是确定总体规划中的具体技术指标与城市合理布局的前提与依据,因此合理预测城市人口对城市的总体规划与城市的可持续发展有着十分重要的意义。

1、含义城市人口预测(urban population forecast)就是对未来一定时期内城市人口数量与人口构成的发展趋势所进行的测算。

2、传统人口预测方法传统的人口预测方法包括平均增长率法、带眷系数法、剩余劳动力转化法与劳动平衡法等。

1)平均增长率法在城市进行总体规划时,对人口规模预测的常见方法之一为平均增长率法,计算时应分析近年来人口的变化情况,确定每年的人口增长率。

人口规模预测公式为: P = P0 (1 + K1 + K2)n。

式中, P为规划期末城市人口规模, P0 为城市现状人口规模, K1 为城市年平均自然增长率, K2 为城市年平均机械增长率, n 为规划年限。

这种方法适合初步经济发展稳定的城市,人口增长会逐步增加,人口增长率变化不大。

但就是随着人口基数的增大,人口结构逐步趋于老龄化,人口增长的速度将会越来越慢,不可能都以平均的速度增长。

若要考虑到未来社会经济发展等因素对人口变动的影响,则可按预见的趋势改变人口增长率进行测算。

该方法具有普遍的适用性,但它对人口增长率的精度要求较高。

2)带眷系数法带眷系数法就是根据新建工业项目的职工数及带眷情况计算的。

当建设项目已经落实,规划期内人口机械增长稳定的情况下,宜按带眷系数法计算人口发展规模。

计算时应分析从业人员的来源、婚育、落户等状况以及城镇的生活环境与建设条件等因素,确定增加的从业人员及其带眷系数。

具体预测公式为: P =P1 (1 + a) + P2 + P3。

式中, P为规划期末城镇人口规模,P1 为带眷职工人数,a 为带眷系数, P2 为单身职工人数, P3 为规划期末城镇其她人口数。

人口预测模型模型概述人类社会进入20世纪以来，在科学技术和生产力飞速发展的同时，世界人口也以空前的规模增长，人口老龄化的现象日益明显，使得我国调整人口生育政策成为可能，人类开始研究人和自然的关系，人口数量的变化规律，以及如何进行控制等问题模型一我国人口现状及人口增长的预测1.1指数增长型英国人口学专家马尔萨斯研究得出了著名的人口指数增长模型，记时刻t的人口为某为了利用微积分这一数学工具，将某视为连续可微函数。

记初始时刻的人口为某，即有微积分知识可得满足微分方程即r>0时（3）式表示人口将按指数规律随时间无限增长，利用最小二乘法将(3)式取对数，可得：经计算与验证，指数增长模型能比较准确的预测人口的增长，但对于长期预报不够准确，因此必须修改指数增长模型关于人口增长率是常数这个基本假设1.2阻滞增长模型分析人口增长到一定数量后增长率下降的主要原因，自然环境，环境条件等因素对人口的增长起着阻滞作用，并且随着人口的增加，阻滞作用越来越大。

阻滞作用体现在增长率R的影响上，使得R随着人口数量某的增加而下降。

若将R表示为某的函数，则它应该是减函数，于是方程（2）写作对R的一个简单的假定是，设为的线性函数，即这里R称固有增长率，表示人口很少时（理论上是某=0）的增长率。

为了确定系数S的意义，引入自然资源和环境条件所能容纳的最大人口数量某称人口容量。

当时人口不再不再增长，即增长率代入（6）式可得于是（6）式为（7）式的另一种解释是，增长率与人口尚未实现部分的比例成正比，比例系数为固有增长率R方程（8）右端的因子体现人口自身增长趋势，因子则体现了资源和环境对人口增长的阻滞作用。

如果以某为横轴为纵轴做出方程（8）的图形可以分析人口增长速度随着某的变化而变化的情况，从而大致地看出的变化规律方程（8）可以用分离变量的方法求解得到。