自回归模型的参数估计案例

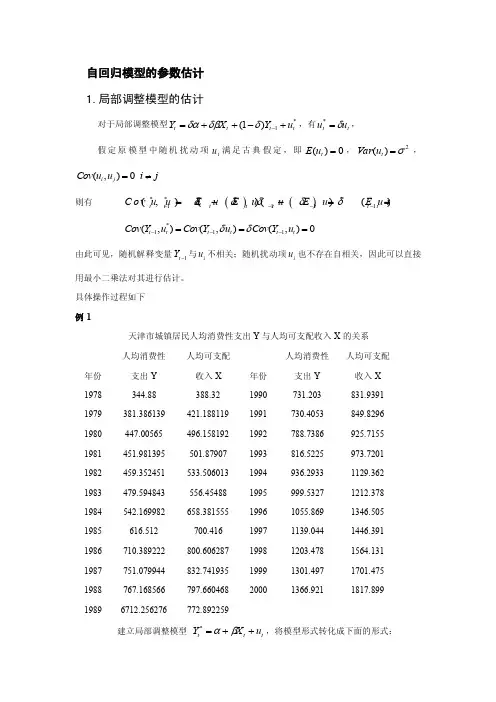
自回归模型的参数估计 1.局部调整模型的估计对于局部调整模型*1)1(t t t t u Y X Y +-++=-δδβδα，有t t u u δ=*，假定原模型中随机扰动项t u 满足古典假定，即0)(=t u E ，2)(σ=t u Var ，(,)0i j Cov u u i j =≠则有 ()()**21111(,)()()()0t t t t t tt t C o v u u E uE u uE u E u u δδδδδ----=--==*111(,)(,)(,)0t t t t t t Cov Y u Cov Y u Cov Y u δδ---===由此可见，随机解释变量1-t Y 与i u 不相关；随机扰动项i u 也不存在自相关，因此可以直接用最小二乘法对其进行估计。

具体操作过程如下 例1天津市城镇居民人均消费性支出Y 与人均可支配收入X 的关系 年份 人均消费性支出Y 人均可支配 收入X 年份 人均消费性支出Y 人均可支配收入X 1978 344.88 388.32 1990 731.203 831.9391 1979 381.386139 421.188119 1991 730.4053 849.8296 1980 447.00565 496.158192 1992 788.7386 925.7155 1981 451.981395 501.87907 1993 816.5225 973.7201 1982 459.352451 533.506013 1994 936.2933 1129.362 1983 479.594843 556.45488 1995 999.5327 1212.378 1984 542.169982 658.381555 1996 1055.869 1346.505 1985 616.512 700.416 1997 1139.044 1446.391 1986 710.389222 800.606287 1998 1203.478 1564.131 1987 751.079944 832.741935 1999 1301.497 1701.475 1988 767.168566 797.660468 2000 1366.9211817.89919896712.256276772.892259建立局部调整模型 t t t u X Y ++=βα*，将模型形式转化成下面的形式：*1*1*0*t t t t u Y X Y +++=-ββα然后直接用OLS 法估计模型参数。

一阶自回归的方差协方差矩阵
一阶自回归模型（AR(1)）的方差协方差矩阵可以通过自回归模型的参数估计来计算。

假设AR(1)模型为：
X_t = c + φ*X_{t-1} + ε_t
其中，X_t表示时间t的随机变量，c是常数项，φ是自回归系数，ε_t是时间t的随机误差项。

方差协方差矩阵可以表示为：
Var(X_t) = Var(c + φ*X_{t-1} + ε_t)
= φ^2 * Var(X_{t-1}) + Var(ε_t)
因为AR(1)模型中的随机变量是序列相关的，所以需要计算时间t-1的随机变量X_{t-1}的方差。

根据AR(1)模型，可以得到X_{t-1}的方差为：
Var(X_{t-1}) = Var(c + φ*X_{t-2} + ε_{t-1})
= φ^2 * Var(X_{t-2}) + Var(ε_{t-1})
通过递归计算，可以得到方差协方差矩阵的形式为：
Var(X_t) = φ^2 * Var(X_{t-1}) + Var(ε_t)
= φ^2 * (φ^2 * Var(X_{t-2}) + Var(ε_{t-1})) + Var(ε_t)
= φ^4 * Var(X_{t-2}) + φ^2 * Var(ε_{t-1}) + Var(ε_t)
= …
可以发现，方差协方差矩阵的形式为无穷级数。

一般情况下，我们可以假设时间序列满足平稳性（即方差和自相关系数随时间不变），从而简化方差协方差矩阵的计算。

自回归模型的参数估计案例案例一：建立中国长期货币流通量需求模型。

中国改革开放以来，对货币需求量（Y）的影响因素，主要有资金运用中的贷款额（X）以及反映价格变化的居民消费者价格指数（P）。

长期货币流通量模型可设定为Y—B o "iX t +為只+片（1）其中，Y t e为长期货币流通需求量。

由于长期货币流通需求量不可观测，作局部调整:Y t -YL（Y t e-Y.）（2）其中，Y为实际货币流通量。

将（1）式代入（2）得短期货币流通量需求模型：Y 二o Mt 2p （1- ）Y「J表1中列出了1978年到2007年我国货币流通量、贷款额以及居民消费者价格指数的相关数据。

居民消费者价格指数年份货币流通量Y （亿元）贷款额X （亿元）P （1990 年=100）1978212.046.21850.01979267.747.12039.61980346.250.62414.31981396.351.92860.21982439.152.93180.61983529.854.03589.91984792.155.54766.11985987.860.65905.6 19861218.464.67590.819871454.569.39032.519882134.082.310551.3 19892344.097.014360.1 19902644.4100.017680.7 19913177.8103.421337.8 19924336.0110.026322.9 19935864.7126.232943.1 19947288.6156.739976.0 19957885.3183.450544.1 19968802.0198.761156.6 199710177.6204.274914.1 199811204.2202.686524.1 199913455.5199.793734.3200014652.7200.699371.1 200115688.8201.9112314.7 200217278.0200.3131293.9 200319746.0202.7158996.2 200421468.3210.6178197.8 200524031.7214.4194690.4 200627072.6217.7225347.2 200730375.2228.1261690.9对局部调整模型1X t + P2r t(1-「JYx ”运用OLS法估计结果如图1:D E餐n血nt Vanable Y fJethac Least Squares Date Tima 21 12Sample r3C|U3tedj 1979 2007Included otsen'aticns 29 after adj」wtnignt辱Vansble Coefficient Std Errcr t-Statistic ProbC-202 5275 221 964S -O 91Z430 0 3703X0D36T100012565 2842001 C 003SP 7 4557283065733 2.431956 C 022bYM)0 723634 0 132796 5 449199 0 0030^squared 0.9985B2F^ean depencent /ar 9059.631Adjjsted R-squared 0.998412S.D lepsndent ,ar 9007.257S.E of regression358.9392 Akaike irfir ci iltn uri14.73163Sum squand rssid 3220934Schwarz cnterior U 92022Loc likelihcod-209.6086 F-statisti：50E8 997L;urb i r-atscn sta:1724407ProbiF-statistic)U U'JUUJU图1回归估计结果由图1短期货币流通量需求模型的估计式:Y = -202.5+ 0.0357Xt + 7.4557R + 0.7236Y T 由参数估计结果? 0.7236,得? 0.2764o由于= -202.5= 0.0357, 、2 = 7.4557。

ARIMA模型预测案例假设我们要预测公司未来一年的销售额，已经收集到了该公司过去几年的销售额数据，我们希望通过ARIMA模型对未来的销售额进行预测。

首先，我们需要对销售额数据进行初步的可视化和分析。

通过绘制时间序列图，可以观察到销售额的趋势、季节性和随机性。

这些特征将有助于我们选择ARIMA模型的参数。

接下来，我们需要对数据进行平稳性检验。

ARIMA模型要求时间序列具有平稳性，即序列的均值和方差不随时间变化。

可以通过ADF检验或单位根检验来判断序列是否平稳。

如果序列不平稳，我们需要对其进行差分处理，直到达到平稳性。

接下来，我们需要确定ARIMA模型的参数。

ARIMA模型由AR（自回归）、I（差分）和MA（移动平均）三个部分组成。

AR部分反映了序列的自相关性，MA部分反映了序列的滞后误差，I部分反映了序列的差分情况。

我们可以使用自相关函数（ACF）和部分自相关函数（PACF）的图像来帮助确定ARIMA模型的参数。

根据ACF和PACF图像的分析，我们可以选择初始的ARIMA模型参数，并使用最大似然估计方法来进行模型参数的估计和推断。

然后，我们可以拟合ARIMA模型，并检查拟合优度。

接着，我们需要进行模型诊断，检查模型的残差是否满足白噪声假设。

可以通过Ljung-Box检验来判断残差的相关性。

如果残差不满足白噪声假设，我们需要重新调整模型的参数，并进行重新拟合。

最后，我们可以利用已经训练好的ARIMA模型对未来的销售额进行预测。

通过调整模型的参数，我们可以得到不同时间范围内的销售额预测结果。

需要注意的是，ARIMA模型的预测结果仅仅是一种可能的情况，并不代表未来的真实情况。

因此，在实际应用中，我们需要结合其他因素和信息来进行决策。

综上所述，ARIMA模型是一种经典的时间序列预测方法，在实际应用中具有广泛的应用价值。

通过对时间序列数据的分析和模型的建立，我们可以对未来的趋势进行预测，并为决策提供参考。

然而，ARIMA模型也有一些限制，如对数据的平稳性要求较高，无法考虑其他因素的影响等。

时变参数向量自回归模型1. 引言时变参数向量自回归模型（Time-Varying Parameter Vector Autoregressive Model，TVAR）是一种用于分析时间序列数据的经济计量模型。

它可以捕捉到时间序列数据中的动态性和非线性关系，因此在经济学、金融学等领域被广泛应用。

本文将介绍时变参数向量自回归模型的基本原理、建模方法以及应用案例，帮助读者全面了解该模型。

2. 基本原理2.1 自回归模型自回归模型（Vector Autoregressive Model，VAR）是一种多元时间序列分析方法。

它假设时间序列数据之间存在线性关系，并可以通过过去若干期的数据来预测未来的值。

VAR模型可以表示为：Y t=c+Φ1Y t−1+Φ2Y t−2+⋯+Φp Y t−p+εt其中，Y t是一个n维向量，表示第t期的观测值；c是一个常数向量；Φ1,Φ2,…,Φp是n×n的系数矩阵，表示自回归系数；εt是一个n维向量，表示误差项。

2.2 时变参数向量自回归模型时变参数向量自回归模型是在VAR模型的基础上引入了时变参数的扩展模型。

它认为自回归系数在时间上是可变的，可以通过某种方式来描述其动态性。

时变参数向量自回归模型可以表示为：Y t=c+Φ1(t)Y t−1+Φ2(t)Y t−2+⋯+Φp(t)Y t−p+εt其中，Φi(t)表示第i个滞后期的自回归系数在时间t上的取值。

3. 建模方法3.1 参数估计对于时变参数向量自回归模型，参数估计是一个关键步骤。

常用的方法有贝叶斯方法、频域方法和局部似然方法等。

贝叶斯方法通过引入先验分布来估计参数，可以获得参数的后验分布。

频域方法利用频域上的特征来估计参数，可以捕捉到数据的周期性。

局部似然方法则在每个时间点上估计参数，可以灵活地适应时变性。

3.2 模型选择在建立时变参数向量自回归模型时，需要选择合适的滞后阶数和模型形式。

滞后阶数决定了过去多少期的数据被考虑进模型中，一般通过信息准则（如AIC、BIC等）来选择最优阶数。

自回归模型（Autoregressive Model）是一种经典的时间序列预测模型，在许多领域中都有着广泛的应用。

它的核心思想是利用过去时间点的观测值来预测未来的观测值。

在本文中，我将介绍自回归模型的概念，并使用Python实现一个简单的自回归模型。

1.自回归模型概述自回归模型是建立在时间序列数据上的统计模型。

它假设当前时刻的观测值是过去时刻的观测值的线性组合，其中线性关系由模型的参数确定。

自回归模型可以被表示为如下形式：X_t = c + Σ(φ_i *X_(t-i)) + ε_t 其中，X_t是当前时刻的观测值，c是常数项，φ_i是参数，ε_t是误差项。

根据历史观测值和参数的不同，自回归模型可以分为不同阶数的自回归模型，如一阶自回归模型（AR(1)）、二阶自回归模型（AR(2)）等。

2.自回归模型的Python实现为了实现自回归模型，我们需要借助Python中的统计分析库statsmodels。

我们需要安装statsmodels库，可以使用以下命令进行安装： pip install statsmodels接下来，我们使用一个示例数据集来演示自回归模型的实现。

假设我们有一个包含100个观测值的时间序列数据，可以使用以下代码生成一个随机的时间序列数据：import numpy as np生成随机时间序列数据np.random.seed(0) data = np.random.randn(100)我们可以使用statsmodels库中的AR模型来建立自回归模型，并进行参数估计和预测。

以下是一个简单的自回归模型的实现代码示例： fromstatsmodels.tsa.ar_model import AutoReg构建AR模型model = AutoReg(data, lags=1)拟合模型model_fit = model.fit()打印模型系数print(model_fit.params)进行单步预测predictions = model_fit.predict(start=len(data), end=len(data))print(predictions)在上述代码中，我们首先使用AutoReg类构建了一个自回归模型，其中lags参数指定了模型的阶数，这里我们选择了一阶自回归模型（lags=1）。

案例二 ARMA 模型建模与预测指导一、实验目的学会通过各种手段检验序列的平稳性；学会根据自相关系数和偏自相关系数来初步判断ARMA 模型的阶数p 和q ，学会利用最小二乘法等方法对ARMA 模型进行估计，学会利用信息准则对估计的ARMA 模型进行诊断，以及掌握利用ARMA 模型进行预测。

掌握在实证研究中如何运用Eviews 软件进行ARMA 模型的识别、诊断、估计和预测和相关具体操作.二、基本概念宽平稳:序列的统计性质不随时间发生改变,只与时间间隔有关。

AR 模型：AR 模型也称为自回归模型.它的预测方式是通过过去的观测值和现在的干扰值的线性组合预测， 自回归模型的数学公式为：1122t t t p t p t y y y y φφφε---=++++式中: p 为自回归模型的阶数i φ(i=1，2， ，p ）为模型的待定系数，t ε为误差, t y 为一个平稳时间序列。

MA 模型：MA 模型也称为滑动平均模型。

它的预测方式是通过过去的干扰值和现在的干扰值的线性组合预测。

滑动平均模型的数学公式为:1122t t t t q t q y εθεθεθε---=----式中： q 为模型的阶数; j θ（j=1，2, ，q ）为模型的待定系数；t ε为误差； t y 为平稳时间序列。

ARMA 模型:自回归模型和滑动平均模型的组合， 便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA, 数学公式为：11221122t t t p t p t t t q t q y y y y φφφεθεθεθε------=++++----三、实验内容及要求1、实验内容:（1）根据时序图判断序列的平稳性；（2）观察相关图，初步确定移动平均阶数q 和自回归阶数p ；（3）运用经典B —J 方法对某企业201个连续生产数据建立合适的ARMA （,p q ）模型，并能够利用此模型进行短期预测。

2、实验要求:（1）深刻理解平稳性的要求以及ARMA 模型的建模思想；（2）如何通过观察自相关，偏自相关系数及其图形，利用最小二乘法，以及信息准则建立合适的ARMA 模型；如何利用ARMA 模型进行预测; （3）熟练掌握相关Eviews 操作，读懂模型参数估计结果.四、实验指导 1、模型识别 （1）数据录入打开Eviews软件，选择“File"菜单中的“New--Workfile”选项，在“Workfile structure type”栏选择“Unstructured /Undated”，在“Date range”栏中输入数据个数201，点击ok，见图2—1，这样就建立了一个工作文件。

自回归模型的参数估计案例自回归模型（AutoRegressive Model, AR）是一种用来描述时间序列数据的统计模型，它的基本思想是将当前时间点的观测值与前一时间点的值相关联，通过线性组合来预测未来的观测值。

在本文中，我们将介绍一个用于估计自回归模型参数的案例。

假设我们有一个每日销售额的时间序列数据，我们希望建立一个自回归模型来预测未来的销售额。

我们使用美国家零售商的销售数据作为案例数据，数据集中包含了该零售商自2000年1月1日至2024年12月31日每天的销售额。

我们将使用Python中的statsmodels库进行模型拟合和参数估计。

首先，我们需要导入相关的库和数据集。

```pythonimport pandas as pdimport statsmodels.api as sm#读取数据data = pd.read_csv('sales_data.csv')```接下来，我们可以先观察一下数据的基本情况。

```pythondata.head```日期，销售额----------，--------2000/1/2，1605.02000/1/3，2096.02000/1/4，2579.02000/1/5，2894.0我们可以看到，数据集包含两列，一列是日期，另一列是销售额。

接下来，我们将日期列设置为数据的索引，并将销售额列转换为时间序列对象。

```python#将日期列设置为索引data.set_index('Date', inplace=True)#将销售额列转换为时间序列对象ts = data['Sales']```现在，我们可以开始建立自回归模型。

AR模型的一项关键任务是确定时滞（lag），即前一时间点（或多个时间点）对当前时间点的影响。

我们可以使用自相关图（ACF,Autocorrelation Function）和偏自相关图（PACF, Partial Autocorrelation Function）来帮助我们选择合适的时滞。

[编辑]案例一:ARlMA模型在海关税收预测中的应用2008年。

海关税收预算计划8400亿元.比2007年实际完成数增加10.8％，比2007年预算数增加22.1％。

为了对2008年江门海关税收总体形势进行把握，笔者尝试利用SAS 统计分析软件的时间序列预测模块建立ARIMA模型，对2008年江门海关税收总值进行预测。

从预测结果来看，预测模型拟合度较高，预测值也切合实际情况，预测模型具有一定的应用价值。

现将预测的方法、原理以及影响税收工作的相关因素分析。

一、ARlMA模型原理ARIMA模型全称为自回归移动平均模型(Autoregressive Integrated Moving Average Model，简记ARIMA)。

是由博克思(Box)fFfl詹金斯(Jenkins)于70年代初提出的一著名时问序列预测方法，所以又称为box--jenkins模型、博克思一詹金斯法。

其中ARIMA(p，d.q)称为差分自回归移动平均模型，AR是自回归，P为自回归项；MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数。

ARIMA模型可分为3种：(1)自回归模型(简称AR模型)；(2)滑动平均模型(简称MA模型)；(3)自回归滑动平均混合模型(简称ARIMA模型)。

ARIMA模型的基本思想是：将预测对象随时问推移而形成的数据序列视为—个随机序列.以时间序列的自相关分析为基础.用一定的数学模型来近似描述这个序列。

这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。

ARlMA模型在经济预测过程中既考虑了经济现象在时间序列上的依存性，又考虑了随机波动的干扰性，对于经济运行短期趋势的预测准确率较高，是近年应用比较广泛的方法之一。

二、应用ARIMA模型进行预测每月税收数据.可以看作是随着时间的推移而形成的一个随机时间序列，通过对该时间序列上税款值的随机性、平稳性以及季节性等因素的分析，将这些单月税收值之间所具有的相关性或依存关系用数学模型描述出来，从而达到利用过去及现在的税收值信息来预测未来税收情况的目的。