上海宝山区2009年第一学期九年级数学期中考试试卷

2009学年度第一学期九年级数学期中试卷（时间：100分钟，满分150 分）一、 选择题：（本大题共6题，每题4分，满分24分） 1．已知1:2:=y x ，那么 x y x :)2(- 等于（ ） （A ）3:2；（B ）3:1； （C ）1:2； （D ）2:3．2．如图1，已知1l ∥2l ∥3l ，则下列结论中，正确的是（ ）（A ）EF DE BC AB =； （B ）CF BEBE AD =； （C ）CF BE AC AB =； （D ）EFDEAC AB =． 3．如图2，已知梯形ABCD 中，AB ∥CD ，∠ABC = 90º， AB=4，BC = 2，CD=1，那么A cot 的值是（ ）． （A ）32 （B ）23 （C ）21 （D ）45 4．已知a b 3-=，则下列判断错误．．的是（ ） （A ）b ∥a ； （B ）a b 3=； （C ）b 与a 的方向相反； （D ）03=+b a ． 5．根据你对相似的理解，下列命题中，不．正确的是（ ）． （A ）三边之比为2：3：4的两个三角形一定相似 （B ）三内角之比为2：3：4的两个三角形一定相似 （C ）两邻边之比为2：3的两个直角三角形一定相似 （D ）两邻边之比为2：3的两个矩形一定相似6．下列四个三角形中，与图3中△ABC 的相似的是（ ）（图3）B CA（A ）(B)(C)(D) （图1）1l AD EF B C2l3lBACD （图2）二、 填空题：（本大题共12题，每题4分，满分48分）7．计算：=---)26(21)2(b a b a . 8．如果两个相似三角形的周长比是1:2，那么它们的面积比是 ． 9．线段4a =厘米，9c =厘米，如果线段b 是线段a 和c 的比例中项， 那么b =_________厘米．10．已知△ABC ∽△DEF ，且点D 与点A 对应，点E 与点B 对应， 若︒=∠50A ，︒=∠70B ，则=∠F 度. 11．如图4，已知ABC ∆中，点D 、E 分别在边AB 、AC 上， 若AD = 2、BD = 3，AC = 4.5，则EC = 。

上海市宝山区2024--2025学年上学期九年级期中考试数学试卷一、单选题1．如果两个相似三角形对应边之比是1∶2，那么它们的对应高之比是（）A ．1∶2；B ．1∶4；C ．1∶6；D ．1∶8．2．下列选项中的两个图形一定相似的是（）A ．两个等边三角形B ．两个矩形C ．两个菱形D ．两个等腰三角形3．如图，DE ∥AB ，如果CE ∶AE =1∶2，DE =3，那么AB 等于（）A ．6；B ．9；C ．12；D ．13．4．已知非零向量a 、b ，且有2a b =-，下列说法中，不正确的是（）A ．2a b=B ．a b∥ C ．a与b方向相反D ．0a b +=5．如图，点D 、E 分别在ABC V 的两边BA 、CA 的延长线上，下列条件能判定ED BC ∥的是（）．A ．AD DEAB BC=B ．AD AEAC AB=C ．AD AEAB AC=D ．AD AB DE BC⋅=⋅6．如图，在△ABC 中，点D 在边BC 上，点G 在线段AD 上，GE ∥BD ，且交AB 于点E ，GF ∥AC ，且交CD 于点F ，则下列结论一定正确的是（）A ．AE CFAB CD=；B ．AE DFEB FC=；C ．=EGFG BDAC；D ．=AE ADAG AB．二、填空题7．如果tan a =α的度数是8．如果()230a b b =≠，那么ab=．9．已知在Rt ABC 中，90C ∠=︒，1cot 3B =，2BC =，那么AC =.10．已知线段2AB =，如果点P 是线段AB 的黄金分割点，且AP BP >，那么AP 的值为．11．已知向量m 与单位向量e 方向相反，且3a = ，那么m=（用向量e的式子表示）12．如图，已知AD ∥BE ∥CF ，它们依次交直线1l 、2l 于点A 、B 、C 和点D 、E 、F ．如果23=AB BC ，DF=15，那么线段DE 的长是．13．如图，ABC V 的中线AD 、CE 交于点G ，点G 是ABC V 的重心，点F 在边AC 上，GF BC ∥，那么GF BC =∶．14．如图，ABC V 是边长为3的等边三角形，,D E 分别是边,BC AC 上的点，60ADE ∠= ，如果1BD =，那么CE =15．矩形的一条对角线长为26，这条对角线与矩形一边夹角的正弦值为513，那么该矩形的面积为.16．如图，在菱形ABCD 中，对角线AC 、BD 交于点O ，点E 是AD 的中点，联结OE ．如果3AB =，4AC =，那么cos AOE ∠=．17．平行于梯形两底的直线截梯形的两腰，当两交点之间的线段长度是两底的比例中项时，称这条线段是梯形的“比例中线”．在梯形ABCD 中，49AD BC AD BC ==∥，，，点E 、F 分别在边AB 、CD 上，如果EF 是梯形ABCD 的“比例中线”，那么DFDC的值为．18．如图，在△ABC 中，AB=AC ，BC=8，tanB=32，点D 是AB 的中点，如果把△BCD 沿直线CD 翻折，使得点B 落在同一平面内的B′处，联结A B′，那么A B′的长为．三、解答题19．计算：22cot 602tan 30tan 60sin 452sin 30︒︒︒︒︒++-20．如图，在平行四边形ABCD 中，点E 在边AD 上，且2AE ED =，联结BE 并延长交边CD 的延长线于点F ，设，,BA a BC b ==．（1）用,a b表示，,BE DF ；（2）先化简，再求作：32()2a b a b ⎛⎫-++- ⎪⎝⎭（不要求写作法，但要写明结论）21．如图，在ABC V 中，45B ∠=︒，AD 是边BC 上的中线，3sin5DAB ∠=，BD =求：(1)AB 的长；(2)CAB ∠的余切值．22．如图，在ABC V 中，点D 、E 分别在边AB 、AC 上，且3AD =，6AC =，4AE =，8AB =．(1)如果7BC =，求线段DE 的长；(2)设DEC 的面积为2，求BDC 的面积．23．如图，平行四边形ABCD 中，AF BC ⊥，垂足为点F ，点E 是边AB 中点，连接DE 交线段AF 于点G ，2AE EG ED =⋅，连接EF ．(1)求证：DE EF ⊥；(2)连接DF ，求证：22CD DF BF =⋅．24．在平面直角坐标系xOy 中，放置一个矩形OABC ，使矩形的一个顶点O 和坐标原点重合，点C 和点A 分别在第一和第四象限内，若点C 和点A 的纵坐标满足“C A y y m -=”，则称矩形OABC 具有“条件m ”．如图，矩形OABC 中，15OC =，10BC =．(1)当矩形OABC 具有“条件0”，求此时点C 坐标；(2)当矩形OABC 具有“条件1”，求此时OC 与x 轴正半轴所夹角的正弦值；(3)若矩形OABC 具有“条件m ”，当点B 在第一象限内，连接CB 并延长交x 轴正半轴于点F ，连接AC ，AF ，若OAC 与ABF △相似，直接写出此时m 的值．25．如图1，在ABC V 中，C ∠是锐角，AB AD =交边BC 于点D ，点F 是边AC 上一点，连接BF 且满足FBC C ∠=∠，BF 交边AD 于点E ．(1)如图2，当点E 是边AD 中点时，求证：AF BDFC BC=；(2)当:1:8FE BE =，且ABE 是直角三角形时，求此时ACB ∠的正切值；(3)记AEF △的面积为1S ，ABF △的面积为2S ，ABC V 的面积为3S ，若2S 是1S 和3S 的比例中项，求:BD DC 的值．。

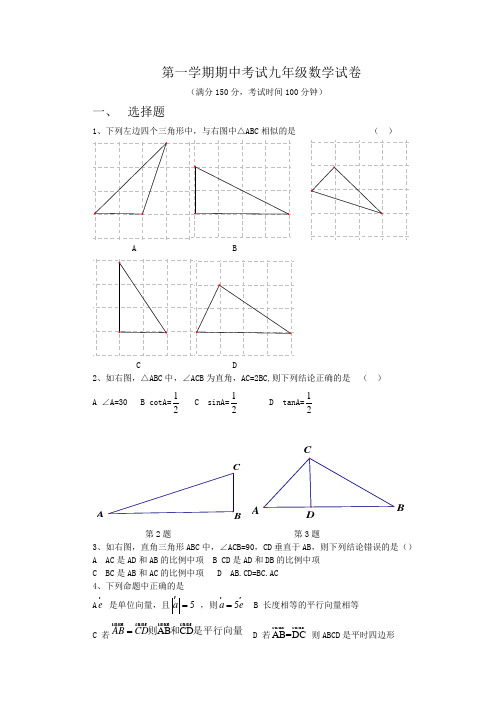
第一学期期中考试九年级数学试卷（满分150分，考试时间100分钟）一、 选择题1、下列左边四个三角形中，与右图中△ABC 相似的是 （ ）A BC D2、如右图，△ABC 中，∠ACB 为直角，AC=2BC,则下列结论正确的是 （ ） A ∠A=30 B cotA=12 C sinA=12D tanA=12CABCABD第2题 第3题3、如右图，直角三角形ABC 中，∠ACB=90，CD 垂直于AB ，则下列结论错误的是（） A AC 是AD 和AB 的比例中项 B CD 是AD 和DB 的比例中项 C BC 是AB 和AC 的比例中项 D AB.CD=BC.AC4、下列命题中正确的是A e 是单位向量，且5a = ，则5a e =B 长度相等的平行向量相等C 若AB CD AB CD =则和是平行向量 D 若AB=DC 则ABCD 是平时四边形5、已知线段a，b，c求做线段X，使bx=ac，下列哪种做法满足要求（）ac xbcbxaxabccbaxA B C D6、在三角形ABC中∠A=36，AB=AC，AB的垂直平分线OD交AB于点O，交AC于点D，连接BD，下列结论错误的是（）A ∠C=2∠AB BD平分∠ＡＢＣC ＡＢＣ面积是△ＢＣＤ面积的３倍D点Ｄ为线段ＡＣ的黄金分割点BACDOMAB CGN G FD EAB C 第6题第10题第12题二、填空题7、2、3、4成比例的数可以是填一个即可)8、已知a3,2b=那么a ba b-=+9、sin60+tan30=10、如图G为△ABC的重心，GN平行AC交BC与N，如果MN=1，那么BC=11、两个相似三角形对应边上的高之比为2:3，且已知较大的三角形的周长为12，则较小的三角形的周长为12、如图已知边长为2的正方形DEFG的四个顶点都在△ABC的边上，若BC=5，则△ABC的面积是13、已知45°＜α＜90°。

则sinα、cosα、tanα从小到大的次序是14,、在一个坡度为1:2.4的斜坡上行走米后，行走者水平高度上升了10米。

2024学年第一学期期中检测九年级数学试卷（考试时间：100分钟 满分150分）考生注意：请将所有答案写在答题卡上，写在试卷上不计分一、选择题：（本大题共6题，每题4分，满分24分）1.在中，所对的边分别为，下列等式成立的是（）A.；B.C.； D.．2.已知是线段的黄金分割点，且，那么下列等式不成立的是（ ）A.； B.；C.D.3.在中，点分别在边的延长线上，下列四个选项中，能判定的是（）A.； B.；C.； D.．4.下列说法中，错误的是（ ）A.长度为1的向量叫做单位向量；B.如果，且，那么的方向与的方向相同；C.如果是一个单位向量，是非零向量，；D.如果，其中是非零向量，那么．5.已知一次函数和二次函数部分自变量和对应的函数值如表：0245013560059当时，自变量的取值范围是（）Rt ABC 90,C A B C ∠∠∠∠= ､､a b c ､､cot b a B =sin ;a c B =sin a c A=cos a b A =P AB AP BP >AB AP AP BP =AB BP BP AP=BP AP =AP AB =ABC D E ､BA CA ､DE ∥BC BD CE AB AC =AB AE AD AC=AB BC AD DE =AB AE AC AD =0k >0a ≠ ka a e a a e a =51,22a cbc ==- c a ∥b ()10y kx m k =+≠()220y ax bx c a =++≠x1- 1y ⋯ 2y ⋯1- 21y y >xA.；B.；C.或；D.或．6.如图，在中于点于点为边的中点，联结、、以下是甲、乙两位同学得到的研究结果：（甲）当为中点时，为等边三角形；（乙）为等边三角形．对于甲、乙两位同学的结论，下列判断正确的是（）A.甲正确乙错误；B.甲错误乙正确；C.甲、乙皆正确；D.甲、乙皆错误．二、填空题：（本大题共12题，每题4分，满分48分）7.已知线段，如果是的比例中项，那么线段等于__________．8.如果两个相似三角形的周长比为，那么它们的对应中线的比为__________．9.在锐角中，锐角A的正切值是，如果将这个三角形三边的长都扩大为原来的2倍，那么锐角A 的余弦值是__________．10.如图，，它们依次交直线于点和点．如果，那么的值是__________．11.已知一个斜坡的坡比为，则坡角的度数为__________．12.如果抛物线在对称轴的左侧，的值随的增大而增大，那么的取值范围是__________．13.如图，点分别在边上，且．若12x -<<45x <<1x <-5x >1x <-4x >ABC 60,A BM AC ∠=⊥ ,M CN AB ⊥,N P BC PM PN MN ､M AC ABC PMN 12cm,6cm a b ==b a c ､c cm 1:2ABC 34AD ∥BE ∥FC 12l l ､A B C ､､D E F ､､2,5AB AC ==DE EF1:()223y a x =+-y x a D E F ､､ABC AB AC BC ､､111,,333AD AB AE AC BF BC ===的面积是，那么的面积是__________．14如果抛物线向右平移一个单位后，顶点落在抛物线上，那么的值等于__________．15.如图，中，点、点分别是的中点，与交于点．若，那么的值是__________．16.如图，在边长为1的正方形网格中，四边形的顶点都在小正方形顶点的位置上，我们称这样的四边形叫做“格点四边形”．联结相交于点，那么的面积等于__________．17.梯形中，相交于点，过点作，交于点．若是直角三角形，那么__________．18.如图，中，．把绕点逆时针旋转（旋转角小于）点的对应点分别是，射线与交于点，若，则__________．ABC 218cm DEF 2cm 21:1C y x =+22:24C y x ax =-+a ABC D E AB AC ､BE CD O ACO EBC ∠∠=:CD BC ABCD AC BD ､O AOB ABCD AD ∥,45,12,BC ABC BC AC BD ∠== ､,tan 2O DAC ∠=D DE ∥AB AC E DOE AD =Rt ABC 90,8,6ACB AC BC ∠=== ABC B 180 A C ､A C ''､CC 'AA 'E BA '∥CC 'C E '=三、解答题：（本大题共7题，满分78分）19.（本题满分10分）计算：20.（本题满分10分）如图，在梯形中，是的中点，且与交于点．（1）若，请用来表示；（2）在原图中直接在图中作出在方向上的分向量（不要求写作法，但要写出所作图中表示结论的向量）．21.（本题满分10分，每小题5分）如图，已知在梯形中，，对角线相交于点，．（1）求的值；（2）求的正切值．22.（本题满分10分）如图是某路灯在铅垂面内的示意图，灯柱的高为11.2米，灯柱与灯杆的夹角为，路灯采24cos60sin 45tan30tan601+-ABCD AB ∥,CD E CD 1,3EC AB AC =BE F ,AB m AD n == ,m n DC AF ､AC ,m n ABCD AD ∥,90,BC ABC BD CD ∠== AC BD ､O 2,3AD AB ==:AO CO ACD ∠BC BC AB 120用锥形灯罩，在地面上的照射区域的长为14.7米，从、两处测得路灯的仰角分别为和，且，求灯杆的长度．23.（本题满分12分，每小题6分）如图，中，是斜边上的中点，是边上的点，与交于点，且．（1）求证：；（2）联结，如果点E 是BC 中点，求证：．24.（本题满分12分，每小题4分）如图，抛物线与轴交于两点（在左侧），与轴交于点．联结交对称轴于点，点为抛物线的顶点．（1）联结，若①求抛物线解析式；②线段上一点，联结，求．（2）平移抛物线，使新抛物线顶点在射线上，新抛物线与轴交于点．若平分，DE D E A α45 tan 6α=AB Rt ABC 90,ACB D ∠= AB E BC AE CD F 2AC CE CB =⋅AE CD ⊥BF 2AE BF BE CD ⋅=⋅()230y x mx m =-++>x A B ､A B y C CB E D AC CD ､45CED ∠=BC ,F ACB FAB ∠∠=FD tan FDE ∠D 'CD y C 'C D 'CDE ∠且，求新抛物线解析．25.（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）中，分别在上，，联结，作交于，交于交于．（1）如图1，．①求的正弦值；②若，求；（2）如图2，，联结，若四边形为梯形，请直接写出的长．2CD CC '='ABC 12,BC D E =､AB AC ､ACB ADE ∠∠=DC MEN DCB ∠∠=DC M BC ,N EN DC O ,2,10AB AC BD AD DC ===DCB ∠:7:18DM MO =DM 45,MEN ABC EC ∠∠===MN MNCE DM。

卢湾区2009学年第一学期九年级期中考试数学试卷（时间100分钟,满分150分）2009.11（本试卷所有答案请书写在答题卷规定位置上）一、选择题（本大题共6题，每题4分，满分24分）1．把ad bc =写成比例式（其中,,,a b c d 均不为0），下列选项中错误．．的是……………………………………………………………………（ ） A ．a cb d =; B ．b d ac =； C ．c a bd =; D ．a bc d=．2．如果一个三角形保持形状不变,但周长扩大为原来的4倍，那么这个三角形的边长扩大为原来的…………………………………………（ ） A ．2倍； B ．4倍； C ．8倍； D ．16倍．3．下列命题中正确的是……………………………………………… ( ） A ．所有的菱形都相似；B ．所有的矩形都相似;C ．所有的等腰三角形都相似；D ．所有的等边三角形都相似．4．在Rt△ABC 中，∠B =90º，若AC =a ，∠A =，则AB 的长为…………( ) A ．sin a θ； B ．cos a θ; C ．tan a θ； D ．cot a θ．5．点C 在线段AB 上,如果AB =3AC ， AB a =,那么等于…………（ ） A ．13a ; B ．23a ； C ．13a -; D ．23a -． 6．已知△ABC 的三边长分别为6 cm,7.5 cm ，9 cm,△DEF 的一边长为5cm ，若这两个三角形相似，则△DEF 的另两边长可能是下列各组中的…（ ) A ．2 cm ，3 cm;B ．4 cm,6 cm ；C ．6 cm ，7 cm ；D ．7 cm ，9 cm ．二、填空题(本大题共12题,每题4分，满分48分) 7．若35a c b d ==（其中0b d +≠），则a cb d+=+__________．8．若线段AB 长为2cm,P 是AB 的黄金分割点，则较长线段PA =cm ． 9．如图,点G 为△ABC 重心,若AG =1，则AD 的长度为_________． 10．求值：cot30ºsin60-º_________． 11．在Rt△ABC 中，∠C =90º，若1tan 3A =，则cot A 的值为_________． 12．如图，在△ABC 中，点D 、E 分别在AB 、AC 边上,DE ∥BC ，若13AD BD =，DE ＝2，则BC 的长为_______．13．如图,∥∥，AB =2，AC =5，DF =7.5，则DE =_________．14．如图，在平行四边形ABCD 中,点E 、F 是边CD 、BC 边的中点，若AD a =，AB b =,则EF =___________．（结果用、表示）15．如图,已知AB ∥CD ,AD 与BC 交于点O ,若AD ∶BC = 5∶4，BO =1，DO =2.5,则AD =___________．(第13题图)B(第9题图)B(第12题图)A(第14题图)16．如图，在△ABC 的边BC 上,若DAC B ∠=∠，且BD =5，AC = 6，则CD 的长为___________．17．在△ABC 中，点D 、E 分别在AB 、AC 边上，若2AD =,4BD =,4AC =，且△ADE 与ABC 相似,则AE 的长为___________．18．在答题纸的方格图中画出与矩形ABCD 相似的图形''''A B C D (其中AB 的对应边''A B 已在图中给出）．三、简答题(本大题共4题，每题10分，满分40分)19．已知两个不平行的向量, a b ，求作向量:32()()2a b a b ---．20．如图，已知点D 、F 在△ABC 的边AB 上,点E 在边AC 上， 且DE ∥BC ，AF AD ADAB=．求证：EF ∥DC ．(第19题图)AC(第18题图)B DB ’A ’(第16题图)CC(第15题图)21．如图,在Rt △ABC 中,∠C =90º，AC = 3,1tan 2B ． (1) 求BC 的长； (2） 求cos A 的值．22．如图，竖立在点B 处的标杆AB 长2.1米，某测量工作人员站在D 点处，此时人眼睛C 与标杆顶端A 、树顶端E 在同一直线上(点D 、B 、F 也在同一直线上，已知此人眼睛与地面的距离CD 长1.6米,且BD = 1米，BF = 5米，求所测量树的高度．四、解答题(本大题共2题，每题12分，满分24分）CAB(第21题图)B(第20题图)BC A 树标杆人FED(第22题图)23．如图,BE 、CF 分别是△ABC 的边AC 、AB 上的高,BE 与CF 相交于点D ． (1） 求证:△ABE ∽△ACF ； （2） 求证：△ABC ∽△AEF ； （3) 若4ABC AEFSS=,求cos BAC ∠的值．24．如图所示，在△ABC 中，已知6BC =，边上中线5AD =。

一、选择题（每题3分，共30分）1. 若a、b是实数，且a+b=0，则a的取值范围是（）A. a > 0B. a < 0C. a ≥ 0D. a ≤ 02. 下列函数中，y是x的二次函数的是（）A. y = 2x + 3B. y = x^2 + 2x + 1C. y = x^2 - 4x + 5D. y = x^3 + 2x^2 + 13. 已知一次函数y = kx + b的图象经过点（1，2）和（-1，0），则k和b的值分别是（）A. k = 1, b = 1B. k = 1, b = 0C. k = -1, b = 2D. k = -1, b = 04. 在△ABC中，∠A = 60°，∠B = 45°，则∠C的度数是（）A. 75°B. 105°C. 120°D. 135°5. 若x^2 - 3x + 2 = 0，则x的值为（）A. x = 1B. x = 2C. x = 1 或 x = 2D. x = 0 或 x = 36. 下列各数中，属于无理数的是（）A. √4B. √9C. √16D. √257. 若等腰三角形底边长为8cm，腰长为10cm，则该三角形的周长是（）A. 26cmB. 24cmC. 22cmD. 18cm8. 已知一元二次方程x^2 - 5x + 6 = 0的解为x1和x2，则x1 + x2的值是（）A. 5B. 6C. 7D. 89. 下列图形中，是正多边形的是（）A. 正方形B. 等腰梯形C. 长方形D. 等腰三角形10. 已知直线l的方程为y = 2x - 3，若直线l与y轴的交点坐标为（0，-3），则直线l的斜率k是（）A. 2B. -3C. 1D. -2二、填空题（每题3分，共30分）11. 若a = -1，则a^2 + 2a + 1的值为______。

12. 已知等腰三角形的底边长为6cm，腰长为8cm，则该三角形的周长是______cm。

中考数学模拟卷2010.1（时间：100分钟，满分：150分）一、单项选择题：（本大题共6题，每题4分，满分24分）[下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上]1下列运算结果正确的是…………………………………………………………………（ ）Ａ．632a a a =⋅； Ｂ．6332)(b a ab =；Ｃ．532)(a a =；Ｄ．3232a a a =+．2. 在49，a 9，25xy ，92+a ，23+x ，1.0中，是最简二次根式的个数是（ ）. (A) 1； (B) 2； (C) 3； (D) 4.3．据媒体报道，我国因环境污染造成的巨大经济损失，每年高达680000000元，这个数用科学记数法表示正确的是 （A ）元； （B ） 元；（C ）元 ；（D ） 元． 4．在平面直角坐标系中，直线1y x =-经过……………………………（ ）A ．第一、二、三象限 ；B ．第一、二、四象限；C ．第一、三、四象限 ；D ．第二、三、四象限． 5．下列命题中假命题是……………………………………………………………………（ ） Ａ．两组对边分别相等的四边形是平行四边形； Ｂ．两组对角分别相等的四边形是平行四边形；Ｃ．一组对边平行一组对角相等的四边形是平行四边形； Ｄ．一组对边平行一组对边相等的四边形是平行四边形．6. 给出下列关于三角形的条件：①已知三边；②已知两边及其夹角；③已知两角及其夹边；④已知两边及其中一边的对角. 利用尺规作图，能作出唯一的三角形的条件是…（ ）. (A) ①②③； (B) ①②④； (C) ②③④； (D) ①③④. 二、填空题：（本大题共12题，每题4分，满分48分）[请将结果直接填入答题纸的相应位置] 7．化简：=-+-xx x 222 ． 8．不等式12-x ≤3的正整数解是 ． 9．函数x y -=1的定义域是 ． 10．在方程223343x x x x+=--中，如果设23y x x =-，那么原方程可化为关于y 的整式方程是 ．11．已知正比例函数y k x =（k ≠ 0）的图像经过点（-4，2），那么函数值y 随自变量x 的值的增大而____________．（填“增大”或“减小”）12．四张大小、质地都相同的卡片上分别标有数字1，2，3，4，现将标有数字的一面朝下放在桌子上，从中随机抽取两张卡片，那么两张卡片上的数字的乘积为偶数的概率是_________．13．写出一个开口向下且对称轴为直线1x =-的抛物线的函数解析式 ． 14．请写出一个既是轴对称图形又是旋转对称图形的图形：_________． 15．在︒=∠∆90C ABC Rt 中，，21tan =A ， 若1=BC ，则AB 边的长是 ． 16．如图，在平行四边形ABCD 中，E 是边CD 上的点，BE 与AC 交于点F ，如果31=CD CE ,那么=FBEF．17．⊙O 的直径为10，⊙O 的两条平行弦8=AB ，6=CD ，那么这两条平行弦之间的距离是________________． 18．平行四边形ABCD 中，3,4==BC AB ，∠B ＝60°，AE 为BC 边上的高，将△ABE沿AE 所在直线翻折后得△AFE ，那么△AFE 与四边形AECD 重叠部分的面积是 ． 三、解答题（本大题共7题，其中第19---22题每题10分，第23、24题每题12分，第25题14分， 满分78分） 19．计算：3197233112211--⎪⎭⎫ ⎝⎛+-+-． .20．解方程组：⎩⎨⎧=+-=-.065,6222y xy x y x21．某商品根据以往销售经验，每天的售价与销售量之间有如下表的关系：C B A DEF每千克售价（元） 38 37 36 35 … 20 每天销售量（千克）50525456…86设当单价从38元/千克下调到x 元时，销售量为y 千克,已知y 与x 之间的函数关系是一次函数．（1）求y 与x 的函数解析式；（2）如果某商品的成本价是20元/千克，为使某一天的利润为780元，那么这一天的销售价应为多少元？（利润=销售总金额-成本）21．为了解本区初三学生体育测试自选项目的情况，从本区初三学生中随机抽取了部分学生的自选项目进行统计，绘制了扇形统计图和频数分布直方图，请根据图中信息，回答下列问题：（1）本次调查共抽取了 名学生； （2）将频数分布直方图补充完整；（3）样本中各自选项目人数的中位数是 ；（4）本区共有初三学生4600名，估计本区有 名学生选报立定跳远．23．如图，在ABC ∆中，B C ∠=∠2，D 是BC 边上一点，且AB AD ⊥，点E 是线段BD 的篮球其他 立定跳远 排球20% 50米60 5040人数 项目篮球排球50米 立定跳远其他20中点，连结AE ． （1）求证：AC BD 2=；（2）若BC DC AC ⋅=2，求证：AEC ∆是等腰直角三角形．24．如图，抛物线c bx ax y ++=2与y 轴正半轴交于点C ，与x 轴交于点），（、04)0,1(B A ，OBC OCA ∠=∠．（1）求抛物线的解析式； （3分）（2）在直角坐标平面内确定点M ，使得以点C B A M 、、、为顶点的四边形是平行四边形，请直接写出点M 的坐标； （3分） （3）如果⊙P 过点C B A 、、三点，求圆心P 的坐标． （6分）25．如图8，在ABC ∆中，90C ∠=︒，6AC =，3tan 4B =，D 是BC 边的中点，E 为AB A BCO yx边上的一个动点，作90DEF ∠=︒，EF 交射线BC 于点F ．设BE x =，BED ∆的面积为y ．（1）求y 关于x 的函数关系式，并写出自变量x 的取值范围；（2）如果以线段BC 为直径的圆与以线段AE 为直径的圆相切，求线段BE 的长； （3）如果以B 、E 、F 为顶点的三角形与BED ∆相似，求BED ∆的面积.AC D EFB图8ACD B备用图·。

卢湾区2009学年第一学期九年级期中考试数学试卷（时间100分钟，满分150分）2009. 11（本试卷所有答案请书写在答题卷规定位置上）一. 选择题（本大题共6题，每题4分，满分24分）1 .把ad = he 写成比例式（其中a.h.c.d 均不为0 ）,下列选项中错误的c- rz D- H2.如果一个三角形保持形状不变，但周长扩大为原來的4倍，那么这个三角形的边长扩大为原來的所冇的等腰三角形都相似；0.所冇的等边三角形都相似.在RtA^r 屮，Z 作90°,若AR Z 用则初的长为 两个三角形相似，则△财的另两边长可能是下列各组中的…（ ） A. 2 cm, 3 cm ； B ・ 4 cm, 6 cm ； C. 6 cm, 7 cm ； D. 7 cm, 9 cm.A. 2倍;B. 4 倍;C. 8 倍;D. 16 倍.3. 下列命题中正确的是 A- 所有的菱形都相似; B.所有的矩形都相似;C. 4. A. aSin 0 :B. tzEbos 0 ；C.d tan 0 ； D. albot 6. 5. 点Q 在线段上，如果A 片3AG AB = a,那么航等于A-6.r2- D. ------ CL •31 一，2-— ci ；B. —a ；33已知△/!%的三边长分别为6 cm, 7.5 cm, 9 cm, △狞的一边长为5cm, C.若这二、填空题（本大题共12题，每题4分，满分48分） ci c 3a + c7. 若--（其中 b + dHO ）,则上二= _______________________ .b d 5 b+d8. 若线段昇〃长为2cm, P 是昇〃的黄金分割点，则较长线段以二 ______ cm. 9. 如图，点0为4血力重心，若力二1,则肋的长度为 ___________ ・ 10. 求值：cot30O-sin6（T= _______________ .11. 在 Rt/XABC 中，Z^90°,若 tanA = -,则 cotA 的值为3 4D 112. 如图，在△肋C 中，点从Z?分別在初、化边上，DE//BQ ^T —= -, DE=2,BD 3则比的长为 _______ .IJ/ IJ/l" AB=2, SU5, 〃戶 7. 5,贝 lj DE=14.如图，在平行四边形ABCD 中，点E 、尸是边CD 、兀边的中点，若AD = a, AB = b , 则EF= ________________ ・（结果用/、乙表示）13.如图, A（第9题图）（第12题图）（第14题图）15.如图，已知肋〃Q, AD与BC交于点、0,若AD： 80= 5 ： 4, B0 =1, DO =2.5,则肋= _____________ .16. 如图，在△加疋的边％上，若ZDAC = ZB ,且妙5, AC= 6,则皿的长为17. 在中，点〃、农分别在畑、化边匕 若AD = 2, BD = 4t AC = 4, H △昇励与畀比相似，则畀F 的长为 __________ .18. 在答题纸的方格图中画出与矩形理血9相似的图形A'B'C'D 1（其中肋的对应边AW 已在图中给出）.三、简答题（本大题共4题，每题10分，满分40分）19-已知两个不平行的向量讥，求作向豊 込初-（二爭）.20.如图，已知点〃、F 在'ABC 的边初上，点E 在边 M 上,且化'〃必—=AD ■AD AB求证：EF//DC.D如图,在Rt △磁中，ZO90。

2009年宝山区初三模拟测试数学试卷（满分150分，考试时间100分钟） 2009.4.考生注意：1．本试卷含三个大题，共25题；2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分） 【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】 1．4的平方根是（A ）2； （B ）2-； （C ）2±； （D ）2±．2．下列等式中，一定成立的是（A ）222)(b a b a +=+； （B ）3232a a a =+；（C ）aa2121=-； （D ）523a a a =⋅． 3．1=x 是下列哪个方程的解（Ａ）01=+x ； （Ｂ）1112-=-x x x ； （Ｃ）1=+y x ； （Ｄ）0433=-+x x ． 4．已知点A (-2，3 )在双曲线xky =上，则下列点中，一定在该双曲线上的点是 （A ）A (3，-2 )； （B ）A (-2，-3 )； （C ）A (2，3 )； （D ）A (3，2) . 5．下列图形中，是旋转对称图形，但不是中心对称图形的是（A ）等腰梯形； （B ）等边三角形； （C ）平行四边形； （D ）直角梯形．6.在研究圆的有关性质时，我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条 直径翻折，可以看到直径两侧的两个半圆互相重合”。

由此说明：（Ａ）圆是中心对称图形，圆心是它的对称中心；（Ｂ）圆是轴对称图形，任意一条直径所在的直线都是它的对称轴； （Ｃ）圆的直径互相平分；（Ｄ）垂直弦的直径平分弦及弦所对的弧．一、填空题：（本大题共12题，每题4分，满分48分） [请将结果直接填入答题纸的相应位置] 7．计算：28-= ▲ ．8．因式分解：a a 2213-= ▲ .9．方程21=-x 的解为 ▲ .10．已知一次函数y=kx+b 的图象经过点A （2，1）（如图1）， 当x ▲ 时，y ≥1.11．从1、2、3、…… 9九个自然数中任选一个数，选出的数被2整除的概率是 ▲ .12．小明家离开学校的距离是a 米，他上学时每分钟走b 米，放学回家时每分钟比上学时少走 15米，则小明从学校回家用的时间是 ▲ 分钟（用含a 、b 的代数式表示）． 13．请你写出一个．．二次函数解析式，使其图像的顶点在y 轴上，且在y 轴右侧图像是下降的。

OA B（第3题A OB2009学年第一学期期中考试九年级数学试卷一．仔细选一选(本题共10小题，每小题3分）1．已知⊙O的半径为4cm,点A到圆心O的距离为3cm，则点A与⊙O的位置关系是（ )A．点A在⊙O 内B．点A在⊙O 上C．点A在⊙O 外D．不能确定2．已知点P1(，)和P2(，）都在反比例函数xy2=的图象上,若021<<xx，则（ )A．012<<yy B．021<<yy C．012>>yy D．021>>yy3．如图，已知⊙O的半径为5mm，弦AB＝8mm，则圆心O到AB的距离是( )A．1mmB．2mmC．3mmD．4mm4。

下列四个三角形，与左图中的三角形相似的是（)5。

二次函数y=ax2+bx+c的图象如图所示，则下列结论:①abc > 0；②b2—4ac 〉0;③。

4a-2b+c〈0;④a+b+c=0，⑤b+2a=0。

其中正确的个数是（）A。

1个 B。

2个 C.3个 D。

4个6。

在平面直角坐标系中，如果抛物线y＝2x2不动，而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是（）A．y＝2（x－2）2 + 2 B．y＝2（x + 2)2－2C．y＝2（x－2）2－2 D．y＝2(x + 2)2 + 27．如图,现有一圆心角为90°,半径为8cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为（）A．4cm B．3cmC．2cm D．1cm8．如图，一块含有30º角的直角三角形ABC，在水平桌面上绕点C按顺时针方向旋转到△A/B/C（B、C、A/在同一直线上）的位置.若BC的长为6cm，那么顶点A从开始到结束所经过的路程长为（）A．8πcm B．10πcm C．4πcm D．4πcm9．如图，⊙O的半径OA、OB,且OA⊥OB，连接AB.现在⊙0上找一点C，使OA2+AB2=BC2, 则∠OAC的度数为（ )（A）15°或75° （B） 20°或70° （C） 20° (D)30°10、如图，直角梯形ABCD中，∠A=90°,∠B=45°，底边AB=5，高AD=3,点E由B沿折线BCD向点D移动，EM⊥AB于M，EN⊥AD于N，设BM=x，矩形AMEN的面积为y,那么y与x之间的函数关系的图像大致是（)二、认真填一填(本题有6个小题，每小题4分，共24分)11．请写出一个开口向上，且对称轴为直线2=x的二次函数解析式▲。