1.4 矩阵的分块

分块矩阵及其应用
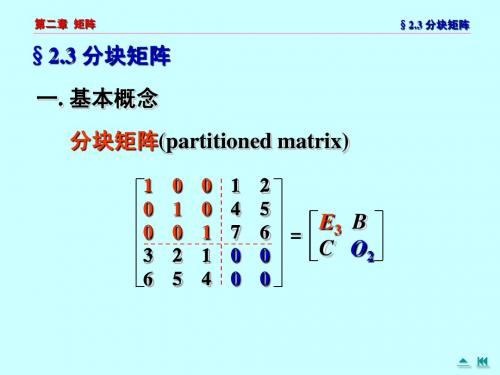
分块矩阵是由若干个子矩阵组成的大矩阵，通常将行和列分成若干块，每块均为矩阵，因而得名。

分块矩阵在数学和工程领域有广泛应用。

一些应用包括：
1.矩阵求逆：对于大规模矩阵求逆，可以先将矩阵分成较小的块，在每个块的范围内求逆并重新组合。

2.矩阵乘法：矩阵乘法的时间复杂度与矩阵的大小有关，但矩阵块的大小也会影响乘法的效率。

分块矩阵可以提高矩阵乘法的效率。

3.矩阵分解：对于某些特定类型的矩阵，如对称正定矩阵和稀疏矩阵，分块矩阵分解可以有效地降低计算复杂度。

4.图像处理：分块矩阵可以用于图像处理中的分块压缩和离散余弦变换等算法，以提高图像处理的效率和质量。

5.结构力学：分块矩阵广泛应用于结构力学和有限元方法中，可以描述复杂的结构系统和分析结构系统的动态行为。

分块矩阵及其应用徐健,数学计算机科学学院摘要：在高等代数中，分块矩阵是矩阵内容的推广. 一般矩阵元素是数量，而分块矩阵则是将大矩阵分割成小矩形矩阵，它的元素是每个矩阵块.分块矩阵的引进使得矩阵工具的利用更加便利，解决相关问题更加强有力，所以其应用也更广泛. 本文主要研究分块矩阵及其应用，主要应用于计算行列式、解决线性方程组、求矩阵的逆、证明与矩阵秩有关的定理.关键词：分块矩阵；行列式；方程组；矩阵的秩On Block Matrixes and its ApplicationsXu Jian, School of Mathematics and Computer ScienceAbstract In the higher algebra, block matrix is a generalization of matrix content.In general, matrix elements are numbers. However, the block matrix is a large matrix which is divided into some small rectangular matricies, whose elements are matrix blocks. The introduction of the block matrix makes it more convenient to use matrix, and more powerful to solve relevant problems. So the application of the block matrix is much wider. This paper mainly studies the block matrix and its application in the calculation of determinant, such as solving linear equations, calculating inverse matrix, proving theorem related to the rank of matrix , etc.Keywords Block matrix; Determinant; System of equations; Rank of a matrix11 ⎪1 引 言我们在高等代数中接触到矩阵后，学习了矩阵的相关性质，但是对于一些复杂高阶矩阵，我们希望能将问题简化. 考虑将矩阵分割为若干块，并将矩阵的部分性质平移至分块矩阵中，这样的处理往往会使问题简化.定义 1.1 [1] 分块矩阵是把一个大矩阵分割成若干“矩阵的矩阵”，如把 m ⨯ n 矩阵分割为如下形式的矩阵：⎛A 11A ⎫ 1n ⎪A m ⨯n = ⎪A m 1 A m n特别地，对于单位矩阵分块：⎝ ⎭ ⎛E 0 0 ⎫ ⎪ E n ⨯n = 0 0 0 ⎪ 0 E ⎝n n ⎭ 显然，这里我们认识的矩阵元素不再局限于数字，而是一个整体，这里的A 所代表的是大矩阵囊括的小矩阵，而小矩阵一般是我们熟知的常见矩阵.ij依照以上设想，有关矩阵性质的一些问题,我们可以考虑用分块矩阵的思路来解决.2.1 矩阵的相关概念2 分块矩阵在矩阵的学习中，我们学过一些最基本的概念，比如矩阵的行列式、矩阵 的秩、矩阵的逆、初等变换、初等矩阵等等.事实上，我们发现：分块后的矩阵同样用到这些概念.a 11 定义 2.1.1[2]n 级行列式a 21a 12 a 22 a 1n a 2n等于所有取自不同行不同列的a n 1 a n 2a nn 个元素的乘积a 1j a 2ja n j的代数和，这一定义又可写成:12na 11 a 21 a 12a 22a 1na 2n =(-1) (j 1j 2 j n )a aa .a n 1 a n 2a n∑j 1j 2 j n1j 1 2j 2n j n[2]定义 2.1.2向量组的极大无关组所含向量的个数称为这个向量组的的秩.所O I ⎪ ⎪ ⎪1谓矩阵的行秩就是指矩阵的行向量组的秩；矩阵的列秩就是矩阵列向量组的秩. 定义 2.1.3 [2] n 级方阵称为可逆的，如果有n 级方阵 B ，使得A B = A -1 .BA = E （这里 E 是n 级单位矩阵），那么B 就称为 A 的逆矩阵，记为定义 2.1.4 [3] 对分块矩阵施行下列三种初等变换： (1) 互换分块矩阵的某两行(列)；(2) 用一个非奇异阵左（右）乘分块矩阵的某一行(列)；(3) 用一个非零阵左(右)乘分块矩阵的某一行(列)加至另一行(列)上， 分别称上述三种初等行(列)变换为分块矩阵的初等行(列)变换. 定义 2.1.5 [3] m + n 2 ⨯ 2 ⎛I m O ⎫对 阶单位矩阵作 分块，即I m +n = O I ⎪ ，然后⎝ n ⎭对其作相应的初等变换所得到的矩阵称为分块初等矩阵. 分块矩阵具有以下形式：(1) 分块初等对换阵⎛I n O ；⎫ ⎝ m ⎭⎛P O ⎫ ⎛I m O ⎫(2) 分块初等倍乘阵 0 I ⎪ ， ⎪ ；⎝ n ⎭ (3) 分块初等倍加阵⎛I m R 1 ⎫ O I ⎝ 0 Q ⎭ ，⎛I m O ⎫ ； S I ⎝ n ⎭ ⎝ n ⎭其中 P , Q 分别是m 阶和n 阶可逆方阵，且R ∈ R m ⨯n ，S ∈ R n ⨯m为非零阵.2.2 矩阵的运算性质矩阵的运算包括加法、乘法、数乘，这里主要讨论矩阵的运算性质： 定义 2.2.1 [4] 矩阵加法：设A = (a ) ， B = (b ) 是两个同型矩阵，ij snij sn则矩阵C = (c i j )= (a i j+ b i j )称为 A 和 B 的和，记为C = A + B .元素全为零的矩阵称为零矩阵，记为O s n ，可简单记为O,对于矩阵 A 、 B ，有:(1) A + O = A(2) A + ( -A ) = 0(3) A - B = A + ( -B )(4) ( A + B ) + C = A + ( B + C )snsnn11 (5)A + B = 定义 2.2.2 [4] B + A矩阵乘法：设A = (a ) ，B = (b ) 是两个不同型矩阵，i k s nk j n m那么矩阵C = A B =(c i j )，称为矩阵 A 与 B 的乘积，其中：smc i j = a i 1b 1j + a i 2b 2j+ a i n b n j= ∑a i k b k jk =1在乘积的定义中，我们要求第二个矩阵行数和第一个矩阵列数相等.特别地，矩阵的乘法和加法满足以下性质：(1) A ( B + C ) = A B + A C(2) ( B + C )A = B A + C A(3) (A B )D =A (B D )⎛k a 11 k a 1k a 1 ⎫定义 2.2.3 [4] 矩阵数乘： k a 21k ak a 2n ⎪ ⎪A = (a ) 与 数 22 ⎪称为矩阵 ⎪⎪ ij sn k a k a k a ⎝ s 1 s 2 s n ⎭k 的数量乘积，记为kA ，有以下性质：(1) 1 * A = A ；(2) k(l A ) = (k l )A ;(3) k ( A + B )= kA + kB ;(4) (k + l )A = kA +lA ; (5) k (A + B ) = kA +kB .2.3 分块矩阵的初等变换性质我们对于分块矩阵，也有其运算性质：设 A 、 B 是m ⨯ n 矩阵，若对它们有相同的划分，也就有：⎛A 11 + B A 1t + B 1t ⎫ ⎪ 加法：A + B = ⎪ . ⎪ A + B A + B ⎪ ⎝ s 1 s 1 st st ⎭乘法：C = A B , 其中：∑ ⎪ 1 C i j = A i 1B 1j + A i 2B 2j+ + A i n B n j⎛k A 11k A 1 ⎫⎪ n= A i k B k j .k =1数乘：k A =⎪ .⎪ k Ak A⎝s 1 s t ⎭总结了矩阵的运算性质，我们主要看看分块矩阵初等变换性质：定义 2.3.1 [2] 由单位矩阵 E 经过一次初等变换得到的矩阵称为初等矩阵. 初等矩阵都是方阵，包括以下三种变换：(1) 互换矩阵 E 的i 行与 j 行的位置; (2) 用数域 P 中的非零数c 乘 E 的i 行; (3) 把矩阵 E 的 j 行的k 倍加到i 行.定义 2.3.2 [5] 将单位矩阵分块，并施行如下三种变换中的一种变换而得到的方阵称为分块初等矩阵:(1) 对调两块同阶的块所在的行或列; (2) 某一块乘以同阶的满秩方阵;(3) 某一块乘以一个矩阵后加到另一行上(假定这种运算可以进行).如：我们对分块矩阵⎛ A B ⎫进行相应变换，只要应用矩阵的计算性质，左乘对⎝C D ⎭ 应分块矩阵： ⎛ O E m ⎫ ⎛ A B ⎫ ⎪⎪⎛C D ⎫ ⎪ ⎝E n O ⎭ ⎝C D ⎭⎝ A B ⎭ ⎛P O ⎫ ⎛ A B ⎫ ⎛P A = P B ⎫ O E ⎪C D ⎪ ⎪⎝ n ⎭ ⎝⎭ ⎝ C D ⎭ ⎛E m O ⎫ ⎛ A B ⎫ ⎛ = A B⎫P E ⎪C D ⎪ ⎪C + P AD + P B⎝ n ⎭ ⎝⎭ ⎝ ⎭2.4 矩阵的分块技巧对矩阵的分块不是唯一的，我们往往根据问题的不同进行不同的分块，分块的合适与否，都对问题的解决至关重要，最常见的有四种分块方法[6] ：(1) 列向量分法，即A =(1,⎛ ⎫ ⎪, n )，其中j 为 A 的列向量.(2) 行向量分法，即A = ⎪ ，其中j 为 A 的行向量.⎪ ⎝ m ⎭=1⎪ (3)分两块，即A = (A 1, A 2 ),其中A 1 ,A 2 分别为A 的各若干列作成.或 A = ⎛B ⎫ ，其中B ，B 分别为 A 的若干行作成. B ⎪1 2 ⎝ 2 ⎭⎛C 1 C 2 ⎫(4) 分四块，即A =C C ⎪ .⎝ 3 4 ⎭我们在进行分块时，希望分割的矩阵块尽可能是我们所熟悉的简单矩阵，于是，我们有必要熟悉一些常见的矩阵.2.5 常见的矩阵块我们把高等代数中学习过的一些常见矩阵总结如下： （1） 单位矩阵：对角线元素都为1，其余元素为0 的n 阶方阵. （2） 对角矩阵：对角线之外的元素都为0 的n 阶方阵. （3） 三角矩阵：对角线以上（或以下）元素全为0 的n 阶方阵. （4） 对称矩阵：满足矩阵 A 的转置和 A 相等. （5） 若尔丹（Jordan ）块：形如⎛ 0 1 0 0 ⎫ 0 ⎪J ( ,t ) ⎪= ⎪0 0 ⎪ 0 0 0 1 ⎝ ⎭（6） 若尔丹形矩阵：由若干个若尔丹块组成的准对角矩阵, 其一般形状形如：⎛A 1 ⎫⎪ A 2⎪ ⎪ ⎪A ⎪ ⎝n ⎭在复杂矩阵中，找到这些矩阵块，会使计算简化.3.1 行列式计算的应用3 分块矩阵及其应用定理 3.1.1 [2] 拉普拉斯（Laplace ）定理:设在行列式 D 中任意取定了k 个 行.由这k 行元素所组成的一切k 级子式与它们的代数余子式的乘积的和等于行列式 D .事实上，行列式计算中的拉普拉斯定理就包括了矩阵分块的思想，它通过取k 级子式的方法，提取出矩阵内的矩阵块. 然而，在行列式计算中，行列式a ⎪ a 按行或列的展开更为常用. 这里，我们最常用到的是取列向量分块和行向量分块.例 3.1.1 [7] ：（爪形行列式）计算行列式：a 01 1 1 1 a 10 0 1 0 a 2 0 ,其中a i ≠ 0(i = 1, 2, , n ) .1 0 0 a n解:设Q =A D ,其中A = (a )C B a 1 B =，C = ( 1, 1, , 1)T ，D = ( 1, 1, , 1) .a n因为a i ≠ 0(i = 1, 2, , n ) ，所以 B 是可逆矩阵.-1⎛n 1 ⎫又易知: A - D B C = a 0 - ∑ ⎪ . ⎝ i =1 i ⎭根据分块矩阵乘法： ⎛ E0 ⎫ ⎛ A D ⎫ --1 ⎪ ⎪= ⎛A D ⎫-1 ⎝ C A E ⎭ ⎝C B ⎭ ⎝ 0 B - C A D ⎭A D -1 -1 ⎛ n 1 ⎫则：= AB - C A D =B A - D BC = a a a a-∑ a ⎪C B⎛n 1 ⎫ 12n 0⎝i =1 i ⎭故：原行列式=a 1a 2 a n a 0 - ∑ ⎪ . ⎝ i =1 i ⎭例 3.1.2 [7] ：(对角行列式)计算行列式：adH 2n= a d.c bcb解：令⎪ a x A =⎛a ⎫⎪ ，B = ⎛b ⎫⎪ ，C = ⎛ c ⎫ ⎛ ，D = d ⎫⎪ ⎪ ⎪ ⎪ ⎪ a ⎪ b ⎪ c ⎪ d ⎪ ⎝ ⎭ 为n 阶方阵. 由于a ≠ ⎝ ⎭ ⎝ ⎭ ⎝ ⎭ 0,故 A 为可逆方阵.⎛ b - c a -1d⎫⎪ 又易知：B - C A -1D =⎝ b - c a -1d ⎪ b - -1 ⎪ ca d ⎭故 H 2n= A D = C BAB - C A -1D = a n (b - c a -1d )n= (a b - c d )n .例 3.1.3 [8] ：设 A 、 B 、C 、 D 都是n 阶矩阵，证明当 AC = CA 时， A 可逆时，有A D= A B - C DC B⎛ A D ⎫ ⎛E -A 1D-⎛ A 0 ⎪ ⎫,证明：若 A 可逆，⎪ ⎪ =-1 ⎝C B ⎭ ⎝OE ⎭ ⎝C B - C A D ⎭A D故：=C BAB - C A -1D = A B - A C A-1D = A B - C D .注意到，这里计算分块矩阵行列式和计算一般数字矩阵行列式有所区别，不是简单的a d c b= a b - c d ，其矩阵块限制条件有所加强. 所以本例告诉我们，在矩阵分块以后，并非所有一般矩阵性质都可以应用到分块矩阵中.3.2 线性方程组的应用对于线性方程组，我们有以下四种表述： （1） 标准型：⎧a 11x 1 + a 12x 2+ + ax = b ⎪ 1nn 1⎨ax + ax + + a x = b ; ⎪a 21 x 1+ 22 2 + + 2n n a x = b ⎩ m1 1 m2 2 m n n m （2） 矩阵型：令A = ⎣a i j ⎦m ⨯n，x = (x 1, x 2, , x n )' ，B = (b 1, b 2, b m )' 方程组可以表述为： Ax = B ;（3） 列向量型：令2⎢a ⎥ ⎝O O⎪ ⎪ ⎪ ⎡a 11 ⎤ ⎢21 ⎥⎡a 12 ⎤⎥ 22 ⎡a 1n ⎤ ⎢ ⎥ = ， 1 ⎢ ⎥ 2 = ， ， ⎢ ⎥= ⎢a 2n ⎥ n ⎢ ⎥ ⎢ ⎥ ⎣a m 1 ⎦ ⎢ ⎥ ⎣a m 2 ⎦ ⎢ ⎥ ⎣a m n ⎦则方程组又可以表述为：x 11 + x22+ + x nn = B ;（4）行向量型： x ' + x ' + + x' = B ' .1 12 2n n可见，矩阵分块为我们解方程组提供了新的思路.事实上，在求齐次线性方程组系数矩阵的秩时，在判断非齐次线性方程组是否有解时，行列向量组的合理应用，使得问题解决更加便捷、明了.例 3.2.1：（齐次线性方程组）求解方程组：⎧ x 1 + 2x 2 2x ⎪ + x + 2x 3 - 2x + x 4 = 0 - 2x = 0 ⎨ 1 x -2x - 4x 3 - 3x 4=0 ⎩ 1 2 3 4 解：对系数矩阵施行行变换,并将结果用分块矩阵表示：⎛1 0 -25 ⎫ - 3⎪ ⎛ 1 2 2 1 ⎪⎫ ⎛ 1 2 2 1 ⎪⎫4 ⎪ ⎛E C ⎫ A = 2 1 -2 -2 0 -3 -6 -4 0 1 2 ⎪ = 2 ⎪ ⎪1 -1 -4 -3⎪ 0 -3 -6 -4⎪ 3 ⎪ 12 ⎭ ⎝ ⎭ ⎝ ⎭ 0 0 0 0 ⎪⎪ ⎝ ⎭R ( A ) = 2，基础解系含4 - 2 = 2 个.而方程又满足：相应的可以取：⎛E 2 C ⎫ ⎛1 ⎫ = ⎛ 0⎫⎪ ,⎝O 1 O 2 ⎭ ⎝2 ⎭⎝ 0⎭⎛ 5 ⎫ 2 3 ⎪ ⎛ -C ⎫⎪⎝ E 2 ⎭⎪ = -2 4 ⎪3 ⎪1 0 ⎪ ⎝ 0 1 ⎭-⎪ 0 3 ⎪⎭⎛ 2 ⎫ ⎛ 5 ⎫3 ⎪有通解： = k + k，其中= -2⎪1， =- ⎪ 4 ⎪ . 1 12 21 ⎪2 ⎪ ⎪ ⎝ 0 ⎭⎪ 1 ⎪ ⎝ ⎭例 3.2.2 [9] ：（非齐次线性方程组）求解方程组：⎧⎪ x 1 + 2x 2- 3x 4 + 2x 5 = 1 x - x - 3x + x - 3x = 2 ⎪ ⎨ 1 2 3 4 52x - 3x + 4x - 5x + 2x = 7 ⎪ 9x ⎩ 1= 25 解：我们分别对于方程组的系数矩阵和增广矩阵求秩：r ( A ) = 3，而r ( A ) = 4 , 故r ( A ) ≠ r ( A) . 从而方程组无解. ⎛ Λ45 -b ⎫事实上，我们可以利用分块矩阵叙述：经对分块矩阵 ⎝ E变换，都不能把最后一列变成0 ,所以该方程组无解.例 3.2.3：证明： n 阶方阵 A 的秩为n- 1，则r a n k ( A* )=1首先证明此例需要利用的一个引理： 4进行行列0 引理：A = (a i j )n ⨯n ，B = (b i j )n ⨯n ，r( A ) = r ，A B =0 ，则r ( B ) ≤ n - r证明：对矩阵 B 进行列向量的分块，B = (B 1, B 2, B n ) ,A B = 0 则有：A B i= 0 ，B i 是AX = 0 的解. 而A X =0 基础解系有n - r 个解.故：r ( B ) ≤ n - r 再证明本例： 因为r ( A )= n - 1，则 A = 0 ，A 至少有一个n -1级子式不为零,r a n k ( A* ) ≥ 1.而：A * =AE = 0 .利用引理得：r a n k ( A * ) ≤ 1，故r a n k ( A )=*.51 - 9 x +2 6x - 163 x4 + 2x 52 3 4 5⎝⎪ 1 2= ⎪ ⎪ 得证.3.3 求矩阵逆的应用我们在求矩阵逆的时候包括很多方法：利用定义求逆、利用伴随矩阵求逆、 利用初等变换求逆、混合采用初等行列变换求逆等等.这里我们统一用矩阵分块的思路来求矩阵的逆.例 3.3.1 [6] ：设 A 、 B 是n 阶方阵，若 A + B 与 A - B 可逆，试证明： ⎛ A B ⎫可逆，并求其逆矩阵. B A ⎭ ⎪ 解：令D = ⎛ A B ⎫，由假设知 A + B ≠ 0 , A - B ≠ 0B A ⎪ .那么：D =A B⎝ ⎭A +B B =A + BB= A + B A - B ≠ 0 .B AB + A AA - B即 D 可逆. 再令D -1 ⎛D 1= D 2⎫ , 由D -1 = E ，即：可得：D D ⎝ 3 4 ⎭⎛ A B ⎫ ⎛D D ⎫ ⎛E 0 ⎫ ⎪ ⎪⎪ ⎝B A ⎭ ⎝D 3D 4 ⎭ ⎝ 0E ⎭⎪⎧A D 1 + B D 3 = E B D + A D = 0⎪12⎨A D +B D = 0 B D 2 + A D 4 = E ⎩ 2 4将第一行和第二行相加、相减，得：⎪D + D = ( A + B )-1 ⎨1 3⎩D 1 - D 3= ( A - B )-1 解之得：D = 1 ⎡( A + B )-1 + ( A - B )-1 ,D = 1⎡( A + B )-1 - ( A - B )-11 2 ⎣⎦ 2 2 ⎣⎦类似地：D 2所以： = D 3 ,D 4= D 1 .⎛ A B ⎫-11 ⎛( A + B )-1 + ( A - B )-1 ( A + B )-1 - ( A - B )-1 ⎫⎪ = 2 -1 -1 -1-1 ⎪ . ⎝B A ⎭ ⎝( A + B ) - ( A - B )( A + B ) + ( A - B ) ⎭ =⎝⎭ ⎝ - ⎪⎪ ⎪0 例 3.3.2 [6] ：已知分块形矩阵M = ⎛ A B ⎫可逆，其中 B 为p ⨯ p 块， C 为C 0 ⎪ ⎝ ⎭q ⨯ q 块，求证： B 与C 都可逆，并求M-1 . 解：由0 ≠M = (-1)p qBC ，则： B ≠0 , C ≠ 0 ,即证 B 、C 都可逆.这里用分块矩阵的广义初等变换来求逆： ⎛ A B E p0 ⎫ → ⎛ A B E 0 ⎫ → ⎛ 0B E -AC -1 ⎫⎪ ⎪ -1 ⎪ -1⎝C 0 0 Eq ⎭ ⎝E 0 0 C ⎭ ⎝E 0 0 E ⎭→ ⎛ 0 E B -1-B -1A C -1 ⎫ → ⎛E 0 0 C-1 ⎫E 0 0 C-1⎪ 0 E B -1-B -1A C -1 ⎪ ⎭-1⎛C -1 ⎫故 ：M = B -1-B -1A C-1 ⎪ . ⎝⎭备注：本例和上例属于同一个类型的问题，但我们利用分块矩阵，可以有两种不同的方法来解决，待定系数法和广义初等变换都是求逆的有效方法.值得注意的是，在题目没有直接给出分块矩阵的情况时，我们要学会自己构造:⎛ 1 0 1 ⎫ 例 3.3.3 [10] ：求矩阵A = 2 1 0 ⎪的逆矩阵.⎝ ⎭ 解：构造矩阵：⎛ 10 1 1 00⎫⎪⎛ 1 0 1 1 0 0⎫⎪2 0 0 1 -2 -2 1 0 D = ⎛ A E ⎫= -3 1 0 0 1 2 -5 0 0 1⎪ → 0 2 -2 3 0 1⎪ ⎪⎪ ⎪ ⎝E O ⎭6⨯6 1 0 0 0 00 1 0 0 0 0⎪ 1 0 0 0 0 0⎪ 0⎪ 0 1 0 0 0 0⎪0 0 1 0 0 0 0 1 0 0 0 ⎝ ⎭ ⎝ ⎭⎛ 1 0⎫⎪ 00 1⎪ →1 0⎪ ⎛ 1 0 1 1 0 0⎫ 0 1 -2 -2 1 0 0 1⎪ → 1 0⎪⎪ ⎪ 0 0⎪ 0 0⎪ 00⎪ 0 0⎪ ⎝⎭ ⎝ ⎭ 0 1 1 0 1 -2 -2 1 0 2 7 -2 0 0 0 0 1 0 0 0 0 1 0 00 2 7 -2 0 -1 0 0 1 0 0 0 0 1 0 0- - ⎪ ⎝ ⎭ ⎝ ⎭1 ⎛ 1 0 0 1 0 0⎫⎪0 1 0 2 1 0 ⎛ 10 0 1 0 0⎪⎫ 0 1 0 2 1 0 0 0 17 -2 1⎪0 0 2 7 -2 1⎪1 ⎪→ ⎪ → 10 - 0 0 0⎪ .1 0 -1 0 0 0⎪2⎪ 0 1 2 0 0 0⎪ 00 10 01 0 0 0⎪0 0 1 0 0 0⎪⎝所以;⎭⎪⎝2⎭⎛1 0 1 ⎫ ⎛ 5 1 ⎫- 2 ⎪⎛ 1 0 0⎫ - 2 -1 - 2 ⎪ A -1 = 0 1 1 ⎪ -2 1 0⎪ = 5 -1 1 ⎪ . ⎪ ⎪ ⎪ 1 ⎪ 7 -2 17 1 ⎪ 0 0 2 ⎪ ⎝ ⎭ 2 -1 2 ⎪ 此方法在计算上并不简单，但是它把平常的单纯的一种变换变成了两种变换同时应用，把已知的可逆矩阵置于含单位矩阵的分块矩阵中，以此求逆矩阵， 有时比较简单.3.4 矩阵秩基本不等式矩阵理论中， 矩阵的秩是一个重要的概念，而矩阵经过运算后所得新矩阵 的秩往往与原矩阵的秩有一定关系. 现把高等代数书中有关矩阵秩最基本的不等式总结如下：（1）矩阵和的秩不超过两矩阵秩的和.即：设 A 、 B 均为m ⨯ n 矩阵，则：r ( A + B ) ≤ r(A ) + r ( B ) .（2）矩阵乘积的秩不超过各因子的秩.即：设 A 是m ⨯ n 矩阵 , B 是n ⨯ s 矩（3）r ⎛A B ⎫阵，则：r ( A B ) ≤≥ r ( A ) + r ( B ) . m i n {r ( A ) , r ( B )}.（4）r ⎝ 0 C ⎭ ⎪ ⎛A ⎫ ⎪⎪ ≥ A i j .A ⎪ ⎝ m ⎭再来介绍由分块矩阵证明导出的两个基本不等式例 3.4.1[11] ：（薛尔弗斯特不等式）设A = (a ) ，B = (b ) ，证明：ij s ⨯nij n ⨯mr a n k ( A B ) ≥ r a n k ( A ) + r a n k ( B ) - n⎪ 证明：由分块矩阵的乘积⎛ E n 0⎪ ⎫ ⎛E B ⎫ ⎪⎛E n -B ⎫⎛E n 0 ⎫ -A E A n0 0 E ⎪ = ⎪0 - ⎝ s ⎭ ⎝ ⎭ ⎝ 知：m ⎭⎝ A B ⎭ r a n k⎛E n B⎫ = r a n k (E ) + r a n k ( -A B ) = n + r a n k ( A B )A 0 ⎪n.⎝ ⎭但,r a n k⎛E nB ⎫ A 0⎪= r a n k⎛B E n ⎫ ≥ r a n k ( A ) + r a n k ( B ) ⎪故：得证.⎝⎭ ⎝ 0 A ⎭.n + r a n k ( A B )≥ r a n k ( A ) + r a n k ( B )备注：在矩阵秩不等式的证明过程中，我们往往会构造如下的分块矩阵： (1) 矩阵不等式中含两个不同矩阵：构造 ⎛A 0 ⎫⎪;⎝ 0 B ⎭(2) 矩阵不等式中含有两个不同矩阵及阶数：构造⎛ A E ⎫ ⎪ 或者 ⎛ A 0 ⎫ ⎪.⎝ 0 B ⎭ ⎝E B ⎭具体分块矩阵的元素则要看题目所给的条件.例 3.4.2 [6] ：（Frobenius 不等式）设 A 、 B 、C 是任意3 个矩阵，乘积ABC 有意义，证明：r ( A B C ) ≥ r ( A B ) + r ( B C ) - r ( B )证明：设 B 是n ⨯ m 矩阵，r ( B ) = r那么存在n 阶可逆阵 P ， m 阶可逆阵Q ，使B = ⎛Er0⎫ P ⎪ Q .⎝ 0 0⎭把 P 、Q 适当分块：P = (M , S ),Q =⎛N ⎫, 由上式有： T ⎝ ⎭故：r ( A B C )= r ( A M N C ) B = (M , S )⎛E r0⎫ ⎛N ⎫ = M N .⎪ ⎪ ⎝ 0 0⎭ ⎝T ⎭≥ r ( A M ) + r ( N C ) - r0 ≥ r ( A M N ) + r ( M N C ) - r ( B )得证.= r ( A B ) + r ( B C ) - r ( B ) .3.5 矩阵秩不等式证明的应用矩阵基本不等式的证明思路，在一般不等式中也常常用到， 以下例题是对矩阵秩不等式的推广及其应用：例 3.5.1[11] ：设 A 为m ⨯ k 矩阵， B 为k ⨯ n 矩阵，则证明：r a n k ( A )+r ank( B ) - k≤ r ank( AB) ≤ m i n {r a n k ( A ) , r a n k ( B )}证明：先证明右边的不等式，由：(A 0)(E k0 B ) = ( A A B ) ;E n可得：⎛E k A E 0⎪ ⎫ ⎛B ⎪⎫ = ⎛ B A B ⎫⎪ ,⎝m ⎭ ⎝ ⎭⎝ ⎭r a n k ( A ) =r ank( A 0) = r a n k ( A A B ) ≥ r a n k ( A B ) ;r a n k ( B ) = r a n k ⎛ B ⎫ = r a n k ⎛ B ⎫≥ r a n k ( A B ) .⎪ ⎪⎝ 0 ⎭ ⎝AB ⎭ 再证左边的不等式.注意到下列事实：⎛E m -A ⎫ ⎛ A 0 ⎫ ⎛E ⎪k -B ⎫ = ⎛ 0 -A B ⎫⎪ 0 E ⎪E B 0E⎪ E 0 ⎝k ⎭ ⎝ k 则：⎭ ⎝ n ⎭⎝ k ⎭0 ⎫⎛ 0r a n k ⎛ A ⎪ = r a n k-A B ⎫ ⎪于是：⎝E kB ⎭ ⎝E k0 ⎭⎛ A 0 ⎫r a n k ( A ) + r ank ( B ) ≤r ank ⎪ = r a n k ( -A B ) + r a n k (E k )= r a n k ( A B ) + k⎝E kB ⎭ 从而: r a n k ( A ) + r a n k ( B ) - k ≤ r a n k ( A B ) .这里也是用到构造矩阵的方法.例 3.5.2 [6] ：设n 阶矩阵 A 、 B 可交换，证明：r a n k ( A + B ) ≤ r a n k ( A ) + r a n k ( B ) - r a n k ( A B )→ → , ⎝ ⎭ 解：利用分块初等变换，有：⎛A O ⎫ ⎛A B ⎫ ⎛A + B B ⎫⎪ ⎪⎪ ⎝O B ⎭ ⎝O B ⎭ ⎝ B B ⎭ 因为 AB = BA ，所以：⎛ E O ⎫ ⎛A + B B ⎫ = ⎛A + B B ⎫ .B -A - ⎪ B ⎪ O- ⎪B B A B ⎝ 于是，有：⎭ ⎝ ⎭ ⎝ ⎭r a n k ( A ) + r a n k ( B )= r a n k⎛A + B B ⎫≥ r a n k ⎛A + B B ⎫B ⎪⎝ B ⎭ ⎝ ⎪O-A B ⎭即：r a n k ( A + B )得证.≥ r a n k ( A + B ) + r a n k ( A B ) .≤ r a n k ( A ) + r a n k ( B ) - r a n k ( A B ) .例 3.5.3：设 A 是n 阶方阵，且r ( A ) = r ( A 2 ,证明：对任意自然数k ,有r ( A k ) = r ( A )⎛A 2O ⎫证：构造分块矩阵 O A 2 ⎪，由 Frobenius 不等式： 2 2 2 ⎛A O ⎫ ⎛A 2 -A 3 ⎫ ⎛O -A 3 ⎫ 3 r ( A )+r( A ) ≤ r ⎪ = r A A 2 A O ⎪ = r A O ⎪ = r ( A ) + r ( A ) . 由：r ( A ) = r ( A 2 ) ⎝ ⎭ ⎝ ⎭ ⎝ ⎭所以，r ( A3 ) = r ( A 2 * A )≤ r ( A2 ) .故： r(A 2 ) = r ( A 3 .由此可推得：r ( A3) = r ( A 4) , r ( A4) = r ( A5 ) , .故：对任意自然数k , 有：r ( A k ) = r ( A ) .3.6 综合应用在掌握了分块矩阵的技巧之后，可以由其导出的一个重要的定理：特征多项式的降阶定理，以下主要讨论该定理及其结论的应用.例 3.6.1 [6] ：（特征多项式的降阶定理）设 A 是m ⨯n 矩阵， B 是n ⨯ m 矩阵. 证明: AB 的特征多项式f A B ( ) 与 BA 的特征多项式f B A( ) 有如下的关系：nm1 2 s证：先要把上式改写为：n f () =m f () .A BB AnE -m A B =mEE 1 Bn - B A .用构造法，设 ≠ 0 ，令： H =n.A E m⎛1 ⎫ ⎛E 1 B ⎫对 ⎛E n 0⎪ ⎫ E n B ⎪= n ⎪ ⎝ -A E⎪⎪ 1 ⎪ 两边取行列式得： n ⎭ A E⎝ m ⎭ 0 E - ⎝A B ⎪⎭ H = E -1 A B = 1 m E - A B .⎛E 1 B ⎫ ⎛E nm 0 ⎫⎛ 1( ) m1 B ⎫ 再对 n ⎪ -A E ⎪ E - B A ⎪ 两边取行列式得： ⎪ ⎪ = n⎪⎝ A E m ⎭⎝ n ⎭ ⎝ H = E -0 1B A = E m ⎭ 1 n E - B A .故： 1nE n- B A =1Em mn- A B() nmE n - B A = nE m - A B .上述等式是假设了 ≠ 0 ，但是两边均为的n + m 次多项式，有无穷多个值使它们成立（0）≠ ，从而一定是恒等式，即证.这个等式也称为薛尔弗斯特（Sylvester ）公式. 以下例题是定理的应用. 例 3.6.2 [6] ：设 A 为m ⨯ n 矩阵， B 为n ⨯ m 矩阵，证明： AB 与 BA 有相同的非零特征值.证：由定理：m E - B A = n E - A B .设 E m- A B = m -s (- ) ( - ) ( - ) ,其中12 m ≠么有：0 ，即 AB 有s 个非零特征值：1, 2, , s , 由上面两式,那nE - B A = ( - 1) ( - ) 2 (- )n- s s即证 BA 也只有s 个非零特征值：1, 2, , s .m∑ 例 3.6.3 [6] ：设 A 、 B 分别是m ⨯n 和n ⨯ m 矩阵，证明：t r A B = t r B A .解：由上例知，若E - A B = m -s ( - a ) ( - a )m1s其中a 1a 2 a s ≠ 0. 则 AB 的全部特征值为1 = a 1, , s= a s , s +1= = m = 0 ,且：E - B A = n -s ( - a ) ( - a ) .n1s即 BA 的全部特征值为:1 = a 1,2 = a2, ,s +1= = n = 0 .从而 t r A B =sa ii=1=t r B A .可见，在一些问题中，直接利用特征多项式的降阶定理会更加方便处理，这里则要求我们对分块矩阵的了解更加深刻.结论本文主要通过“分块矩阵、分块矩阵及其应用”两个部分，分别简单介绍了分块矩阵的性质概念、导出的定理结论和相关应用.主要是将分块矩阵的技巧和推广做了一个内容的总结.本文简单的将矩阵工具应用于计算行列式、解决线性方程组、求矩阵的逆、证明矩阵秩的相关定理等，对应不同问题也举了几个重要的应用以及它们的综合应用.将以前出现的矩阵思想整体化，并对相关知识也做了一个系统的复习.最后，本文还有一些不足之处，有待于进一步的改善和提高.参考文献[1] 上海交通大学线性代数编写组. 线性代数[M]. 高等教育出版社, 1982. [2] 北京大学. 高等代数{M}. 高等教育出版社, 1998.[3] 高百俊. 分块矩阵的初等变换及其应用[J]. 伊犁师范学院学报, 2007(4):14-18.[4]张红玉, 魏慧敏. 矩阵的研究[M]. ft 西人民出版社, 2010.[5]雷英果. 分块初等方阵及其应用[J].工科数学, 1998, 14(4):150-154. [6]钱吉林. 高等代数题解精粹(第二版)[M]. 中央民族大学出版社, 2010.[7] 王莲花, 李念伟, 梁志新. 分块矩阵在行列式计算中的应用[J]. 河南教育学院学报(自然科学版), 2005, 14(3):12-15.[8] 张贤科, 许甫华. 高等代数学[M]. 清华大学出版社, 1998:91-96.[9]杨子胥. 高等代数习题集[M]. ft东科学技术出版社, 1981.[10]鲁翠仙. 分块矩阵在求矩阵逆的应用[D]. 云南:云南大学数学系数学研究所,2009：14-15.[11]刘丁酉. 高等代数习题精解[M].中国科学技术大学出版社, 1999.“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

分块矩阵的计算反三角矩阵分块矩阵的计算是矩阵理论中的一个重要概念，它可以将大型矩阵划分成若干个小块进行计算，从而简化计算过程。

反三角矩阵是指一个矩阵的每个元素都是该元素在原矩阵中的倒数。

本文将介绍分块矩阵的计算方法以及如何计算反三角矩阵。

1.分块矩阵的基本概念分块矩阵是指将一个大型矩阵分成若干个子块的矩阵。

分块矩阵的好处是可以将复杂的计算过程划分成若干个简单的子过程，从而简化计算。

分块矩阵可以按照行、列或者更复杂的方式进行划分。

2.分块矩阵的计算方法对于一个分块矩阵A=[A11,A12;A21,A22]，其中A11、A12、A21和A22都是矩阵，那么矩阵A的运算可以表示为：A=[A11,A12;A21,A22]=[A11*A11+A12*A21,A11*A12+A12*A22;A21*A11+A22*A21,A21*A12+A22*A22]3.反三角矩阵的计算方法反三角矩阵是指一个矩阵的每个元素都是该元素在原矩阵中的倒数。

要计算反三角矩阵，首先需要求出原矩阵的每个元素在倒数后的矩阵中的位置。

然后，可以通过遍历原矩阵的每个元素，将其倒数值放入对应位置的新矩阵中。

具体地，如果有一个三角矩阵A=[a11,0, 0a21,a22, 0...,...,...,...;an1, an2, ..., ann]那么其反三角矩阵B=[1/a11,0, 0-1*(a21/a11^2),1/a22, 0...,...,...,...;-1*(an1/a11^2), -1*(an2/a22^2), ..., 1/ann]注意到，对于非主对角线上的元素，其位置上的元素需要除以主对角线上的元素的平方，而非主对角线上的元素需要除以主对角线上的元素。

4.反三角矩阵的计算实例假设有一个三角矩阵A=[2,0,0;1,3,0;4,5,6]首先我们需要求出每个元素在新的矩阵中的位置：B=[1/2,0,0;-1*(1/2^2),1/3,0;-1*(4/2^2),-1*(5/3^2),1/6]=[1/2,0,0;-1/4,1/3,0;-1/8,-5/9,1/6]可以看到，反三角矩阵中的每个元素都是对应的原矩阵元素的倒数。

矩阵分块求行列式
矩阵分块是一种将一个大的矩阵划分成几个较小的子矩阵的方法。

在计算行列式时，利用矩阵分块可以简化计算过程。

具体步骤如下：
1. 将原始矩阵按照某种规则进行分块，可以按行分块，也可以按列分块。

2. 对于每个子矩阵，计算其行列式。

3. 利用分块矩阵的行列式性质进行计算。

具体来说，如果一个矩阵被分为两个子矩阵，并且这两个子矩阵的维度分别为
n1×n1 和 n2×n2，那么整个矩阵的行列式可以表示为：det(A)
= det(A1) × det(A2) ，其中 A1 是 n1×n1 子矩阵的行列式，A2
是 n2×n2 子矩阵的行列式。

4. 对于每个子矩阵的行列式，可以继续应用分块矩阵的行列式性质，直到得到一个维度较小的子矩阵，其行列式可直接计算得到。

5. 将得到的所有行列式进行求和或相乘，得到最终的行列式值。

需要注意的是，具体的矩阵分块方法和分块矩阵的行列式性质会根据具体的矩阵形式而有所不同。

在实际计算中，可以根据矩阵的性质和分块的需要选择合适的分块方法。