第3章静定结构的受力分析(刚架-组合结构)_图文(精)
- 格式:doc
- 大小:19.00 KB
- 文档页数:4





第三章静定结构受力分析主要任务:要求灵活运用隔离体的平衡条件,熟练掌握静定梁、刚架、桁架、拱、组合结构等的支反力和内力计算、内力图的绘制,及它们的受力性能分析§3-1 单跨静定梁的内力分析一、截面上内力符号的规定:轴力—截面上应力沿杆轴切线方向的合力,使杆产生伸长变形为正,画轴力图要注明正负号;剪力—截面上应力沿杆轴法线方向的合力, 使杆微段有顺时针方向转动趋势的为正,画剪力图要注明正负号;弯矩—截面上应力对截面形心的力矩之和, 水平杆件下侧受拉的弯矩为正。
弯矩图画在杆件受拉一侧,不注符号。
F N F N F Q F Q M M2、截面法若要求某一横截面上的内力,假想用一平面沿杆轴垂直方向将该截面截开,使结构成两部分;在截开后暴露的截面上用力(内力)代替原相互的约束。
对于截开后结构的两部分上,截面上的内力已成为外力,因此,由任一部分的静力平衡条件,均可列出含有截面内力的静力平衡方程。
解该方程即将内力求出。
内力计算式(用截面一侧上外力表达的方式):FN =截面一侧所有外力在杆轴平行方向上投影的代数和。
左左为正,右右为正。
FQ =截面一侧所有外力在杆轴垂直方向上投影的代数和。
左上为正,右下为正。
Μ =截面一侧所有外力对截面形心力矩代数和。
弯矩的竖标画在杆件受拉一侧。
例3-1-1求图(a )所示简支梁在图示荷载下截面的内力。
解:1)支座反力∑ΜA =0F By ×4﹣10×4×2﹣100×(4/5)×2=0F by =60kN (↑)∑ΜB =0F Ay =60kN (↑) ∑F x = 0F Ax +100×(3/5)=0F Ax =-60kN (← )由∑Fy = 0校核,满足。
2)C截面内力∑Fx =0FNC -60=0FNC =60 kN∑Fy =0FQC -60+10×1.5=0FQC =45kN∑ΜC =0ΜC -60×1.5-10×1.5×(1.5/2)=0ΜC =101.25 kNm (下侧受拉)说明:计算内力要点:1)所取的隔离体(包括结构的整体、截面法截取的局部),其隔离体周围的所有约束必须全部切断并代以约束力、内力。



1 结构力学多媒体课件◆几何特性:无多余约束的几何不变体系◆静力特征:仅由静力平衡条件可求全部反力和内力◆常见静定结构:梁、刚架、三铰拱、桁架和组合结构。
◆静定结构受力分析的内容:反力和内力的计算,内力图的绘制和受力性能分析。
◆静定结构受力分析的基本方法:选取脱离体,建立平衡方程。
◆注意静力分析(拆)与构造分析(搭)的联系◆学习中应注意的问题:多思考,勤动手。
本章是后面学习的基础,十分重要,要熟练掌握!容易产生的错误认识:“静定结构内力分析无非就是选取隔离体,建立平衡方程,以前早就学过了,没有新东西”一、反力的计算4kN1kN/mDCBA2m2m 4mCB A20kN/m 4m4m2m6mDCB A(1)上部结构与基础的联系为3个时,对整体利用3个平衡方程,就可求得反力。
(2)上部结构与基础的联系多于三个时,不仅要对 整体建立平衡方程,而且必须把结构打开, 取隔离体补充方程。
1、内力分量及正负规定轴力F N :截面上应力沿杆轴法线方向的合力。
以拉力为正,压力为负。
剪力F Q :截面上应力沿杆轴切线方向的合力。
以绕隔离体顺时针转为正,反之为负。
弯矩M :截面应力对截面中性轴的力矩。
不规定正负,但弯矩图画在受拉侧。
在水平杆中, 当弯矩使杆件下部纤维受拉时为正。
A 端B 端杆端内力 F Q ABF N ABM AB正 F N BA F Q BAM BA 正2、内力的计算方法K截面法:截开、代替、平衡。
内力的直接算式(截面内力代数和法)=截面一边所有外力沿截面法线方向投影的代数和。
轴力FN外力背离截面投影取正,反之取负。
剪力F=截面一边所有外力沿截面切线方向投影代数和。
Q外力绕截面形心顺时针转动,投影取正,反之取负。
弯矩M =截面一边所有外力对截面形心的外力矩之和。
外力矩和弯矩使杆同侧受拉时取正,反之取负。
2、内力的计算方法【例】如图所示简支梁,计算截面C 、D 1、D 2的内力。
2m 4m 2mA2kN/mCBD 1 D 210kN0.2m10kN3.75kN0.25kN3、绘制内力图的规定内力图是表示结构上各截面的内力各杆件轴线分布规律的图形, 作图规定:弯矩图一律绘在受拉纤维一侧,图上不注明正负号;剪力图和轴力图可绘在杆轴线的任一侧(对水平杆件通常把正号的剪力和轴力绘于上方),但必须注明正负号,且正负不能绘在同一侧。
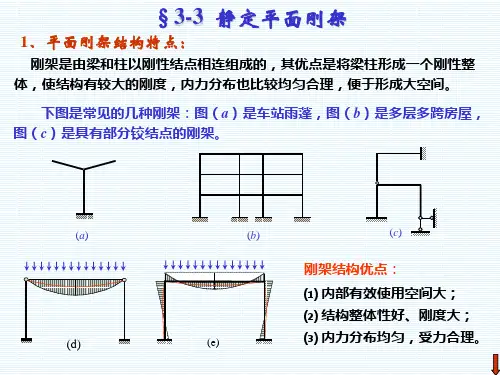


2013-6-25 3-3 静定平面刚架 教学要求: „ 了解刚架的特点。 „ 掌握刚架的支座反力和截面内力的计算。 „ 掌握刚架内力图的绘制。 主要内容: „ 刚架的特点 „ 刚架的内力计算和内力图 3-3 静定平面刚架 3-3 静定平面刚架 (2)静定平面刚架的分类 火车站站台 起重机的刚支架 小型厂房、仓库 1. 刚架的特点 (1)平面刚架的定义 刚架:由若干根直杆(梁和柱)用刚结点(部分可为铰 结点)所组成的结构。 平面刚架:组成刚架的各杆的轴线和外力在同一平面 平面刚架:组成刚架的各杆的轴线和外力在同一平面。 刚结点 铰结点 悬臂刚架 简支刚架 三铰刚架 3-3 静定平面刚架 3-3 静定平面刚架 (3)刚架的特点: ¾ 内部空间大,便于利用。 ¾ 刚结点处各杆不能发生相对转动,因而各 杆件的夹角始终保持不变。 ¾ 刚结点处可以承受和传递弯矩。 2. 刚架的内力计算 ™ ™ ™ 内力类型:弯矩、剪力、轴力 计算方法:截面法 内力的符号规定: 弯矩 弯矩 弯矩:弯矩图画在受拉一侧。 在 拉 侧 剪力:使杆段顺时针转动为正。 轴力:拉力为正。 1
2013-6-25 3-3 静定平面刚架 示例 3-3 静定平面刚架 示例 例1: 10kN/m B 2m m 计算步骤: (1)计算支座反力 (2)求杆端内力 (3)作内力图 例2: B VC C 10kN/m 1 HA VA A MA (4)结点校核 HA VA A 2m 1m 3-3 静定平面刚架 示例 3-3 静定平面刚架 小结 例3: 20kN/m D ¾ 刚架特点 刚结点处各杆件的夹角始终保持不变, C E 1 1m HB B 主要内力是弯矩; HA VA A 1m ¾ 刚架内力图绘制的解题步骤 求支座反力,杆端内力,作内力图。 1m VB 3-4 静定平面桁架 教学要求: „ 了解静定平面桁架的受力特点。 „ 掌握静定平面桁架内力计算的方法: ——结点法、截面法 3-4 静定平面刚架 主要内容: „ 桁架的特点和组成 „ 桁架内力计算方法 钢筋混凝土组合屋架 2m 2
2013-6-25 3-4 静定平面刚架 3-4 静定平面刚架 武汉长江大桥采用的桁架形式 3-4 静定平面刚架 3-4 静定平面刚架 1. 桁架的特点和组成 ¾ 定义: 结点均为铰结点的结构。 杆的内力主要是轴力。 ¾ 内力计算中的基本假定 桁架的结点为光滑的铰结点。 各杆的轴线均为直线且通过铰心。 荷载和支座反力都作用在结点上。 ¾ 桁架的各部分名称 上弦杆 腹杆 竖杆 斜杆 节间长度d 下弦杆 跨度 L 3-4 静定平面刚架 ¾ 按几何组成分 简单桁架: 分类 3-4 静定平面刚架 ¾ 按不同特征分 平行弦桁架 分类 折弦桁梁 由基本铰结三角形或基础, 依次增加二元体组成。 联合桁架: 由几个简单桁架联合组成的 几何不变的铰结体系。 复杂桁架: 非前两种为复杂桁架。 三角形桁架 梯形桁架 3
2013-6-25 3-4 静定平面刚架 B 2. 桁架内力的计算方法 D 3-4 静定平面刚架 B 3m 2. 桁架内力的计算方法 D E 3m C F 15kN 4m 15kN 4m G 15kN 例:求杆FC的内力。 例:求杆FC的内力。 ⅠE A 4m C 15kN Ⅰ 15kN 4m F G 15kN 4m E A 4m 分析: 截面法 截—代—平 NED NEC NFC Ⅰ 分析: 结点法 G 15kN 隔离体: 结点F NFE F 结点G NGE G 15kN Ⅰ F 15kN NFC 15 NFG NGF 3-4 静定平面刚架 B D E 3m 3-4 静定平面刚架 3. 零杆 A 4m C 15kN 4m 零杆 D F 15kN 4m G 15kN N1 =0 N2 =0 0 L形结点 N1 N2 隔离体:结点D 内力为零的杆 N3 =0 T形结点 NDB NDE NDC =0 3-4 静定平面刚架 3. 零杆 3-4 静定平面刚架 ¾ 零杆的判断 0 0 0 0 0 0 0 0 ¾ 截面单杆 任意隔离体中,除某一杆件外,其它所有待求内力的 杆件均相交于一点时,则此杆件为该截面的截面单杆。 0 0 O y 截面单杆的内力可直接根据隔离体平衡条件求出 4
2013-6-25 3-4 静定平面刚架 示例 3-4 梁静定平面刚架 示例 1. 求图示平面桁架结构中指定杆件a~d的内力。 1’ Ι 2’ 3’ 4’ a A V A = 1. 5 P 1. 求图示平面桁架结构中指定杆件a~d的内力。 Ι Ι 1’ 2’ 3’ ΙΙ 4’ Ι c d B 4 d 3 d A V A = 1. 5 P a b 1 2 P c d B 4 d 3 d 1 b 2 Ι 3 4 5 P P P 6d 1’ 2’ V B = 1. 5 P 3 ΙΙ 4 5 Ι Ι P P Ι 6d V B = 1. 5 P 解:(1)求支座反力 (2)求内力 (2)求内力 Nc Nd N k 5 P B 2d 1. 5 P 2d Na 1. 5 P Na Nb 4 d 3 4’ e B 1. 5 P 1 2 Nb P Nc d 4 P 5 Nd 4 3-4 静定平面刚架 示例 3-4 静定平面刚架 P 示例 b ¾ 求图示桁架指定杆件内力(只需指出所选截面 b P P b P 0 b 0 a 对称性 b 0 b a P 0 P 0 b 0 0 a a 正对称性 反对称性 3-5 组合结构 3 1 ——桁架和梁 3-5 组合结构 桥梁 屋架 加固工程 5
2013-6-25 3-5 组合结构 3-5 组合结构 高层建筑 3 2 内力计算——截面法 ¾ 区分桁架杆件和受弯杆件。 ¾ 选取脱离体时不要切断受弯杆件。 ¾ 先计算桁架杆件,后计算受弯杆件。 3-5 组合结构 示例 3-5 组合结构 例:绘制内力图 F D F C F D F C A 讨论: MA大小 h h a A A a E B XE E B a A YE YE A XE h 3-6 三铰拱 ¾ 杆 轴线为曲线; ¾ 在竖向荷载作用下产生水平反力。 3-6 三铰拱 ¾ 应用 桥梁,也适用于宽敞的大厅,如礼堂、展览馆、体育 馆和商场等。 6
2013-6-25 3-6 三铰拱 3-6 三铰拱 ¾ 类型 1. 内力计算 ¾ 内力类型 M、Q、N 拉杆拱 三铰拱 两铰拱 拱顶 拱 趾 无铰拱 拱轴线 拱 趾 内侧受拉为正 轴力压为正 顺时针转动为正 ¾ 拱的各部分名称 f L 拱高ƒ 起拱线 跨度L ¾ 计算方法 截面法 高跨比 3-6 三铰拱 a b FP D C HA A VA A 0 VA 0.5l 0.5l FP D C l b 0 VA = FP = VA l a 0 VB = FP = VB f l B 0 HB 0.5 V l M H A = H B= = C B VB f f b V0 = F a 0 VA = FP B P B l l 0 M = 0.5V l VB 0 C 0 B (1 支座反力 3-6 三铰拱 NK FP C ϕK y D K ( x ,M K QKy K K a b (2 内力的计算 0 QK = QK cos ϕ K − H sin ϕ K f A B x HA H B = M 0 − Hy M H K K K VA 0.5l 0.5l VB 0 FP QK 0 0 QK = VA − FP D 0 A B K 0 N K = QK sin ϕ K +H cos ϕ K MK V 0 A l 0 VB 0 0 MK = VA x K − FP ( x K − a 3-6 三铰拱 示例 3-6 三铰拱 示例 例:三铰拱的轴线为抛物线: y = 4f x(l − x l2 试求支座反力,D截面的内力,并绘制内力图。 (2 内力的计算 截面D的几何参数: Q = Q 0 cosϕ − H sin ϕ N = Q0 sin ϕ + H cosϕ M = M 0 − Hy y D = 3m sin ϕ D = −0.447 cos ϕ D = 0.894 1kN /m 6 A y x 4kN 0右 QD = −5kN 0左 QD = −1kN 1kN /m H A 4kN (1 支座反力 H 4m B 0 VA = VA = 7kN ( ↑ y x 8m C D C D 4m VA 4m VB VB = V = 5kN ( ↑ 0 B 6 4m B 4m 0 MD = 2kN ⋅ m M0 H = C = 6kN f 7 8m y= 4m 5 Q 左 = 1.79kN D M D = 2kN ⋅ m 左 ND = 5.81kN 右 QD = −1.79kN 右 N D = 7.61kN 4f x(l − x l2 7
2013-6-25 3-6 三铰拱 (3 内力图 示例 3-6 三铰拱 示例 (3 内力图 3-6 三铰拱 3-6 三铰拱 合理轴线 y( x = 2. 合理轴线 在给定的荷载作用下,拱上各截面的弯矩均为零。 例:试求图示三铰拱的合理拱轴线。 q M 0 ( x H M = M 0 − Hy A y x 0.5l C f B 0.5l q H= 0 MC ql 2 = f 8f M0 y= H y( x = M 0 ( x 1 1 M 0 ( x = qlx − qx 2 2 2 H y( x = 4f x (l − x l2 3-6 三铰拱 合理轴线 均匀分布的水压力,合理轴线是园弧曲线。 q 3-7 静定结构的基本特征 教学目标: „ 理解静定结构的受力特点和分析方法; 填土荷载 填土表面为 水平面 合理轴线是悬链线。 填土荷载,填土表面为一水平面,合理轴线是 悬链线 qc+γ.f qc f y q = qc + γ ⋅ y y y* „ 掌握静定结构的基本特征。 x y ( x = A ⋅ ch γ H ⋅ x + B ⋅ sh γ H ⋅x {e x = shx + chx e−x = chx − shx } 8