当前位置：文档之家 › 第三章3静定结构受力分析(平面刚架)

第三章3静定结构受力分析(平面刚架)

  • 格式：ppt
  • 大小：1.23 MB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

结构力学第三章静定结构受力分析

结构力学第三章静定结构受力分析


MA

0, FP

l 2
YB
l

0,YB

FP 2
()
Fy

0,YA
YB

0,YA

YB


Fp 2
()
例2: 求图示刚架的约束力 q
C
A
ql
l
l
l
B
A
ql
ql
C
XC
YC
FNAB
解:
Fy 0,YC 0
MA

0, ql
l 2

XC
l

0,
XC

1 2
ql()
弹性变形，而附属部分上的荷载可使其自身和基本部分均产生内力和 弹性变形。因此，多跨静定梁的内力计算顺序也可根据作用于结构上 的荷载的传力路线来决定。
40k N
80k N·m
20k N/m
AB
CD
EF
G
H
2m 2m 2m 1m 2m 2m 1m
4m
2m
50构造关系图 40k N
C 20 A B 50
Fy 0,YA YB 2ql 0,YA ql() 3)取AB为隔离体
2)取AC为隔离体
Fy 0, YC YA ql 0
Fx 0, XB X A ql / 2()
l MC 0, X A l ql 2 YB l 0, X A ql / 2()
A
B
C D E FG
1m 1m 2m 2m 1m 1m
A C D E FG B
13 17
26 8
7 15 23 30
第三章静定平面刚架讲解

第三章静定平面刚架讲解


A C
x
L
B 斜梁的反力与相应简支 梁的反力相同。
（2）内力 求斜梁的任意截面C的内力，取隔离体AC：
a
相应简支梁C点的内力为：
FP1 A
FYA
x
MC FNC C
FQC
MC0
=
FY
0 A
x
FP1 (x
a)
FQ0C = FY A FP1 FN0C = 0
Fp1 M0
C
斜梁C点的内力为：
MC = FYA x FP1 (x a) = MC0
F0 YA
F0 QC
FQC = (FYA FP1)Cos = FQ0CCos
FNC = (FYA FP1)Sin = FQ0CSin
结论：斜梁任意点的弯矩与水平梁相应点相同， 剪力和轴力等于水平梁相应点的剪力在沿斜梁 切口及轴线上的投影。
例：求图示斜梁的内力图。
q
A
L
解：a、求反力
B
XA =0
FNDC=8k0N
A
MDC=24kN.m（下拉）
FQDB=8kN D FNDB=6kN
MDB=16kN.m（右拉）
8kN
B
6kN C 6kN
2m
8kN
B24kN.m
6kN
4m
6kN

－6kN 8kN
∑Fx = 8－8 = 0 ∑Fy = －6－（－6） = 0
16kN.m 6kN
∑M = 24－8 － 16 = 0
Fx = 0 : FNCE = 0 .45 kN
校核 Fy= (3.13+0.45)sin +(1.793.58)cos
= 3.58 1.79×2 = 0
§3-3 静定平面刚架

§3-3 静定平面刚架

qa ∑ M A = 0，FyB = (↑) 2 qa ∑ Fy = 0，FyA = − (↓) 2
qa
q
A
qa 2
qa 2
Step2：求控制截面的内力。设弯矩内侧受拉为正。
FNAC
M AC
M AC = 0 FQAC = qa FNAC qa = 2
M CB
FNCB
C
B qa
FQCB
2
qa
F A QAC
FNBA
M BA
M BC = −6.23KN .m FQBA M = −6.23KN .m BA FQBC = 3.86 KN FNBC = −2.74 KN FQBA = −1.348 KN FNBA = −4.5 KN
1.384 KN 4.5 KN
A
1KN / m
FNCB
FQCB
M CB
C B A 1.384 KN 4.5 KN
§3-3 静定平面刚架
平面刚架：由直杆组成的具有刚结点的结构，且各杆轴线和外力作用 线都处于同一平面内。
一、刚架的特征
变形特征：刚结点处，各杆端不能产生 变形特征 相对移动和转动，变形前后各杆所夹角 度不变。
受力特征：刚结点能够承 受力特征 受和传递弯矩 使 结构中内力分布相对比较 均匀、合理，减小弯矩的 峰值，节省材料
3、组合刚架：先进行几何组成分析，分清附属部分和基本部分，先计 算附属部分的支座反力，再计算基本部分的支座反力
例1：三铰刚架支座反力的求解
思路：尽量每列一个方程就能求解一个未知力 FAy=30KN(↑),FBy=10KN(↑) FBx=6.67KN(←) ,FAx=6.67KN(→)
例2：组合刚架支座反力的求解
结构力学第3章

结构力学第3章

D (a)
B C YC A C
Q
q P
D
XD (b) C YC XC XC
q
Q
B YB A YA XA
(c)
刚架指定截面内力计算
与梁的指定截面内力计算方法相同（截面法）.
注意未知内力正负号的规定（未知力先假定为正）
注意结点处有不同截面（强调杆端内力） 注意正确选择隔离体（选外力较少部分）
注意利用结点平衡（用于检验平衡，传递弯矩） 连接两个杆端的刚结点,若结点上无外力偶作用, 则两个杆端的弯矩值相等,方向相反
刚架内力图的绘制
弯矩图
取杆件作隔离体
剪力图
轴力图
取结点作隔离体
静定刚架的内力图绘制方法： 一般先求反力，然后求控 制弯矩，用区段叠加法逐杆 绘制，原则上与静定梁相同。
例一、试作图示刚架的内力图
求反力
(单位：kN . m)
48 192
144 126
12
48 kN
42 kN
22 kN
例一、试作图示刚架的内力图
计算关键
正确区分基本结构和附属结构 熟练掌握单跨静定梁的绘制方法
多跨度梁形式
并列简支梁
多跨静定梁
超静定连续梁
为何采用 多跨静定梁这 种结构型式?
作内力图
例
叠层关系图
先附属，后基本， 先求控制弯矩，再区段叠加
18 10 10
5
12
例
9
12
18
+ 9 9
4
其他段仿 此计算 5
5
2.5 FN 图（kN）
l
q
A
ql2 8 l
B
a m l m A b m l a b l B
第三章3静定结构受力分析(平面刚架)

第三章3静定结构受力分析(平面刚架)


MA= qa2+2qa2-2aYB=0 (1)
2） 对中间铰C建立矩平衡方程 qa
MB=0.5qa2+2aXB -aYB=0 (2) 解方程(1)和(2)可得
a
XB=0.5qa YB=1.5qa 3） 再由整体平衡 X=0 解得 XA=-0.5qa Y=0 解得 YA=0.5qa
qa/X2 A YA
1/2qa2
↓↓↓↓↓↓↓↓↓↓↓↓↓↓
C
1/2qa2
A
a
a
qa2 q
B XqBa/2 YB
2 绘制弯矩图
注意：三铰刚架绘制弯矩图往往只须求一水平反力,然后由 支座作起！！
画三铰刚架弯矩图
CM
O M
M/2
M/2
a
C
A
B
a
a
Mo=m－2a×XB=0, 得 XB=M/2a
注意：
A
RA
B
XB
YB
1、三铰刚架仅半边有荷载，另半边为二力体，其反力沿两铰连线，
§3-3 静定平面刚架
一. 刚架的受力特点
梁
1 8
ql2
l
1 ql2 8
刚架
桁架
弯矩分布均匀 可利用空间大
§3-3 静定刚架受力分析
一. 刚架的受力特点 二. 刚架的支座反力计算
静定刚架的分类:
三铰刚架 (三铰结构)
简支刚架 悬臂刚架
单体刚架 (联合结构)
复合刚架 (主从结构)
1.单体刚架(联合结构)的支座反力(约束力)计算
三. 刚架指定截面内力计算
四.刚架的内力分析及内力图的绘制
①分段：根据荷载不连续点、结点分段。 ②定形：根据每段内的荷载情况，定出内力图的形状。 ③求值：由截面法或内力算式，求出各控制截面的内力值。
第3章 多跨静定梁和静定平面刚架

第3章 多跨静定梁和静定平面刚架


A
q
YB
MB
MA
O
YA

+
M
YB
M M

M

MA
MB
M M M
（二） 多跨静定梁的组成形式及分层关系图 单跨静定梁组成的多跨静定梁形式：
（三） 多跨静定梁的受力分析及内力图的绘制
多跨静定梁的受力分析要利用分层关系图。 从力的传递来看：荷载作用在基本部分时，附 属部分不受影响；荷载作用在附属部分时，则基本部 分产生内力。 多跨静定梁的计算是先计算附属部分，后计算 基本部分。将附属部分的支座反力反向，就得附属部 分作用于基本部分的载荷。 先利用分层关系拆成单跨梁，从附属程度最高 跨开始，向下逐跨计算。
dM Q dx d 2M q 2 dx
（2）增量关系
Q P
M m
（3）积分关系 由d Q = – q· dx
MA
q(x)
MB
QB QA q( x) dx
xA
xB
由d M = Q· dx
QA QB
M B M A Q( x) dx
xA
xB
弯矩和剪力的图形特征： 1. 在无荷载的梁段上，剪力为常量，Q图是一水平直线，M 图为一倾斜直线。 2. 在均布荷载的梁段上，Q图是一倾斜直线，弯矩图为二次 抛物线形，曲线的凸向与荷载指向相同。 3. 在集中荷载作用处，Q图有突变呈阶形变化，突变数值等 于集中力的大小，而M图有一转折点，其尖顶的突出方向 与荷载的指向相同。 4. 在集中力偶作用处，Q图无变化，而M图有阶形突变，突 变数值等于集中力偶的大小，集中力偶两侧M图的切线相 互平行。
Q 图没有变化。
Q 图为斜直线，荷载向
结构力学 第三章 静定梁和静定平面钢架

结构力学 第三章 静定梁和静定平面钢架


２、截面法 若要求某一横截面上的内力，假想用一平面沿杆轴垂直方向将该 截面截开，使结构成两部分；在截开后暴露的截面上用力（内力）代 替原相互的约束。
对于截开后结构的两部分上，截面上的内力已成为外力，因此，
由任一部分的静力平衡条件，均可列出含有截面内力的静力平衡方程。 解该方程即将内力求出。
３、截面内力 截开一根梁式杆件的截面上有三个内力（分量），即：轴力ＦN 、 剪力ＦQ和弯矩Μ 。
dFN/dx=-qx
dFQ/dx=-qy dM/dx=Q
d2M/dx2=-qy
增量关系： DFN=-FPx
DFQ=-FPy
DM=m
１）微分关系及几何意义： dFN/dx=-qx dFQ/dx=-qy dM/dx=Q d2M/dx2=-qy （１）在无荷载区段，ＦQ图为水平直线；
当ＦQ≠０时，Μ图为斜直线;
右右为正。
ＦQ＝截面一侧所有外力在杆轴垂直方向上投影的代数和。左上为正， 右下为正。
Μ ＝截面一侧所有外力对截面形心力矩代数和。弯矩的竖标画在杆
件受拉一侧。
例3-1-1 求图（a）所示简支梁在图示荷载下截面的内力。
解：1）支座反力 ∑ΜA=0 FBy×4﹣10×4×2﹣100× (4/5)×2=0 Fby=60kN (↑) ∑ΜB=0 FAy=60kN (↑) ∑Fx= 0 FAx+100×(3/5)=0 FAx=－60kN (← ) 由 ∑Ｆy= 0 校核，满 足。
(下侧受拉)
区段叠加法求Ｅ、Ｄ截面弯矩； ΜE＝20×42/8＋120/2＝100kNm ΜＤ＝40×4/4＋120/2＝100kNm
(下侧受拉) (下侧受拉)
内力应考虑
说明：集中力或集中力偶作用点，注意对有突变的 分两侧截面分别计算。
结构力学 第3章静 定梁、平面刚架受力分析

结构力学 第3章静 定梁、平面刚架受力分析

工程中，斜梁和 斜杆是常遇到的，如楼梯梁、刚架中的斜梁等。斜梁 受均布荷载时有两种表示方法： （1）按水平方向分布的形式给出（人群、雪荷载等），用 q 表示。 （2）按沿轴线方向分布方式给出（自重、恒载），用 q’ 表示。
q 与 q’间的转换关系：
qdx qds q q
cos
第3章
[例题] 试绘制图示斜梁内力图。
q
B
C
A
α
D VB
HA
l/3 l/3
l/3
VA
（1）求支座反力：
解：
X 0 MB 0 MA 0
HA 0
VA
ql 6
()
VB
ql 6
()
校核：
Y
qj 6
qj 6
ql 3
0
第3章
（2）AC段受力图：
（3）AD段受力图：
HAcosα HAsinα
HA VAsinα
VA VAcosα
MC
C
NC
α QC
HAcosα
dx
d2M dx2
q(x)
（1）在无荷区段q(x)＝０，剪力图为水平直线，弯矩图为斜直线。
（2）在q(x)＝常量段，剪力图为斜直线，弯矩图为二次抛物线。其凹下去的曲 线象锅底一样兜住q(x)的箭头。
（3）集中力作用点两侧，剪力值有突变、弯矩图形成尖点；集中力偶作用点两 侧，弯矩值突变、剪力值无变化。
解：
10KN/m A HA=0
4m VA=26.25kN
30KN.m
20KN
C
D
B
E
2m
2m
32.5 2.5
3m VB=33.75KN 60
（1）计算支座反力
结构力学 第三章 静定结构

结构力学 第三章 静定结构

• 由结点弯矩平 衡校核弯矩计算是 否正确。
MBC=1kN· m
B
MBE= 4kN· m
MBA=5kN· m
FP1=1kN FP2=4kN
• 用计算中未使 用过的隔离体平衡 条件校核结构内力 计算是否正确。
5kN· m
1kN
3kN
FP3=1kN
2、简支刚架
• 解: • （1）、求支座 反力 • ∑y=0 • FCy =80kN(↑) • ∑m0=0 • FAx=120kN(←) •∑x=0 •FBx=80kN(→)
§3-2 静定多跨梁
•
由中间铰将若干根梁（简单梁） 联结在一起而构成的静定梁，称为静 定多跨梁。
1、几何组成：
• 基本部分+附属部分。 • （1）、基本部分：不依赖其它部分， 本身能独立承受荷载并维持平衡。 • （2）、附属部分：依赖于其它部分而 存在。
2、层叠图和传力关系
（1）、附属部分荷载 传 基本部分或 支撑它的附属部分。 • （2）、基本部分的荷载对附属部分无 影响，从层叠图上可清楚的看出来。 •
练习: 分段叠加法作弯矩图
q
A B
C
1 2 ql 4
l
q
1 ql 2
ql
l l l
例题
4kN· m
4kN
3m
3m
（1）集中荷载作用下
6kN· m
（2）集中力偶作用下
4kN· m 2kN· m
（3）叠加得弯矩图
4kN· m
4kN· m
例题
3m
8kN· m
2kN/m
3m
2m
（1）悬臂段分布荷载作用下
FP2=4kN
q=0.4kN/m
结构力学第三章静定结构的受力分析

结构力学第三章静定结构的受力分析


例2： MA
A
MA
FP L/2 L/2
FP
MB
B 结论
把两头的弯矩标在杆
端，并连以直线，然
后在直线上叠加上由
节间荷载单独作用在
简支梁上时的弯矩图
MB MA
FPL/4
FPL/4
2020年5月29日星期五7时56分M25秒B
§3-1 梁的内力计算的回顾
3）画剪力图
要求杆件上某点的剪力，通常是以弯矩图为
C
B FQBA
由： MA 0 FQBA (81 26) 2 9kN
也可由： Y 0 FQCA 17 8 9kN
剪力图要注意以下问题： ▲ 集中力处剪力有突变； ▲ 没有荷载的节间剪力是常数； ▲ 均布荷载作用的节间剪力是斜线； ▲ 集中力矩作用的节间剪力是常数。
2020年5月29日星期五7时56分25秒
L/2
M/2
FPL/4
L/2
M
M/2
2020年L5/月229日星期五L7/时2 56分25秒
§3-1 梁的内力计算的回顾
2）用叠加法画简支梁在几种简单荷载共同作用下 的弯矩图
例1： MA
q
MB
q
A
B=
qL2/8
MA
MB
+
+
MA
=A
qL2/8
MB
B
2020年5月29日星期五7时56分25秒
§3-1 梁的内力计算的回顾
2020年5月29日星期五7时56分25秒
§3-1 梁的内力计算的回顾
正 MAB
杆端内力
FNAB
A端 FQAB
MBA 正
B端
FNBA
FQBA
结构力学课件 第三节平面刚架

结构力学课件 第三节平面刚架

FP FP FP
G
H
I
a FP a FP a FP a a B a/2 M图 C FP a a/2 FP a D a/2 FP a FP a FP a a/2 F
A
E
【例3-16】试求作图3-33a所示多跨刚架的弯矩图。
20kN/m C F 10kN/m E A B H G D 20kN/m K I 4m 4m
例
作下图所示刚架的弯矩图。
【例3-14】试绘出图3-31a所示静定结构在荷载 作用下的弯矩图轮廓。
6 7
8
9
10
11 12
13
14 15
16 17 18
1
2
3
4
5
7 6
8
9 10 11 12 3 13
14
15
16 17 18
1
2
4
5
【例3-15】试求作图3-32所示刚架的弯矩图(不求支反力)。
cosa = 0.894 sina = 0.447
FAx=11.43kN
FBx=11.43kN
A
2m
FBy=17.14kN B A
9 1.0 M图(kN· m) 5 C ND F
4m
FAy=62.86kN
4m
FQCD m 4.47
.0 51
9
F NDC
解：DC(1) 求支反力 FQ
FQCD .47m
3) 取图3-32h所示隔离体，由∑Fx = 0，可得
FNCE×0.894+10.22×0.447+11.43 = 0 F NCD
FNCE = -17.90 kN .43
20
x
FN
2.58

《结构力学》_龙驭球_第3章_静定结构的受力分析(2)


一、求支座反力
40 kN
在支座反力的计算过程中，应尽可能建立 独立方程。
B
D
C
20 kN/m
4m
MA 0 FY 0
FDY 4 40 2 (20 4) 2 0 FDY 60kN () FAY 40 60 0 FAY 20kN ()
FX 0 FAX 80kN ()
二、绘制内力图
⑴ 分段：根据荷载不连续点、结点；
解，本题剪力很容易用投影方程求得。
4kN/m
1kN
C
MDE D
E
8
14kN
4m
1kN B 4m
2kN
28 24
4
4D
8
E
F
A
B
M 图（kN·m）
14
D
E
2
2
16
1
F
A
B
FQ 图（kN）
③ 作FN 图 各杆轴力可以用投影方程求
解。也可根据剪力图， 取各结点 为隔离体，用投影方程求轴力。
④ 校核
16
14
40
载和B端外力偶作用的简支梁(图C)。
画M图时，将 B 端弯矩竖标画在受拉 80 A
侧，连以虚直线，再叠加上横向荷载产生
20
的简支梁的弯矩图，如图(d)示。
(b)
A
A
(c)
(d)
B 160
D
160
120
20 60
120
20
A M图 (kN·m）
80 F Q 图（kN)
F N 图（kN)
练习3-3.1：试计算图示简支刚架的支座反力，并绘制Ｍ、F Q 和 F N 图。
Fx 0, FBx 2 11kN()

第三章 静定结构的受力分析


斜直线
FS=0处
有突变
突变值为P
如变号
无变化
M图
斜直线
抛物线
有尖角
↓
↑
有极值
尖角指向同P
有极值
有突变
M=0
利用上述关系可迅速正确地绘制梁的内力图（简易法）8
Structural mechanics
静定结构的受力分析
简易法绘制内力图的一般步骤：
（1）求支反力。
2）分段：凡外力不连续处均应作为分段点，如集中力
15
Structural mechanics
基本部分：
静定结构的受力分析
不依赖其它部分的存在而能独立地维持其几何不变性的部 分。 如：AB、CD部分。
（a）
基本部分
（b） A
B
层叠图：
基本部分
C
附属部分：
必须依靠基本部分 才能维持其几何不变 D 性的部分。如BC部分 。
为了表示梁各部分之间的支撑关系，把基本部分画在下层， 而把附属部分画在上层， （b）图所示，称为层叠图。
3
Structural mechanics
静定结构的受力分析
§3—1 梁的内力计算的回顾
单跨静定梁应用很广，是组成各种结构的基构件之一，其受 力分析是各种结构受力分析的基础。这里做简略的回顾和必
要的补充。
1. 单跨静定梁的反力
常见的单跨静定梁有：
简支梁
外伸梁
悬臂梁
↷
→↑
↙ ↑
→↙ ↑↑
→↑ ↙
反力只有三个，由静力学平衡方程求出。 4
16
Structural mechanics
（2）受力分析方面:
静定结构的受力分析

第3章静定结构的受力分析


M0
1 2 ql 8
弯矩图的叠加指纵坐标的叠加， 不是图形的简单拼合。
任意直段杆的弯矩图：以(a)中的AB端为例，其隔离体如图(b)。
与图(c)中的简支梁相比， 显然二者的弯矩图相同。
因此：作任意直杆段弯矩图
就归结为作相应简支 梁的弯矩图。 AB段的弯矩图如图(d)。
M0 1 2 ql 8
§3-5 静定平面桁架
武汉长江大桥
1
桁架的特点和组成 由杆件组成的格构体系， 荷载作用在结点上， 各杆内力主要为轴力。
钢筋混凝土组合屋架
优点：重量轻，受力合理，能承受较大荷载，可作成较大 跨度。
武汉长江大桥采用的桁架形式
第3 章
静定结构的内力分析
§3-1 杆件内力计算 §3-2 静定梁 §3-3 静定刚架 §3-4 三铰拱 §3-5 静定桁架 §3-6 静定结构的内力分析和受力特点
第3章 静定结构的内力分析
本章讨论静定结构。 内容：静定结构的内力分析。 静定结构分析的要点： 1、如何选择“好的”隔离体； 2、怎样建立比较简单而又恰当的平衡方程， 计算最为简捷。
FQB FQA q y dx xA xB M B M A FQ dx xA
xB
积分关系的几何意义： B端的剪力=A端的剪力-该段荷载qy图的面积
B端的弯矩=A端的弯矩+此段剪力图的面积
5. 分段叠加法作弯矩图
图(a)结构荷载有两部分： 跨间荷载q和端部力偶MA、MB 端部力偶单独作用时，弯 矩图为直线，如图(b): 跨间荷载q单独作用时，弯 矩图如图(c): 总弯矩图为图(b)基础上叠加图 (c)，如图(d):
FQ >0 F <0 增函数 降函数 Q 自左向右折角 斜直线 曲线

结构力学I-第三章 静定结构的受力分析(桁架、组合结构)

FNEC FNED 33.54 kN
Y 0 FNEC sin FNED sin FNEA sin 10 kN 0
联立解出
FNEC FNED 10 5 33.5 思考：能否更快呢？ FNEC 22.36 kN， FNED 11.18 kN
00:44
静定平面桁架
• 桁架的内力计算
由力矩平衡方程 ∑ ME = 0，可求CD杆内力。
FA×d - FNCD×h = 0
FNCD = FAd / h = M0E / h
F1 F2 F3 F4 F5
M0E FA
6d
M FB
若M0E > 0，则FNCD >0 (下弦杆受拉 )
M0E是什么？
00:44
I
II
静定平面桁架
I
II
• 桁架的内力计算
简支梁
悬臂梁
伸臂梁
刚架：受弯构件，由若干直杆联结而成的结构，其中全部或部份 结点为刚结点；
A
D
B
C
简支刚架
悬臂刚架
三铰刚架
00:44
回顾
• 结构内力图
M–AB (表0) 示结构上各截面内力值的图形：弯矩图、M剪BA (0)
力图、A端轴力图；
A
B
FNA横B 坐标 -- 截面位置；
内力图 - 弯矩
A
FA
FB
– 截面法
• 例1：试求图示桁架中杆EF、ED，CD，DG的内力。
解: ⑶ 求上弦杆EF内力，力矩法；
取 ED 和 CD 杆 的 交 点 D 为 矩 心 ， 先 求 EF 杆 的 水 平 分 力
FxEF，由力矩平衡方程∑MD = 0，
FA×2d - F1×d + FxEF×H = 0

第三章静定结构受力分析

内力的概念和表示在平面杆件的任意截面上，将内力一般分为三个分量：轴力F N 、剪力F Q 和弯矩MM A轴力----截面上应力沿杆轴切线方向的合力。

轴力以拉力为正。

剪力----截面上应力沿杆轴法线方向的合力。

剪力以绕微段隔离体顺时针转者为正。

内力的概念和表示弯矩----截面上应力对截面形心的力矩。

在水平杆件中，当弯矩使杆件下部受拉时，弯矩为正。

作图时，轴力图和剪力图要注明正负号，弯矩图规定画在杆件受拉的一侧，不用注明正负号。

内力的计算方法梁的内力的计算方法主要采用截面法。

截面法可用“截开、代替、平衡”六个字来描述：1.截开----在所求内力的截面处截开，任取一部分作为隔离体；隔离体与其周围的约束要全部截断。

2.代替----用截面内力代替该截面的应力之和；用相应的约束力代替截断约束。

3.平衡----利用隔离体的平衡条件，确定该截面的内力。

内力的计算方法利用截面法可得出以下结论：1.轴力等于截面一边的所有外力沿杆轴切线方向的投影代数和；2.剪力等于截面一边所有外力沿杆轴法线方向的投影代数和；3.弯矩等于截面一边所有外力对截面形心力矩的代数和。

以上结论是解决静定结构内力的关键和规律，应熟练掌握和应用。

分段叠加法画弯矩图1.叠加原理：几个力对杆件的作用效果，等于每一个力单独作用效果的总和。

= +=+2.分段叠加原理：上述叠加法同样可用于绘制结构中任意直杆段的弯矩图。

例例：下图为一简支梁，AB段的弯矩可以用叠加法进行计算。

（1）（2）（3）（4）静定多跨连续梁的实例现实生活中，一些梁是由几根短梁用榫接相连而成，在力学中可以将榫接简化成铰约束,这样由几个单跨梁组成几何不变体系，称作为静定多跨连续梁。

下图为简化的静定多跨连续梁。

静定多跨梁的受力特点结构特点：图中AB依靠自身就能保持其几何不变性的部分称为基本部分，如图中AB；而必须依靠基本部分才能维持其几何不变性的部分称为附属部分，如图中CD。

受力特点：作用在基本部分的力不影响附属部分，作用在附属部分的力反过来影响基本部分。

静定平面钢架受力分析

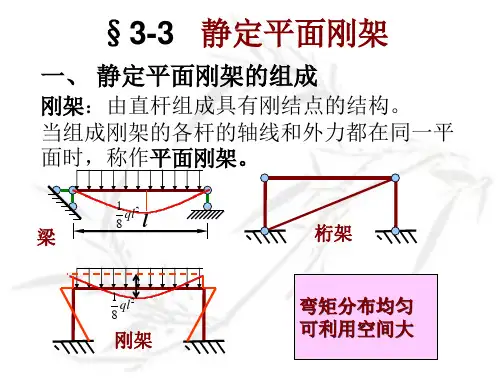
静定平面钢架受力分析XXX摘要：刚架的特点:杆件少，内部空间大，便于利用。

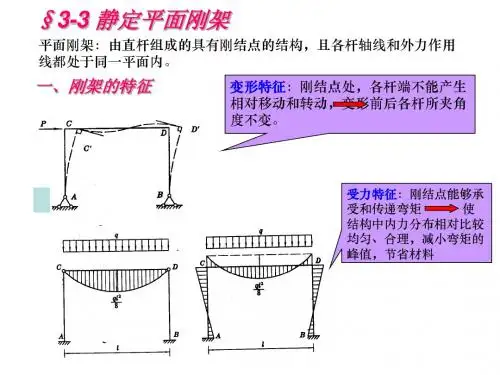
刚结点处各杆不能发生相对转动，因而各杆件的夹角始终保持不变。

刚结点处可以承受和传递弯矩，因而在刚架中弯矩是主要内力。

刚架中的各杆通常情况下为直杆，制作加工较方便。

根据结构组成特点，静定平面刚架可分为：悬臂刚架：常用于火车站站台雨棚等。

简支刚架：常用于起重机的刚支架及渡槽横向计算所取的简图等三铰刚架：常用于小型厂房、仓库、食堂等结构。

刚架结构在土木工程中应用较广。

但静定的刚架在工程中应用不多，多为超静定刚架，如房屋建筑结构中的框架结构。

解算超静定刚架的内力是建立在静定刚架内力计算基础之上的。

所以，必须熟练掌握静定刚架的内力计算方法。

关键词：平面刚架；超静定刚架；内力Statically determinate planar steel stress analysisShaoxiangyangAbstract：The characteristics of the frame: bar, less internal space is big, easy to use. Just the rod cannot occur relatively rotation at junctions, and Angle of the bar is always remains the same. Just at junctions can absorb and transmit bending moment and bending moment are the main internal force in rigid frame. Frame of the rod as the straight rod, normally make processing more convenient. According to the structure characteristics of statically determinate planar frame can be divided into: cantilever frame: often used in the railway platform canopy, etc. Simply supported frame: commonly used in cranes just stents and diagram of aqueduct transverse calculations take three hinged frame: often used in small workshop, warehouse, canteen and structure. Frame structure is widely used in civil engineering. But statically determinate frame in engineering application is not much, more than for statically indeterminate frame, such as building the structure of the frame structure. Solving statically indeterminate frame internal force is based on the determinate frame internal force calculation. So, must be skilled in statically determinate frame internal force calculation methodKey words:plane rigid frame; Statically indeterminate frame; The internal force引言刚架是由若干根直杆（梁和柱）用刚结点（部分可为铰结点）所组成的结构。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2
YA
解: YB P / 2()
2
B
l
XB
2
YB
YA P / 2()
X B P / 4() X A P / 4()
P/4
P/4
M 2 Pl / 4(右侧受拉) M1 Pl / 4(上侧受拉) M1 M 2 (外侧受拉)
§3-3 静定刚架受力分析
一. 刚架的受力特点 二. 刚架的支座反力计算
另外，根据这些关系，常可不经计算直观检查 M 图的轮廓是否正确。 ①M图与荷载情况不符。 ②M图与结点性质、约束情况不符。 ③作用在结点上的各杆端弯矩及结点集中力偶不满足平衡条件。
内力图形状特征
Q图 M图
1.无何载区段 2.均布荷载区段 3.集中力作用处
平行轴线
↓↓↓↓↓↓
＋ －
发生突变
＋P －
斜直线
2.三铰刚架(三铰结构)的支座反力(约束力)计算
方法:取两次隔离体,每个隔离体包含一或两个刚片,建立六
个平衡方程求解--双截面法.
例1: 求图示刚架的支座反力
解:1)取整体为隔离体
P
XA YA
XC
C
A
B
l
l
l 2
l 2
MA Fy
0, P 0,YA
l 2
YB
l
0,
YB
YB 0,YA YB
对O点取矩可求出B点水平反力，由B支座开始做弯矩图。
2、集中力偶作用处，弯矩图发生突变，突变前后弯矩两条线平行。
3、三铰刚架绘制弯矩图时，关键是求出一水平反力！！
4、主从结构绘制弯矩图 可以利用弯矩图与荷载、支承及连结之
间的对应关系，不求或只求部分约束力。
绘制图示刚架的
↓↓↓↓↓↓↓↓↓↓
D
E
弯矩图
＋，－号；竖标大致成比例。
NDC QDC
1m
8kN
QDA MDA NDA
QDA=8kN NDB MDB NMDDAA==08k0NQ.DmB （左D拉）
8kN.m 8kN
MDC
8QkNDC=－6kAN NDC=0 MDC=24kDN.m（下拉）
6kN C
QDB=8kN
6kN
NM8DDkBBN==61k6NkN.mB（右拉）
1/2qa2
↓↓↓↓↓↓↓↓↓↓↓↓↓↓
C
1/2qa2
A
a
a
qa2 q
B XqBa/2 YB
2 绘制弯矩图
注意：三铰刚架绘制弯矩图往往只须求一水平反力,然后由 支座作起！！
画三铰刚架弯矩图
CM
O M
M/2
M/2
a
C
A
B
a
a
Mo=m－2a×XB=0, 得 XB=M/2a
注意：
A
RA
B
XB
YB
1、三铰刚架仅半边有荷载，另半边为二力体，其反力沿两铰连线，
MA= qa2+2qa2-2aYB=0 (1)
2） 对中间铰C建立矩平衡方程 qa
MB=0.5qa2+2aXB -aYB=0 (2) 解方程(1)和(2)可得
a
XB=0.5qa YB=1.5qa 3） 再由整体平衡 X=0 解得 XA=-0.5qa Y=0 解得 YA=0.5qa
qa/X2 A YA
120 q=20kN/m
2m 2m
仅绘M图,并不需要 求出全部反力.
A
80kN 90
120 ↓↓↓↓↓↓↓↓
F
C
先由AD
180 MEA=80×6-½×2200×kN6²=120
60
120
62.5
180
3m
∑Y=0 得 YA=80kN
20kN
M60图 B kM.m
再由整体平衡方程 ∑X=0
得 XB=20kN
NEF 4P()
MA 0, P3l YB l 0,YB 3P()
Fy 0, NCD 6P()
Fx 0, X A 0
Fy 0,YA YB P 0,YA 2P()
3.复合刚架(主从结构)的支座反力(约束力)计算
例1: 求图示刚架的支座反力
方法:先算附属部分,后算基本部 分,计算顺序与几何组成顺序相
然后先由A.B支座开始 作弯矩图.
4m
2m
5m
5、对称性的利用
对称结构在对称荷载作用下，反力和内力都呈对称分布；对 称结构在反对称荷载作用下，反力和内力都呈反对称分布。
m
m
m
h
q ↓↓↓↓↓↓↓↓↓↓↓
ql2/8
ql2/8
ql2/8
h
l/2
l/2
静定刚架的 M图正误判别
利用上述内力图与荷载、支承和联结之间的对应关系，可在绘制内力图时减 少错误，提高效率。
2
2kN
3kN sin 1
5
3.13
－3
3m
3m 9kN
cos 2 5
lDC lEC 3.35m
－
0.45
－
5.82D
ααQQC1CC.NEC7DNC9EDC↓↓↓47α↓k.↓1N↓6α↓/m3.58 E
1.79 3.13QDC2
Q 2
EC
NC 9E
校∑Q核NX∑Q∑QNXCMCNMMECEEDCEXC(D==CED=NC32===13－C066EY6.N..－+547N75－58D3339.3.kC1k(.E.831×.(3N1CNc65Q32k.3×o81k)kkNCs32N4cNNDo1×)4s.0×=75.×1194Q..×53751()D973+.s.235Ci.s.35n1+i5.8n363＝05.13Q(.157012E.9Q7C)9＝Cs50iEn3＝0.5008)0cos
二次抛物线
凸向即q指向
出现尖点
尖点指向即P的指向
4.集中力偶作用处
无变化
发生突变
m
两直线平行
注备
Q=0区段M图 Q=0处，M 平行于轴线 达到极值
集中力作用截 集中力偶作用点
面剪力无定义
弯矩无定义
5、在自由端、铰支座、铰结点处，无集中力偶作用，截面弯矩等于零， 有集中力偶作用，截面弯矩等于集中力偶的值。
方法:切断两个刚片之间的约束,取一个刚片为隔离体,假定 约束力的方向,由隔离体的平衡建立三个平衡方程.
例1: 求图示刚架的支座反力
C
B
C
B
l
2
YB
P
lP
A
l
2
A X A YA
解:
Fx 0, X A P 0, X A P()
MA
0, P
l 2
YB
l
0,YB
P 2
()
Fy
0,YA
YB
0,YA
QDC=－6kN NDC=0 MDC=24kN.m（下拉）
8 6
－ ＋
Q kN
6
＋
N kN
§3-3 静定刚架受力分析
一. 刚架的受力特点 二. 刚架的支座反力计算 三. 刚架指定截面内力计算 四.刚架的内力分析及内力图的绘制 五.刚架弯矩图的绘制
做法:拆成单个杆,求出杆两端的弯矩,按与单跨 梁相同的方法画弯矩图.
l
2
解:
Fx 0, X B P() l P
MB
Fy 0,YA 0
2
A
MB 0, MB pl / 2(顺时针转) YA
l
例4: 求图示刚架的约束力 q
C
A
ql
l
l
l
B
A
ql
ql
C
XC
YC
N AB
解:
Fy 0,YC 0
MA
0, ql
l 2
XC
l
0,
XC
1 2
ql()
1 Fx 0, NAB XC 2 ql()
P
2
() P () 2
X B Fx 0, X A P XB 0
2
2
YB
2)取右部分为隔离体
C YC
B
XB
l
P
MC
0,
XB
l
YB
2
0,
XB
P4
()
Fy Fx
0,YC YB 0, X B
0,YC YB XC 0, XC
P
4
() 2 ()
YB
例2: 求图示刚架的支座反力和约束力
ql l
5ql / 4
q
l
l 5ql / 4 l
5ql2 / 4
ql2
3ql2 / 2
5ql2 / 4
例四: 作图示结构弯矩图
3M / 4
M /2
M
M /4 M /2
M / 4l
2ql 2 ql2
0
ql
l
l
l
ql2 / 2 ql
3、三铰刚架弯矩图
1 反力计算 0
1） 整体对左底铰建立矩平衡方程
a
例题2: 作图示结构弯矩图 练习: 作图示结构弯矩图
ql2 / 2
q
q ql / 2 l
ql
l
ql l / 2 l/2
l
练习: 作图示结构弯矩图
P
l
P l/2
l
l/2
l
l
l
例题3: 作图示结构弯矩图
P
Pl / 2
Pl / 4
P
Pl / 2
l
Pl / 4
l 3Pl / 4
3Pl / 4
l
l