第3讲 动态信号特征分析2_随机信号特征
- 格式:ppt
- 大小:4.84 MB
- 文档页数:47




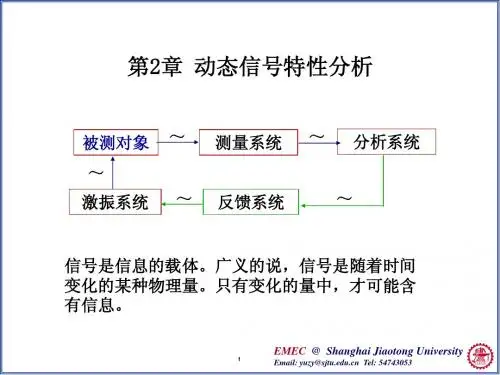

第1章 动态信号特性分析在动态测试中,我们会遇到大量的信号或数据需记录和分析,这些动态信号或数据就是激励与响应的测量结果。
所有动态信号或数据可分为两大类,即确定性与非确定性,非确定性信号也称为随机信号。
所谓确定性信号,是可用明确的数学方程精确地描述一个物理现象的动态过程。
它包括周期信号和非周期信号。
确定性动态信号无论在时域或频域都有自身的特点。
1.1确定性动态信号的时域和频域特性1.1.1周期信号周期信号又可按其复杂程度分为最简单的正弦信号和一般的周期信号。
例如,单自由度无阻尼振动系统的自由振动位移就是典型的正弦信号,可用下列时变函数表示)2sin()(0θπ+=t f X t x (1.1)式中,为振动位移振幅,单位是m ;f X 0为频率,单位时间内重复出现的循环数,单位是Hz ;θ为相对于时间原点的初始相角,单位是弧度;为振动位移在时间t 瞬时的值,单位是m 。
方程(1.1)描述的随时间变化的记录曲线,即时间历程,常称正弦波。
实践中分析正弦信号时,常忽略相角)(t x θ,有t f X t x 02sin )(π= (1.2)方程(1.2)可画成时间历程图或振幅频率图-频谱,见图1-1。
图1-1正弦信号完成一个循环所需时间,称为周期。
如上述,单位时间内出现的循环数称为频率f p T 0,两者的关系是1f T p =(1.3)注意到,图1.1的频谱仅由一个具体频率f 0上的振幅构成。
这样的频谱称为离散谱或线谱。
从分析的观点来看,正弦信号是时变数据的最简形式。
X一般的周期信号是经过一定的时间间隔重复出现的信号,能用周期性的时变函数表示L ,3,2,1),()(=±=n nT t x t x p (1.4)在时域中,这一函数的最简单形式可表现为周期是的正弦波(称基波)的整数倍的波形(称谐波)。
显然,为一般的周期信号的周期。
p T p nT T =在实践中,除少数例外,一般的周期信号都可按下列公式展开为Fourier 级数)2sin 2(2)(1110t f b t f con a at x n n n ππ++=∑∞= (1.5)其中pT f 11=,称为基频 ∫∫====ppT pn T pn n tdt nf t x T b n tdt nf t x T a 0101,2,1,0,2sin )(2,2,1,0,2cos )(2LLππ它们还可表达为另一种Fourier 级数形式)2cos()(110n n n t nf X X t x θπ−+=∑∞= (1.6)其中 20a X =LL,3,2,1),(tan ,3,2,1,122===+=−n a b n b a X nnn n n n θ图1-2式(1.6)表明周期信号由一个静态分量和无限个称为谐波的简谐(正弦或余弦)分量组成,这些谐波分量的振幅为,相位为0X n X n θ,频率是基频的整数倍。

动态信号分析引言动态信号分析是指对一系列随时间变化的信号进行分析和解释的过程。
这些信号可以是任何随时间变化的数据,如声音、振动、电信号等。
动态信号分析可以帮助我们了解信号的周期性、频谱特征、幅度变化等信息,对于理解信号的特性和进行相关应用具有重要意义。
常见的动态信号分析方法1. 傅里叶变换傅里叶变换是一种将信号从时域转换为频域的数学方法。
通过傅里叶变换,可以将信号分解为一系列不同频率的正弦波的叠加。
傅里叶变换可以帮助我们了解信号的频谱分布,找出信号中的主要频率成分,并进一步分析信号的周期性和频谱特征。
2. 小波变换小波变换是一种将信号从时域转换为时频域的数学方法。
与傅里叶变换不同,小波变换可以提供信号在时间和频率上的更为精细的分析。
通过小波变换,可以得到信号在不同时间段和频率段上的能量分布,帮助我们了解信号的局部特征和瞬态特性。
3. 自相关分析自相关分析是一种研究信号相关性的方法。
它通过计算信号与其在不同时间延迟下的自身的相关性,来分析信号的周期性和重复性。
自相关分析可以用来判断信号中的周期性成分,并估计信号的主要周期。
4. 谱分析谱分析是一种将信号在频域上进行分析的方法。
它通过计算信号在不同频率段上的能量分布,来了解信号的频谱特性。
谱分析可以帮助我们找到信号中的主要频率成分,并估计信号的频率范围和带宽。
动态信号分析的应用领域动态信号分析在许多领域都具有广泛的应用。
以下是一些常见的应用领域:1. 声音分析动态信号分析可以用来分析声音信号的频率特征、音调、语速等信息,对语音识别、音频处理和声音品质评估具有重要意义。
2. 振动分析动态信号分析可以帮助我们分析机械振动信号的频谱成分、振动模态、共振频率等信息,对机械故障诊断、结构健康监测等具有重要应用。
3. 电信号分析动态信号分析可以用来分析电信号的频谱特征、噪声成分、幅度调制等信息,对于电力系统分析、通信系统优化等具有重要意义。
4. 生物信号分析动态信号分析可以帮助我们研究生物信号的周期特征、频率变化、相位调制等信息,对心电图分析、脑电图分析和生物信号处理等具有重要应用价值。