人教版数学必修一 第二章 2.3幂函数2

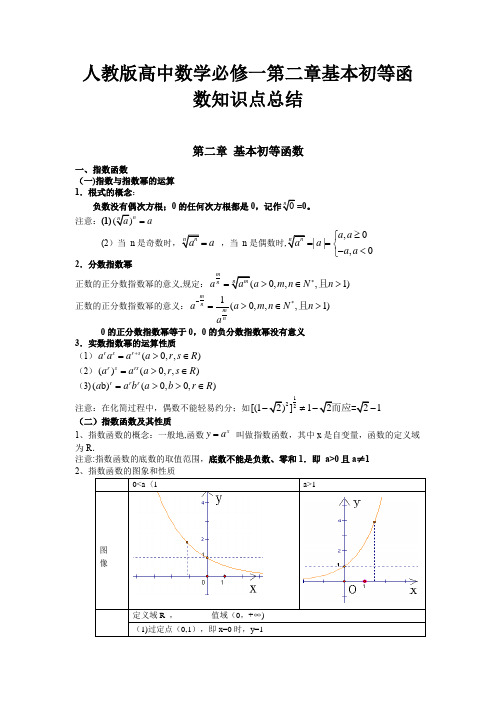
人教版高中数学必修一第二章基本初等函数知识点总结第二章 基本初等函数一、指数函数（一)指数与指数幂的运算 1．根式的概念：负数没有偶次方根；0的任何次方根都是0=0。

注意：(1)na =(2）当 n a = ，当 n 是偶数时,0||,0a a a a a ≥⎧==⎨-<⎩2．分数指数幂正数的正分数指数幂的意义,规定：0,,,1)m na a m n N n *=>∈>且正数的正分数指数幂的意义：_1(0,,,1)m nm naa m n N n a*=>∈>且0的正分数指数幂等于0，0的负分数指数幂没有意义 3．实数指数幂的运算性质 （1）(0,,)rsr s a a aa r s R +=>∈（2）()(0,,)r s rsa a a r s R =>∈ （3)(b)(0,0,)rrra ab a b r R =>>∈注意：在化简过程中，偶数不能轻易约分；如122[(1]11≠ （二）指数函数及其性质1、指数函数的概念：一般地,函数xy a = 叫做指数函数，其中x 是自变量，函数的定义域为R ．注意:指数函数的底数的取值范围，底数不能是负数、零和1．即 a>0且a ≠1 2a>1注意： 指数增长模型：y=N （1+p)指数型函数： y=ka 3 考点：(1)a b =N, 当b>0时，a,N 在1的同侧;当b 〈0时，a,N 在1的 异侧.（2）指数函数的单调性由底数决定的，底数不明确的时候要进行讨论。

掌握利用单调性比较幂的大小，同底找对应的指数函数,底数不同指数也不同插进1(=a 0）进行传递或者利用（1）的知识。

（3）求指数型函数的定义域可将底数去掉只看指数的式子，值域求法用单调性. （4)分辨不同底的指数函数图象利用a 1=a ，用x=1去截图象得到对应的底数。

(5）指数型函数：y=N （1+p)x 简写：y=ka x 二、对数函数 （一)对数1．对数的概念：一般地，如果x a N = ,那么数x 叫做以a 为底N 的对数，记作:log a x N = （ a - 底数， N — 真数，log a N — 对数式）说明：1。

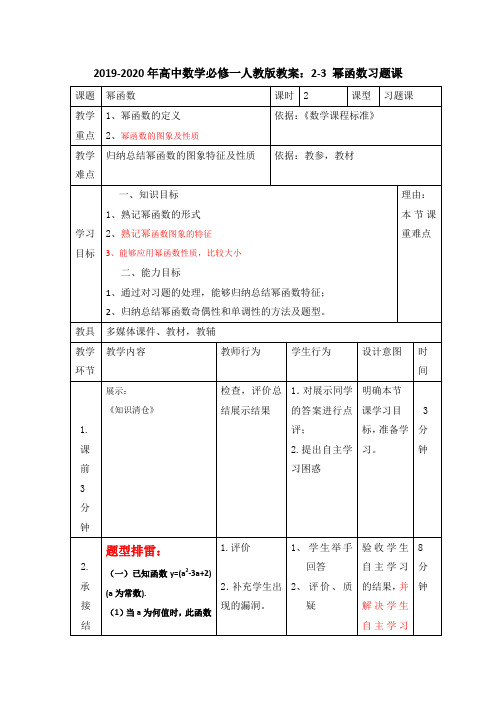
2.3幂函数基础训练1.下列函数为幂函数的是()①y=-x2;②y=2x;③y=xπ;④y=(x-1)3;⑤y=1x2;⑥y=x2+1x.A.①③④⑤B.①②⑤⑥C.③⑤D.⑤解析:①y=-x2的系数是-1,而不是1,故不是幂函数;②y=2x是指数函数;④y=(x-1)3的底数是x-1,而不是x,故不是幂函数;⑥y=x2+1x是两个幂函数和的形式,也不是幂函数.很明显③⑤是幂函数.答案:C2.已知m=(a2+3)-1(a≠0),n=3-1,则()A.m>nB.m<nC.m=nD.m与n的大小不确定解析:设f(x)=x-1,已知a≠0,则a2+3>3>0,f(x)在(0,+∞)上是减函数,则f(a2+3)<f(3),即(a2+3)-1<3-1,故m<n.答案:B3.下列幂函数在区间(-∞,0)内为减函数的是()A.y=x 13 B.y=x2 C.y=x3 D.y=x解析:函数y=x 13,y=x3,y=x在区间(-∞,0)内均是增函数,y=x2在(-∞,0)内是减函数.答案:B4.设α∈{-1,1,12,3},则使函数y=xα的定义域为R,且为奇函数的所有α的值为() A.1,3 B.-1,1 C.-1,3 D.-1,1,3解析:函数y=x-1的定义域是{x|x≠0},函数y=x 12的定义域是[0,+∞),函数y=x和y=x3的定义域为R,且为奇函数.答案:A5.函数y=x 13的图象是()解析:函数y=x 13是幂函数,幂函数在第一象限内的图象恒过定点(1,1),排除A,D.当x>1时,x>x13,故幂函数y=x 13图象在直线y=x的下方,排除C.答案:B6.已知幂函数f(x)=(m2-2m-2)x2-m(m>0),则m=.解析:由于函数f(x)是幂函数,则m2-2m-2=1,解得m=3或-1.又m>0,则m=3.答案:37.若(a+1)3<(3a-2)3,则实数a的取值范围是.解析:构造函数y=x3,它在R上是增函数,所以a+1<3a-2,解得a>32.答案:(32,+∞)8.已知幂函数f(x)=x-m2+2m+3(m∈Z)为偶函数,且在区间(0,+∞)内是增函数,则函数f(x)的解析式为.解析:因为幂函数f(x)=x-m2+2m+3(m∈Z)为偶函数,所以-m2+2m+3为偶数.又f(x)在区间(0,+∞)内是增函数,所以-m2+2m+3>0,所以-1<m<3.又m∈Z,-m2+2m+3为偶数,所以m=1,故所求解析式为f(x)=x4.答案:f(x)=x49.若函数f(x)是幂函数,且满足f(4)f(2)=3,则f(12)的值等于____________________________.解析:设f(x)=xα,∵f(4)f(2)=3,∴4α2α=3,∴2α=3,∴α=log23,∴f(x)=x log23,∴f(12)=(12)log23=13.答案:1310.已知函数f(x)=(m2-m-1)x m2+m-3是幂函数,且当x∈(0,+∞)时,f(x)是增函数,求f(x)的解析式.解:根据幂函数的定义,得m2-m-1=1,解得m=2或m=-1.当m=2时,f(x)=x3在区间(0,+∞)内是增函数;当m=-1时,f(x)=x-3在区间(0,+∞)内是减函数,不符合要求.故f(x)=x3.。

必修1第一章集合与函数概念1．1 集合1．2 函数及其表示1．3 函数的基本性质第二章基本初等函数（Ⅰ）2．1 指数函数2．2 对数函数2．3 幂函数第三章函数的应用3．1 函数与方程3．2 函数模型及其应用必修2第一章空间几何体1．1 空间几何体的结构1．2 空间几何体的三视图和直观图1．3 空间几何体的表面积与体积第二章点、直线、平面之间的位置关系2．1 空间点、直线、平面之间的位置关系2．2 直线、平面平行的判定及其性质2．3 直线、平面垂直的判定及其性质第三章直线与方程3．1 直线的倾斜角与斜率3．2 直线的方程3．3 直线的交点坐标与距离公式必修3第一章算法初步1．1 算法与程序框图1．2 基本算法语句1．3 算法案例阅读与思考割圆术第二章统计2．1 随机抽样阅读与思考一个著名的案例阅读与思考广告中数据的可靠性阅读与思考如何得到敏感性问题的诚实反应2．2 用样本估计总体阅读与思考生产过程中的质量控制图2．3 变量间的相关关系阅读与思考相关关系的强与弱第三章概率3．1 随机事件的概率阅读与思考天气变化的认识过程3．2 古典概型3．3 几何概型必修4第一章三角函数1．1 任意角和弧度制1．2 任意角的三角函数1．3 三角函数的诱导公式1．4 三角函数的图象与性质1．5 函数y=Asin（ωx+ψ）1．6 三角函数模型的简单应用第二章平面向量2．1 平面向量的实际背景及基本概念2．2 平面向量的线性运算2．3 平面向量的基本定理及坐标表示2．4 平面向量的数量积2．5 平面向量应用举例第三章三角恒等变换3．1 两角和与差的正弦、余弦和正切公式3．2 简单的三角恒等变换必修5第一章解三角形1.1正弦定理和余弦定理1.2应用举例1.3实习作业第二章数列2.1数列的概念与简单表示法2.2等差数列2.3等差数列的前n项和2.4等比数列2.5等比数列的前n项和第三章不等式3.1不等关系与不等式3.2一元二次不等式及其解法3.3二元一次不等式（组）与简单的线性规划问题二元一次不等式（组）与平面区域简单的线性规划问题3.4基本不等式选修1-1第一章常用逻辑用语1.1命题及其关系1.2充分条件与必要条件1.3简单的逻辑联结词1.4全称量词与存在量词第二章圆锥曲线与方程2.1椭圆2.2双曲线2.3抛物线第三章导数及其应用3.1变化率与导数3.2导数的计算3.3导数在研究函数中的应用3.4生活中的优化问题举例选修1-2第一章统计案例1．1回归分析的基本思想及其初步应用1．2独立性检验的基本思想及其初步应用第二章推理与证明2．1合情推理与演绎证明2．2直接证明与间接证明第三章数系的扩充与复数的引入3．1数系的扩充和复数的概念3．2复数代数形式的四则运算第四章框图4．1流程图4．2结构图选修2-1第一章常用逻辑用语1.1命题及其关系1.2充分条件与必要条件1.3简单的逻辑联结词1.4全称量词与存在量词第二章圆锥曲线与方程2.1曲线与方程2.2椭圆2.3双曲线2.4抛物线第三章空间向量与立体几何3.1空间向量及其运算3.2立体几何中的向量方法选修2-2第一章导数及其应用1.1变化率与导数1.2导数的计算1.3导数在研究函数中的应用1.4生活中的优化问题举例1.5定积分的概念1.6微积分基本定理1.7定积分的简单应用第二章推理与证明2.1合情推理与演绎推理2.2直接证明与间接证明2.3数学归纳法第三章数系的扩充与复数的引入3.1数系的扩充和复数的概念3.2复数代数形式的四则运算选修2-3第一章计数原理1.1分类加法计数原理与分步乘法计数原理1.2排列与组合1.3二项式定理第二章随机变量及其分布2.1离散型随机变量及其分布列2.2二项分布及其应用2.3离散型随机变量的均值与方差2.4正态分布第三章统计案例3.1回归分析的基本思想及其初步应用3.2独立性检验的基本思想及其初步应用选修3-1第一讲早期的算术与几何第二讲古希腊数学第三讲中国古代数学瑰宝第四讲平面解析几何的产生第五讲微积分的诞生第六讲近代数学两巨星第七讲千古谜题第八讲对无穷的深入思考第九讲中国现代数学的开拓与发展选修3-2选修3-3第一讲从欧氏几何看球面第二讲球面上的距离和角第三讲球面上的基本图形第四讲球面三角形第五讲球面三角形的全等第六讲球面多边形与欧拉公式第七讲球面三角形的边角关系第八讲欧氏几何与非欧几何选修3-4第一讲平面图形的对称群第二讲代数学中的对称与抽象群的概念第三讲对称与群的故事选修4-1第一讲相似三角形的判定及有关性质第二讲直线与圆的位置关系第三讲圆锥曲线性质的探讨选修4-2第一讲线性变换与二阶矩阵第二讲变换的复合与二阶矩阵的乘法第三讲逆变换与逆矩阵第四讲变换的不变量与矩阵的特征向量选修4-3选修4-4第一讲坐标系第二讲参数方程选修4-5第一讲不等式和绝对值不等式第二讲证明不等式的基本方法第三讲柯西不等式与排序不等式第四讲数学归纳法证明不等式选修4-6第一讲整数的整除第二讲同余与同余方程第三讲一次不定方程第四讲数伦在密码中的应用选修4-7第一讲优选法第二讲试验设计初步选修4-8选修4-9第一讲风险与决策的基本概念第二讲决策树方法第三讲风险型决策的敏感性分析第四讲马尔可夫型决策简介高中人教版（B）教材目录介绍必修一第一章集合1．1 集合与集合的表示方法1．2 集合之间的关系与运算第二章函数word格式-可编辑-感谢下载支持 2．1 函数2．2 一次函数和二次函数2．3 函数的应用（Ⅰ）2．4 函数与方程第三章基本初等函数（Ⅰ）3．1 指数与指数函数3．2 对数与对数函数3．3 幂函数3．4 函数的应用（Ⅱ）必修二第一章立体几何初步1．1 空间几何体1．2 点、线、面之间的位置关系第二章平面解析几何初步2．1 平面真角坐标系中的基本公式2．2 直线方程2．3 圆的方程2．4 空间直角坐标系必修三第一章算法初步1．1 算法与程序框图1．2 基本算法语句1．3 中国古代数学中的算法案例第二章统计2．1 随机抽样2．2 用样本估计总体2．3 变量的相关性第三章概率3．1 随机现象3．2 古典概型3．3 随机数的含义与应用3．4 概率的应用必修四第一章基本初等函(Ⅱ)1．1 任意角的概念与弧度制1．2 任意角的三角函数1．3 三角函数的图象与性质第二章平面向量2．1 向量的线性运算2．2 向量的分解与向量的坐标运算2．3 平面向量的数量积2．4 向量的应用第三章三角恒等变换3．1 和角公式3．2 倍角公式和半角公式3．3 三角函数的积化和差与和差化积必修五第一章解直角三角形1．1 正弦定理和余弦定理1．2 应用举例第二章数列2．1 数列2．2 等差数列2．3 等比数列第三章不等式3．1 不等关系与不等式3．2 均值不等式3．3 一元二次不等式及其解法3．4 不等式的实际应用3．5 二元一次不等式（组）与简单线性规划问题选修1－1第一章常用逻辑用语1．1 命题与量词1．2 基本逻辑联结词1．3 充分条件、必要条件与命题的四种形式第二章圆锥曲线与方程2．1 椭圆2．2 双曲线2．3 抛物线第三章导数及其应用3．1 导数3．2 导数的运算3．3 导数的应用选修1－2第一章统计案例第二章推理与证明第三章数系的扩充与复数的引入第四章框图选修4－5第一章不等式的基本性质和证明的基本方法1．1 不等式的基本性质和一元二次不等式的解法1．2 基本不等式1．3 绝对值不等式的解法1．4 绝对值的三角不等式1．5 不等式证明的基本方法第二章柯西不等式与排序不等式及其应用2．1 柯西不等式2．2 排序不等式2．3 平均值不等式(选学)2．4 最大值与最小值问题，优化的数学模型第三章数学归纳法与贝努利不等式3．1 数学归纳法原理3．2 用数学归纳法证明不等式，贝努利不等式。

数学必修一第二章函数知识点
第二章函数知识点包括以下几点：
1. 函数的定义：函数是一种确定的关系，把一个数集的每一个元素都对应到另一个数集的唯一元素上。

函数可以用公式、图像或者表格来表示。

2. 自变量和因变量：函数中，自变量是输入的数值，通常用x表示；因变量是输出的数值，通常用y表示。

函数表示为y = f(x)。

3. 定义域和值域：函数的定义域是自变量的取值范围，值域是因变量的取值范围。

4. 函数的图像：函数的图像是函数关系的几何反映，通常用平面直角坐标系或者极坐标系来表示。

5. 常见函数的类型：
- 线性函数：y = ax + b，其中a和b是常数，直线图像。

- 幂函数：y = x^n，其中n是正整数，曲线图像。

- 指数函数：y = a^x，其中a是大于0且不等于1的常数，曲线图像。

- 对数函数：y = log_a(x)，其中a是大于0且不等于1的常数，曲线图像。

- 三角函数：包括正弦函数、余弦函数、正切函数等。

6. 函数的性质：
- 奇偶性：如果对于任意x，有f(-x) = f(x)，则函数为偶函数；如果对于任意x，有f(-x) = -f(x)，则函数为奇函数。

- 单调性：函数在某个区间上的函数值随着自变量的增加或减小而单调增加或减小。

- 周期性：如果函数存在一个正数T，对于任意x，有f(x+T) = f(x)，则函数具有周期T。

这些是数学必修一第二章函数的主要知识点，还有一些其他的概念和性质需要进一步学习和理解。

高中数学必修1幂函数的基本性质幂函数是数学中一种常见的函数类型，它的表达式形式为 $y = x^a$，其中 $x$ 是自变量，$a$ 是常量指数。

幂函数的基本性质有以下几个方面：1. 定义域和值域对于幂函数 $y = x^a$，当指数 $a$ 是有理数时，定义域为正实数集，即 $x > 0$；当指数 $a$ 是整数时，定义域为实数集；当指数 $a$ 是负有理数时，定义域为整个实数集。

其中，当指数 $a$ 是正偶数时，值域为正实数集，$y > 0$；当指数 $a$ 是正奇数时，值域为整个实数集；当指数 $a$ 是负偶数时，值域为正实数集，$y > 0$；当指数 $a$ 是负奇数时，值域为负实数集，$y < 0$。

2. 奇偶性对于幂函数 $y = x^a$，当指数 $a$ 是偶数时，函数为偶函数，即 $f(-x) = f(x)$；当指数 $a$ 是奇数时，函数为奇函数，即 $f(-x) = -f(x)$。

3. 单调性当指数 $a$ 是正数时，幂函数是递增函数，即 $a > 0, x_1 <x_2 \Rightarrow f(x_1) < f(x_2)$；当指数 $a$ 是负数时，幂函数是递减函数，即 $a < 0, x_1 < x_2 \Rightarrow f(x_1) > f(x_2)$。

4. 极值点和拐点当指数 $a$ 是正数时，幂函数不具有极值点和拐点；当指数$a$ 是负数时，幂函数具有极值点和拐点。

具体的极值点和拐点的位置需要根据具体的指数和函数图像来判断。

以上是关于高中数学必修1幂函数的基本性质的简要介绍。

幂函数作为数学中常见的函数类型，在数学的应用中具有重要的作用。

描述：例题：高中数学必修1(人教B版)知识点总结含同步练习题及答案
第二章 函数 2.3 函数的应用（I）
一、学习任务
了解一次函数、二次函数模型的意义，并能进行简单应用．
二、知识清单
函数模型的应用
三、知识讲解
1.函数模型的应用
函数模型的概念
函数模型就是用函数知识对日常生活中普遍存在的成本最低、利润最高、产量最大、收益最好、用料最省等实际问题进行归纳加工，建立相应的目标函数，确定变量的取值范围，运用函数的方法进行求解，最后用其解决实际问题．
几种函数模型的增长速度比较
在区间 上，尽管函数 ， 和 都是增函数，但它们的增长速度不同，随着 的增大，指数函数 的增长速度会越来越快，会超过并远远大于幂函数 的增长速度，而 的增长则会越来越慢，因此总会存在一个 ，当 时，就有 ．
(0,+∞)y =(a >1)a x y =x (a >1)log a y =(a >0)x a x y =(a >1)a x y =(a >0)x a y =x (a >1)log a x 0x >x 0x <<log a x a a
x
向高 为的水瓶内注水，注满为止，如果注水量 与水深 的函数关系的图像如图所示，那
么水瓶的形状是（ ）
解：B
取 的中点 作 轴的垂线，由图可知，当水深 达到容量高度的一半时，体积大于一
H V
h OH E h h
高考不提分，赔付1万元，关注快乐学了解详情。

答案：A ． 分钟B ． 分钟C ． 分钟D ． 分钟B
3.50 3.75
4.00
4.25。

高一上：必修1第一章集合与函数概念1．1 集合1．2 函数及其表示1．3 函数的基本性质第二章基本初等函数（Ⅰ）2．1 指数函数2．2 对数函数2．3 幂函数第三章函数的应用3．1 函数与方程3．2 函数模型及其应用必修4第一章三角函数1．1 任意角和弧度制1．2 任意角的三角函数1．3 三角函数的诱导公式1．4 三角函数的图象与性质1．5 函数y=Asin（ωx+ψ）1．6 三角函数模型的简单应用第二章平面向量2．1 平面向量的实际背景及基本概念2．2 平面向量的线性运算2．3 平面向量的基本定理及坐标表示2．4 平面向量的数量积2．5 平面向量应用举例高一下必修4第三章三角恒等变换3．1 两角和与差的正弦、余弦和正切公式 3．2 简单的三角恒等变换必修5第一章解三角形1.1正弦定理和余弦定理1.2应用举例第二章数列2.1数列的概念与简单表示法2.2等差数列2.3等差数列的前n项和2.4等比数列2.5等比数列的前n项和第三章不等式3.1不等关系与不等式3.2一元二次不等式及其解法3.3二元一次不等式（组）与简单的线性规划问题3.3.1二元一次不等式（组）与平面区域3.3.2简单的线性规划问题3.4基本不等式高二上必修3第一章算法初步1．1 算法与程序框图1．2 基本算法语句1．3 算法案例第二章统计2．1 随机抽样2．2 用样本估计总体2．3 变量间的相关关系第三章概率3．1 随机事件的概率3．2 古典概型3．3 几何概型必修2第一章空间几何体1．1 空间几何体的结构1．2 空间几何体的三视图和直观图1．3 空间几何体的表面积与体积第二章点、直线、平面之间的位置关系2．1 空间点、直线、平面之间的位置关系2．2 直线、平面平行的判定及其性质2．3 直线、平面垂直的判定及其性质第三章直线与方程3．1 直线的倾斜角与斜率3．2 直线的方程3．3 直线的交点坐标与距离公式第四章圆与方程4．1 圆的方程4．2 直线、圆的位置关系4．3 空间直角坐标系选修2-1第三章空间向量与立体几何 ---理科学3.1 空间向量及其运算3.2 立体几何中的向量方法高二下---理科选修2-1第一章常用逻辑用语1.1 命题及其关系1.2 充分条件与必要条件1.3 简单的逻辑联结词1.4 全称量词与存在量词第二章圆锥曲线与方程2.1 曲线与方程2.2 椭圆2.3 双曲线2.4 抛物线选修2-2第一章导数及其应用1.1 变化率与导数1.2 导数的计算1.3 导数在研究函数中的应用1.4 生活中的优化问题举例第三章数系的扩充与复数的引入3.1 数系的扩充和复数的概念3.2 复数代数形式的四则运算选修2-3第一章计数原理1.1 分类加法计数原理与分步乘法计数原理1.2 排列与组合1.3 二项式定理高二下---文科选修1-1第一章常用逻辑用语1.1命题及其关系1.2充分条件与必要条件1.3简单的逻辑联结词1.4全称量词与存在量词第二章圆锥曲线与方程2.1椭圆2.2双曲线2.3抛物线第三章导数及其应用3.1变化率与导数3.2导数的计算3.3导数在研究函数中的应用3.4生活中的优化问题举例选修1-2第三章数系的扩充与复数的引入3．1数系的扩充和复数的概念3．2复数代数形式的四则运算。