函数的图象第二课时导学案教案

第2课时1.会用描点法画函数图象.2.通过由解析式画函数图象的过程,体会数形结合思想.3.重点:描点法画函数图象.问题探究阅读教材本节中的“例3”至第一个“练习”止,解决下列问题.1.函数y=x+0.5,自变量的取值范围是全体实数,自变量的取值兼顾到三种情况正数、0、负数.2.函数y=(x>0),自变量规定为x>0,所以y> 0.这样得到的每一个点都在第一象限.3.函数y=x+0.5的图象是一条直线,从左到右上升,x由小变大,y随之增大;函数y=的图象是一条曲线,从左到右下降,x由小变大,y随之减小.4.给出函数y=2x+1,如果将上述的任意一对有序实数对(x,y)作为点的坐标,在坐标系内描出这些点,可知道这些点在同一条直线上,我们把这条直线叫做函数y=2x+1的图象.【归纳总结】描点法画函数图象的一般步骤如下:第一步:列表——在表中列出一些自变量的值及其对应的函数值;第二步:描点——在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中的数值对应的各点;第三步:连线——按照横坐标由小到大的顺序,把所描出的各点用平滑的曲线连接起来.【讨论】在画函数图象时,自变量与对应的函数值取值多少对所画的函数图象有什么影响?自变量与对应的函数值取值越多,即函数图象上选取的点越多,作出的函数图象越准确.【预习自测】下列图象中,与关系式y=-x+1表示的是同一个函数的图象是( D )互动探究1:一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( D )互动探究2:(1)在直角坐标系中画出函数y=x+1的图象.解:列表:描点,连线:(2)判断点(-4,5)、(-0.5,0.5)、(1.5,3)在不在该函数图象上?当x=-4时,y=x+1=-4+1=-3,所以(-4,5)不在函数y=x+1的图象上.同理,(-0.5,0.5)在函数y=x+1的图象上,(1.5,3)不在函数y=x+1的图象上.互动探究3:在同一坐标系中,试画出下列函数的图象.(1)y=x; (2)y=2x-1.解:列表:(2)描点,连线,图象如图所示.【方法归纳交流】列表时所选的对应值应选取一些特殊值,如整数值等,方便描点.见《导学测评》P33。

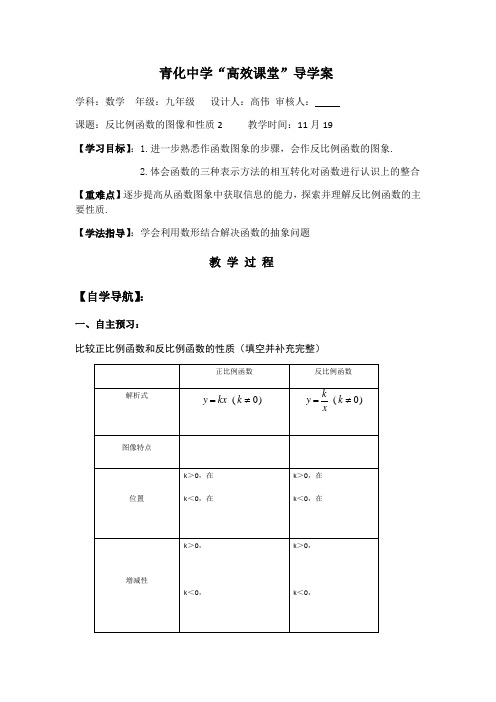
青化中学“高效课堂”导学案学科：数学年级：九年级设计人：高伟审核人：_____课题：反比例函数的图像和性质2 教学时间：11月19【学习目标】：1.进一步熟悉作函数图象的步骤，会作反比例函数的图象.2.体会函数的三种表示方法的相互转化对函数进行认识上的整合【重难点】逐步提高从函数图象中获取信息的能力，探索并理解反比例函数的主要性质.【学法指导】：学会利用数形结合解决函数的抽象问题教学过程【自学导航】：一、自主预习：比较正比例函数和反比例函数的性质（填空并补充完整）二．预习检测：小组合作探究1．若ab < 0，则函数y = ax 与y = b x在同一平面直角坐标系中的图象大致是( )2．已知点P 、Q 在反比函数y =−3x的图象上。

(1)若P (1，a )，Q (2，b ), 比较a 、b 的大小； (2)若P (−1，a )，Q (−2，b )，比较a 、b 的大小； (3)你能从中发现y 随x 增大时的变化规律吗? (4)若P (x 1，y 1),Q (x 2，y 2)，x 1<x 2，你能比较 y 1 与 y 2的大小吗？ 3，观察课本154页图6-4，回答问题4，思考课本155页图6-5，当K 取不同值时，函数图像有什么区别？【新知探究】：反比例函数xky的图象是由 组成的.（通常称为 ） 当k ＞0时，两支曲线分别位于第 象限内，在每一象限内．．．．．．，y 的值 当k ＜0时，两支曲线分别位于第 象限内，在每一象限内．．．．．．，y 的值 【课堂检测】1.一次函数y = kx – k 与反比例函数y =kx在同一直角坐标系内的图象大致是（ ）2．已知直线y ax b =+如图所示，则函数aby x=的图像应在（ ） A ．第一、二象限 B ．第二、三象限C ．第一、三象限D ．第二、四象限3．反比例函数y=1m x-的图象在第二、四象限，则m 的取值范围是（ ）4．已知反比例函数xky -=3，分别根据下列条件求出字母k 的取值范围 （1）函数图象位于第一、三象限 （2）在第二象限内，y 随x 的增大而增大5．函数y ＝－ax ＋a 与xay -=（a ≠0）在同一坐标系中的图象可能是（ ）教师评价： 我的疑惑：。

19.2.2 一次函数落红不是无情物，化作春泥更护花。

出自龚自珍的《己亥杂诗·其五》李坑学校李忠华第2课时一次函数的图象与性质一、新课导入1.导入课题正比例函数y=kx(k≠0)的图象是一条直线，那么，一次函数的图象会是什么形状呢？这节课我们来探讨一次函数的图象及它的性质，由此导入课题(板书课题).2.学习目标（1）会画一次函数的图象，会根据图象(或k的符号)说出一次函数的性质.（2）知道正比例函数y=kx（k≠0）与一次函数y=kx+b（k≠0）的图象之间的平移关系.（3）掌握一次函数的图象和性质与k,b的关系.3.学习重、难点重点：一次函数的图象和性质.难点：一次函数图象与性质的运用.二、分层学习1.自学指导（1）自学内容：P91的例2到P92的例3以上内容.（2）自学时间：10分钟.（3）自学要求：结合所画的图象、比较图象位置，说出y=kx（k≠0）与y=kx+b(k≠0)的图象之间的位置关系.（4）自学参考提纲：①完成P91到P92的思考，并说明一次函数的图象是什么形状.②结合例2说明直线y=kx（k≠0）与直线y=kx+b(k≠0)之间的平移关系.③一次函数y=2x+5的图象是由y=2x的图象向上平移5个单位得到的.④把函数y=－2x的图象向上平移3个单位后得到函数y=-2x+3的图象.2.自学：学生可参考自学参考提纲进行自学.3.助学（1）师助生：①明了学情：关注学生能否从例2中看出y=kx（k≠0）与y=kx+b(k≠0)的图象的位置变化关系.②差异指导：对共性问题共同指导，个性问题针对性指导.（2）生助生：小组研讨，帮助解决疑点.4.强化：直线y=kx（k≠0）与直线y=kx+b(k≠0)之间的平移关系.1.自学指导（1）自学内容：P92例3到P93练习上面的内容.（2）自学时间：10分钟.（3）自学要求：画图、看图，猜想图象从左到右的升与降与什么有关.（4）自学参考提纲：①阅读例3，说说画一次函数图象的简单方法，并说明理由.②按例3画一次函数图象的方法画出探究中的四个函数的图象.③观察上述四个函数图象，你能发现一次函数y=kx+b(k≠0)有何性质？④完成下表：⑤完成P9的练习题.2.自学：学生可参考自学参考提纲进行自学.3.助学（1）师助生：①明了学情：关注学生是否明白画一次函数图象的简单画法的道理或依据是什么？从探究中你发现k 值与图象的什么有关系,存在什么困难？②差异指导：指导学生结合图象位置及k值符号总结一次函数的性质.（2）生助生：同桌之间相互交流、研讨.4.强化（1）点四位学生板演自学参考题纲中的第②题，并点评.（2）总结一次函数的性质.（3）总结k,b的符号与直线在直角坐标系中的位置的关系.（4）总结P93的练习题中的规律.（5）展示本节所学知识点和数学思想方法.三、评价1.学生的自我评价(围绕三维目标)：各小组学生代表介绍自己的课堂学习方法、学习收获及疑点.2.教师对学生的评价：（1）表现性评价：对学生在课堂学习中的态度、方法、成果及不足进行点评.（2）纸笔评价：课堂评价检测.3.教师的自我评价(教学反思).本课时的教学先引导学生画出一次函数的图象（根据两点确定一条直线画出），然后根据图象确定过的象限和增减性.本课时遵循了“画——读——用”的教学流程，使整堂课在教师的指导下由学生全程动手、观察、发现并实用实际解题的方式进行，指导学生认识“由数到形”“由形到数”的数学方法，培养解决问题、研究问题的基本素质，有利于加强研究更复杂知识的能力.(时间：12分钟满分：100分)一、基础巩固（70分）1.(10分)一次函数y=x+2的图象大致是（A）A B C D2.(10分)在同一直角坐标系中，对于函数：①y=-x-1，②y=x+1，③y=-x+1，④y=-2x-1的图象，下列说法不正确的是(A)A.通过点(-1，0)的是①和③B.两直线的交点在y轴负半轴上的是①和④C.相互平行的是①和③D.关于y轴对称的②和③3.(10分)已知正比例函数y=(k-3)x，若y随x的增大而增大，则k的取值范围是(D)A.k＜0B.k＞0C.k＜3D.k＞34.(10分)若一次函数y=(2m-1)x+3-2m的图象经过第一、二、四象限，则m的取值范围是m＜12.5.(10分)下列关于一次函数y=-2x+1的说法：①y随x的增大而减小；②图象与直线y=-2x平行；③图象与y轴的交点坐标是(0，1)；④图象经过第一、二、四象限. 其中正确的有4 个.6.(20分)在平面直角坐标系中画出函数y=－12x+3的图象.（1）在图象上标出横坐标为-4的点A，并写出它的坐标；（2）在图象上标出与y轴的距离是2个单位长度的点，并写出它的坐标.二、综合应用（20分）7.一次函数y=(2a+4)x-(3-b)，当a，b为何值时：（1）y随x的增大而增大；（2）图象经过第二、三、四象限；（3）图象与y轴的交点在x轴上方；（4）图象过原点.解：（1）a＞-2,b为任意实数；（2）a＜-2，b＜3；（3）a≠-2，b＞3；(4)a≠-2，b=3.三、拓展延伸（10分）8.如图，有一种动画程序，屏幕上正方形区域ABCD表示黑色物体甲，其中，A(1，1)，B(2，1)，C(2，2)，D(1，2)，用信号枪沿直线y=2x+b发射信号，当信号遇到区域甲时，甲由黑变白.若甲能由黑变白，则b的取值范围为(B)A.0≤b≤3B.-3≤b≤0C.-3≤b≤3D.b≤3【素材积累】1、黄鹂方才唱罢，摘村庄的上空，摘树林子里，摘人家的土场上，一群花喜鹊便穿戴着黑白相间的朴素裙裾而闪亮登场，然后，便一天喜气的叽叽喳喳，叽叽喳喳叫起来。

第二十二章二次函数知人者智，自知者明。

《老子》 原创不容易，【关注】，不迷路！22.1.3二次函数y =a (x －h )2+k 的图象和性质 第2课时二次函数y =a (x －h )2的图象和性质 学习目标：1.会画二次函数y =a (x －h )2的图象. 2.掌握二次函数y =a (x －h )2的性质. 3.比较函数y =ax 2与y =a (x －h )2的联系. 重点：会画二次函数y =a (x －h )2的图象.难点：掌握二次函数y =a (x －h )2的性质并会应用其解决问题.一、知识链接1.说说二次函数y =ax 2+c (a ≠0)的图象的特征.2.二次函数y =ax 2+k (a ≠0)与y =ax 2(a ≠0)的图象有何关系？3.函数21(2)2yx 的图象，能否也可以由函数212y x 平移得到？ 二、要点探究探究点1：二次函数y =a (x －h )2的图象和性质 引例在同一直角坐标系中，画出二次函数212y x 与21(2)2y x 的图象． 根据所画图象，填写下表：试一试画出二次函数2112yx ，()2112y x =--的图象，并分别指出它们的开口方向、对称轴和顶点坐标.想一想通过上述例子，函数y =a (x －h )2的性质是什么？ 要点归纳：二次函数y =a (x －h )2(a ≠0)的性质当a ＞0时，抛物线开口方向向上，对称轴为直线x =h ，顶点坐标为(h ，0)，当x =h 时，y 有最小值为0.当x ＜h 时，y 随x 的增大而减小；x ＞h 时，y 随x 的增大而增大. 当a ＞0时，抛物线开口方向向下，对称轴为直线x =h ，顶点坐标为(h ，0)，当x =h 时，y 有最大值为0.当x ＜h 时，y 随x 的增大而增大；x ＞h 时，y 随x 的增大而减小. 典例精析例1已知二次函数y ＝(x -1)2 （1）完成下表；x … … y……（2）在如图坐标系中描点，画出该二次函数的图象．（3）写出该二次函数的图象的对称轴和顶点坐标； （4）当x 取何值时，y 随x 的增大而增大． （5）若3≤x ≤5，求y 的取值范围； 想一想：若-1≤x ≤5，求y 的取值范围；（6）若抛物线上有两点A (x 1，y 1)，B (x 2，y 2)，如果x 1＜x 2＜1，试比较y 1与y 2的大小．变式：若点A (m ，y 1)，B (m +1，y 2)在抛物线的图象上，且m ＞1，试比较y 1，y 2的大小，并说明理由．探究点2：二次函数y =ax 2与y =a (x －h )2的关系 想一想抛物线2112yx ，2112y x 与抛物线212y x 有什么关系？ 要点归纳：二次函数y =a (x －h )2与y =ax 2的图象的关系y =ax 2向右平移︱h ︱得到y =a (x －h )2； y =ax 2向左平移︱h ︱得到y =a (x +h )2.左右平移规律：括号内左加右减，括号外不变.例2抛物线y ＝a 2向右平移3个单位后经过点(－1，4)，求a 的值和平移后的函数关系式．方法总结：根据抛物线左右平移的规律，向右平3个单位后，a 不变，括号内应“减去3”；若向左平移3个单位，括号内应“加上3”，即“左加右减”．练一练将二次函数y ＝－2x 2的图象平移后，可得到二次函数y ＝－2(x ＋1)2的图象，平移的方法是( )A ．向上平移1个单位B ．向下平移1个单位C ．向左平移1个位D ．向右平移1单位 三、课堂小结1.指出下列函数图象的开口方向，对称轴和顶点坐标. 22(3)x 22(2)x23(1)4x 2.如果二次函数y ＝a (x -1)2（a ≠0）的图象在它的对称轴右侧部分是上升的，那么a 的取值范围是_____．3.把抛物线y=－x2沿着x轴方向平移3个单位长度，那么平移后抛物线的解析式是.4.若（-134，y1）（-54，y2）（14，y3）为二次函数y=(x-2)2图象上的三点，则y1，y2，y3的大小关系为___________.5.在同一坐标系中，画出函数y＝2x2与y＝2(x-2)2的图象，分别指出两个图象之间的相互关系．能力提升已知二次函数y＝（x-h）2（h为常数），当自变量x的值满足-1≤x≤3时，与其对应的函数值y的最小值为4，求h的值.参考答案自主学习知识链接1.二次函数y=ax2+c(a≠0)的图象，对称轴为y轴，顶点坐标为（0，c）,当a＞0时，图象的开口向上，有最低点（即最小值c），当x0时，y随x增大而增大.当a＜0时，图象的开口向下，有最高点（即最大值c），当x0时，y随x 增大而减小.2.答：二次函数y=ax2+k(a≠0)的图象可以由y=ax2(a≠0)的图象平移得到：当k>0时，向上平移k个单位长度得到.当k<0时，向下平移-k个单位长度得到.3.能课堂探究二、要点探究探究点1：二次函数y=a(x－h)2的图象和性质引例列表如下：描点、连线，画出这两个函数的图象如图①所示.图①图② 填表如下：试一试 填表如下：1212-292-892-21212-2描点、连线，画出这两个函数的图象如图②所示. 例1解：（1）填表如下：x…-10 1 2 3 …y… 2 120 122 …（2）解：描点，画出该二次函数图象如下：（3）对称轴为直线x=1.顶点坐标为(1,0).（4）当x＞1时，y随x的增大而增大.（5）∵当x＞1时，y随x的增大而增大，当x=3时，y=2;当x=5时，y=8,∴当3≤x≤5时，y的取值范围为2≤y≤8.想一想∵当-1≤x≤5时，y的最小值为0，∵当-1≤x≤5时，y的取值范围是0≤y≤8.（6）∵当x＜1时，y随x的增大而减小，∴当x1＜x2＜1时，y1＞y2.变式∵m＞1，∴1＜m＜m+1，∵当x＞1时，y随x的增大而增大，∴y1＜y2.探究点2：二次函数y=ax2与y=a(x－h)2的关系想一想抛物线向左平移1个单位得到抛物线，抛物线向右平移1个单位得到抛物线.例2解：二次函数y＝ax2的图象向右平移3个单位后的二次函数关系式可表示为y＝a(x－3)2，把x＝－1，y＝4代入，得4＝a(－1－3)2，a=14，∴平移后二次函数关系式为y＝14(x－3)2.练一练C当堂检测 1.填表如下： 22(3)x 22(2)x23(1)4x2.a ＞03.y =-(x +3)2或y =-(x -3)24.y 1＞y 2＞y 35. 解：图象如图.函数y =2(x -2)2的图象由函数y =2x 2的图象向右平移2个单位得到. 能力提升解：∵当x ＞h 时，y 随x 的增大而增大，当x ＜h 时，y 随x 的增大而减小，∴①若h ＜-1≤x ≤3，x ＝-1时，y 取得最小值4，可得（-1-h ）2＝4，解得h ＝-3或h ＝1（舍）；②若-1≤x ≤3＜h ，当x ＝3时，y 取得最小值4，可得：（3-h ）2＝4，解得：h ＝5或h ＝1（舍）；③若-1＜h ＜3时，当x ＝h 时，y 取得最小值为0，不是4，∴此种情况不符合题意，舍去．综上，h 的值为-3或5.【素材积累】阿达尔切夫说过：“生活如同一根燃烧的火柴，当你四处巡视以确定自己的位置时，它已经燃完了。

高中数学1.3.2 第2课时正切函数的图象和性质导学案苏教版必修4 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学1.3.2 第2课时正切函数的图象和性质导学案苏教版必修4）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学1.3.2 第2课时正切函数的图象和性质导学案苏教版必修4的全部内容。

1。

3。

2 三角函数的图象和性质第2课时 正切函数的图象和性质单问题。

正切函数的图象与性质正切函数的图象叫做正切曲线．正切函数在整个定义域内是增函数吗？提示:不是．正切曲线由被互相平行的直线x ＝错误!＋k π（k ∈Z ）所隔开的无穷多支曲线组成,且不连续．例如取x 1＝错误!，x 2＝错误!，显然x 1＜x 2，但y 1＝tan 错误!＝1,y 2＝tan 错误!＝－错误!， ∴y 1＞y 2，不符合增函数定义．预习交流2如何作出正切函数的图象？提示：（1)几何法利用单位圆中的正切线来作出正切函数的图象,该方法作图较为精确,但画图时较繁琐．（2)三点两线法“三点”是指错误!，(0,0），错误!；“两线”是指x ＝－错误!和x ＝错误!.在三点、两线确定的情况下，类似于五点法作图，可大致画出正切函数在错误!上的简图，然后向右、向左扩展即可得到正切曲线．一、正切函数的定义域、值域问题求函数y ＝tan x ＋1＋lg （1－tan x ）的定义域．思路分析：先列出使每个式子有意义的不等式组,然后解不等式组．解:由题意得错误!即－1≤tan x ＜1。

在错误!内，满足上述不等式的x 的取值范围是错误!.又因为y ＝tan x 的周期为π，所以所求x 的范围是错误!（k ∈Z ）．故函数的定义域为错误!(k ∈Z ）．求函数y ＝1lg tan x的定义域． 解:要使y ＝错误!有意义,必须满足错误!即错误!∴函数y ＝错误!的定义域为错误!∪错误!(k ∈Z )．求正切函数的定义域、值域的方法及注意点:(1)求与正切函数有关的函数的定义域时，除了求函数定义域的一般要求外，还要保证正切函数y ＝tan x 有意义，即x ≠k π＋错误!（k ∈Z ）,而对于构建的三角函数不等式，常利用三角函数的图象求解．(2）求解与正切函数有关的函数的值域时，要注意函数的定义域，在定义域内求值域；对于求由正切函数复合而成的函数的值域时，常利用换元法，但要注意新“元”的范围．二、与正切函数有关的函数的单调性问题求函数y ＝tan 错误!的单调减区间．思路分析:将函数化为y ＝－tan 错误!，再利用整体代换求解．解：∵y ＝tan 错误!＝－tan 错误!，∴只需求函数y ＝tan 错误!的单调增区间，即为原函数的单调减区间．令μ＝x 4－错误!,则μ∈错误!(k ∈Z ），即－错误!＋k π＜μ＜错误!＋k π（k ∈Z )． ∴－错误!＋k π＜错误!－错误!＜错误!＋k π（k ∈Z ）．解得4k π－错误!＜x ＜4k π＋错误!（k ∈Z ）．∴函数y ＝tan 错误!的单调减区间为错误!(k ∈Z )．1．比较大小：tan 1__________tan 4。

公开课导学案——正弦函数余弦函数的图像学教案第一章：正弦函数图像的基本特征1.1 学习目标：了解正弦函数图像的形状和基本特点。

1.2 教学内容：(1) 引导学生观察正弦函数图像的波形，理解其周期性和振幅的概念。

(2) 分析正弦函数图像在各个象限的符号和变化规律。

1.3 课堂活动：(1) 让学生自主绘制正弦函数图像，观察其特点。

(2) 分组讨论正弦函数图像在各个象限的变化规律。

1.4 练习题目：(1) 描述正弦函数图像的一个周期内的变化情况。

(2) 判断给定的点在正弦函数图像的哪个象限。

第二章：余弦函数图像的基本特征2.1 学习目标：了解余弦函数图像的形状和基本特点。

2.2 教学内容：(1) 引导学生观察余弦函数图像的波形，理解其周期性和相位的概念。

(2) 分析余弦函数图像在各个象限的符号和变化规律。

2.3 课堂活动：(1) 让学生自主绘制余弦函数图像，观察其特点。

(2) 分组讨论余弦函数图像在各个象限的变化规律。

2.4 练习题目：(1) 描述余弦函数图像的一个周期内的变化情况。

(2) 判断给定的点在余弦函数图像的哪个象限。

第三章：正弦函数和余弦函数图像的比较3.1 学习目标：掌握正弦函数和余弦函数图像的异同点。

3.2 教学内容：(1) 分析正弦函数和余弦函数图像的形状和周期的关系。

(2) 比较正弦函数和余弦函数图像在各个象限的变化规律。

3.3 课堂活动：(1) 让学生对比绘制正弦函数和余弦函数图像，观察其异同点。

(2) 分组讨论正弦函数和余弦函数图像的比较。

3.4 练习题目：(1) 说明正弦函数和余弦函数图像的异同点。

(2) 绘制一个给定角度的正弦函数和余弦函数图像，并比较它们的特点。

第四章：正弦函数余弦函数图像的应用4.1 学习目标：学会利用正弦函数和余弦函数图像解决实际问题。

4.2 教学内容：(1) 引导学生利用正弦函数和余弦函数图像解决物理、工程等领域的问题。

(2) 分析正弦函数和余弦函数图像在实际问题中的应用。