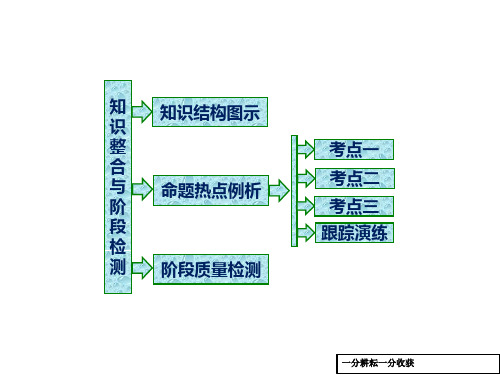
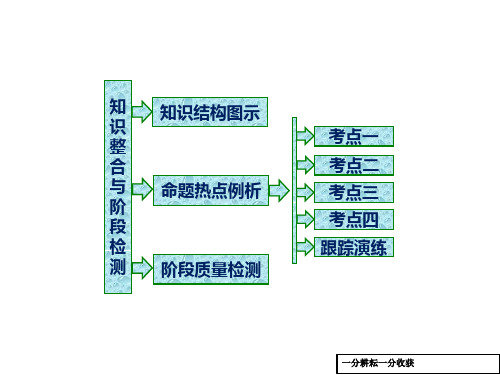
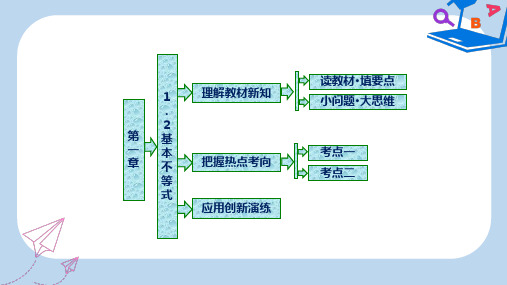
高二数学人教B版选修4-5课件:第一章 章末小结 知识整合与阶段检测
- 格式:ppt
- 大小:1.53 MB
- 文档页数:41

1. 5 不等式证明的基本方法1 . 5.1 比较法扭氢问龙索弟葯幻比卅匚诸[对应学生用书P16][读教材填要点]1. 定义要证a>b,只需要证 a —b>0;要证a<b,只需证a —b<0,这种证明不等式的方法,称为比较法.2. 用比较法证明不等式的步骤⑴求差.(2) 变形:可用因式分解、配方、乘法公式等,把差变形为乘积式平方和的形式.(3) 作出判断.[小问题大思维]作差比较法的主要适用类型是什么?实质是什么?提示:作差比较法尤其适用于具有多项式结构特征的不等式的证明. 实质是把两个数或式子的大小判断问题转化为一个数(或式子)与0的大小关系•:爲爲疋企壮至它-字,hi:…点軌迪[对应学生用书P16]比较法证明不等式4 3 2[例1]求证:⑴当x€ R时,1 + 2x >2x + x ;a ba b ----(2)当a, b € (0,+s )时,a b > (ab) 2 .[思路点拨](1)利用作差比较法,注意变形分解 :(2)利用作商比较法,注意判断底数大小决定商的大小.[精解详析]⑴法一:(1 + 2x4) —(2x3+ x2)3=2x (x—1)—(x+ 1)(x—1)=(x—1)(2x3—x—1)=(x—1)(2x3—2x+ x—1)1. 5 不等式证明的基本方法=(x—1)[2x(/ —1) + (x—1)]11(x 1)2(2X 22x 1)(x 1)2 2 x 122 1101 2x 4 2x 3x 2.(1 2x 4 )(2 x 3 x 2) x 4 2x 3 x 2 x 4 2x 2 1 (x 1)2x 2 (x 2 1)2 01 2x 4 2x 3 x 2.⑵一a ab ba-baa bb _aPa 竽 babPa b a 竽 b1a>b>0 a >Ia b |1■ x a ba jb>a>00<a <1a b 2 <0b>1.a “ba b(0 )a ab b (ab)—规』l 沁 姑(i 2)x> 11 x>0 ■\/iX >0.x2.=-2【(x+ 1) - 2 x+ 1 + 1]-2( .x+ 1- 1)2w 0,•••寸1+x w 1+ 2.[例2]甲、乙二人同时同地沿同一路线走到同一地点,甲有一半时间以速度m行走,另一半以速度n行走;乙有一半路程以速度m行走,另一半路程以速度n行走.如果m^ n, 问甲、乙二人谁先到达指定地点?[思路点拨]本题考查比较法在实际问题中的应用,解答本题需要设出从出发点到指定地点的路程s,甲、乙二人走完这段路程各自需要的时间如t2,然后利用作差法比较t1, t2的大小即可.[精解详析]设从出发地点至指定地点的路程为s,甲、乙二人走完这段路程所用的时间分别为如t2,依题意有:t1 t1^m+ 尹=s,2m+影t2mn m+ n '其中s, m, n都是正数,且m^ n,• •屯—t2< 0,即t r V t2.从而知甲比乙先到达指定地点.应用不等式解决问题时,关键是如何把等量关系不等量关系转化为不等式的问题来解决,也就是建立数学模型是解应用题的关键,最后利用不等式的知识来解.解答不等式问题,一般可分为如下步骤:①阅读理解材料;②建立数学模型;③讨论不等式关系;④作出问题结论.2 .某人乘出租车从A地到B地,有两种方案.第一种方案:乘起步价为10元,超过规定里程后每千米 1.2元的出租车;第二种方案:乘起步价为8元,超过规定里程后每千米1.4元的出租车.按出租车管理条例, 在起步价内,不同型号的出租车行驶的路程是相等的,则此人从A 地到B 地选择哪一种方案比较合适?解:设A 地到B 地的距离为m 千米.起步价内行驶的路程为 a 千米.显然当m w a 时,选起步价为 8元的出租车比较合适.当m>a 时,设m = a + x(x>0),乘坐起步价为10元的出租车费用为 P(x)元.乘坐起步价 为8元的出租车费用为 Q(x)元,贝U P(x)= 10+ 1.2x , Q(x) = 8+ 1.4x. •/ P(x) — Q(x) = 2 — 0.2x = 0.2(10 — x)•••当x>10时,P(x)<Q(x),此时选择起步价为 10元的出租车较为合适. 当x<10时,P(x)>Q(x),此时选择起步价为 8元的出租车较为合适. 当x = 10时,P(x)= Q(x),两种出租车任选,费用相同.、选择题 1.下列关系中对任意 a v b v 0的实数都成立的是(2 .2A . a v b b C . a>1解析:■/ a v b v 0, •— a> — b>0.2 2 (—a) >( — b) >0. 即 a 2>b 2>0. b 2 • a2v 1.b 2又 lg b 2— Ig a 2= Ig^v Ig 1 = 0. a• lg b 2v Ig a 2答案:B1 o2.已知P =?++!,Q= a 2— a +1,那么P 、Q的大小关系是()A . P>Q C . P >Q解析:2 21 — (a — a + 1 f a + a + 1 } P — Q = 24 i 2—++T ,YING YONG课下训练经撫化.贵在鮭类旁通P18][对应学生用书)2 2B . lgb <ig aB . P<QD .>3 (A C A D4 A C56a 2 a 1 0a 4 a 2 0P Q 0. QP.m主彩石⑴w p wm n>p B m>n p n> m>pD n m>pB C.n.D.(ab k a k b) (a k 1 b k 1)(k N )(ab k a "b) b k (a b) a k (b a) b k 1a>0 b>0 a>b (a b)(b k a k ) a k >b k(a b)(b k a k )<0 a<ba k <b k(a b)(b k a k )<o.2 2(x y )(x y) N (x y )(x y) MN 2, 、 z 2 . 2X z 、 x y 0 M M N (x y 2)(x y) (x 2y 2)(x y)(x y)[(x 2y 2) (x y)2]2xy(x y)x<y<0 xy 0 x y<0.2xy(x y)>0 M N>0. M>N. M>N0<x<1a换b 1 X c 匕得c>b,知c最大.答案:c17.如果a>0, b>0,则下列两式的大小关系为lg(1 + Vab) _______ 艮lg(1 + a) + lg(1 +b)].(填不等关系符号)解析:T (1 + a)(b+ 1) = 1 + a+ b+ ab,1•- 2[lg(1 + a) + lg(1 + b)]=lg 1 + a+ b+ ab.T (1 + :.;ab)2 —(-;”;1 + a+ b + ab)?= 2 ■'ab —(a + b),又 a + b》2、.;ab,.°. 2・..;ab —(a + b)w 0.1•- lg(1 + ■.ab)w 2【lg(1 + a) + lg(1 + b)].答案:w&一个个体户有一种商品,其成本低于^■器元.如果月初售出可获利100元,再将本利存入银行,已知银行月息为2.5%,如果月末售出可获利120元,但要付成本的2%的保管费,这种商品应_______________________ 出售(填“月初”或“月末”).解析:设这种商品的成本费为a元.月初售出的利润为L1= 100+ (a+ 100) X 2.5% ,月末售出的利润为L2= 120-2%a,则L1-L2= 100 + 0.025a+ 2.5- 120 + 0.02a=0.045 a-...av3器,•. L1<L2,月末出售好.答案:月末三、解答题9.已知a> 1,求证.a+ 1 - '.a< ,a- .a —1,证明:•/ ( a + 1 - .a) —( a —a- 1)= 1 -1.a+ 1 + \ a .a + a- 1m 0/什昇1 ) 0 f(a) f(b)a 3b 3 剧(a 2 b 2)a p a &a 並)b 乐(伍翻(帝佝[(佝5(W )5]a by/a y/b(回5(W )5(击承)[(W )5 (W )5] 0 a <b 羽<训 (诉)5<(托)5b a<0.a 1b 1m b a (a1 • 1<0f (a)<f(b )m•— >0 f(a)>f(b) a 1 b 12 2 2 2a 22x b 2 1 x 2 2x>a 2 a>0 b>0a 3b 3 何a 211m R a>b>1 mxf(x)'丿x 1f(a)f(a) f(b) ma 1a 1mb m b ab 1(a1 b1.a>b>1b a<0 a 1>0 b 1>0(⑴ 佝(何(何]>0.f(b)m>0m<0b>a.c b — x) 5^)产>01 x 1 x 1 xI -a + 1 + \a+ \; a—1 i,a+ 1 - .a<, a —, a- 1.10.设a, b是非负实数,求证:a3+ b3> ab(a I 2+ b2).什昇1) 0 f(a) f(b)m 0 /。

P24][ P24]() ()[1] |x 1| |x|<2.[] 3x 1x 1 x<2 一<x 1 2 1<x<0 x 1x<21<x<0x 1 x<2x<2.不等式的基木性质解不等式p 1元一次不等式含绝对值的不等式一元二次不等式因此,原不等式的解集为# —2<x<1匚法二:利用方程和函数的思想方法.令f(x) = |x+ 1|+ 凶一22x—1 x> 0 ,1=—1 —K x<0 ,—2x — 3 x<—1 .作函数f(x)的图象(如图),3 1知当f(x)<0 时,一2<x<?.3 1故原不等式的解集为X1 — 3<x<1 .法三:利用数形结合的思想方法.由绝对值的几何意义知,x+ 11表示数轴上点P(x)到点A(—1)的距离,|x|表示数轴上点P(x)到点0(0)的距离.由条件知,这两个距离之和小于 2.3 1 |--------------- 1作数轴(如图),知原不等式的解集为吠一3 v x</ .2 2丿3-1 0 1L.~2T 法四:利用等价转化的思想方法.原不等式? 0W|x+ 1|<2 —|x|,•••(x+ 1)2<(2 —|x|)2,且|X|<2,即0<4|x|<3—2x,且xi<2.• 16x <(3 —2x),且—2<x<2.3 1 3 1、解得—2<x<2・故原不等式的解集为<x|—2v x<2 r.[例2]已知f(x) =|ax+ 1|(a € R),不等式f(x) < 3 的解集为{x|—2< x< 1}.(1) 求a的值;⑵若f(x 一2f $ j w k恒成立,求k的取值范围.[解](1)由|ax+ 1|w 3 得—4w ax w 2.又f(x) w 3的解集为{x|—2w x w 1},所以当a w 0时,不合题意.当a>0 时,一4w x w2,得 a = 2.a a(2) 法一:记h(x) = f(x)—2fQ ,kk 1.B 2 .3 D 4 . 31.5(1x 1 」 4x 31<x< h(x) <【11 x212k 1.2|x 1||[3]0<x<21 cos 2x 8sin 2x22cos x8sin 2x 1 .. f(x)- 2sin xcos x 丄4ta n x. tan xI r 、 1x! P n 丿 tan x>0 tan x>0.f(x)1 4ta n x2 1 4ta nxtan x、:tan x[]C[4]xm11164.2014k (m 0) x 3(k )m 120148|h(x)| 1 k1| 1f(x) 2fg) k⑴将2014年该产品的利润y 万元(利润=销售金额—生产成本—技术改革费用 )表示为技术改革费用 m 万元的函数;⑵该企业2014年的技术改革费用投入多少万元时,厂家的利润最大? [解] ⑴由题意可知,当 m = 0时,x = 1(万件), 1 = 3— k.「. k = 2.「. x = 3 — _2—m + 1 每件产品的销售价格为 1.5 X 8±^6X (元),X ••• 2014年的利润16⑵「m >0,• mV (m +1)》216=8,• y w 29 — 8= 21.16当 =m + 1,即 m = 3, y max = 21. m +1•该企业2014年的技术改革费用投入 3万元时,厂家的利润最大证明不等式是近几年新课标高考的一个热点考向,常以解答题的形式出现,常与函数、 数列等知识交汇命题,常用到的证明方法有:1. 比较法证明不等式比较法证明不等式的依据是: 不等式的意义及实数比较大小的充要条件.作差比较法证明的一般步骤是:①作差;②恒等变形;③判断结果的符号;④下结论•其中,变形是证明 推理中一个承上启下的关键,变形的目的在于判断差的符号,而不是考虑差能否化简或值是多少,变形所用的方法要具体情况具体分析, 可以配方,可以因式分解,可以运用一切有效的恒等变形的方法.[例 5]已知 a > b>0,求证:2a 3 — b 3 >2ab 2— a 2b. [证明]2a 3— b 3— (2ab 2— a 2b) =2a(a 2— b 2) + b(a 2— b 2)22=(a — b )(2 a + b) =(a — b)(a + b)(2a + b).因为 a > b>0 ,所以 a — b >0, a + b>0,2a + b>0,从而(a — b)(a + b)(2a + b) > 0, 即 2a ‘— b ‘》2ab ?— a ^b.y = x • 1.5X8 + 16xx —(8 + 16x)— m -16m + 1卜 m + 1 + 29(m > 0).2. 综合法证明不等式综合法证明不等式的思维方向是“顺推” 件(由因导果),最后推导出所要证明的不等式成立.综合法证明不等式的依据是:已知的不等式以及逻辑推证的基本理论: 证明时要注意的是:作为依据和出发点的几个重要不等式(已知或已证)成立的条件往往不同,应用时要先考虑是否具备应有的条件,避免错误、如一些带等号的不等式,应用时要清楚取等号的条件, 即对重要不等式中“当且仅当…时,取等号”的理由要理解掌握.[例 6] 设 x>0 , y>0 , z>0,求证: ,x 2+ xy + y 2 + y 2 + yz + z 2>x + y + 乙 >x +y ,① 7y 2+ zy + z[z+ 2/+ 4y 2 >z + 2,②•••由①②得:x 2 + xy + y 2 + y 2 + zy + z>x + y + 乙 3. 分析法证明不等式分析法证明不等式的依据也是不等式的基本性质、 已知的重要不等式和逻辑推理的基本理论•分析法证明不等式的思维方向是“逆推”,即由待证的不等式出发,逐步寻找使它成立的充分条件(执果索因),最后得到的充分条件是已知 (或已证)的不等式.当要证的不等式不知从何入手时, 可考虑用分析法去证明,特别是对于条件简单而结论 复杂的题目往往更为有效.由教材内容可知,分析法是“执果索因”,步步寻求上一步成立的充分条件,而综合法是“由因导果”,逐步推导出不等式成立的必要条件,两者是对立统一的两种方法•一般来 说,对于较复杂的不等式, 直接用综合法往往不易入手, 因此,通常用分析法探索证题途径,然后用综合法加以证明,所以分析法和综合法可结合使用.[例 7]已知 a>0, b>0,且 a + b = 1,求证:[证明]即证 a + b + 1 + 2,即由已知的不等式出发,逐步推出其必要条[证明]8]2 .2 a2 1a孑<21 1 1112 12 31 1 1[ ] 1 23 <k 1 2 •2小11)2n<3.a>0 b>0 a b 1.(1)(ab1 1ab 2(a b) 4 114.] 22.212a12aaa2 4[9]22 )<1 +1 +1+ 步+ {+ …+ 十=1=3 — 2°-1V 3.爪匚'■■叭[对应学生用书P26] 一、选择题A . [ — 1,4) D . (— 1,4)解析:A = {x|x — 1|>2} = {x|x>3 或 x< — 1},2B = {x|x — 6x + 8<0} = {x|2<x<4}, •••(?u A) n B = {x|2<x w 3}. 答案:C12. a>1 ”是“才<1 ”成立的( )A .充分不必要条件B •必要不充分条件 C. 充要条件D. 既不充分也不必要条件1 1 一 a解析:当一<1时,有 <0,即a<0或a>1, a a 1所以a>1 ”是“丄<1”成立的充分不必要条件.a 答案:A 3.已知a ,b ,c 满足c<b<a 且a>0, ac<0,则下列选项中不一疋能成立的是()c b A . -<aa ab — a B . >0c .2 2b a c.—> —c ca — c D . <0 ac解析:由b>c , a>0,即丄>0,可得->c ,故A 恒成立.a a a-b<a ,…b — a<0.b _ a又c<0,•—厂>0,故B 恒成立.c -c<a ,・• a — c>0.1.已知全集 U = R ,且 A = {x|X — 1|>2}, B = {x|x 2— 6x + 8<0},则(?u A) n B 等于( B . (2,3) C . (2,3]ac<0 ----------- <0 Dac b 2 a 1b 2>a 2 c<0.2 2b a <—c cC4 |x 2| |x 3|>a x RA ( 5)B [0,5)C (1) D [0,1]A B A B |x 2| X 3|5Aa b不肩也何2占曙|x 1| |x 3|M >N6()x|ax 2|<3!x —I 33l32 a5一3 7a 71- 336 a引X132|x 2| |x 3|5 AB5a<5. A( 3)B(2)5.[-2x — 2,(X W — 3 , *;4, (— 3<x<1 ,(2x + 2, (X 》1 .当 x < — 3 时,一2x — 2>6? x < — 4; 当 x > 1 时,2x + 2>6? x >2; 当一3<x<1时,4W 6,舍去. 故不等式的解集为{x|x > 2或x < — 4}. 答案:{x|x > 2 或 x <— 4}1 , ,8.已知 a>0,贝U ---- , ~: ----- , ---------- 从大至U 小的顺序为2如 2pa + 1 >/a+p a + 1 解析:T a>0, — 2、a<• J a +、a + 1<2 .j a + 1 1 ______ 1 _______ 12 H a a + a + 1 2 ;:a + 1 1 1 _______ 12 ja a + \:a + 1 2\: a + 1 三、解答题(1)证明:对n 》2总有x n 》,a ; ⑵证明:对n 》2总有X n 》X n + 1.证明:(1)由x 1 = a>0,及X n + 1 = 1X n +旦可以归纳证明21 X n 丿X n • = a(n € N +),所以当n 》2时,x *》a 成立. X n (2)当 n 》2 时,因为 X n 》a>0 , X n + 1= 2 X n + X , 所以 x n +1 — x n =# 、 21 , a 1 a — x n= 1X n +X n —冷=2 - X n 仝故当n 》2时,Xn 》Xn + 1成立.10.已知关于x 的不等式 |ax — 1|+ |ax — a|》1(a>0).(1)当a = 1时,求此不等式的解集;(2)若此不等式的解集为 R ,求实数a 的取值范围. 解: (1)当 a = 1 时,得 2|x — 1|》1, 13 1••• ix -1》2 x 》3或 x < 2,•••不等式的解集为 *| x < 1或X 》2 .答案:9.某数列由下列条件确定:1 X 1 = a>0, xn + 1=-刈+x n , Xn >0,从而有 X n +1= £1-0(2) |ax 1| |ax a| |a 1|b a 小 C・a a 2b 2 ab ab a 2 A B|a| |b| 0 |a b| 0.Ra 2 a 0. |a 1| 1a[2 ) 11 (1) x(x 1)(x 21)(x 31) 8x(2) x R(x 1)(x 2 1)(x 3 1) 8x 3xx 12五 12 x 2xx 31 2品(x 1)(x 21)(x 3 1)2乐 2x 2欢8x 3(⑵ x R(x 21)(x1)(x 3 31) 8x 3(1)x>0x 0 8x 3 0.(x 1)(x 2 1)(x 3 1)(x 1)2(x 21)(x 2 x 1)(x 1)2(x 2 1)[(x 2)刃P49]1090120 ) 50 )A a 2 b 2B ab b 2 D |a||b| |a b|ABCD b a 0? ai |b|.a>0 a 2. (1) x答案:D2.设 a , b , c € R J 则"abc = 1” 是"芈 + -1 +-1 < a + b + c ” 的( p aQ b A /CA .充分条件但不是必要条件B •必要条件但不是充分条件C .充分必要条件D .既不充分也不必要的条件 解析:当a = b = c = 2时,有辛+¥ a + b + c ,但abc 丰1,所以必要性不成立; a . b . c当 abc = 1 时,"a * I * 1广J " * ac * ab , a* b 土 *2* c a * c > ab * bc * ac ,所以充分性成立, a * b * c ”的充分不必要条件. 答案:A x > 0,3.不等式3 -x 2 — x 的解集是()> | |3* x 2*X A . (0,2) B . (0,2.5) C . (0, .6) D . (0,3)5解析:用筛选法,容易验证 x = 2是不等式的解,否定A ; x = 5不是不等式的解,否定D ; X=V 6使汙% 瓷!取 “ = ”,7 V 2,故否定 B.3十x 2十X | 2 答案:C4•若a>b>0,则下列不等式中一定成立的是 () 1 1 A . a * b>b *a b b * 1B.a 诂 112a * b aC .a -b>b -aD .O *十航解析:a>b>0?右〉1〉。

1.5不等式证明的基本方法1.5.1 比 较 法[对应学生用书P16][读教材·填要点]1.定义要证a >b ,只需要证a -b >0;要证a <b ,只需证a -b <0,这种证明不等式的方法,称为比较法.2.用比较法证明不等式的步骤 (1)求差.(2)变形:可用因式分解、配方、乘法公式等,把差变形为乘积式平方和的形式. (3)作出判断.[小问题·大思维]作差比较法的主要适用类型是什么?实质是什么?提示:作差比较法尤其适用于具有多项式结构特征的不等式的证明.实质是把两个数或式子的大小判断问题转化为一个数(或式子)与0的大小关系.[对应学生用书P16][例1] 求证:(1)当x ∈R 时,1+2x 4≥2x 3+x 2; (2)当a ,b ∈(0,+∞)时,a a b b≥(ab )2a b.[思路点拨] (1)利用作差比较法,注意变形分解; (2)利用作商比较法,注意判断底数大小决定商的大小. [精解详析] (1)法一:(1+2x 4)-(2x 3+x 2) =2x 3(x -1)-(x +1)(x -1) =(x -1)(2x 3-x -1)=(x -1)(2x 3-2x +x -1) =(x -1)[2x (x 2-1)+(x -1)] =(x -1)2(2x 2+2x +1) =(x -1)2⎣⎡⎦⎤2⎝⎛⎭⎫x +122+12≥0, ∴1+2x 4≥2x 3+x 2. 法二:(1+2x 4)-(2x 3+x 2) =x 4-2x 3+x 2+x 4-2x 2+1 =(x -1)2·x 2+(x 2-1)2≥0, ∴1+2x 4≥2x 3+x 2. (2)2a b a ba b ab +()=a2a b -b2b a -=⎝⎛⎭⎫a b 2a b-,当a =b 时,⎝⎛⎭⎫a b 2a b-=1;当a >b >0时,a b >1,a -b 2>0,则⎝⎛⎭⎫a b 2a b->1; 当b >a >0时,0<ab <1,a -b 2<0,则⎝⎛⎭⎫a b 2a b->1.综上可知,当a ,b ∈(0,+∞)时,a a b b≥(ab )2a b +成立.(1)比较法证明不等式的过程中,变形具有承上启下的作用,变形的目的在于判断差的符号,而不用考虑差能否化简或值是多少.(2)变形所用的方法要具体情况具体分析,可以配方,可以因式分解,可以运用一切有效的恒等变形的方法.(3)因式分解是常用的变形手段,为了便于判断“差式”的符号,常将“差式”变形为一个常数,或几个因式积的形式,当所得的“差式”是某字母的二次三项式时,常用判别式法判断符号.有时会遇到结果符号不能确定,这时候要对差式进行分类讨论.1.已知x >-1,求证:1+x ≤1+x2.证明:∵x >-1, ∴1+x >0,1+x >0.∵1+x -(1+x2)=1+x -x +1+12=x +1-x +12-12=-12[(x +1)-2x +1+1]=-12(x +1-1)2≤0,∴1+x ≤1+x2.[例2] 甲、乙二人同时同地沿同一路线走到同一地点,甲有一半时间以速度m 行走,另一半以速度n 行走;乙有一半路程以速度m 行走,另一半路程以速度n 行走.如果m ≠n ,问甲、乙二人谁先到达指定地点?[思路点拨] 本题考查比较法在实际问题中的应用,解答本题需要设出从出发点到指定地点的路程s ,甲、乙二人走完这段路程各自需要的时间t 1、t 2,然后利用作差法比较t 1,t 2的大小即可.[精解详析] 设从出发地点至指定地点的路程为s ,甲、乙二人走完这段路程所用的时间分别为t 1、t 2,依题意有:t 12m +t 12n =s , s 2m +s2n=t 2. ∴t 1=2sm +n,t 2=s (m +n )2mn .∴t 1-t 2=2sm +n -s (m +n )2mn =s [4mn -(m +n )2]2mn (m +n )=-s (m -n )22mn (m +n ).其中s ,m ,n 都是正数,且m ≠n , ∴t 1-t 2<0,即t 1<t 2.从而知甲比乙先到达指定地点.应用不等式解决问题时,关键是如何把等量关系不等量关系转化为不等式的问题来解决,也就是建立数学模型是解应用题的关键,最后利用不等式的知识来解.解答不等式问题,一般可分为如下步骤:①阅读理解材料;②建立数学模型;③讨论不等式关系;④作出问题结论.2.某人乘出租车从A 地到B 地,有两种方案.第一种方案:乘起步价为10元,超过规定里程后每千米1.2元的出租车;第二种方案:乘起步价为8元,超过规定里程后每千米1.4元的出租车.按出租车管理条例,在起步价内,不同型号的出租车行驶的路程是相等的,则此人从A 地到B 地选择哪一种方案比较合适?解:设A 地到B 地的距离为m 千米.起步价内行驶的路程为a 千米. 显然当m ≤a 时,选起步价为8元的出租车比较合适.当m >a 时,设m =a +x (x >0),乘坐起步价为10元的出租车费用为P (x )元.乘坐起步价为8元的出租车费用为Q (x )元,则P (x )=10+1.2x ,Q (x )=8+1.4x . ∵P (x )-Q (x )=2-0.2x =0.2(10-x )∴当x >10时,P (x )<Q (x ),此时选择起步价为10元的出租车较为合适. 当x <10时,P (x )>Q (x ),此时选择起步价为8元的出租车较为合适. 当x =10时,P (x )=Q (x ),两种出租车任选,费用相同.[对应学生用书P18]一、选择题1.下列关系中对任意a <b <0的实数都成立的是( ) A .a 2<b 2 B .lg b 2<lg a 2 C .ba>1D .⎝⎛⎭⎫12a 2>⎝⎛⎭⎫12b 2解析:∵a <b <0,∴-a >-b >0. (-a )2>(-b )2>0. 即a 2>b 2>0. ∴b 2a2<1.又lg b 2-lg a 2=lg b 2a2<lg 1=0.∴lg b 2<lg a 2. 答案:B2.已知P =1a 2+a +1,Q =a 2-a +1,那么P 、Q 的大小关系是( )A .P >QB .P <QC .P ≥QD .P ≤Q解析:P -Q =1-(a 2-a +1)(a 2+a +1)a 2+a +1=-(a 4+a 2)a 2+a +1, ∵a 2+a +1>0恒成立且a 4+a 2≥0, ∴P -Q ≤0.即Q ≥P . 答案:D3.已知a >0,b >0,m =a b +ba,n =a +b ,p =a +b ,则m ,n ,p 的大小顺序是( )A .m ≥n >pB .m >n ≥pC .n >m >pD .n ≥m >p解析:由已知,知m =a b +ba,n =a +b ,得a =b >0时m =n ,可否定B 、C.比较A 、D 项,不必论证与p 的关系.取特值a =4,b =1,则m =4+12=92,n =2+1=3,∴m >n .可排除D. 答案:A4.若a ,b 为不等的正数,则(ab k +a k b )-(a k +1+b k +1)(k ∈N +)的符号( )A .恒正B .恒负C .与k 的奇偶性有关D .与a ,b 大小无关解析:(ab k +a k b )-a k +1-b k +1 =b k (a -b )+a k (b -a )=(a -b )(b k -a k ). ∵a >0,b >0,若a >b ,则a k >b k ,∴(a -b )(b k -a k )<0;若a <b ,则a k <b k ,∴(a -b )(b k -a k )<0. 答案:B 二、填空题5.若x <y <0,M =(x 2+y 2)(x -y ),N =(x 2-y 2)(x +y ),则M ,N 的大小关系为________. 解析:M -N =(x 2+y 2)(x -y )-(x 2-y 2)(x +y ) =(x -y )[(x 2+y 2)-(x +y )2]=-2xy (x -y ). ∵x <y <0,∴xy >0,x -y <0.∴-2xy (x -y )>0,∴M -N >0.即M >N . 答案:M >N6.设0<x <1,则a =2x ,b =1+x ,c =11-x 中最大的一个是________.解析:由a 2=2x ,b 2=1+x 2+2x >a 2,a >0,b >0, 得b >a .又c -b =11-x -(1+x )=1-(1-x 2)1-x =x 21-x>0,得c >b ,知c 最大. 答案:c7.如果a >0,b >0,则下列两式的大小关系为lg(1+ab )________12[lg(1+a )+lg(1+b )].(填不等关系符号)解析:∵(1+a )(b +1)=1+a +b +ab , ∴12[lg(1+a )+lg(1+b )] =lg1+a +b +ab .∵(1+ab )2-(1+a +b +ab )2=2ab -(a +b ),又a +b ≥2ab ,∴2ab -(a +b )≤0. ∴lg(1+ab )≤12[lg(1+a )+lg(1+b )].答案:≤8.一个个体户有一种商品,其成本低于3 5009元.如果月初售出可获利100元,再将本利存入银行,已知银行月息为2.5%,如果月末售出可获利120元,但要付成本的2%的保管费,这种商品应________出售(填“月初”或“月末”).解析:设这种商品的成本费为a 元.月初售出的利润为L 1=100+(a +100)×2.5%, 月末售出的利润为L 2=120-2%a , 则L 1-L 2=100+0.025a +2.5-120+0.02a =0.045⎝⎛⎭⎫a -3 5009, ∵a <3 5009,∴L 1<L 2,月末出售好.答案:月末 三、解答题9.已知a ≥1,求证a +1-a <a -a -1, 证明:∵(a +1-a )-(a -a -1)=1a +1+a-1a +a -1=a -1-a +1(a +1+a )(a +a -1)<0,∴a +1-a <a -a -1. 10.设a ,b 是非负实数,求证:a 3+b 3≥ab (a 2+b 2). 证明:由a ,b 是非负实数,作差得 a 3+b 3-ab (a 2+b 2)=a 2a (a -b )+b 2b (b -a ) =(a -b )[(a )5-(b )5].当a ≥b 时,a ≥b ,从而(a )5≥(b )5, 得(a -b )[(a )5-(b )5]≥0; 当a <b 时,a <b ,从而(a )5<(b )5,得(a -b )[(a )5-(b )5]>0. 所以a 3+b 3≥ab (a 2+b 2). 11.设m ∈R ,a >b >1,f (x )=mxx -1,比较f (a )与f (b )的大小. 解:f (a )-f (b )=ma a -1-mbb -1=m ·(b -a )(a -1)·(b -1).∵a >b >1,∴b -a <0,a -1>0,b -1>0, ∴b -a(a -1)·(b -1)<0.当m >0时,m ·(b -a )(a -1)·(b -1)<0,f (a )<f (b );当m <0时,m ·(b -a )(a -1)·(b -1)>0,f (a )>f (b ); 当m =0时,m ·(b -a )(a -1)·(b -1)=0,f (a )=f (b ).。