八上月考成绩统计表

初二年级八上期末成绩分析及提分对策
庄定炯
一、期末成绩分析
1、成绩：从A、B、C三个层次的班级还是能从成绩上有所体现。

但是A班的成绩没有达到学校要求的至少第二名；B班的成绩在全区中还是没有体现出B班的优势，；C班确实在学的人不多，尾巴也大。

2、原因：（1）从A、B班来说还是有太多这两个层次不该有的那么大的尾巴。

（2）确实因为跨年级，办公室又不在该年级，对初二学生关注要少些，抽学生背的时候太少，主要还是依靠班主任。

二、本期提升对策
1、初二下期的知识点在会考中所占比例较大。

对A班的学生可以适当延伸，要考虑到与高中知识的衔接。

2、对B班、C班的学生，主要少讲、多背、多练。

每节课花5—10分钟时间背上节课的内容，5—10分钟时间做当节课的联系。

3、按照年级安排，做好月考、期中、期末考试的复习安排。

4、期末复习的时候还是要给学生印复习资料。

5、B、C班的学生只背重点中的重点。

5、多读多练多背。

XX—2018学年度第一学期八年级英语第一次月考成绩试卷分析一、试题特点本次英语试题是梯级强化训练月考试题，难易程度适中，严格按照中考的出题模式出的试卷，测查的范围就是Units1—2的知识，知识点考查详细，采用各种形式检测学生对英语基础知识的掌握程度及灵活综合运用语言的能力。

二、考试总体情况两个班的两极分化非常严重，普遍成绩较低。

本次考试学生整体情况都不理想。

一方面是孩子们做这类试卷形式的题很少，另一方面孩子们比较浮躁，考试态度不是很端正。

三、试卷分析、听力此次考试的听力题目的是从一开始就要让孩子们重视听力，听说读写全面发展。

孩子们的听力层次不齐，有的孩子可以拿满分，有的孩子低至10来分。

以后还是要加强孩子们的听力训练。

2、完形填空完形填空是考试的基本题型，本次完形填空孩子们都比较熟悉。

比较简单，但是答题情况并不理想。

3、阅读理解三篇阅读理解，严格按照中考模式出题。

A篇阅读是判断正误，考察第一单元的知识。

B篇阅读和篇阅读的题都很简单，答题较为理想。

4、完成句子这道题可以很好的反映出孩子们记单词的情况。

通过试卷答题情况，反映出孩子们平时没有好好记单词，即使我们每节都有听写单词的环节，但是孩子们知识当成任务完成即可，没有灵活的运用知识。

、短文填空本次短文填空有10个空，是比较简单的，但是男孩子们的答题情况不好。

主要是因为他们对待英语考试的态度不端正。

6、任务型阅读这个阅读是文的类似版本，读起来比较流畅，试题也比较简单，但是大部分学生没有写出来。

7、完成对话这道题是要求孩子们写出英文句子，但是有部分学生理解英文太弱，没有英语的语言沟通思维，同时大部分孩子不记单词，所以这道题做的不是很好。

8、作文作文历来都是考试的一个重中之重的任务。

这次的考试作文题是我从第五单元的知识提取出来的，但是孩子答得不好，能的满分的学生寥寥无几。

而且孩子的作文反映出很强的中文思维。

四、教学建议综合学生答卷中的问题，为了今后更好的教学，提出以下教学建议：、基础知识的落实要常抓不懈，尤其在复习期间应巧抓落实。

宿迁市泗阳县2023-2024学年八年级上学期第一次月考语文试题注意事项:1.本试卷共8页，分值150分，考试时间150分钟。

2.答案一律用黑色钢笔或墨水笔写在答卷纸上，不能写在本试卷上。

第一部分(24分)一、积累与运用(24分)1.阅读下面语段，完成题目。

(9分)自古以来，浩hàn (▲)的长江在这片土地上流过，从qí(▲)岖的山路到浩渺的东海，它以锐不可当．(▲)的气势，冲刷出一条引领风骚的诗文之路，多少文人骚客在这里[甲]!这是一条镌．(▲)刻文明、充满灵性的诗歌之江，更是一条滋润人类、养育万物的生命之江。

(1)请根据拼音写汉字或给加点字注音。

(4分)浩 (hàn) ▲ (qí) ▲岖锐不可当．▲镌．刻▲(2)结合语境，填入甲处最恰当的一项是(▲)(3分)A.寻欢作乐纵情歌唱B.寻幽探胜纵情歌唱C.寻幽探胜惆怅徘徊D.寻欢作乐惆怅徘徊(3)语段中划线句子有语病，请你写出修改意见。

(2分)2.写出下列句子中的空缺部分。

(8分)山川之美，古来共谈，“树树皆秋色，(1) ”是秋意颇浓的山野之美;“重岩叠嶂，(2) ”是三峡山高谷深的险峻之美;“ (3)，长河落日圆”是塞外大漠雄浑壮丽之美;“ (4)，浅草才能没马蹄”是白居易笔下西湖早春的花草之美。

然览物之情，各有不同,面对傲雪凌霜的松柏，刘祯发出了“(5) ?松柏有本性”的赞叹;面对黄鹤楼下的美景，(6) (人名)抒发的是“ (7) (8)”的思乡之情。

3.综合性学习。

(7分)5.杜甫为什么自称“腐儒”，又言“心犹壮”?请结合全诗，谈谈你的看法。

(3分)(二)阅读下面的文言文，完成题目。

(15分)观月记(节选)(宋)张孝祥月极明于中秋，观中秋之月，临水胜;临水之观，宜独往;独往之地，去人远者又胜也。

然中秋多无月，城郭宫室，安得皆临水?盖有之矣，若夫远去人迹，则必空旷幽绝之地。

诚有好奇之士，亦安能独行以夜而之空旷幽绝，蕲顷刻之玩也哉?今余之游金沙堆，其具是四美者欤 ?中国科学界正举全国之力，缩小与世界科学珠峰的距离。

八年级上数学第一次月考试卷分析一、试题的结构、特点的分析１．试题结构的分析本套试题满分120分，七道大题包含24道小题，其中客观性题目占42分，主观性题目占78分。

２．试题的特点（1）强调能力，注重对数学思维过程、方法的考查试卷中不仅考查学生对第一章、第二章数学基础知识的掌握情况，而且也考查了学生以这些知识为载体，在综合运用这些知识的过程中所反映出来的基本的数学能力。

（2）重视阅读理解、获取信息和数据处理能力的考查从文字、图象、数据中获取信息和处理信息的能力是新课程特别强调的。

如第16题、17题、19题、题24题等，较好地实现了对这方面能力的考查，强调了培养学生在现代社会中获取和处理信息能力的要求。

（3）重视联系实际生活，突出数学应用能力的考查二、试题做答情况分析试题在设计上保持了一定的梯度，学生对客观题完成教好，后面的主观题完成较差，特别是应用方面，分析原因是：平时对阅读题较少，不能从题中找出有用的数学信息，缺乏耐心。

三、存在情况：1、好学生的学习态度可以，但进步不大，后进生情况令人担忧，缺乏学习数学的兴趣，譬如课前不预习、上课不听讲，课后不作业，考试不认真做；两级分化严重；差生面较多，特别是二班2、数学思维缺乏（分组讨论思想），学生一遇到难题就怕，不愿开动脑筋思考，对实际应用题型缺乏突破，对基础掌握不扎实，导致后面的大题失分非常严重3、对所学数学概念理解不透彻，对所学知识不会融会贯通，只会就题论题，不能用所学知识解决实际问题；4、审题意识不强，粗心，没有做阅读题的耐心；四、教学启示与建议通过对以上试卷的分析，在今后的教学过程中应注意以下几个方面：１．研读新课程标准，以新课程理念指导教学工作平时教学要从学生已有知识和生活经验出发，创设问题情境，激发学生的学习积极性，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学经验。

２．面向全体，夯实基础数学教学中应重视基本概念、基本图形、基本思想方法的教学和基本运算及分析问题、解决问题、运用等能力的培养，同时要特别关心数学学习困难的学生，通过学习兴趣培养学习方法指导，使他们达到学习的基本要求。

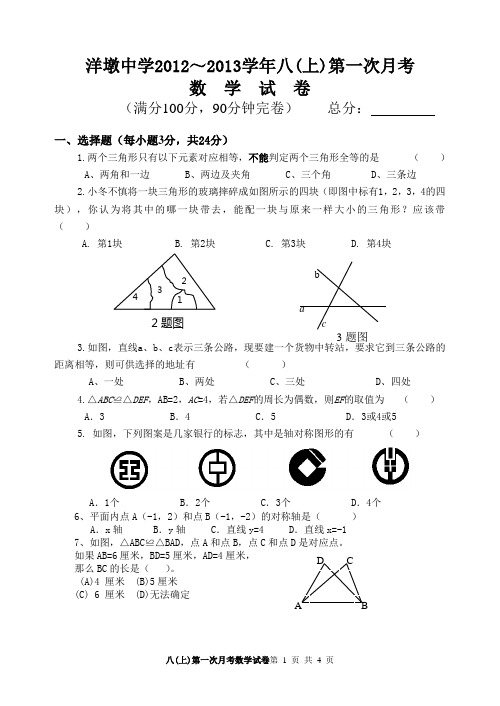
洋墩中学2012～2013学年八(上)第一次月考数 学 试 卷（满分100分，90分钟完卷） 总分：一、选择题（每小题3分，共24分）1.两个三角形只有以下元素对应相等，不能判定两个三角形全等的是 （ ）A 、两角和一边B 、两边及夹角C 、三个角D 、三条边2.小冬不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1，2，3，4的四块），你认为将其中的哪一块带去，能配一块与原来一样大小的三角形？应该带 （ ）A. 第1块B. 第2块C. 第3块D. 第4块3.如图，直线a 、b 、c 表示三条公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有 （ ）A 、一处B 、两处C 、三处D 、四处4.△ABC ≌△DEF ，AB=2，AC =4，若△DEF 的周长为偶数，则EF 的取值为 （ ）A ．3B ．4C ．5D ．3或4或55. 如图，下列图案是几家银行的标志，其中是轴对称图形的有 （ ）A ．1个B ．2个C ．3个D ．4个6、平面内点A （-1，2）和点B （-1，-2）的对称轴是（ ）A ．x 轴B ．y 轴C ．直线y=4D ．直线x=-17、如图，△ABC ≌△BAD ，点A 和点B ，点C 和点D 是对应点。

如果AB=6厘米，BD=5厘米，AD=4厘米， 那么BC 的长是（ ）。

(A)4 厘米 (B)5厘米(C) 6 厘米 (D)无法确定2题图D C A BA CB D E 8、如图，△ABN ≌△ACM ，AB=AC ，BN=CM ，∠B=50°，∠ANC=120°，则∠MAC 的度数等于（ ）A ．120° B.70°C.60°D.50°.二、选择题（每题3分，共15分）9.点(-2,1)关于x 轴对称的点坐标为__________.10.若△ABC ≌△DEF ，则_________＝DE ，BC ＝_________,∠ACB=_________.11.如图,在△ABC 中，∠C ＝90°，AD 是∠BAC 的角平分线，若BC ＝5㎝，BD ＝3㎝，则点D 到AB 的距离为 .．第11题图 第12题图 第13题图12．如图，已知∠1=∠2，请你添加一个条件：___________，使△ABD ≌△ACD .13．如图：沿AM 折叠，使D 点落在BC 上，如果AD=7cm ，DM=5cm ，∠DAM=30°，则AN=_________ cm ，∠NAM=_________。

试卷分析（沪科版八数上月考一）霍邱县乌龙镇中心学校龚家林一、试卷结构本次考试卷基本模仿着升学考试卷的结构，其中选择题10题，每题4分，填空题4题，每题5分，第三大题两题，第四大题两题，第五大题两题，六、七、八三大题，共２３个小题，满分１５０分，考试时间两个小时。

包括页面设置上也是象升学考试卷一样，分成每一页，共６页，这样的考试可让孩子们提前感知正规考试的题型和试卷结构，是一次很重要的锻炼。

二、试卷覆盖此次考试是我们学校的第一次月考，试卷是从外引入的现成试卷即2016——2017学年度八年级第一次大联考数学试卷，考试时间早已确定，十月八号至十月九号，考试内容为：第十一章：平面直角坐标系、第十二章的前两节（12.1函数，21.2一次函数），其中平面直角坐标系占小部分内容，约50分，大部分内容是一次函数，约占100分。

内容和结构安排比较合理，符合这一学期月考一的进度和内容要求。

三、难易程度这次考试全校八年级共参加224人，最高分150分，共两人，八（4）班的赵阳和本班的刘培煜，其次，140至150分共十四人，130分至140分二十四人。

我代的八(5)班除刘培煜最高分150分，其次陈寿瑞140分、黄维维141分，可见试卷还是有一定难度的，同时有些题学生关键不细心，丢分也十分严重。

选择题中也只有第9题，第10题难些。

填空题很多孩子第14题没有得到分，不是难，关键是不细心，都是习惯了算好就填数，而没有注意到是要求求a+b的值，丢失了5分。

第15题、第16题丢分也比较严重，主要是计算能力差。

第22题稍难些，是一个开放题，很多孩子脑海中还没有形成函数的模型，不能够进行分类讨论，然后归纳，再画出函数图象。

第23题是一个一次函数的模型题，其实这一题我们在上课过程中不止一次做过，甚至有的比这还难些，关键不能结合文字与实际生活做具体的分析，导致列不出式子，或者分析错误。

总体而言，试卷难易程度中等，这样的月考试卷也让孩子们知难而进，今后更加努力学习。

2020-2021学年四川省成都市双流中学实验学校八年级第一学期月考数学试卷（12月份）一、选择题（共10小题，每题3分，共30分）.1．下列实数中，属于无理数的是（）A．0B．3.14C．D．2．使代数式有意义的x的取值范围是（）A．x≥﹣1B．x＞﹣1C．x≥1D．x＞13．已知A，B两点在y＝2x+1上，A的坐标为（1，m），B的坐标为（3，n），则（）A．m＝n B．m＜n C．m＞n D．无法确定4．在平面直角坐标系中，一次函数y＝kx﹣3（k＜0）的图象大致是（）A．B．C．D．5．在平面直角坐标系xOy中，点P（x，y）在第二象限，且点P到横轴的距离等于3，到纵轴的距离等于4，则点P坐标是（）A．（﹣3，4）B．（3，﹣4）C．（﹣4，3）D．（4，﹣3）6．将函数y＝﹣4x的图象沿y轴向下平移2个单位后，所得到的函数图象对应的函数表达式（）A．y＝﹣4x+2B．y＝﹣6x C．y＝﹣4x﹣2D．y＝﹣2x7．学习了《数据的分析》后，小王同学对其学习小组内甲、乙、丙、丁四名同学的三次数学单元考试成绩的平均分（）、方差（s2）统计如下表，则数学成绩最好、最稳定的同学是（）甲乙丙丁平均分（）1009510095方差（s2）0.890.89 1.01 1.01A．甲B．乙C．丙D．丁8．如图所示，数轴上点A所表示的数为a，则a的值是（）A．+1B．C．﹣1D．﹣+19．某公司去年的利润（总产值﹣总支出）为200万元．今年总产值比去年增加了20%，总支出比去年减少了10%，今年的利润为780万元．如果去年的总产值x万元、总支出y 万元，则下列方程组正确的是（）A．B．C．D．10．如图所示，边长分别为1和2的两个正方形靠在一起，其中一边在同一水平线上．大正方形保持不动，小正方形沿该水平线自左向右匀速运动，设运动时间为t，大正方形内去掉小正方形重叠部分后的面积为s，那么s与t的大致图象应为（）A．B．C．D．二、填空题（本大题共4小题，每小题4分，共16分）11．比较大小：2；﹣5﹣5．12．已知：如图，∠1＝∠2＝∠3＝55°，则∠4的度数是．13．如图所示，一根长为7cm的吸管放在一个圆柱形杯中，测得杯的内部底面直径为3cm，高为4cm，则吸管露出在杯外面的最短长度为cm．14．如图，已知函数y＝x+1和y＝ax+3图象交于点P，点P的横坐标为1，则关于x，y的方程组的解是．三、解答题（本大题共6小题，共54分）15．计算：（1）×﹣（1﹣）2；（2）（π﹣2020）0+6﹣|5﹣|﹣（）﹣2．16．解方程组：．17．为了提高学生阅读能力，“双中实验校”倡议八年级学生利用双休日加强课外阅读，为了解同学们阅读的情况，学校随机抽查了部分同学周末阅读时间，并且得到数据绘制了不完整的统计图，根据图中信息回答下列问题：（1）将条形统计图补充完整：被调查的学生周末阅读时间众数是小时，中位数是小时．（2）计算被调查学生阅读时间的平均数．（3）我校八年级共有1200人，试估计周末阅读时间不低于1.5小时的人数．18．某旅馆的客房有三人间和两人间两种，三人间每人每天25元，两人间每人每天35元，一个50人的旅游团到该旅馆住宿，租住了若干客房，且每个客房正好住满，一天花去住宿费1510元，两种客房各租住多少间？19．如图，在平面直角坐标系xOy中，直线y＝﹣x+4与x轴、y轴分别交于点A、点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．（1）求AB的长；（2）求点C和点D的坐标；（3）y轴上是否存在一点P，使得S△PAB＝S△OCD？若存在，直接写出点P的坐标；若不存在，请说明理由．20．在等腰Rt△ABC中，∠ABC＝90°，AB＝BC．（1）如图1，D为线段BC的延长线上一点，连接AD，过点B作BE⊥AD，已知AB＝8，AD＝17，求CD和BE的长．（2）如图2，点F是线段AC上一点，连接BF，过点B作BG⊥AC于点G，过点C作CH⊥BF于点H，连接GH．①若＝，AC＝5，求S△BCH的值．②求证：CH﹣BH＝HC．四、填空题（本大题共5小题，每小题4分，共20分）21．若（a﹣2）+3y b﹣2＝2是关于x，y的二元一次方程，则a﹣b＝．22．已知关于x，y的二元一次方程组的解满足x﹣y＝3，则m的值为23．如图，已知直线上l：y＝x，过点A（0，1）作y轴的垂线交直线l于点B，过点B 作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线的垂线交轴于点A2；按此作法继续下去，则A1的坐标为，A2020的坐标．24．如图，已知a，b，c分别Rt△ABC是的三条边长，∠C＝90°，我们把关于x的形如y ＝x+的一次函数称为“勾股一次函数”．若点P（1，）在“勾股一次函数”的图象上，且Rt△ABC的面积是10，则c的值是．25．如图，已知x轴上一点A（4，0），B为y轴上的一动点，连接AB，以B为直角顶点，AB为腰作等腰直角△ABC，连接OC，则AC+OC的最小值是．五、解答题（本大题共3小题，共30分）26．甲、乙两个仓库要向A、B两地运送水泥，已知甲库可调出水泥100吨，乙库可调出水泥80吨；A地需水泥70吨，B地需水泥110吨，两仓库到A、B两地的路程和运费如下表：路程（千米）运费（元/吨•千米）甲库乙库甲库乙库A地20151212B地2520108（1）设甲库运往A地水泥x吨，求总运费y（元）关于x（吨）的函数关系式及x的取值范围；（2）当甲、乙两个仓库各运往A、B两地水泥多少吨时总运费最少？最少运费是多少？27．已知：直线m∥n，点A，B分别是直线m，n上任意两点，在直线m上取一点C，使AC＝AB，连接BC，在直线BC上任取一点E，作∠AEF＝∠BAC，EF交直线n于点F．（1）如图1，当点E在线段BC上，目∠BFE＝20°时，求∠BAE的度数．（2）若点E是线段BC上任意一点，求证：EF＝AE．（3）如图2，当点E在线段BC的延长线上时，若∠BAC＝90°，请判断线段EF与AE 的数量关系，并说明理由．28．如图，直线y＝kx+k分别交x轴、y轴于点A，C，直线BC过点C交x轴于点B，且OA＝OC，∠CBA＝45°，点P是直线BC上的一点．（1）求直线BC的解析式；（2）若动点P从点B出发沿射线BC方向匀速运动，速度为个单位长度/秒，连接AP，设△PAC的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式，并写出t的取值范围；（3）若点Q是直线AC上且位于第三象限图象上的一个动点，点M是y轴上的一个动点，当以点B、M、Q为顶点的三角形为等腰直角三角形时，求点Q和点M的坐标．参考答案一、选择题（共10小题，每题3分，共30分）.1．下列实数中，属于无理数的是（）A．0B．3.14C．D．【分析】根据无限不循环小数叫无理数，可得答案．解：A.0是整数，属于有理数；B.3.14是有限小数，属于有理数；C.是分数，属于有理数；D.是无理数．故选：D．2．使代数式有意义的x的取值范围是（）A．x≥﹣1B．x＞﹣1C．x≥1D．x＞1【分析】根据二次根式的被开方数是非负数列出不等式，解不等式得到答案．解：使代数式有意义，则x﹣1≥0，解得，x≥1，故选：C．3．已知A，B两点在y＝2x+1上，A的坐标为（1，m），B的坐标为（3，n），则（）A．m＝n B．m＜n C．m＞n D．无法确定【分析】利用一次函数图象上点的坐标特征可得出m，n的值，比较后即可得出结论．解：∵点A（1，m），B（3，n）在y＝2x+1上，∴m＝3，n＝7．∵3＜7，∴m＜n．故选：B．4．在平面直角坐标系中，一次函数y＝kx﹣3（k＜0）的图象大致是（）A．B．C．D．【分析】根据题目中的函数解析式和一次函数的性质，可以得到该函数图象经过哪几个象限，本题得以解决．解：∵一次函数y＝kx﹣3（k＜0），b＝﹣3，∴该函数图象经过第二、三、四象限，故选：C．5．在平面直角坐标系xOy中，点P（x，y）在第二象限，且点P到横轴的距离等于3，到纵轴的距离等于4，则点P坐标是（）A．（﹣3，4）B．（3，﹣4）C．（﹣4，3）D．（4，﹣3）【分析】P在第二象限，那么点P的横纵坐标的符号为负，正；进而根据P到x轴的距离为纵坐标的绝对值．到y轴的距离为横坐标的绝对值判断出具体坐标．解：∵点P在第二象限，且第二象限内的点横坐标小于0，纵坐标大于0；∴点P的横坐标小于0，纵坐标大于0∵点P到x轴的距离等于3，到y轴的距离等于4，∴点P的坐标是（﹣4，3）．故选：C．6．将函数y＝﹣4x的图象沿y轴向下平移2个单位后，所得到的函数图象对应的函数表达式（）A．y＝﹣4x+2B．y＝﹣6x C．y＝﹣4x﹣2D．y＝﹣2x【分析】直接利用一次函数平移规律，“上加下减”得出即可．解：将函数y＝﹣4x的图象沿y轴向下平移2个单位后，所得图象对应的函数关系式为：y＝﹣4x﹣2．故选：C．7．学习了《数据的分析》后，小王同学对其学习小组内甲、乙、丙、丁四名同学的三次数学单元考试成绩的平均分（）、方差（s2）统计如下表，则数学成绩最好、最稳定的同学是（）甲乙丙丁平均分（）1009510095方差（s2）0.890.89 1.01 1.01A．甲B．乙C．丙D．丁【分析】此题有两个要求：①成绩较好，②最稳定．于是应选平均数大、方差小的运动员参赛．解：由于甲的平均数较大且方差较小，故选甲．故选：A．8．如图所示，数轴上点A所表示的数为a，则a的值是（）A．+1B．C．﹣1D．﹣+1【分析】根据勾股定理，可得圆的半径，根据圆的性质，可得答案．解：如图，在Rt△BCD中，由勾股定理，得BD＝＝＝，由圆的性质，得AD＝BD＝，1﹣a＝，∴a＝1﹣，故选：D．9．某公司去年的利润（总产值﹣总支出）为200万元．今年总产值比去年增加了20%，总支出比去年减少了10%，今年的利润为780万元．如果去年的总产值x万元、总支出y 万元，则下列方程组正确的是（）A．B．C．D．【分析】根据：①去年总产值﹣去年总支出＝200，②今年总产值﹣今年总支出＝780，可列方程组．解：设去年的总产值x万元、总支出y万元，根据题意，可列方程：，故选：A．10．如图所示，边长分别为1和2的两个正方形靠在一起，其中一边在同一水平线上．大正方形保持不动，小正方形沿该水平线自左向右匀速运动，设运动时间为t，大正方形内去掉小正方形重叠部分后的面积为s，那么s与t的大致图象应为（）A．B．C．D．【分析】根据题意和函数图象可以得到各个过程中S随着t的变化如何变化，注意选项A 和选项D中的区别是一个变化比较大，一个变化比较小，这个可以根据两个正方形的面积进行判断正误．解：由题意可得，小正方形的面积为：1×1＝1，大正方形的面积为：2×2＝4，∴刚开始小正方形从左向右运动，到小正方形正好完全进入大正方形的过程中，S随t的增大而减小，面积由4减小到3；当小正方形刚好完全进入大正方形到一边刚好要出大正方形的过程中，S随t的增大不变，一直是S＝3，从小正方形刚好出大正方形到完全出大正方形的过程中，S随t的增大而增大，S由3增加到4，故选项A、B、C不符合题意，选项D符合题意，故选：D．二、填空题（本大题共4小题，每小题4分，共16分）11．比较大小：＜2；﹣5＜﹣5．【分析】根据算术平方根估算大小，然后利用实数的大小比较法则进行比较．解：∵，∴，∵，∴5＞5，∴﹣5＜﹣5．故答案为：＜，＜．12．已知：如图，∠1＝∠2＝∠3＝55°，则∠4的度数是125°．【分析】由∠1＝∠2及对顶角相等可得出∠1＝∠5，利用“同位角相等，两直线平行”可得出l1∥l2，利用“两直线平行，同旁内角互补”可求出∠6的度数，再利用对顶角相等可得出∠4的度数．解：给各角标上序号，如图所示．∵∠1＝∠2，∠2＝∠5，∴∠1＝∠5，∴l1∥l2，∴∠3+∠6＝180°．∵∠3＝55°，∴∠6＝180°﹣55°＝125°，∴∠4＝∠6＝125°．故答案为：125°．13．如图所示，一根长为7cm的吸管放在一个圆柱形杯中，测得杯的内部底面直径为3cm，高为4cm，则吸管露出在杯外面的最短长度为2cm．【分析】吸管露出杯口外的长度最少，即在杯内最长，可用勾股定理解答．解：设在杯里部分长为xcm，则有：x2＝32+42，解得：x＝5，所以露在外面最短的长度为7cm﹣5cm＝2cm，故吸管露出杯口外的最短长度是2cm，故答案为：2．14．如图，已知函数y＝x+1和y＝ax+3图象交于点P，点P的横坐标为1，则关于x，y的方程组的解是．【分析】先把x＝1代入y＝x+1，得出y＝2，则两个一次函数的交点P的坐标为（1，2）；那么交点坐标同时满足两个函数的解析式，而所求的方程组正好是由两个函数的解析式所构成，因此两函数的交点坐标即为方程组的解．解：把x＝1代入y＝x+1，得出y＝2，函数y＝x+1和y＝ax+3的图象交于点P（1，2），即x＝1，y＝2同时满足两个一次函数的解析式．所以关于x，y的方程组的解是．故答案为．三、解答题（本大题共6小题，共54分）15．计算：（1）×﹣（1﹣）2；（2）（π﹣2020）0+6﹣|5﹣|﹣（）﹣2．【分析】（1）根据二次根式的乘法法则和完全平分公式计算；（2）利用零指数幂、负整数指数幂和绝对值的意义计算．解：（1）原式＝﹣（1﹣2+3）＝2﹣4+2＝4﹣4；（2）原式＝1+2+5﹣3﹣4＝2﹣．16．解方程组：．【分析】方程组利用加减消元法求出解即可．解：，①×3得：6x﹣3y＝9③，②+③得：7x＝7，解得：x＝1，将x＝1代入①得：2﹣y＝3，解得：y＝﹣1，则方程组的解为．17．为了提高学生阅读能力，“双中实验校”倡议八年级学生利用双休日加强课外阅读，为了解同学们阅读的情况，学校随机抽查了部分同学周末阅读时间，并且得到数据绘制了不完整的统计图，根据图中信息回答下列问题：（1）将条形统计图补充完整：被调查的学生周末阅读时间众数是 1.5小时，中位数是 1.5小时．（2）计算被调查学生阅读时间的平均数．（3）我校八年级共有1200人，试估计周末阅读时间不低于1.5小时的人数．【分析】（1）根据众数，中位数的定义解决问题即可．（2）根据平均数的定义求解即可．（3）用样本估计总体的思想解决问题即可．解：（1）由题意可得，本次调查的学生数为：30÷30%＝100（人），阅读时间1.5小时的学生数为：100﹣12﹣30﹣18＝40（人），补全的条形统计图如图所示：由补全的条形统计图可知，抽查的学生阅读时间的众数是1.5小时，中位数是1.5小时．故答案为：1.5；1.5．（2）所有被调查同学的平均阅读时间为：（小时），即所有被调查同学的平均阅读时间为1.32小时．（3）不低于1.5小时所占比例；，∴1200×58%＝696（人），故我校八年级阅读不低于1.5小时的人数696人．18．某旅馆的客房有三人间和两人间两种，三人间每人每天25元，两人间每人每天35元，一个50人的旅游团到该旅馆住宿，租住了若干客房，且每个客房正好住满，一天花去住宿费1510元，两种客房各租住多少间？【分析】设租住三人间x间，租住两人间y间，就可以得出3x+2y＝50，3×25x+2×35y ＝1510，由这两个方程构成方程组求出其解就可以得出结论．解：设租住三人间x间，租住两人间y间，由题意，得，解得：．答：租住三人间8间，租住两人13间．19．如图，在平面直角坐标系xOy中，直线y＝﹣x+4与x轴、y轴分别交于点A、点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．（1）求AB的长；（2）求点C和点D的坐标；（3）y轴上是否存在一点P，使得S△PAB＝S△OCD？若存在，直接写出点P的坐标；若不存在，请说明理由．【分析】（1）先求得点A和点B的坐标，则可得到OA、OB的长，然后依据勾股定理可求得AB的长，（2）依据翻折的性质可得到AC的长，于是可求得OC的长，从而可得到点C的坐标；设OD＝x，则CD＝DB＝x+4．，Rt△OCD中，依据勾股定理可求得x的值，从而可得到点D（0，﹣6）．（3）先求得S△PAB的值，然后依据三角形的面积公式可求得BP的长，从而可得到点P 的坐标．解：（1）令x＝0得：y＝4，∴B（0，4）．∴OB＝4令y＝0得：0＝﹣x+4，解得：x＝3，∴A（3，0）．∴OA＝3．在Rt△OAB中，AB＝＝5．（2）∵AC＝AB＝5，∴OC＝OA+AC＝3+5＝8，∴C（8，0）．设OD＝x，则CD＝DB＝x+4．在Rt△OCD中，DC2＝OD2+OC2，即（x+4）2＝x2+82，解得：x＝6，∴D（0，﹣6）．（3）存在，理由如下：∵S△PAB＝S△OCD，∴S△PAB＝××6×8＝12．∵点P在y轴上，S△PAB＝12，∴BP•OA＝12，即×3BP＝12，解得：BP＝8，∴P点的坐标为（0，12）或（0，﹣4）．20．在等腰Rt△ABC中，∠ABC＝90°，AB＝BC．（1）如图1，D为线段BC的延长线上一点，连接AD，过点B作BE⊥AD，已知AB＝8，AD＝17，求CD和BE的长．（2）如图2，点F是线段AC上一点，连接BF，过点B作BG⊥AC于点G，过点C作CH⊥BF于点H，连接GH．①若＝，AC＝5，求S△BCH的值．②求证：CH﹣BH＝HC．【分析】（1）先利用勾股定理求出BD，CD，再利用S△ABD＝•AB•BD＝•AD•BE，求出BE，即可解决问题；（2）①如图2中，设BH＝x，CH＝2x，利用勾股定理可得x，求出BH，CH可得结论；②如图3，在CH上截取CM＝BH，连接GM，证明△GCM≌△GBH，根据线段的差可得结论．解：（1）在Rt△ABD中，AB＝8，AD＝17，∠ABC＝90°，∴，∵AB＝BC＝8，∴CD＝BD﹣BC＝15﹣8＝7，∵．∴BE＝＝＝．（2）①∵AB＝BC，∠ABC＝90°，∴，∴BC＝5，∵，设BH＝x，则HC＝2x，在Rt△BCH中，BC2＝BH2+HC2＝5x2，∴5x2＝52，∴，∴，∴．②在CH上截取CM＝BH，连接GM，∵AB＝BC，BG⊥AC，∠ABC＝90°，∴BG＝AG＝CG，∵BH⊥CH，∴∠BHC＝∠BGC＝90°，由8字模型倒角得∠GCM＝∠GBH，在△GCM和△GBH中，，∴△GCM≌△GBH（SAS），∴CM＝CH，∠CGM＝∠BGH，∴∠CGM+∠BGM＝∠BGH+∠BGM＝90°，∴∠HGM＝90°，∴△HGM是等腰直角三角形，∴，∴，∴．四、填空题（本大题共5小题，每小题4分，共20分）21．若（a﹣2）+3y b﹣2＝2是关于x，y的二元一次方程，则a﹣b＝﹣5．【分析】根据二元一次方程的定义得到且a﹣2≠0，联立方程组并解答．解：依题意得且a﹣2≠0，解得，则a﹣b＝﹣2﹣3＝﹣5．故答案为：﹣5．22．已知关于x，y的二元一次方程组的解满足x﹣y＝3，则m的值为1【分析】②﹣①得到x﹣y＝4﹣m，代入x﹣y＝3中计算即可求出m的值．解：，②﹣①得：x﹣y＝4﹣m，∵x﹣y＝3，∴4﹣m＝3，解得：m＝1，故答案为：123．如图，已知直线上l：y＝x，过点A（0，1）作y轴的垂线交直线l于点B，过点B 作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线的垂线交轴于点A2；按此作法继续下去，则A1的坐标为（0，4），A2020的坐标（0，24040）．【分析】根据所给直线解析式可得l与x轴的夹角，进而根据所给条件依次得到点A1，A2的坐标，通过相应规律得到A2020坐标即可．解：∵直线l的解析式为上，当y＝1，时，代入上式x＝，即AB＝，AO＝1，∴tan∠AOB＝＝，∴∠AOB＝60°，∵A（0，1），AB⊥y轴，∴OB＝2，∵A1B⊥l，∴OA1＝4，∴A1（0，4），同理可得A2（0，16）...A n（0，22n），∴A2020的纵坐标为24040，∴A2021（0，24040），故答案为：A2020（0，24040）．24．如图，已知a，b，c分别Rt△ABC是的三条边长，∠C＝90°，我们把关于x的形如y ＝x+的一次函数称为“勾股一次函数”．若点P（1，）在“勾股一次函数”的图象上，且Rt△ABC的面积是10，则c的值是．【分析】依据题意得到三个关系式：，ab＝20，a2+b2＝c2，运用完全平方公式即可得到c的值．解：∵点在“勾股一次函数”乌的图象上，∴把代入得，，即，∵a，b，c分别是Rt△ABC的三条边长，∠C＝90°，Rt△ABC的面积为10，∴，a2+b2＝c2，故ab＝20，∴（a+b）2﹣2ab＝c2，∴，∴，解得：，故答案为：．25．如图，已知x轴上一点A（4，0），B为y轴上的一动点，连接AB，以B为直角顶点，AB为腰作等腰直角△ABC，连接OC，则AC+OC的最小值是4．【分析】过C作CH⊥y轴于H，根据等腰直角三角形，的性质得到AB＝BC，∠ABC＝90°．根据全等三角形的性质得到OB＝HC，OA＝BH．设B点坐标为（0，n），得到OB＝HC＝n，推出点C在直线y＝x+4上．设直线y＝x+4与x轴交于点P，与y轴交于点Q，令y＝0，得到P（﹣4，0），Q（0，4），过O点作直线y＝x+4的对称点M，连结PM，AM，CM，根据轴对称的性质得到PO＝PM，CO＝CM，∠OPQ＝∠MPQ＝45°，求得M点坐标为（﹣4，4）．当且仅当A，M，C三点共线时，AC+OC取得最小值，根据勾股定理即可得到结论．解：过C作CH⊥y轴于H，∴△ABC是等腰直角三角形，∴AB＝BC，∠ABC＝90°．∵∠AOB＝∠CHB＝90°，∴∠OBA+∠OAB＝90°，∠0BA+∠HBC＝90°，∴∠OAB＝∠HBC，在△AOB和△BHC中，∴△AOB≌△BHC（AAS），∴OB＝HC，OA＝BH．∵A点坐标为（4，0），∵OA＝4，∴BH＝4，设B点坐标为（0，n），∴OB＝HC＝n，∴OH＝OB+BH＝4+n，∴C点坐标为（n，4+n），∴点C在直线y＝x+4上．设直线y＝x+4与x轴交于点P，与y轴交于点Q，令y＝0，x+4＝0，解得x＝﹣4，令x＝0，y＝4，∴P（﹣4，0），Q（0，4），∴OP＝OQ＝4．∵∠POQ＝90°，∴∠OPQ＝45°，过O点作直线y＝x+4的对称点M，连结PM，AM，CM，由对称性可知，PO＝PM，CO＝CM，∠OPQ＝∠MPQ＝45°，∴∠MPO＝90°，∴M点坐标为（﹣4，4）．∵AC+OC＝AC+CM≥AM，∴当且仅当A，M，C三点共线时，AC+OC取得最小值，∴AC+OC的最小值即为线段AM的长度．∴，∴AC+OC的最小值为．故答案为：．五、解答题（本大题共3小题，共30分）26．甲、乙两个仓库要向A、B两地运送水泥，已知甲库可调出水泥100吨，乙库可调出水泥80吨；A地需水泥70吨，B地需水泥110吨，两仓库到A、B两地的路程和运费如下表：路程（千米）运费（元/吨•千米）甲库乙库甲库乙库A地20151212B地2520108（1）设甲库运往A地水泥x吨，求总运费y（元）关于x（吨）的函数关系式及x的取值范围；（2）当甲、乙两个仓库各运往A、B两地水泥多少吨时总运费最少？最少运费是多少？【分析】（1）由甲库运往A地水泥x吨，根据题意首先求得甲库运往B地水泥（100﹣x）吨，乙库运往A地水泥（70﹣x）吨，乙库运往B地水泥（10+x）吨，然后根据表格求得总运费y（元）关于x（吨）的函数关系式；（2）根据（1）中的一次函数解析式的增减性，即可知当x＝70时，总运费y最省，然后代入求解即可求得最省的总运费．解：（1）设甲库运往A地水泥x吨，依题意得y＝12×20x+10×25×（100﹣x）+12×15×（70﹣x）+8×20×（10+x）＝﹣30x+39200 （0≤x≤70）（2）上述一次函数中k＝﹣30＜0∴y的值随x的增大而减小，∴x＝70时，总运费y最少，最少的总运费为37100元．27．已知：直线m∥n，点A，B分别是直线m，n上任意两点，在直线m上取一点C，使AC＝AB，连接BC，在直线BC上任取一点E，作∠AEF＝∠BAC，EF交直线n于点F．（1）如图1，当点E在线段BC上，目∠BFE＝20°时，求∠BAE的度数．（2）若点E是线段BC上任意一点，求证：EF＝AE．（3）如图2，当点E在线段BC的延长线上时，若∠BAC＝90°，请判断线段EF与AE 的数量关系，并说明理由．【分析】（1）由三角形的内角和定理可求解；（2）由“AAS”可证△EMF≌△EBA，可得EF＝AE；（3）由“SAS”可证△ABE≌△NBE，可得AE＝EN，∠EAB＝∠ENB，由补角的性质可证EF＝EN＝AE．【解答】证明：（1）如图1，设AB与EF交于点O，∵m∥n，∴∠BAC＝∠ABF，∵∠BAC＝∠ABF，∴∠AEF＝∠ABF，∵∠AOE＝∠BOF，∠OAE＝180°﹣∠AEF﹣∠AOE，∠BFE＝180°﹣∠ABF﹣∠BOF，∴∠OAE＝∠BFE＝20°．（2）如图1﹣1，以E为圆心，BE为半径画弧交直线n于点M，连接EM，∴EM＝EB，∴∠EMB＝∠EBM，∵m∥n，∴∠ACB＝∠EBM，∵AC＝AB，∴∠ACB＝∠ABC，∴∠EMF＝∠ABC，由（1）可知，∠EAB＝∠EFB，在△EMF和△EBA中，，∴△EMF≌△EBA（AAS），∴EF＝AE．（3）EF＝AE，理由如下：如图2，在BF上截取BN＝AB，连接EN，∴AB＝AC，∴∠ACB＝∠ABC，∵m∥n，∴∠ACB＝∠NBC，∴∠ABC＝∠NBC，在△ABE和△NBE中，，∴△ABE≌△NBE（SAS），∴AE＝EN，∠EAB＝∠ENB，∵∠AEF＝∠BAC＝90°，∠BAC＝∠ABF＝90°，∴∠EAB+∠EFB＝180°，∵∠ENB+∠ENF＝180°，∴∠EFB＝∠ENF，∴EF＝EN，∴EF＝AE．28．如图，直线y＝kx+k分别交x轴、y轴于点A，C，直线BC过点C交x轴于点B，且OA＝OC，∠CBA＝45°，点P是直线BC上的一点．（1）求直线BC的解析式；（2）若动点P从点B出发沿射线BC方向匀速运动，速度为个单位长度/秒，连接AP，设△PAC的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式，并写出t的取值范围；（3）若点Q是直线AC上且位于第三象限图象上的一个动点，点M是y轴上的一个动点，当以点B、M、Q为顶点的三角形为等腰直角三角形时，求点Q和点M的坐标．【分析】（1）点A（﹣1，0），且OA＝OC，则点C（0，3），则k＝3，∠CBA＝45°，则OB＝OC＝3，即可求解；（2）利用S＝S△ABC﹣S△ABP或S＝S△ABP﹣S△ABC，即可求解；（3）分∠BMQ＝90°、∠MQB＝90°、∠QBM＝90°三种情况，分别求解即可．解：（1）直线y＝kx+k分别交x轴、y轴于点A，C，则点A（﹣1，0），且OA＝OC，则点C（0，3），则k＝3，故直线AC的表达式为：y＝3x+3，∵∠CBA＝45°，∴OB＝OC＝3，∴点B（3，0），∵点C（0，3）、点B（3，0），则直线BC的表达式为：y＝﹣x+3；（2）当点P在线段BC时，过点P作PH⊥x轴于点H，∵∠CBA＝45°，PH＝PB sin45°＝t×＝t，S＝S△ABC﹣S△ABP＝×BA×（OC﹣PH）＝4×（3﹣t）＝6﹣2t，（0≤t≤3）；当点P在y轴右侧的射线BC上时，同理可得：S＝S△ABP﹣S△ABC＝2t﹣6，（t＞3）；故S＝；（3）设点M（0，m），点Q（n，3n+3），①如图2（左侧图），当∠BMQ＝90°时，（点M在x轴上方），分别过点Q、P作y轴的平行线QG、BH，过点M作x轴的平行线分别交GQ、BH于点G、H，∵∠GMQ+∠MQG＝90°，∠GMQ+∠HMB＝90°，∴∠HMB＝∠GQM，∠MHB＝∠QGM＝90°，MB＝MQ，∴△MHB≌△QGM（AAS），∴GQ＝MH，BH＝GM，即：m＝﹣n，m﹣3n﹣3＝3，解得：m＝，n＝﹣；故点M（0，）、点Q（﹣，﹣）；同理当点M在x轴下方时，3n+3﹣m＝3且﹣m＝﹣n，解得：m＝n＝0（舍去）；②当∠MQB＝90°时，同理可得：﹣n＝﹣3n﹣3，3n+3﹣m＝3﹣n，解得：m＝﹣6，n＝﹣，故点M（0，﹣6）、点Q（﹣，﹣）；③当∠QBM＝90°时，同理可得：﹣3n﹣3＝3，m＝3﹣n解得：m＝5，n＝﹣2，点M（0，5）、点Q（﹣2，﹣3）；综上，M（0，）、Q（﹣，﹣）或M（0，﹣6）、Q（﹣，﹣）或M（0，5）点Q（﹣2，﹣3）．。

（考试时间：120 分钟；满分：120 分）1.根据要求完成下题。

（6 分）我们的文化遗产是历史的见证。

秦朝的兵马俑至今仍然A．无动于衷地挺立着，隋朝大运河的波澜依旧拍打着千年的岸堤……这些文化遗产镂刻着历史的痕迹，将肃穆呈于世人。

我们的文化遗产是中华民族的魂。

万里长城记载了中华民族积极反抗侵略、抵 y ù ( ) 压迫的民族精神。

B. 自出心裁的剪纸、年画、刺绣体现了生动的民族特性。

这些文化遗产向世界诠释了中华民族的精神风貌。

我们的文化遗产是中国人的根。

君不见，每年都有 C. 络绎不绝的海外游子经过D. 长途跋涉寻回家来，在黄帝陵前捧上一回黄土。

我们的文化遗产情牵了亿万炎黄子孙的心。

历史的见证，民族的魂，民族的根使我们的文化遗产历经千年而巍然屹立于世界民族文化之林。

所以，①。

（1）给加点字注音或者根据拼音写汉字。

（2 分）镂刻( ) 抵 yù( )（2）文中划横线的四字短语使用不正确的一项是（）（2 分）A．无动于衷 B．自出心裁 C．络绎不绝 D．长途跋涉（3）根据文意，在横线①处补写一句祈使句。

（2 分）2.依次填入下面一段文字横线处的语句,衔接最恰当的一项是（）(2 分)牡丹是芍药科芍药属植物。

__ 。

,来年新叶和新枝直接从老枝上生出;芍药组则是亚灌木和草本植物,它们的茎只有基部木质化或完全为草质,冬天地上部分大都枯死或完全枯死,来年不得不从茎基上再生出新枝叶。

①它们的茎高度地木质化,冬天地上部分只落叶不枯死②芍药属全世界一共有30 多种,除北美洲西部的两个种外都产自旧大陆③尽管牡丹组和芍药组在花型上极其相似,但牡丹组是灌木④这些旧大陆的种可以分成两组--牡丹组和芍药组A.②③④①B.②④③①C.①②③④D.①③②④3.古诗文默写。

（8 分）（ 1 ）孟子在《富贵不能淫》阐述大丈夫应该遵守 “ 仁 ” “ 礼 ” “ 义 ” 原则的句子是：，，。

（2）《得道多助，失道寡助》，指出决定战争胜利的三要素及其关系的句子是：，。