高数下期中考B

高等数学模拟题A ．上册：上册期中（一）一、试解下列各题： 1．求。

2．求。

3．设处连续，在处不连续，试研究在处的连续性。

4．求在上的最大值与最小值。

二、试解下列各题： 1．判断的奇偶性。

2．[5分]设，其中，求。

3．[5分]设，求。

4．[5分]验证罗尔定理对在上的正确性。

三、试解下列各题：1．[6分]设函数由方程所确定，且，其中是可导函数，，求的值。

2．求极限。

3．求的极值。

四、设圆任意一点M （点M 在第一象限）处的切线与轴，轴分别交于A 点和B 点，试将该切线与两坐标轴所围成的三角形AOB 的面积S 表示为的函数。

1cos cos 21cos 2cos 8lim223-+--→x x x x x π242320)1()1(limx x x x --+→0)(x x x f =在)(x g 0x )()()(x g x f x F +=0x x x x f +=2)(]1,1[-)11(11ln 11)(<<-+-+-=x x x e e x f x x )]1ln 1ln(1ln[x x x y ++=10<<x y 'x xy +-=11)(n y 1074)(23--+=x x x x f ]2,1[-)(x y y =)()(22y x f y x f y +++=2)0(=y )(x f 1)4(,21)2(='='f f 0=x dxdy xx x 10)(cos lim +→22)13()(e x x e x f x +++=-222a y x =+),(y x ox oy x五、用函数连续性“”的定义，验证函数在任意点处连续。

六、求极限七、求与的公切线方程。

八、证明：当时，。

九、]一气球从距离观察员500米处离地匀速铅直上升，其速率为140米/分，当此气球上升到500米空中时，问观察员的视线的倾角增加率为多少？ 参考答案：一、1．2。

中国农业大学2019 ~2020学年秋季学期（2019.12 ） 高等数学A （上） 课程试题解答一、单项选择题（本题共有8道小题，每小题3分，满分24分）1. 设函数()f x 可微，则2d ()f x =【 C 】．(A) ()22d x f x x '； (B) ()2d f x x '； (C) ()22d x f x x '； (D) ()22x f x '.2. 设2sin ()sin x t xF x e tdt π+=⎰，则()F x 【 A 】．(A) 为正常数； (B) 为负常数； (C) 恒为零； (D) 不为常数.3. 已知函数()y f x =对一切x 满足[]2()3()1x xf x x f x e -'''+=-，若()00()00f x x '=≠，则【 C 】.(A) 0()f x 是()f x 的极大值； (B) ()00,()x f x 是曲线()y f x =的拐点； (C) 0()f x 是()f x 的极小值；(D) 0()f x 不是()f x 的极小值，()00,()x f x 不是曲线()y f x =的拐点.4. 设10()20，，x e x f x x x ⎧-≥=⎨<⎩, 则()f x 在0x =处【 D 】.(A) 0lim ()x f x →不存在； (B) 0lim ()x f x →存在, 但在0x =处不连续；(C) (0)f '存在； (D) ()f x 在0x =处连续, 但不可导.5. 设当0x →时，2(1cos )ln(1)x x -+是比sin n x x 高阶的无穷小，而sin nx x 是比2(1)x e -高阶的无穷小，则正整数n = 【 B 】.(A) 1 ; (B) 2 ; (C) 3 ; (D) 4.6. 0x =是函数12sin ()||1xxf x x e=++的【 B 】间断点. (A) 跳跃； (B) 可去； (C) 无穷； (D) 振荡.7. 下列积分的值为0的是【 C 】. (A)111dx x -⎰； (B)11sin(2)x dx -+⎰； (C)11cos x xdx -⎰； (D)21xdx x +∞-∞+⎰. 8. 已知一阶线性微分方程()x y p x y e '+=有特解x y xe =，则该微分方程的通解是【 B 】.(A) ()xy e C x =-； (B) ()xy e C x =+；(C) (2)x y e C x =-； (D) (2)x y e C x =+.二、填空题（本题共有4道小题，每小题3分，满分12分） 1. ()1lim 12xx x →+ =2e .2. 已知函数()y y x =由方程2610ye xy x ++-=确定，则(0)y ''= -2 .3. 设lim ()x f x k →∞'=，则 []lim ()()x f x a f x →∞+-=ka .4. 11xdx e=+⎰ ln(1)x x e C -++ .三、求解下列各题（本题共有4道小题，每小题7分，满分28分）.(1) 求极限 20ln(1)lim sec cos x x x x→+-　.【解】 解一 22200ln(1)lim lim sec cos 1cos x x x x x x x→→+=-- =1解二 22002ln(1)1lim lim 1sec cos sec tan sin x x xx x x x x x x→→++==-+ (2) 证明：当1x >时，ln(1)ln 1x xx x+>+. 【解】令()(1)ln(1)ln f x x x x x =++-1()ln(1)11ln ln0xf x x x x+'⇒=++--=> ， 于是()f x 在1x >时单调递增，所以()(1)2ln20f x f >=> ， 所以，当1x >时，(1)ln(1)ln x x x x ++>⇒ln(1)ln 1x xx x+>+ .(3) 设0()()cos f x x f x xdx π=-⎰，求()f x .【解】 原等式两端同时乘以cos x ，并从0到π积分得()cos cos cos ()cos f x xdx x xdx xdxf x xdx ππππ=-⎰⎰⎰⎰，求得0()cos 2f x xdx π=-⎰ ，所以 ()2f x x =+ .(4)求微分方程2109xy y y e '''-+=的通解.【解】特征方程21090r r -+= ， 特征根121,9r r ==对应齐次方程的通解为912x x y C e C e =+ 设*2x y Ae =是原微分方程的一个特解，求得17A =-，即*217x y e =-所以原微分方程的通解为 921217x x x y C e C e e =+-.四、（本题满分10分）在曲线21(0)y x x =>上求一点M , 使过该点的切线被两坐标轴所截得的长度最短, 并求出这最短的长度.解 设点M(t,21)t即为所求的切点(也可设为(0201,x x ))， 切线方程为 2312()y x t t t-=-- 两截距分别为 233,2t t ,于是所截线段长度为 l241()4t f t t=+ 在()0,+∞内的最小值点.由54()2t f t t '=-=0，得唯一驻点为t，且0,f ''> t. 由实际问题可知， t是最小值点，故点12)即为所求的点，且最短距离为2. 五、（本题满分10分）设函数()f x 在(),-∞+∞内二阶可导且()0f x ''>，又()0lim1x f x x→=.1. 求()(0),0f f '；2. 试证：在()0,+∞内，函数()()f x g x x=是单调增加的.解 1. 因为()0lim1x f x x→=, 要使此式成立，必 ()0lim 0x f x →=. 又因为可导必连续，()f x 在(),-∞+∞内二阶可导，所以 ()()0lim 00x f x f →== ()()()()000limlim10x x f x f f x f x x→→-'===-2. ()()()2x f x f x g x x'-'=，设()()()h x x f x f x '=-，下证()0h x ≥.因为()h x 在[)0,+∞上连续，且()()()()()()()0,0,h x f x x f x f x x f x x '''''''=+-=>∈+∞所以()h x 在()0,+∞内单调增加， ()()00h x h >=，所以()0g x '>，()g x 在()0,+∞内单调增加.六、（本题满分10分）已知()f x 有连续导数，当0x →时，220()()()xF x x t f t dt '=-⎰的导数与2x 为等价无穷小，求0f '（）.解 22220()()()()()xxxF x x t f t dt x f t dt t f t dt '''=-=-⎰⎰⎰220()2()()()xF x x f t dt x f x x f x ''''=+-⎰2()2(()(0))xx f t dt x f x f '==-⎰由题意22000()2(()(0))()(0)lim=lim 2lim 1x x x F x x f x f f x f x x x→→→'--== 所以 (0)=f '12七、（本题满分6分）已知函数()f x 在闭区间[],a b 上连续（0a >），且()0baf x dx =⎰，求证：存在(,)a b ξ∈，使得()()af x dx f ξξξ=⎰.证明：令1F()()xa x f t dt x=⎰，由于()f x 在[],a b 上连续，故F()x 在[],a b 上可导，且F()0,F()0a b ==，应用罗尔定理可知，存在(,)a b ξ∈，使得F ()0ξ'=，而 2()()F ()xa xf x f t dtx x-'=⎰，故()()()aaf t dt f x dx f ξξξξ==⎰⎰ .。

课程名称:高等数学(一、一）（期中考试）学 院: 专 业: 学号: 姓名:―――――――――――――装――――――――――――订――――――――――――线――――――――――――――一、填空题（每小题2分,共20分）1.数列 ,41,0,31,0,21,0,1,0的一般项=n x . 答：nn)1(1-+.2. 极限0sin 3lim tan 5x xx→= .答：35. 3. 极限=-→xx x 10)1(lim .答：1e. 4. 设函数1()cos f x x=，则[(1)]f '= . 答：0.5. 函数()ln ||f x x =的导数()f x '= .答:1x . 注：答为1||x 不给分 6. 已知x y sin =，则(20)y = . 答:sin x . 7. 已知21()1df x dx x =+, 则()f x = . 答: arctan x C +. 注：答为arctan x 扣1分8.当∞→n 时，如果nk1sin 与n1为等价无穷小，则k = . 答:2.9. 若函数31,1(), 1.x x f x a x -+<⎧=⎨≥⎩，在),(+∞-∞上连续，则a = .答:2-.10. 设函数)(x f 在闭区间[]b a ,上连续，在开区间()b a ,内可导，根据拉格朗日定理，则在开区间()b a ,内至少存在一点ξ，使得)(ξf '= .答:()()f b f a b a--.二、单项选择题（每小题3分,共18分）1. 若极限0lim =∞→n n x ，而数列}{n y 有界，则数列}{n n y x （ Ａ ）.(A) 收敛于0； (B) 收敛于1； (C) 发散； (D) 收敛性不能确定. 2. 0=x 是函数1()12xf x =-的（ C ）间断点. (A) 可去； (B) 跳跃； (C) 无穷； (D) 振荡. 3．设函数()(1)(2)(2011)f x x x x x =+++ ，则=')0(f （ C ）. (A) !n ； (B) 2010!； (C) 2011!； (D) 2012!. 4．若函数)(x f 、()g x 都可导，设[()]y f g x =，则d d yx=（ B ）. (A) {[()]}()f g x g x ''⋅； (B) [()]()f g x g x ''⋅； (C) [()]()f g x g x '⋅； (D) [()]f g x '.5．若函数)(x f 与)(x g 对于开区间),(b a 内的每一点都有)()(x g x f '='，则在开区间),(b a 内必有（ D ）(其中C 为任意常数).(A) )()(x g x f =； (B) C x g x f =+)()(； (C) 1)()(=+x g x f ； (D) C x g x f +=)()(. 6．下列函数中，在区间]1,1[-上满足罗尔定理条件的是（ A ）.课程名称:高等数学(一、一）（期中考试）学 院: 专 业: 学号: 姓名:―――――――――――――装――――――――――――订――――――――――――线――――――――――――――(A) 21x -； (B) xe ； (C) x ln ； (D)211x -.三、求下列极限（每小题6分,共24分）1. xx x 11lim-+→. 解：0011limlim(11)x x x xxx x →→+-=++ (2分) 011lim211x x →==++. (6分)2. 1lim 1xx x x →∞+⎛⎫ ⎪-⎝⎭解：211212lim lim 111x x x xx x x x x --→∞→∞⎡⎤+⎛⎫⎛⎫⎢⎥=+ ⎪ ⎪⎢⎥--⎝⎭⎝⎭⎣⎦(4分)2e = (6分)3. xxx ln cot ln lim 0+→ 解：原式=x x x xx x x x cos sin lim 1)sin 1(cot 1lim 020++→→-=-⋅ (3分)1cos 1lim sin lim 00-=⋅-=++→→xx x x x ．(6分)4. 222111lim 12n nn n n →∞⎛⎫+++⎪+++⎝⎭解：设22212111nn nnx n ++++++=，(1分)则，≤n xn y nnn ==+++1111222； (2分) ≥n xn z nnn n nn nn nn =+=+=++++++/1111112222，(3分) 因为1lim lim ==∞→∞→n n n n z y ，(4分)由夹逼定理112111lim 222=⎪⎪⎭⎫⎝⎛++++++∞→n n n n n . (6分)课程名称:高等数学(一、一）（期中考试）学 院: 专 业: 学号: 姓名:―――――――――――――装――――――――――――订――――――――――――线――――――――――――――四. 求导数或微分（每小题6分,共18分）1．已知)1sin(ln x y -=,求y d 解：cos(1)(1)sin(1)x dy dx x -=-- (4分)cot(1)x dx =--. (6分)２．求由参数方程2arctan ,ln(1)x t y t =⎧⎨=+⎩所确定的函数()y y x =的导数dydx .解：2[ln(1)][arctan ]dy t dx x '+='(2分) 2221/211t t t t==++ .(6分)3. 设函数)(x y y =由方程y x y e 1+=确定, 求)(x y y =在0x =处的切线方程. 解：当0, 1.x y ==(1分)方程yx y e 1+=两边对x 求导，有xy x x y y y d d e e d d +=，(3分) 得d e d 1eyy y x x =-(4分) 所以,x dy e dx==. (5分)因此,所求的切线方程为1y e x =+. (6分)五.（8分）已知函数2arcsin(),0,()2b,0ax x f x x x x >⎧=⎨++≤⎩在0x =点可导, 求常数ba 、的值.解：要使)(x f 在0x =处可导，必须)(x f 在0x =处连续，(1分)而0(0)lim arcsin()0x f ax ++→==；(0)f b =.(2分) 由(0)(0)f f +=，有0b =. (3分) 又 000()(0)arcsin()(0)lim lim lim 0x x x f x f a x a xf a x x x++++→→→-'====-，(4分) 200()(0)2(0)lim lim 20x x f x f x xf x x---→→-+'===-.(5分)由)(x f 在0x =处可导，有(0)(0)f f -+''=(6分), 得2a =.(7分) 故当0,2a b ==时，函数)(x f 在0x =处可导. (8分)六．证明题（12分）若函数)(x f 在闭区间[0,1]上连续，在开区间(0,1)内可导，且(0)0f =,(1)1f =.证明: (1) 存在(0,1)ξ∈，使得()1f ξξ=-;(2) 存在两个不同的点,(0,1)a b ∈,使得()()1f a f b ''=. 证明：(1) 令()()1g x f x x =+-, (1分) 则()g x 在[0,1]上连续, (2分)又(0)10g =-<，(1)10g =>(3分)，由零点定理知,存在(0,1)ξ∈,使得()()10g f ξξξ=+-=(5分), 即()1f ξξ=-.(6分)(2) 分别在[0,]ξ和[,1]ξ上应用拉格朗日中值定理 (7分),课程名称:高等数学(一、一）（期中考试）学 院: 专 业: 学号: 姓名:―――――――――――――装――――――――――――订――――――――――――线――――――――――――――存在(0,)a ξ∈,(,1)b ξ∈使得()(0)1()f f f a ξξξξ--'==, (9分)(1)()1(1)()111f f f b ξξξξξξ---'===---, (11分)因此()()1f a f b ''=. (12分)附加题（10分,不计入总成绩，只作为参考） 如果)(x f 和()g x 满足下列三个条件：（1）在闭区间[]b a ,上连续；（2）在开区间()b a ,内可导；（3）对任意(),x a b ∈，均有()0g x '≠．则存在一点(),a b ξ∈，使得()()()()()()f a f fg g b g ξξξξ'-='-．证明：令()[()()][()()]F x f a f x g x g b =--.(2分)因为()F x 在闭区间[]b a ,上连续，在开区间()b a ,内可导，且()()0F a F b ==,(3分)由罗尔定理, 存在一点(),a b ξ∈,使得()0F ξ'=. (5分)由于()[()()]()[()()]()F x f a f x g x g x g b f x '''=-⋅--⋅, (6分)所以()[()()]()[()()]()0F f a f g g g b f ξξξξξ'''=-⋅--⋅=,(8分)整理,得()()()()()()f a f fg g b g ξξξξ'-='-.(10分)大一上学期高数期末考试卷一、单项选择题 (本大题有4小题, 每小题4分, 共16分)1. )(0),sin (cos )(　处有则在设=+=x x x x x f .（A ）(0)2f '= （B ）(0)1f '=（C ）(0)0f '= （D ）()f x 不可导.2. ）时（　，则当，设133)(11)(3→-=+-=x x x x xx βα.（A ）()()x x αβ与是同阶无穷小，但不是等价无穷小； （B ）()()x x αβ与是等价无穷小；（C ）()x α是比()x β高阶的无穷小； （D ）()x β是比()x α高阶的无穷小.3. 若()()()02xF x t x f t dt=-⎰，其中()f x 在区间上(1,1)-二阶可导且'>()0f x ，则（ ）.（A ）函数()F x 必在0x =处取得极大值； （B ）函数()F x 必在0x =处取得极小值；（C ）函数()F x 在0x =处没有极值，但点(0,(0))F 为曲线()y F x =的拐点；（D ）函数()F x 在0x =处没有极值，点(0,(0))F 也不是曲线()y F x =的拐点。

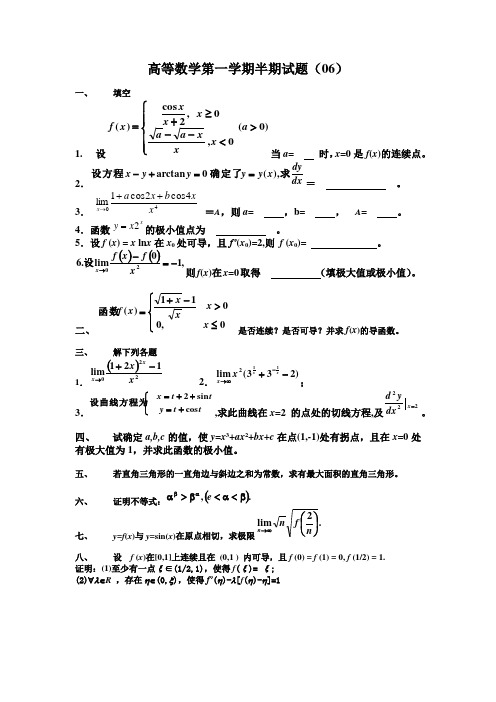
一、 填空1. 设当a= 时，x =0是f (x )的连续点。

2．＝ 。

3． ＝A ，则a= ，b = ， A = 。

4．函数的极小值点为 。

5．设f (x ) = x ln x 在x 0处可导，且f’(x 0)=2,则 f (x 0)= 。

则f (x )在x =0取得 （填极大值或极小值）。

二、是否连续？是否可导？并求f (x )的导函数。

三、 解下列各题1．2．；3．,求此曲线在x =2 的点处的切线方程,及。

四、 试确定a,b,c 的值，使y =x 3+ax 2+bx +c 在点(1,-1)处有拐点，且在x =0处有极大值为1，并求此函数的极小值。

五、 若直角三角形的一直角边与斜边之和为常数，求有最大面积的直角三角形。

六、 证明不等式：七、 y =f (x )与y =sin(x )在原点相切，求极限八、 设 f (x )在[0,1]上连续且在 (0,1 ) 内可导，且f (0) = f (1) = 0, f (1/2) = 1. 证明：(1)至少有一点ξ∈(1/2,1)，使得f (ξ)= ξ; (2)∀λ∈R ，存在η∈(0,ξ)，使得f’(η)-λ[f (η)-η]=1)0(0,0,2cos )(>⎪⎪⎩⎪⎪⎨⎧<--≥+=a x x x a a x x xx f dx dyx y y y y x 求确定了设方程),(0arctan ==+-404cos 2cos 1limx xb x a x ++→xx y 2=()(),10lim .620-=-→x f x f x 设⎪⎩⎪⎨⎧≤>-+=0,0011)(x x xx x f 函数()220121limx x xx -+→)233(lim 112-+-∞→xx x x ⎩⎨⎧+=++=tt y tt x cos sin 2设曲线方程为222=x dxy d ().,β<α<β>ααβe .2lim ⎪⎭⎫⎝⎛∞→n f n n一、 填空1. 设当a= 时，x =0是f (x )的连续点。

1 / 2大一上学期高数期中考试一、单项选择题 (本大题有4小题, 每小题4分, 共16分)1. )(0),sin (cos )(　处有则在设=+=x x x x x f .（A ）(0)2f '= （B ）(0)1f '=（C ）(0)0f '= （D ）()f x 不可导.2. ）时（　，则当，设133)(11)(3→-=+-=x x x x x x βα.（A ）()()x x αβ与是同阶无穷小，但不是等价无穷小； （B ）()()x x αβ与是等价无穷小；（C ）()x α是比()x β高阶的无穷小； （D ）()x β是比()x α高阶的无穷小.34二、填空题（本大题有4小题，每小题4分，共16分）5 =+→x x x sin 20)31(lim .6 ,)(cos 的一个原函数是已知x f x x =⋅⎰x x x x f d cos )(则7. lim (cos cos cos )→∞-+++=22221n n n n n n ππππ .8 设x e f x +='1)(， 则=)(x f三、解答题（本大题有5小题，每小题8分，共40分）9 设函数=()y y x 由方程sin()1x y e xy ++=确定，求'()y x 以及'(0)y .10.d )1(177x x x x ⎰+-求11 求 x xx x x c b a 10)3(lim ++→ )0,0,0(>>>c b a 12 x x x sin 1(sin lim -++∞→） 13 判别间断的类型，对可去间断点，将间断点去掉。

设 x e x f -+=1111)(四、 解答题（本大题7分）14将一个边长为a 的正方形铁皮，从每个角截去同样的小方块，然后把四边折起来，能做成一个无盖的方盒，为了使这个方盒的体积最大，问应截去多少。

五、解答题（本大题7分）15、已知)(x f 是周期为5的连续函数，它在0=x 的某个邻域内满足关系式)(8)sin 1(3)sin 1(x o x x f x f +=--+且)(x f 在1=x 处可导，求曲线)(x f y =在点))6(,6(f 处的切线方程。

高数A 期中测试题答案一、填空题（每小题4分，共20分） 1. 设γβα,,为给定的实数，则=++∞→γβαn n n)1(lim解： =++∞→γβαn n n)1(lim αβγβαααe nn nn n =++⋅⋅∞→)()1(lim 。

2．设)(x f y =是由方程1-=yxe y 所确实的隐函数，则==0|x dxdy解：两边同时对x 求导，有''y xe e y yy+=，得yyxe e y -=1'，又0=x 时，1-=y ，于是==0|x dxdy 110|1--===-e xe e y x y y 。

3．若,3)(',2)(==a f a f 则=--+→h h a f h a f h )()2(lim220 解： ha f h a f a f h a f h )]()([)]()2([lim 22220----+→h a f h a f h 2)()2(lim 2220-+=→h a f h a f h ---+→)()(lim 22036)(')(6|)]'([32====a f a f x f a x 。

4．设)()(x f xee f y =，其中f 可微，则=dy _______xde 。

解：因为dx e de x x=，有dx e de dxx x ==，于是])([)(x f x e e f d dy =)()()()(x f x x x f de e f e df e +=)()()(')()(x df e e f de e f e x f x x x x f += dx x f e e f de e f e x f x x x x f )(')()(')()(+=x x x f x x x x f de e x f e e f de e f e -+=)(')()(')()( x x x x x f de e x f e f e f e ])(')()('[)(-+=。

《高等数学》（上）期中考试题及评分标准1．（6分）已知11()()()212xF x f x =+-为偶函数，判断()f x 的奇偶性。

解：令11()212xx ϕ=+-，于是1121()212122xx xx ϕ--=+=+--11()()212x x ϕ=-+=-- （4分）()()()()()F x f x x f x x ϕϕ-=--=--()()f x f x =-- （5分） ()f x ∴为奇函数。

（6分） 2．求极限（每小题4分，共12分） （1）lim 1)x x x →+∞--解：原式=22(2321)lim1x x x x x x x →+∞++---++ （2分）=22lim 1211x x→+∞==++ （4分） （2）cot 0lim(sin cos )xx x x →+解：原式=12tan 0lim(12sin cos )xx x x →+ （1分）1sin cos 2sin cos tan 0lim(12sin cos )x xx x xx x x ⋅→+ （2分）=sin lim cos tan 0x x xx e ⋅→ （3分） =e （4分）（3）22ln(122)lim1x x x x x e →++-2220(24)ln(122)122lim 2x x x x x x x x xe→++++++ (1分） 、 =2220001ln(122)24lim [lim lim ]2122x x x x x x x e x x x-→→→++++++ （2分）=20122(lim 2)2x x xx →++ （3分）=1(22)22+= （4分）3．（8分）当x →+∞时，判断下列各式哪些是无穷小，并指出其中是否有等价无穷小（写出判断过程）。

（1）- （2）3221x x ++ （3）11sin sin x x x x-解:2lim lim sin 0x x →+∞→+∞-==+ （2分）32122lim lim 011x x x x →+∞→+∞+==++ （4分）1sin11sin lim(sin sin )lim lim 1011x x x x x x x x xx→+∞→+∞→+∞-=-=-= （6分）x ∴→+∞时，（1），（2）两式是无穷小，（3）不是无穷小。