2017秋六年级数学上册3.6等可能事件课件沪教版
- 格式:ppt
- 大小:873.00 KB
- 文档页数:19
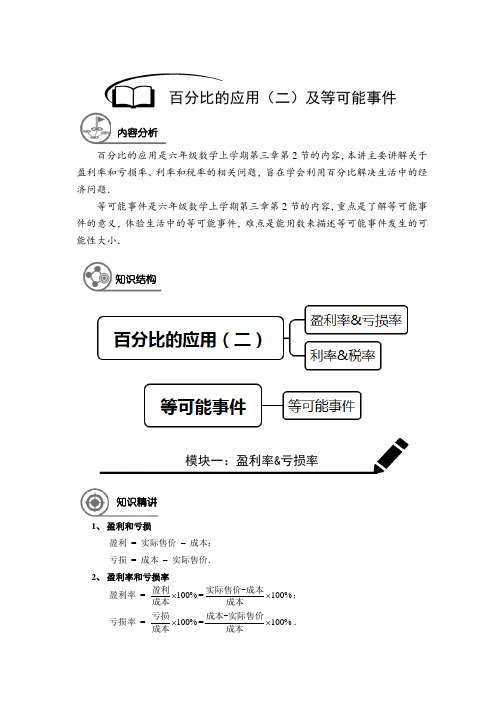
知识精讲百分比的应用是六年级数学上学期第三章第2节的内容,本讲主要讲解关于盈利率和亏损率、利率和税率的相关问题,旨在学会利用百分比解决生活中的经济问题.等可能事件是六年级数学上学期第三章第2节的内容,重点是了解等可能事件的意义,体验生活中的等可能事件,难点是能用数来描述等可能事件发生的可能性大小.1、 盈利和亏损盈利 = 实际售价 – 成本; 亏损 = 成本 – 实际售价.2、 盈利率和亏损率盈利率 = 100%⨯盈利成本=100%⨯实际售价-成本成本;亏损率 =100%⨯亏损成本=100%⨯成本-实际售价成本. 百分比的应用(二)及等可能事件内容分析知识结构模块一:盈利率&亏损率例题解析【例1】一耳机进价800元,现以1000元售出,盈利______元,盈利率为______%.【例2】某羽绒服品牌专卖店,冬天以每件800元购进一批羽绒服,春天来了,举行换季跳楼大甩卖活动,每件售价500元,则每件的亏损率为______%.【例3】某种商品进价100元,以盈利50%的定价出售,每件商品的售价为()A.125元B.50元C.105元D.150元【例4】一款书包的生产成本是40元,如果生产厂家赚15%的生产利润,销售商赚20%,问:(1)销售商购进这款书包需要多少钱?(2)顾客购买这款书包需要多少钱?【例5】春节期间一服装店同时以210元的价格出售两种羊毛衫,其中一件盈利40%,另一件亏损40%,问最终商家是盈利的还是亏损的?盈利或亏损的金额是多少?【例6】某商品按20%的利润定价,然后按八八折出售,共得利润84元,这种商品的成本是多少元?【例7】一种商品若以180元卖出就亏本10%,若要盈利15%,应标价多少元?【例8】一果品商店采购100个哈密瓜,成本为每只10元,商店将其中80个以单价30元卖出,余下的20个因损坏以单价5元卖出.问商店是盈利还是亏损了?盈利率或亏损率是多少?【例9】某商品如果成本降低10%,售价不变,那么利润率可增加12%,问原来的利润率是多少?【例10】一数码相机售价1500元,第一次打八折后仍盈利180元,如果在第一次打折的基础上再打折,问打几折以上才能保证不亏本?模块二:利率&税率知识精讲1、利率将钱存入银行,银行根据不同的存期制定了相应的利率,存款人取出存款时,银行在返还存款时还向存款人支付利息.向银行借款时(或称贷款),也需要向银行支付利息.存款额或借款额称为本金.利率又称利息率,表示一定时期内利息与本金的百分比,按年计算则称为年利率;按月计算则称为月利率;按日计算则称为日利率.2、税率税金= 应缴税额×税率.在特定的时期,国家规定,到银行存款时获取利息的同时,还需按一定的税率,向国家缴纳利息税.3、利息利息= 本金×利率×期数×(1-利息税率)本利和= 本金+利息例题解析【例11】一家饭店十月份的营业额约是30万元.如果按营业额的5%缴纳营业税,这家饭店十月份应缴纳营业税约多少万元?【例12】计税金额是400000元,应交税额是4200元,税率是______ %.【例13】若月利率为0.98%,则年利率为______%.【例14】小兰家买了一套普通住房,房子的总价为180万元,如果一次付清房款,就有九五折的优惠价.(1)打完折后,房子总价是多少?(2)买房还要缴纳实际房价的1.5%的契税,契税是多少钱?【例15】张先生把10000存入银行,存整存整取2年,年利率是3%,到期时张先生可取出多少元钱?(利息要按20%征利息税).【例16】徐明在银行存了8000元钱,定期一年,月利率为2%.到期时他应得利息多少元?如果按20%缴纳利息税,他应缴纳利息税多少元?他可以获得本金和税后利息一共多少元?【例17】某人将2000元存入银行,年利率为5%,一年到期后,取出全部存款及利息,再存一年,但利率又下降1.5个百分点,求第二次存款到期的利息与本利和.【例18】某银行存款有两种选择:一年期、二年期.一年期存款利率是1.98%,二年期存款利率是2.25%,如果有10000元存入银行两年后取出,怎样存获利较多?.【例19】小明家已经订购了一套商品房,到结算时还差10万元,他的父母准备向银行贷款或者向亲戚朋友借用.第一种办法:向银行贷款10万元,年利率为5.5%,贷款一年;第二种办法:向朋友借5万,两年后归还,年利率为3%;剩下的5万向亲戚借,不付利息,但在归还时小明的父母准备给亲戚买2000元的礼物作为酬谢金.为了节省开支,请通过计算说明,李平的父母应该采取哪种办法解决这笔资金?如下:其中“全月应纳税所得额”是指从工资、薪金收入中减去3500元的余额.(1)若某人一月份的收入为6000元,他应交税多少元?(2)若某人一月份扣除税后拿了6575元,他交了多少税?(3)若某人一月份纳税额为400元,他的收入是多少?\1、 事件学校组织六年级八个班进行“元旦联欢会”活动,每个班都准备了一个节目,活动的时候用抽签的方式确定各个班级的出场顺序.那么哪个年级可能第一个出场?此时,每个班级都有第一个出场的可能,但无法确定具体哪个班级第一个出场. 像上述的问题,我们把它称为事件.类似的事件有许多,如抛掷一枚硬币,落地后是正面朝上还是背面朝上?掷骰子停止后,哪一点朝上?等等. 2、 等可能事件上述事件具有共同的特点,就是事先知道出现的结果会有几种可能性,但是又无法确定到底会出现哪一种结果.我们将这类事件叫做等可能事件. 3、 等可能事件中发生某种结果可能性的大小用字母“P ”表示可能性的大小.P发生的结果数所有等可能的结果数. 可能性的大小一般用分数表示,也可以用百分数表示.【例20】 有一个正方体,6个面分别标有1~6这6个整数,投掷这个正方体一次,则出现向上一面的数字是偶数的可能性大小为( )A .13B .16C .12D .14【例21】 如图所示,小区公园里有一块圆形地面被黑白石子铺成了面积相等的八部分,阴影部分是黑色石子,小华随意向其内部抛一个小球,则小球落在黑色石子区域内的可能性大小是多少?模块三:等可能事件知识精讲例题解析【例22】假设你班有男生24名,女生26名,班主任要从班里任选一名红十字会的志愿者,则你被选中的可能性大小是______.【例23】现有分别标有1~10数字的相同大小的纸片10张,那么抽到标有素数的纸片的可能性的大小为()A.13B.310C.25D.15【例24】如图,一个圆形转盘被等分成五个扇形区域,上面分别标有数字1、2、3、4、5,转盘指针的位置固定,转到转盘后任其自由停止.转动转盘一次,当转盘停止转动时(若指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止),求:(1)指针指向标有数字“1”所在区域的可能性的大小P(1)(2)指针指向标有偶数所在区域的可能性的大小P(偶数);(3)指针指向标有奇数所在区域的可能性的大小P(奇数).【例25】甲、乙两人在石头、剪刀、布这个传统的游戏中,(1)若甲出剪子,能赢对方的可能性是多少?(2)两人出相同手势的可能性是多少?【例26】任取一个标有1~30数字的相同大小的乒乓球,标号既是2的倍数也是3的倍数的球的可能性的大小是______.【例27】把只有颜色不同的1个红球和2个白球装入一个不透明的口袋里搅匀,从中随机地一次摸出2个球,得1红球1白球的可能性大小是______.【例28】一只口袋中放着若干只红球和白球,这两种球除了颜色以外没有任何其他的区别,袋中的球已经搅匀,蒙上眼睛从口袋中取出一只球,取出红球的可能性的大小是14.(1)取出白球的可能性的大小是多少?(2)如果袋中的白球有18只,那么袋中的红球有多少只?【例29】如图所示是两个各自分割均匀的转盘,同时转动两个转盘,转盘停止时(若指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止),求两个指针所指区域的数字和为偶数的可能性是多少?【习题1】甲商店以400元每双的批发价购进一批运动鞋,售价每双500元;乙商店以500元每双的批发价购进一批皮鞋,售价每双650元.试问,卖运动鞋和卖皮鞋,甲、乙两家商店哪家的盈利率高?【习题2】计税金额是200000元,税率是15%,应交税额是______元.【习题3】盒子里有3支红色笔芯,2支黑色笔芯,每支笔芯除颜色外均相同,从中任意拿出一支笔芯,则拿出黑色笔芯的可能性的大小是______.【习题4】将圆盘分成7块,其中有三块红色区域,三块蓝色区域,一块白色区域,指针绕着中心旋转,以下判断正确的是()A.指针箭头停在红色区域的可能性大小是1 3B.指针箭头停在红色区域的可能性是停在白色区域可能性的3倍C.指针停在红色区域的可能性是停在蓝色区域的可能性大小一样D.以上说法都不对【习题5】上周五,李阿姨将自己买的甲乙两种股票同时抛出,各得1200元,在不计交易费用的前提下甲种股票赚了25%,乙种股票亏了25%,你能否帮李阿姨算算,到底是赚还是亏?随堂检测【习题6】某人今年存入银行10万元,定期二年,年利率3.6%.到期后需扣除利息税20%,此时他得到的利息能买一台5000元的笔记本电脑吗?【习题7】从一副52张扑克牌中(没有大小王)随意抽出一张,(1)抽到2的可能性大小是多少?(2)抽到黑桃的可能性大小是多少?(3)抽到黑桃2的可能性大小是多少?【习题8】《中华人民共和国个人所得税法》中的个人所得税税率表(工资、薪金所其中“全月应纳税所得额”是指从工资、薪金收入中减去3500元的余额.(1)若张先生九月份的收入为5500元,他应交税多少元?(2)若张先生十月份交纳此项税350元,他这个月的收入是多少元?【习题9】元旦将至,某商场搞促销活动,已知一种服装每套标价600元,第一次打8折出售,每套能盈利25%,店家售出这样的服装100套后,对剩下的8套服装再打8.5折出售,当服装全部售完后,商店共可盈利多少元?【习题10】 如图所示,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A 、B ,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则如下:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为偶数时,甲获胜;数字之和为奇数时,乙获胜.(若指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止) (1)求乙获胜的可能性的大小;(2)这个游戏规则对甲乙双方公平吗?请判断并说明理由.【作业1】一台汽车模型的成本价为120元,若商家准备盈利15%,则售价应定为______元.【作业2】下列说法中,正确的是( )A .“明天降雨的可能性是80%”表示明天有80%的时间降雨B .“抛一枚硬币正面朝上的可能性是0.5”表示每抛硬币2次就有一次出现正面朝上C .“彩票中奖的可能性是1%”表示买100张彩票一定有1张会中奖D .同一年出生的367名学生中,至少有两人的生日是同一天【作业3】某人将2000元存入银行,年利率是2.25%,存满三年到期后需支付20%的利息税,问到期后他可以拿回多少元?课后作业A B【作业4】 一个新玩具的成本价是50元,零售商从生产厂家用出厂价买入,然后卖出.如果生产厂家的利润率为40%,零售商的利润率为50%,则这个新玩具的售价为多少?【作业5】一宗出口商品共50件,每件价值24万元,按规定要征税8%,为了鼓励出口,实际按应征税额的九折征税,这宗商品共应交税多少元?【作业6】一种三年期的国债年利率是3.73%,王阿姨买了这种国债4万元,到期可得本息和______.(免交利息税)【作业7】如图所示,转盘指针的位置固定,转动转盘一次任其自由停止.记指针指向标有偶数所在区域的可能性大小为P (偶数),指针指向标有奇数所在区域的可能性大小为P (奇数),则P (偶数)______ P (奇数).(填“>”“<”或“=”)【作业8】某厂为职工投保“团体人身保险”,保险金额共计600万元.按保险费率0.6%计算,该厂每年为每个职工交纳保险费72元.这个厂共有职工多少人?【作业9】盒子内有黑、白、红三种球共100个.如果黑球个数 : 白球个数 = 1 : 3,白球个数 : 红球个数 = 1 : 2,那么从盒子中,任意拿一个球: (1)求拿到红球的可能性的大小;(2)求拿到一个黑球或一个白球的可能性的大小.【作业10】 一个不透明的口袋中装有红球6个,黄球9个,绿球3个,这些球除颜色外没有区别.从中任意摸出一个球.(1)计算摸到的是绿球的可能性的大小;(2)如果要使摸到绿球的可能性为14,需要在这个口袋中再放入多少个绿球?。

的可能性为。
7、圆的周长是28.26米,它的直径是()厘米,半径是()厘米。
8、一圆的周长是12.56厘米,如果用圆规画这个圆,圆规两脚的距离是()厘米。
9、一条弧所对的圆心角为120°,半径为3,那么这条弧长为。
(结果用π表示)10、已知弧长的长为20πcm,弧所对的圆心角为150°,那么弧所在圆的半径是.11、一本40页的书,随手翻开一页。
求:(1)页数码是偶数的可能性大小。
(2)页码数的末位是5的可能性大小。
(3)页码数能被5整除的可能性大小。
12、一只挂钟的分针长20厘米,经过30分钟后,分针的尖端所走的路程是多少厘米?经过45分钟呢?13、一圆弧的圆心角为300°,它所对的弧长等于半径为6cm的圆的周长,求该圆弧所在圆的半径.精解名题例1、掷两枚骰子,点数之和为10的可能性大小。
例2、(1)轧路机前轮直径 1.2米,每分钟滚动6周。
1小时能前进多少米?(2)自行车轮胎外直径 71厘米,每分钟滚动100圈。
通过一座 1000米的大桥约需几分钟?例3、求下图中阴影部分的周长。
例4、一个人要从A地到B地,有两条路可走,是按哪一号箭头所走的路线近一些?为什么?例5、将一细铅丝圆圈剪成A、B、C三段弧,A弧长是B弧长的31,B弧长是C弧长的21,则最长的弧A B1222多少分钟?(得数保留整数)15、一只挂钟分针的针尖在41小时内,正好走了25.12厘米。
它的分针长多少?16、抛出两枚相同的硬币。
(1)两枚同时朝上的可能性的大小。
(2)一枚朝上,一枚朝下的可能性大小。
17、求下列阴影图形的周长。
4自我测试1、有30张卡片,上面的编号为1到30,丛中任取1张,则抽到卡号为质数的可能性为( ) A 、301 B 、3011 C 、103 D 、3114、有一个圈环,外周长是π40厘米,内周长是π10厘米,求这个圆环的宽?15、如图,扇形纸扇完全打开后,外侧两竹条AB ,AC 夹角为120°,AB 的长为30cm ,贴纸部分BD 的长为20cm ,则贴纸部分的周长为 ?。


等可能事件【教学目标】1.了解等可能事件和简单的等可能事件概率的计算方法。
2.通过动手试验,用试验的方法来证明数学问题;通过情景、活动,感受数学与现实生活的密切联系。
3.通过交流合作,体验在解决问题的过程中与他人合作的重要性。
【教学重难点】1.重点:等可能事件的意义。
2.难点:等可能事件的计算。
【教学过程】一、问题呈现,情景导入情景一:某商场开展抽奖活动,满88元就可以参加抽奖一次(若压线则可以重新转一次),转盘如图所示。
提问:请同学观察,抽到冰箱和抽到雪碧的可能性一样吗?为什么呢?学生可以直观的发现,通过面积不同得到:抽到冰箱和雪碧的可能性不同这样一个结论。
情景二:如果做了如上的改动,那么,抽到冰箱和抽到雪碧的可能性一样吗?学生会发现,转盘被分割为5个形状大小完全相同的区域,那么指针落在的区域可以是5个中任意的一个,并且这个可能性是相同。
引入课题——等可能事件。
提问:如转盘所示,你能说说抽到冰箱的可能性是多少吗?有些同学可以直接得到答案,有些同学还有些困难,那么多给他们一些时间思考,然后请一位同学说说他的想法。
二、探索发现实验1:大家来做个讨论:谁去听演唱会?某组合要到上海来开演唱会,但是,我们只有一张票,而同学们都想去,那你有什么公平的方式来决定谁去听这个演唱会吗?方案一:我们抓阄的方法,准备51张白纸,其中50张写“不去”,1张写“去”;方案二:还是抓阄的方法,也准备51张白纸,但其中50张写“去”,一张写“不去”,然后选出“不去”的那个学生,然后再准备50张白纸,其中49张写“去”,1张写“不去”,依此类推,就可以选出最后一个要去的学生了。
请你说说哪种方案好,如果认为都不好,那么你有什么好的方案?讨论后,请小组发表各自的意见。
每种方案的分析:方案一:不公平,万一第一个学生就抓到“去”的这张纸片,那么对于后面的34个学生来说,就不要抓了,所以对于后抓的学生来说不公平。
大家否定了这个方案。
方案二:既不公平,也很麻烦,要抓很多次……教师:这些方法都不公平,那么你们有什么好的方法吗?学生:还是抓阄,准备51张白纸,每张白纸上,写上学生的学号,然后放在一个箱子里,由老师来抓,并且抓之前要摇一下,然后抓出其中一张,是几号就是他(她)去。


沪教版六年级下册数学3.6等可能事件(教案)一. 教材分析《沪教版六年级下册数学3.6等可能事件》这一节主要让学生理解等可能事件的定义,并能够运用等可能事件的概念解决实际问题。
教材通过生动的例题和丰富的练习,让学生在实际操作中感受和理解等可能事件的本质特征。
二. 学情分析六年级的学生已经具备了一定的逻辑思维能力和数学基础,但是对于等可能事件这一概念可能还比较陌生。
因此,在教学过程中,教师需要从学生的实际出发,通过具体的例子和实际操作,让学生理解和掌握等可能事件的概念。
三. 教学目标1.让学生理解等可能事件的定义,能够识别和判断等可能事件。
2.培养学生运用等可能事件的概念解决实际问题的能力。
3.提高学生的数学思维能力和逻辑推理能力。
四. 教学重难点1.等可能事件的定义和判断。
2.运用等可能事件的概念解决实际问题。
五. 教学方法1.实例教学:通过具体的例子,让学生理解和掌握等可能事件的概念。
2.问题解决法:引导学生运用等可能事件的概念解决实际问题,提高学生的应用能力。
3.分组讨论法:让学生分组讨论,培养学生的合作能力和沟通能力。
六. 教学准备1.准备相关的例子和练习题,用于引导学生理解和运用等可能事件的概念。
2.准备一些实际问题,让学生解决,培养学生的应用能力。
七. 教学过程1.导入(5分钟)通过一个简单的游戏,让学生初步感受等可能事件的性质。
例如,抛硬币游戏,让学生观察和思考硬币正反面出现的概率是否相等。
2.呈现(10分钟)呈现教材中的例子,引导学生理解和掌握等可能事件的概念。
通过具体的例子,让学生判断哪些是等可能事件,哪些不是。
3.操练(10分钟)让学生分组讨论,每组选择一个实际问题,运用等可能事件的概念进行解决。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)让学生进行一些相关的练习题,巩固对等可能事件的理解和掌握。
教师及时批改和反馈,帮助学生纠正错误。
5.拓展(10分钟)引导学生思考和讨论等可能事件在实际生活中的应用,让学生体会数学的实用价值。
六、挑战成功(1)1;(2)2;(3)4,5;(4)7,8或92:圆盘等分为7块,其中有三块红色区域,三块蓝色区域,一块白色区域,指针绕着中心旋转,求指针落在红色区域内的可能性的大小。
练习1:(1)投一枚骰子,求点数1朝上的可能性的大小。
(2)投一枚骰子,求点数是偶数朝上的可能性的大小。
(3)投一枚骰子,求点数素数朝上的可能性的大小。
练习2:两个圆盘一个6等份,一个4等分,用字母和数字分别表示区域(1)以数字分别表示两个指针停的所在区域,写出所有可能的结果,用1-1、 2-3 等表示(2)求以下每小题可能性的大小①两数相同②两数相加等于5③两数相乘等于6练习3:小明家里只有一台电视机,星期天爸爸、妈妈和小明都想看自己喜爱的节目,怎么办呢?爸爸出了一个主意,抛出两个硬币,都是正面的给妈妈看,都是反面的给小明看,一正一反的爸爸看,你说爸爸的主意好会把各种情况表示出来进行分析。
七、思考八、小结不好?为什么?商场搞促销抽奖活动,广告宣传说中奖率为1/10,某位消费者已经抽了9次,都没有中奖,他想再抽一次就肯定中奖了。
他的想法正确吗?商场搞促销抽奖活动,广告宣传说中奖率为1/10,某位消费者已经抽了9次,都没有中奖,他想再抽一次就肯定中奖了。
他的想法正确吗?☐这一节课,你学会了什么?☐如何求等可能事件可能性的大小?分哪几个步骤?☐你还有什么样的求可能性大小的问题?正大中学沈水荣作业布置练习册3.6作业反馈本节课通过实验,学生对等可能理解比较深入,作业反馈良好。
教学反思学生学习的主动性,关键是老师在课堂设计时,要为学生创设情景,创设机会,并关注学生的兴趣爱好等方面,这样才能使学生积极主动地参与到课堂学习中,才能产生良好的学习效果。
-------------等可能事件(★★)1.了解等可能事件的意义.2.掌握简单等可能事件概率的计算方法.【课堂引入】 【情景一】某商场开展抽奖活动,满88元就可以参加抽奖一次(若压线则可以重新转一次),转盘如图所示.提问:请同学观察,抽到冰箱和抽到雪碧的可能性一样吗?为什么呢?学生可以直观的发现,通过面积不同得到:抽到冰箱和雪碧的可能性不同这样一个结论.【情景二】如果做了如上的改动,那么,抽到冰箱和抽到雪碧的可能性一样吗?学生会发现,转盘被分割为5个形状大小完全相同的区域,那么指针落在的区域可以是5个中任意的一个,并且这个可能性是相同.引入课题——等可能事件。
提问:如转盘2所示,你能说说抽到冰箱的可能性是多少吗?【答案:51】【知识结构】【典型例题】【例1】如图,圆盘平均分成7块,其中有三块红色的区域,三块蓝色的区域,一块白色的区域,指针绕着中心旋转,求:(1)指针落在红色区域的可能性的大小. (2)求指针落在非红色区域的可能性的大小. 解:【巩固】(1)从1、2、3、5这四个数中任取一个,这个数是奇数的可能性是( ) (2)将圆盘8等分,指针绕中心旋转,指针落在区域2的可能性大小是( ) (3)投掷一枚骰子,点数3朝上的可能性大小是( ) 【答案】(1)43(2)81(3)61 【例2】一副52张的扑克牌(无大王、小王),从中任意取出一张,共有52种等可能的结果。
(1)列出抽到K 的所有可能的情况; (2)求抽出红桃K 的可能性的大小; (3)求抽到K 的可能性的大小. 解:(1)红桃K 、黑桃K 、梅花K 和方块K 共4种. (2)521 (3)131524= 【小结】所有等可能的结果数事件发生的结果数=P【巩固】(4)在红桃这个花色中,抽到5的倍数的牌的可能性大小是多少?3P 7P =(1)4(2)=7(5)在红桃这个花色中,抽到偶数的牌的可能性大小为多少? (6)在四个花色中,抽到5的倍数的牌的可能性大小是多少?【答案】(4)132;(5)Q 看作12的话,概率为136;(6)132【例3】把100张已编号的卡片(从1号到100号),从中任取1张,计算:(1)卡片号是偶数的概率; (2)卡片号是5的倍数的概率; (3)卡片号是素数的概率; (4)卡片号是合数的概率; (5)卡片号是3的倍数的概率;(6)卡片号是从1号到100号中任意一号的数的概率; (7)卡片号是3和5的倍数的概率。