北师大版七年级下册第三章三角形讲义
- 格式:docx
- 大小:323.76 KB
- 文档页数:13
D C B A
C
常见辅助线的作法有以下几种:
1) 遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角
形。
2) 遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,构造全等三
角形。
3) 截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,
或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.
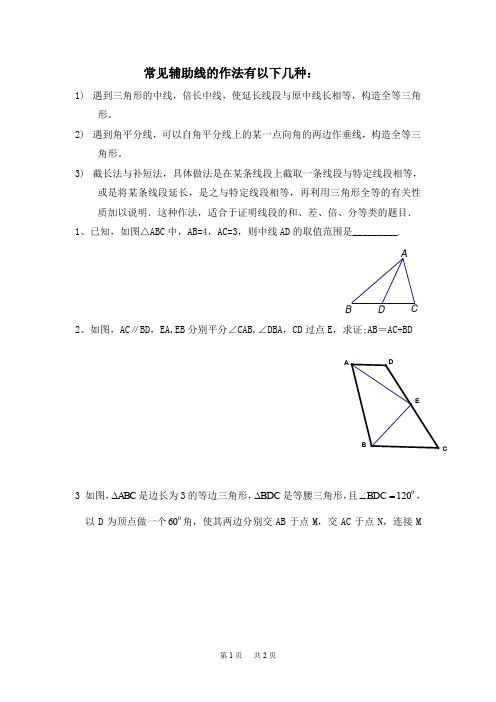
1、已知,如图△ABC 中,AB=4,AC=3,则中线AD 的取值范围是_________.
2、如图,AC ∥BD ,EA,EB 分别平分∠CAB,∠DBA ,CD 过点E ,求证;AB =AC+BD
3 如图,ABC ∆是边长为3的等边三角形,BDC ∆是等腰三角形,
且0120BDC ∠=,以D 为顶点做一个060角,使其两边分别交AB 于点M ,交AC 于点N ,连接M
B C
则AMN
的周长为。


第三章三角形3.1 认识三角形第一课时三角形的概念与内角和【学习目标】1.能说出三角形的概念,能正确表示三角形的三顶点、三边、三角.2.能说明三角形的内角和为什么是︒180,并能应用这个规律解决问题.3.会对三角形按角进行分类.4.能正确表示直角三角形,能解释直角三角形为什么两锐角互余,并能应用这个规律解决问题.【课前导学温故与预习】课前热身1.在小学我们学习了三角形的哪些知识?答案不惟一,例如三角形有三条边、三个角,面积等于底乘高的一半,内角和等于180度等.2.请举出两个生活中的三角形的例子.例如自行车的三角杠、路边的警示标志等.自主学习自学教材62页—64页,初步感知后回答下面的问题:1.图1中的三角形记作ABC∆,三个角是CBA∠∠、、,三条边是CABCAB、、.AC B AC B图1 图22.一个三角形有两个角分别是︒40和︒70,那么第三个角的度数是︒70.3.三角形按角分类,可分为钝角三角形、直角三角形、锐角三角形.4.如图2,直角三角形ABC中,︒=∠90C,则=∠+∠BA︒90.【互动课堂探究与合作】探究点一:三角形的概念1.观察下面生活中的三角形。
我们发现它们都是由不在同一条直线上的三条线段首尾顺次相接所组成的图形,我们将这样的图形叫做三角形.2.三角形的表示:B如图,组成三角形的三条线段AB、BC、CA叫做三角形的边,相邻两边组在的角叫做三角形的内角,简称三角形的角;相邻两边的公共端点是三角形的顶点,三角形通常用表示顶点的三个大写字母来表示,如上面的三角形就表示为△ABC ;某个角的对边通常也可以用这个角的顶点对应的小写字母来表示,如:AB也可以表示为c.3.与同桌一起找一找,填一填。
ABCD(1)图中有三个三角形,分别是ABD∆、ADC∆、ABC∆;.(2)ABD∆的三边为:AB、BD、DA;(3)ADC∆的三角为:ADC∠、ACD∠、DAC∠;(4)在ABD∆中,ABD∠的对边是AD、BD的对角是BAD∠.探究点二:三角形的内角和1.做一做(1)如图1,做一个三角形纸片,它的三个内角分别为1∠,2∠和3∠图1 图2(2)如图2,将1∠撕下摆放,1∠的顶点与2∠的顶点重合.(3)请观察图2,撕下前的1∠与撕下后摆放的1∠恰好构成一组相等的内错角,由此可以推断直线a 与直线b 的位置关系是 平行 ,这说明1∠,2∠和3∠的和是 180°.归纳:三角形内角和 等于180° . 2.想一想:在撕纸的过程中,我们发现了三角形内角和是︒180,受撕纸的启发,我们用下面这种推理的方法来证明三角形内角和是︒180: 已知:ABC ∆ 求证:︒=∠+∠+∠180ACB B A 证明:过点C 作AB 的平行线CE∵AB ∥CE (辅助线的作法)∴ A ∠ =ACE ∠(两直线平行,内错角相等)又∵ AB ∥CE∴ B ∠+BCE ∠=180°(两直线平行,同旁内角互补) ∴︒=∠+∠+∠180ACB B A .3.议一议,与同伴一起完成下面的推理过程。

第三章三角形第一节认识三角形知识点一、三角形相关概念1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
表示为“ ABC”2.边:组成三角形的线段叫做三角形的边;表示:AB,AC,BC 或a, b, c3.顶点:相邻两边的公共端点叫做三角形的顶点;4.角:相邻两边所组成的角叫做三角形的内角,简称三角形的角。
5.三角形有三条边、三个内角、三个顶点例:如图,共有三角形的个数是()A.3 B.4 C.5 D.6练习1.如做下图所示,图中的三角形有()A.6个B.8个C.10个D.12个2. 如右上图所示,图中三角形的个数为().A.3个B.4个C.5个D.6个知识点二、三角形的三边关系1.三角形的两边之和大于第三边。
2.三角形的两边之差小于第三边。
3.作用:①判断三条已知线段能否组成三角形②当已知两边时,可确定第三边的范围。
③证明线段不等关系。
例1.七(1)班某同学想利用下列长度的木棒制成一个三角形工具,下列各组你认为可行的是()A.5,2,2 B.2,3,6 C.5,3,4 D.7,13,6例2.一个三角形两边长为5和7,且有两边长相等,这个三角形的周长是()A.17B.19C.17或19D.无法确定练习1.有下列长度(cm)的三条小木棒,如果首尾顺次连结,能钉成三角形的是()A.10、14、24 B.12、16、32 C.16、6、4 D.8、10、122.有5根小木棒,长度分别为2cm、3cm、4cm、5cm、6cm,任意取其中的3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为()A.5个 B.6个 C.7个 D.8个3.已知等腰三角形的周长为16,且一边长为3,则腰长为()A.3 B.10 C.6.5 D.3或6.54.甲地离学校4km,乙地离学校1km,记甲乙两地之间的距离为d km,则d的取值范围为____________5.如果三角形的两边长分别是2和4,且第三边是奇数,那么第三边长为,如果第三边长为偶数,则此三角形的周长为 .知识点三、三角形的内角的关系1.三角形三个内角和等于180°。


【关键字】数学三角形几何A级概念:(要求深刻理解、熟练运用、主要用于几何证明)几何B级概念:(要求理解、会讲、会用,主要用于填空和选择题)一基本概念:三角形、不等边三角形、锐角三角形、钝角三角形、三角形的外角、全等三角形、角平分线的集合定义、尺规作图、辅助线、线段笔直平分线的集合定义、轴对称的定义、轴对称图形的定义。
二常识:1.三角形中,第三边长的判断:另两边之差<第三边<另两边之和.2.三角形中,有三条角平分线、三条中线、三条高线,它们都分别交于一点,其中前两个交点都在三角形内,而第三个交点可在三角形内,三角形上,三角形外.注意:三角形的角平分线、中线、高线都是线段.3.如图,三角形中,有一个重要的面积等式,即:若CD⊥AB,BE⊥CA,则CD·AB=BE·CA. 4.三角形能否成立的条件是:最长边<另两边之和.5.直角三角形能否成立的条件是:最长边的平方等于另两边的平方和.6.分别含30°、45°、60°的直角三角形是特殊的直角三角形.7.如图,双垂图形中,有两个重要的性质,即:(1)AC·CB=CD·AB ;(2)∠1=∠B ,∠2=∠A .8.三角形中,最多有一个内角是钝角,但最少有两个外角是钝角.9.全等三角形中,重合的点是对应顶点,对应顶点所对的角是对应角,对应角所对的边是对应边.10.等边三角形是特殊的等腰三角形.11.几何习题中,“文字叙述题”需要自己画图,写已知、求证、证明.12.符合“AAA”“SSA”条件的三角形不能判定全等.13.几何习题经常用四种方法进行分析:(1)分析综合法;(2)方程分析法;(3)代入分析法;(4)图形观察法.14.几何基本作图分为:(1)作线段等于已知线段;(2)作角等于已知角;(3)作已知角的平分线;(4)过已知点作已知直线的垂线;(5)作线段的中垂线;(6)过已知点作已知直线的平行线.15.会用尺规完成“SAS”、“ASA”、“AAS”、“SSS”、“HL”、“等腰三角形”、“等边三角形”、“等腰直角三角形”的作图.16.作图题在分析过程中,首先要画出草图并标出字母,然后确定先画什么,后画什么;注意:每步作图都应该是几何基本作图.17.几何画图的类型:(1)估画图;(2)工具画图;(3)尺规画图.※18.几何重要图形和辅助线:(1)选取和作辅助线的原则:①构造特殊图形,使可用的定理增加;②一举多得;③聚合题目中的分散条件,转移线段,转移角;④作辅助线必须符合几何基本作图.(2)已知角平分线.(若BD是角平分线)。
三角形 1.认识三角形1、它的三个顶点分别是 ,三条边分别 是 ,三个内角分别是 。
2、分别量出这三角形三边的长度,并计算任意两边之和以及任意两边之差。
你发现了什么?结论:三角形任意两边之和大于第三边三角形任意两边之差小于第三边C b A c a B例:有两根长度分别为 5cm 和 8cm 的木棒, 用长度为 2cm 的木棒与它们能摆成三角形吗?为什么?长度为 13cm 的木棒呢?长度为 7cm 的木棒呢? 二、巩固练习:1、下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?为什么?(单位: cm )(1) 1 , 3 , 3 (2) 3 , 4 , 7 (3) 5 , 9 , 13(4) 11 , 12 , 22 (5) 14 , 15 , 302、已知一个三角形的两边长分别是 3cm 和 4cm ,则第三边长 X 的取值范围 是 。
若 X 是奇数, 则 X 的值是 。
这样的三角形有 个;若 X 是偶数,则 X 的值是 , 这样的三角形又有 个3、一个等腰三角形的一边是 2cm ,另一边是 9cm , 则这个三角形的周长是 cm 夯实基础1、填空:(1)当 0°< <90°时, 是 角;(2)当 = °时, 是直角;(3)当 90°< < 180°时, 是 角;(4)当 = °时, 是平角。
A2、如右图,E2 ∵AB ∥CE , 13 B(已知)C D∴∠A = ,( )∴∠ B=,()(第 2 题)二、探索练习:根据知道三角形的三个内角和等于 180°,那么是否对其他的三角形也有这样的一个结论呢?(提出问题,激发学生的兴趣)结论:三角形三个内角和等于180°(几何表示)练习 1:1、判断:(1)一个三角形的三个内角可以都小于60°;()(2)一个三角形最多只能有一个内角是钝角或直角;()2、在△ ABC中,( 1)∠ C=70°,∠ A=50°,则∠ B= ( 2)∠ B=100°,∠ A=∠C ,则∠ C=( 3) 2∠ A=∠ B+∠ C ,则∠A=度。
度; 度; 3、如右图,在△ ABC 中,∠ A = 3x °∠= 2 x °∠= x °求三个内角的度数。
解:∵∠ A+∠ B+∠ C=180°,( )∴ 3x 2x xA ∴ 6x =3x∴ x =B 2xx C 从而,∠ A= ,∠ B= ,∠ C=三、 探究交流(第 3 题) 练习 1:一个三角形中三个内角可以是什么角? (提醒:一个三角形中能否有两个直角? 钝角呢?)★ 按三角形内角的大小把三角形分为三类锐角三角形 直角三角形 钝角三角形 ( acute trangle )( right triangle ) ( obtuse triangle )三个内角都是锐角有一个内角是直角有一个内角是钝角练习 2:1、观察三角形,并把它们的标号填入相应的括号内:锐角三角形( ) 直角三角形( ) 钝角三角形( )2、一个三角形两个内角的度数分别如下,这个三角形是什么三角形?(1) 30°和60°()(2) 40°和70°()(3) 50°和30°()(4) 45°和45°()四、猜想结论:简单介绍直角三角形,和表示方法,Rt △思考:直角三角形中的两个锐角有什么关系?结论:直角三角形的两个锐角互余练习 3:1、观察下列的直角三角形,分别写出它们符号表示、直角边和斜边。
B DCEG F(图 1)(图 2)(1)图 1 中的直角三角形用符号写成,直角边是和,斜边是;(2)图 2 中的直角三角形用符号写成,直角边是和,斜边是;2、如下图,在Rt △CDE,∠ C 和∠ E 的关系是,其中∠C=55°,则∠E=度CE AD B C3、如上图,在 Rt△ ABC中,∠ A=2∠ B,则∠ A= 度,∠ B= 度;2.认识三角形的中线和高1、任意画一个三角形,设法画出它的一个内角的平分线。
1、你能通过折纸的方法得到它吗?(可以用量角器来量出这个角的大小的方法画出这个角的平分线。
也可以用折纸的方法得到角平分线)。
结论:三角形一个角的角平分线和这个角的对边相交,这个角的顶点和对边交点之间的线段叫做三角形中这个角的角平分线。
简称三角形的角平分线。
A如图:∵ AD是三角形ABC的角平分线。
1 2∴∠ 1=∠2=∠ BAC或:∠ BAC= 2 ∠ 1= 2 ∠ 2请画出△ ABC(锐角三角形)的所有角平分线,并且观察这些角平分线有什么规律?对于钝角三角形呢 ?直角三角形呢 ?它们的角平分线也有这样的规律吗?一个三角形共有三条角平分线,它们都在三角形内部,而且相交于一点。
连结三角形一个顶点和它对边中点的线段,叫做三角形这个边上的中线。
简称三角形的中线。
注:规范书面表达,按下面的示范书写:如图:∵ AD是三角形ABC的中线。
A∴BD= DC=1 BC2或: BC= 2BD= 2DCB D C结论:一个三角形共有三条中线,它们都在三角形内部,而且相交于一点。
如图 , 已知 ,AD 是 BC边上的中线 ,AB=5cm,AD=4cm, ▲ ABD的周长是12cm,求 BD的长 .1、★三角形的高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高。
2.如图,线段 AM是 BC边上的高。
∵ AM 是 BC边上的高∴AM⊥ BC3、议一议:画出一个直角三角形和一个钝角三角形(1)画出直角三角形的三条高,并观察它们有怎样的位置关系?(2)能折出钝角三角形的三条高吗?能画出它们吗?( 3)钝角三角形的三条高交于一点吗?它们所在的直线交于一点吗?结论: 1、直角三角形的三条高交于直角顶点处。
2、钝角三角形的三条高所在直线交于一点,此点在三角形的外部。
3.图形的全等一、看一看1.多举一些比较熟悉的能全等或不全等图形的实例,进行想象全等力形与不全等图形的区别。
例如:(1)同一张底片冲印出两张相同尺寸的相片与两张不同尺寸的相片。
(2)同一人的两只手掌与一大人左手掌和一小孩的左手掌。
(3)一个三角形和一个四边形2.把下列两组图形(1)3.能够重合的两个图形称为全等图形。
全等图形的形状和大小都相同小结:本节课学习了能够重合的图形称为全等图形,全等图形的形状和大小都相同。
全等三角形(1) 课前复习三角形的有关知识:一个三角形共有______个顶点 ,_________ 个角 ,_______ 条边.(2)已知△ ABC,它的顶点是 _________, 它的角是 ______________, 它的边是 ____________(3) 两个图形完全重合指的是它们的形状 ___________, 大小 ___________.(4)完全重合的两条线段 _________( 填“相等”或“不相等” )(5)完全重合的两个角 _________( 填“相等”或“不相等” )1.全等三角形的定义及有关概念和性质.(1) 定义:全等三角形是能够完全重合的两个三角形或形状相同、大小相等的两个三角形.( 2)三角形中对应元素的关系,发现对应边相等,对应角相等.2.学习全等三角形的符号表示及读法和写法:解释“≌”的含义和读法,并强调对应顶点写在对应位置上.举例说明:如图,∵△ ABC≌ DFE, ( 已知 )∴AB=DF, AC=DE, BC=FE, ( 全等三角形的对应边相等 ) ∠ A=∠ D,∠ B=∠ F,∠ C=∠ E.( 全等三角形的对应角相等 ).二、总结寻找全等三角形对应元素的方法,渗透全等变换的思想(1)全等用符号 _________ 表示 . 读作 __________.(2)三角形 ABC全等于三角形 DEF,用式子表示为 ______________(3)已知△ ABC和△ A′ B′ C′中 , ∠ A=∠A′ , ∠ B=∠B′∠ C=∠ C′ ; AB=A′B′ ,BC=B′ C′ ,AC=A′ C′.则△ ABC_______△A′ B′ C′.(4)如右图△ ABC≌△ BCD,∠A 的对应角是∠ D, ∠B 的对应角∠ E, 则∠ C 与____是对应角 ;AB 与 _____是对应边 , BC 与 _____是对应边 ,AC与 ____是对应边 .(5)判断题 :①全等三角形的对应边相等, 对应角相等 .( )②全等三角形的周长相等.( )③面积相等的三角形是全等三角形.( )④全等三角形的面积相等.( )三、性质应用举例1.性质的基本应用.例1 已知:△ ABC≌△ DFE,∠ A=96°,∠ B=25°, DF=10cm.求∠ E的度数及 AB的长。
例 2 如图,已知 CD ⊥ AB 于 D ,BE ⊥ AC 于E ,△ ABE ≌△ ACD ,∠ C= 20 °, AB=10, AD= 4,G 为 AB 延长线上一点.求∠ EBG 的度数和 CE 的长.探索三角形全等的条件 探索、归纳总结。
1、全等三角形的 2、如图 1,已知△ =OB , =OD 相等, AOC ≌△ BOD ,则∠ A=∠ B ,∠ C= 。
相等。
, = ∠2,对应边有AC= , 3、如图 OC= 4、如图 2,已知△ AOC ≌△ DOB ,则∠ A=∠ D ,∠ C= , = ∠2,对应边有 , AO= 。
3,已知∠ B=∠D ,∠1=∠ 2,∠ 3=∠ 4, AB=CD ,AD=CB ,AC=CA 。
则△ AC =,≌ △5、判定两个三角形全等,依定义必须满足( (A )三边对应相等 (C )三边对应相等和三角对应相等一、 巩固练习:1、 下列三角形全等的是)(B )三角对应相等 (D )不能确定2、三边对 应相等的两个三角形 例全等,简 写 为或3、如图, AB=AC ,BD=DC 4 、如图,AM=AN ,求证:△ ABD ≌△ ACD证明:在△ ABD 和△ ACD 中BM=BN求证:△ AMB≌△ ANB证明:在△ AMB和△ ANB中A B AC (已知 ) AM_______(__ ____)_______ _______(已知 ) _______ BN (已知 )A D AD (公共边) _______ _________( 公共边)∴ △ ABD △ ACD()∴≌()A N MBB CD A5、如图, AD=CB, AB=CD 6 、如图, PA=PB, PC是△ PAB的中线,∠ A=55°求证:∠ B=∠ D 求:∠ B 的度数证明:在中解:∵ PC是 AB边上的中线,∴ AC= (中线的定义)在中∴ △≌△()∴≌()∴∠ B=∠ D(全等三角形对应角相等)P∴ ∠ A=∠ B()AD∵∠A=55°(已知)∴ ∠ B=∠ A=55°(等量代换)B 第 5 题C A C B第6题小结:本节学习并且掌握了三角形全等的条件,全等三角形对应的三条边和角都相等。