基于四元数法的捷联式惯性导航系统的姿态解算
- 格式:pdf
- 大小:425.77 KB
- 文档页数:8





哈尔滨工张大学硕士学位论文摘要撼联式惯性导航系统是一种十分先进的惯性导航技术,它采用数学平台代替实体乎台,即通过导舷计算机实时计算出姿态矩阵,建立起数学平台, 所汉导靛诗算辊跫建整个系统麓谈心寇关毽。
瓣薅,捷联矮浮簸系统聂澎衮精度、商可靠性、低成本、小型化、数字化的方向发展。
怒现代数字信号处理中的一门新兴技术,作为一零孛专魏数字售号处理器,它具骞毫激、麓这秘裹蕤凄等貔点。
本文应用单片机和设计了一套被捷联导航计算机系统。
以高速、高精度的?作为导航计算机数据处理的核心,以高速、商性能的离档位单片枧为作为整个系统的控铡器,构成了~褰双勺捷联导簸计簿枫系统。
这为导虢系统瀚小型纯、低藏本、数字化提供了一种设计思想。
如果再加上、电子罗擞和计程仪等,就可以完整的组合一个定位和导航系统。
本文蠹绕基予蕊导菠诗算壤系统,具,零巧震了以下尼方囊骚究工作:.论文分析了捷联惯导系统的基本原理,讨论了捷联懒导系统的算法。
.提出并论证了导航计算机的总体方案,同时分析了和单片枕这两牵申微处理器的特点和应用方法。
.讨论了基予麓捷联镄导系统静硬俘设计,包括基本功能静实现、原理框图及外围电路的设计。
本文对周围的接口电路作了较详细的介绍,主要电路有存储器系统、引导装载程序系统、通用异步串行蹦电路以及复位电路等。
.论述了系统的各种软件的舆体设计方法。
采用汇编语言和语言混台编程的方法来实现麟个系统软件。
并且详细讨论了实现该导航系统过程中的软件、硬件的调试和考核过程。
关键词:捷联惯性导航系统:数字信号处理器;数据处理;单片机哈尔滨工程太学硕士学位论文拄. , ,, ,, 。
,曲,跏,,它 .。
, 拉. ?曲 ?;圆 .,.‘’., ? ,:......髓接。
.?。
.. , , .,, 南撞哈尔滨工程大学硕士学位论文. 掣硼娃..: ;;; ?哈尔滨工程大学学位论文原创性声明本人郑重声明:本论文的所有工作,是在导师的指导下,由作者本人独立完成灼。
2019年第3期 信息通信2019(总第 195 期)INFORMATION&COMMUNICATIONS(Sum.N o 195)四元数算法在姿态矩阵解算中的研究陈国通,范圆圆,孙敬(河北科技大学信息科学与工程学院,河北石家庄050018)摘要:SIN S是直接利用计算机来模拟载体的姿态矩阵,然后根据模拟出的姿态矩阵解算出载体的姿态和航向信息。
姿 态矩阵的计算是捷联惯导算法中最重要的一部分,也是捷联式系统所特有的。
所以,对于姿态矩阵的研究是非常必要的,文章以四元数算法为基袖,主要研究整体-四元数和分解-四元数算法。
通过建立线性化误差模型,将这两种算法的精 度进行比较分析和仿真对比,结果表明分解-四元数算法比整体-四元数算法精度更高。
关键词:SINS.姿态矩阵;整体-四元数;分解-四元数中图分类号:TN927 文献标识码:A文章编号:1673-1131(2019)03-0046-03Research on Quaternion Algorithm in Attitude Matrix SolutionChen Guotong,Fan Yuanyuan,Sun Jing(College of Information Science and Engineering,Hebei University o f Science and Technology,Shijiazhuang050018, China) AbstractrSE^S directly uses the computer to simulate the attitude matrix o f t he earner,and then calculates the attitude and heading information o f t he carrier based on the simulated attitude matrix.The calculation of t he attitude matrix is the most important part o f t he strapdown inertial navigation algorithm and is unique to the strapdown system.Therefore,the study of attitude matrix is very necessary.Based on the quaternion algorithm,this paper mainly studies the whole-quaternion and decomposition-quaternion algorithm.By establishing a linearized error model,the accuracy o f the two algorithms is compared and analyzed.The results show that the decomposition-quaternion algorithm is more accurate than the global-quaternion algorithm.K ey words:SINS;attitude matrix;whole-quaternion;decomposition-quaternion〇引言捷联惯导系统(strap-down inertial navigation system,SINS)是惯性导航系统(Inertial navigation system,INS)的一[6] SLIMANI K,BENEZETH Y,SOUAMI F.Human interaction recognition based on the co-occurrence o f visual words[C]//Proceedings o f IEEE Conference on Computer Msionand Pattern Recognition Workshops.Columbus,Ohio,U SA: IEEE,2014:461-466.[7] NAM G YU CHO,SE HO PARK,JEONG SEON PARK.Compositional interaction descriptor for human interaction recognitiont^.Neurocomputing,2017,(267) 169-181.[8] JUNEJO I,DEXTER E,LAPTEV I.Cross-view action recognition from temporal self-similarities[C]//European Conference on Computer Vision.Berlin:Springer-Verlags2008: 293-306.[9] WRIGHT J,YANG A,GANESH A.Robust face recognition via sparse representation[C]//IEEE Trans,on Pattern Analysis and Machine Intelligence.IEEE,2009:354-371. [10] HUANG Zhi-wu,WANG Rui-pings SHAN Shi-guang.Facerecognition on large-scale video in the wild with hybrid Eu-clidean-and-Riemannian metric learning [J].Mixture Research Article Pattern Recognition,2015,48(10): 3113-3124.[11] VAHDAT A,G A O B,RANJBAR M.A discriminative keypose sequencemodel for recognizing human interactions[C]/ /Proceedings o f t he IEEE International Conference on Computer Vision Workshops.IEEE,2011:1729-1736.[12] RYOO MS.Human activity prediction:early recognition ofongoing activitiesfrom streaming videos[C]//Proceedings of 种。
1.初始对准得到载体的姿态角后,由欧拉角得到四元数初始值:其中q=a+bi+cj+dk,[a,b,c,d]也即[q0,q1,q2,q3]。
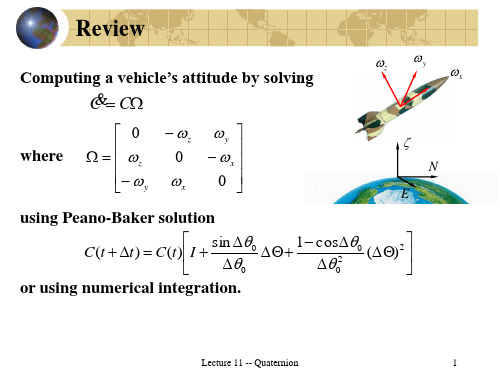
2.由四元数初始值构造姿态转移矩阵nc——载体坐标系b系到导航b坐标系(也即地理坐标系)n系的转移矩阵其中,俯仰角θ,滚转角φ,航向角ψ3.由n b C求出e b Cn b e n e b C C C =其中:其中,ϕ和λ分别为纬度和经度。
4. 由eb C 反求e 系下四元数的初始值[a,b,c,d]也即[q0,q1,q2,q3]。
5. 由四元数按时间传递的特性:也即:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡32103210000021q q q q q q q q xyzx zyy zx z yx ωωωωωωωωωωωω (2-24) 利用毕卡逼近法求解可得:()()()*120M dt q t e q t ω⎰= (2-25)令:[]()*0000x y z xz y y z x zyxM dt θθθθθθθωθθθθθθ-∆-∆-∆⎡⎤⎢⎥∆∆-∆⎢⎥∆==⎢⎥∆-∆∆⎢⎥∆∆-∆⎢⎥⎣⎦⎰ (2-26) (2-25)可简写为:()[]()120q t e q θ∆= (2-27)将[]12eθ∆展开可得:()[][][][]()231111022!23!2!2nq t I q n θθθθ⎡⎤⎛⎫⎛⎫⎛⎫∆∆∆⎢⎥=+∆+++++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦(2-28) 由于:[][][][]224222203040x y z I IIθθθθθθθθθθ⎡⎤∆==-∆+∆+∆=-∆⎣⎦∆=-∆∆∆=-∆ (2-29) 将式(2-29)代入式(2-28)整理可得:[]000sin 2()cos (0)2q t I q θθθθ∆⎧⎫⎪⎪∆=+∆⎨⎬∆⎪⎪⎩⎭(2-30) 在实际解算中,把0cos 2θ∆和0sin 2θ∆展为级数形式并取有限项,得四元数的各阶近似算法。