四轴姿态解算
- 格式:docx
- 大小:346.53 KB
- 文档页数:8

给四轴调了好久的PID,总算是调好了,现分享PID参数整定的心得给大家,还请大家喷的时候手下留情。
首先说明一下,这篇文章的主旨并不是直接教你怎么调,而是告诉你这么调有什么道理,还要告诉大家为什么…只‟使用PID的四轴会在飞行中震荡,告诉大家为什么光使用PID并不能实现对四轴姿态‘足够好’的控制。
文章中还是涉及了不少自控原理和其他控制相关的姿势,没有一点底子的话确实会看着很困惑(不然那么些人花好几年学控制还有什么意义?)。
如果你只想知道结论的话,直接看文章开头和结尾部分就好了(作者也支持大家这么做,这样被喷的几率就小了=_=)。
本人是刚刚转行学控制,思考错误的地方还请各位大神批评指正。
Ps:用wps画系统框图太费劲了,于是就一个豆没有画……,大家不会怪罪我吧?PID控制器是什么?我想每一个看到这里的人都对PID的概念有了足够的了解,我一遍遍叽歪比例积分微分没有任何意义。
这里我只想说一些大家提的较少的‘重点’内容:PID控制器是一个线性的控制器!从这里开始我们进入正题了,虽然若干年来PID已然成为了世界上使用最普遍的控制方法,也逐渐被人们神话到几乎可以控制一切………………但是,从理论上来说,只有‘线性的,符合要求的’被控系统才能在PID控制下实现良好的控制效果。
所以说,我们首先第一步,要保证我们的被控系统在被PID控制的区域‘表现为’一个线性系统才行。
于是这里有人会说了,现实中没有哪个系统是线性的,自然,我们的四轴飞行器在大范围内是一个非常典型的非线性系统(随便按照理论推推模型就会出现漫天的三角函数),也就是说,我们‘仅’使用标准PID控制的话是不可能让四轴从各个姿态回到目标状态的过程都能保持稳定。
于是这里出现我们使用PID时要注意的第一个问题:我们的PID控制只能工作在四轴角度偏移不大的一个近似线性的区域内。
这个区域没有定论,不过你要是飞机偏了90°的话想用PID调回到水平状态指定是非常危险的事情。

四轴飞行器报告(高级篇)姓名: 阿力木江艾合买提江高瞻完成日期: 2014年12月29日星期一报告内容1.姿态解算用到的常用数学方法和处理手段2.自动控制原理PID和系统建模姿态解算用到的常用数学方法和处理手段姿态有多种数学表示方式,常见的是四元数,欧拉角,矩阵和轴角。
他们各自有其自身的优点,在不同的领域使用不同的表示方式。
在四轴飞行器中使用到了四元数和欧拉角。
四元数是由爱尔兰数学家威廉·卢云·哈密顿在1843年发现的数学概念。
从明确地角度而言,四元数是复数的不可交换延伸。
如把四元数的集合考虑成多维实数空间的话,四元数就代表着一个四维空间,相对于复数为二维空间。
四元数大量用于电脑绘图(及相关的图像分析)上表示三维物件的旋转及方位。
四元数亦见于控制论、信号处理、姿态控制、物理和轨道力学,都是用来表示旋转和方位。
相对于另几种旋转表示法(矩阵,欧拉角,轴角),四元数具有某些方面的优势,如速度更快、提供平滑插值、有效避免万向锁问题、存储空间较小等等。
以上部分摘自维基百科-四元数。
莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。
对于在三维空间里的一个参考系,任何坐标系的取向,都可以用三个欧拉角来表现。
参考系又称为实验室参考系,是静止不动的。
而坐标系则固定于刚体,随着刚体的旋转而旋转。
以上部分摘自维基百科-欧拉角。
下面我们通过图例来看看欧拉角是如何产生的,并且分别对应哪个角度。
姿态解算的核心在于旋转,一般旋转有4种表示方式:矩阵表示、欧拉角表示、轴角表示和四元数表示。
矩阵表示适合变换向量,欧拉角最直观,轴角表示则适合几何推导,而在组合旋转方面,四元数表示最佳。
因为姿态解算需要频繁组合旋转和用旋转变换向量,所以采用四元数保存组合姿态、辅以矩阵来变换向量的方案。
总结来说,在飞行器中,姿态解算中使用四元数来保存飞行器的姿态,包括旋转和方位。
在获得四元数之后,会将其转化为欧拉角,然后输入到姿态控制算法中。

作者:nieyong本文需要讲清楚在无人机飞行器算法中,什么是姿态,怎么表示姿态,如何得到姿态。
姿态就是指飞行器的俯仰/横滚/航向情况。
在咱们地球上,就是指飞行器在地球坐标系中的俯仰/横滚/航向情况。
飞行器需要实时知道当前自己的姿态,才能够根据需要操控其接下来的动作,例如保持平稳,例如实现翻滚。
下面是学术型的严密论述。
数学模型姿态是用来描述一个刚体的固连坐标系和参考坐标系之间的角位置关系,有一些数学表示方法。
很常见的就是欧拉角,四元数,矩阵,轴角。
地球坐标系又叫做地理坐标系,是固定不变的。
正北,正东,正向上构成了这个坐标系的X,Y,Z轴,我们用坐标系R表示。
四轴飞行器上固定着一个坐标系,我们一般称之为机体坐标系,用坐标系r表示。
那么我们就可以用欧拉角,四元数等来描述r和R的角位置关系。
这就是四轴飞行器姿态解算的数学模型和基础。
姿态有多种数学表示方式,常见的是四元数,欧拉角,矩阵和轴角。
他们各自有其自身的优点,在不同的领域使用不同的表示方式。
在四轴飞行器中使用到了四元数和欧拉角。
Crazepony开源四轴飞行器也是一样的。
四元数四元数是由爱尔兰数学家威廉·卢云·哈密顿在1843年发现的数学概念。
从明确地角度而言,四元数是复数的不可交换延伸。
如把四元数的集合考虑成多维实数空间的话,四元数就代表着一个四维空间,相对于复数为二维空间。
四元数大量用于电脑绘图(及相关的图像分析)上表示三维物件的旋转及方位。
四元数亦见于控制论、信号处理、姿态控制、物理和轨道力学,都是用来表示旋转和方位。
相对于另几种旋转表示法(矩阵,欧拉角,轴角),四元数具有某些方面的优势,如速度更快、提供平滑插值、有效避免万向锁问题、存储空间较小等等。
以上部分摘自维基百科-四元数。
欧拉角莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。
对于在三维空间里的一个参考系,任何坐标系的取向,都可以用三个欧拉角来表现。


正文开始:这篇文章分为三个部分:•PID原理普与•常用四轴的两种PID算法讲解(单环PID、串级PID)•如何做到垂直起飞、四轴飞行时为何会飘、如何做到脱控?PID原理普与1、对自动控制系统的基本要求:稳、准、快:稳定性(P和I降低系统稳定性,D提高系统稳定性):在平衡状态下,系统受到某个干扰后,经过一段时间其被控量可以达到某一稳定状态;准确性(P和I提高稳态精度,D无作用):系统处于稳态时,其稳态误差;快速性(P和D提高响应速度,I降低响应速度):系统对动态响应的要求。
一般由过渡时间的长短来衡量。
2、稳定性:当系统处于平衡状态时,受到某一干扰作用后,如果系统输出能够恢复到原来的稳态值,那么系统就是稳定的;否则,系统不稳定。
3、动态特性(暂态特性,由于系统惯性引起):系统突加给定量(或者负载突然变化)时,其系统输出的动态响应曲线。
延迟时间、上升时间、峰值时间、调节时间、超调量和振荡次数。
通常:上升时间和峰值时间用来评价系统的响应速度;超调量用来评价系统的阻尼程度;调节时间同时反应响应速度和阻尼程度;4、稳态特性:在参考信号输出下,经过无穷时间,其系统输出与参考信号的误差。
影响因素:系统结构、参数和输入量的形式等5、比例(P)控制规律:具有P控制的系统,其稳态误差可通过P控制器的增益Kp来调整:Kp越大,稳态误差越小;反之,稳态误差越大。
但是Kp越大,其系统的稳定性会降低。
由上式可知,控制器的输出m(t)与输入误差信号e(t)成比例关系,偏差减小的速度取决于比例系数Kp:Kp越大,偏差减小的越快,但是很容易引起振荡(尤其是在前向通道中存在较大的时滞环节时);Kp减小,发生振荡的可能性小,但是调节速度变慢。
单纯的P控制无法消除稳态误差,所以必须要引入积分I控制。
原因:(R为参考输入信号,Kv为开环增益)当参考输入信号R不为0时,其稳态误差只能趋近于0,不能等于0。
因为开环增益Kv不为0。
6 比例微分(PD)控制规律:可以反应输入信号的变化趋势,具有某种预见性,可为系统引进一个有效的早期修正信号,以增加系统的阻尼程度,而从提高系统的稳定性。

四轴飞行器的设计随着电子技术的快速发展,四轴飞行器被越来越多的人们喜欢和使用,特别是用于航拍和军事领域,在不久的将来必然也会应用于越来越多的其他领域。
文章设计一款基于STM32F103C8T6为主控系统的小型四轴飞行器,采用keil5为软件开发环境,用MPU6050芯片进行姿态采集,根据采集到的数据进行姿态分析,进而控制其稳定飞行。
标签:四轴飞行器;单片机;PID1 无人机的发展历史及意义无人飞行器是指具有动力装置,而不要求有专业操纵人员的飞行器。
它利用螺旋桨通过转动形成向地面的气流来抵消机身的质量,可实现独立飞行或者远程控制飞行。
相对于固定翼无人机,旋翼无人飞行器的发展就较为缓慢,这是因为旋翼无人飞行器的控制系统较为复杂,早期的技术不能满足飞行要求。
然而旋翼机具备所有飞机和固定翼无人机的优点,其成本低,结构简单,无大机翼的限制,具有自主起飞及下降功能,事故代价低等特点。
四轴飞行器是多旋翼飞行器中结构最简单的一种,由于其应用前景广泛,很快就吸引了众多研究者的注意,特别是以美国等西方国家为主的大学在无人机的控制算法研究以及导航等方面取得了不少成果。
在我国,北京理工大学在基于PID控制算法,姿態控制方面也取得一定的成果。
国防科技大学从2004年开始对四轴飞行器相关技术展开研究,并自主设计了四轴飞行器的原型样机。
但四轴飞行器真正的进入公众视野却是2012年2月,美国宾夕法尼亚大学的VijayKumar教授在TED上做出四旋翼飞行器里程碑式的演讲[2]。
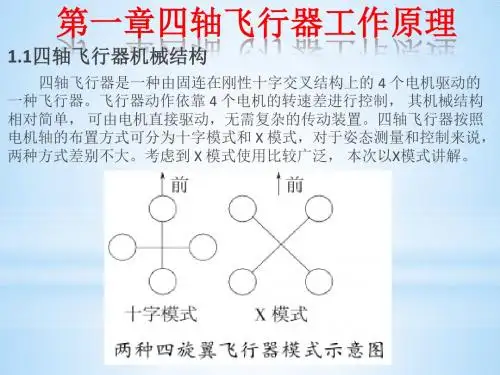
2 四轴飞行器的动力分析2.1 四轴飞行器的飞行模式四轴飞行器的飞行模式主要包括十字模式和X字模式两种,如图1所示。
十字模式下的飞行方向与其中一个电机的安装方向一致,而X模式下的四轴飞行器前进方向指向两个电机中间。
由于十字模式可以直接明了的分清四个电机在四轴飞行器飞行过程的作用,所以操纵简单,但动作灵活性差。
X模式飞行模式复杂,但动作灵活。
本次课题的四旋翼飞行器设计采用X模式。

四轴飞行器姿态控制算法四轴飞行器姿态控制是指通过调整四个电机的转速,使得飞行器能够保持所需的姿态,例如平稳飞行、转弯、盘旋等。
姿态控制算法主要包括传感器采集、姿态估计和控制指令生成等几个部分。
以下将详细介绍四轴飞行器姿态控制的算法原理。
1.传感器采集:四轴飞行器通常会配备三个主要的传感器:加速度计、陀螺仪和磁力计。
加速度计用于测量飞行器的重力加速度,陀螺仪用于测量飞行器的角速度,磁力计用于测量地磁场强度。
这些传感器的数据将用于后续的姿态估计和控制。
2.姿态估计:姿态估计是根据传感器提供的数据计算出飞行器的当前姿态角。
一种常用的姿态估计方法是互补滤波器。
互补滤波器将加速度计和陀螺仪的数据进行融合,通过加速度计估计出的姿态角和陀螺仪估计出的姿态角进行加权平均,从而得到更准确的姿态估计。
3.控制指令生成:姿态控制器的目标是生成适当的转速指令,使得飞行器能够达到所需的姿态。
在四轴飞行器中,姿态控制通常分为俯仰控制、滚转控制和偏航控制三个方向。
俯仰控制用于调整飞行器的前后倾斜角度,滚转控制用于调整飞行器的左右倾斜角度,偏航控制用于调整飞行器的旋转角度。
在控制指令生成中,通常会采用PID控制器。
PID控制器根据目标姿态角和当前姿态角的误差,计算出相应的控制指令。
PID控制器包括三个参数:比例项、积分项和微分项。
比例项用于快速响应误差,积分项用于消除稳态误差,微分项用于抑制系统的振荡。
通过将三个方向的控制指令进行线性叠加,得到最终的转速指令。
转速指令将被发送到四个电机,控制它们的转速,从而实现飞行器的姿态调整。
值得注意的是,四轴飞行器还需要考虑到动力学和非线性因素。
动力学因素包括电机的动态响应和旋转惯量的影响,通常会使用动态模型进行补偿。
非线性因素包括旋翼的非线性动力学和空气动力学特性的影响,通常会采用非线性控制器进行补偿。
综上所述,四轴飞行器姿态控制算法主要包括传感器采集、姿态估计和控制指令生成等几个部分。

(转)四轴飞⾏器6050六轴传感器软件姿态解算使⽤MPU6050硬件DMP解算姿态是⾮常简单的,下⾯介绍由三轴陀螺仪和加速度计的值来使⽤四元数软件解算姿态的⽅法。
我们先来看看如何⽤欧拉⾓描述⼀次平⾯旋转(坐标变换):设坐标系绕旋转α⾓后得到坐标系,在空间中有⼀个⽮量在坐标系中的投影为,在内的投影为由于旋转绕进⾏,所以Z坐标未变,即有。
转换成矩阵形式表⽰为:整理⼀下:所以从旋转到可以写成上⾯仅仅是绕⼀根轴的旋转,如果三维空间中的欧拉⾓旋转要转三次:上⾯得到了⼀个表⽰旋转的⽅向余弦矩阵。
不过要想⽤欧拉⾓解算姿态,其实我们套⽤欧拉⾓微分⽅程就⾏了:上式中左侧,,是本次更新后的欧拉⾓,对应row,pit,yaw。
右侧,是上个周期测算出来的⾓度,,,三个⾓速度由直接安装在四轴飞⾏器的三轴陀螺仪在这个周期转动的⾓度,单位为弧度,计算间隔时T陀螺⾓速度,⽐如0.02秒0.01弧度/秒=0.0002弧度。
间因此求解这个微分⽅程就能解算出当前的欧拉⾓。
前⾯介绍了什么是欧拉⾓,⽽且欧拉⾓微分⽅程解算姿态关系简单明了,概念直观容易理解,那么我们为什么不⽤欧拉⾓来表⽰旋转⽽要引⼊四元数呢?⼀⽅⾯是因为欧拉⾓微分⽅程中包含了⼤量的三⾓运算,这给实时解算带来了⼀定的困难。
⽽且当俯仰⾓为90度时⽅程式会出现神奇的“GimbalLock”。
所以欧拉⾓⽅法只适⽤于⽔平姿态变化不⼤的情况,⽽不适⽤于全姿态飞⾏器的姿态确定。
四元数法只求解四个未知量的线性微分⽅程组,计算量⼩,易于操作,是⽐较实⽤的⼯程⽅法。
我们知道在平⾯(x,y)中的旋转可以⽤复数来表⽰,同样的三维中的旋转可以⽤单位四元数来描述。
我们来定义⼀个四元数:我们可以把它写成,其中,。
那么是⽮量,表⽰三维空间中的旋转轴。
w是标量,表⽰旋转⾓度。
那么就是绕轴旋转w度,所以⼀个四元数可以表⽰⼀个完整的旋转。
只有单位四元数才可以表⽰旋转,⾄于为什么,因为这就是四元数表⽰旋转的约束条件。

姿态解算姿态解算(attitude algorithm),是指把陀螺仪,加速度计, 罗盘等的数据融合在一起,得出飞行器的空中姿态,飞行器从陀螺仪器的三轴角速度通过四元数法得到俯仰,航偏,滚转角,这是快速解算,结合三轴地磁和三周加速度得到漂移补偿和深度解算。
姿态的数学模型坐标系姿态解算需要解决的是四轴飞行器和地球的相对姿态问题。
地理坐标系是固定不变的,正北,正东,正上构成了坐标系的X,Y,Z轴用坐标系R表示,飞行器上固定一个坐标系用r表示,那么我们就可以适用欧拉角,四元数等来描述r和R的角位置关系。
姿态的数学表示姿态有多种数学表示方式,常见的是四元数,欧拉角,矩阵和轴角。
在四轴飞行器中使用到了四元数和欧拉角,姿态解算的核心在于旋转。
姿态解算中使用四元数来保存飞行器的姿态,包括旋转和方位。
在获得四元数之后,会将其转化为欧拉角,然后输入到姿态控制算法中。
姿态控制算法的输入参数必须要是欧拉角。
AD值是指MPU6050的陀螺仪和加速度值,3个维度的陀螺仪值和3个维度的加速度值,每个值为16位精度。
AD值必须先转化为四元数,然后通过四元数转化为欧拉角。
在四轴上控制流程如下图:下面是用四元数表示飞行姿态的数学公式,从MPU6050中采集的数据经过下面的公式计算就可以转换成欧拉角,传给姿态PID控制器中进行姿态控制.PID控制算法先简单说明下四轴飞行器是如何飞行的,四轴飞行器的螺旋桨与空气发生相对运动,产生了向上的升力,当升力大于四轴的重力时四轴就可以起飞了。
四轴飞行器飞行过程中如何保持水平:我们先假设一种理想状况:四个电机的转速是完全相同的是不是我们控制四轴飞行器的四个电机保持同样的转速,当转速超过一个临界点时(升力刚好抵消重力)四轴就可以平稳的飞起来了呢?答案是否定的,由于四个电机转向相同,四轴会发生旋转。
我们控制四轴电机1和电机3同向,电机2电机4反向,刚好抵消反扭矩,巧妙的实现了平衡, 但是实际上由于电机和螺旋浆本身的差异,造成我们无法做到四个电机产生相同的升力,这样飞行器起飞之后就会失去平衡。

姿态角解算(MPU6050 加速度计加陀螺仪)本文持续更新…I2C通信AHRS是自动航向基准系统(Automatic Heading Reference System)的简称。
目前,使用四元数来进行AHRS姿态解算的算法被广泛采用于四轴飞行器上。
IMU部分:IMU是惯性测量装置(Inertial Measurement Unit)的简称,通常包含陀螺仪和加速度计。
1.陀螺仪:测量的是角速度,即物体转动的速度,把速度和时间相乘,即可以得到某一时间段内物体转过的角度。
(但是积分运算得来的角度本身就存在误差,随着时间的累加,误差会加剧,此时就需要加速度计辅助计算出姿态角度)2.加速度计:测量的是物体的加速度,我们知道,重力加速度是一个物体受重力作用的情况下所具有的加速度。
当物体处于静止状态时,加速度计测量出来的值就等于重力加速度1g, 约等于9.8米每平方秒。
重力加速度g的方向总是竖直向下的,通过获得重力加速度在其X轴,Y轴上的分量,我们可以计算出物体相对于水平面的倾斜角度。
典型的IMU惯性测量芯片为MPU6050,它被广泛采用在四轴飞行器上。
mpu6050便是这两种传感器结合测出姿态角,通常运用卡尔曼滤波得出最终角度根据加速度计和地磁计的数据,转换到地理坐标系后,与对应参考的重力向量和地磁向量进行求误差,这个误差用来校正陀螺仪的输出,然后用陀螺仪数据进行四元数更新,再转换到欧拉角陀螺仪的角速度测量:如果他的速度是1度不加秒,我们用速度乘以时间就可以知道他从起点走了多少度。
加速度计来测量倾角:一个简单的例子如下: 一个单轴的加速计位于重力水平面上的时候,它在垂直方向上受到的加速度为1g,在水平方向上受到的加速度为0。
当我们把它旋转一个角度的时候,就会在水平轴上产生一个加速度分量。
通过它们的关系,就可以计算出该单轴加速计的倾角。
1.通过陀螺仪的积分来获得四轴的旋转角度2.然后通过加速度计的比例和积分运算来修正陀螺仪的积分结果。
又花了将近一个星期,终于把姿态解算的框架完成了。
仅仅是把陀螺仪、加速度计、罗盘融合在一起,得出旋转姿态,没有对加速度积分,没有用到气压计,几乎没有滤波。
算是阶段性的工作吧,把框架设计得合理一点,以后添加/修改就很简单了。
从传感器的读取,到四元数的学习,到空间旋转的处理方法,循序渐进,逐个击破。
主要参考了以下资料(按阅读的时间循序):《计算机图形学几何工具算法详解》(四元数转矩阵的公式是错的!)《交互式计算机图形学——基于OpenGL的自顶向下方法》维基百科——四元数框框的日记——四元数青衫湮痕——四元数Heath's blog——四元数与欧拉角之间的转换阿莫电子论坛——【原创】姿态估计下面总结一下“姿态解算”的过程,分为“传感器”、“四元数与旋转”、“姿态解算框架”、“长期融合”、“快速融合”四部分。
1.传感器我用的是10轴姿态传感器模块,其中陀螺仪是L3G4200D,加速度计是ADXL345,罗盘是HMC5883L,气压计是BMP085。
全部都通过一条共用的I2C总线访问,速度都支持400kHz。
先讲讲I2C库。
要配置、读取传感器,首先把通信做好,这里就是I2C库了。
现在大部分单片机都有支持中断的硬件I2C了,可以写个高效的I2C库。
我只实现了主机发送和主机接收模式,这里简单介绍一下接口。
接口函数主要有2个:uint8_t I2C_transmit (uint8_t which,I2C_transmitCallback cb);void I2C_setNextCallback (uint8_t which,I2C_transmitCallback cb);I2C_transmit()用于触发一次传输(发送或接收),异步执行,调用后马上返回。
其中有一个I2C_transmitCallback类型的参数,就是决定发送或接收、如何处理数据的回调函数了,其定义如下:/* 数据传输回调函数。
* 每(准备)传输一个字节都调用一次。
PID的整定是个让很多人都感到头痛的问题,在此,我想强调一句,PID整定必须建立在良好的姿态解算的基础上才能进行,否则根本没法弄出一个很好的效果。
举个例子,我的这个四轴,用互补滤波进行姿态处理,P最多调到3。
再调大由于姿态解算不过关,P 越大输出的姿态震动越大,即使D调大系统也没法收敛,也就是说这个系统发散了。
而用卡尔曼滤波我可以把P调到4.5而且回复也有力,飞起来也稳。
在姿态解算中,有很多种方法,我这采用的就是普通的姿态角,其他的解算方法还有四元素,欧拉角,等等,其实四元数还是要转化为欧拉角才能用于PID,不过四元数没有欧拉角中万向节死锁的问题。
具体请百度:四元数,欧拉角,万向节死锁。
在此不一一赘述。
我这的姿态解算原理比较简单,就是对三轴加速度的值进行三角函数运算即可。
举个例子,首先我从加速度计中获取数据。
Accel_y= GetData(ACCEL_YOUT_H);Accel_x= GetData(ACCEL_XOUT_H);Accel_z= GetData(ACCEL_ZOUT_H);再进行转化,转化公式在MPU6050数据手册里有Angle_ax=(Accel_x)/8192;Angle_az=(Accel_z)/8192;Angle_ay=(Accel_y)/8192;好了,这里得到的就是我们需要的加速度的值,取值范围0-1,也就是多少个g,g是重力加速度这个就不用说了吧。
之后用反三角函数进行运算:AngleAx=atan(Angle_ax/sqrt(Angle_ay*Angle_ay+A ngle_az*Angle_az))*180/3.141592657;公式:X轴角度=arctan(Angle_ax/开根号(Angle_ay^2+Angle_az^2))好了,这里得到的是弧度制的角度,再乘180除以π即可得到所需的角度值。
之后要对得到的值进行滤波,为什么要滤波呢,因为加速度计对震动特别敏感,一点震动就大姨妈,得到的角度值是不怎么准确的,不过大致在实际角度的上下。
四轴飞行器控制系统设计及其姿态解算和控制算法研究四轴飞行器控制系统设计及其姿态解算和控制算法研究一、引言四轴飞行器是一种飞行机械,通过四个对称分布的旋翼作为动力驱动,能够实现各种姿态的飞行。
在日常生活中,四轴飞行器被广泛应用于飞行摄影、物流配送、农业植保等领域。
为了保证四轴飞行器的稳定性和精确控制,需要设计合适的控制系统以及姿态解算和控制算法。
二、四轴飞行器控制系统设计1. 框架设计四轴飞行器控制系统的框架一般包括硬件和软件两个部分。
硬件部分主要包括传感器模块、执行器模块以及通讯模块。
传感器模块用于获取飞行器的姿态信息,执行器模块用于产生控制信号,通讯模块用于与地面站进行数据传输。
软件部分主要包括姿态解算模块和控制算法模块。
2. 传感器模块传感器模块是四轴飞行器控制系统中非常重要的一部分,它提供了飞行器当前姿态信息的反馈。
一般而言,传感器模块包括陀螺仪、加速度计和磁力计。
陀螺仪用于测量飞行器的角速度,加速度计用于测量飞行器的加速度,磁力计用于测量飞行器所处的磁场。
通过这些传感器的数据,可以实现对飞行器的姿态和位置的估计。
3. 执行器模块执行器模块是四轴飞行器控制系统中的输出模块,它能够控制四个旋翼的转速,从而产生所需的推力和力矩。
一般而言,执行器模块包括电机和电调。
电机负责将电能转化为机械能,电调则控制电机的转速。
通过对四个电机的控制,可以实现对飞行器的姿态和位置的调整。
4. 通讯模块通讯模块是四轴飞行器控制系统中的数据传输模块,它负责与地面站进行通讯,并将传感器模块获取到的数据传输给地面站进行处理。
通讯模块一般采用无线通信方式,例如蓝牙、Wi-Fi等。
通过与地面站的通讯,可以实现对飞行器的遥控和数据监测。
5. 姿态解算模块姿态解算是四轴飞行器控制系统中的关键部分,它负责从传感器获取到的数据中解算出飞行器的当前姿态信息。
一般而言,姿态解算模块采用卡尔曼滤波算法对传感器数据进行融合处理,以提高姿态解算的精度和稳定性。
四轴飞⾏器1.4姿态解算和Matlab实时姿态显⽰原创⽂章,欢迎转载,转载请注明出处MPU6050数据读取出来后,经过⼀个星期的努⼒,姿态解算和在matlab上的实时显⽰姿态终于完成了。
1:完成matlab的串⼝,并且实时通过波形显⽰数据2:添加RTT查看CPU使⽤率的扩展功能,MPU6050读取数据的优化3:四元素表⽰的坐标变化,四元素与欧拉⾓的关系和Madgwick的IMUupdate算法4:飞控数据采集线程和数据处理线程的安排,类似于⽣产者与消费者的关系。
先放个效果视频。
1:matlab串⼝初始化还是⽐较简单的,⽹上的资料也很多,这⾥就直接贴初始化代码了。
1 % --- Executes on button press in pb_OpenSerialPort.2 function pb_OpenSerialPort_Callback(hObject, eventdata, handles)3 % hObject handle to pb_OpenSerialPort (see GCBO)4 % eventdata reserved - to be defined in a future version of MATLAB5 % handles structure with handles and user data (see GUIDATA)6 %7global o_SerialPort;8 %______________________________________________9 %GUI全局变量101112 %---------------------串⼝初始化-----------------------13 %%%COM端⼝初始化14 int_Index_COM=get(handles.pop_SerialPort,'Value');15 string_COM=get(handles.pop_SerialPort,'String');16 string_Select_COM=string_COM{int_Index_COM};17 o_SerialPort=serial(string_Select_COM);18 %%%Baud初始化19 int_Index_Baud=get(handles.pop_BaudRate,'Value');20 string_Baud=get(handles.pop_BaudRate,'String');21 string_Select_Baud=string_Baud{int_Index_Baud};22 double_Baud=str2double(string_Select_Baud);23set(o_SerialPort,'BaudRate',double_Baud);24 %%%设置数据长度25 int_Index_DataBit=get(handles.pop_DataBit,'Value');26 string_DataBit=get(handles.pop_DataBit,'String');27 string_Select_DataBit=string_DataBit(int_Index_DataBit);28 double_DataBit=str2double(string_Select_DataBit);29set(o_SerialPort,'DataBits',double_DataBit);30 %%%设置停⽌位长度31 int_Index_StopBits=get(handles.pop_StopBits,'Value');32 string_StopBits=get(handles.pop_StopBits,'String');33 string_Select_StopBits=string_StopBits(int_Index_StopBits);34 double_StopBits=str2double(string_Select_StopBits);35set(o_SerialPort,'StopBits',double_StopBits);36 %%%设置输⼊缓冲区⼤⼩为1M37set(o_SerialPort,'InputBufferSize',1024000);38 %%%串⼝事件回调设置3940set(o_SerialPort,'BytesAvailableFcnMode','terminator');41set(o_SerialPort,'terminator','!'); %!标识结束符结束,⽅便处理和读取数据4243 o_SerialPort.BytesAvailableFcn={@EveBytesAvailableFcn,handles};44 % ----------------------打开串⼝-----------------------45 fopen(o_SerialPort);matlab串⼝我们采⽤回调函数,类似于中断⽅式哈,但是mtalb的串⼝⼗分的不好⽤哈,没有多线程,⽽我们在中断⾥⾯需要进⾏波形显⽰,四元素旋转等各种数据操作,是需要花费点时间的,这就导致我们的数据平率不能很⾼。
又花了将近一个星期,终于把姿态解算的框架完成了。
仅仅是把陀螺仪、加速度计、罗盘融合在一起,得出旋转姿态,没有对加速度积分,没有用到气压计,几乎没有滤波。
算是阶段性的工作吧,把框架设计得合理一点,以后添加/修改就很简单了。
从传感器的读取,到四元数的学习,到空间旋转的处理方法,循序渐进,逐个击破。
主要参考了以下资料(按阅读的时间循序):《计算机图形学几何工具算法详解》(四元数转矩阵的公式是错的!)《交互式计算机图形学——基于OpenGL的自顶向下方法》维基百科——四元数框框的日记——四元数青衫湮痕——四元数Heath's blog——四元数与欧拉角之间的转换阿莫电子论坛——【原创】姿态估计下面总结一下“姿态解算”的过程,分为“传感器”、“四元数与旋转”、“姿态解算框架”、“长期融合”、“快速融合”四部分。
1.传感器我用的是10轴姿态传感器模块,其中陀螺仪是L3G4200D,加速度计是ADXL345,罗盘是HMC5883L,气压计是BMP085。
全部都通过一条共用的I2C总线访问,速度都支持400kHz。
先讲讲I2C库。
要配置、读取传感器,首先把通信做好,这里就是I2C库了。
现在大部分单片机都有支持中断的硬件I2C了,可以写个高效的I2C库。
我只实现了主机发送和主机接收模式,这里简单介绍一下接口。
接口函数主要有2个:uint8_t I2C_transmit (uint8_t which,I2C_transmitCallback cb);void I2C_setNextCallback (uint8_t which,I2C_transmitCallback cb);I2C_transmit()用于触发一次传输(发送或接收),异步执行,调用后马上返回。
其中有一个I2C_transmitCallback类型的参数,就是决定发送或接收、如何处理数据的回调函数了,其定义如下:/* 数据传输回调函数。
* 每(准备)传输一个字节都调用一次。
* 参数:* seq =>序号,第一次调用时为0,以后每次调用递增。
* data => seq==0时写(从机地址+W/R)到data。
* seq!=0时data是数据。
发送就写data,接收就读data。
* 返回值表示下一步的行为:* I2C_RT_START =>发送开始信号。
* I2C_RT_STOP =>发送停止信号。
* I2C_RT_REPEAT_START_OR_STOP =>如果有下一次传输,就发送RepeatStart,否则发送Stop。
* I2C_RT_ACK =>继续传送,回应ACK。
* I2C_RT_NACK =>继续传送,回应NACK。
*/typedef uint8_t (* I2C_transmitCallback)(uint8_t seq,uint8_t * data);当用I2C_transmit()成功触发一次传输后,I2C库会根据需要调用回调函数,所以使用这个I2C 库就是写回调函数了。
而I2C_setNextCallback()则是用来设置紧接着的一次传输的。
当本次传输结束时,不发送“Stop”信号,而是发送“Repeat Start”信号,然后开始下一个传输。
利用这个函数可以发起连续多次传输。
有了I2C库就可以操作传感器了,以L3G4200D为例讲解。
先看看DataSheet,操作L3G4200D 有两个步骤,首先配置好寄存器,然后不断获取数据。
配置寄存器比较简单,就是发送一段数据,用到两个函数:/** 初始化芯片。
* 返回值:{L3G4200D_RT_NORMAL,L3G4200D_RT_BUS_BUSY} */uint8_t l3g4200d_init(void){if(I2C_transmit(L3G4200D_WHICH_I2C,l3g4200d_init_callback) == I2C_RT_TRANSMIT_NORMAL)return L3G4200D_RT_NORMAL;return L3G4200D_RT_BUS_BUSY;}/** 初始化使用的I2C回调函数。
*/uint8_t l3g4200d_init_callback(uint8_t seq,uint8_t * data){const static uint8_t value[] = {I2C_addressToByte_write(L3G4200D_ADDRESS), /* 总线地址。
*/(0x80 | 0x20), /* 寄存器地址。
或0x80表示连续写。
*/0xEF, /* CTRL_REG1 */0x00, /* CTRL_REG2 */0x00, /* CTRL_REG3 */0x00, /* CTRL_REG4,250dps量程。
*//* 其它默认。
*/};//if(seq == sizeof(value))return I2C_RT_STOP;//*data = value[seq];return I2C_RT_ACK;}读取数据就有点麻烦,因为读之前要设置寄存器指针,所以其实包含两次传输:第一次是发送,设置当前寄存器指针;第二次是接收,获取测量值。
第一次传输结束前要用I2C_setNextCallback()设置第二次传输的回调函数。
见代码:/** 获取角速度。
* 异步,读取成功后,l3g4200d_measureCompleted()会被调用。
* 返回值:{L3G4200D_RT_NORMAL,L3G4200D_RT_BUS_BUSY} */uint8_t l3g4200d_measureOmega(void){if(I2C_transmit(L3G4200D_WHICH_I2C,l3g4200d_measureOmega_callback_reg) == I2C_RT_TRANSMIT_NORMAL)return L3G4200D_RT_NORMAL;return L3G4200D_RT_BUS_BUSY;}/** 读角速度的I2C回调函数,设置当前寄存器地址。
*/uint8_t l3g4200d_measureOmega_callback_reg(uint8_t seq,uint8_t * data){if(seq == 0){*data = I2C_addressToByte_write(L3G4200D_ADDRESS);return I2C_RT_ACK;}if(seq == 1){*data = L3G4200D_REG_OMEGA; /* 角速度数据的寄存器地址。
*/return I2C_RT_ACK;}//I2C_setNextCallback(L3G4200D_WHICH_I2C,l3g4200d_measureOmega_callback_read);return I2C_RT_REPEAT_START_OR_STOP;}/** 读角速度的I2C回调函数,读取数据。
*/uint8_t l3g4200d_measureOmega_callback_read(uint8_t seq,uint8_t * data){if(seq == 0){*data = I2C_addressToByte_read(L3G4200D_ADDRESS);return I2C_RT_ACK;}if(seq > L3G4200D_BUFFER_SIZE)return I2C_RT_STOP;//l3g4200d_var.buffer_8u[seq-1] = *data;if(seq == L3G4200D_BUFFER_SIZE){l3g4200d_measureCompleted();return I2C_RT_NACK;}return I2C_RT_ACK;}这样就可以读取角速度了。
所有数据都是在I2C中断里处理,所以要注意数据安全性,合理利用volatile。
其他传感器的工作方式几乎一样,Crtl+C,Ctrl+V,然后改改名字,改改参数就可以用了。
2.四元数与旋转姿态解算的核心在于旋转,一般旋转有4种表示方式:矩阵表示、欧拉角表示、轴角表示和四元数表示。
矩阵表示适合变换向量,欧拉角最直观,轴角表示则适合几何推导,而在组合旋转方面,四元数表示最佳。
因为姿态解算需要频繁组合旋转和用旋转变换向量,所以采用四元数保存组合姿态、辅以矩阵来变换向量的方案。
下面介绍一下四元数,然后给出几种旋转表示的转换。
四元数可以理解为一个实数和一个向量的组合,也可以理解为四维的向量。
这里用一个圈表示q是一个四元数(很可能不是规范的表示方式)。
四元数的长度(模)与普通向量相似。
下面是对四元数的单位化,单位化的四元数可以表示一个旋转。
四元数相乘,旋转的组合就靠它了。
旋转的“轴角表示”转“四元数表示”。
这里创造一个运算q(w,θ),用于把绕单位向量w转θ角的旋转表示为四元数。
通过q(w,θ),引伸出一个更方便的运算q(f,t)。
有时需要把向量f的方向转到向量t的方向,这个运算就是生成表示对应旋转的四元数的(后面会用到)。
然后是“四元数表示”转“矩阵表示”。
再次创造运算,用R(q)表示四元数q对应的矩阵(后面用到)。
多个旋转的组合可以用四元数的乘法来实现。
“四元数表示”转“欧拉角表示”。
用于显示。
3.姿态解算框架姿态解算框架其实就是程序框架了。
设计框架既要准确,又要高效。
总体设计是这样的:用一个计时器定时触发测量;所有测量过程都靠中断推进;在main函数里不断检查测量是否完成,完成就进行解算。
测量过程比较耗时间,而这样设计,测量和解算可以同时进行,不会浪费CPU时间在(等待)测量上。
而通过计时器触发测量,最大限度保证积分间隔的准确。
长期融合的目的有两个:一、得到初始姿态;二、用直接测量的姿态(下称直接姿态),纠正陀螺仪积分得出的姿态。
直接测量的量包括加速度和磁场强度。
长期融合有两个阶段,第一阶段是获得直接姿态,第二阶段是用直接姿态纠正当前姿态。
首先讲第一阶段:用加速度和磁场强度计算直接姿态。
获取直接姿态的过程,其实是利用了空间中的两个场——重力场和地磁场,把测得的加速度和磁场强度旋转到“原来的位置”,其中的“旋转”就是我们需要的直接姿态了。
但由于干扰和误差,测得的值不可能旋转到与实际的场一致。
用了净两天的时间来思考,还是想不出高效的办法。
下面讲我的笨办法。
首先定义几个量("w" for world,"m" formeasure):单位化:变换到对角线和平面法线。
因为不能把加速度和磁场强度旋转到与对应的场一致,于是变换一下,使他们的对角线和平面法线与场对应的量重合,这是可以做到的。