系统工程-第5章节 系统评价方法-层次分析法资料文档
- 格式:ppt
- 大小:1.20 MB
- 文档页数:86



系统:由两个及以上有机联系、相互作用的要素组成,具有特定结构、功能和环境的整体。
系统边界:从空间结构上看,把系统和环境分开的所有点的集合;从逻辑上看,边界是系统构成关系从起作用到不起作用的边界,系统质从存在到消失的边界。
系统的属性:整体性{是系统最核心的特性,是系统性最集中的体现}关联性(由多个有机联系、相互作用的要素组成,具备独立要素所不具备的功能)环境适应性(环境输入系统,系统输出环境,系统要生存,一定要适应环境)层次性(作为总体来看,系统可以分解一系列子系统,并有一定的层次结构)目的性(有一定目的,为达到既定目的而具备一定的功能)集合性(把具备某种属性的一些对象看成一个整体,从而形成一个集合)系统的类型:人造系统和自然系统实体系统和概念系统、动态系统和静态系统、封闭系统和开发系统系统工程的概念:是组织管理系统的规划、研究、设计、制造、试验、使用的科学方法,是一种对所有系统具有普遍意义的科学方法。
系统工程方法论:是研究、探索系统问题的一般规律和途径重要思想:最优思想、总体思想、组合思想、分解和协调思想、反馈思想霍尔三维结构:知识维、时间维、逻辑维时间维(6个阶段):规划阶段、方案阶段、研制阶段、生产阶段、运行阶段、更新阶段逻辑维(7个步骤):明确问题、选择目标、系统综合、系统分析、方案优化、做出决策、付诸实施特点:强调目标明确,核心是最优化,认为一切现实问题都可以规划为工程系统问题,运用定量分析法,做最优解答。
该方法论在研究方法上有整体性,在技术应用上有综合性,在组织管理上有科学性,在系统工程上有问题导向性。
切克兰德方法论:主要内容:问题、根底定义、建立概念模型、比较与探索、选择、设计与实施、评估与反馈主要步骤(略)比较:同:同为系统工程方法论,均以问题为起点,具备相应的逻辑结构异:前者主要研究工程系统问题,后者更适用于“软”系统问题的研究前者以优化分析为核心,后者以比较学习为核心前者使用定量分析方法,后者使用定性、定量与定性相结合的方法前者研究对象为良结构,后者则为不良结构系统分析:运用建模及预测、优化、仿真、评价等技术,对系统的各方面进行定性与定量相结合的分析,为选择最优或满意的方案提供决策依据的分析研究过程。



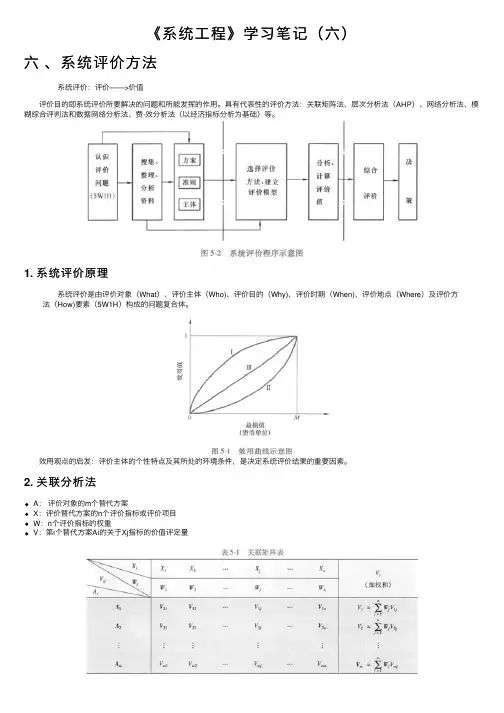
《系统⼯程》学习笔记(六)六、系统评价⽅法 系统评价:评价——>价值 评价⽬的即系统评价所要解决的问题和所能发挥的作⽤。
具有代表性的评价⽅法:关联矩阵法、层次分析法(AHP)、⽹络分析法、模糊综合评判法和数据⽹络分析法、费-效分析法(以经济指标分析为基础)等。
1. 系统评价原理 系统评价是由评价对象(What)、评价主体(Who)、评价⽬的(Why)、评价时期(When)、评价地点(Where)及评价⽅法(How)要素(5W1H)构成的问题复合体。
效⽤观点的启发:评价主体的个性特点及其所处的环境条件,是决定系统评价结果的重要因素。
2. 关联分析法A:评价对象的m个替代⽅案X:评价替代⽅案的n个评价指标或评价项⽬W:n个评价指标的权重V:第i个替代⽅案Ai的关于Xj指标的价值评定量3. 逐对⽐较法 确定评价指标的简便⽅法。
对各替代⽅案的评价指标进⾏逐对⽐较,对相对重要的指标给予较⾼得分,据此可得到各评价项⽬的权重Wj 。
再根据评价主体给定的评价尺度,对各替代⽅案在不同的评价指标下⼀⼀进⾏评价,得到相应的评价值,进⽽求加权和得到综合评价值。
4. 古林法 从上向下⽐较得Rj,从下向上链式相乘得Kj,归⼀化“因为最后加权和V2>V1>V3, 所以A2为最优⽅案”5. 层次分析法(Analytic Hierarchy Process, AHP) 提出者:T.L.萨迪(T.L.Saaty), 20世纪70年代,核⼼思想:分解-判断-综合⼤致步骤: (1)分析评价系统中各基本要素之间的关系,建⽴系统的递阶层次结构; (2)对同⼀层次的各元素关于上⼀层次中某⼀准则的重要性进⾏两两⽐较,构造两两⽐较判断矩阵,并进⾏⼀致性检验; (3)由判断矩阵计算被⽐较要素对于该准则的相对权重; (4)计算各层要素对系统⽬的(总⽬标)的合成(总)权重,并对各备选⽅案进⾏排序。
求各要素相对于上层某要素(准则等)的归⼀化相对重要度向量。




层次分析法课程设计一、课程目标知识目标:1. 理解层次分析法的概念、原理及基本步骤;2. 学会运用层次分析法构建问题层次结构,进行判断矩阵的构建和权重计算;3. 能够运用层次分析法解决实际问题,并对其结果进行分析和解释。
技能目标:1. 培养学生运用层次分析法进行问题分析和解决的能力;2. 提高学生运用数学软件进行层次分析运算的技能;3. 培养学生的逻辑思维和团队协作能力。
情感态度价值观目标:1. 培养学生积极探究问题、主动学习的态度;2. 增强学生对层次分析法的兴趣,激发学生运用数学工具解决实际问题的热情;3. 培养学生的批判性思维和创新意识,使学生在面对复杂问题时能保持独立、客观的判断。
课程性质:本课程为方法论课程,旨在教授学生层次分析法这一实用工具,提高学生的问题分析解决能力。
学生特点:学生具备一定的数学基础和逻辑思维能力,但对层次分析法及其应用尚不熟悉。
教学要求:结合学生特点,通过案例教学、小组讨论等形式,使学生掌握层次分析法的原理和应用,培养其独立分析和解决问题的能力。
教学过程中注重启发式教学,引导学生主动参与,提高课程学习的趣味性和实用性。
教学评估侧重于学生的实际操作能力和问题解决能力的提升。
二、教学内容1. 引言:介绍层次分析法的背景、应用领域及重要性。
2. 基本概念:讲解层次结构、判断矩阵、权重、一致性指标等基本概念。
- 章节关联:课本第二章第二节3. 方法原理:阐述层次分析法的原理、步骤及注意事项。
- 章节关联:课本第二章第三节4. 案例分析:选取实际案例,讲解如何构建层次结构、进行判断矩阵的构建和权重计算。
- 章节关联:课本第二章第四节5. 数学软件应用:介绍如何运用数学软件(如MATLAB、yaaph等)进行层次分析运算。
- 章节关联:课本第二章第五节6. 实践操作:布置实际操作题目,指导学生分组进行问题分析和解决,培养学生的团队协作能力。
- 章节关联:课本第二章第六节7. 结果分析与评价:对实践操作结果进行分析和评价,总结层次分析法的优缺点及适用范围。
系统工程试卷1一、名词解释:1、反馈:2、层次分析法:3、控制论:4、三维结构分析法:5、系统评价的概念:二、单项选择题:1、我国古代运用系统工程建造的大型水利工程典范是()。
A、都江堰B、京杭大运河C、黄河治理D、灵宝渠2、系统科学的产生与()有关。
A、科技背景、社会经济水平、军事政治B、科技背景、军事政治C、社会经济水平、军事政治D、科技背景、社会经济水平3、下列关于系统定义描述错误的是()oA. 系统是一个整体B.二个系统的结构就是所有组分间关联方式的总和C.对于系统中的任意两个组分,它们之间的关系只有一种D.模型是对原系统特性的简化表达形式4、关于切克兰德模式,下面说法中()是错误的。
A.霍尔结构主要解决“硬”问题,而切克兰德模式主要解决“软”问题B.切克兰德模式实质上是一种调查学习法C.切克兰德使用概念模型代替数学模型,用可行满意解代替最优解D.切克兰德模式适合解决工程系统的问题5、关于综合集成工程方法学说法错误的是()。
A.它是从定性到定量的综合集成法 b.处在成熟期的产品C.生产集中、消费分散的产品D.技术性强、价格昂贵的产品6、关于系统分析,下面说法错误的是()。
A、无狭义和广义之分B、通过对情况的全面分析,对可能采取的方案进行优选,为决策者提供可靠的依据C、系统分析应首先明确分析的目的D、既是系统工程中的一个阶段,又贯穿于整个系统工程活动过程7、系统分析和系统设计是系统工程中的两个核心阶段,下列说法错误的是()。
A、系统设计的10个阶段要严格遵循一种线性的进程B、系统设计是选择和安排系统的各个组成部分来实现规定的功能C、可以采用分析和综合两种方法进行系统设计D、系统分析是对某一给定的系统的各个组成部分的一种调查和分析研究8、系统功能分析一般不用()来描述A.功能流程框图法B.时间基线法C.系统流程图D. M图法9、建立递阶结构模型,一般要经过①级位划分②区位划分③多级递阶有向图绘制④骨架矩阵提取四个阶段,下列排列正确的是()A、①②③④B、①②④③C、②①④③D、②①③④10、关于系统评价,下面论述正确的是()oA、系统评价只是在系统即将终结之时进行B、系统评价越晚其意义越显著C、在系统工程的每一阶段都应进行系统评价D、系统评价活动与系统需求、系统开发无关三、填空题:1、系统是具有特定功能的、相互间具有有机联系的许多要素所构成的一个整体,一般系统具有集合性、相关性、、、目的性和ji df 等特性。
层次分析法及其应用摘要层次分析法是美国运筹学家匹兹堡大学教授萨迪于20世纪70年代初,为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时,应用网络系统理论和多目标综合评价方法,提出的一种层次权重决策分析方法。
本文主要介绍层次分析法原理及其在实际工作上的应用。
层次分析法(Analytic Hierarchy Process,简称AHP)是将与决策总是有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法。
这种方法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的难于完全定量的复杂决策问题提供简便的决策方法。
基本原理:应用AHP解决问题的思路:首先,把要解决的问题分层次系列化,即根据问题的性质和要达到的目标,将问题分解为不同的组成因素,按照因素之间的相互影响和隶属关系将其分层聚类组合,形成一个递阶的、有序的层次结构模型。
然后,对模型中每一层此因素的相对重要性,根据人们对客观现实的判断给予定量表示,再利用数学方法确定每一层此因素相对重要性次序的权值。
最后,通过综合计算各层因素相对重要性的权值,得到最底层(方案层)相对于最高层(总目标)的相对重要性次序的组合权值,以此作为评价和选择方案的依据。
基本步骤:1.明确问题,建立层次结构模型;2.构造判断矩阵;3.层次单排序及一致性检验;4.层次总排序及一致性检验。
实际案例应用在这个信息化的时代,通讯是必不可少的一部分。
如今,我们的生活也越来越离不开手机,几乎每一个人都拥有一部手机。
同时,生产手机的厂商越来越多,手机的款式五花八门,选择哪款手机这个问题也困扰了许多人。
以下运用层次分析法进行分析:1.将决策分解为三个层次目标层A:购买手机准则层B:价格,性能,外观方案层P:华为,苹果,三星层次结构模型如下图:构造判断矩阵A B1 B2 B3 B1 P1 P2 P3B1 1 3 5 P1 1 5 3B2 1/3 1 3 P2 1/5 1 1/3B3 1/5 1/3 1 P3 1/3 3 1判断矩阵A-B 判断矩阵B1-PB2 P1 P2 P3 B3 P1 P2 P3P1 1 1/3 1/5 P1 1 1/5 3P2 3 1 1/3 P2 5 1 7P3 5 3 1 P3 1/3 1/7 1判断矩阵B2-P 判断矩阵B3-P计算判断矩阵的特征值,特征向量和一致性检验1)13/15/1313/1531=A ,归一化后为:111.0077.0130.0333.0231.0217.0556.0692.0652.02)列正规化后的判断矩阵按行相加:900.1556.0692.0652.0111=++==∑=nj j a W 781.0333.0231.0217.0122=++==∑=nj j a W318.0111.0077.0130.0133=++==∑=nj j a W3)将向量=W []w w w T321,,列归一化后,得特征向量:[]106.0,260.0,634.0TW =4)计算判断矩阵的最大特征根λmax⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=321)()()(106.0260.0634.013/15/1313/1531AW AW AW AW 320.0106.01260.03/1634.05/1)(789.0106.03260.01634.03/1)(944.1106.05260.03634.01)(321=⨯+⨯+⨯==⨯+⨯+⨯==⨯+⨯+⨯=AW AW AW 04.33/)()()()(3322111max =⎥⎦⎤⎢⎣⎡++==∑=W AW W AW W AW nW AW ni i i λ 5)对A 进行一致性检验 02.02304.31max =-=--=n n CI λ 由1~9阶矩阵的平均随机一致性指标得:58.0=RI1.0034.058.002.0〈===RI CI CR 满足一致性要求6)对1B ,2B ,3B 进行一致性检验 同理5)步骤进行计算可得:矩阵P B -1:[]TW 260.0,106.0,634.0=,04.3max =λ,1.0034.0〈=CR矩阵P B -2:[]TW 633.0,260.0,106.0=,04.3max =λ,1.0034.0〈=CR矩阵P B -3:[]TW 08.0,724.0,193.0=,067.3max =λ,1.0058.0〈=CR根据上表可得层次总排序的组合权向量:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=319.0202.0457.0321WP WP WP W 故最终决策为:P1首选,P3次之,P2最后。
层次分析法例题专题:层次分析法一般情况下,物流系统的评价属于多目标、多判据的系统综合评价。
如果 仅仅依靠评价者的定性分析和逻辑判断,缺乏定量分析依据来评价系统方案的 优劣,显然是十分困难的。
尤其是物流系统的社会经济评价很难作出精确的定 量分析°层次分析法(Analytical Hierarchy Process)由美国著名运筹学家萨蒂(T.L. Saaty)于1982年提出,它综合了人们主观判断,是一种简明、实用的定性 分析与定量分析相结合的系统分析与评价的方法。
目前,该方法在国内已得到 广泛的推广应用,广泛应用于能源问题分析、科技成果评比、地区经济发展方 案比较,尤其是投入产出分析、资源分配、方案选择及评比等方面。
它既是一 种系统分析的好方法,也是一种新的、简洁的、实用的决策方法。
♦层次分析法的基本原理人们在日常生活中经常要从一堆同样大小的物品中挑选出最重的物品。
这 时,一般是利用两两比较的方法来达到目的。
假设有n 个物品,其真实重量用 W1 , W2,--W n 表示。
要想知道W1 , W2,--W n 的值,最简单的就 是用秤称出它 们的重量,但如果没有秤,可以将几个物品两两比较,得到它们的重量比矩阵 A 。
W/叫/讥zWVV.VVPW/1V如果用物品重量向量W=[W1,W2右乘矩阵A,则有:由上式可知,n 是A 的特征值,W 是A 的特征向量。
根据矩阵理论, 矩阵A 的唯一非零解,也是最大的特征值。
这就提示我们,可以利用求物/W2 /W2叫/W]叫/叫/W]W1"'2/ W] W’r / us• • •/w” • • •■nw 2/ W]叫/ “2 叫=nW品重量比判断矩阵的特征向量的方法来求得物品真实的重量向量W。
从而确定最重的物品。
将上述n个物品代表n个指标(要素),物品的重量向量就表示各指标(要素)的相对重要性向量,即权重向量;可以通过两两因素的比较,建立判断矩阵,再求出其特征向量就可确定哪个因素最重要。