离散数学假言推理的例子

假言判断推理公式
（原创版）
目录
1.假言判断推理的定义和基本概念
2.假言判断推理的公式和符号表示
3.假言判断推理的例子和应用
正文
1.假言判断推理的定义和基本概念
假言判断推理，也称为条件推理，是一种逻辑推理方法，用于确定一个陈述（前提）与另一个陈述（结论）之间的关系。

在这种推理方法中，前提和结论之间的关系是基于某种条件或假设。

简单来说，假言判断推理是一种根据已知条件推导出新结论的推理方式。

2.假言判断推理的公式和符号表示
在假言判断推理中，我们通常使用“如果…那么…”这样的表述来表示前提和结论之间的关系。

在逻辑符号中，我们用“→”表示这种关系，其中“→”左边的陈述是前提，右边的陈述是结论。

例如，如果 A→B，表示如果 A 成立，那么 B 就成立。

除了“如果…那么…”这种表述，假言判断推理还有其他形式，如“只要…就…”（表示充分条件）和“只有…才…”（表示必要条件）。

在逻辑符号中，我们分别用“”和“”表示充分条件和必要条件。

3.假言判断推理的例子和应用
假言判断推理在日常生活和学术研究中都有广泛的应用。

以下是一个简单的例子：
前提：如果你吃多了，那么会觉得肚子疼。

结论：如果你觉得肚子疼，那么你一定吃多了。

在这个例子中，前提和结论之间的关系是充分条件。

也就是说，如果你吃多了，那么会觉得肚子疼，但如果你觉得肚子疼，并不能确定你一定吃多了，因为肚子疼还可能有其他原因。

假言判断推理在数学、物理、化学等科学领域以及法律、经济学等社会科学领域都有广泛应用。

离散数学假言三段论假言三段论在离散数学中是一种重要的推理方式。

其形式为：如果A成立，那么B成立；如果B成立，那么C成立。

因此，如果A成立，那么C也成立。

在这种推理方式中，A、B、C都是命题，每个命题都有T（真）和F（假）两种可能性。

为了更好地理解假言三段论，我们可以通过具体的例子来解释。

比如说，如果我明天放假，那么我会去旅行；如果我去旅行，那么我会拍照。

据此，我们可以得出结论：如果我明天放假，那么我会拍照。

这个结论是正确的吗？我们可以通过列出真值表进行判断：假定明天放假为真，那么我会去旅行为真，我会拍照为真，结论为真。

（如果我放假，我一定会去旅行，并且旅行的时候我会拍照。

）假定明天放假为假，结论为真。

（这种情况下结论可以是任何值，因为条件不成立。

）因此，我们可以得知，假言三段论并不是一定正确的推理方式，它的正确性取决于前提的真假。

在上述例子中，只有当我明天放假并且去旅行的情况下，才能得到正确的结论。

在离散数学中，假言三段论有着广泛的应用。

例如，在逻辑门电路设计中，如果我们想要设计一个与门，就可以使用假言三段论的推理方式。

我们可以假设两个输入信号为A和B，如果A=1，那么与门的输入信号也为1；如果与门的输入信号为1，那么输出信号为1。

因此，我们可以得出结论：如果A=1，那么与门的输出信号也为1。

这个结论也是正确的。

除了逻辑门设计，假言三段论也可以用于证明数学定理。

例如，欧几里得的算法定理（即最大公因数定理）可以通过假言三段论来证明。

该定理的形式如下：如果a和b是正整数，那么a和b的最大公因数等于b和a mod b的最大公因数。

我们可以使用假言三段论来证明该定理：假设a和b的最大公因数为d，那么我们可以表示a=md、b=nd（其中m和n是互质的正整数）。

根据定义，我们可以得到a mod b=a-kb，其中k是一个正整数。

因此，a=nb+(m-nk)d，意味着d是a和b的公因数，也是b和a mod b的公因数。

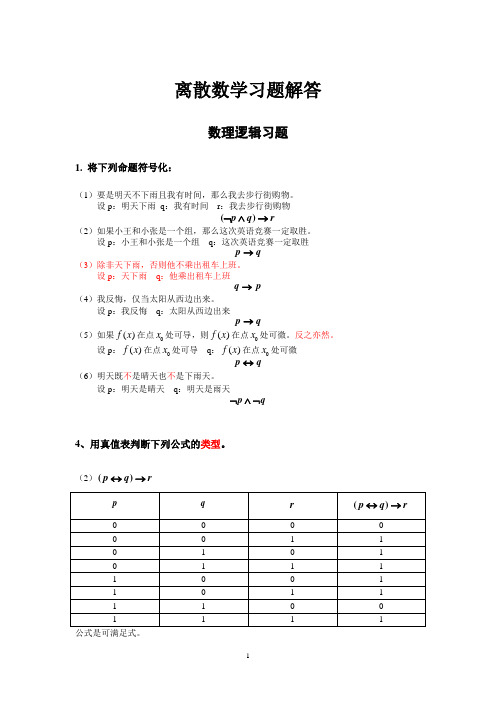
数理逻辑习题判断题1．任何命题公式存在惟一的特异析取范式 （ √ ） 2． 公式)(q p p →⌝→是永真式 （ √ ） 3．命题公式p q p →∧)(是永真式 （ √ ） 4．命题公式r q p ∧⌝∧的成真赋值为010 （ × ） 5．))(()(B x A x B x xA →∃=→∀ （ √ ）6．命题“如果1＋2＝3，则雪是黑的”是真命题 （ × ） 7．p q p p =∧∨)( （ √ ）8．))()((x G x F x →∀是永真式 （ × ） 9．“我正在撒谎”是命题 （ × ） 10． )()(x xG x xF ∃→∀是永真式（ √ ）11．命题“如果1＋2＝0，则雪是黑的”是假命题 （ × ） 12．p q p p =∨∧)( （ √ ）13．))()((x G x F x →∀是永假式 （ × ）14．每个命题公式都有唯一的特异（主）合取范式 （ √ ） 15．若雪是黑色的:p ，则q →p 公式是永真式 （ √ ） 16．每个逻辑公式都有唯一的前束范式 （ × ） 17．q →p 公式的特异（主）析取式为q p ∨⌝ （ × ） 18．命题公式 )(r q p →∨⌝的成假赋值是110 （ √ ） 19．一阶逻辑公式)),()((y x G x F x →∀是闭式（ × ）单项选择题1． 下述不是命题的是（ A ）A．花儿真美啊! B．明天是阴天。

C．2是偶数。

D．铅球是方的。

2．谓词公式（∀y）（∀x）（P（x）→R（x,y））∧∃yQ（x,y）中变元y （B）A．是自由变元但不是约束变元B．是约束变元但不是自由变元C．既是自由变元又是约束变元D．既不是自由变元又不是约束变元3．下列命题公式为重言式的是（ A ）A．p→ （p∨q）B．（p∨┐p）→qC．q∧┐q D．p→┐q4．下列语句中不是．．命题的只有（A ）A．花儿为什么这样红？B．2+2=0C．飞碟来自地球外的星球。

离散数学（一）知识梳理逻辑和证明部分命题逻辑题型命题符号化问题将自然语言转为符号化逻辑命题用命题变量来表示原子命题用命题联结词来表示连词命题公式的类型判断判断命题公式是否是永真式、矛盾式、可能式利用真值表判断利用已知的公式进行推理判断利用主析取和合取范式判断定理：A为含有n个命题变元的命题公式，若A的主析取范式含有2^n个极小项，则A为重言式，若极小项在0到2^n之间，则为可满足式，若含有0个极小项，则A为矛盾式；若A的主合取范式含有2^n个极大项，则A为矛盾式，若极小项在0到2^n之间，则为可满足式，若含有0个极小项，则A为重言式翻译：一个命题公式化成主范式后，若所有项都分布在主析取范式中（主合取范式为1）则为重言式；若所有项都分布在主合取范式中（主析取范式为0）则为矛盾式；若均有分布，则为可满足式。

【思想来源：真值表法求主范式】一个质析取式是重言式的充要条件是其同时含有某个命题变元及其否定式；一个质合取式是矛盾式的充要条件是其同时含有某个命题变元及其否定式一个析取范式是矛盾式当且仅当它的每项都是矛盾式；一个合取范式是重言式当且仅当它的每项都是重言式求（主）析取或合取范式等值演算法1. 利用条件恒等式消除条件（蕴含和双条件）联结词，化简得到一个范式2. 在缺项的质项中不改变真值地添加所缺项，化简得到一个主范式3. 找出包含所有命题变元排列中剩余项，凑出另一个主范式（思想上类似于真值表法）真值表法1. 画出命题公式真值表2. 根据真值表结果求出主范式主析取范式：真值为1的所有项，每一项按对应01构成极小项主合取范式：真值为0的所有项，每一项按对应01构成极大项形式证明与命题推理利用推理规则构造一个命题公式的序列，证明结论形式证明：命题逻辑的论证是一个命题公式的序列，其中每个公式或者是前提，或者是由它之前的公式作为前提推得的结论，序列的最后一个是待证的结论，这样的论证也称为形式证明。

核心方法把非条件语句全部转为条件语句利用条件的逆否命题和双条件的拆分利用重言式/矛盾式来不改变真值地添项蕴含证明规则：A1,A2, …, An⇒ A → B 等价于A1,A2, …,An,A⇒ B【意义：使用结论的前提时应标为附加前提】（适用：结论为条件语句）反证法：若要证A1,A2, …, An⇒ B，将ØB加入前提，通过证明：A1,A2, …, An, ØB⇒ C, ØC完成证明。

离散数学重点笔记第一章，0命题逻辑素数=质数，合数有因子和或假必真同为真(p T q) A (q <--> r) , (p A q) An r, p A (q An r)等都是合式公式，而若公式A是单个的命题变项，则称A为0层合式n p A q) T r , (n (p q)) A ((r V s)斥甬p)分别为3层和4层公式r, ( p r (r T q)等不是合式公式。

p A q) Tn r【例】求下列公式的真值表，并求成真赋值和成假赋值。

公式(1)的成假赋值为011，其余7个赋值都是成真赋值(1)双重否定律(2)等幂律A A; A V(3)交换律A A A A ; A V V A(4) 结合律(A A B) A A(BA C);(5) 分配律(A A B)V C(A V C)A(B V C)(6) 德•摩根律(A V B)A A B;(7) 吸收律A V( A A B)A; A A(A V B)(8)零一律A V 1 1 ； A A 00(9) 同一律A V 0A A A 1A(10) 排中律A V A1(11) 矛盾律A A A0(12) 蕴涵等值式A T V B(13) 假言易位A T A(14) 等价等值式(A T B)A( B T A)第二章，命题逻辑等值演算A(A V B)V；(A V B)(A A B)V( B V C)A C (A A C) V(B A C)A V B离散数学重点笔记(15) 等价否定等值式 (16) 归缪式 (A T B )A( A TB )A一个析取范式是矛盾式当且仅当它的每个简单合取式都是矛盾式 一个合取范式是重言式当且仅当它的每个简单析取式都是重言式 主范式【A 小真，V 大假】 A 成真 小写极小项极大项1 盘我真赋值 名称舍式1成假赋值 名称-1 pA~i qA~i T 0 0 0P V<J V TI 0 0 0 n pAn 小工0 0 1pVqVn r 0 0 1 pAqAn T 0 1 0 血2 pV n qVr 0 1 0 n P A<I A T 0 1 1 口3 pVn qVn T 0 1 1pAn 10 0n pV-iVr 10 0 P A~I 1 0 1TLI5 1 pVqVn T 1 0 1 r 1 1 0 ms t pVn qVr 1 1 0 pA-qAr111 IDy n pVn aVn r ill【例】(p T q)T (n qp) =n (n p V q) V (q V n =(p An q) Vn p V q =(p An q) V (n p Anp) (消去宀) (n 内移)(已为析取范式) q) V (n p A q) V (n p A q) V (p A q) ( *) = m2 V m0 V ml V ml V m3 =m0 V ml V m2 V m3(幂等律、排序) (*)由n p 及q 派生的极小项的过程如下: n p = n p A (n q V q) =(n p An q)V (n p A q)q = (n p V p) A q =(n p A q) V (p A q)熟练之后，以上过程可不写在演算过程中。

离散数学证明题解题方法（5篇范例）离散数学是现代数学的一个重要分支，是计算机科学中基础理论的核心课程。

离散数学以研究离散量的结构和相互间的关系为主要目标，其研究对象一般地是有限个或可数个元素，因此他充分描述了计算机科学离散性的特点。

1、定义和定理多。

离散数学是基于大量定义的逻辑推理学科。

所以，理解概念是我们学习这门学科的核心。

在这些概念的基础上，要特别注意概念之间的关系，描述这些关系的实体是大量的定理和性质。

●证明等价关系：即要证明关系有自反、对称、传递的性质。

●证明偏序关系：即要证明关系有自反、反对称、传递的性质。

（特殊关系的证明就列出来两种，要证明剩下的几种只需要结合定义来进行）。

●证明满射：函数f：XY，即要证明对于任意的yY，都有x或者对于任意的f(x1)=f(x2)，则有x1=x2。

●证明集合等势：即证明两个集合中存在双射。

有三种情况：第一、证明两个具体的集合等势，用构造法，或者直接构造一个双射，或者构造两个集合相互间的入射；第二、已知某个集合的基数，如果为א，就设它和R之间存在双射f，然后通过f 的性质推出另外的双射，因此等势；如果为א0，则设和N之间存在双射；第三、已知两个集合等势，然后再证明另外的两个集合等势，这时，先设已知的两个集合存在双射，然后根据剩下题设条件证明要证的两个集合存在双射。

●证明群：即要证明代数系统封闭、可结合、有幺元和逆元。

（同样，这一部分能够作为证明题的概念更多，要结合定义把它们全部搞透彻）。

●证明子群：虽然子群的证明定理有两个，但如果考证明子群的话，通常是第二个定理，即设<g,*>是群，S是G的非空子集，如果对于S中的任意元素a和b有a*b-1是<g,*>的子群。

对于有限子群，则可考虑第一个定理。

●证明正规子群：若<g,*>是一个子群，H是G的一个子集，即要证明对于任意的aG，有aH=Ha，或者对于任意的hH，有a-1 *h*aH。

推理理论中的推理规则（离散数学）推理理论是一个研究推理方法与规则的学问，其中推理规则是重要的一部分。

推理规则是指在一定的条件下，由一个或多个命题出发，推出另一个命题的规则。

在离散数学中，推理规则包括一些基础的规则和一些复杂的规则。

1. 充分必要条件充分必要条件是指一个命题P能成立的充分必要条件是命题Q 成立。

即P⇔Q。

这里的充分必要条件是指两个命题是等价的，即当且仅当P成立时Q成立，Q成立时P也成立。

例如，一个三角形是等腰三角形的充分必要条件是它有两个相等的角。

2. 反证法反证法是一种常用的推理规则，它常用于证明一个命题的反命题成立。

即假设命题P不成立，通过推理得到矛盾，从而证明了P成立。

例如，证明“所有偶数都不是素数”这个命题可以采用反证法，假设有一个偶数是素数，然后推导出矛盾，从而证明“所有偶数都不是素数”。

3. 等价变形等价变形是指在推理过程中将命题变形成等价的命题。

例如，将P∧Q推导为Q∧P是一种等价变形。

等价变形可以通过逻辑符号的转换、语法规则的变换等方式实现。

4. 全称推理全称推理是指从一个全称命题出发，推出另一个全称命题。

例如，从“对于任意一个自然数n，n+1>n”这个全称命题可以推出“对于任意一个自然数m，m+2>m”。

5. 假言推理假言推理是指从一个条件命题和它的前件出发，推出它的后件的命题。

例如，从“如果今天下雨，那么他就不去逛公园。

今天不下雨”这两个命题可以推出“他会去逛公园”。

6. 假命题推理假命题推理是指从一个假命题出发进行推理，最终得到矛盾。

例如，从假设“1=2”出发，我们可以通过推导得到矛盾，并证明1不等于2。

7. 归谬法归谬法是指从前提推导出矛盾的方法，一般用于证明前提错误的情况。

例如，如果要证明“所有汉语拼音都是辅音加韵母”这个命题是错误的，可以通过归谬法证明，即找出一个汉语拼音不符合这个规则。

8. 消解法消解法是推理中常用的一种方法，可用于在两个命题中推导得到新的命题。

3.9解：符号化：p：a是奇数. q：a是偶数. r：a能被2整除前提：(p→¬r),(q→r)结论：(q→¬p)证明：确。

方法2（等值演算法）(p→¬r)∧(q→r)→(q→¬p)⇔(¬p∨¬r)∧(¬q∨r) →(¬q∨¬p)⇔(p∧r) ∨(q∧¬r) ∨¬q∨¬p⇔((p∧r) ∨¬p)∨((q∧¬r) ∨¬q)⇔(r∨¬p) ∨(¬r∨¬q)⇔¬p∨(r∨¬r) ∨¬q⇔ 1即证得该式为重言式，则原结论正确。

方法3（主析取范式法）(p→¬r)∧(q→r)→(q→¬p)⇔(¬p∨¬r)∧(¬q∨r) →(¬q∨¬p)⇔(p∧r) ∨(q∧¬r) ∨¬q∨¬p⇔m0+ m1+ m2+ m3+ m4+ m5+ m6+ m7可知该式为重言式，则结论推理正确。

3.10. 解：符号化：p：a是负数. q：b是负数. r：a、b之积为负前提：r→(p∧¬q) ∨(¬p∧q)结论：¬r→(¬p∧¬q)方法1（真值法）证明：不正确。

方法2（主析取范式法）证明：(r→(p∧¬q) ∨(¬p∧q))→(¬r→(¬p∧¬q))⇔¬ (¬r∨(p∧¬q) ∨(¬p∧q))∨(r∨(¬p∧¬q))⇔r∨(¬p∧¬q)⇔m0+m2+m4+m6+m7只含5个极小项，课件原始不是重言式，因此推理不正确3.11.填充下面推理证明中没有写出的推理规则。

假言推理定律
假言推理定律是一种逻辑推理规则，用于推导假言命题之间的关系。

假言命题是一个条件语句，形式为“如果A，则B”。

假言推理定律有以下几种形式：
1. 假言三段论定律（Modus Ponens）：如果有一个条件语句“If A, then B”为真，且前提A为真，则结论B也为真。

符号表示为：“A→B, A ⊢ B”。

例如，如果有一个假设：“如果下雨，那么路会湿”，并且已经确定“下雨”为真，则可以推论出“路会湿”为真。

2. 反证法定律（Modus Tollens）：如果有一个条件语句“If A, then B”为真，且结论B为假，则可以推断出前提A为假。

符号表示为：“A→B, ¬B ⊢ ¬A”。

例如，如果有一个假设：“如果这个电路正常工作，那么指示灯会亮”，并且已经确定“指示灯不亮”为真，则可以推论出“电路不正常工作”为真。

3. 寻常假设法定律（Hypothetical Syllogism）：如果有两个条件语句“A→B”和“B→C”为真，则可以推断出条件语句“A→C”也为真。

符号表示为：“A→B, B→C ⊢ A→C”。

例如，如果有两个假设：“如果天气晴朗，那么我会去公园”和“如果我去公园，那么我会玩得开心”，则可以推论出“如果天
气晴朗，那么我会玩得开心”为真。

这些假言推理定律是逻辑推理中经常使用的推理规则，可以帮助我们在给定条件下推导出新的结论。

量词的辖域定义:量词的辖域是邻接量词之后的最小子公式，故除非辖域是个原子公式，否则应在该子公式的两端有括号。

例：∀XP(X)→Q(X)∀X的辖域是P(X)∃X(P(X,Y)→Q(X，Y) ) ∨ P(Y,Z)∃X的辖域是P(X，Y)→Q(X，Y)有限个体域上消去量词例15: 个体域D={a,b,c}, 则消去下面公式中的量词∃x∀yF(x,y)⇔∃x (F(x,a)∧F(x,b)∧F(x,c))⇔ (F(a,a)∧F(a,b)∧F(a,c))∨(F(b,a)∧F(b,b)∧F(b,c))∨(F(c,a)∧F(c,b)∧F(c,c)) 例16：设个体域D={a,b}，消去下面各公式中的量词：(1) ∀x∃y(F(x) →G(y)) ⇔∀x(F(x)→∃y G(y))⇔∃xF(x)→∃y G(y) ⇔ (F(a)∨F(b))→(G(a)∨G(b))(2) ∀x∃y(F(x,y) →G(x,y))⇔∀x((F(x,a) →G(x,a))∨(F(x,b)→G(x,b))⇔((F(a,a) →G(a,a))∨(F(a,b)→G(a,b)))∧((F(b,a) →G(b,a))∨(F(b,b)→G(b,b)))注：(1)中量词辖域可以缩小，先缩小量词辖域，再消量词，演算简单；但在(2)中，因为全称量词和存在量词均约束F与G中个体变量，因而它们的辖域不能缩小，消去量词后的公式也不易化的更简单。

例17 将下面命题用两种形式符号化, 并证明两者等值:(1) 没有不犯错误的人解令F(x)：x是人，G(x)：x犯错误.⌝∃x(F(x)∧⌝G(x)) 或∀x(F(x)→G(x⌝∃x(F(x)∧⌝G(x))⇔∀x⌝(F(x)∧⌝G(x)) 量词否定等值式⇔∀x(⌝F(x)∨G(x)) 置换⇔∀x(F(x)→G(x)) 置换(2) 不是所有的人都爱看电影解令F(x)：x是人，G(x)：爱看电影.⌝∀x(F(x)→G(x)) 或∃x(F(x)∧⌝G(x))⌝∀x(F(x)→G(x))⇔∃x⌝(F(x)→G(x)) 量词否定等值式⇔∃x⌝(⌝F(x)∨G(x)) 置换⇔∃x(F(x)∧⌝G(x)) 置换例18 求下列公式的前束范式(1) ⌝∃x(M(x)∧F(x))解⌝∃x(M(x)∧F(x))⇔∀x(⌝M(x)∨⌝F(x)) （量词否定等值式）⇔∀x(M(x)→⌝F(x))后两步结果都是前束范式，说明公式的前束范式不惟一.(2) ∀xF(x)∧⌝∃xG(x)解∀xF(x)∧⌝∃xG(x)⇔∀xF(x)∧∀x⌝G(x) （量词否定等值式）⇔∀x(F(x)∧⌝G(x)) （量词分配等值式）或∀xF(x)∧⌝∃xG(x)⇔∀xF(x)∧∀x⌝G(x) 量词否定等值式⇔∀xF(x)∧∀y⌝G(y) 换名规则⇔∀x∀y(F(x)∧⌝G(y)) 辖域收缩扩张规则(3) ∀xF(x)→∃y(G(x,y)∧⌝H(y))解∀xF(x)→∃y(G(x,y)∧⌝H(y))⇔∀zF(z)→∃y(G(x,y)∧⌝H(y)) 换名规则⇔∃z∃y(F(z)→(G(x,y)∧⌝H(y))) 辖域收缩扩张规则或⇔∀xF(x)→∃y(G(z,y)∧⌝H(y)) 代替规则⇔∃x∃y(F(x)→(G(z,y)∧⌝H(y)))推理定理第一组命题逻辑推理定理的代换实例如, ∀xF(x)∧∃yG(y) ⇒∀xF(x)第二组基本等值式生成的推理定理如, ∀xF(x) ⇒⌝⌝∀xF(x), ⌝⌝∀xF(x) ⇒∀xF(x)⌝∀xF(x)⇒∃x⌝F(x), ∃x⌝F(x) ⇒⌝∀xF(x)第三组其他常用推理定律(1) ∀xA(x)∨∀xB(x) ⇒∀x(A(x)∨B(x))(2) ∃x(A(x)∧B(x))⇒∃xA(x)∧∃xB(x)(3) ∀x(A(x)→B(x)) ⇒∀xA(x)→∀xB(x)(4) ∃x(A(x)→B(x)) ⇒∃xA(x)→∃xB(x)一个公式如果它的所有量词均非否定的出现在公式的最前面，且它们的辖域一直延伸到公式的末尾，此种形式的公式就叫前束范式。

离散数学推理证明1、在自然推理系统F中，构造下面推理的证明不存在能表示成分数的无理数，有理数都能表示成分数。

因此，有理数都不是无理数。

个体域为实数集合。

令F ( x ) : x F(x):xF(x):x是无理数G ( x ) : x G(x):xG(x):x是有理数H ( x ) : x H(x):xH(x):x能表示成分数命题符号化：不存在能表示成分数的无理数：¬ ∃x ( H ( x ) ∧F ( x ) ) \lnot \exist x (H(x) \wedge F(x))¬∃x(H(x)∧F(x))有理数都能表示成分数：∀x ( G ( x ) →H ( x ) ) \forall x(G(x)\rightarrow H(x))∀x(G(x)→H(x))有理数都不是无理数：∀x ( G ( x ) →¬ F ( x ) ) \forall x(G(x) \rightarrow \lnot F(x))∀x(G(x)→¬F(x))证明：（1）¬ ∃x ( H ( x ) ∧F ( x ) ) \lnot \exist x (H(x) \wedge F(x))¬∃x(H(x)∧F(x))（2）∀x ( ¬ H ( x ) ∨¬ F ( x ) ) \forall x (\lnot H(x) \vee \lnot F(x))∀x(¬H(x)∨¬F(x)) 量词转换、摩根律（3）¬ H ( a ) ∨¬ F ( a ) \lnot H(a) \vee \lnot F(a)¬H(a)∨¬F(a) 去掉全称量词（4）H ( a ) →¬ F ( a ) H(a) \rightarrow \lnot F(a)H(a)→¬F(a)（5）∀x ( G ( x ) →H ( x ) ) \forall x(G(x)\rightarrow H(x))∀x(G(x)→H(x))（6）G ( a ) →H ( a ) ) G(a)\rightarrow H(a))G(a)→H(a)) 去掉全称量词（7）G ( a ) →¬ F ( a ) G(a) \rightarrow \lnot F(a)G(a)→¬F(a) (4)与(6)（8）∀x ( G ( x ) →¬ F ( x ) ) \forall x(G(x) \rightarrow \lnot F(x))∀x(G(x)→¬F(x)) 添加全称量词2、在自然推理系统中，构造下面推理的证明任何自然数都是整数；存在着自然数。