【推荐】北师大初中数学中考总复习：实数--知识讲解(基础)

实数的运算知识梳理 1．知识结构2．知识要点在实数范围内，加、减、乘、除、乘方运算都可以进行，但开方运算不一定能行，如负数不能开偶次方。

实数的运算基础是有理数运算，有理数的一切运算性质和运算律都适用于实数运算。

正确的确定运算结果的符号和灵活的使用运算律是掌握好实数运算的关键。

3．中考预测对于实数运算的考查，是考查“双基”的重要体现，其题型主要有选择题、填空题、解答题。

近几年题型变化比较大，创设了一些新的情境，考查学生灵活运用所学知识的能力，需要将问题化为熟知的知识来处理，仅凭死记或套用模式是不行的，并且对于运算的考查，降低了运算的难度，并避免出现繁难的计算或有意编造的偏题。

解题指导例1 （1）计算：(-3)2-1= ；（2）计算：（2－3）2004·（2+3）2005=______；（3）计算：102)14.3(-+-π+____________（4）下列运算中，错误的有_____________________（只填序号）①1251144251=，②4)4(2±=-，③22222-=-=-，④2095141251161=+=+分析：本题是对实数的基本运算的考查，应准确把握实数的各种运算法则和运算律。

解答：（1）8；（2）2+3；（3）23；（4）①、③、④。

点评：以填空题、选择题形式出现的实数的运算问题比较简单，应以运算法则和性质为依据，细心计算，不难做对。

拓广：（1）计算：()12-=___________；（2）计算： －3＋|－1| ＝________； （3）计算： 45sin 281++-=_________.解：（1）1；（2）－2；（3）2251+。

例2：计算：实数的运算加、减、乘、除、乘方、开方运算法则运算律（1）（-2）3+21（2004-3）0-|-21|； （2）－22+ (12－1 )0+ 2sin30º（3）102)121()52()21(1)2(2--+--++－分析：混合运算，除了要注意每一种运算法则之外，更要注意运算顺序及符号的确定。

中考北师大版数学知识点总结一、数与代数1. 实数- 有理数和无理数统称为实数。

有理数包括整数（正整数、0、负整数）和分数（有限小数和无限循环小数）；无理数是无限不循环小数，如√(2)，π等。

- 实数的运算：- 加法：同号两数相加，取相同的符号，并把绝对值相加；异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值；互为相反数的两个数相加得0。

- 减法：减去一个数等于加上这个数的相反数。

- 乘法：两数相乘，同号得正，异号得负，并把绝对值相乘；任何数与0相乘都得0。

- 除法：除以一个数等于乘以这个数的倒数（除数不能为0）。

- 乘方：a^n表示n个a相乘，其中a是底数，n是指数。

- 实数的大小比较：- 正数大于0，0大于负数，正数大于负数。

- 两个正数比较大小，绝对值大的数大；两个负数比较大小，绝对值大的反而小。

- 数轴上右边的数总比左边的数大。

2. 代数式- 用运算符号（加、减、乘、除、乘方、开方）把数或表示数的字母连接而成的式子叫做代数式，单独的一个数或者一个字母也是代数式。

- 整式：单项式和多项式统称为整式。

- 单项式：由数与字母的积组成的代数式叫做单项式，单独的一个数或一个字母也是单项式。

单项式中的数字因数叫做单项式的系数，一个单项式中，所有字母的指数的和叫做这个单项式的次数。

- 多项式：几个单项式的和叫做多项式。

其中每个单项式叫做多项式的项，不含字母的项叫做常数项。

多项式里次数最高项的次数，叫做这个多项式的次数。

- 整式的加减：- 合并同类项：所含字母相同，并且相同字母的指数也相同的项叫做同类项。

合并同类项就是把同类项的系数相加，字母和字母的指数不变。

- 去括号法则：括号前面是“+”号，把括号和它前面的“+”号去掉后，原括号里各项的符号都不改变；括号前面是“ - ”号，把括号和它前面的“ - ”号去掉后，原括号里各项的符号都要改变。

- 整式的乘除：- 幂的运算性质：- 同底数幂相乘：a^m· a^n = a^m + n（m，n为正整数）。

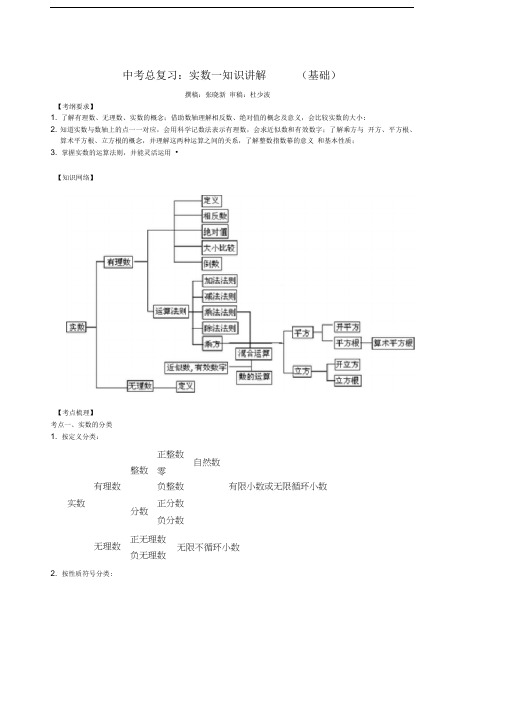
中考总复习：实数一知识讲解（基础）撰稿：张晓新审稿：杜少波【考纲要求】1. 了解有理数、无理数、实数的概念；借助数轴理解相反数、绝对值的概念及意义，会比较实数的大小;2. 知道实数与数轴上的点一一对应，会用科学记数法表示有理数，会求近似数和有效数字；了解乘方与开方、平方根、算术平方根、立方根的概念，并理解这两种运算之间的关系，了解整数指数幕的意义和基本性质；3. 掌握实数的运算法则，并能灵活运用•【知识网络】【考点梳理】考点一、实数的分类1. 按定义分类：2. 按性质符号分类:整数正整数零自然数有理数负整数有限小数或无限循环小数实数分数正分数负分数无理数正无理数负无理数无限不循环小数负无理数无理数：无限不循环小数叫无理数. 实数：有理数和无理数统称为实数. 要点诠释： 常见的无理数有以下几种形式：(1)字母型：如n 是无理数， 一、一等都是无理数，而不是分数；2 4(2) 构造型：如2.100…(每两个1之间依次多一个 0)就是一个无限不循环的小数； (3) 根式型：…都是一些开方开不尽的数；(4) 三角函数型：sin35 °、tan 27 °、cos29。

等.考点二、实数的相关概念1. 相反数(1)代数意义：只有符号不同的两个数，我们说其中一个是另一个的相反数.0的相反数是0;(2) 几何意义：在数轴上原点的两侧，与原点距离相等的两个点表示的两个数互为相反数； (3)互为相反数的两个数之和等于 0.a 、b 互为相反数 a+b=0.2. 绝对值(1)代数意义：正数的绝对值是它本身；负数的绝对值是它的相反数；0的绝对值是0.a(a 0) 可用式子表示为：|a(a 0)a (a 0)tr(2)几何意义：一个数 a 的绝对值就是数轴上表示数 a 的点与原点的距离.距离是一个非负数，所 以绝对值的几何意义本身就揭示了绝对值的本质，即绝对值是一个非负数.用式子表示：若a 是实数，则|a| > 0. 要点诠释：若a a,则a 0； a -a,则a 0； a-b 表示的几何意义就是在数轴上表示数a 与数b 的点之间的距离.3. 倒数1(1) 实数a(a 0)的倒数是一；0没有倒数；正实数正有理数 正整数 正分数实数零负实数正无理数负有理数 负整数 负分数有理数：整数和分数统称为有理数或者“形如m(m n 是整数n ^O )”的数叫有理数.na(2)乘积是1的两个数互为倒数.a、b互为倒数a b 1.4. 平方根(1)如果一个数的平方等于a，这个数就叫做a的平方根.一个正数有两个平方根，它们互为相反数;0有一个平方根，它是0本身；负数没有平方根. a (a> 0)的平方根记作.a .(2)一个正数a的正的平方根，叫做a的算术平方根.a (a>0)的算术平方根记作.a .5. 立方根如果x3=a，那么x叫做a的立方根.一个正数有一个正的立方根；一个负数有一个负的立方根；0的立方根仍是0.考点三、实数与数轴规定了原点、正方向和单位长度的直线叫做数轴，数轴的三要素缺一不可.每一个实数都可以用数轴上的一个点来表示，反过来，数轴上的每一个点都表示一个实数.要点诠释：(1)数轴的三要素：原点、正方向和单位长度(2) -------------------------------------- 实数和数轴上的点是对应的.考点四、实数大小的比较1. 对于数轴上的任意两个点，靠右边的点所表示的数较大2. 正数都大于0,负数都小于0,正数大于一切负数；两个负数；绝对值大的反而小3. 对于实数a、b,若a-b>0 a>b; a-b=0 a=b；a-b<0 a<b.4. 对于实数a, b, c,若a>b, b>c，贝U a>c.5. 无理数的比较大小：利用平方转化为有理数：如果a>b>0, a 2>b2a>b . a . b ；或利用倒数转化：如比较17 4与4 .15.要点诠释：实数大小的比较方法：(1)直接比较法：正数都大于0,负数都小于0，正数大于一切负数；两个负数，绝对值大的反而小.(2)数轴法：在数轴上，右边的数总比左边的数大考点五、实数的运算1. 加法同号两数相加，取相同的符号，并把绝对值相加；绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值；互为相反数的两个数相加得0；一个数同0相加,仍得这个数.满足运算律：加法的交换律a+b=b+a，加法的结合律(a+b)+c=a+(b+c).2. 减法减去一个数等于加上这个数的相反数.3. 乘法两数相乘，同号得正，异号得负，并把绝对值相乘几个非零实数相乘，积的符号由负因数的个数决定，当负因数有偶数个时，积为正；当负因数有奇数个时，积为负.几个数相乘，有一个因数为0，积就为0.乘法运算的运算律：(1)乘法交换律ab=ba ； (2)乘法结合律(ab)c=a(bc) ； (3)乘法对加法的分配律a(b+c)=ab+ac .4. 除法(1)除以一个数，等于乘上这个数的倒数.(2)两个数相除，同号得正，异号得负，并把绝对值相除.0除以任何一个不等于0的数都得0.5. 乘方与开方(1)求n个相同因数的积的运算叫做乘方，a n所表示的意义是n个a相乘. 正数的任何次幕是正数，负数的偶次幕是正数，负数的奇次幕是负数.(2)正数和0可以开平方，负数不能开平方；正数、负数和0都可以开立方.1(3)零指数与负指数a0 1(a^0), a p --(a^0).a p要点诠释：加和减是一级运算，乘和除是二级运算，乘方和开方是三级运算. 这三级运算的顺序是三、二、一•如果有括号，先算括号内的；如果没有括号，同一级运算中要从左至右依次运算.考点六、有效数字和科学记数法一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位•一个近似数，从左边第一个不是0的数字起，到精确到的数位为止，所有的数字，都叫做这个近似数的有效数字.精确度的形式有两种：(1 )精确到哪一位；(2)保留几个有效数字.把一个数用土a x 10n (其中1w£|v 10, n为整数)的形式记数的方法叫科学记数法.要点诠释：(1)当要表示的数的绝对值大于1时，用科学记数法写成a x 10n，其中K a v 10, n 为正整数，其值等于原数中整数部分的数位减去1;(2)当要表示的数的绝对值小于1时，用科学记数法写成a x 10n，其中K a v 10, n 为负整数，其值等于原数中第一个非零数字前面所用零的个数的相反数(包括小数点前面的零)【典型例题】类型一、实数的有关概念1. (1) a的相反数是丄，则a的倒数是5(2)实数a、b在数轴上对应点的位置如图所示：则化简J(a+ b)2= _______________ .* «* b 0 a(3) (泉州市)去年泉州市林业用地面积约为10200000亩，用科学记数法表示为约 _____________________ . 【答案】(1) 5 ; (2) -a-b ; ( 3) 1.02 x 107亩.【解析】(1 )注意相反数和倒数概念的区别，互为相反数的两个数只有性质符号不同，互为倒数的两个数要改变分子分母的位置；或者利用互为相反数的两个数之和等于0,互为倒数的两个数乘积等于1来计算.(2)此题考查绝对值的几何意义，绝对值和二次根式的化简.注意要去掉绝对值符号，要判别绝对值内的数的性质符号.由图知：a 0,b 0, |a | | b |, a b 0, . (a b)2 |a b| (a b) a b.(3 )考查科学记数法的概念.【点评】本大题旨在通过几个简单的填空，让学生加强对实数有关概念的理解. 举一反三：【变式】据市旅游局统计，今年“五•一”小长假期间，我市旅游市场走势良好，假期旅游总收入达到8. 55亿元，用科学记数法可以表示为（ ）A . 8. 55X 106B . 8. 55X 107C . & 55X 108D . 8.55X 109【答案】C.类型二、实数的分类与计算举一反三：【高清课程名称： 实数 高清ID 号：369214 关联的位置名称(播放点名称)：经典例题1】【变式】在 3.14, . 8, . 4,( 3 2)°,n, cos30 , tan 45 , , 0.1010010001, 5 1, 3%, 0.31 中,2 7哪些是有理数？哪些是无理数？12【答案】3.14,「4, ( 32)0, tan 45 ,〒，5 1, 3%, 0.31 都是有理数；8, n, cos30o , 0.1010010001L ,都是无理数.23•计算：计算：(-1)2001(丄厂2(..3)0—2| .2【答案与解析】(—1 )2001 (2)—2 ")0—|—2|14 12 1【点评】该题是实数的混合运算，包括绝对值，0指数幕、负整数指数幕，正整数指数幕•只要准确把握各自的意义，就能正确的进行运算.举一反三：【高清课程名称：实数高清ID 号：369214关联的位置名称(播放点名称)：经典例题8-9】73A . 1B . 2C. 3D . 4【答案】 c.i【解析】 无理数有sin60 °、—、83【点评】 对实数进行分类不能只看表面 形式，应先化简，再根据结果去判断8 中无理数有()个22 0F 列实数 、sin 60 °、一、 、2 、3.14159、- . 9、 .72 2「3)2 (n 3.14)°8si n 45 .V【答案】—4【变式2】计算：2001 2002 2003 2004 1【答案】设n=2001，则原式=n(n 1)(n 2)(n 3) 1(n23n)(n2 3n 2) 1 (把n2+3n 看作一个整体)=(n2 3n)22( n2 3n) 1=n 2+3n+1=n(n+3)+1=2001 x 2004+1=4010005.1(1) 17 4 与4 .. 15 (2) a 与(0)a【答案与解析】(1) . 17 4 —10 , 4 .15 一1 ~如 4 4 V15而一17 4与4 .15可以很容易进行比较得到:.17 4 4 15 0 ,所以,17 4 4 15 ;1(2 )当a<-1 或O<a<1 时，a< -;a1当-1<a<0 或a>1 时，a> ;a当a= 1 时，a=1.a【点评】(1)有时无理数比较大小，通过平方转化以后也无法进行比较，那么我们可以利用倒数关系比【变式1】计算:类型三、实数大小的比较较；(2 )这道题实际上是互为倒数的两个数之间的比较大小，我们可以利用数轴进行比较，我们知道，0没有倒数，土1的倒数等于它本身，这样数轴就被这3个数分成了4部分，下面就可6 •细心观察图形，认真分析各式，然后解答问题以分类讨论每种情况•我们还可以利用函数图象来解决这个问题， 把1的值看成是关于a 的a反比例函数，把 a 的值看成是关于 a 的正比例函数，在坐标系中画出它们的图象，可以很 直观的比较出它们的大小.举一反三：【答案】(1 )将其通分，转化成同分母分数比较大小，17 85 11 8817 11840， 5 40， 8 5，1711所以852(2).2 . 57 2,10 7 ,40.3 227 4、3 7 48，所以.2类型四、平方根的应用【点评】此题考查的是非负数的性质类型五、实数运算中的规律探索【变式】 (1)比较下列每组数的大小:17 知 11 和 - 85(2) 、2 .5 和.3因为.40.48，y 是实数,.3x 4 y 2 6y9 0，若axy-3x=y ，则实数a 的值是【解析】3x 46y 9 0，即，3x 4 (y3)2 0两个非负数相加和为 •••、3x 40, (y-3) 2=0,又••• axy-3x=y , - a=逖0,则这两个非负数必定同时为4 •- x= , y=33 43(-)3.' 3 1 4 4 4 3 43yxy0,x ,1 2,S 52 22 2 1 3,S 22 32 1 4,S3 仝 2L L(1 )请用含有n (n 是正整数)的等式表示上述变化规律; (2) 推算出OA o 的长；(3) 求出 S 2+ S 22+ S 32+…+ S 102的值.【答案与解析】(1)由题意可知，图形满足勾股定理,(2)因为 OA= . 1 , OA= . 2 , OA F 3 …,所以OA o = 102222(3) S 1 + S 2 + S 3+…+ S 10=(」)2 (丄)2 (込2 (_!£)22 2 2 2 1= —(12 3 10)4=554【点评】 近几年各地的中考题中越来越多的出现了一类探究问题规律的题目，这些问题素材的选择、文字的表述、题型的设计不仅考察了数学的基础知识，基本技能，更重点考察了创新意识和能力,还考察了认真观察、分析、归纳、由特殊到一般，由具体到抽象的能力举一反三:【变式】图中是一幅“苹果图”，第一行有1个苹果，第二行有2个，第三行有4个，？第四行有8个,【答案】29( 512)A 2A 1。

初中数学知识点总结（中考复习用）（34页）第一章实数考点一、实数的概念及分类1、实数的分类正有理数厂有理数实数v匕无理数十"无限不循环小数「负无理数 」2、无理数 在理解无理数时，要抓住“无限不循环”这一时之，归纳起来有四类：（1）开方开不尽的数，如 、、7,32等；n（2） 有特定意义的数，如圆周率 n,或化简后含有 n 的数，如一+8等；3（3） 有特定结构的数，如 0.1010010001…等； （4）某些三角函数，如 sin60°等考点二、实数的倒数、相反数和绝对值1、 相反数：实数与它的相反数时一对数（只有符号不同的两个数叫做互为相反数，零的相反数是零），从数轴上看，互为相反数的两个数所对应的点关于原点对称，如果 a 与b 互为相反数，则有a+b=0, a= —b ,反之亦成立。

2、 绝对值：一个数的绝对值就是表示这个数的点与原点的距离，|a|为。

零的绝对值时它本身，也可 看成它的相反数， 若|a|=a ，则a%;若|a|=-a ，则a 切。

正数大于零，负数小于零，正数大于一切负数， 两个负数，绝对值大的反而小。

3、 倒数：如果a 与b 互为倒数，则有ab=1，反之亦成立。

倒数等于本身的数是1和-1。

零没有倒数。

考点三、平方根、算数平方根和立方根1、 平方根：如果一个数的平方等于 a ,那么这个数就叫做 a 的平方根（或二次方跟）。

一个数有两个平方根，他们互为相反数；零的平方根是零；负数没有平方根。

正数a 的平方根记做“ a ”。

2、 算术平方根：正数 a 的正的平方根叫做 a 的算术平方根，记作“ < a ”。

正数和零的算术平方根都只有一个，零的算术平方根是零。

厂 a （ a >0）厂、；a 兰 0■Va 2 = a = Y ；注意J；的双重非负性：Y--a （ a <0）- a -03、 立方根：如果一个数的立方等于a ,那么这个数就叫做 a 的立方根（或a 的三次方根）。

中考复习专用北师大版初中数学知识点总结北师大版初中数学是根据学生的认知心理特点和数学发展规律，注重培养学生数学思维能力和解决问题的能力，使数学学习真正走进学生日常生活中。

下面是北师大版初中数学的知识点总结。

一、整数和有理数1.整数的概念、相等和大小比较、绝对值。

2.整数的加、减、乘、除及分配率。

3.有理数的概念、加、减、乘、除运算规则。

4.实数的概念与分类。

二、平方根和立方根1.平方根的概念与性质。

2.平方根的运算与应用。

3.立方根的概念与性质。

4.立方根的运算与应用。

三、代数与方程式1.代数表达式的概念和表示方法。

2.一元一次方程的概念、解法及应用。

3.一元一次方程组的概念、解法及应用。

4.二元一次方程组的概念、解法及应用。

5.代数运算律与应用。

四、几何与图形1.点、线、线段、射线和角的概念与性质。

2.直角、锐角和钝角的概念与判别。

3.圆的性质与相关概念。

4.三角形的分类、性质和判定。

5.二次图形的性质与规律。

五、相似与全等1.图形的相似概念、判定及性质。

2.图形的全等概念、判定及性质。

六、比例与比例关系1.比例的概念与性质。

2.比例的四种特殊情况及应用。

3.相似比例的性质与应用。

七、图形的计算1.三角形的面积与计算公式。

2.平行四边形和梯形的面积与计算公式。

3.圆的面积与计算公式。

八、统计与概率1.数据的收集与整理。

2.数据的分组与统计方法。

3.统计图的制作与分析。

4.概率的概念与计算。

九、函数与图像1.函数的概念与性质。

2.函数的表示与运算。

3.函数的应用与意义。

4.图像的描述与应用。