固体物理学第二章

第21. 有一晶体,平衡时体积为 0V ， 原子间相互作用势为0.如果相距为 r 的两原子互作用势为 ()n m r r a r u β+-= 证明(1) 体积弹性模量为 K=.90V mnU (2) 求出体心立方结构惰性分子的体积弹性模量.[解答]设晶体共含有 N 个原子,则总能量为U(r)=()∑∑i jij r u '21. 由于晶体表面层的原子数目与晶体内原子数目相比小得多,因此可忽略它们之间的基异,于是上式简化为 U=().2'∑jijr u N设最近邻原子间的距离为R 则有j ij a r =R再令 A ,1'∑=j m j m a A ,1'∑=jn j n a 得到 U=.200⎪⎪⎭⎫ ⎝⎛+-n n m m R A R A N βα 平衡时R=R 0,则由已知条件U(R 0) = 0U 得0002U R A R A N n n m m =⎪⎪⎭⎫⎝⎛+-βα 由平衡条件 0)(0=R dRR dU得021010=⎪⎪⎭⎫⎝⎛-++n nm m R A n R A m N βα. 由(1),(2)两式可解得.)(2,)(20000n n m m nR n m N U A nR n m N U A -=-=βα利用体积弹性模量公式[参见《固体物理教程》(2.14)式]K=0220209R R U V R ⎪⎪⎭⎫ ⎝⎛∂∂得K= ⎥⎦⎤⎢⎣⎡+++-n n m m R A n n R A m m N V 000)1()1(291βα = ⎥⎦⎤⎢⎣⎡-++-+-)(2)1()(2)1(2910000000n m N mR U R n n n m N nR U R m m N V nnm m = .900V mn U - 由于,00<U 因此,00U U -= 于是 K= .90V mnU (1) 由《固体物理教程》(2.18)式可知,一对惰性气体分子的互作用能为.)(126r B r A r u +-=若令 61,42⎪⎭⎫⎝⎛==A B B A σε,则N 个惰性气体分子的互作用势能可表示为⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=6612122)(R A R A N r U σσε.由平衡条件0)(0=R dRR dU 可得 R .2616120⎪⎪⎭⎫ ⎝⎛=A A σ进一步得 .2)(122600A A N R U U ε-==代入K=.900V mn U 并取 m =6，n =12，V 300334R N =得 K=5126123233⎪⎪⎭⎫⎝⎛A A A σε.对体心立方晶体有 A .11.9,25.12126==A 于是.1.703σε=K 2. 一维原子链,正负离子间距为a ,试证:马德隆常数为2=μ1n2. [解答] 相距ij r 的两个离子间的互作用势能可表示成.4)(2n ijij ij r br q r u +=πμ设最近邻原子间的距离为R 则有 R a r j ij =, 则总的离子间的互作用势能 U=()∑∑∑-⎪⎪⎭⎫ ⎝⎛±-=jn jn j j j ij a bRa R q N r u N ''0'114[22πε. 基中 jja 1'±=∑μ 为离子晶格的马德隆常数,式中+;- 号分别对应于与参考离子相异和相同的离子.任选一正离子作为参考离子,在求和中对负离子到正号,对正离子取负号,考虑到对一维离子两边的离子是正负对称分布的,则有.413121112)1('⎥⎦⎤⎢⎣⎡+-+-=±=∑Λj ja μ利用正面的展开式 1n(1+x ),432432Λ+-+-x x x x 并令 1=x 得Λ+-+-41312111=1n(1+1)=1n2.于是,一维离子链的马德常数为2=μ1n23. 计算面心立方面简单格子的6A 和12A(1) 只计最近邻; (2) 计算到次近邻; (3) 计算到次近邻.[解答]图2.26示出了面心立方简单格子的一个晶胞.角顶O 原子周围有8个这样的晶胞,标号为1的原子是原子O 的最近邻标号为2的原子是O 原子的最近邻,标号为3的原子是O 原子的次次近邻.由此得到,面心立方简单格子任一原子有12个最近邻,6个次近邻及24个次次近邻.以最近邻距离度量,其距离分别为:.3,2,1===j j j a a a 由 .1,112'126'6⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=∑∑jj j j a A a A图2.6 面心立方晶胞得(1) 只计最近邻时1211*12)1(66=⎪⎭⎫⎝⎛=A ， 1211*12)1(1212\=⎪⎭⎫⎝⎛=A .(2) 计算到次近邻时.094.1221*611*12)2(,750.1221*611*12)2(121212666=⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛==⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=A A(3) 计算到次次近邻时.127.12033.0094.1231*2421*611*12)3(,639.13899.0750.1231*2421*611*12)3(121212126666=+=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛==+=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=A A 由以上可以看出,由于12A中的幂指数较大,12A 收敛得很快,而6A 中的幂指数较小,因此 6A 收敛得较慢,通常所采用的面心立方简单格子的 6A 和 12A 的数值分别是14.45与12.13.4. 用埃夫琴方法计算二维正方离子(正负两种)格子的马德隆常数. [解答]马德隆常数的定义式为 jja 1'±=∑μ,式中+、-号分别对应于与参考离子相异和相同的离子,二维正方离子(正负两种)格子,实际是一个面心正方格子,图 2.7示出了一个埃夫琴晶胞.设参考离子O 为正离子,位于边棱中点的离子为负离子,它们对晶胞的贡献为4*(1/2).对参考离子库仑能的贡献为图2.7二维正方离子晶格.121*4顶角上的离子为正离子,它们对晶胞的贡献为4*(1/4), 对参考离子库仑能的贡献为 .241*4-因此通过一个埃夫琴晶胞算出的马德隆常数为 .293.1241*4121*4=-=ν再选取422=个埃夫琴晶胞作为考虑对象,这时离子O 的最的邻,次近邻均在所考虑的范围内,它们对库仑能的贡献为,2414-而边棱上的离子对库仑能的贡献为 ,521*8221*4+- 顶角上的离子对为库仑能的贡献为 ,841*4-这时算出的马德隆常数为图 2.8 4个埃夫琴晶胞同理对932=个埃夫琴晶胞进行计算,所得结果为611.11841*41321*81021*8321*48458242414=⎪⎪⎪⎪⎭⎫ ⎝⎛-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛-=μ 对 1642=个埃夫琴晶胞进行计算,所得结果为614.13241*42521*81721*81021*8421*4184138108348458242414=⎪⎪⎪⎪⎭⎫ ⎝⎛-+-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛-=μ当选取 n 2个埃夫琴晶胞来计算二维正方离子(正负两种)格子的马德隆常数,其计算公式(参见刘策军,二维NaC1 晶体马德隆常数计算,《大学物理》，Vo1.14,No.12,1995.)为 [][].1,8411>+++=--n D C B A n n n n μ其中 ,21)1(,1)1(11111nB t A n n n t t n +-=+--=-=∑,1)1(1)1()2()1(1)1()1(2112212221112122122222222221⎪⎪⎪⎪⎪⎭⎫⎝⎛+--+--+-+-+--++⎪⎪⎭⎫⎝⎛+++-+⎪⎪⎭⎫ ⎝⎛+---n n n n n C n n ΛΛ.121)1()1(2181222222+-+-++++-=n n n n n D n n Λ5. 用埃夫琴方法计算CsCl 型离子晶体的马德隆常数(1) 只计最近邻 (2) 取八个晶胞 [解答](1) 图2.29是CsCl 晶胸结构,即只计及最近邻的最小埃夫琴晶胞,图2.29()a 是将Cs +双在体心位置的结构,图2.9(a)是将 Cl -取在体心位置的结构,容易求得在只计及最近邻情况下,马德隆常数为1.图2.29 （a ）Cs 取为体心的CsC1晶胞,(b) C1取为体心的CsC1晶胞(2)图2.10是由8个CsCl 晶胞构成的埃夫琴晶胞,8个最近邻在埃夫琴晶胞内,每个离子对晶胞的贡献为1,它们与参考离子异号,所以这8个离子对马德隆常数的贡献为8埃夫琴晶胞6个面上的离子与参考离子同号,它们对埃夫琴晶胞的贡献是21,它们与参考离子的距离为32R 它们对马德隆常数的贡献为-()3/2*621图 2.10 8个CsCl 晶胞构成的一个埃夫琴晶胞埃夫琴晶胞楞上的12个离子,与参考离子同号,它们对埃夫琴晶胞的贡献是41它们与参考离子的距离为322R 它们对马德隆常数的贡献为-()3224/1*12埃夫琴晶胞角顶上的 8个离子,与参考离子同号,它们对埃夫琴晶胞的贡献是81它们与参考离子的距离为2R 它们对马德隆常数的贡献为 -()281*8,由8个CsCl 晶胞构成的埃夫琴晶胞计算的马德隆常数.064806.32)8/1(*8322)4/1(*123/2)2/1(*68=---=μ 为了进一步找到马德常数的规律,我们以计算了由27个CsCl 晶胞构成的埃夫琴晶胞的马德隆常数,结果发现,由27个CsCl 晶胞构成的埃夫琴晶胞的马德隆常数是0.439665.马德隆常数的不收敛,说明CsCl 晶胞的结构的马德隆常数不能用传统的埃夫琴方法计算.为了找出合理的计算方法,必须首先找出采用单个埃夫琴晶胞时马德隆常数不收敛的原因.为了便于计算,通常取参考离子处于埃夫琴晶胞的中心.如果以Cs +作参考离子,由于埃夫琴晶胞是电中性的要求,则边长为pa 2(p 是大于或等于1的整数)的埃夫琴晶胞是由(2p )3个CsCl 晶胞所构成,埃夫琴晶胞最外层的离子与参考离子同号,而边长为(2p +1)的埃夫琴晶胞是由(2p +1)3 个 CsCl 晶胞所构成,但埃夫琴晶胞的最外层离子与参考离子异号,如果以C1-作参考离子也有同样的规律,设参考离子处于坐标原点O ,沿与晶胞垂直的方向(分别取为x,y,z 图2.11示出了z 轴)看去,与参考郭同号的离子都分布在距O 点ia 的层面上,其中i 是大于等于 1的整数,与 O 点离子异号的离子都分布在距O 点(i -0.5)a 的层面上,图 2.11(a) 示出了同号离子层,图2.11(b)示出了异号离子层.图2.11 离子层示意图(a)表示同号离子层, O 离子所在层与 O '离子所在层相距ia(b)表示异号离子层, O 离子所在层和O ' 离子所在层相距(i -0.5)a当 CsCl 埃夫琴晶胞边长很大时,晶胞最外层的任一个离子对参考离子的库仑能都变得很小,但它们对参考离子总的库仑能不能忽略.对于由(2p )3个CsCl 晶胞所构成的埃夫琴晶胞来说,最外层有6*(2p )2个与参考离子同号的离子,它们与参考离子的距离为(1/2)pa ~(23)pa ,它们与参考离子的库仑能为a pe 024πε量级,这是一个相对大的正值.对于由(2p +1)3个CsCl 晶胞所构成的埃夫琴晶胞来说,离外层有6*(2p +1)2个与参考离子异号的离子,它们与参考离子的库仑能为a pe 024πε-量级,这是一个绝对值相对大的负值,因此,由(2p )3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能,与由(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能会有较大的差异.即每一情况计算的库仑能都不能代表CsCl 晶体离子间相互作用的库仑能.因此这两种情况所计算的马德隆常数也必定有较大的差异,由1个CsCl 晶胞、8个CsCl 晶胞和27个CsCl 晶胞构成的埃夫琴晶胞的计算可知, CsCl 埃夫琴晶胞体积不大时,这种现象已经存在.为了克服埃夫琴方法在计算马德隆常数时的局限性,可采取以下方法,令由 (2p )3个CsCl 晶胞构成的埃夫琴晶胞计算的库仑能为1U ，由(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能为1U ，则CsCl 晶体离子间相互作用的库仑能可近似取作 )(2121U U U +=(1) 因子1/2 的引入是考虑除了(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞最外层离子外,其他离子间的库仑能都累计了两偏,计算1U 和2U 时要选取体积足够大的埃夫琴晶胞,此时埃夫琴晶胞最外层离子数与晶胞内的离子数相比是个很小的数,相应的马德隆常数应为 )(2121μμμ+=(2) 其中：=1μ⎪⎪⎭⎫ ⎝⎛±∑i ja 1'是由(2p )3个CsC1晶胞构成的埃夫琴晶胞计算的值; =1μ⎪⎪⎭⎫ ⎝⎛±∑i ja 1'由 (2p +1)3 个CsC1晶胞构成的埃夫琴晶胞所计算成本的值.为简化计算,特选取晶胞边长a 为计算单位,由于,32a R =所以,23'μμ= ⎪⎪⎭⎫ ⎝⎛±=∑'''1i i a μ (3) 其中'i a 是某一离子到参点的距离与a 的比值.考虑到对称性,对选定的埃夫琴晶胞,把晶胞的离子看成分布在一个个以参考离子为对称心的正六面体的六个面上,体积不同的正六面六个面上的离子分别计算.由(2p )3个CsC1晶胞构成埃夫琴晶胞时,由分析整理可得,231111⎪⎪⎭⎫ ⎝⎛++=∑∑=-=p pi i p i i C B A μ (4) 由(2p +1)3个 CsC1 晶胸构成埃夫琴晶胞时,,231112⎪⎪⎭⎫ ⎝⎛++=∑∑=-=p pi i p i i D B A μ (5)其中：),1(''''22'2'p i i y x k A i x iy y x i <≤++-=∑∑(6)i A 表示与 O 点距离为ia 的6个面上所有的离子对马德隆常数的面贡献,因为这些离子与参考离子同号,故到负号.'x 、'y 是离子在平面 '''y x o 上的坐标, ''y x k 代表 6个面上等价离子的个数,其取值规则为:(1) 在角上(如E 点),即'x =i 且 'y = i. 时, ''y x k =8；(2) 在棱与坐标轴的交点(如 F 点)，'x =i 且'y = 0或 'x =0且'y = 0时, ''y x k =6 (3) 在棱上的其他点(如H 、I 点)即不满足上述条件,且'x =i 或'y = i.时, ''y x k =12 (4) 在'O 点,即'x =0且'y = 0时, ''y x k =6(5) 在除'O 点外的面上的点(如J 点),即不满足上述条件时，''y x k =24.),1()5.0(5.05.05.05.022'2''''''p i i y x k B i x i y yx i ≤≤-++=∑∑-=-=(7)i B 代表距O 点距离为(i -0.5)a 的6个面上的离子对马德隆常数的贡献,因为这种些离子与参考离子异号,故取正号. 'x ,'y 是离子在平面'''y x o 上的坐标, '''y x k 代表这6个面上等价离子的个数,其取值规则为:(1) 在角上(如K 点),即'x =i 且 'y = i.时, '''y x k =8;(2) 在棱下(如L 、M 点),即不满足不述条件,且'x =i 或'y = i 时，'''y x k =12； (3) 在面上(如N 点)好不满足上述条件时, '''y x k =24.),(0022'2'"''''p i i y x k C i x iy i yx =++-=∑∑==i C 表示在边长为2pa 的晶胞最外层,即与参考离子相距pa 的6个面上的离子对马德隆常数的贡献,应取负号,与iA 的不同在于"''y x k的取值: (1) 在角上, "''y x k =''y x k /8; (2) 在棱上, "''y x k =''y x k /4; (3) 在面上, "''y x k=''y x k /2.),()5.0(5.05.05.05.022'2''''''''p i i y x k D i x i y yx i =-++=∑∑-=-=i D 表示在边长为2a p )1(+的晶胞最外层,即与参考离子相距(p +0.5)a 的离子层对马德隆常数的贡献,应取正号,与i B 的不同在于'''''yx k 的取值: (1) 在角上, '''''y x k ='''y x k /8; (2) 在棱上, '''''y x k ='''y x k /4; (3) 在面上, '''''y x k ='''y x k /2.表2.1给出了计算结果,给出的μ是由分别对应2p 和2p+1的1μ和2μ求得的,实际上, 1μ和2μ只需对应边长相近的埃夫琴晶胞即可,如取对应2p 和2p-1的埃夫琴晶胞也可得到一样的收敛结果,由以上数据可见,马德隆常数μ随晶胞边长的增大而迅速收敛.该方法适用于NaC1结构以外离子晶体马德隆常数的计算.6.只计及最近邻间的排斥作用时,一离子晶体离子间的互作用势为⎪⎪⎩⎪⎪⎨⎧±-=-)2(,)1(,)(22r e R e e r u R ρλ(1)最近邻(2)最近邻以外 式中ρλ,是常数,R 是最近邻距离,求晶体平衡时,原子间总的互作用势.[解 答]设离子数目为2N,以j ij a r =R 表示第j 个离子到参考离子i 的距离,忽略表面效应,则总的相互作用能可表示为U =N ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛±-∑∑-ρλR j j e R a e 2' (∑表示最近邻)=N ,2⎥⎦⎤⎢⎣⎡+--ρλμR e Z R e其中⎪⎪⎭⎫⎝⎛±=∑j ia 1'μ 为马德隆常数,+号对应于异号离子,-号对应于同号离子;Z 为任一离子的最近邻数目,设平衡时R=R 0 ,由平衡条件,02020=⎥⎦⎤⎢⎣⎡+=-ρρλμR R e Z R e N dRdU 得.0202ρλμρR e Z R e -=平衡时的总相互作用为.1)(0020200⎪⎪⎭⎫⎝⎛-=⎥⎦⎤⎢⎣⎡+-=-R R e N e Z R e N R U R ρμλμρ 7. 设离子晶体中,离子间的互作用势为⎪⎪⎩⎪⎪⎨⎧±+-=最近邻以外最近邻,,)(22re R b R e r u m(1) 求晶体平衡时,离子间总的相互作用势能)(0R U (2) 证明: )(0R U 11-⎪⎪⎭⎫⎝⎛∝m mZ μ其中μ是马德隆常数，Z 是晶体配位数 [解答](1)设离子数目为2N , 以j ij a r =R 表示第j 个离子到参考离子i 的距离,忽略表面效应,则总的相互作用能可表示U =N ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛±-∑∑m j j R b R a e 2'(∑表示最近邻) =N ,2⎥⎦⎤⎢⎣⎡+-m R b Z Re μ其中⎪⎪⎭⎫ ⎝⎛±=∑j i a 1'μ,为马德隆常数,+号对应于异号离子,-号对应于同号离子.Z 为任一离子的最近邻数目,设平衡时R=R 0由平衡条件,0102020=⎥⎦⎤⎢⎣⎡-=+m R R Zmb R e N drdUμ得10-m R Zmb=2e μ即1120-⎪⎪⎭⎫ ⎝⎛=m e Zmb R μ.于是,晶体平衡时离子间总的相互作用势能0U =).1(000--=⎥⎦⎤⎢⎣⎡+-m R NZbR b Z R Zmb N m m m(2)晶体平衡时离子间的相互作用势能可进一步化为0U =.)()()1()1(1111121211--------=⎪⎪⎭⎫ ⎝⎛--m m m m mm m m m m mb Ze Nbm e Zmb ZNbm μμ由上式可知 .110-⎪⎪⎭⎫⎝⎛∝m mZ U μ8.一维离子链,其上等间距载有正负2N 个离子,设离子间的泡利排斥只出现在最近邻离子之间,且为b/R n,b,n 是常R 是两最近邻离子的间距,设离子电荷为q ,(1) 试证明平衡间距下 )(0R U =;114212002⎪⎭⎫⎝⎛--n R n Nq πε(2) 令晶体被压缩,使0R )1(0δ-→R , 试证明在晶体被压缩单位长度的过程中外力作功的主项为c 2δ其中c=;21)1(02R n q n -(3) 求原子链被压缩了2)1(0<<e e NR δδ时的外力[解答](1) 因为离子间是等间距的,且都等于R ,所以认定离子与第j 个离子的距离j r 总可表示成为R a r j j =ja 是一整数,于是离子间总的互作用势能⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛±-=⎥⎥⎦⎤⎢⎢⎣⎡+=∑∑n i in j j j R b a R q N r b r q N R U 214242)('202'0πεπεμ,其中+、-分别对应相异离子和相同离子的相互作用.一维离子晶格的马德隆常数(参见本章习题2)为=⎪⎪⎭⎫ ⎝⎛±∑i ia 1'21n2. 利用平衡条件0)(0=R dRR dU得到b=nq 01-n 0241n2R πε,)(R U =⎪⎪⎭⎫ ⎝⎛---n n nR R R Nq 102141n22πε. 在平衡间距下⎪⎭⎫⎝⎛--n R Nq R U 1141n22)(0020πε.(2) 将互作用势能在平衡间距附近展成级数Λ+-⎪⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛+=202200)(21)()()(0R R dR U d R R dR dU R U R U R R 由外力作的功等于晶体内能的增量，可得外力作功的主项为W=20220)(21)()(0R R dR U d R U R U R-⎪⎪⎭⎫ ⎝⎛=-, 其中利用平衡条件，将R=R )1(0δ- ，代入上式，得到W=δδπε)2(421)1(2102002NR R n q n ⎥⎥⎦⎤⎢⎢⎣⎡-. 晶体被压缩单位长度的过程中，外力作的功的主项δ02W NR =δπε⎥⎥⎦⎤⎢⎢⎣⎡-2002421)1(21R n q n 令c=202421)1(R n q n πε-(CGS)得到在晶体被压缩单位长度的过程中，外力作的功的主项为2δc . （3）设e δδ=时外力为F e ,由于在弹性范围内，外力与晶格的形变成正比，所以 F= )2(0δαNR , F e = )2(0e NR δα,其中α为比例系数离子链被压缩e NR δ02过程中外力作的功W e =δδαδδd NR NR Fdx e eNR e 020002)]2([0⎰⎰== e e e F NR NR δδα022022121)2(=.由于 W e =)2(20e eNR c δδ,所以离子链被压缩了e NR δ02时的外力为F e =202)1(21R n n q c ee δδ-=.9．设泡利排斥项的形式不变，讨论电荷加倍对NaC1晶格常数，体积弹性模量以及结合能的影响。

海纳百川大道致远海纳百川大道致远2.1原子的电负性一、原子的电子壳层结构(atomic shell structure)原子内带正电的密实部分集中于一个很小的核，带负电的电子分布于核外，中性原子的核外电子数等于原子序数Z。

Z个电子在核外分布:原子内的电子可处于各种可能的定态，电子的运动状态由n、l、ml、ms4个量子数描述。

海纳百川大道致远n: 主量子数,总能量的主要部分，描述轨道的大小主量子数取正整数1、2、3、4、5…；分别用大写字母K、L、M、N、O、P…等表示。

l: 角量子数，代表轨道的形状和轨道的角动量；可取0、1、2、…n－1，共n个值，分别用s、p、d、f、g、h…表示。

ml: 轨道量子数可取－l、－l＋1、…、l，共2 l＋1个值，代表轨道有空间可能的取向。

ms : 自旋方向磁量子数ms = +1/2，-1/2。

电子自旋量子数S= ½，对所有电子均相同。

海纳百川大道致远原子核外电子的排布遵从两条规律：①泡利不相容原理。

原子内不可能有两个或两个以上的电子具有完全相同的四个量子数。

由此可确定原子内每个支壳层可容纳的电子数为2l＋1个，每个壳层可容纳的电子数为2n2个，对于第1、2、3、4等壳层可容纳的电子数分别为2、8、18、32、50。

②能量最低原理。

电子尽可能先填充能量较低的状态，各状态能量高低的顺序可由经验规律n＋0.7l值的大小加以判断。

由此可以确定随着原子序数增大，核外电子填充支壳层的顺序是：1s2s2p3s3p4s3d4p5s4d5p6s4f5d6p7s5f…电子的壳层排布与元素周期表一致。

海纳百川大道致远费密子与玻色子•凡是自旋为1/2或其它半整数的粒子都遵循泡利原理，这类粒子称为费密子，例如电子、质子和中子都是费密子。

还有一些粒子的自旋为整数，则不受泡利原理的约束，这一类粒子称为玻色子，例如光子、介子等。

海纳百川大道致远二、电离能与电子亲和能气态原子失去一个电子成为一价气态正离子所需的最低能量，称为原子的第一电离能（I1）。

2 正四面体的对称操作四个原子位于正四面体的四个顶角上，显然正四面体的对称操作包含在立方体操作之中。

如图XCH001_027所示。

1) 绕三个立方轴转动：π，共有3个对称操作；2) 绕4个立方体对角线轴转动34,32ππ，共有8个对称操作； 3) 正交变换也是一个对称操作；⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛1000100014) 绕三个立方轴转动：23,2ππ，加上中心反演，共有6个对称操作；5) 绕6条面对角线轴转动π，加上中心反演，共有6个对称操作；因此正四面体的对称操作共有24个。

3 正六面柱的对称操作1) 绕中心轴线转动：35,34,,32,3πππππ，共有5个对称操作；如图XCH001_028所示。

2) 绕对棱中点连线转动π，共有3个对称操作； 3) 绕相对面中心连线转动π，共有3个对称操作；4) 正交变换也是一个对称操作；⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛1000100015) 以上12个对称操作加中心反演仍是对称操作 因此正六面柱的对称操作共有24个。

4 对称素为简洁明了地概括一个物体的对称性，不去一一列举所有的对称操作，而是描述它所具有的“对称素”。

对称素就是一个物体的旋转轴，以及旋转－反演轴。

一个物体绕某一个转轴转动nπ2，以及其倍数不变时，称该轴为物体n 重旋转轴，计为n 。

一个物体绕某一个转轴转动nπ2加上中心反演的联合操作，以及其联合操作的倍数不变时，称该轴为物体n 重旋转－反演轴轴，计为n 。

+ 立方体—— 立方轴（23,,2πππ）为4重轴，计为4；同时也是4重旋转－反演轴，计为4； —— 面对角线（π）为2重轴，计为2；同时也是2重旋转－反演轴，计为2；—— 体对角线轴（34,32ππ）为3重轴，计为3；同时也是3重旋转－反演轴，计为3；+ 正四面体—— 立方轴是4重旋转－反演轴，但不是4重轴； —— 面对角线是2重旋转－反演轴，但不是2重轴； —— 体对角线轴是3重轴，但不是3重旋转－反演轴。

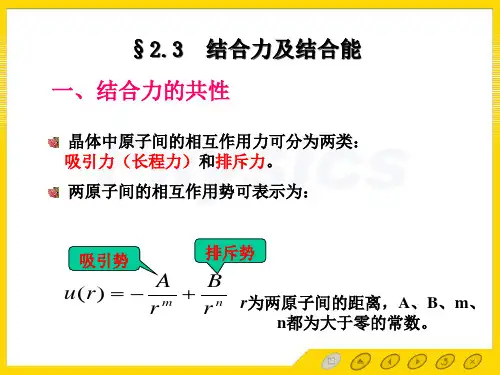
第二章 固体的结合晶体中粒子的相互作用力可以分为两大类，即吸引力和排斥力，前者在远距离是主要的，后者在近距离是主要的；在某一适当的距离，两者平衡，使晶格处于稳定状态。

吸引作用来自于异性电荷的库仑作用；排斥作用源于：一、同种电荷之间的库仑作用，二、泡利原理所引起的作用。

固体的结合根据结合力的性质分为四种基本形式：⎪⎪⎩⎪⎪⎨⎧范德瓦尔结合金属性结合共价性结合离子性结合 实际结合可能是兼有几种结合形式或者具有两种结合之间的过渡性质。

§2-1 离子性结合离子性结合的基本特点是以离子而不是以原子为结合的单位，结合的平衡依靠较强的静电库仑力，要求离子间相间排列。

其结构比较稳定，结合能为800千焦耳/摩尔数量级。

结合的稳定性导致导电性能差、熔点高、硬度高和膨胀系数小等特点。

以N a Cl 晶体为例，由于N a +和 Cl -离子满壳层的结构，具有球对称结构，可以看成点电荷，若令r 表示相邻离子的距离，则一个正离子的平均库仑能为：∑++-++321321,,2122322222102)(4)1(21n n n n n n r n r n r n q πε这里n 1，n 2，n 3为整数且不能同时为零。

一个元胞的库仑能为：απεπεr q n n n r q n n n n n n 02,,21232221024)()1(4321321-≡∑++-++上式中α为无量纲量，称为马德隆常数。

当邻近离子的电子云显著重叠时，将出现排斥，其能量可以由下式描述：n r rr bbe 或者0-因此含N 个元胞的晶体的系统内能可以表示为：)(nr B r A N U +-= 其和体积或者晶格常数的关系如下图（1） 晶格常数结合最稳定时的原子间距即为晶格常数，由下式决定0)(0=∂∂=r r r r U（2） 压缩系数压缩系数定义为单位体积的改变随单位压强的变化的负值，即：T pV V )(1∂∂-=κ 由热力学第一定律有：pdV dU -=（这里忽略了热效应），则压缩系数为：TV UV )(122∂∂=κ 体弹性模量为：κ1=K（3） 抗张强度晶体能够承受的最大张力，叫抗张强度。

固体物理讲义第二章2.1 晶体结构的实验确定晶体的结构可以通过衍射的方法来确定，即利用入射的射线束受晶体内部原子的相干散射产生衍射。

目前常用的衍射方法有X射线衍射、电子衍射和中子衍射。

其中，X射线衍射是最常用的方法，可以用于测量晶体内部结构，而电子衍射则适用于表面结构的测量，中子衍射则适用于磁性物质结构的测量。

晶体衍射的条件是波长与晶格常数同数量级。

现在，我们可以利用高分辨电子显微镜、场粒子显微镜和扫描透射电子显微镜直接观察原子排列和晶格结构。

虽然往往只能看到表面和局部的原子排列，但无论如何这是一种直接的观察，一种对原子规则结构的周期排列的直接验证。

2.2 晶体的倒格子和布里渊区晶体的倒格子是通过___格子的基矢量定义三个新的基矢量得到的，它们之间的关系为：b1 = 2π(a2×a3)/Ω，b2 =2π(a3×a1)/Ω，b3 = 2π(a1×a2)/Ω。

其中，a1、a2、a3为构成晶体正格子的基矢，Ω为正格子的体积。

倒格子中每个格点的位置为：Kh = h1b1 + h2b2 + h3b3，其中Kh称为倒格矢量，简称倒格矢。

倒格子空间也叫倒易点阵，每一个___正格子都有与之对应的倒格子。

正格子中的一族晶面(h1h2h3)和倒格矢Kh = h1b1 + h2b2+ h3b3正交，即d(h1h2h3)·Kh = 2π。

晶面族(h1h2h3)面间距d(h1h2h3)的长度正比于倒格矢Kh的倒数：d(h1h2h3) = 2π/|Kh|。

正格子原胞体积与倒格子原胞体积之间的关系为Ω = b1·b2×b3.倒格点与晶体中的一晶面相对应。

晶体中任一处r的物理量具有晶格周期性，可以展开为___级数。

比较展开式可得，周期为l的函数的倒格矢量一定是GG。

倒格子和正格子互相是对应的傅立叶空间。

每个晶体结构都有两套格子与之相联系，倒格子是与真实空间相联系的傅立叶空间中的格子，一定是___点阵。

第二章晶体的结合填空体1.晶体的结合类型为：离子结合分子结合、金属结合和氢键结合。

2.共价结合的特点—方向性和饱和性。

3.晶体中原子的相互作用力可分为两类吸引力—和排斥力。

4.一般固体的结合可概括为范德瓦耳斯结合、金属结合、离子结合和共价结合四种基本类型。

5.金属具有延展性的微观根源是金属原子容易相对滑动。

6.石墨晶体的结合涉及到的结合类型有共价结合、氢键结合和金属结合。

7.GaAs晶体的结合涉及到的结合类型有共价结合和离子结合。

二、基本概念1.电离能始原子失去一个电子所需要的能量。

2.电子的亲和能电子的亲和能：一个中性原子获得一个电子成为负离子所释放出的能量。

3.电负性描述化合物分子中组成原子吸引电子倾向强弱的物理量。

4.共价键原子间通过共享电子所形成的化学键。

5.离子键两个电负性相差很大的元素结合形成晶体时，电负性小的原子失去电子形成正离子，电负性大的得到电子形成负离子，这种靠正、负离子之间库仑吸引的结合成为离子键。

6.范德瓦尔斯力答：分子晶体的粒子间偶极矩相互作用以及瞬时偶极矩相互诱生作用力称为范德瓦耳斯力。

7.氢键答：氢原子处于两个电负性很强的原子（如氟、氧、氮、氯等）之间时，可同时受两个原子的吸引而与它们结合，这种结合作用称为氢键。

8.金属键答：在金属中，组成金属的原子的价电子已脱离母原子而成为自由电子，自由电子为整个晶体共有，而剩下的离子实就好像沉浸在自由电子的海洋中。

自由电子与离子实间的互相吸引作用具有负的势能，使势能降低形成稳定结构。

这种公有化的价电子（自由电子）与离子实间的互作用称为金属键。

三、简答题1.共价结合为什么有“饱和性”和“方向性”答：饱和性：当一个原子与其它原子结合时，能够形成共价键的数目有一个最大值，这个最大值决定于它所含的未配对的电子数，这个特性称为共价键的饱和性。

方向性：两个原子在以共价键结合时，必定选取尽可能使其电子云密度为最大的方位，电子云交迭得越厉害，共价键越稳固。

固体物理二章知识点总结固体物理第二章是关于晶体结构的内容，围绕着晶体的结晶结构、晶体点阵和基本晶胞的概念来展开讨论。

晶体是由周期性排列的原子或分子组成的，具有高度有序的结构，其结晶结构决定了晶体的性质和行为。

在这一章中，我们将从晶体的基本概念出发，逐步展开对晶体结构的探讨。

晶体的结晶结构是指晶体中原子或分子的排列方式和规律。

晶体的结晶结构包括晶体点阵和晶体的基本晶胞。

晶体点阵描述了晶体原子或分子的周期性排列方式，而晶体的基本晶胞则是由最小的重复单元构成，可以描述晶体的整体结构。

在这一部分，我们将介绍常见的晶体点阵和基本晶胞的类型以及它们之间的关系。

晶体点阵包括简单立方晶体、体心立方晶体和面心立方晶体等多种类型。

这些不同类型的晶体点阵具有不同的原子或分子排列方式和周期性，从而导致了晶体具有不同的性质和行为。

而晶体的基本晶胞则由部分晶胞和全部晶胞构成，它们决定了晶体的整体结构和周期性。

在这一章中，我们将深入探讨不同类型的晶体点阵和基本晶胞的性质和特点，并对它们进行详细的介绍和比较。

此外，我们还将介绍晶体缺陷和晶体生长的原理。

晶体缺陷是指晶体中存在的一些不规则排列的原子或分子，这些缺陷对晶体的性质和行为有着重要的影响。

晶体生长则是指晶体通过物质的沉积和积累形成有序结构的过程，它是晶体的产生和发展的基本原理。

在这一章中，我们将对晶体缺陷和晶体生长的机制和规律进行详细的阐述和分析。

总的来说，固体物理第二章是关于晶体结构的内容，围绕着晶体的结晶结构、晶体点阵和基本晶胞的概念展开讨论，同时还包括晶体缺陷和晶体生长的原理。

这些知识点对于理解固体物质的结构和性质，以及相关材料的性能和应用有着重要的意义。

在今后的学习和研究中，我们需要深入掌握这些知识点，并不断拓展和深化自己的理解，以便更好地应用和发展固体物理的相关理论和方法。