高等数学教学教案 格林公式及其应用
- 格式:doc
- 大小:359.00 KB
- 文档页数:7
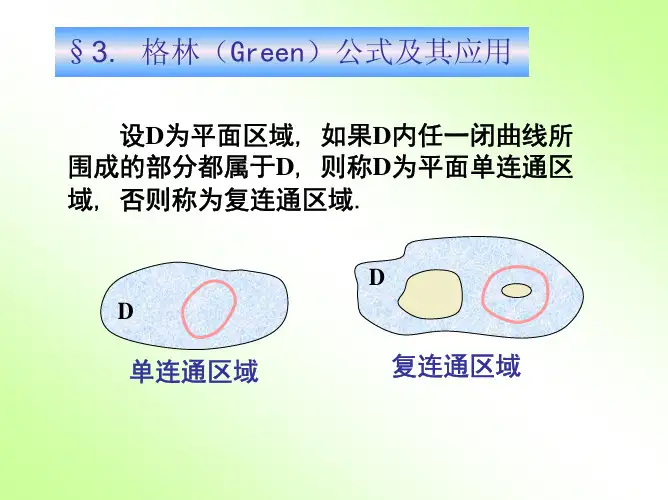







§10.3格林公式及其应用10.3.1格林公式1.单连通区域与复连通区域若平面区域D 内任一封闭曲线围成的部分都D 属于,则称为 D 单连通区域,否则称为复连通区域。
例如:圆形区域⎭⎬⎫⎩⎨⎧<+1),(22y x y x 、上半平面{}0),(>y y x 是单连通区域;圆环区域⎭⎬⎫⎩⎨⎧<+<41),(22y x y x 、⎭⎬⎫⎩⎨⎧<+<20),(22y x y x 是复连通区域。
通俗地说,单连通域就是不含有“洞”(包括点“洞” )的区域。
2.区域D 的边界曲线C 的正向规定的 C 正向如下:当观察者沿的 C 此方向行走时,靠近 D 他的部分总在他的左侧。
例如是 D 由边界曲线1C 和2C 所围成的复连通区域,的 1C 正向是逆时针方向,的 2C 正向是顺时针方向。
3.定理1设是 D 以逐段光滑曲线为C 边界的平面闭区域,函数),(y x P 、),(y x Q 在上 D 具有一阶连续偏导数,则有dxdy yPx Q Qdy Pdx DC ⎰⎰⎰∂∂-∂∂=+)(—格林(Green )公式 其中的取正向的边界曲线是D C 。
公式(1)称为格林(Green )公式。
证明:先假设穿过区域内部 D 且平行坐标轴的直线与的 D 边界曲线的 C 交点恰好为两点。
即D 既是型的区域型的又是 Y X 。
设}),()(),{(21b x a x y y x y y x D ≤≤≤≤=,∵yP ∂∂连续, ∴=σ∂∂⎰⎰d y P D⎰⎰∂∂bax y x y dy yPdx )(2)(1dx x y x P x y x P b a)]}( ,[)]( ,[{ 12⎰-=另一方面,有⎰⎰⎰⋂⋂+=BNAAMB C dx y x P ),(dx x y x P dx x y x P abb a)]( ,[ )]( ,[ 2 1⎰⎰+=dx x y x P x y x P ba)]}( ,[)]( ,[{ 21⎰-=,∴σ∂∂-=⎰⎰⎰d yPdx y x P DC),(。
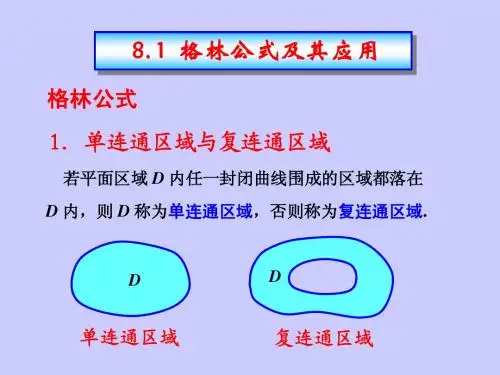

§113 格林公式及其应用 授课次序69 教 学 基 本 指 标 教学课题 §113 格林公式及其应用 教学方法 当堂讲授,辅以多媒体教学
教学重点 格林公式及其应用 教学难点 各种不同情况下的计算
参考教材 同济大学编《高等数学(第6版)》 自编教材《高等数学习题课教程》 作业布置 《高等数学》标准化作业
双语教学 微分 :differential calculus;全微分:total differential;偏微分:partial differential ; 积分:integral;重积分:multiple integral;二重积分:double integral;三重积分:threefold integral
课堂教学目标
1. 掌握格林公式;
2. 会运用平面曲线积分与路径无关的条件; 3. 会求全微分的原函数。
教学过程 1.格林公式(45min); 2.平面曲线积分与路径无关的条件(20min); 3.全微分的原函数(25min)
教 学 基 本 内 容
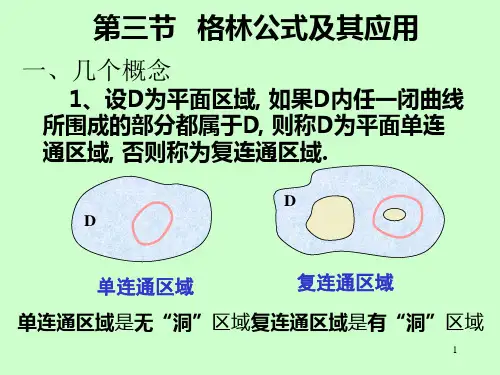
§113 格林公式及其应用 一、格林公式 单连通与复连通区域设D为平面区域如果D内任一闭曲线所围的部分都属于D则称D为平面单连通区域否则称为复连通区域 对平面区域D的边界曲线L 我们规定L的正向如下 当观察者沿L的这个方向行走时D内在他近处的那一部分总在他的左边 区域D的边界曲线L的方向 定理1设闭区域D由分段光滑的曲线L围成函数P(xy)及Q(xy)在D上具有一阶连续偏导数则有LDQdyPdxdxdyyPxQ)( 其中L是D的取正向的边界曲线 简要证明 备注栏 仅就D即是X-型又是Y-型的情形进行证明 设D{(xy)|1(x)y2(x)axb}因为yP连续所以由二重积分的计算法有
dxxxPxxPdxdyyyxPdxdyyPbaxxbaD)]}(,[)](,[{}),({12)()(21
另一方面由对坐标的曲线积分的性质及计算法有 abbaLLLdxxxPdxxxPPdxPdxPdx)](,[)](,[
21
21
dxxxPxxPba)]}(,[)](,[{21因此LDPdxdxdyyP
设D{(xy)|1(y)x2(y)cyd}类似地可证LDQdxdxdyxQ 由于D即是X-型的又是Y-型的所以以上两式同时成立两式合并即得 LDQdyPdxdxdy
yPx
Q
应注意的问题对复连通区域D格林公式右端应包括沿区域D的全部边界的曲线积分且边界的方向对区域D来说都是正向 设区域D的边界曲线为L 取PyQx则由格林公式得
LDydxxdydxdy2
或LDydxxdydxdyA21
例1椭圆xa cosyb sin所围成图形的面积A 分析只要1yPxQ 就有AdxdydxdyyPxQDD)( 解设D是由椭圆x=acosy=bsin所围成的区域 令yP21xQ21 则12121yPxQ于是由格林公式
例2 设L是任意一条分段光滑的闭曲线证明Ldyxxydx022 证令P2xyQx2则022xxyPxQ 因此由格林公式有0022dxdydyxxydxDL (为什么二重积分前有“”号? ) 3计算Dydxdye2其中D是以O(0 0)A(1 1)B(0 1)为顶点的三角形闭区域 分析 要使2yeyPxQ只需P02yxeQ 解令P02yxeQ则2yeyPxQ 因此由格林公式有 BOABOAyDy
dyxedxdye
22
)1(2111022edxxedyxexOAy
例4计算Lyxydxxdy22其中L为一条无重点、分段光滑且不经过原点的连续闭曲线L的方向为逆时针方向 解 令22yxyP22yxxQ
则当x2y20时有yPyxxyxQ22222)( 记L所围成的闭区域为D 当(0 0)D时由格林公式得022Lyxydxxdy 当(0 0)D时 在D内取一圆周lx2y2r 2(r>0) 由L及l围成了一个复连通区域D 1应用格林公式得02222lLyxydxxdyyxydxxdy其中l的方向取逆时针方向 于是lLyxydxxdyyxydxxdy22222022222sincosdrrr2 二、平面上曲线积分与路径无关的条件 曲线积分与路径无关设G是一个开区域P(xy)、Q(xy)在区域G内具有一阶连续偏导数如果对于G内任意指定的两个点A、B以及G内 从点A到点B的任意两条曲线L 1、L 2等式
21LLQdyPdxQdyPdx
恒成立就说曲线积分LQdyPdx在G内与路径无关否则说与路径有关 设曲线积分LQdyPdx在G内与路径无关L 1和L 2是G内任意两条从点A到点B的曲线则有21LLQdyPdxQdyPdx
因为
21LLQdyPdxQdyPdx021LLQdyPdxQdyPdx
021LLQdyPdxQdyPdx0)(21LLQdyPdx 所以有以下结论曲线积分LQdyPdx在G内与路径无关相当于沿G内任意 闭曲线C的曲线积分LQdyPdx等于零 定理2 设开区域G是一个单连通域函数P(xy)及Q(xy)在G内具有一阶连续偏导数则曲线积分LQdyPdx
在G内与路径无关(或沿G内任意闭曲线的曲线积分为零)的充分必要条件是等
式xQyP在G内恒成立 充分性易证 若xQyP则0yPxQ由格林公式对任意闭曲线L 有DLdxdyyPxQQdyPdx0 必要性假设存在一点M0G使0yPxQ不妨设>0则由yPxQ的连续性存在M0
的一个邻域U(M0, )使在此邻域内有2yPxQ 于是沿邻域U(M0, )边界l 的闭曲线积分 02)(2),(0MUldxdyyPxQQdyPdx
这与闭曲线积分为零相矛盾 因此在G内0yPxQ 应注意的问题定理要求区域G是单连通区域且函数P(xy)及Q(xy)在G内具有一阶连续偏导数如果这两个条件之一不能满足那么定理的结论不能保证成立
破坏函数P、Q及yP、xQ连续性的点称为奇点
例5计算Ldyxxydx22 其中L为抛物线yx2上从O(0 0)到B(1 1)的一段弧 解因为xxQyP2在整个xOy面内都成立所以在整个xOy面内积分Ldyxxydx22与路径无关ABOALdyxxydxdyxxydxdyxxydx22222211102dy 讨论 设L为一条无重点、分段光滑且不经过原点的连续闭曲线L的方向为逆时针方向 问
022Lyxydxxdy是否一定成立?提示 这里22yxyP和22yxxQ在点(0 0)不连续 因为
当x2y20时yPyxxyxQ22222)( 所以如果(0 0)不在L所围成的区域内则结论成立而当(00)在L所围成的区域内时 结论未必成立 三、二元函数的全微分求积 曲线积分在G内与路径无关 表明曲线积分的值只与起点从点(x0y0)与终点(xy)有关 如果
LQdyPdx
与路径无关则把它记为),(),(00yxyxQdyPdx
即),(),(00yxyxLQdyPdxQdyPdx 若起点(x0y0)为G内的一定点终点(xy)为G内的动点则u(xy)),(),(00yxyxQdyPdx 为G内的的函数 二元函数u(xy)的全微分为du(xy)ux(xy)dxuy(xy)dy 表达式P(xy)dx+Q(xy)dy与函数的全微分有相同的结构但它未必就是某个函数的全微分那么在什么条件下表达式P(xy)dx+Q(xy)dy是某个二元函数u(xy)的全微分呢?当这样的二元函数存在时怎样求出这个二元函数呢? 定理3 设开区域G是一个单连通域函数P(xy)及Q(xy)在G内具有一阶连续偏导数则
P(xy)dxQ(xy)dy在G内为某一函数u(xy)的全微分的充分必要条件是等式xQyP在G内恒成立 简要证明必要性假设存在某一函数u(xy)使得duP(xy)dxQ(xy)dy
则有yxuxuyyP2)(xyuyuxxQ2)(
因为yPyxu2、xQxyu2连续 所以xyuyxu22即xQyP 充分性因为在G内xQyP 所以积分LdyyxQdxyxP),(),(在G内与路径无关考虑函数u(xy)),(),(00),(),(yxyxdyyxQdxyxP 因为 u(xy)),(),(00),(),(yxyxdyyxQdxyxPxxyydxyxPdyyxQ00),(),(0 所以 ),(),(),(000yxPdxyxPxdyyxQxxuxxyy 类似地有),(yxQyu从而duP(xy)dxQ(xy)dy 即P(xy)dxQ(xy)dy是某一函数的全微分 求原函数的公式),(),(00),(),(),(yxyxdyyxQdxyxPyxu
yyxxdyyxQdxyxPyxu00),(),(),(0xxyydxyxPdyyxQyxu00),(),(),(
0
例6 验证22yxydxxdy在右半平面(x>0)内是某个函数的全微分并求出一个这样的函数
解 这里22yxyP22yxxQ