时域分析法习题及解答
- 格式:docx
- 大小:374.04 KB
- 文档页数:16

第3章离散系统的时域分析3.1 复习笔记一、基本概念1.前向差分与后向差分一阶前向差分一阶后向差分2.差分方程包含未知序列及其各阶差分的方程式称为差分方程。
将差分展开为移位序列,得一般形式二、离散系统的时域分析与连续系统的时域分析类似,离散系统的时域分析也是分析求解系统响应的过程,全部在时间域里进行。
不同的是离散系统的数学模型是借助差分方程,求解系统响应常用两种方法:时域经典法与时域卷积和法。
1.经典解法与微分方程经典解类似,全解y(k)=齐次解y h(k)+特解y p(k)。
(1)齐次解y h(k)齐次解由齐次方程解出。
设差分方程的n个特征根为。
齐次解的形式取决于特征根,y h(k)又称自由响应。
①当特征根λ为单根时,齐次解y h(k)形式为:②当特征根λ为r重根时,齐次解y h(k)形式为:③有一对共轭复根,齐次解y h(k)形式为:,其中(2)特解y p(k)特解y p(k)的求解过程类同连续系统时求y p(t)的过程。
差分方程的齐次解又称为系统的自由响应,特解又称强迫响应。
2.卷积和法全响应y(k)=零输入响应y zi(k)+零状态响应y zs(k)其求解过程如下:①建立系统的差分方程;②特征值→求零输入响应y zi(k);③单位样值响应→利用卷积和求零状态响应y zs(k)=h(k)*f(k);④全响应y(k)=y zi(k)+y zs(k)。
三、零输入响应和零状态响应1.零输入响应y zi(k)激励为零时,仅由系统的初始状态引起的响应,若特征根为单根时,则零状态响应为起始条件代入上式求出。
2.零状态响应y zs(k)当系统的初始状态为零,仅由激励所产生的响应,若特征根为单根时,则零状态响应为y p(k)求法同经典解法一样。
由零状态条件用递推法导出,再代入上式求出。
系统的全响应既可以分解为自由响应和强迫响应,又可以分解为零输入响应和零状态响应。
四、单位序列响应和阶跃响应1.单位序列响应由单位序列δ(k)所引起的零状态响应,称为单位序列响应或单位样值响应或单位取样响应,或简称单位响应,记为h(k),即。

时间序列分析习题解答第一章 P. 7 1.5 习题1.1 什么是时间序列?请收集几个生活中的观察值序列。
答:按照时间的顺序把随机事件变化发展的过程记录下来就构成一个时间序列。
例1:1820—1869年每年出现的太阳黑子数目的观察值;年份黑子数年份黑子数年份黑子数年份黑子数年份黑子数1820 16 1830 71 1840 63 1850 66 1860 96 1821 7 1831 48 1841 37 1851 64 1861 77 1822 4 1832 28 1842 24 1852 54 1862 59 1823 2 1833 8 1843 11 1853 39 1863 44 1824 8 1834 13 1844 15 1854 21 1864 47 1825 17 1835 57 1845 40 1855 7 1865 30 1826 36 1836 122 1846 62 1856 4 1866 16 1827 50 1837 138 1847 98 1857 23 1867 7 1828 62 1838 103 1848 124 1858 55 1868 37 1829 67 1839 86 1849 96 1859 94 1869 74 例2:北京市城镇居民1990—1999年每年的消费支出按照时间顺序记录下来,就构成了一个序列长度为10的消费支出时间序列(单位:亿元)。
1686,1925,2356,3027,3891,4874,5430,5796,6217,6796。
1.2 时域方法的特点是什么?答:时域方法特点:具有理论基础扎实,操作步骤规范,分析结果易于解释的优点,是时间序列分析的主流方法。
1.3 时域方法的发展轨迹是怎样的?答:时域方法的发展轨迹:一.基础阶段:1. G.U. Yule 1972年AR模型2. G.U.Walker 1931年 MA模型、ARMA模型二.核心阶段:G.E.P.Box和G.M.Jenkins1. 1970年,出版《Time Series Analysis Forecasting and Control》2. 提出ARIMA模型(Box-Jenkins模型)3. Box-Jenkins模型实际上主要运用于单变量、同方差场合的线性模型三.完善阶段:1.异方差场合:a.Robert F.Engle 1982年 ARCH模型b.Bollerslov 1985年 GARCH模型2.多变量场合:C.Granger 1987年提出了协整(co-integration)理论3.非线性场合:汤家豪等 1980年门限自回归模型1.4 在附录1中选择几个感兴趣的序列,创建数据集。


第一章 概论 习题及及解答1-1 试列举几个日常生活中的开环控制和闭环控制系统实例,并说明它们的工作原理。
略1-2. 图1-17是液面自动控制系统的两种原理示意图。
在运行中,希望液面高度0H 维持不变。
1.试说明各系统的工作原理。
2.画出各系统的方框图,并说明被控对象、给定值、被控量和干扰信号是什么()a 工作原理:出水量2θ与进水量一致,系统处于平衡状态,液位高度保持在0H 。
当出水量大于进水量,液位降低,浮子下沉,通过连杆使阀门1L 开大,使得进水量增大,液位逐渐回升;当出水量小于进水量,液位升高,浮子上升,通过连杆使阀门1关小,液位逐渐降低。
其中被控对象是水槽,给定值是液面高度希望值0H 。
被控量是液面实际高度,干扰量是出水量2θ。
()b 工作原理:出水量与进水量一致系统处于平衡状态,电位器滑动头位于中间位置,液面为给定高度0H 。
当出水量大于(小于)进水量,浮子下沉(上浮)带动电位器滑动头向上(下)移动,电位器输出一正(负)电压,使电动机正(反)转,通过减速器开大(关小)阀门1L ,使进水量增大(减小),液面高度升高(降低),当液面高度为0H 时,电位器滑动头处于中间位置,输出电压为零,电动机不转,系统又处于平衡状态。
其中被控对象是水槽,给定值为液面高度希望值0H ,被控量是液面实际高度,干扰量是出水量2θ。
()a ,()b 系统结构图如下图1-3 什么是负反馈控制在图1-17(b)系统中是怎样实现负反馈控制的在什么情况下反馈极性会误接为正,此时对系统工作有何影响解:负反馈控制就是将输出量反馈到输入端与输入量进行比较产生偏差信号,利用偏差信号对系统进行调节,达到减小或消除偏差的目的。
图1-17()b系统的输出量液面实际高度通过浮子测量反馈到输入端与输入信号(给定液面高度)进行比较,如果二者不一致就会在电位器输出一电压值——偏差信号,偏差信号带动电机转动,通过减速器使阀门1开大或关小,从而进入量改变,当输出量——液面实际高度与给定高度一致偏差信号为0,电机,减速器不动,系统又处于平衡状态。


第3章平稳时间序列分析本章教学内容与要求:了解时间序列分析的方法性工具;理解并掌握ARMA 模型的性质;掌握时间序列建模的方法步骤及预测;能够利用软件进行模型的识别、参数的估计以及序列的建模与预测。
本章教学重点与难点:利用软件进行模型的识别、参数的估计以及序列的建模与预测。
型来息。
t x 为t x 的1阶差分: ▽1t t t x x x --=对1阶差分后的序列再进行一次1阶差分运算称为2阶差分,记▽2tx 为t x 的2阶差分:▽2t x =▽t x -▽1-t x以此类推,对p-1阶差分厚序列再进行一次1阶差分运算称为p 阶差分。
记▽p t x 为t x 的p 阶差分:▽p t x =▽p-1t x -▽p-11-t x (二)k 步差分kt x 为t x 的10,,1t = 10,,2 = 即2阶差分序列▽2t x :3,22,-63,-54,-6,16,-52,-40,10,,3t = 2步差分:▽29x x x 133=-= ▽234x x x 244=-=……▽2-28x x x 81010=-=即2步差分序列:9,34,-7,-26,12,21,-16,-28 二、延迟算子(滞后算子) (一)定义延迟算子类似于一个时间指针,当前序列值乘以一个延迟算子,就相x因此,15-18+6=343-30+9=222.k 步差分▽k =t k t k t k t t x )B 1(x B x x x -=-=--三、线性差分方程在实践序列的时域分析中,线性差分方程是非常重要的,也是极为有效的工具,事实上,任何一个ARMA模型都是一个现象差分方程。
因此,ARMA模型的性质往往取决于差分方程的性质。
为了更好地讨论ARMA 模型的性质,先简单介绍差分方程的一般性质。
设,,方程两边同除以,得特征方程(这是一个一元p次方程,应该至少有p个非零实根,称这p个实根为特征方程(3)的特征根,不防记作.特征根的取值情况不同,齐次线性差分方程的解会有不同的表达形式。

第二章第一节信号特征检测一、填空题(10)1.常用的滤波器有、低通、带通、四种。
2.加速度传感器,特别是压电式加速度传感器,在及的振动监测与诊断中应用十分广泛。
3.传感器是感受物体运动并将物体的运动转换成的一种灵敏的换能器件。
4.振动传感器主要有、速度传感器、三种。
5.把模拟信号变为数字信号,是由转换器完成的。
它主要包括和两个环节。
6.采样定理的定义是:。
采样时,如果不满足采样定理的条件,会出现频率现象。
7.电气控制电路主要故障类型、、。
8.利用对故障进行诊断,是设备故障诊断方法中最有效、最常用的方法。
9.振动信号频率分析的数学基础是变换;在工程实践中,常运用快速傅里叶变换的原理制成,这是故障诊断的有力工具。
10.设备故障的评定标准常用的有3种判断标准,即、相对判断标准以及类比判断标准。
可用制定相对判断标准。
二、选择题(10)1.()在旋转机械及往复机械的振动监测与诊断中应用最广泛。
A位移探测器B速度传感器C加速度计D计数器2.当仅需要拾取低频信号时,采用()滤波器。
A高通B低通C带通D带阻3.()传感器,在旋转机械及往复机械的振动监测与诊断中应用十分广泛。
A压电式加速度B位移传感器C速度传感器 D 以上都不对4.数据采集、谱分析、数据分析、动平衡等操作可用()实现。
A传感器B数据采集器C声级计D滤波器5.()是数据采集器的重要观测组成部分。
A. 滤波器B. 压电式传感器C数据采集器D数据分析仪6.传感器是感受物体运动并将物体的运动转换成模拟()的一种灵敏的换能器件。
A力信号B声信号C光信号 D. 电信号7.在对()进行电气故障诊断时,传感器应尽可能径向安装在电机的外壳上。
A单相感应电机B三相感应电机C二相感应电机D四相感应电机8.从理论上讲,转速升高1倍,则不平衡产生的振动幅值增大()倍。
A1 B2 C3 D49.频谱仪是运用()的原理制成的。
A绝对判断标准B阿基米德C毕达哥拉斯D快速傅立叶变换10.伺服控制上常用三环结构,三个环都是调节器,其中有的采用P调节器,有的采用PI 调节器,有的采用PID调节器。




第一章绪论1-1试比较开环控制系统和闭环控制系统的优缺点.解答:1开环系统(1)优点:结构简单,成本低,工作稳定。
用于系统输入信号及扰动作用能预先知道时,可得到满意的效果。
(2)缺点:不能自动调节被控量的偏差。
因此系统元器件参数变化,外来未知扰动存在时,控制精度差。
2闭环系统⑴优点:不管由于干扰或由于系统本身结构参数变化所引起的被控量偏离给定值,都会产生控制作用去清除此偏差,所以控制精度较高。
它是一种按偏差调节的控制系统。
在实际中应用广泛。
⑵缺点:主要缺点是被控量可能出现波动,严重时系统无法工作。
1-2什么叫反馈?为什么闭环控制系统常采用负反馈?试举例说明之。
解答:将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反馈。
闭环控制系统常采用负反馈。
由1-1中的描述的闭环系统的优点所证明。
例如,一个温度控制系统通过热电阻(或热电偶)检测出当前炉子的温度,再与温度值相比较,去控制加热系统,以达到设定值。
1-3试判断下列微分方程所描述的系统属于何种类型(线性,非线性,定常,时变)?(1)22()()()234()56() d y t dy t du ty t u t dt dt dt++=+(2)()2() y t u t=+(3)()()2()4() dy t du tt y t u t dt dt+=+(4)()2()()sin dy ty t u t t dtω+=(5)22()()()2()3() d y t dy ty t y t u t dt dt++=(6)2()()2() dy ty t u t dt+=(7)()()2()35()du ty t u t u t dtdt=++⎰解答:(1)线性定常(2)非线性定常(3)线性时变(4)线性时变(5)非线性定常(6)非线性定常(7)线性定常1-4如图1-4是水位自动控制系统的示意图,图中Q1,Q2分别为进水流量和出水流量。
控制的目的是保持水位为一定的高度。

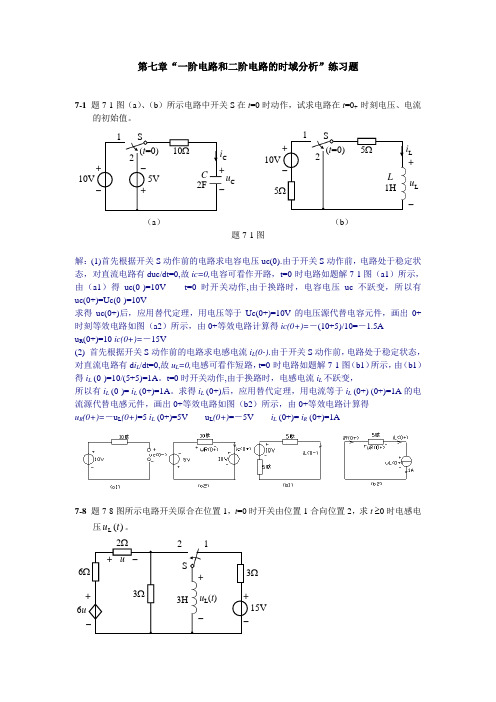

第三章 时域分析法习题及解答 3-1. 假设温度计可用11Ts传递函数描述其特性,现在用温度计测量盛在容器内的水温。发现需要min1时间才能指示出实际水温的98%的数值,试问该温度计指示出实际水温从10%变化到90%所需的时间是多少?
解: 41min, =0.25TT
1111()=1-e0.1, =ln0.9thttTT
21T22()=0.9=1-e ln0.1thttT,
210.9ln2.20.55min0.1rtttTT 3-2. 系统在静止平衡状态下,加入输入信号tttr)(1)(,测得响应为 tettC109.0)9.0()(
试求系统的传递函数。
解:2210.90.910(s+1)()=10s(s+10)Cssss
22111R(s)=ssss
()10()()10CssRss
3-3. 某惯性环节在单位阶跃作用下各时刻的输出值如下表所示。试求环节的传递函数。 t 0 1 2 3 4 5 6 7
h(t) 0 1.61 2.97 3.72 4.38 4.81 5.10 5.36 6.00
解: 设()1KsTs 11()()()()1(1)KCssRsKsTsssT
1()tThtKKe ()6hK
1161.61()661.61, ln0.3126ThteT
6 3.2 ()3.21Tss
3-4. 已知系统结构图如图3-49所示。试分析参数a对输出阶跃响应的影响。 解:1()()111KKTssKasTKasTs 1()()()()1KCssRssTKas
11=1sTaKKsTaK
11=()1sKsTaK
1h(t)=(1-e)tTaKK
当a>0时,系统响应速度变慢; 0TaK时,系统响应速度变快。
3-5. 设控制系统闭环传递函数为
2222)(nnnsss
试在[s]平面上绘出满足下列各要求的系统特征方程式根的可能分布的区域。 1.707.01, 2n
2.05.0, 24n 3.5.0707.0, 2n 解:①0.707<<1, 2n ②0<0.5, 24n ③0.50.707, 2n 3-6. 已知某前向通路的传递函数(如图3-50所示) 12.010)(ssG
今欲采用负反馈的办法将阶跃响应的调节时间st减小为原来的1.0倍,并保证总放大系数不变。试选择HK和0K的值。 解: 000
10()10110()0.21()0.21101110HHHHK
KGsKKsKGssKsK
010K101100.2T0.20.10.02110HHKKKK
解得:00.9 =10HKK
题解3-5(1) 题解3-5(2) 题解3-5(3) 3-7. 设一单位反馈控制系统的开环传递函数为 )11.0()(ssKsG
试分别求出当110sK和120sK时系统的阻尼比,无阻尼自然频率n,单位阶跃响应的超调量%及峰值时间pt,并讨论K的大小对系统性能指标的影响。
解: 22()10()1()0.11010GsKKsGsssKssK
2100=10, (s)=s10100K
s
210100 12102nnn
21%=e100%16.3%
2 0.3621pnts
2200=20 (s)=s10200Ks,
214.14200 0.353210nnn
21%=e100%30%
20.2371pnts
K增大使%,pt,但不影响调节时间。
3-8. 设二阶控制系统的单位阶跃响应曲线如图3-51所示。如果该系统属于单位反馈控制系统,试确定其开环传递函数。
解: 222()2nnnsss
212%=e100%30%0.357 33.63 0.1 1npnt
21131()1131() ()2411311()(24)ssGssssss
3-9. 设系统闭环传递函数
121)()()(22TssTsRsCs
试求1.2.0;sT08.0;4.0;sT08.0;0.8;sT08.0时单位阶跃响应的超调量%、调节时间st及峰值时间pt。 2.4.0;sT04.0和4.0;sT16.0时单位阶跃响应的超调量%、调节时间st和峰值时间pt。 3.根据计算结果,讨论参数、T对阶跃响应的影响。
解:2222221()212nnnTsssssTT 21%e100%
23.51psnntt
1. 0.08T 0.2 0.4 0.8 % 52% 25% 0.5% 0.26 0.27s 0.42s 1.2s 0.6s 0.38spstst
2. =0.4 0.04 0.08 0.16% 25% 25% 25% 0.14 0.27 0.55 0.3 0.6 1.2psT
tssstsss
3. ,T改变使闭环极点位置改变,从而系统动态性能发生变化。,%,,,,,%,pspsTttTtt不变,不变不变。 3-10. 已知图3-52(a)所示系统的单位阶跃响应曲线图3-52(b),试确定1K、2K和a的数值。 解: 由系统阶跃响应曲线有 oooopth3.333)34(1.03)( 系统闭环传递函数为 222212212)(nnnssKKassKKs (1)
由 oooonpet3.331.01212 联立求解得 28.3333.0n 由式(1)222110821nnaK 另外 3lim1)(lim)(2122100KKassKKssshss 3-11. 测得二阶系统图3-53(a)的阶跃响应曲线如图3-53(b)所示。试判断每种情况下系统内、外两个反馈的极性(其中“0”为开路),并说明其理由。
解:121()1KKsGsKss
2111221112
2
1
1()11KKKKKssssKsKsKKKsKss
(1) 单位阶跃响应为等幅振荡,故闭环极点为纯虚根,故内回路断开,外回路为负反馈; (2) 单位阶跃响应为发散,内回路为正反馈,外回路为负反馈; (3) 单位阶跃响应为近似斜坡信号,故外回路断开,内回路为负反馈; (4) 单位阶跃响应为加速度信号,闭环极点为原点上2个极点,故内回路开路,外回路也开路。
3-12. 试用代数判据确定具有下列特征方程的系统稳定性。 1. 010092023sss
2. 020092023sss 3. 025103234ssss 解: 321. 2091000sss 3 2
10
. 1 9 20 100209100 =4 020 100Routhss
ss
Routh表第一列系数均大于0,故系统稳定。 322. 2092000sss