1.21典型题

50道典型计算题解析1.【基准法】93+96+97+95+89+90+94+87+95+92原式=(90+3)+(90+6)+(90+7)+(90+5)+(90-1)+90+(90+4)+(90-3)+(90+5)+(90+2)=90×10+(3+6+7+5-1+4-3+5+2)=900+28=9282.【位值原理】(123456+234561+345612+456123+561234+612345)÷3【分析】仔细观察我们可以发现1、2、3、4、5、6分别在个、十、百、千、万、十万，六个数位上各出现过一次，所以原式=[(1+2+3+4+5+6)×111111]÷3=21×111111÷3=7×111111=7777773.【巧妙分组】2005+2004-2003-2002+2001+2000-1999-1998+1997+1996-……-7-6+5+4-3-2+1【分析】将后四项每四项分为一组，每组的计算结果都是0，后2004项的计算结果都是0，剩下第一项，结果是2005。

原式=123420012002200320042005+--+--+=20054.【拆分取整】2999+999×999【分析】计算时9、99、999类的数字时可以将其看成10-1、100-1、1000-1或者拆出1和其凑整计算，故原式=2000+999+999×999=2000+999×(1+999)=2000+999000=10010005.【乘法凑整】333333×333333【分析】将333333拆成3×111111，3×3=9，999999看成1000000-1。

原式=3×111111×3×111111=999999×111111=(1000000-1)×111111=111111000000-111111=1111108888896.【乘法分配律逆用】2005×2004-2004×2003+2003×2002-2002×2001+……+3×2-2×1原式=(2005-2003)×2004+(2003-2001)×2002+……+(3-2)×2=2×(2004+2002+2000+ (2)=2×2×(1002+1001+1000+ (1)=2×2×(1002+1)×1002÷2=20100127.【乘法分配律逆用】80×1995-3990+1995×22【分析】把3990分解为1995×2，这样80×1995、2×1995、22×1995中都有相同的乘数，可以利用乘法分配律进行巧算。

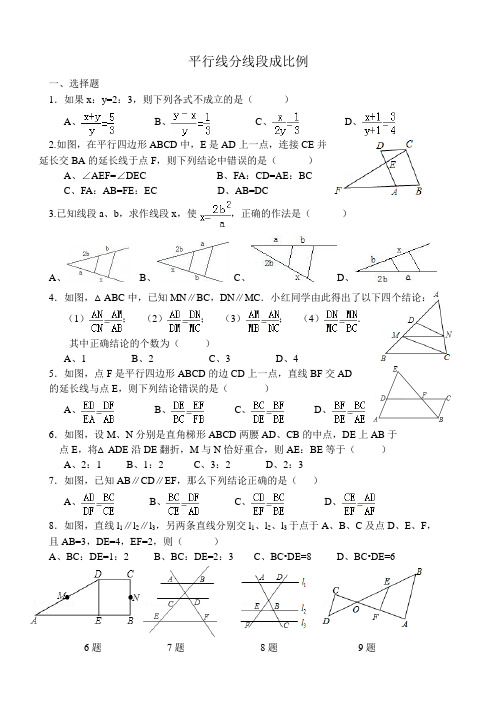
平行线分线段成比例一、选择题1．如果x：y=2：3，则下列各式不成立的是（）A、B、C、D、2.如图，在平行四边形ABCD中，E是AD上一点，连接CE并延长交BA的延长线于点F，则下列结论中错误的是（）A、∠AEF=∠DECB、FA：CD=AE：BCC、FA：AB=FE：ECD、AB=DC3.已知线段a、b，求作线段x，使，正确的作法是（）A、B、C、D、4．如图，△ABC中，已知MN∥BC，DN∥MC．小红同学由此得出了以下四个结论：（1）；（2）；（3）；（4）．其中正确结论的个数为（）A、1B、2C、3D、45．如图，点F是平行四边形ABCD的边CD上一点，直线BF交AD的延长线与点E，则下列结论错误的是（）A、B、C、D、6．如图，设M、N分别是直角梯形ABCD两腰AD、CB的中点，DE上AB于点E，将△ADE沿DE翻折，M与N恰好重合，则AE：BE等于（）A、2：1B、1：2C、3：2D、2：37．如图，已知AB∥CD∥EF，那么下列结论正确的是（）A、B、C、D、8．如图，直线l1∥l2∥l3，另两条直线分别交l1、l2、l3于点于A、B、C及点D、E、F，且AB=3，DE=4，EF=2，则（）A、BC：DE=1：2B、BC：DE=2：3C、BC•DE=8D、BC•DE=66题7题8题9题9．如图，若DC∥FE∥AB，则有（）A、B、C、D、10．如图所示，△ABC中若DE∥BC，EF∥AB，则下列比例式正确的是（）A、B、C、D、二．简答题1.如图，已知直线a∥b∥c，直线m、n与直线a、b、c分别交于点A、C、E、B、D、F，AC=4，CE=6，BD=3，求BF等于多长？2.如图所示：△ABC中，DE∥BC，AD=5，BD=10，AE=3．求CE的值。

3.如图，直线AB∥CD∥EF，若AC=3，CE=4，则的值是多少？4.如图，在△ABC中，AD=DE=EF=FB，AG=GH=HI=IC，已知BC=2，则DG+EH+FI的长是多少？5.如图，在△ABC中，CD平分∠ACB，过D作BC的平行线交AC于M，若BC=m，AC=n，求DM等于多少？。

1.21易错题练习1.Do you know there is some good news_____ todays newspaper? A in B. on C. at D. /2. Ill leave Beijing_____ Shanghai tomorrow. A for B. in C. to D. at3. A lot of French wines are made____ grape. A of B. from C. in D.for4. This is a good dictionary____ English grammar. A in B. for C. on D. about5. Do you have the key_____ the door. A in B. to C. of D. from6. It was good ____you to help my little boy. A for B. to C. as D.of7. My parents were very pleased ____ my studying. A at B. with C. to D.for8. He ____ me. A. is agree with B. against C. is against with D. is against9. Help yourself to _________. A. some chickensB. a chickenC. some chickenD. any chicken10. Which is the way to the __________?A. shoe factoryB. shoes factoryC. shoe’s factoryD. shoes’factory11. .This class ________ now. Miss Gao teaches them.A. are studyingB. is studyingC. be studyingD. studying12.Our sports meeting will be held ________.A. on 24, Tuesday, April B. in April 24, TuesdayC. on Tuesday, April 24D.13. –When shall we meet again next week?-- ___day is possible. It’s no problem with me.A. Either B. Neither C. EveryD. Any14. .Robert has gone to _________ city and he’ll be back in a week. A. otherB. the otherC. anotherD. any other15. –Which book would you like to borrow?-- ____ of the two books is OK with me.A. Either B. Both C. Any D. None16. 81. .He knows _________ English ________ French. But he’s very good at Japanese.A. either; orB. both; andC. neither; norD. either; nor17. 22.There are many trees on ________ side of the street. A. either B. any C. all D. both18. ________ is the population of the city?A. How many B. What C. How many peopleD. How much19. He hasn’t heard from his friend __________ last month. A. since B. by the end of C. for D. until20. I’m going to look for another job ________ the company offers me more money.A. afterB. unlessC. whenD. For3. A. take B. spend C. cost D. pay4. A. possible B. easy C. good D. hard5. A. read B. learn C. win D. download6. A. lose B. try C. waste D. watch7. A. come B. live C. study D. eat 8. A. watch TV B. go out C. stay there D. work9. A. better B. exciting C. even worse D. interesting 10. A. lessons B. games C. families D. sports11. A. classes B. rooms C. schools D. shops 12. A. classmates B. teachers C. sisters D. parents13. A. lucky B. unlucky C. careful D. polite 14. A. good B. bad C. rich D. poor15. A. important B.wonderful C. unusual D. seriousMr. Read was born in a small village with high mountains all around it．He has few fields and he can’t get enough food for his family．He’s often worried about it．So he works harder and harder and tries his best to get more money．One afternoon，Mr. Read went out to look for some grass for his cows．It was very hot and he had to have a swim．Suddenly he saw a big tortoise in the water．He swam there and caught it．The next morning he went to the town to sell it in the markets．When he was walking in the street, a car hit him down and he was hurt．He was sent to hospital at once．The doctors looked him over and had an operation on him．Two weeks later he felt much better．The doctors were satisfied with the operation and said，“You’ll be fully recovered in a week．We’re sure you can write when you leave hospital．”“It’s really a miracle（奇迹）！”shouted Mr. Read，“I could neither read nor write before！”1．The Reads have little food because ．A．they live in a small village B．they have few fields C．they’re too lazy to work D．nobody would help them to get money 2．Mr. Read jumped into the river because ．A．he wanted to get some grass in the water B．he wanted to look for a tortoise in the waterC．he wanted to have a good rest in the water D．he wanted to have a swim3．Mr. Read’s was hurt in the traffic accident．A．head B．leg C．right hand D．left hand4．In Chinese the phrase“be fully recovered”means ．A.完全覆盖B．全部找回C．恢复疲劳D．恢复健康5. What the doctor said meant that ______________ .A. he did a very successful operationB. the farmer was lucky enough to write after the operationC. the accident helped the farmer to writeD. he taught the farmer to write while he was staying in hospital1.〔析〕在报纸上的新闻要用in, 而在具体某一版上，或某一页上则要用on。

分数乘法练习题
1、92
× 5.4 = 83× 2.4 = 115× 1.21 = 13
7
×0.39 =
95×72+95×75 73×(14+87) 112×4+112×8-112 (72-9
1
)×6.3
2、解决问题
（1）一条路，第一天修了全长的6
1，第二天修了全长的3
2，两天共 修了全场的几分之几？
（2）一头鲸长7m ，头部长占5
2，这头鲸的其他部分长多少米？
（3）食堂买回大米5
4吨，第一周吃了它的3
1，第二周吃了它的4
1，第
二周吃了多少吨？
（4）某年级计划植树200棵，实际多植了25
1
，实际植树多少棵？
（5）学校有足球20个，篮球比足球少5
2，篮球有多少个？
（6）养鸡场有400只母鸡，公鸡的只数比母鸡的只数多5
1，公鸡有多少只？
（7）一根绳长2米，剪下它的8
7，还剩多少米？
（8）一条路长100千米，第一天修了全长的20
3
，第二天修了第一天 的5
4，第二天修了多少千米？
（9）我校五年级有故事书200本，科技书的本数是故事书的5
3，文艺书的本数是科技书的
53
，
文艺书有多少本？
（10）一台电视机原价2350元，现价比原价降低了50
3
，现价是多少？。

2022年高考物理100考点最新模拟题千题精练第一部分直线运动专题1.21．追击和相遇问题计算题（基础篇）二．计算题1．（8分）（2021安徽六市十校联考）在一直径为200m的圆形滑冰场上，教练和运动员分别站在直径AB 的两端，教练从A端沿与AB成53︒角的方向以16m/s的速度沿冰面击出冰球的同时，运动员从B点出发沿直线匀加速运动，在冰球到达圆形场地边缘时恰好拦住冰球，已知冰球被拦住时速度大小为4m/s，10m/s求：sin530.8︒=，g取2︒=，cos530.6（1）冰球的加速度大小；（2）运动员的加速度大小．2．（2021江西兴国三中质检）如图所示，在粗糙的水平路面上，一小车以v0=4m/s的速度向右匀速行驶，与此同时，在小车后方相距s0=40m处有一物体在水平向右的推力F=20N作用下，从静止开始做匀加速直线运动，当物体运动了x1=25m撤去力。

已知物体与地面之间的动摩擦因数μ=0.2，物体的质量m=5kg，重力加速度g取10m/s2。

求：(1)在推力F作用下，物体运动的加速度a1的大小；(2)物体运动过程中与小车之间的最大距离；(3)物体刚停止运动时与小车的距离d。

3.（12分）（2020福建华安一中、龙海二中第一次联考）现有甲、乙两辆汽车同时从汽车站由静止驶出，甲车先做匀加速直线运动，10s后速度达到72km/h，之后开始做匀速直线运动；乙车出发后一直做匀加速直线运动，发现自己和甲车之间的距离在发车20s后才开始变小。

求：（1）甲、乙车的加速度分别为多大？（6分）（2）甲、乙两车在相遇之前的最大距离是多少？（6分）4、 (2020·菏泽模拟)水平地面上有一足球距门柱的距离为x ＝32 m ，某同学将足球以水平速度v 1＝10 m/s 踢向球门，足球在地面上做匀减速直线运动，加速度大小为a 1＝1 m/s 2，足球撞到门柱后反向弹回，弹回瞬间速度大小是碰撞前瞬间速度大小的14。

数学小数点移动试题答案及解析1.填上适当的数．（1）把3.6的小数点向左移动一位是．（2）把3.14的小数点向左移动两位是．（3）把0.03扩大到它的倍是30．（4）把42缩小到它的是0.042．【答案】0.36，0.0314，1000，【解析】根据小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立；进行解答即可．解：（1）把3.6的小数点向左移动一位是0.36．（2）把3.14的小数点向左移动两位是0.0314．（3）把0.03扩大到它的1000倍是30．（4）把42缩小到它的是0.042．故答案为：0.36，0.0314，1000，．点评：此题考查了小数点置移动引起数的大小变化规律，应注意灵活运用．2.把0.2缩小100倍是，把3.06扩大倍，也就是把小数点向边移，得到3060．【答案】0.002，1000，右，三位【解析】把0.2缩小100倍，也就是把0.2的小数点向左移动两位，为0.002；由3.06变为3060，相当于把3.06的小数点向右移动三位，即扩大了1000倍；据此解答即可．解：把0.2缩小100倍是0.002，把3.06扩大1000倍，也就是把小数点向右边移三位，得到3060；故答案为：0.002，1000，右，三位．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．3.一个小数先向右移动三位小数点，接着向左移动一位是67.25，这个小数是．【答案】0.6725【解析】小数点位置移动引起数的大小变化规律，小数点先向右移动三位，这个数比原来扩大了1000倍，再向左移动一位，就又缩小了10倍，1000÷10=100，所以得到的数比原来扩大了了100倍，即所得的数是原数的100倍，据此解答．解：67.25÷100=0.6725；故答案为：0.6725．点评：此题主要考查了小数点位置移动引起数的大小变化规律．4.把10.258的小数点先向右移动两位，再向左移动三位，这个数是，原数就到它的．【答案】1.0258，缩小，【解析】把10.258的小数点先向右移动两位，再向左移动三位，相当于把这个数的小数点向左移动了一位，这个数是1.0258，即缩小了10倍，缩小到原数的；据此解答即可．解：根据小数点的位置移动引起小数大小变化的规律可知：把10.258的小数点先向右移动两位，再向左移动三位，这个数是1.025，原数就缩小到它的；故答案为：1.0258，缩小，．点评：此题考查小数点的位置移动引起小数大小变化的规律：一个数的小数点向右（或向左）移动一位、两位、三位…，这个数就扩大（或缩小）10倍、100倍、1000倍…，反之也成立．5.甲数是12.1，如果甲数的小数点向左移动一位，就与乙数相等，乙数是，甲数扩大100倍是．【答案】1.21，1210【解析】根据小数点位置移动引起数的大小变化规律可知：12.1的小数点向左移动一位，这个数就缩小10倍，是乙数，则乙数为1.21；如果把12.1扩大100倍，相当于把12.1的小数点向右移动两位，结果是1210；据此解答．解：甲数是12.1，如果甲数的小数点向左移动一位，就与乙数相等，乙数是1.21，甲数扩大100倍是1210；故答案为：1.21，1210．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．6.将50.95缩小10倍是；3.025扩大倍是302.5．【答案】5.095，100【解析】根据小数点位置移动引起小数大小变化的规律进行解答即可．解：将50.95缩小10倍即小数点向左移动一位是5.095；3.025到302.5小数点向右移动了两位，即扩大了100倍，故答案为：5.095，100．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．7.数A与数B的和是5.28，如果数A的小数点向右移动一位，就与数B相等，数A是．【答案】0.48【解析】根据小数点位置移动引起数的大小变化规律的运用．把A数的小数点向右移动1位就与B相等，即A数是1份数，B数就是10份数，再根据甲乙两数的和是5.28，进一步求出甲数即可．解：设甲数为x，乙数为10x，x+10x=5.28，11x=5.28，x=0.48；答：甲数是 0.48．故答案为：0.48．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．8.把6.57扩大100倍就是把小数点向移动位，得．【答案】右，2，657【解析】根据小数点位置移动引起数的大小变化规律进行解答即可．解：把6.57扩大100倍就是把小数点向右移动2位，得657，故答案为：右，2，657．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就扩大（缩小）10倍、100倍、1000倍…，反之也成立．9.①把20.178 的小数点移到最高位的左边，小数就到原数的．②把扩大到原数的1000倍后，再把小数向左移动两位是3.04．【答案】缩小，100倍；0.304【解析】①把20.178 的小数点移到最高位的左边就是向左移动2位；②这一问可用倒推法解，原题变成“把3.04的小数点先向右移动两位，再把得到的结果缩小1000倍”，可求出答案．解：①把20.178 的小数点移到最高位的左边就是向左移动2位，小数就缩小到原数的100倍；②把3.04的小数点先向右移动两位是304，再把304缩小1000倍是0.304．故答案为：缩小，100倍；0.304．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．10.0.04读作，表示．28个百分之一组成的数是．1.03的小数点向右移动三位，再向左移动两位是．把0.35 扩大倍是35．【答案】零点零四，4个百分之一，0.28，10.3，100【解析】（1）小数的读法：整数部分要按整数的读法去读，小数部分要依次读出每一位上的数字；（2）小数的数位顺序表中，小数点后第一位是十分位，第二位是百分位，第三位是千分位…，分别表示十分之一、百分之一，千分之一…，据此填写；（3）根据小数点的移动变化规律：小数点向右移动一位，小数就扩大到原数的10倍；小数点向右移动两位，小数就扩大到原数的100倍；小数点向右移动三位，小数就扩大到原数的1000倍…；小数点向左移动一位，小数就缩小到原数的；小数点向左移动两位，小数就缩小到原数的；小数点向左移动三位，小数就缩小到原数的…，据此解答．解：根据小数的读法，0.04读作：零点零四，因4在百分位上，表示4个百分之一，28个百分之一，是28个0.01，就是0.28；1.03小数点向右移动三位，再向左移动两位，实际向右移动了一位是10.3，0.35小数点向右移动了两位后是35，就扩大了100倍．故答案为：零点零四，4个百分之一，0.28，10.3，100．点评：考查了小数的读法、小数的数位以及小数点移动变化的规律．11.把6.05的小数点向左移动三位、再向右移动两位，6.05就．【答案】缩小到原数的【解析】把6.05的小数点向左移动三位，再向右移动两位后，实际上相当于把这个小数的小数点向左移动1位，即缩小了10倍．缩小到原数的；由此解答即可．解：把6.05的小数点向左移动三位、再向右移动两位，6.05就缩小到原数的；故答案为：缩小到原数的．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．12.一个一位小数去掉小数点后，就会扩大倍，如果把这个小数去掉小数点后比原数增加了10.8，那么原数是．【答案】10，1.2【解析】一个一位小数去掉小数点就是把这个一位数扩大了10倍，把扩大的数平均分成10份，那么原数就是其中的1份，去掉小数点就比原来增加10.8，即是10﹣1=9份所对应的数，由此求出1份是多少即可解决问题．解：一个一位小数去掉小数点后，就会扩大10倍；10.8÷（10﹣1）=10.8÷9=1.2；故答案为：10，1.2．点评：根据小数点移动引起小数大小的变化规律得出：新数是原数的10倍，由此即可解答．13.一个数与0.01相乘，也就是把这个数缩小到它的千分之一．．【答案】错误【解析】0.01有两位小数，一个数乘0.01，也就是要把小数点向左移动两位，此数则会缩小100倍．解：一个数乘0.01，小数点向左移动两位，也就是把这个数缩小到它的百分之一；故答案为：错误．点评：此题考查小数乘法，根据小数点的移动引起数的大小变化解决问题．14.一个小数的小数点向右移动一位，就比原来大3.33，这个小数是．【答案】0.37【解析】把一个小数的小数点向右移动一位即所得的数是原来的10倍，由题意知比原来多 3.33，也就是原数的9倍是3.33，求原来的数用除法可求出答案．解：3.33÷（10﹣1），=3.33÷9，=0.37；故答案为：0.37．点评：此题主要考查小数点位置移动引起数的大小变化规律和差倍问题的知识．15.把一个小数的小数点先向右移动两位，再向左移动三位，得到的数比原数．【答案】小【解析】把一个小数的小数点先向右移动两位，即扩大100倍；再向左移动三位，即缩小1000倍；相当于把原数小数点向左移动了一位，即缩小了10倍，缩小到原数的；由此解答即可．解：把一个小数的小数点先向右移动两位，再向左移动三位，得到的数比原数小；故答案为：小．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．16.把4.5扩大到它的100倍是，缩小它的是0.73．【答案】450，730【解析】（1）把4.5扩大到它的100倍，即4.5×100，小数点向右移动两位是450；（2）一个数缩小它的是0.73，即该数缩小了1000倍，小数点向左移动三位是0.73，所以原数应为0.73的小数点向右移动三位，为：730．解：（1）4.5×100=450，（2）0.73×1000=730，故答案为：450，730．点评：根据小数点位置的移动与小数大小的变化的规律进行解答．17.扩大到原来的100倍是21.8．【答案】0.218【解析】要求原数，就把21.8缩小100倍，根据小数点的位置移动规律，只要把21.8的小数点向左移动2位即可．解：把21.8缩小100倍，只要把21.8的小数点向左移动2位是0.218，所以 0.218扩大到原来的100倍是21.8．故答案为：0.218．点评：此题考查小数点的位置移动引起小数大小变化的规律：把一个数扩大（或缩小）10倍、100倍、1000倍…只要把这个数的小数点向右（或向左）移动一位、两位、三位…，反之也成立．18.去掉一个一位小数的小数点，这个数就扩大到原来的10倍．．【答案】√【解析】根据小数点位置移动引起数的大小变化规律可知：去掉一个一位小数的小数点，这个数就扩大到原来的10倍；据此解答．解：去掉一个一位小数的小数点，这个数就扩大到原来的10倍；故答案为：√．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．19.把一个数扩大100倍，就是在这个数的后面添上两个0．．【答案】错误【解析】根据小数点的移动与小数的大小变化可知：把一个数扩大100倍，即小数点向右移动2位，不一定就是在这个数的后面添上两个0；然后举例证明即可．解：一个数扩大100倍，就是在这个数的后面添上两个0，说法错误，如这个数是0.3，在后面填上两个0，数值不变；故答案为：错误．点评：本题主要考查小数点的移动与小数的大小变化的规律，应注意本题这个数是小数、还是非0自然数．20.一个数先缩小10倍，再把小数点向右移动两位，结果是8.05，这个数是．【答案】0.805【解析】根据小数点的位置移动与小数点大小的变化规律可知：小数点再向右移动两位是扩大100倍，这时得到8.05，那么在此之前是8.05÷100=0.0805，因为这个数先缩小10倍，所以在扩大10倍就是原来的数，即0.0805×10，即可得到原来的数，据此解答．解：8.05÷100×10，=0.0805×10，=0.805，答：这个数是0.805．故答案为：0.805．点评：本题主要考查小数点的位置移动与小数点大小的变化规律，通过逆向思维缩小的再扩大，扩大的再缩小即可得到原来的数．21.甲、乙两数的和是24.2．如果甲的小数点向右移动一位就与乙相等．甲数是．【答案】2.2【解析】根据小数点位置移动引起数的大小变化规律的运用．把甲数的小数点向右移动1位就与乙相等，即甲数是1份数，乙数就是10份数，再根据甲乙两数的和是24.2，进一步求出甲数即可．解：设甲数为x，乙数为10x，x+10x=24.2，11x=24.2，x=2.2；答：甲数是 2.2．故答案为：2.2．点评：此题主要考查小数点的位置移动引起数的大小变化规律：一个数的小数点向右（或向左）移动一位、两位、三位…，这个数就扩大（或缩小）10倍、100倍、1000倍…，反之也成立．22.一个小数的小数点向左移动两位后是0.509，这个小数是，一个小数的小数点向右移动两位后是3048，则原来的数是．【答案】50.9，30.48【解析】（1）一个小数的小数点向左移动两位，相当于此数缩小了100倍，要求原数就把0.509再扩大100倍，将其小数点向右移动两位即可；（2）一个小数的小数点向右移动两位，相当于此数扩大了100倍，要求原数就把3048再缩小100倍，将其小数点向左移动两位即可．解：一个小数的小数点向左移动两位后是0.509，这个小数是50.9，一个小数的小数点向右移动两位后是3048，则原来的数是30.48．故答案为：50.9，30.48．点评：此题考查小数点的位置移动引起小数大小变化的规律：一个数的小数点向右（或向左）移动一位、两位、三位…，这个数就扩大（或缩小）10倍、100倍、1000倍…，反之也成立．23.甲+乙=25.3，如果将乙数的小数点向右移动一位，则两数相等，甲是，乙是．【答案】23，2.3【解析】根据小数点位置移动引起数的大小变化规律的运用．把这个数的小数点向右移动1位，此数就扩大了10倍，乙数是1份数，甲数就是10份数，再根据甲乙两数的和是25.3，进一步求出乙数，即可求出甲数．解：设乙数为x，甲数为10x，x+10x=25.3，11x=25.3，x=2.3；10×2.3=23．答：甲数是23，乙数是2.3．故答案为：23，2.3．点评：此题主要考查小数点的位置移动引起数的大小变化规律：一个数的小数点向右（或向左）移动一位、两位、三位…，这个数就扩大（或缩小）10倍、100倍、1000倍…，反之也成立．24.把69.08的小数点向右移动2位，小数就到原来的倍；如果把小数点向左移动位，小数就缩小原来的1000倍．【答案】扩大，100，3【解析】根据小数点位置移动引起数的大小变化规律直接填空．解：把69.08的小数点向右移动2位，小数就扩大到原来的100倍；如果把小数点向左移动3位，小数就缩小原来的1000倍；故答案为：扩大，100，3．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．25. 58.987缩小到原来的是，4.985扩大到原来的1000倍是．【答案】0.58987，4985【解析】（1）根据小数点位置移动与小数大小的变化规律可知：缩小到原来的就是小数点向左移动两位，据此解答；（2）根据小数点位置移动与小数大小的变化规律可知：扩大到原来的1000倍就是小数点向右移动三位，据此解答．解：（1）58.987缩小到原来的是 0.58987；（2）4.985扩大到原来的1000倍是 4985；故答案为：0.58987，4985．点评：本题主要考查小数点位置移动与小数大小的变化规律．26.一个数，如果将它缩小为原来的，得到的新数比原来的数少3.6，原来的数是．【答案】4【解析】设原来的数为x，缩小原来的，即缩小10倍，根据小数点位置移动引起数的大小变化规律可知：新数为0.1x，进而根据“原数﹣新数=3.6”列出方程，解答即可．解：设原来的数是x，x﹣0.1x=3.6，0.9x=3.6，x=4，答：原来的数是4，故答案为：4．点评：本题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．27.把一个一位小数的小数点去掉后，比原数大39.6，这个小数是．【答案】4.4【解析】一个一位小数去掉小数点就是把这个一位数扩大了10倍，把扩大的数平均分成10份，那么原数就是其中的1份，去掉小数点就比原来大39.6，即是10﹣1=9份所对应的倍数，由此求出1份是多少即可解决问题．解：39.6÷（10﹣1）=39.6÷9=4.4；故答案为：4.4．点评：根据小数点移动引起小数大小的变化规律得出：新数是原数的10倍，由此即可解答．28.填上合适的数．把3.4扩大100倍是． 2.3小数点向左移动两位是．【答案】340，0.023【解析】（1）把3.4扩大100倍，就用3.4×100，只要把3.4的小数点向右移动2位即可；（2）把2.3的小数点向左移动两位，就用2.3÷100，直接把2.3小数点向左移动两位即可．解：（1）把3.4扩大100倍是340；（2）2.3小数点向左移动两位是0.023．故答案为：340，0.023．点评：此题考查小数点位置移动引起数的大小变化规律：把一个数扩大（或缩小）10倍、100倍、1000倍…只要把这个数的小数点向右（或向左）移动一位、两位、三位…，反之也成立．29.把3.14的小数点向移动两位，就扩大到它的倍．【答案】右，100【解析】小数点向右移动一位就扩大10倍，两位就扩大100倍，三位就扩大1000倍…解：3.14×100=314，扩大100倍要向右移动两位．故答案为：右，100．点评：此题主要考查小数点的位置移动引起小数大小的变化规律．30. 0.04扩大到原数的倍是4．【答案】100【解析】由0.04变为4，是把0.084的小数点向右移动了2位，就是把0.04扩大了100倍；据此解答．解：4÷0.04=100（倍）；故答案为：100．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．31.把50缩小到它的是；把0.64扩大到它的倍是640．【答案】0.5，1000【解析】根据小数点位置移动引起数的大小变化规律可知：把50缩小到它的，即50的小数点向左移动2位，是0.5；由0.64到640，相当于把0.64的小数点向右移动了3位，即扩大了1000倍；据此解答．解：把50缩小到它的是0.5； 0.64扩大它的1000倍是640；故答案为：0.5，1000．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．32. 0.76扩大到原来的10倍等于760缩小到原来的．．【答案】错误【解析】（1）0.76扩大到原来的10倍，是把0.76的小数点向右移动一位，列式为0.76×10=7.6；（2）760缩小到原来的，是把760的小数点向左移动三位，列式为760÷1000=0.76，由此即可判断．解：0.76×10=7.6；760÷1000=0.76，所以原题说法错误．故答案为：错误．点评：本题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．33.把0.8缩小10倍是，把0.32的小数点去掉，这个数就扩大倍．【答案】0.08，100【解析】把0.8缩小10倍，只要把0.8的小数点向左移动一位即可；把0.32的小数点去掉，相当于把0.32扩大100倍．解：把0.8缩小10倍是0.08，把0.32的小数点去掉，这个数就扩大100倍．故答案为：0.08，100．点评：此题考查了小数点位置移动引起数的大小变化规律：把一个数扩大（缩小）10倍、100倍、1000倍…只要把这个数的小数点向右（向左）移动一位、两位、三位…，反之也成立．34.把0.09扩大100倍是；把23.7缩小倍是0.0237．【答案】9，1000【解析】（1）把0.09扩大100倍，用0.09×100，只要把0.09的小数点向右移动2位即可；（2）把23.7缩小多少倍是0.0237，用23.7÷0.0237，即可．解：①0.09×100=9；②23.7÷0.0237=1000，故答案为：9，1000点评：此题考查小数点位置移动引起数的大小变化规律：把一个数扩大（或缩小）10倍、100倍、1000倍…只要把这个数的小数点向右（或向左）移动一位、两位、三位…，反之也成立．35. 0.65扩大10倍等于650缩小100倍．．【答案】正确【解析】0.65扩大10倍，小数点向右移动一位是6.5，650缩小100倍，小数点向左移动两位是6.5．解：0.65扩大10倍是6.5，650缩小100倍是6.5，故答案为：正确．点评：此题主要考查的是小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．36.把一个数扩大10倍后是0.9，原来这个数是0.009．．【答案】×【解析】把一个数扩大10倍后是0.9，可知0.9是原数小数点向右移动一位得到的，则将0.9小数点向左移动一位可得原数．解：0.9小数点向左移动一位是0.09，所以把一个数扩大10倍后是0.9，原来这个数是0.009的说法是错误的．故答案为：×．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…，反之也成立．37.把一个小数扩大100倍得735，这个小数原来是．【答案】7.35【解析】由于一个小数扩大100倍得735，将735的小数点位置向左移动2位可得原来的小数．解：735÷100=7.35．答：这个小数原来是7.35．故答案为：7.35．点评：本题考查了小数点位置的移动与小数大小的变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…．38. A÷B=1.28，如果B扩大1000倍，要使商不变，A的小数点应向移动位．【答案】右，3【解析】依据商不变的性质，再除法算式里被除数、除数同时扩大相同的倍数（0除外）商的大小不变，因此，在题干中除数B扩大1000倍，也就是说小数点向右移动了3位，要使商不变，所以被除数A的小数点也要向右移动3位．解：根据商不变的性质可知：在A÷B=1.28，如果B扩大1000倍，要使商不变，A的小数点应向右移动3位．故答案为：右，3．点评：本题主要考查了学生对“商不变的性质”的理解和应用．39. 0.045去掉小数点后，这个数就扩大倍．【答案】1000【解析】0.045去掉小数点后是45，也就是小数点向右移动了三位，所以这个数就扩大1000倍．解：0.045去掉小数点后是45，小数点向右移动三位，这个数就扩大1000倍．故答案为：1000．点评：此题主要根据小数点位置的移动与小数大小的变化规律．40.把3.78的小数点向右移动2位，原来的数就大2倍．．【答案】错误【解析】一个数的小数点向右移动扩大，当移动位数为1、2、3、…位，相应的倍数为10、100、1000…，依据此规律，就能确定扩大的倍数．解：把3.78的小数点向右移动2位，原来的数就大100倍．故答案为：错误．点评：此题主要考查小数点位置移动引起数的大小变化规律：一个数的小数点向右（向左）移动一位、两位、三位…，这个数就比原来扩大（缩小）10倍、100倍、1000倍…41. 0.8的计数单位是，再加上个这样的计算单位等于1；扩大100倍是56．【答案】0.1，2，0.56【解析】（1）小数的计数单位有0.1，0.01，0.001，0.0001，0.00001等，所以0.8的计数单位是0.1，问题得解；（2）0.8表示8个0.1，1是10个0.1，10﹣8=2，所以再加2个0.1就是1，问题得解；（3）扩大100倍是56，那么56缩小100倍就是原来的数，即56÷100，也可以由小数点的移动规律可知，小数点向左移动两位就是缩小100倍即可得到原来的数，问题即可解答．解：（1）0.8的表示8个0.1，它的计数单位是0.1；（2）0.8的表示8个0.1，1等于10个0.1，10﹣8=2；（3）56÷100=0.56；故答案为：0.1，2，0.56．点评：本题主要考查小数的意义和小数点的移动规律．42.一个小数由8个十，8个十分之一组成，这个数是，把它的小数点向右移动3位，得到的数是．【答案】80.8，80800【解析】①由题意可知，这个数十位上是8，十分位上是8，从高位到低位写起，一级一级地写，哪一个数位上一个数字也没有，就在那个数位上写0，据此写出即可；②把它的小数点向右移动3位即扩大了1000倍，据此解答即可．解：①一个小数由8个十，8个十分之一组成，这个数是80.8；②把它的小数点向右移动3位，得到的数是80800；故答案为：80.8，80800．点评：这是一道综合题，既考查了小数的组成，又考查小数的读写以及小数点位置的移动与小数大小的变化规律．43. 10.35读作，把它扩大100倍得，再缩小1000倍是．【答案】十点三五，1035，1.035【解析】根据小数的读法：整数部分按整数的读法来读，小数点读作点，小数部分要依次读出每个数字；把10.35扩大100倍，即10.35的小数点向右移动两位，是1035；再缩小1000倍，即1035的小数点向左移动3位，即1.035；据此解答．解：10.35读作十点三五，把它扩大100倍得1035，再缩小1000倍是1.035；故答案为：十点三五，1035，1.035．点评：此题考查了小数的读法及小数点移动引起数的大小变化规律．。

微观经济学典型计算题1、某消费者每年用于商品的价格分别为P1=20元和P2=30元，收入I=1800，该消费者的效用函数为U=3某1某22。

求：（1）消费者每年购买这两种商品的数量各应是多少？（2）每年从中获得的总效用是多少？解：（1）由消费者均衡条件MU1/P1=MU2/P2P1某1+P2某2=I3某22/20=6某1某2/3020某1+30某2=1800某1=30某2=40(2)每年获得的总效用U=3某1某22=1440002、已知某厂商只有一种可变生产要素L，产出一种产品Q，固定成本为既定，短期生产函数为Q=21L+9L2-L3，求：（1）总产量TP的最大值。

（2）平均产量AP的最大值（3）边际产量MP的最大值。

解：（1）MP=dQ/dP=21+18L-3L2MP=0，21+18L-3L2=0，L=7（2）AP=TP/L=21+9L-L2=MPL=4或者5，AP的最大值41（3）MP=dQ/dP=21+18L-3L2L=3，MP的最大值为483、设生产函数Q=LK-0.2L2-K2，K=10。

求：（1）L的平均产量函数和边际产量函数（2)当L分别为何值时，APL=0，MPL=0解：当K=10时，生产函数为Q=10L-0.2L2-100(1)平均产量APL=(10L-0.2L2-100)/L边际产量MPL=10-0.4L(2)APL=(10L-0.2L2-100)/L=0，L=36MPL=10-0.4L，L=251.1.经济人从事经济活动的人所采取的经济行为都是力图以自己的最小经济代价去获得自己的最大经济利益。

1.2.需求消费者在一定时期内在各种可能的价格水平愿意而且能够购买的该商品的数量。

1.3.需求函数表示一种商品的需求数量和影响该需求数量的各种因素之间的相互关系的函数。

1.4.供给生产者在一定时期内在各种价格水平下愿意并且能够提供出售的该种商品的数量。

1.5.供给函数供给函数表示一种商品的供给量和该商品的价格之间存在着一一对应的关系。

z 一元二次方程应用题经典题型汇总一、增长率问题例 1 恒利商厦九月份的销售额为200 万元，十月份的销售额下降了20% ，商厦从十一月份起加强管理，改善经营，使销售额稳步上升，十二月份的销售额达到了193.6 万元，求这两个月的平均增长率.解设这两个月的平均增长率是X.,则根据题意，得200(1 —20%)(1+ x)2= 193.6 ,即(1+x)2= 1.21，解这个方程，得x i = 0.1 , X2=— 2.1 (舍去).答这两个月的平均增长率是10%.说明这是一道正增长率问题,对于正的增长率问题,在弄清楚增长的次数和问题中每一个数据的意义，即可利用公式m(1+x)2= n求解，其中m v n.对于负的增长率问题，若经过两次相等下降后，则有公式m(1 —x)2= n即可求解，其中m >n.二、商品定价例2 益群精品店以每件21 元的价格购进一批商品, 该商品可以自行定价, 若每件商品售价a元，则可卖出(350 —10a)件，但物价局限定每件商品的利润不得超过20%，商店计划要盈利400 元,需要进货多少件？每件商品应定价多少？解根据题意，得(a—21)(350 —10a) = 400，整理，得a2—56a+775 = 0 ,解这个方程，得a1 = 25 , a2 = 31.因为21 p+20%) = 25.2，所以a2=31不合题意，舍去.所以350 —10 a= 350 —10 X25 = 100 (件).答需要进货100 件,每件商品应定价25元.说明商品的定价问题是商品交易中的重要问题,也是各种考试的热点例3 王红梅同学将1000元压岁钱第一次按一年定期含蓄存入“少儿银行”，到期后将本金和利息取出，并将其中的500元捐给“希望工程”，剩余的又全部按一年定期存入，这时存款的年利率已下调到第一次存款时年利率的90%，这样到期后，可得本金和利息共530元，求第一次存款时的年利率•(假设不计利息税)解设第一次存款时的年利率为X.则根据题意，得[1000(1+ x)- 500](1+0.9 x) = 530.整理，得90X2+145 x —3 = 0.解这个方程，得X i~0.0204 = 2.04% , X21.63.由于存款利率不能为负数，所以将X2~—1.63 舍去.答第一次存款的年利率约是 2.04%.说明这里是按教育储蓄求解的，应注意不计利息税四、趣味问题例4 一个醉汉拿着一根竹竿进城，横着怎么也拿不进去，量竹竿长比城门宽4米，旁边一个醉汉嘲笑他，你没看城门高吗，竖着拿就可以进去啦，结果竖着比城门高2米，二人没办法，只好请教聪明人，聪明人教他们二人沿着门的对角斜着拿，二人一试，不多不少刚好进城，你知道竹竿有多长吗？解设渠道的深度为x m，那么渠底宽为(x+0.1)m，上口宽为(x+0.1+1.4)m.则根据题意，得2(x+0.1+ x+1.4+0.1) x= 1.8，整理，得x2+0.8 x—1.8 = 0.解这个方程，得X1 = — 1.8 (舍去)，X2= 1.所以x+1.4+0.1 = 1 + 1.4+0.1 = 2.5.答渠道的上口宽2.5m，渠深1m.说明求解本题开始时好象无从下笔，但只要能仔细地阅读和口味，就能从中找到等量关系，列出方程求解例5 读诗词解题：(通过列方程式，算出周瑜去世时的年龄)大江东去浪淘尽，千古风流数人物；而立之年督东吴，早逝英年两位数；十位恰小个位三，个位平方与寿符；哪位学子算得快，多少年华属周瑜？解设周瑜逝世时的年龄的个位数字为X,则十位数字为x - 3.则根据题意，得x2= 10(x —3)+ x，即X2-11X+30 = 0，解这个方程，得x= 5或x= 6.当x = 5时，周瑜的年龄25岁，非而立之年，不合题意，舍去；当x = 6时，周瑜年龄为36岁，完全符合题意.答周瑜去世的年龄为36岁.六、象棋比赛例6 象棋比赛中，每个选手都与其他选手恰好比赛一局，每局赢者记2分，输者记0分.如果平局，两个选手各记1分，领司有四个同学统计了中全部选手的得分总数，分别是1979 , 1980 , 1984 , 1985.经核实，有一位同学统计无误•试计算这次比赛共有多少个选手参加•解设共有n个选手参加比赛，每个选手都要与(n —1)个选手比赛一局，共计n(n —1)1局，但两个选手的对局从每个选手的角度各自统计了一次，因此实际比赛总局数应为2 n(n —1)局由于每局共计2分，所以全部选手得分总共为n(n —1)分•显然(n—1)与n为相邻的自然数，容易验证，相邻两自然数乘积的末位数字只能是0, 2 , 6，故总分不可能是1979 , 1984 , 1985，因此总分只能是1980，于是由n(n —1) = 1980，得n2—n —1980 = 0 ,解得n1 = 45 , n2=—44 (舍去).答参加比赛的选手共有45人.说明类似于本题中的象棋比赛的其它体育比赛或互赠贺年片等问题, 法求解• 七、情景对话例7 春秋旅行社为吸引市民组团去天水湾风景区旅游，推出了如图1对话中收费标准. 某单位组织员工去天水湾风景区旅游，共支付给春秋旅行社旅游费用27000元•请问该单位 这次共有多少员工去天水湾风景区旅游？解设该单位这次共有 x 名员工去天水湾风景区旅游 •因为1000 >25 = 25000 V 27000，所以员工人数一定超过 25人.则根据题意，得[1000 — 20(x — 25)] x = 27000.整理，得 x 2 — 75X +1350 = 0,解这个方程，得 x i = 45 , X 2= 30.当 x = 45 时，1000 — 20( x — 25) = 600 V 700，故舍去 x i ；当 X 2= 30 时，1000 — 20(x — 25) = 900 >700，符合题意.答：该单位这次共有30名员工去天水湾风景区旅游说明 求解本题要时刻注意对话框中的数量关系，求得的解还要注意分类讨论，从中找出符合题意的结论都可以仿照些如果人数不超过25人 如果人数超过25人，每増加1 人人均放游费用降低20元 旦人均册费用不得低于700人均旅游费用海1000元.八、等积变形例8 将一块长18米，宽15米的矩形荒地修建成一个花园（阴影部分）所占的面积为 原来荒地面积的三分之二•（精确到0.1m ）（1 ）设计方案1 （如图2）花园中修两条互相垂直且宽度相等的小路（2）设计方案2 （如图3）花园中每个角的扇形都相同 .以上两种方案是否都能符合条件？若能，请计算出图2中的小路的宽和图3中扇形的半径；若不能符合条件，请说明理由 解 都能.(1)设小路宽为 X ,则 18x +16x — x 2=^ X18 X15,即 x 2— 34X +180 = 0 ,解这个方程，得x = 2 ，即x ~ 6.6.(2)设扇形半径为 r ，则 3.14 r 2 =X18 X15 ,即卩 r 2疋 57.32，所以 r ~7.6.明 等积变形一般都是涉及的是常见图形的体积，面积公式；其原则是形变积不变; 积也变，但重量不变，等等九、动态几何问题例9 如图 4所示，在△ ABC 中，/ C = 90?/SPAN> , AC = 6cm , BC = 8cm ，点 P 从 点A 出发沿边AC 向点C 以1cm/s 的速度移动，点Q 从C 点出发沿CB 边向点B 以2cm/s 的速度移动（1）如果P 、Q 同时出发，几秒钟后，可使△ PCQ 的面积为8平方厘米?X ,或形变(2)点P 、Q 在移动过程中，是否存在某一时刻，使得△ PCQ 的面积等于△ ABC 的面积的一半•若存在，求出运动的时间；若不存在，说明理由(1 )设 x s 后，可使△ PCQ 的面积为 8cm 2,所以 AP = x cm , PC = (6 — x )cm , CQ =2x cm.则根据题意，得(6 — x ) 2x = 8.整理，得X 2— 6x +8 = 0,解这个方程，得 x i = 2, X 2=4. 所以P 、Q 同时出发，2s 或4s 后可使△ PCQ 的面积为8cm 2.(2)设点P 出发x 秒后，△ PCQ 的面积等于△ ABC 面积的一半•1 1 1则根据题意，得 2(6 — x ) 2x =2 x2 x6 X8.整理，得 x 2— 6x +12 = 0.由于此方程没有实数根，所以不存在使厶 PCQ 的面积等于ABC 面积一半的时刻•说明 本题虽然是一道动态型应用题，但它又要运用到行程的知识，求解时必须依据路程=速度x 时间.十、梯子问题例10 一个长为10m 的梯子斜靠在墙上，梯子的底端距墙角6m.(1) 若梯子的顶端下滑1m ，求梯子的底端水平滑动多少米？ (2) 若梯子的底端水平向外滑动 1m ，梯子的顶端滑动多少米？(3 )如果梯子顶端向下滑动的距离等于底端向外滑动的距离，那么滑动的距离是多少米？解 依题意，梯子的顶端距墙角 =8 (m ).(1 )若梯子顶端下滑1m ，则顶端距地面7m.设梯子底端滑动x m.因为/ C = 90?/SPAN>，所以AB ="汙\取匸=用卜『=10(cm )(2)点P、Q在移动过程中，是否存在某一时刻，使得△PCQ的面积等于△ ABC的则根据勾股定理，列方程72+(6+ x)2= 102，整理，得x2+12 x—15 = 0 ,解这个方程，得X i~ 1.14 , X213.14 (舍去)，所以梯子顶端下滑1m，底端水平滑动约1.14m.(2)当梯子底端水平向外滑动1m时，设梯子顶端向下滑动x m.则根据勾股定理，列方程(8 —X)2+(6+1)2= 100.整理，得X2—16X+13 = 0.解这个方程，得X1~ 0.86 , X2 ~ 15.14 (舍去).所以若梯子底端水平向外滑动1m，则顶端下滑约0.86m.(3)设梯子顶端向下滑动x m时，底端向外也滑动x m.则根据勾股定理，列方程(8 —X)2+(6+X)2= 102，整理，得2x2—4x = 0,解这个方程，得X1 = 0 (舍去)，X2= 2.所以梯子顶端向下滑动2m时，底端向外也滑动2m.说明求解时应注意无论梯子沿墙如何上下滑动，梯子始终与墙上、地面构成直角三角形.十一、航海问题例11如图5所示，我海军基地位于A处，在其正南方向200 海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D恰好位于AC 的中点，岛上有一补给码头；小岛F位于BC上且恰好处于小岛D的正南方向，一艘军舰从A出发，经B到C匀速巡航•一艘补给船同时从D出发，沿南偏西方向匀速直线航行，欲将一批物品送往军舰.(1)小岛D和小岛F相距多少海里?(2)已知军舰的速度是补给船的2倍，军舰在由B到C的途中与补给船相遇于E处，那么相遇时补给船航行了多少海里？(精确到0.1海里)解(1) F位于D的正南方向，贝U DF丄BC•因为AB丄BC, D为AC的中点，所以DF =2 AB = 100海里，所以，小岛D与小岛F相距100海里.(2 )设相遇时补给船航行了x海里，那么DE = x海里，AB+BE= 2x海里，EF= AB+BC -(AB+ BE)—CF= (300 - 2x)海里.在Rt△ DEF中，根据勾股定理可得方程x2= 100 2+(300 - 2x)2，整理，得3x2-1200 x+100000 = 0.lOtK/6 10(K/6解这个方程，得X1 = 200 —孑 ~ 118.4 , X2 = 200+3 (不合题意，舍去)•所以，相遇时补给船大约航行了118.4海里.说明求解本题时，一定要认真地分析题意，及时发现题目中的等量关系，并能从图形中寻找直角三角形，以便正确运用勾股定理布列一元二次方程十二、图表信息例12 如图6所示，正方形ABCD的边长为12，划分成12 X12个小正方形格，将边长为n (n 为整数，且2w n< 11 )的黑白两色正方形纸片按图中的方式，黑白相间地摆放，第一张n Xi的纸片正好盖住正方形ABCD左上角的n刈个小正方形格，第二张纸片盖住第一张纸片的部分恰好为(n - 1) X n —1)个小正方形.如此摆放下去，直到纸片盖住正方形ABCD的右下角为止.请你认真观察思考后回答下列问题：(1)由于正方形纸片边长n的取值不同，冼成摆放时所使用正方形纸片的张数也不同，请填写下表：纸片的边长n23456使用的纸片张数（2 ）设正方形ABCD被纸片盖住的面积（重合部分只计一次）为S i，未被盖住的面积为S2.①当n = 2时，求S i : S2的值;解（1 ）依题意可依次填表为: 11、10、9、8、7.②是否存在使得S i = S2的n值？若存在，请求出来；若不存在，请说明理由(2) S1 = n2+(12 - n)[n2—(n - 1)2] = - n2+25 n - 12.①当n = 2 时，S1 = - 22+25 X2 - 12 = 34 , S2= 12 X12 - 34 = 110.所以S1 : S2 = 34 : 110 = 17 : 55.1②若S1 = S2，则有—n2+25 n —12 =? X122，即n2—25 n +84 = 0 ,解这个方程，得n1 = 4 , n2= 21 (舍去).所以当n = 4时，S1= S2.所以这样的n值是存在的.说明求解本题时要通过阅读题设条件及提供的图表，及时挖掘其中的隐含条件，对于求解第（3）小题，可以先假定问题的存在，进而构造一元二次方程，看得到的一元二次方程是否有实数根来加以判断.十三、探索在在问题例13 将一条长为20cm 的铁丝剪成两段，并以每一段铁丝的长度为周长做成一个正方形.（1）要使这两个正方形的面积之和等于17cm 2，那么这段铁丝剪成两段后的长度分别是多少？(2)两个正方形的面积之和可能等于 12cm 2吗？若能，求出两段铁丝的长度； 若不能, 请说明理由解(1)设剪成两段后其中一段为 x cm ，则另一段为(20 — x ) cm.当 x = 16 时，20 — x = 4，当 x = 4时，20 — x = 16 , 答 这段铁丝剪成两段后的长度分别是4cm 和16cm.(2)不能.理由是：不妨设剪成两段后其中一段为 y cm ，则另一段为(20 — y ) cm.则由题意得I 4丿+1 4丿=12，整理，得 y 2— 20 y +104 = 0,移项并配方，得(y — 10) 2 =—4v 0,所以此方程无解，即不能剪成两段使得面积和为12cm 2.说明 本题的第(2 )小问也可以运用求根公式中的 b 2 — 4ac 来判定 若b 2 — 4ac >0,方程有两个实数根，若 b 2— 4ac v 0，方程没有实数根，本题中的b 2 — 4ac =— 16 v 0即无解.十四、平分几何图形的周长与面积问题例14 如图7,在等腰梯形 ABCD 中，AB = DC = 5 , AD = 4 , BC = 10.点E?^下底边BC 上，点F 在腰AB 上.(1 )若EF 平分等腰梯形 ABCD 的周长，设BE 长为X ,试用含x 的代数式表示 △ BEF 的面积； (2) 是否存在线段 EF 将等腰梯形ABCD 的周长和面积同时平分？若存在，求出此时BE 的长；若不存在，请说明理由；(3) 是否存在线段 EF 将等腰梯形ABCD 的周长和面积同时分成1 : 2的两部分？若存在，求此时BE 的长；若不存在，请说明理由则根据题意，得 =17,解得 X i = 16X 2 = 4 ,Be K解(1 )由已知条件得，梯形周长为12，高4，面积为28.过点F作FG丄BC于G,过点A作AK丄BC于K.12 - K则可得，FG= 总,込24所以S A BEF=BEFG=—§ x2+ x (7 < x < 10).2 24(2)存在.由 (1 )得—5 x2+ 5 x = 14，解这个方程，得x i = 7, X2 = 5 (不合题意，舍去),所以存在线段EF将等腰梯形ABCD的周长与面积同时平分，此时BE= 7.(3)不存在•假设存在，显然有S A BEF : S多边形AFECD = 1 : 2,2 16 28即(BE+BF)：(AF+AD + DC) = 1 : 2.则有一5 x2+ 5 x =3 ,整理，得3x2—24x+70 = 0,此时的求根公式中的b2—4ac = 576 —840 V 0,所以不存在这样的实数X.即不存在线段EF将等腰梯形ABCD的周长和面积同时分成1 : 2的两部分.说明求解本题时应注意：一是要能正确确定x的取值范围；二是在求得X2 = 5时，并不属于7 < X W 10,应及时地舍去；三是处理第(3)个问题时的实质是利用一元二次方程来探索问题的存在性.十五、利用图形探索规律例15 在如图8中，每个正方形有边长为1的小正方形组成:（1 ）观察图形，请填写下列表格：正方形边长 13黑色小正方形个数 正方形边长 24黑色小正方形个数（2 ）在边长为n （n > 1）的正方形中，设黑色小正方形的个数为个数为P 2,问是否存在偶数.n ,使P 2= 5P i ?若存在，请写出 n 的值；若不存在，请说明 理由.解（1）观察分析图案可知正方形的边长为 1、3、5、7、…、n 时，黑色正方形的个 数为1、5、9、13、2n — 1 （奇数）；正方形的边长为2、4、6、8、…、n 时，黑色正方形 的个数为4、& 12、16、2n （偶数）•（2 ）由（1 ）可知n 为偶数时P 1 = 2 n ,所以P 2= n 2— 2n .根据题意，得n 2 — 2 n = 5 x 2n ,即n 2 —12 n = 0,解得n 1= 12 , n 2 = 0 （不合题意，舍去）.所以存在偶数n = 12，使得P 2 =5P 1.n （奇数）n （偶数）P i ，白色小正方形的说明本题的第（2）小问是属于存在性问题，求解时，可以先假设结论存在，进而从中找到数量关系，使问题获解综上所言，列一元二次方程解应用题是列一元一次方程、二元一次方程组解应用题的延续和发展，列方程解应用题就是先把实际问题抽象为方程模型，然后通过解方程获得对实际问题的解决.列一元二次方程解应用题的关键是：找出未知量与已知量之间的联系，从而将实际问题转化为方程模型，要善于将普通语言转化为代数式，在审题时，要特别注意关键词语，如“多少、快、慢、和、差、倍、分、超过、剩余、增加、减少”等等，此外，还要掌握一些常用的公式或特殊的等量关系，如特殊图形的面积公式、行程问题、工程问题、增长率问题中的一些特殊关系等等.。