2014届高三理科数学一轮复习试题选编9：正余弦定理(教师版)--带详细答案

第七节 正弦定理和余弦定理1．正弦定理 2．余弦定理 3．三角形的面积公式第一课时 正弦定理和余弦定理(一) 考点一 利用正、余弦定理解三角形考法(一) 正弦定理解三角形[典例] (1)在△ABC 中，a ＝3，b ＝2，A ＝30°，则cos B ＝________.(2)设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .若a ＝3，sin B ＝12，C ＝π6，则b ＝________.考法(二) 余弦定理解三角形[典例] (1)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若b cos A ＋a cos B ＝c 2，a ＝b ＝2，则△ABC 的周长为( ) A ．7.5 B ．7 C ．6 D ．5(2)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且c －b 2c －a ＝sin Asin B ＋sin C，则角B ＝________. [题组训练]1.△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若b 2＝ac ，c ＝2a ，则cos C ＝( ) A.24 B ．－24 C.34 D ．－342.△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知sin B ＋sin A (sin C －cos C )＝0，a ＝2，c ＝2，则C ＝( ) A.π12 B.π6 C.π4 D.π33.在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知sin 2B ＋sin 2C ＝sin 2A ＋sin B sin C . (1)求角A 的大小；(2)若cos B ＝13，a ＝3，求c 的值．考点二 判定三角形的形状[典例] (1)设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若b cos C ＋c cos B ＝a sin A ，则△ABC 的形状为( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不确定(2)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若sin A sin B ＝a c ，(b ＋c ＋a )(b ＋c －a )＝3bc ，则△ABC 的形状为( ) A ．直角三角形B ．等腰非等边三角形C ．等边三角形D ．钝角三角形[变透练清]1.(变条件)若本例(1)条件改为“a sin A ＋b sin B <c sin C ”，那么△ABC 的形状为________．2.(变条件)若本例(1)条件改为“c －a cos B ＝(2a －b )cos A ”，那么△ABC 的形状为________．3.(变条件)若本例(2)条件改为“cos A cos B ＝ba＝2”，那么△ABC 的形状为________．[课时跟踪检测]1．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .若sin A a ＝cos Bb ，则B 的大小为( )A ．30°B ．45°C ．60°D ．90°2．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .已知b ＝40，c ＝20，C ＝60°，则此三角形的解的情况是( )A ．有一解B ．有两解C ．无解D ．有解但解的个数不确定3．在△ABC 中，cos B ＝ac (a ，b ，c 分别为角A ，B ，C 的对边)，则△ABC 的形状为( )A ．直角三角形B ．等边三角形C ．等腰三角形D ．等腰三角形或直角三角形4．在△ABC 中，a ，b ，c 分别是内角A ，B ，C 的对边．若b sin A ＝3c sin B ，a ＝3，cos B ＝23，则b＝( )A ．14B ．6 C.14 D. 65．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，若a sin B cos C ＋c sin B cos A ＝12b ，且a >b ，则B ＝( )A.π6B.π3C.2π3D.5π66．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若2(b cos A ＋a cos B )＝c 2，b ＝3,3cos A ＝1，则a ＝( )A. 5 B ．3 C.10 D ．47．在△ABC 中，AB ＝6，A ＝75°，B ＝45°，则AC ＝________.8．设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且a ＝2，cos C ＝－14，3sin A ＝2sin B ，则c＝________.9．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .若a ＝7，b ＝2，A ＝60°，则sin B ＝________，c ＝________.10．在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对的边，sin A ，sin B ，sin C 成等差数列，且a ＝2c ，则cos A ＝________.11．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且A ＝2B . (1)求证：a ＝2b cos B ； (2)若b ＝2，c ＝4，求B 的值．12．在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且2a sin A ＝(2b ＋c )sin B ＋(2c ＋b )sin C . (1)求A 的大小； (2)若sin B ＋sin C ＝1，试判断△ABC 的形状．第二课时 正弦定理和余弦定理(二)考点一 有关三角形面积的计算[典例] (1)△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，已知b ＝7，c ＝4，cos B ＝34，则△ABC 的面积等于( ) A ．37 B.372 C ．9 D.92(2)△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .若△ABC 的面积为34(a 2＋c 2－b 2)，则B ＝______. [变透练清]1.(变条件)本例(1)的条件变为：若c ＝4，sin C ＝2sin A ，sin B ＝154，则S △ABC ＝________. 2.(变结论)本例(2)的条件不变，则C 为钝角时，ca 的取值范围是________．3．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，(2b －a )cos C ＝c cos A . (1)求角C 的大小；(2)若c ＝3，△ABC 的面积S ＝433，求△ABC 的周长．考点二 平面图形中的计算问题[典例] 如图，在平面四边形ABCD 中，∠ABC ＝3π4，AB ⊥AD ，AB ＝1.(1)若AC ＝5，求△ABC 的面积； (2)若∠ADC ＝π6，CD ＝4，求sin ∠CAD .[题组训练]1.如图，在△ABC 中，D 是边AC 上的点，且AB ＝AD,2AB ＝3BD ，BC ＝2BD ，则sin C 的值为________．2.如图，在平面四边形ABCD 中，DA ⊥AB ，DE ＝1，EC ＝7，EA ＝2，∠ADC ＝2π3，且∠CBE ，∠BEC ，∠BCE 成等差数列．(1)求sin ∠CED ；(2)求BE 的长．考点三 三角形中的最值、范围问题[典例] (1)在△ABC 中，内角A ，B ，C 对应的边分别为a ，b ，c ，A ≠π2，sin C ＋sin(B －A )＝2sin 2A ，则角A 的取值范围为( )A.⎝⎛⎦⎤0，π6B.⎝⎛⎦⎤0，π4C.⎣⎡⎦⎤π6，π4D.⎣⎡⎦⎤π6，π3 (2)已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且cos 2A ＋cos 2B ＝2cos 2C ，则cos C 的最小值为( )A.32 B.22 C.12 D ．－12[题组训练]1．在钝角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，B 为钝角，若a cos A ＝b sin A ，则sin A ＋sin C 的最大值为( ) A. 2 B.98 C ．1 D.782．在△ABC 中，已知c ＝2，若sin 2A ＋sin 2B －sin A sin B ＝sin 2C ，则a ＋b 的取值范围为________． 3．已知在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且cos B b ＋cos C c ＝sin A3sin C .(1)求b 的值；(2)若cos B ＋3sin B ＝2，求△ABC 面积的最大值．考点四 解三角形与三角函数的综合应用考法(一) 正、余弦定理与三角恒等变换[典例] 在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知 b sin A ＝ac os ⎝⎛⎭⎫B －π6. (1)求角B 的大小；(2)设a ＝2，c ＝3，求b 和sin(2A －B )的值．考法(二) 正、余弦定理与三角函数的性质[典例] 已知函数f (x )＝c os 2x ＋3sin(π－x )c os(π＋x )－12.(1)求函数f (x )在[0，π]上的单调递减区间；(2)在锐角△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知f (A )＝－1，a ＝2，b sin C ＝a sin A ，求△ABC 的面积．[对点训练]在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，(2a －c )cos B －b cos C ＝0. (1)求角B 的大小；(2)设函数f (x )＝2sin x cos x cos B －32cos 2x ，求函数f (x )的最大值及当f (x )取得最大值时x 的值． [课时跟踪检测]1．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，cos 2A ＝sin A ，bc ＝2，则△ABC 的面积为( ) A.12 B.14C ．1D ．22．在△ABC 中，a ，b ，c 分别是角A ，B ，C 所对的边，若(2a ＋c )cos B ＋b cos C ＝0，则角B 的大小为( ) A.π6 B.π3 C.2π3 D.5π63．在锐角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若sin A ＝223，a ＝3， S △ABC ＝22，则b 的值为( ) A ．6 B ．3 C ．2 D ．2或34．在△ABC 中，已知AB ＝2，AC ＝5，t a n ∠BAC ＝－3，则BC 边上的高等于( ) A ．1 B. 2 C. 3 D ．25．已知a ，b ，c 分别是△ABC 的内角A ，B ，C 的对边，且a sin B ＝3b cos A ，当b ＋c ＝4时，△ABC 面积的最大值为( )A.33 B.32C. 3 D ．2 3 6．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若bc ＝1，b ＋2c cos A ＝0，则当角B 取得最大值时，△ABC 的周长为( )A ．2＋ 3B ．2＋ 2C ．3D ．3＋ 27．在△ABC 中，B ＝120°，AC ＝7，AB ＝5，则△ABC 的面积为________．8．在△ABC 中，三个内角A ，B ，C 的对边分别为a ，b ，c ，若 12b cos A ＝sin B ，且a ＝23，b ＋c ＝6，则△ABC 的面积为________．9．已知在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，∠BAC ＝π2，点D 在边BC 上，AD ＝1，且BD ＝2DC ，∠BAD ＝2∠DAC ，则sin Bsin C＝________.10．如图所示，在△ABC 中，C ＝π3，BC ＝4，点D 在边AC 上，AD ＝DB ，DE ⊥AB ，E为垂足，若DE ＝22，则cos A ＝________.11．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知c (1＋cos B )＝b (2－cos C )． (1)求证：2b ＝a ＋c ；(2)若B ＝π3，△ABC 的面积为43，求b .12．在△ABC 中，AC ＝6，cos B ＝45，C ＝π4.(1)求AB 的长；(2)求c os ⎝⎛⎭⎫A －π6的值．。

易失分点清零（十一)解析几何（一)1。

若过点A（4,0）的直线l与曲线(x－2）2＋y2＝1有公共点,则直线l的斜率的取值范围为（)．A．［－3,错误!］B．（－错误!，错误!）C.错误!D.错误!解析易知直线的斜率存在，设直线方程为y ＝k（x－4),即kx－y－4k＝0，直线l与曲线(x－2）2＋y2＝1有公共点，圆心到直线的距离小于等于半径，d＝错误!≤1，得4k2≤k2＋1，k2≤错误!，解得－错误!≤k≤错误!，故选C.答案C2．已知点P在曲线y＝错误!上，α为曲线在点P处的切线的倾斜角，则α的取值范围为（）．A.错误!B。

错误!C。

错误!D。

错误!解析设曲线在点P处的切线斜率为k，则k＝y′＝错误!＝错误!，因为e x>0,所以由均值不等式，得k≥错误!。

又k〈0,所以－1≤k〈0,即－1≤tan α〈0.所以错误!≤α〈π.答案D3．直线x－2y＋1＝0关于直线x＝1对称的直线是（)．A．x＋2y－1＝0 B．2x＋y－1＝0C．2x＋y－3＝0 D．x＋2y－3＝0解析点（x，y）关于直线x＝1的对称点为(2－x，y），2－x－2y ＋1＝0⇒x＋2y－3＝0.答案D4．圆（x＋2）2＋y2＝5关于原点（0,0)对称的圆的方程为（)．A．（x－2）2＋y2＝5 B．x2＋(y－2)2＝5C．（x＋2）2＋（y＋2）2＝5 D．x2＋（y＋2）2＝5解析根据圆自身的对称性，原圆心(－2，0）对称后的圆心(2，0）,两圆为等圆,不同处在于圆心变化了,所以对称后圆的方程为（x－2)2＋y2＝5。

答案A5．已知圆的方程为(x－1)2＋(y－1）2＝9，点P（2,2）是该圆内一点，过点P的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积是（）．A．3错误!B．4错误!C．5错误!D．6错误!解析依题意，知圆的最长弦为直径,最短弦为过点P且垂直于最长弦的弦，所以|AC|＝2×3＝6.又因为圆心到BD的距离为2－12＋2－12＝错误!,所以|BD|＝2错误!＝2错误!。

2014年全国高考理科数学试题选编五.三角函数及解三角形试题一.选择题和填空题1全国课标Ⅰ6．如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示成x 的函数f (x )，则y ＝f (x )在[0，π]的图像大致为( )．2.全国课标Ⅰ.8．.设π0,2α⎛⎫∈ ⎪⎝⎭，π0,2β⎛⎫∈ ⎪⎝⎭，且1sin tan cos βαβ+=，则( )．A ．π32αβ-＝B ．π32αβ+=C ．π22αβ-=D ．π22αβ+=3.(课标全国Ⅱ4)钝角三角形ABC 的面积是12，AB ＝1，BC ，则AC ＝( )． A ．5 BC ．2D ．14.(2014课标全国Ⅱ.12)设函数π()3sin xf x m=.若存在f (x )的极值点x 0满足22200+[()]x f x m <，则m 的取值范围是( )． A ．(－∞，－6)∪(6，＋∞) B ．(－∞，－4)∪(4，＋∞) C ．(－∞，－2)∪(2，＋∞) D ．(－∞，－1)∪(1，＋∞) 5. (大纲全国.3)设a ＝sin 33°，b ＝cos 55°， c ＝tan 35°，则( )． A ．a ＞b ＞c B ．b ＞c ＞a C ．c ＞b ＞a D ．c ＞a ＞b 6.（陕西2)函数()πcos 26f x x ⎛⎫- ⎪⎝⎭＝的最小正 周期是( )．A ．π2B ．πC ．2πD ．4π 7.(安徽.6)设函数f (x )(x ∈R )满足f (x ＋π)＝f (x )＋sin x ．当0≤x ＜π时， f (x )＝0，则23π6f ⎛⎫⎪⎝⎭＝( )． A ．12 BC ．0D ．12-8.(浙江4)为了得到函数y ＝sin 3x ＋cos 3x 的图象，可以将函数 3y x =的图象( )．A ．向右平移π4个单位 B ．向左平移π4个单位 C ．向右平移π12个单位 D ．向左平移π12个单位9.(江西4)在△ABC 中，内角A ，B ，C 所对的边 分别为a ，b ，c ，若c 2＝(a －b )2＋6，π3C =， 则△ABC 的面积是( )．A ．3 B．2 C．2D．10.(辽宁9)将函数π3sin 23y x ⎛⎫=+ ⎪⎝⎭的图象向右平移π2个单位长度，所得图象对应的函数( )．A ．在区间π7π1212⎡⎤⎢⎥⎣⎦，上单调递减B ．在区间π7π1212⎡⎤⎢⎥⎣⎦，上单调递增C ．在区间ππ63⎡⎤-⎢⎥⎣⎦，上单调递减D ．在区间ππ63⎡⎤-⎢⎥⎣⎦，上单调递增11.(四川3)为了得到函数y ＝sin(2x ＋1)的图象， 只需把函数y ＝sin 2x 的图象上所有的点( )．A ．向左平行移动12个单位长度 B ．向右平行移动12个单位长度C ．向左平行移动1个单位长度D ．向右平行移动1个单位长度12.(重庆10)已知△ABC 的内角A ，B ，C 满足 sin 2A ＋sin(A －B ＋C )＝sin(C －A －B )＋12， 面积S 满足1≤S ≤2，记a ，b ，c 分别为 A ，B ，C 所对的边，则下列不等式一定成 立的是( )．A ．bc (b ＋c )＞8B ．ab (a ＋b )＞ C ．6≤abc ≤12 D ．12≤abc ≤2413.全国课标Ⅰ.16．已知a ，b ，c 分别为△ABC 三个内角A ，B ，C 的对边，a ＝2， 且(2＋b )(sin A －sin B )＝(c －b )sin C ， 则△ABC 面积的最大值为__________． 14.（全国课标Ⅱ.14)函数f (x )＝sin(x ＋2φ)－2sin φcos(x ＋φ)的最 大值为__________．15.（大纲全国.16)若函数f (x )＝cos 2x ＋a sin x 在区间ππ,62⎛⎫⎪⎝⎭是减函数，则a 的取值范围是__．16.（北京14)设函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ是常数，A ＞0，ω＞0)．若f (x )在区间ππ,62⎡⎤⎢⎥⎣⎦上具有单调性，且π2ππ236f f f ⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则f (x )的最小正周期为__________．17.（安徽.11)若将函数()πsin 24f x x ⎛⎫+ ⎪⎝⎭＝的图象向右平移φ个单位，所得图象关于y 轴对称，则φ的最小正值是__________．18.（天津.12)在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c .已知14b c a -=,2sin B ＝3sin C ，则cos A 的值为__________．19.（福建.12)在△ABC 中，A ＝60°，AC ＝4，BC =ABC 的面积等于_____． 20. (广东12)在△ABC 中，角A ，B ，C 所对应的 边分别为a ，b ，c ，已知b cos C ＋c cos B ＝2b ， 则ab＝________. 21.(四川13)如图，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为67°，30°，此时气球的高是46 m ，则河流的宽度BC 约等于__________m ．(用四舍五入法将结果精确到个位．参考数据：sin 67°≈0.92，cos 67°≈0.39，sin 37°≈0.60，cos 37°≈0.801.73)二.解答题1. (大纲全国117满分10分)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知3a cos C ＝2c cos A ，1tan 3A =，求B .2. (陕西16满分)△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c .(1)若a ，b ，c 成等差数列，证明：sin A ＋sin C ＝2sin(A ＋C )；(2)若a ，b ，c 成等比数列，求cos B 的最小值． 3. (北京15满分13分)如图， 在△ABC 中，π3B ∠=，AB ＝8， 点D 在BC 边上，且CD ＝2，1cos 7ADC ∠=. (1)求sin ∠BAD ； (2)求BD ，AC 的长．4. (天津15满分13分)已知函数()2πcos sin 3f x x x x ⎛⎫⋅+ ⎪⎝⎭=，x ∈R . (1)求f (x )的最小正周期； (2)求f (x )在闭区间ππ,44⎡⎤-⎢⎥⎣⎦上的最大值和最小值． 5. (安徽16满分12分)设△ABC 的内角A ，B ，C 所对边的长分别是a ，b ，c ，且b ＝3，c ＝1， A ＝2B . (1)求a 值；(2)求πsin()4A +的值． 6. (福建16满分13分)已知函数f (x )＝cos x (sin x ＋cos x )－12. (1)若π02α<<，且sin α=，求f (α)的值； (2)求函数f (x )的最小正周期及单调递增区间． 7. (湖北.17满分11分)某实验室一天的温度(单位：℃)随时间t (单位：h)的变化近似满足函数关系：()ππ10sin 1212f t t t -⋅-=，t ∈[0,24)． (1)求实验室这一天的最大温差；(2)若要求实验室温度不高于11 ℃，则在哪段时间实验室需要降温？8. (湖南18满分12分)如图，在平面四边形ABCD中，AD ＝1，CD ＝2，AC =.(1)求cos ∠CAD 的值； (2)若cos BAD ∠=，sin 6CBA ∠=，求BC 的长．9. (浙江18满分14分)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知a ≠b，c =22cos cos cos cos A B A A B B -. (1)求角C 的大小；(2)若4sin 5A =，求△ABC 的面积． 10. (广东.16满分12分)已知函数π()sin 4f x A x ⎛⎫=+ ⎪⎝⎭，x ∈R ，且5π3122f ⎛⎫= ⎪⎝⎭. (1)求A 的值；(2)若()3()2f f θθ-+＝，π02θ⎛⎫∈ ⎪⎝⎭，， 求3π4f θ⎛⎫-⎪⎝⎭. 11. (江西16满分12分)已知函数 f (x )＝sin(x ＋θ)＋a cos(x ＋2θ)，其中a ∈R ，ππ,22θ⎛⎫∈- ⎪⎝⎭. (1)当a =π4θ=时，求f (x )在区间[0，π]上的最大值与最小值； (2)若π02f ⎛⎫=⎪⎝⎭，f (π)＝1，求a ，θ的值． 12. (辽宁17满分12分)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且a ＞c .已知2BA BC ⋅=，1cos 3B =，b ＝3.求：(1)a 和c 的值； (2)c os(B －C )的值．13. (山东16满分12分)已知向量a ＝(m ，cos 2x )， b ＝(sin 2x ，n )，函数f (x )＝a ·b ，且y ＝f (x )的图象过点π12⎛⎝和点2π,23⎛⎫- ⎪⎝⎭. (1)求m ，n 的值；(2)将y ＝f (x )的图象向左平移φ(0＜φ＜π)个单位后得到函数y ＝g (x )的图象，若y ＝g (x )图象上各最高点到点(0,3)的距离的最小值为1，求y ＝g (x )的单调递增区间．14. (四川16满分12分)已知函数()πsin 34f x x ⎛⎫+ ⎪⎝⎭＝.(1)求f (x )的单调递增区间；(2)若α是第二象限角，4πcos cos 2354f ααα⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，求cos α－sin α的值．15. (重庆17满分13分)已知函数 f (x )＝1π)0,22x ωϕωϕ⎛⎫>-≤< ⎪⎝⎭＋的图象关于直线π3x =对称，且图象上相邻两个最高点的距离为π. (1)求ω和φ的值；(2)若π2π263f αα⎛⎫⎫=<< ⎪⎪⎝⎭⎝⎭，求3πcos 2α⎛⎫+ ⎪⎝⎭的值．.五.三角函数及解三角形试题解析一.选择题和填空题1全国课标Ⅰ6．如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示成x 的函数f (x )，则y ＝f (x )在[0，π]的图像大致为( )．解析：由题意|OM |＝|cos x |，f (x )＝|OM ||sin x |＝|sin x cos x |＝1sin 22x ，由此可知C 正确．2.全国课标Ⅰ.8．.设π0,2α⎛⎫∈ ⎪⎝⎭，π0,2β⎛⎫∈ ⎪⎝⎭，且1sin tan cos βαβ+=，则( )．A ．π32αβ-＝B ．π32αβ+=C ．π22αβ-=D ．π22αβ+=解析：由已知，得sin 1sin cos cos αβαβ+=， ∴sin αcos β＝cos α＋cos αsin β.∴sin αcos β－cos αsin β＝cos α. ∴sin(α－β)＝cos α，∴sin(α－β)＝πsin 2α⎛⎫-⎪⎝⎭. ∵π0,2α⎛⎫∈ ⎪⎝⎭，π0,2β⎛⎫∈ ⎪⎝⎭，∴ππ22αβ-<<－，ππ022α<-<，∴π2αβα-=-，∴π22αβ-=.故选C.3.(课标全国Ⅱ4)钝角三角形ABC 的面积是12，AB ＝1，BC ，则AC ＝( )． A ．5 BC ．2D ．1解析：由题意知S △ABC ＝12AB ·BC ·sin B ，即11122B =⨯，解得sin 2B =. ∴B ＝45°或B ＝135°. 当B ＝45°时，AC 2＝AB 2＋BC 2－2AB ·BC ·cos B＝2212112-⨯+. 此时AC 2＋AB 2＝BC 2，△ABC 为直角三角形， 不符合题意； 当B ＝135°时，AC 2＝AB 2＋BC 2－2AB ·BC ·cos B＝22121(5-⨯+＝，解得AC 符合题意．故选B. 4.(2014课标全国Ⅱ.12)设函数π()3sinx f x m=.若存在f (x )的极值点x 0满足22200+[()]x f x m <，则m 的取值范围是( )． A ．(－∞，－6)∪(6，＋∞) B ．(－∞，－4)∪(4，＋∞) C ．(－∞，－2)∪(2，＋∞) D ．(－∞，－1)∪(1，＋∞) 解析：∵x 0是f (x )的极值点，∴f ′(x 0)＝0，即0ππcos 0x m m=， 得0πππ2x k m =+，k ∈Z ， 即012x mk m =+，k ∈Z .∴x 02＋[f (x 0)]2＜m 2可转化为2221π122mk m mk m m m ⎤⎛⎫⎛⎫+++< ⎪ ⎪⎥⎝⎭⎝⎭⎦， k ∈Z ，即2221+32k m m ⎛⎫+< ⎪⎝⎭，k ∈Z ，即221312k m ⎛⎫+<- ⎪⎝⎭，k ∈Z .要使原问题成立，只需存在k ∈Z ，使223112k m ⎛⎫->+ ⎪⎝⎭成立即可．又212k ⎛⎫+ ⎪⎝⎭2的最小值为14，∴23114m ->，解得m ＜－2或m ＞2.故选C.5. (大纲全国.3)设a ＝sin 33°，b ＝cos 55°， c ＝tan 35°，则( )． A ．a ＞b ＞c B ．b ＞c ＞a C ．c ＞b ＞a D ．c ＞a ＞b解析：∵a ＝sin 33°，b ＝cos 55°＝sin 35°，sin 35tan 35cos35c ︒=︒=︒，∴sin 35sin 35sin 33cos35︒>︒>︒︒.∴c ＞b ＞a ，选C.6.（陕西2)函数()πcos 26f x x ⎛⎫- ⎪⎝⎭＝的最小正 周期是( )．A ．π2B ．πC ．2πD ．4π 解析：f (x )的最小正周期2ππ2T ==. 7.(安徽.6)设函数f (x )(x ∈R )满足 f (x ＋π)＝f (x )＋sin x ．当0≤x ＜π时， f (x )＝0，则23π6f ⎛⎫ ⎪⎝⎭＝( )． A ．12 BC ．0D ．12- 解析：由题意得23π17π17π11π11π17πsin sin +sin666666f f f ⎛⎫⎛⎫⎛⎫=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭7π17π11π11π17πsin sin +sin 66666f ⎫⎛⎫+=+⎪ ⎪⎭⎝⎭＝5π5π11π17π+sin +sin+sin 6666f ⎛⎫ ⎪⎝⎭ ＝111102222+-+=.8.(浙江4)为了得到函数y ＝sin 3x ＋cos 3x 的图象，可以将函数 3y x =的图象( )． A ．向右平移π4个单位 B ．向左平移π4个单位 C ．向右平移π12个单位D ．向左平移π12个单位解析：ππsin 3cos 332cos 3412y x x x x ⎡⎤⎛⎫⎛⎫=+=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦=ππcos 33412x x ⎡⎤⎛⎫⎛⎫-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦因此需将函数 3y x =的图象向右平移π12个单位．故选C.9.(江西4)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，若c 2＝(a －b )2＋6，π3C =， 则△ABC 的面积是( )． A ．3 BCD．解析：在△ABC 中，由已知条件及余弦定理可得c 2＝(a －b )2＋6＝a 2＋b 2－π2cos 3ab ， 整理得ab ＝6， 再由面积公式1sin 2S ab C =，得1π6sin 23ABC S ∆=⨯⨯=.故选C.10.(辽宁9)将函数π3sin 23y x ⎛⎫=+ ⎪⎝⎭的图象向右平移π2个单位长度，所得图象对应的函数( )． A ．在区间π7π1212⎡⎤⎢⎥⎣⎦，上单调递减 B ．在区间π7π1212⎡⎤⎢⎥⎣⎦，上单调递增 C ．在区间ππ63⎡⎤-⎢⎥⎣⎦，上单调递减 D ．在区间ππ63⎡⎤-⎢⎥⎣⎦，上单调递增 解析：设平移后的函数为f (x )，则()ππ3sin 223f x x ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦π3sin 2π3x ⎛⎫=+- ⎪⎝⎭π3sin 23x ⎛⎫=-+ ⎪⎝⎭.令πππ2π22π232k x k -≤+≤+，k ∈Z ，解得f (x )的递减区间为5ππππ+1212k k ⎡⎤-⎢⎥⎣⎦，，k ∈Z ，同理得递增区间为π7πππ+1212k k ⎡⎤+⎢⎥⎣⎦，，k ∈Z . 从而可判断得B 正确． 11.(四川3)为了得到函数y ＝sin(2x ＋1)的图象， 只需把函数y ＝sin 2x 的图象上所有的点( )． A ．向左平行移动12个单位长度 B ．向右平行移动12个单位长度 C ．向左平行移动1个单位长度D ．向右平行移动1个单位长度解析：∵y＝sin(2x＋1)＝1 sin 22x⎛⎫+⎪⎝⎭，∴需要把y＝sin 2x图象上所有的点向左平移1 2个单位长度即得到y＝sin(2x＋1)的图象．12.(重庆10)已知△ABC的内角A，B，C满足sin 2A＋sin(A－B＋C)＝sin(C－A－B)＋12，面积S满足1≤S≤2，记a，b，c分别为A，B，C所对的边，则下列不等式一定成立的是()．A．bc(b＋c)＞8 B．ab(a＋b)＞C．6≤abc≤12 D．12≤abc≤24 解析：由sin 2A＋sin(A－B＋C)＝sin(C－A－B)＋1 2得，sin 2A＋sin[A－(B－C)]＋sin[A＋(B－C)]＝12，所以sin 2A＋2sin A cos(B－C)＝1 2 .所以2sin A[cos A＋cos(B－C)]＝12，所以2sin A[cos(π－(B＋C))＋cos(B－C)]＝12，所以2sin A[－cos(B＋C)＋cos(B－C)]＝12，即得sin A sin B sin C＝1 8 .根据三角形面积公式S＝12ab sin C，①S＝12ac sin B，②S＝12bc sin A，③因为1≤S≤2，所以1≤S3≤8. 将①②③式相乘得1≤S3＝18a2b2c2sin A sin B sin C≤8，即64≤a2b2c2≤512，所以8≤abc≤，故排除C，D选项，而根据三角形两边之和大于第三边，故b＋c＞a，得bc(b＋c)＞8一定成立，而a＋b＞c，ab(a＋b)也大于8，而不一定大于，故选A.13.全国课标Ⅰ.16．已知a，b，c分别为△ABC三个内角A，B，C的对边，a＝2，且(2＋b)(sin A－sin B)＝(c－b)sin C，则△ABC面积的最大值为__________．解析：由正弦定理，可得(2＋b)(a－b)＝(c－b)·c.∵a＝2，∴a2－b2＝c2－bc，即b2＋c2－a2＝bc.由余弦定理，得2221cos22b c aAbc+-==.∴sin A=.由b2＋c2－bc＝4，得b2＋c2＝4＋bc.∵b2＋c2≥2bc，即4＋bc≥2bc，∴bc≤4.∴1sin2ABCS bc A∆=⋅≤，即(S△ABC)max＝14.（全国课标Ⅱ.14)函数f(x)＝sin(x＋2φ)－2sin φcos(x＋φ)的最大值为__________．解析：∵f(x)＝sin(x＋2φ)－2sin φcos(x＋φ)＝sin[(x＋φ)＋φ]－2sin φcos(x＋φ)＝sin(x＋φ)cos φ＋cos(x＋φ)sin φ－2sin φcos(x＋φ)＝sin(x＋φ)cos φ－cos(x＋φ)sin φ＝sin[(x＋φ)－φ]＝sin x.∴f(x)max＝1.15.（大纲全国.16)若函数f(x)＝cos 2x＋a sin x在区间ππ,62⎛⎫⎪⎝⎭是减函数，则a的取值范围是__．解析：f(x)＝cos 2x＋a sin x＝1－2sin2x＋a sin x.令t＝sin x，∵x∈ππ,62⎛⎫⎪⎝⎭，∴1,12t⎛⎫∈ ⎪⎝⎭，∴g(t)＝1－2t2＋at＝－2t2＋at＋1112t<<，由题意知1222a-≤⨯(-)，∴a≤2，∴a的取值范围为(－∞，2]．16.（北京14)设函数f(x)＝A sin(ωx＋φ)(A，ω，φ是常数，A＞0，ω＞0)．若f(x)在区间ππ,62⎡⎤⎢⎥⎣⎦上具有单调性，且π2ππ236f f f⎛⎫⎛⎫⎛⎫==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则f(x)的最小正周期为__________．解析：由f(x)在区间ππ,62⎡⎤⎢⎥⎣⎦上具有单调性，且ππ26f f⎛⎫⎛⎫=-⎪ ⎪⎝⎭⎝⎭知，f(x)有对称中心π,03⎛⎫⎪⎝⎭，由π2π23f f⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭知f(x)有对称轴1π27ππ22312x⎛⎫=+=⎪⎝⎭.记f(x)的最小正周期为T ，则1ππ226T ≥-，即2π3T ≥. 故7πππ12344T-==，解得T ＝π. 17.（安徽.11)若将函数()πsin 24f x x ⎛⎫+ ⎪⎝⎭＝的图象向右平移φ个单位，所得图象关于y 轴对称，则φ的最小正值是__________． 解析：把函数()πsin 24f x x ⎛⎫+ ⎪⎝⎭＝的图象向右平移φ个单位，得到()ππsin 2()sin(22)44f x x x ϕϕ⎛⎫-+=-+ ⎪⎝⎭＝的图象．由()πsin 224f x x ϕ⎛⎫-+⎪⎝⎭＝的图象关于y 轴 对称，所以ππ2π42k ϕ-+=+，k ∈Z .即ππ28k ϕ=--，k ∈Z . 当k ＝－1时，φ的最小正值是3π8.18.（天津.12)在△ABC 中，内角A ，B ，C 所对的 边分别是a ，b ，c .已知14b c a -=,2sin B ＝3sin C ， 则cos A 的值为__________． 解析：由2sin B ＝3sin C ，结合正弦定理得2b ＝3c ，又14b c a -=，所以32b c =，a ＝2c . 由余弦定理得222cos =2b c a A bc+-＝222322322c c c c c ⎛⎫+-() ⎪⎝⎭⋅⋅＝14-.19.（福建.12)在△ABC 中，A ＝60°，AC ＝4，BC =ABC 的面积等于_____．解析：由题意及余弦定理得222216121cos 2242b c a c A bc c +-+-===⨯⨯，解得c ＝2.所以S ＝12bc sin A ＝12×4×2×sin 60°＝故答案为20. (广东12)在△ABC 中，角A ，B ，C 所对应的 边分别为a ，b ，c ，已知b cos C ＋c cos B ＝2b ，则ab＝________. 解析：因为b cos C ＋c cos B ＝2b ，所以由正弦定理可得sin B cos C ＋sin C cos B ＝2sin B ， 即sin(B ＋C )＝2sin B ，所以sin(π－A )＝2sin B ，即sin A ＝2sin B . 于是a ＝2b ，即2ab=. 21.(四川13)如图，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为67°，30°，此时气球的高是46 m ，则河流的宽度BC 约等于__________m ．(用四舍五入法将结果精确到个位．参考数据：sin 67°≈0.92，cos 67°≈0.39，sin 37°≈0.60，cos 37°≈0.801.73)解析：如图所示，过A 作AD ⊥CB 且交CB 的延长线于D.在Rt △ADC 中，由AD ＝46 m ，∠ACB ＝30° 得AC ＝92 m.在△ABC 中，∠BAC ＝67°－30°＝37°， ∠ABC ＝180°－67°＝113°，AC ＝92 m ，由正弦定理sin sin AC BCABC BAC =∠∠，得92sin113sin37BC =︒︒，即92sin67sin37BC=︒︒，解得92sin3760m sin67BC ︒≈≈︒. 二.解答题1. (大纲全国117满分10分)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知3a cos C ＝2c cos A ，1tan 3A =，求B . 分析：通过3a cos C ＝2c cos A ，借助于正弦定理把a ，c 转化成关于A ，C 的三角函数值，由已知1tan 3A =，从而求出tan C ，再利用公式 tan B ＝－tan(A ＋C )求出B . 解：由题设和正弦定理得3sin A cos C ＝2sin C cos A .故3tan A cos C ＝2sin C ， 因为1tan 3A =，所以cos C ＝2sin C ，1tan 2C =. 所以tan B ＝tan[180°－(A ＋C )] ＝－tan(A ＋C )＝tan tan tan tan 1A CA C +-＝－1，即B ＝135°.2. (陕西16满分)△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c .(1)若a ，b ，c 成等差数列，证明：sin A ＋sin C ＝2sin(A ＋C )；(2)若a ，b ，c 成等比数列，求cos B 的最小值． 分析：在(1)问中结合等差数列性质，得出a ，b ，c 之间关系，再利用正弦定理转化为角的关系，进而结合三角形内角和为π，利用诱导公式将角B 转化为用角A 和C 来表示，从而达到证明目标等式．在(2)问利用等比数列基本性质，得出a ，b ，c 之间关系，再结合余弦定理，表达出cos B 的式子，依据基本不等式得出其范围，注意等号成立的条件．解：(1)∵a ，b ，c 成等差数列，∴a ＋c ＝2b . 由正弦定理得sin A ＋sin C ＝2sin B . ∵sin B ＝sin[π－(A ＋C )]＝sin(A ＋C )， ∴sin A ＋sin C ＝2sin(A ＋C )．(2)∵a ，b ，c 成等比数列，∴b 2＝ac . 由余弦定理得2222221cos 2222a cb ac ac ac ac B ac ac ac +-+--==≥=，当且仅当a ＝c 时等号成立． ∴cos B 的最小值为12. 3. (北京15满分13分)如图，在△ABC 中，π3B ∠=，AB ＝8，点D 在BC 边上，且CD ＝2，1cos 7ADC ∠=.(1)求sin ∠BAD ；(2)求BD ，AC 的长．分析：(1)先利用三角形中角之间的关系可得 ∠BAD ＝∠ADC －∠B ，然后即可利用两角差的正弦公式求解；(2)在△ABD 中，根据正弦定理，结合(1)即可求得BD ，然后在△ABC 中，直接利用余弦定理求AC 即可．解：(1)在△ADC 中，因为1cos 7ADC ∠=，所以sin ADC ∠. 所以sin ∠BAD ＝sin(∠ADC －∠B ) ＝sin ∠ADC cos B －cos ∠ADC sin B1127-=(2)在△ABD 中，由正弦定理得8sin 3sin AB BAD BD ADB ⋅∠==∠＝. 在△ABC 中，由余弦定理得 AC 2＝AB 2＋BC 2－2AB ·BC ·cos B ＝82＋52－2×8×5×12＝49. 所以AC ＝7.4. (天津15满分13分)已知函数()2πcos sin 3f x x x x ⎛⎫⋅+ ⎪⎝⎭=，x ∈R . (1)求f (x )的最小正周期； (2)求f (x )在闭区间ππ,44⎡⎤-⎢⎥⎣⎦上的最大值和最小值． 分析：(1)先利用两角和与差的正弦公式及二倍角的正弦、余弦公式，化简函数解析式为一个角的三角函数的形式，再求周期． (2)可利用函数f (x )在区间ππ,44⎡⎤-⎢⎥⎣⎦上的单调性求最值．解：(1)由已知，有()21cos sin 2f x x x x x ⎛⎫⋅ ⎪ ⎪⎝⎭=＝21sin cos 2x x x ⋅+＝1sin 2(1cos 2)444x x -++＝1sin 2cos 244x x =-＝1πsin 223x ⎛⎫- ⎪⎝⎭. 所以，f (x )的最小正周期2ππ2T ==. (2)因为f (x )在区间ππ,412⎡⎤--⎢⎥⎣⎦上是减函数，在区间ππ,124⎡⎤-⎢⎥⎣⎦上是增函数，π144f ⎛⎫-=- ⎪⎝⎭，π1122f ⎛⎫-=- ⎪⎝⎭，π144f ⎛⎫= ⎪⎝⎭， 所以，函数f (x )在闭区间ππ,44⎡⎤-⎢⎥⎣⎦上的最大值为14，最小值为12-.5. (安徽16满分12分)设△ABC 的内角A ，B ，C所对边的长分别是a ，b ，c ，且b ＝3，c ＝1，A ＝2B .(1)求a 值； (2)求πsin()4A +的值． 分析：(1)通过观察给出的条件及求解的问题，先将角的关系化为边的关系．首先由A ＝2B ，得sin A ＝sin 2B ，再由倍角公式将2B 的三角函数化为B 的三角函数，再由正弦定理、余弦定理将角的关系化为边的关系进行求解．(2)由(1)知三边都已确定，先由余弦定理求出cos A 的值，再利用平方关系求出sin A 的值，最后利用两角和的正弦公式求解． 解：(1)因为A ＝2B ，所以sin A ＝sin 2B ＝2sin B cos B .由正弦定理、余弦定理得2222a cb a b +-=⋅.因为b ＝3，c ＝1，所以a 2＝12，a =.(2)由余弦定理得22291121cos263b ca A bc +-+-===-. 由于0＜A ＜π，所以sin 3A ===故πππ2221242sin()sin cos cos sin ()44432326A A A -+=+=⨯+-⨯= ππ122c o s c o s 44A ++-.6. (福建16满分13分)已知函数f(x )＝cos x (sin x ＋cos x )－12.(1)若π02α<<，且sin 2α=，求f (α)的值；(2)求函数f (x )的最小正周期及单调递增区间．分析：首先结合已知角的范围，利用同角三角函数的基本关系式及已知的正弦值，求出余弦值，注意符号的判断，然后代入已知的函数关系式，得出结果．在第(2)问中，结合式子特点，利用二倍角公式、两角和与差的三角函数公式以及辅助角公式，得出最终的目标——y ＝A sin(ωx ＋φ)＋B 形式，运用2πT ω=得出周期，再结合三角函数的图象与性质等基础知识求得单调区间，此时要注意复合函数的单调性．另外，也可先化简再分别求解． 解法一：(1)因为π02α<<，sin 2α=，所以cos 2α=. 所以()11(22222fα=+-=. (2)因为 f (x )＝sin x cos x ＋cos 2x －12＝11cos21sin 2222x x ++- ＝11sin 2cos222x x + ＝π)24x +，所以2ππ2T ==. 由πππ2π22π242k x k -≤+≤+，k ∈Z ，得3ππππ88k x k -≤≤+，k ∈Z . 所以f (x )的单调递增区间为3πππ,π88k k ⎡⎤-+⎢⎥⎣⎦，k ∈Z . 解法二：f (x )＝sin x cos x ＋cos 2x －12＝11cos21sin 2222x x ++- ＝11sin 2cos222x x +＝π224x ⎛⎫+ ⎪⎝⎭. (1)因为π02α<<，sin α=， 所以π4α=， 从而()π3π1)442f αα+==.(2) 2ππ2T ==. 由πππ2π22π242k x k -≤+≤+，k ∈Z ，得3ππππ88k x k -≤≤+，k ∈Z . 所以f (x )的单调递增区间 为3πππ,π88k k ⎡⎤-+⎢⎥⎣⎦，k ∈Z. 7. (湖北.17满分11分)某实验室一天的温度(单位：℃)随时间t (单位：h)的变化近似满足函数关系：()ππ10sin 1212f t t t ⋅-=，t ∈[0,24)． (1)求实验室这一天的最大温差；(2)若要求实验室温度不高于11 ℃，则在哪段时间实验室需要降温？分析：由函数f (t )为a cos t ＋b sin t 型，故可利用辅助角公式对f (t )化简为f (t )＝10－2sin ππ123t ⎛⎫+⎪⎝⎭，再根据t ∈[0,24)，把ππ123t +的范围求出，再利用单位圆或者正弦函数的图象求出ππsin 123t ⎛⎫+⎪⎝⎭的范围，从而求得f (t )的最大与最小值．对于第(2)问，要求实验室温度不高于11 ℃，即满足不等式f (t )＞11的t 的范围就是实验室需要降温的时间段，可利用正弦曲线或单位圆来解三角不等式． 解：(1)因为()π1πππ102sin 102sin 12212123f t t t t ⎫⎛⎫+=-+⎪ ⎪⎪⎝⎭⎝⎭＝－，又0≤t ＜24，所以πππ7π+<31233t ≤， ππ1sin +1123t ⎛⎫≤≤ ⎪⎝⎭－.当t ＝2时，ππsin +1123t ⎛⎫= ⎪⎝⎭；当t ＝14时，ππsin +1123t ⎛⎫= ⎪⎝⎭.于是f (t )在[0,24)上取得最大值12，取得最小值8.故实验室这一天最高温度为12 ℃，最低温度 为8 ℃，最大温差为4 ℃.(2)依题意，当f (t )＞11时实验室需要降温． 由(1)得()ππ102sin +123f t t ⎛⎫⎪⎝⎭=-， 故有ππ102sin +11123t ⎛⎫>⎪⎝⎭-， 即ππ1sin +1232t ⎛⎫<- ⎪⎝⎭.又0≤t ＜24，因此7πππ11π61236t <+<， 即10＜t ＜18.在10时至18时实验室需要降温．8. (湖南18满分12分)如图，在平面四边形ABCD中，AD ＝1，CD ＝2，AC =.(1)求cos ∠CAD 的值； (2)若cos BAD ∠=，sin 6CBA ∠=，求BC 的长．分析：对于第(1)问，由已知△ACD 中三边求角，很容易想到利用余弦定理进行求解．对于第 (2)问，目标为求BC 的长度，而BC 是△ABC 中的边．又AC 已知，AC 所对的角∠CBA 的正弦已知，所以联想到利用正弦定理来求，但需要 ∠BAC 的正弦值．而已知中有cos ∠BAD 的值，发现∠BAC ＝∠BAD －∠CAD ，因此用两角差的正弦公式求得sin ∠BAC ，从而问题得解． 解：(1)如题图，在△ADC 中，由余弦定理，得222cos 2AC AD CD CAD AC AD+-∠=⋅.故由题设知，cos CAD ∠==(2)如题图，设∠BAC ＝α，则α＝∠BAD －∠CAD .因为cos 7CAD ∠=，cos 14BAD ∠=-， 所以cos CAD ∠sinBAD ∠于是sinα＝sin(∠BAD －∠CAD )＝sin ∠BAD cos ∠CAD －cos ∠BAD sin ∠CAD＝147⎛-⨯= ⎝⎭. 在△ABC 中，由正弦定理，sin sin BC AC CBAα=∠.故sin 3sin AC BC CBA α⋅===∠ 9. (浙江18满分14分)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知a ≠b，c =22cos cos cos cos A B A A B B -. (1)求角C 的大小；(2)若4sin 5A =，求△ABC 的面积．分析：(1)将已知等式运用二倍角的正、余弦公式和辅助角公式化为2A,2B 的三角函数式，结合角A ，B 的范围求出2A,2B 的关系式，然后求出角C .(2)由(1)知C ，又已知sin A ，c ，则可由sin sin a cA C=求出a ，则由 1sin 2ABC S ac B ＝知，只需求sin B 即可．结合B ＝π－(A ＋C )运用两角和的正弦公式可求sin B .解：(1)由题意得1cos 21cos 2 2 22A B A B ++-=， 11 2cos 2 2cos 222A AB B -=-，ππsin 2sin 266A B ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭，由a ≠b ，得A ≠B ，又A ＋B ∈(0，π)，得ππ22π66A B -+-=， 即2π3A B +=，所以π3C =.(2)由c =4sin =5A ，=sin sin a cA C，得8=5a .由a ＜c ，得A ＜C ，从而3cos 5A =，故sin B ＝sin(A ＋C )＝sin A cos C ＋cos A sin C＝410+. 所以△ABC 的面积为1sin 2S ac B ==10. (广东.16满分12分)已知函数π()sin 4f x A x ⎛⎫=+ ⎪⎝⎭，x ∈R ，且5π3122f ⎛⎫= ⎪⎝⎭. (1)求A 的值；(2)若()3()2f f θθ-+＝，π02θ⎛⎫∈ ⎪⎝⎭，， 求3π4f θ⎛⎫-⎪⎝⎭. 解：(1)∵π()sin 4f x A x ⎛⎫=+ ⎪⎝⎭， 且5π3122f ⎛⎫=⎪⎝⎭， ∴5π5ππ2πsin sin 121243f A A ⎛⎫⎛⎫=+= ⎪⎪⎝⎭⎝⎭＝32A ⋅=.∴A =(2)∵π()4f x x ⎛⎫=+ ⎪⎝⎭，且()3()=2f f θθ-+，∴()ππ()44f f θθθθ⎛⎫⎛⎫+-+-+ ⎪ ⎪⎝⎭⎝⎭ ππππsin cos cos sin sin cos cos sin 4444θθθθ⎤⎛⎫⎛⎫++- ⎪ ⎪⎥⎝⎭⎝⎭⎦π32cos sin=42θθ， ∴cos θ=，且π02θ⎛⎫∈ ⎪⎝⎭，.∴sin θ==. ∵3π3ππ444f θθ⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭π =4θθ-. 11. (江西16满分12分)已知函数f (x )＝sin(x ＋θ)＋a cos(x ＋2θ)，其中a∈R ，ππ,22θ⎛⎫∈- ⎪⎝⎭. (1)当a =π4θ=时，求f (x )在区间[0，π]上的最大值与最小值； (2)若π02f ⎛⎫=⎪⎝⎭，f (π)＝1，求a ，θ的值．分析：(1)先将a =π4θ=代入f (x )，再利用两角和的正弦公式和余弦公式对f (x )进行化简，最终化成一个三角函数值的形式，根据所给角的范围，借助于数形结合求出最大值和最小值；(2)利用所给条件列出方程联立成方程组求出a ，θ. 解：(1)ππ()sin 42f x x x ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭22πcos )cos sin sin 224x x x x x x ⎛⎫=-=- ⎪＋ πcos )2sin cos sin 224x x x x x ⎛⎫-=-=- ⎪⎝⎭＋，因为x ∈[0，π]，从而π3ππ,444x ⎡⎤-∈-⎢⎥⎣⎦.故f (x )在[0，π]，最小值为－1.(2)由π()0,2(π)0,f f ⎧=⎪⎨⎪=⎩得2cos (12sin )02sin sin 1,a a a θθθθ-=⎧⎨--=⎩， 又ππ,22θ⎛⎫∈- ⎪⎝⎭，知cos θ≠0，解得1,π.6a θ=-⎧⎪⎨=-⎪⎩12. (辽宁17满分12分)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且a ＞c .已知2BA BC ⋅=，1cos 3B =，b ＝3.求：(1)a 和c 的值； (2)c os(B －C )的值．分析：(1)将条件中的2BA BC ⋅=，转化为边角的量表示，可得a 与c 的关系，再结合余弦定理列方程组求解．(2)由(1)及正弦定理可得sin C ，进而求出c os C ，再由两角差的余弦公式求出c os(B －C )的值． 解：(1)由2BA BC ⋅=，得c ·ac os B ＝2. 又1cos 3B =，所以ac＝6. 由余弦定理，得a 2＋c2＝b 2＋2acc os B .又b ＝3，所以a 2＋c 2＝9＋2×2＝13.解226,13,ac a c=⎧⎨+=⎩得a ＝2，c ＝3或a ＝3，c ＝2. 因a ＞c ，所以a ＝3，c ＝2.(2)在△ABC 中，sin 3B ===，由正弦定理， 得2sin sin 339c C B b ==⋅=. 因a ＝b ＞c ，所以C 为锐角，因此7cos 9C ===. 于是c os(B －C )＝c os Bc os C ＋sin B sin C 17233927=⋅= 13. (山东16满分12分)已知向量a ＝(m ，cos 2x )， b ＝(sin 2x ，n )，函数f (x )＝a ·b ，且y ＝f (x )的 图象过点π12⎛ ⎝和点2π,23⎛⎫- ⎪⎝⎭. (1)求m ，n 的值；(2)将y ＝f (x )的图象向左平移φ(0＜φ＜π)个单位后得到函数y ＝g (x )的图象，若y ＝g (x )图象上各最高点到点(0,3)的距离的最小值为1，求y ＝g (x )的单调递增区间．分析：在第(1)问中，可先根据向量数量积坐标运算整理出f (x )的解析式，再由图象过两点，代入整理可得关于m ，n 的方程组，利用此方程组即得m ，n 的值．在第(2)问中，通过图象平移知识，可得含参数φ的g (x )的解析式，从中设出最高点，然后根据两点距离为1，可确定最高点的坐标，代入可求出g (x )确定的解析式，从而求出单调区间．解：(1)由题意知f (x )＝a·b ＝m sin 2x ＋n cos 2x . 因为y ＝f (x )的图象过点π12⎛⎝和2π,23⎛⎫- ⎪⎝⎭， 所以ππsin cos 664π4π2sin cos 33m n m n =+⎨⎪-=+⎪⎩，，即1,212,2m n =⎨⎪-=-⎪⎩ 解得m =n ＝1.(2)由(1)知()2cos2f x x x =+π2sin 26x ⎛⎫=+ ⎪⎝⎭.由题意知()π()2sin 226g x f x x ϕϕ⎛⎫=+=++ ⎪⎝⎭.设y ＝g (x )的图象上符合题意的最高点为(x 0,2)， 由题意知2011x +=，所以x 0＝0，即到点(0,3)的距离为1的最高点为(0,2)．将其代入y ＝g (x )得πsin 216ϕ⎛⎫+= ⎪⎝⎭， 因为0＜φ＜π，所以π6ϕ=.因此()π2sin 22cos 22g x x x ⎛⎫=+= ⎪⎝⎭， 由2k π－π≤2x ≤2k π，k ∈Z ，得πππ2k x k -≤≤，k ∈Z ，所以函数y ＝g (x )的单调递增区间 为ππ,π2k k ⎡⎤-⎢⎥⎣⎦，k ∈Z 14. (四川16满分12分)已知函数()πsin 34f x x ⎛⎫+ ⎪⎝⎭＝.(1)求f (x )的单调递增区间；(2)若α是第二象限角，4πcos cos 2354f ααα⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，求cos α－sin α的值．分析：在第(1)问，通过整体思想，将π34x +看作一个整体，借助y ＝sin x 的单调递增区间，解不等式求出x 的范围得到f (x )的单调递增区间，要注意k ∈Z 不要漏掉；在第(2)问，利用已知条件求出3f α⎛⎫⎪⎝⎭，然后利用和角公式展开整理，得到关于sin α＋cos α与cos α－sin α的方程，再对sin α＋cos α与0的关系进行讨论，得到 cos α－sin α的值．解：(1)因为函数y ＝sin x 的单调递增区间为ππ2π,2π22k k ⎡⎤-++⎢⎥⎣⎦，k ∈Z ， 由πππ2π32π242k x k -+≤+≤+，k ∈Z ，得π2ππ2π43123k k x -+≤≤+，k ∈Z .所以，函数f (x )的单调递增区间为π2ππ2π,43123k k ⎡⎤-++⎢⎥⎣⎦，k ∈Z . (2)由已知， 有π4πsin cos 454αα⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭(cos 2α－sin 2α)，所以ππ4ππsin coscos sin (cos cos sin sin )(c 44544αααα+=-， 22ππ4ππsin cos cos sin (cos cos sin sin )(cos sin )44544αααααα+=-- 即sin α＋cos α＝45(cos α－sin α)2(sin α＋cos α)． 当sin α＋cos α＝0时，由α是第二象限角，知α＝3π4＋2k π，k ∈Z . 此时，cos α－sin α＝当sin α＋cos α≠0时， 有(cos α－sin α)2＝54. 由α是第二象限角，知cos α－sin α＜0， 此时cos α－sin α＝2-综上所述，cos α－sin α＝15. (重庆17满分13分)已知函数f (x )＝1π)0,22x ωϕωϕ⎛⎫>-≤< ⎪⎝⎭＋的图象关于直线π3x =对称，且图象上相邻两个最高点的距离为π. (1)求ω和φ的值；(2)若π2π263f αα⎛⎫⎫=<< ⎪⎪⎝⎭⎝⎭，求3πcos 2α⎛⎫+ ⎪⎝⎭的值．分析：在第(1)问中主要考查了三角函数的周期和对称性，两最高点之间的距离是一个周期，从而根据公式2πT ω=，准确求出ω；而求φ，则根据对称轴处取最值并结合φ的取值范围给k赋值才能准确求出φ.第(2)问中已知2f α⎛⎫=⎪⎝⎭，结合α的范围判断并求出πcos 6α⎛⎫- ⎪⎝⎭的值，然后进一步将3cos π2α⎛⎫+ ⎪⎝⎭转化成sin α，而后将α写成π6α-加上π6的形式，从而求出最后的值，该题解答过程中，必须熟练运用诱导公式及两角和差的三角函数公式．解：(1)因f (x )的图象上相邻两个最高点的距离 为π，所以f (x )的最小正周期T ＝π，从而2π=2Tω=. 又因f (x )的图象关于直线π3x =对称， 所以ππ2π+32k ϕ⋅+=，k ＝0，±1，±2，…. 因ππ22ϕ-≤<得k ＝0，所以π2ππ236ϕ=-=-.(2)由(1)得π2226f αα⎛⎫⎛⎫=⋅-= ⎪ ⎪⎝⎭⎝⎭，所以π1sin =64α⎛⎫- ⎪⎝⎭.由π2π63α<<得ππ062α<-<，所以πcos 6α⎛⎫-= ⎪⎝⎭==.因此3πππcos sin sin 266ααα⎡⎤⎛⎫⎛⎫+==-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ππππ13151315sin cos cos sin 666642428αα+⎛⎫⎛⎫=-+-=⨯+⨯=⎪ ⎪⎝⎭⎝⎭ππ11cos sin 6642428α⎛⎫-=+=⎪⎝⎭。

§1.1 正弦定理(二)一、基础过关1．若△ABC 的面积为3，BC ＝2，C ＝60°，则边AB 的长度为________．2．在△ABC 中，若a cos A ＝b cos B ＝c cos C，则△ABC 是______三角形． 3．在△ABC 中，A ＝60°，a ＝3，b ＝2，则B ＝______.4．在△ABC 中，a ＝2，A ＝30°，C ＝45°，则△ABC 的面积S △ABC ＝________.5．下列判断中所有正确命题的序号是________．①当a ＝4，b ＝5，A ＝30°时，三角形有两解；②当a ＝5，b ＝4，A ＝60°时，三角形有两解；③当a ＝3，b ＝2，B ＝120°时，三角形有一解；④当a ＝322，b ＝6，A ＝60°时，三角形有一解． 6．已知△ABC 中，AB ＝3，AC ＝1，且B ＝30°，则△ABC 的面积等于________．7．在△ABC 中，已知23a sin B ＝3b ，且cos B ＝cos C ，试判断△ABC 的形状．8．在△ABC 中，a ，b ，c 分别是三个内角A ，B ，C 的对边，若a ＝2，C ＝π4，cos B 2＝255，求△ABC 的面积S .二、能力提升9．△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，a sin A sin B ＋b cos 2A ＝2a ，则b a ＝________.10．在△ABC 中，若a cos A 2＝b cos B 2＝ccos C 2，则△ABC 是________三角形． 11．在△ABC 中，A ＝60°，a ＝63，b ＝12，S △ABC ＝183，则a ＋b ＋c sin A ＋sin B ＋sin C ＝______，c ＝______.12．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且c ＝10，又知cos A cos B ＝b a ＝43，求a 、b 及△ABC 内切圆的半径．三、探究与拓展13．已知△ABC 的面积为1，tan B ＝12，tan C ＝－2，求△ABC 的各边长以及△ABC 外接圆的面积．答案1．2 2.等边3．45°4.3＋15．①④6.32或34 7．解 ∵23a sin B ＝3b ，∴23·(2R sin A )·sin B ＝3(2R sin B )，∴sin A ＝32，∴A ＝60°或120°.∵cos B ＝cos C ，∴B ＝C .当A ＝60°时，B ＝C ＝60°，△ABC 是等边三角形；当A ＝120°时，B ＝C ＝30°，△ABC 是顶角为120°的等腰三角形．8．解 cos B ＝2cos 2B 2－1＝35， 故B 为锐角，sin B ＝45. 所以sin A ＝sin(π－B －C )＝sin ⎝⎛⎭⎪⎫3π4－B ＝7210. 由正弦定理得c ＝a sin C sin A ＝107， 所以S △ABC ＝12ac sin B ＝12×2×107×45＝87. 9. 2 10.等边 11.12 612．解 由正弦定理知sin B sin A ＝b a， ∴cos A cos B ＝sin B sin A. 即sin A cos A ＝sin B cos B ，∴sin 2A ＝sin 2B .又∵a ≠b ，∴2A ＝π－2B ，即A ＋B ＝π2. ∴△ABC 是直角三角形，且C ＝90°，由⎩⎪⎨⎪⎧ a 2＋b 2＝102b a ＝43，得a ＝6，b ＝8.故内切圆的半径为r ＝a ＋b －c 2＝6＋8－102＝2. 13．解 ∵tan B ＝12>0，∴B 为锐角． ∴sin B ＝55，cos B ＝255. ∵tan C ＝－2，∴C 为钝角．∴sin C ＝255，cos C ＝－55. ∴sin A ＝sin(B ＋C )＝sin B cos C ＋cos B sin C＝55·⎝ ⎛⎭⎪⎫－55＋255·255＝35. ∵S △ABC ＝12ab sin C ＝2R 2sin A ·sin B sin C ＝2R 2×35×55×255＝1.∴R 2＝2512，R ＝536. ∴πR 2＝2512π，即外接圆的面积为2512π. ∴a ＝2R sin A ＝3，b ＝2R sin B ＝153， c ＝2R sin C ＝2153.。

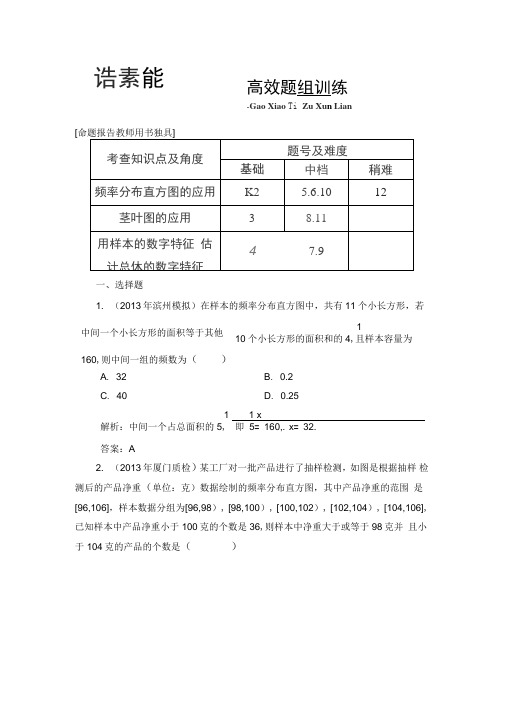
[一、选择题1. （2013年滨州模拟）在样本的频率分布直方图中，共有11个小长方形，若 中间一个小长方形的面积等于其他1 10个小长方形的面积和的4,且样本容量为160,则中间一组的频数为（）A . 32B . 0.2C . 40D . 0.251 1 x解析：中间一个占总面积的5, 即 5= 160,.°x = 32.答案：A2. （2013年厦门质检）某工厂对一批产品进行了抽样检测，如图是根据抽样 检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围 是[96,106]，样本数据分组为[96,98）, [98,100）, [100,102）, [102,104）, [104,106], 已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并 且小于104克的产品的个数是（）诰素能高效题组训练-Gao Xiao Ti Zu Xu n LianA. 90 C . 60解析：产品净重小于100克的频率为（0.050+ 0.100） X 2 = 0.300,设样本容量36为n ,则n = 0.300,所以n = 120,净重大于或等于98克并且小于104克的产品的频率为（0.100+ 0.150+ 0.125）X 2 = 0.75,所以样本中净重大于或等于 98克并 且小于104克的产品的个数是120X 0.75= 90.答案：A3. （2012年高考陕西卷）对某商店一个月内每天的顾客人数进行了统计，得 到样本的茎叶图（如图所示），则该样本的中位数、众数、极差分别是（）1 252 0253 312448945 5577889 5 00114796 1 78A . 46,45,56 C . 47,45,56解析：直接列举求解. 由题意知各数为12,15,20,22,23,23,31,32,34,34,38,39,45,45,45,47,47,48,48,49,50,50,51,51,54,57,59,61,67,68中位数是46,众数是45,最大数为68，最小数为 12,极差为 68- 12= 56.答案：A4. （2013年黄岗模拟）一组数据中的每一个数据都乘以 2,再都减去80,得 组新D . 45B . 46,45,53 D . 45,47,53频率/组距oj.so 0.125 0.100 0.075 0.050B . 75数据，若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是（）A . 40.6,1.1B . 48.8,4.4C . 81.2,44.4D . 78.8,75.6解析：记原数据依次为X 1, X 2, X 3,…，X n ,则新数据依次为2X 1 - 80,2X 2- 2 X 1 + X 2 + …+ X n — 80n X 1 + X 2 + …+ X n80,2X 3-80,…，2X n — 80,且 n = 1.2,因此有 n 1.2+ 80 =2 = 40.6，结合各选项知正确选项为 A. 答案：A5. （2012年高考江西卷）小波一星期的总开支分布如图（1）所示，一星期的食品开支如图（2）所示，则小波一星期的鸡蛋开支占总开支的百分比为 （ ）團（2）A . 30%B . 10%C . 3%D .不能确定解析：利用“整数值”定比例.由题图（2）可知小波一星期的食品开支共计 300元，其中鸡蛋开支30元.又 由题图（1）知，一周的食品开支占总开支的30%，则可知一周总开支为1 000元,肉奶牛鸡他其 菜 蔬图⑴30所以鸡蛋开支占总开支的百分比为1 000100%= 3%.答案：C、填空题6. （2013年南京模拟）一个社会调查机构就某地居民的月收入调查了 10 000 人，并根据所得数据画了样本的频率分布直方图 （如下图所示）•为了分析居民的 收入与年龄、学历、职业等方面的关系，要从这 10 000人中再用分层抽样的方法抽出100人作进一步调查，则在［2 500,3 000）月收入段应抽出 _______ .解析：由图可得月收入在［2 500,3 000）的频率为0.000 5X 500= 0.25,所以在 ［2 500,3 000）月 收入段应抽取 100X 0.25= 25（人）.答案：257. （2013年苏州模拟）甲、乙两名射击运动员参加某大型运动会的预选赛,他们分别射击了 5次，成绩如下表（单位：环）:如果甲、乙两人中只有1人入选，则入选的最佳人选应是 __________ .一 一 1解析：x 甲=x 乙=9，$甲=5X ［（9 — 10）2 + （9- 8）2 + （9-9）2 + （9-9）2 + （9-2 2 2 2—2) + (X 2— 2 ) + (4— X 2 — 2) + (4 — X 1 — 2)甲10 8 乙 10109 9 9 799甲 乙解析：由茎叶图所给数据依次确定两组体能测试的平均成绩分别为 x 甲63+ 65+ 66+ 71 + 77+ 77+ 79+ 81 + 84+ 92_ 10= 75.5, x 乙 =58 + 68+ 69+ 74 + 75+ 78 + 79+ 80+ 82 + 91 10= 75.4,故平均成绩较高的是甲.答案：甲9. （2012年高考广东卷）由正整数组成的一组数据X 1, X 2, X 3, X 4,其平均数 和中位数都是2,且标准差等于1,则这组数据为 ______________ .（从小到大排列）解析：利用平均数、中位数、标准差公式分类讨论求解.假设这组数据按从小到大的顺序排列为 X 1 , X 2, X 3, X 4,X 1+ X 4 = 4 X 2 + X 3 = 4.12 2 2 24[(X 1 — 2) + (X 2— 2)+ (X 3 — 2) + (X 4— 2)]X 1 + X 2 + X 3 + X 44=2,X 2 + X 3 丁 = 2,1 =22 2 由x i, X2,X3, X4 均为正整数，且(X1, X2), (x3, X4)均为圆(x —2) + (y—2)=2上的点，分析知X1 , X2, X3, X4应为1,1,33答案：1,1,3,3三、解答题10. 某市电视台为宣传在伦敦举办的“ 2012年奥运会”，随机对该市15〜65岁的人群抽取了n人，回答问题“2012年奥运会是第几届奥运会？”，统计结果如图表所示：组号分组回答正确回答正确的人的人数数占本组的概率第1组[15,20)50. 5第2组[25,35)a0. 9第3组[35,45〉27.!第4组[45,55〉h0. 36第5组[55,65)3$(1) 分别求出a，b，X，y的值；(2) 在第2,3,4组回答正确的人中用分层抽样的方法抽取6人，则第2,3,4组每组应各抽取多少人？(3) 在(2)的前提下，电视台决定在所抽取的6人中随机抽取2人颁发幸运奖，求所抽取的人中第2组至少有1人获得幸运奖的概率.5解析：(1)由频率分布表中第1组数据可知，第1组总人数为05= io,再结10合频率分布直方图可知n = 0.01010= 100,「a= 1000.020100.9= 18, b27=x X x = , = x X = ,3y= 100X X =(2) v第2,3,4组中回答正确的共有54人，•••利用分层抽样的方法在54人中抽取6人，每组分别抽取的人数为：第218 27组，54X 6= 2,第 3 组，54X 6= 3,第 4 组，54X 6= 1.(3) 设第2组的2人为A1, A2,第3组的3人为B1, B2, B3,第4组的1人为C1,则从6人中抽取2人的所有可能的结果为(A1, A2), (A1, B1), (A1, B2), (A1, B3), (A1, C1), (A2, B1), (A2, B2), (A2, B3), (A2, C1), (B1, B2), (B1, B3), (B1, C1) , (B2 , B3) , (B2 , C1) , (B3 , C”，共15 种情况，其中每2 组至少有1 人被抽中的情况有(A1 , A2) , (A1 , B1) , (A1 , B2) , (A1 , B3), (A , C” , (A2 , B1) , (A, B2) , (A2 , B3) , (A2 , C1),共9 种情况.9 3故第2组至少有1人获得幸运奖的概率为15= 5.11. 在某电脑杂志的一篇文章中，每个句子的字数如下：10,28,31,17,23,27,18,15,26,24,20,19,36,27,14,25,15,22,11,24,27,17.在某报纸的一篇文章中，每个句子中所含的字数如下：27,39,33,24,28,19,32,41,33,27,35,12,36,41,27,13,22,23,18,46,32,22.(1) 将这两组数据用茎叶图表示；(2) 将这两组数据进行比较分析，得到什么结论？解析：(1)茎叶图如图所示.电脑杂志报紙9877554101 2 3 8 9877765443202 234 7 7 27 86 1322335694 1 1 6(2)电脑杂志上每个句子的字数集中在10〜30之间，中位数为22.5；而报纸上每个句子的字数集中在10〜40之间，中位数为27.5.还可以看出电脑杂志上每个句子的平均字数比报纸上每个句子的平均字数要少. 说明电脑杂志作为读物通俗易懂、简明清晰.12. (能力提升)(2013年郑州质检)某中学共有1 000名学生参加了该地区高三第一次质量检测的数学考试，数学成绩如下表所示：(1) 为了了解同学们前段时间的复习情况，学校将采用分层抽样的方法抽取100名同学进行问卷调查，甲同学在本次测试中数学成绩为95分，求他被抽中的概率；(2) 已知本次数学成绩的优秀线为110分，试根据所提供数据估计该中学达到优秀线的人数；(3) 作出频率分布直方图，并估计该学校本次考试的数学平均分. (同一组中的数据用该组区间的中点值作代表)+频率/组距030 60 90 120 150 分数样本容量解析：(1)分层抽样中，每个个体被抽到的概率均为总体中的个体数，故甲丄同学被抽到的概率P= 10.(2)由题意得x= 1 000- (60+ 90+ 300+ 160)= 390.120—110 故估计该中学达到优秀线的人数m= 160+ 390X 茹90 = 290.(3)频率分布直方图如图所示.该学校本次考试的数学平均分60X 15+ 90X 45 + 300X 75 + 390X 105+ 160X 135C/ 22. （2013年咸阳模拟）为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，测试成绩（单位：分）如图所示，假设得分值的中位101064数为m e，众数为m。

第4讲直线与圆、圆与圆的位置关系基础巩固1.直线y=x+1与圆x2+y2=1的位置关系是()A.相切B.相交但直线不过圆心C.直线过圆心D.相离【答案】B【解析】圆心到直线的距离d==<1,∴直线与圆相交但不过圆心.2.圆C1:x2+y2+2x+2y-2=0与圆C2:x2+y2-4x-2y+1=0的公切线有且仅有()A.1条B.2条C.3条D.4条【答案】B【解析】可判断圆C1与C2相交,故公切线有2条.3.圆x2+y2-4x=0在点P(1,)处的切线方程为()A.x+y-2=0B.x+y-4=0C.x-y+4=0D.x-y+2=0【答案】D【解析】设切线方程为y-=k(x-1),由d=r,可求得k=.故所求切线方程为x-y+2=0.4.过点(0,-1)作直线l与圆x2+y2-2x-4y-20=0交于A,B两点,如果|A B|=8,则直线l的方程为()A.3x+4y+4=0B.3x-4y-4=0C.3x+4y+4=0或y+1=0D.3x-4y-4=0或y+1=0【答案】C【解析】圆的标准方程为(x-1)2+(y-2)2=25.圆心为(1,2),半径r=5,又|AB|=8,从而圆心到直线的距离等于3.由点到直线的距离公式得直线方程为3x+4y+4=0或y+1=0.5.已知一圆的方程为x2+y2-6x-8y=0,设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为()A.10B.20C.30D.40【答案】B【解析】圆的方程可化为(x-3)2+(y-4)2=52,∴圆心为P(3,4).∴过点(3,5)的最长弦为直径|AC|=10,过点(3,5)的最短弦|BD|=2=4.故S四边形ABCD=|AC||BD|=×10×4=20.6.设O为坐标原点,C为圆(x-2)2+y2=3的圆心,且圆上有一点M(x,y)满足·=0,则等于()A. B.或-C. D.或-【答案】D【解析】∵·=0,∴OM⊥CM.∴OM是圆C的切线.设OM的方程为y=kx,由=,得k=±,即=±.7.设m,n∈R,若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切,则m+n的取值范围是()A.[1-,1+]B.(-∞,1-]∪[1+,+∞)C.[2-2,2+2]D.(-∞,2-2]∪[2+2,+∞)【答案】D【解析】∵直线与圆相切,∴=1,∴|m+n|=,即mn=m+n+1.设m+n=t,则mn≤=,∴t+1≤.∴t2-4t-4≥0,解得t≤2-2或t≥2+2.8.(2012·北京卷,9)直线y=x被圆x2+(y-2)2=4截得的弦长为.【答案】2【解析】由题意得,圆x2+(y-2)2=4的圆心为(0,2),半径为2,圆心到直线x-y=0的距离d==.设截得的弦长为l,则由+()2=22,得l=2.9.(2012·天津卷,12)设m,n∈R,若直线l:mx+ny-1=0与x轴相交于点A,与y轴相交于点B,且l与圆x2+y2=4相交所得弦的长为2,O为坐标原点,则△AOB面积的最小值为.【答案】3【解析】∵l与圆相交所得弦的长为2.∴=.∴m2+n2=≥2|mn|,即|mn|≤.l与x轴交点A,与y轴交点B,故S△AOB=·=·×6=3.10.求过点P(4,-1)且与圆C:x2+y2+2x-6y+5=0切于点M(1,2)的圆的方程.【解】设所求圆的圆心为A(m,n),半径为r,则A,M,C三点共线,且有|MA|=|AP|=r,因为圆C:x2+y2+2x-6y+5=0的圆心为C(-1,3),则解得m=3,n=1,r=,所以所求圆的方程为(x-3)2+(y-1)2=5.11.已知圆C的圆心与点P(-2,1)关于直线y=x+1对称,直线3x+4y-11=0与圆C相交于A,B两点,且|AB|=6,求圆C的方程.【解】设点P关于直线y=x+1的对称点为C(m,n),则有解得故圆心C(0,-1)到直线3x+4y-11=0的距离d==3,所以圆C的半径的平方r2=d2+=18.故圆C的方程为x2+(y+1)2=18.12.已知圆x2+y2-4x+2y-3=0和圆外一点M(4,-8).(1)过M作圆的割线交圆于A,B两点,若|AB|=4,求直线AB的方程;(2)过M作圆的切线,切点为C,D,求切线长及CD所在直线的方程.【解】(1)圆x2+y2-4x+2y-3=0化为标准方程为(x-2)2+(y+1)2=8,圆心为P(2,-1),半径r=2.①若割线斜率存在,设AB:y+8=k(x-4),即kx-y-4k-8=0,设AB的中点为N,则|PN|==,由|PN|2+=r2,得k=-,此时AB的直线方程为45x+28y+44=0.②若割线斜率不存在,AB:x=4,代入圆方程得y2+2y-3=0,解得y1=1,y2=-3,符合题意. 综上,直线AB的方程为45x+28y+44=0或x=4.(2)切线长为==3.以PM为直径的圆的方程为(x-2)(x-4)+(y+1)·(y+8)=0,即x2+y2-6x+9y+16=0.又已知圆的方程为x2+y2-4x+2y-3=0,两式相减,得2x-7y-19=0,所以直线CD的方程为2x-7y-19=0.拓展延伸13.已知m∈R,直线l:mx-(m2+1)y=4m和圆C:x2+y2-8x+4y+16=0.(1)求直线l的斜率的取值范围;(2)直线l能否将圆C分割成弧长的比值为的两段圆弧?为什么?【解】(1)设直线l的斜率为k.直线l的方程可化为y=x-,此时直线l的斜率k=.因为|m|≤(m2+1),所以|k|=,当且仅当|m|=1时等号成立.所以斜率k的取值范围是.(2)不能.由(1)知直线l的方程为y=k(x-4),其中|k|≤.圆C的圆心为(4,-2),半径r=2,圆心C到直线l的距离为d=,由|k|≤,得d≥>1,即d>,从而,若直线l与圆C相交,则圆C截直线l所得的弦所对的圆心角小于,所以l不能将圆C分割成弧长的比值为的两段圆弧.。

第九章解析几何单元测试一、选择题(本大题共10小题，每小题5分，共50分．每小题中只有一项符合题目要求)1．(2012·浙江)设a∈R，则“a＝1”是“直线l1：ax＋2y－1＝0与直线l2：x＋(a＋1)y＋4＝0平行”的() A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件答案 A解析由a＝1可得l1∥l2，反之，由l1∥l2可得a＝1或a＝－2，故选A.2．(2012·湖北)过点P(1,1)的直线，将圆形区域{(x，y)|x2＋y2≤4|}分为两部分，使得这两部分的面积之差最大，则该直线的方程为() A．x＋y－2＝0 B．y－1＝0C．x－y＝0 D．x＋3y－4＝0答案 A解析两部分面积之差最大，即弦长最短，此时直线垂直于过该点的直径．因为过点P(1,1)的直径所在直线的斜率为1，所以所求直线的斜率为－1，方程为x ＋y－2＝0.3．经过抛物线y2＝4x的焦点且平行于直线3x－2y＝0的直线l的方程是() A．3x－2y－3＝0 B．6x－4y－3＝0C．2x＋3y－2＝0 D．2x＋3y－1＝0答案 A解析∵抛物线y2＝4x的焦点是(1,0)，直线3x－2y＝0的斜率是32，∴直线l的方程是y＝32(x－1)，即3x－2y－3＝0，故选A.4．（2013·广东模拟）已知圆C的半径为2，圆心在x轴的正半轴上，直线3x＋4y＋4＝0与圆C相切，则圆C的方程为A．x2＋y2－2x－3＝0 B．x2＋y2＋4x＝0C ．x 2＋y 2＋2x －3＝0D ．x 2＋y 2－4x ＝0答案 D解析 设圆心C (a,0)(a >0)，由3a ＋45＝2得，a ＝2，故圆的方程为(x －2)2＋y 2＝4，即x 2＋y 2－4x ＝0.5．(2012·江西)椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右顶点分别是A ，B ，左、右焦点分别是F 1，F 2.若|AF 1|，|F 1F 2|，|F 1B |成等比数列，则此椭圆的离心率为( )A.14B.55 C.12 D.5－2答案 B解析 由等比中项的性质得到a ，c 的一个方程，再进一步转化为关于e 的方程，解之即得所求．依题意得|F 1F 2|2＝|AF 1|·|F 1B |，即4c 2＝(a －c )(a ＋c )＝a 2－c 2，整理得5c 2＝a 2，∴e ＝c a ＝55.6．(2012·浙江)如图，中心均为原点O 的双曲线与椭圆有公共焦点，M ，N 是双曲线的两顶点．若M ，O ，N 将椭圆长轴四等分，则双曲线与椭圆的离心率的比值是( )A ．3B ．2 C. 3 D. 2答案 B解析 设焦点为F (±c,0)，双曲线的实半轴长为a ，则双曲线的离心率e 1＝ca ，椭圆的离心率e 2＝c 2a ，所以e 1e 2＝2.选B.7．设F 1、F 2分别是双曲线x 2－y 29＝1的左、右焦点．若点P 在双曲线上，且PF 1→·PF 2→＝0，则|PF 1→＋PF 2→|等于( )A.10 B ．210 C. 5 D ．2 5答案 B解析 F 1(－10，0)，F 2(10，0)，2c ＝210，2a ＝2. ∵PF 1→·PF 2→＝0，∴|PF 1→|2＋|PF 2→|2＝|F 1F 2|2＝4c 2＝40. ∴(PF 1→＋PF 2→)2＝|PF 1→|2＋|PF 2→|2＋2PF 1→·PF 2→＝40. ∴|PF 1→＋PF 2→|＝210.8．过抛物线y ＝14x 2准线上任一点作抛物线的两条切线，若切点分别为M ，N ，则直线MN 过定点( )A ．(0,1)B ．(1,0)C ．(0，－1)D ．(－1,0)答案 A解析 特殊值法，取准线上一点(0，－1)．设M (x 1，14x 21)，N (x 2，14x 22)，则过M 、N 的切线方程分别为y －14x 21＝12x 1(x －x 1)，y －14x 22＝12x 2(x －x 2)．将(0，－1)代入得x 21＝x 22＝4，∴MN 的方程为y ＝1，恒过(0,1)点．9．如图，过抛物线x 2＝4py (p >0)焦点的直线依次交抛物线与圆x 2＋(y －p )2＝p 2于点A 、B 、C 、D ，则AB →·CD →的值是( )A ．8p 2B ．4p 2C ．2p 2D ．p 2答案 D解析 |AB →|＝|AF |－p ＝y A ，|CD →|＝|DF |－p ＝y B ，|AB →|·|CD →|＝y A y B ＝p 2.因为AB →，CD →的方向相同，所以AB →·CD →＝|AB →|·|CD →|＝y A y B ＝p 2.10．已知抛物线y ＝x 2上有一定点A (－1,1)和两动点P 、Q ，当P A ⊥PQ 时，点Q 的横坐标取值范围是( )A ．(－∞，－3]B ．[1，＋∞)C ．[－3,1]D ．(－∞，－3]∪[1，＋∞)答案 D解析 设P (x 1，x 21)，Q (x 2，x 22)，∴k AP ＝x 21－1x 1＋1＝x 1－1，k PQ ＝x 22－x 21x 2－x 1＝x 2＋x 1.由题意得k P A ·k PQ ＝(x 1－1)(x 2＋x 1)＝－1， ∴x 2＝11－x 1－x 1＝1(1－x 1)＋(1－x 1)－1.利用函数性质知x 2∈(－∞，－3]∪[1，＋∞)，故选D.二、填空题(本大题共6小题，每小题5分，共30分，把答案填在题中横线上)11．设l 1的倾斜角为α，α∈(0，π2)，l 1绕其上一点P 逆时针方向旋转α角得直线l 2，l 2的纵截距为－2，l 2绕点P 逆时针方向旋转π2－α角得直线l 3：x ＋2y －1＝0，则l 1的方程为________．答案 2x －y ＋8＝0 解析 ∵l 1⊥l 3，∴k 1＝tan α＝2，k 2＝tan2α＝2tan α1－tan 2α＝－43. ∵l 2的纵截距为－2，∴l 2的方程为y ＝－43x －2. 由⎩⎪⎨⎪⎧y ＝－43x －2，x ＋2y －1＝0，∴P (－3,2)，l 1过P 点．∴l 1的方程为2x －y ＋8＝0.12．过直线2x ＋y ＋4＝0和圆x 2＋y 2＋2x －4y ＋1＝0的交点且面积最小的圆的方程是________．答案 (x ＋135)2＋(y －65)2＝45解析 因为通过两个定点的动圆中，面积最小的是以这两个定点为直径端点的圆，于是解方程组⎩⎨⎧2x ＋y ＋4＝0，x 2＋y 2＋2x －4y ＋1＝0，得交点A (－115，25)，B (－3,2)．因为AB 为直径，其中点为圆心，即为(－135，65)， r ＝12|AB |＝255，所以圆的方程为(x ＋135)2＋(y －65)2＝45.13．(2012·江苏)在平面直角坐标系xOy 中，圆C 的方程为x 2＋y 2－8x ＋15＝0，若直线y ＝kx －2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的最大值是________．答案 43解析 设圆心C (4,0)到直线y ＝kx －2的距离为d ，则d ＝|4k －2|k 2＋1，由题意知问题转化为d ≤2，即d ＝|4k －2|k 2＋1≤2，得0≤k ≤43，所以k max ＝43.14．若椭圆x 2a 2＋y 2b 2＝1过抛物线y 2＝8x 的焦点，且与双曲线x 2－y 2＝1有相同的焦点，则该椭圆的方程是________．答案 x 24＋y 22＝1解析 抛物线y 2＝8x 的焦点坐标为(2,0)，则依题意知椭圆的右顶点的坐标为(2,0)，又椭圆与双曲线x 2－y 2＝1有相同的焦点，∴a ＝2，c ＝ 2.∵b 2＝a 2－c 2，∴b 2＝2，∴椭圆的方程为x 24＋y 22＝1.15．已知两点M (－3,0)，N (3,0)，点P 为坐标平面内一动点，且|MN →|·|MP →|＋MN →·NP →＝0，则动点P (x ，y )到点A (－3,0)的距离的最小值为________．答案 3解析 因为M (－3,0)，N (3,0)，所以MN →＝(6,0)，|MN →|＝6，MP →＝(x ＋3，y )，NP →＝(x －3，y )．由|MN →|·|MP →|＋MN →·NP →＝0，得6(x ＋3)2＋y 2＋6(x －3)＝0，化简整理得y 2＝－12x .所以点A 是抛物线y 2＝－12x 的焦点，所以点P 到A 的距离的最小值就是原点到A (－3,0)的距离，所以d ＝3.16．已知以y ＝±3x 为渐近线的双曲线D ：x 2a 2－y 2b 2＝1(a >0，b >0)的左，右焦点分别为F 1，F 2，若P 为双曲线D 右支上任意一点，则|PF 1|－|PF 2||PF 1|＋|PF 2|的取值范围是________．答案 ⎝ ⎛⎦⎥⎤0，12 解析 依题意，|PF 1|－|PF 2|＝2a ，|PF 1|＋|PF 2|≥2c ，所以0<|PF 1|－|PF 2||PF 1|＋|PF 2|≤a c ＝1e .又双曲线的渐近线方程y ＝±3x ，则ba ＝ 3.因此e ＝ca ＝2，故0<|PF 1|－|PF 2||PF 1|＋|PF 2|≤12.三、解答题(本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤)17．(本题满分10分)已知O 为平面直角坐标系的原点，过点M (－2,0)的直线l 与圆x 2＋y 2＝1交于P ，Q 两点．(1)若OP →·OQ →＝－12，求直线l 的方程；(2)若△OMP 与△OPQ 的面积相等，求直线l 的斜率． 解析 (1)依题意知直线l 的斜率存在， 因为直线l 过点M (－2,0)， 故可设直线l 的方程为y ＝k (x ＋2)．因为P ，Q 两点在圆x 2＋y 2＝1上，所以|OP →|＝|OQ →|＝1.因为OP →·OQ →＝－12，即|OP →|·|OQ →|·cos ∠POQ ＝－12. 所以∠POQ ＝120°，所以点O 到直线l 的距离等于12. 所以|2k |k 2＋1＝12，解得k ＝±1515. 所以直线l 的方程为x －15y ＋2＝0或x ＋15y ＋2＝0.(2)因为△OMP 与△OPQ 的面积相等，所以MP ＝PQ ，即P 为MQ 的中点，所以MQ →＝2MP →.设P (x 1，y 1)，Q (x 2，y 2)，所以MQ →＝(x 2＋2，y 2)，MP →＝(x 1＋2，y 1)． 所以⎩⎨⎧ x 2＋2＝2(x 1＋2)，y 2＝2y 1，即⎩⎨⎧x 2＝2(x 1＋1)，y 2＝2y 1.①因为P ，Q 两点在圆x 2＋y 2＝1上，所以⎩⎨⎧x 21＋y 21＝1，x 22＋y 22＝1.②由①及②得⎩⎨⎧x 21＋y 21＝1，4(x 1＋1)2＋4y 21＝1，解得⎩⎪⎨⎪⎧x 1＝－78，y 1＝±158.故直线l 的斜率k ＝k MP ＝±159.18．(本题满分12分)(2012·北京文)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的一个顶点为A (2,0)，离心率为22.直线y ＝k (x －1)与椭圆C 交于不同的两点M ，N .(1)求椭圆C 的方程；(2)当△AMN 的面积为103时，求k 的值．解析(1)由题意得⎩⎪⎨⎪⎧a ＝2，c a ＝22，a 2＝b 2＋c 2，解得b ＝ 2.所以椭圆C 的方程为x 24＋y 22＝1. (2)由⎩⎪⎨⎪⎧y ＝k (x －1)，x 24＋y 22＝1，得(1＋2k 2)x 2－4k 2x ＋2k 2－4＝0.设点M ，N 的坐标分别为(x 1，y 1)，(x 2，y 2)，则y 1＝k (x 1－1)，y 2＝k (x 2－1)，x 1＋x 2＝4k 21＋2k 2，x 1x 2＝2k 2－41＋2k 2.所以|MN |＝(x 2－x 1)2＋(y 2－y 1)2 ＝(1＋k 2)[(x 1＋x 2)2－4x 1x 2] ＝2(1＋k 2)(4＋6k 2)1＋2k 2.又因为点A (2,0)到直线y ＝k (x －1)的距离d ＝|k |1＋k2， 所以△AMN 的面积为 S ＝12|MN |·d ＝|k |4＋6k 21＋2k 2.由|k |4＋6k 21＋2k2＝103，化简得7k 4－2k 2－5＝0，解得k ＝±1. 19．(本题满分12分)(2012·天津理)设椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右顶点分别为A 、B ，点P 在椭圆上且异于A ，B 两点，O 为坐标原点．(1)若直线AP 与BP 的斜率之积为－12，求椭圆的离心率； (2)若|AP |＝|OA |，证明直线OP 的斜率k 满足|k |> 3. 解析 (1)设点P 的坐标为(x 0，y 0)． 由题意，有x 20a 2＋y 20b 2＝1.① 由A (－a,0)，B (a,0)，得k AP ＝y 0x 0＋a ，k BP ＝y 0x 0－a. 由k AP ·k BP ＝－12，可得x 20＝a 2－2y 20，代入①并整理得(a 2－2b 2)y 20＝0.由于y 0≠0，故a 2＝2b 2.于是e 2＝a 2－b 2a 2＝12，所以椭圆的离心率e ＝22.(2)方法一依题意，直线OP 的方程为y ＝kx ，设点P 的坐标为(x 0，y 0)．由条件得⎩⎪⎨⎪⎧y 0＝kx 0，x 20a 2＋y 20b2＝1.消去y 0并整理得x 20＝a 2b 2k 2a 2＋b2.②由|AP |＝|OA |，A (－a,0)及y 0＝kx 0，得(x 0＋a )2＋k 2x 20＝a 2.整理得(1＋k 2)x 20＋2ax 0＝0.而x 0≠0，于是x 0＝－2a 1＋k 2，代入②，整理得(1＋k 2)2＝4k 2(ab )2＋4.由a >b >0，故(1＋k 2)2>4k 2＋4，即k 2＋1>4.因此k 2>3，所以|k |> 3.方法二 依题意，直线OP 的方程为y ＝kx ，可设点P 的坐标为(x 0，kx 0)．由点P 在椭圆上，有x 20a 2＋k 2x 20b 2＝1.因为a >b >0，kx 0≠0，所以x 20a 2＋k 2x 20a 2<1，即(1＋k 2)x 20<a 2.③由|AP |＝|OA |，A (－a,0)，得(x 0＋a )2＋k 2x 20＝a 2，整理得(1＋k 2)x 20＋2ax 0＝0，于是x 0＝－2a 1＋k 2.代入③，得(1＋k 2)·4a 2(1＋k 2)2<a 2，解得k 2>3，所以|k |> 3.20. (本题满分12分)如图，点A ，B 分别是椭圆x 236＋y 220＝1长轴的左，右端点，点F 是椭圆的右焦点，点P 在椭圆上，且位于x 轴上方，P A ⊥PF .(1)求点P 的坐标；(2)设M 是椭圆长轴AB 的一点，M 到直线AP 的距离等于|MB |，求椭圆上的点到点M 的距离d 的最小值．解析 (1)由已知可得点A (－6,0)，F (4,0)， 设点P 的坐标是(x ，y )，则AP →＝(x ＋6，y )，FP →＝(x －4，y )． 由已知得⎩⎪⎨⎪⎧x 236＋y 220＝1，(x ＋6)(x －4)＋y 2＝0，则2x 2＋9x －18＝0，x ＝32或x ＝－6. ∵点P 位于x 轴上方，∴x ＝－6舍去， 只能取x ＝32.由于y >0，于是y ＝52 3. ∴点P 的坐标是(32，523)． (2)直线AP 的方程是x －3y ＋6＝0. 设点M 的坐标是(m,0)(－6≤m ≤6)， 则M 到直线AP 的距离是m ＋62. 于是m ＋62＝6－m ，解得m ＝2. 椭圆上的点(x ，y )到点M 的距离d 有 d 2＝(x －2)2＋y 2＝x 2－4x ＋4＋20－59x 2 ＝49(x －92)2＋15. 由于－6≤x ≤6，∴当x ＝92时，d 取得最小值15.21．(本题满分12分)已知椭圆x 2m ＋1＋y 2＝1的两个焦点是F 1(－c,0)，F 2(c,0)(c >0)．(1)设E 是直线y ＝x ＋2与椭圆的一个公共点，求|EF 1|＋|EF 2|取得最小值时椭圆的方程；(2)已知点N (0，－1)，斜率为k (k ≠0)的直线l 与条件(1)下的椭圆交于不同的两点A ，B ，点Q 满足AQ →＝QB →，且NQ →·AB →＝0，求直线l 在y 轴上的截距的取值范围．解析 (1)由题意，知m ＋1>1，即m >0. 由⎩⎪⎨⎪⎧y ＝x ＋2，x2m ＋1＋y 2＝1，得(m ＋2)x 2＋4(m ＋1)x ＋3(m ＋1)＝0.又由Δ＝16(m ＋1)2－12(m ＋2)(m ＋1)＝4(m ＋1)(m －2)≥0， 解得m ≥2或m ≤－1(舍去)，∴m ≥2. 此时|EF 1|＋|EF 2|＝2m ＋1≥2 3.当且仅当m ＝2时，|EF 1|＋|EF 2|取得最小值23， 此时椭圆的方程为x 23＋y 2＝1.(2)设直线l 的方程为y ＝kx ＋t .由方程组⎩⎨⎧x 2＋3y 2＝3，y ＝kx ＋t ，消去y 得(1＋3k 2)x 2＋6ktx ＋3t 2－3＝0. ∵直线l 与椭圆交于不同的两点A ，B ， ∴Δ＝(6kt )2－4(1＋3k 2)(3t 2－3)>0， 即t 2<1＋3k 2.①设A (x 1，y 1)，B (x 2，y 2)，Q (x Q ，y Q )，则x 1＋x 2＝－6kt1＋3k 2. 由AQ →＝QB →，得Q 为线段的AB 的中点， 则x Q ＝x 1＋x 22＝－3kt 1＋3k 2，y Q ＝kx Q ＋t ＝t1＋3k 2. ∵NQ →·AB →＝0，∴直线AB 的斜率k AB 与直线QN 的斜率k QN 乘积为－1，即k QN ·k AB ＝－1，∴t1＋3k 2＋1－3kt 1＋3k 2·k ＝－1.化简得1＋3k 2＝2t ，代入①式得t 2<2t ， 解得0<t <2.又k ≠0，即3k 2>0，故2t ＝1＋3k 2>1，得t >12. 综上，直线l 在y 轴上的截距t 的取值范围是(12，2)．22．(本题满分12分)(2012·浙江文)如图，在直角坐标系xOy 中，点P (1，12)到抛物线C ：y 2＝2px (p >0)的准线的距离为54.点M (t,1)是C 上的定点，A ，B 是C 上的两动点，且线段AB 被直线OM 平分．(1)求p ，t 的值；(2)求△ABP 面积的最大值．解析 (1)由题意知⎩⎪⎨⎪⎧ 2pt ＝1，1＋p 2＝54，得⎩⎪⎨⎪⎧p ＝12，t ＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，线段AB 的中点为Q (m ，m )．由题意知，设直线AB 的斜率为k (k ≠0)．由⎩⎨⎧y 21＝x 1，y 22＝x 2，得(y 1－y 2)(y 1＋y 2)＝x 1－x 2. 故k ·2m ＝1.所以直线AB 的方程为y －m ＝12m (x －m )． 即x －2my ＋2m 2－m ＝0.由⎩⎨⎧x －2my ＋2m 2－m ＝0，y 2＝x ，消去x ，整理得y 2－2my ＋ 2m 2－m ＝0.所以Δ＝4m －4m 2>0，y 1＋y 2＝2m ，y 1·y 2＝2m 2－m . 从而|AB |＝1＋1k 2·|y 1－y 2|＝1＋4m 2·4m －4m 2.设点P到直线AB的距离为d，则d＝|1－2m＋2m2|1＋4m2.设△ABP的面积为S，则S＝12|AB|·d＝|1－2(m－m2)|·m－m2.由Δ＝4m－4m2>0，得0<m<1.令u＝m－m2，0<u≤12，则S＝u(1－2u2)．设S(u)＝u(1－2u2)，0<u≤12，则S′(u)＝1－6u2.由S′(u)＝0，得u＝66∈(0，12]．所以[S(u)]max＝S(66)＝69.故△ABP面积的最大值为6 9.1．(2012·辽宁文)将圆x2＋y2－2x－4y＋1＝0平分的直线是() A．x＋y－1＝0B．x＋y＋3＝0C．x－y＋1＝0 D．x－y＋3＝0答案 C解析要使直线平分圆，只要直线经过圆的圆心即可，由题知圆心坐标为(1,2)．A，B，C，D四个选项中，只有C选项中的直线经过圆心，故选C.2．(2012·孝感统考)若直线过点P(－3，－32)且被圆x2＋y2＝25截得的弦长是8，则该直线的方程为()A．3x＋4y＋15＝0 B．x＝－3或y＝－3 2C．x＝－3 D．x＝－3或3x＋4y＋15＝0答案 D解析若直线的斜率不存在，则该直线的方程为x＝－3，代入圆的方程解得y＝±4，故该直线被圆截得的弦长为8，满足条件；若直线的斜率存在，不妨设直线的方程为y ＋32＝k (x ＋3)，即kx －y ＋3k －32＝0，因为该直线被圆截得的弦长为8，故半弦长为4，又圆的半径为5，则圆心(0,0)到直线的距离为52－42＝|3k －32|k 2＋1，解得k ＝－34，此时该直线的方程为3x ＋4y ＋15＝0.综上可知答案为D.3．直线4kx －4y －k ＝0与抛物线y 2＝x 交于A 、B 两点，若|AB |＝4，则弦AB 的中点到直线x ＋12＝0的距离等于( )A.74 B ．2 C.94 D ．4答案 C解析 直线4kx －4y －k ＝0，即y ＝k (x －14)，可知直线4kx －4y －k ＝0过抛物线y 2＝x 的焦点(14，0)．设A (x 1，y 1)，B (x 2，y 2)，则|AB |＝x 1＋x 2＋12＝4，故x 1＋x 2＝72，则弦AB 的中点的横坐标是74，弦AB 的中点到直线x ＋12＝0的距离是74＋12＝94.4．已知l 1和l 2是平面内互相垂直的两条直线，它们的交点为A ，动点B 、C 分别在l 1和l 2上，且BC ＝32，则过A 、B 、C 三点的动圆所形成的区域的面积为( )A ．6πB ．8πC ．16πD ．18π答案 D解析 当A 与B 或C 重合时，此时圆的面积最大，且圆的半径r ＝BC ＝32，所以圆的面积S ＝πr 2＝π(32)2＝18π，则过A 、B 、C 三点的动圆所形成的区域的面积为18π.5．已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)与双曲线x 2m 2－y 2n 2＝1(m >0，n >0)有相同的焦点(－c,0)和(c,0)．若c 是a 与m 的等比中项，n 2是m 2与c 2的等差中项，则椭圆的离心率等于( )A.13B.33C.12D.22答案 B解析 ∵c 2＝am,2n 2＝c 2＋m 2，又n 2＝c 2－m 2， ∴m 2＝13c 2，即m ＝33c .∴c 2＝33ac ，则e ＝c a ＝33.6．椭圆x 24＋y 23＝1离心率为e ，点(1，e )是圆x 2＋y 2－4x －4y ＋4＝0的一条弦的中点，则此弦所在直线的方程是( )A ．3x ＋2y －4＝0B ．4x ＋6y －7＝0C ．3x －2y －2＝0D ．4x －6y －1＝0答案 B解析 依题意得e ＝12，圆心坐标为(2,2)，圆心(2,2)与点(1，12)的连线的斜率为2－122－1＝32，所求直线的斜率等于－23，所以所求直线方程是y －12＝－23(x －1)，即4x ＋6y －7＝0，选B.7．已知圆x 2＋y 2＝1与x 轴的两个交点为A 、B ，若圆内的动点P 使|P A |、|PO |、|PB |成等比数列，则P A →·PB →的取值范围为( )A.⎝ ⎛⎦⎥⎤0，12 B.⎣⎢⎡⎭⎪⎫－12，0 C ．(－12，0) D ．[－1,0)答案 C解析 设P (x ，y )，∴|PO |2＝|P A ||PB |， 即x 2＋y 2＝(x －1)2＋y 2·(x ＋1)2＋y 2， 整理得2x 2－2y 2＝1.∴P A →·PB →＝(1－x ，－y )·(－1－x ，－y )＝x 2＋y 2－1＝2x 2－32.∴P 为圆内动点且满足x 2－y 2＝12. ∴22<|x |<32，∴1<2x 2<32. ∴－12<2x 2－32<0，选C.8．(2012·新课标全国)等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线y 2＝16x 的准线交于A ，B 两点，|AB |＝43，则C 的实轴长为( )A.2 B ．2 2 C ．4 D ．8答案 C解析 抛物线y 2＝16x 的准线方程是x ＝－4，所以点A (－4,23)在等轴双曲线C ：x 2－y 2＝a 2(a >0)上，将点A 的坐标代入得a ＝2，所以C 的实轴长为4.9．已知正方形ABCD ，则以A 、B 为焦点，且过C 、D 两点的椭圆的离心率为________．答案2－1解析 令AB ＝2，则AC ＝2 2. ∴椭圆中c ＝1,2a ＝2＋22⇒a ＝1＋ 2. 可得e ＝c a ＝12＋1＝2－1. 10．(2012·北京理)在直角坐标系xOy 中，直线l 过抛物线y 2＝4x 的焦点F ，且与该抛物线相交于A ，B 两点，其中点A 在x 轴上方．若直线l 的倾斜角为60°，则△OAF 的面积为________．答案3解析 直线l 的方程为y ＝3(x －1)，即x ＝33y ＋1，代入抛物线方程得y 2－433y －4＝0，解得y A ＝433＋163＋162＝23(y B <0，舍去)，故△OAF 的面积为12×1×23＝ 3.11．设椭圆C ：x 2a 2＋y 22＝1(a >0)的左、右焦点分别为F 1、F 2，A 是椭圆C 上的一点，且AF 2→·F 1F 2→＝0，坐标原点O 到直线AF 1的距离为13|OF 1|.(1)求椭圆C 的方程；(2)设Q 是椭圆C 上的一点，过点Q 的直线l 交x 轴于点P (－1,0)，交y 轴于点M ，若MQ →＝2QP →，求直线l 的方程．解析 (1)由题设知F 1(－a 2－2，0)，F 2(a 2－2，0)．由于AF 2→·F 1F 2→＝0，则有AF 2→⊥F 1F 2→，所以点A 的坐标为(a 2－2，±2a )，故AF 1→所在直线方程为y ＝±(x a a 2－2＋1a)．所以坐标原点O 到直线AF 1的距离为a 2－2a 2－1(a >2)．又|OF 1|＝a 2－2，所以a 2－2a 2－1＝13a 2－2，解得a ＝2(a >2)．所求椭圆的方程为x 24＋y 22＝1.(2)由题意可知直线l 的斜率存在，设直线l 斜率为k ， 直线l 的方程为y ＝k (x ＋1)，则有M (0，k )． 设Q (x 1，y 1)，∵MQ →＝2QP →， ∴(x 1，y 1－k )＝2(－1－x 1，－y 1)． ∴⎩⎪⎨⎪⎧x 1＝－23，y 1＝k3.又Q 在椭圆C 上，得(－23)24＋(k 3)22＝1，解得k ＝±4.故直线l 的方程为y ＝4(x ＋1)或y ＝－4(x ＋1)，即4x －y ＋4＝0或4x ＋y ＋4＝0.12．椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点为F 1、F 2，过F 1的直线l 与椭圆交于A 、B 两点．(1)如果点A 在圆x 2＋y 2＝c 2(c 为椭圆的半焦距)上，且|F 1A |＝c ，求椭圆的离心率；(2)若函数y ＝2＋log m x (m >0且m ≠1)的图像，无论m 为何值时恒过定点(b ，a )，求F 2B →·F 2A →的取值范围．解析 (1)∵点A 在圆x 2＋y 2＝c 2上， ∴△AF 1F 2为一直角三角形． ∵|F 1A |＝c ，|F 1F 2|＝2c ， ∴|F 2A |＝|F 1F 2|2－|AF 1|2＝3c . 由椭圆的定义，知|AF 1|＋|AF 2|＝2a ， ∴c ＋3c ＝2a .∴e ＝c a ＝21＋3＝3－1.(2)∵函数y ＝2＋log m x 的图像恒过点(1，2)，由已知条件知还恒过点(b ，a )，∴a ＝2，b ＝1，c ＝1.点F 1(－1,0)，F 2(1,0)，①若AB ⊥x 轴，则A (－1，22)，B (－1，－22)． ∴F 2A →＝(－2，22)，F 2B →＝(－2，－22)． ∴F 2A →·F 2B →＝4－12＝72.②若AB 与x 轴不垂直，设直线AB 的斜率为k ，则AB 的方程为y ＝k (x ＋1)． 由⎩⎨⎧y ＝k (x ＋1)，x 2＋2y 2－2＝0，消去y ，得(1＋2k 2)x 2＋4k 2x ＋2(k 2－1)＝0.(*) ∵Δ＝8k 2＋8>0，∴方程(*)有两个不同的实根．设点A (x 1，y 1)，B (x 2，y 2)，则x 1，x 2是方程(*)的两个根．x 1＋x 2＝－4k 21＋2k 2，x 1x 2＝2(k 2－1)1＋2k 2.∴F 2A →＝(x 1－1，y 1)，F 2B →＝(x 2－1，y 2)． ∴F 2A →·F 2B →＝(x 1－1)(x 2－1)＋y 1y 2 ＝(1＋k 2)x 1x 2＋(k 2－1)(x 1＋x 2)＋1＋k 2 ＝(1＋k 2)2(k 2－1)1＋2k 2＋(k 2－1)(－4k 21＋2k2)＋1＋k 2 ＝7k 2－11＋2k 2＝72－92(1＋2k 2). ∵1＋2k 2≥1，∴0<11＋2k 2≤1,0<92(1＋2k 2)≤92.∴－1≤F 2A →·F 2B →＝72－92(1＋2k 2)<72.综上，由①②，知－1≤F 2A →·F 2B →≤72.13．(2013·衡水调研)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的一个焦点是F (1,0)，且离心率为12.(1)求椭圆C 的方程；(2)设经过点F 的直线交椭圆C 于M ，N 两点，线段MN 的垂直平分线交y 轴于点P (0，y 0)，求y 0的取值范围．解析 (1)设椭圆C 的半焦距是c .依题意，得c ＝1. 因为椭圆C 的离心率为12， 所以a ＝2c ＝2，b 2＝a 2－c 2＝3. 故椭圆C 的方程为x 24＋y 23＝1. (2)当MN ⊥x 轴时，显然y 0＝0.当MN 与x 轴不垂直时，可设直线MN 的方程为y ＝k (x －1)(k ≠0)．由⎩⎪⎨⎪⎧y ＝k (x －1)，x 24＋y 23＝1，消去y 并整理得(3＋4k 2)x 2－8k 2x ＋4(k 2－3)＝0.设M (x 1，y 1)，N (x 2，y 2)，线段MN 的中点为Q (x 3，y 3)， 则x 1＋x 2＝8k 23＋4k 2.所以x 3＝x 1＋x 22＝4k 23＋4k 2，y 3＝k (x 3－1)＝－3k 3＋4k 2. 线段MN 的垂直平分线的方程为y ＋3k 3＋4k 2＝－1k (x －4k 23＋4k 2)．在上述方程中，令x ＝0，得y 0＝k 3＋4k 2＝13k ＋4k. 当k <0时，3k ＋4k ≤－43；当k >0时，3k ＋4k ≥4 3. 所以－312≤y 0<0或0<y 0≤312. 综上，y 0的取值范围是[－312，312]． 14．(2013·北京海淀区期末)已知焦点在x 轴上的椭圆C 过点(0,1)，且离心率为32，Q 为椭圆C 的左顶点．(1)求椭圆C 的标准方程；(2)已知过点(－65，0)的直线l 与椭圆C 交于A ，B 两点． ①若直线l 垂直于x 轴，求∠AQB 的大小；②若直线l 与x 轴不垂直，是否存在直线l 使得△QAB 为等腰三角形？若存在，求直线l 的方程；若不存在，请说明理由．解析 (1)设椭圆C 的标准方程为x 2a 2＋y 2b 2＝1(a >b >0)，且a 2＝b 2＋c 2. 由题意可知：b ＝1，c a ＝32.解得a 2＝4，所以椭圆C 的标准方程为x 24＋y 2＝1.(2)由(1)得Q (－2,0)．设A (x 1，y 1)，B (x 2，y 2)． ①当直线l 垂直于x 轴时，直线l 的方程为x ＝－65. 由⎩⎪⎨⎪⎧x ＝－65，x 24＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝－65，y ＝45或⎩⎪⎨⎪⎧x ＝－65，y ＝－45.即A (－65，45)，B (－65，－45)(不妨设点A 在x 轴上方)， 则k AQ ＝45－0－65－(－2)＝1，k BQ ＝－45－0－65－(－2)＝－1.因为k AQ ·k BQ ＝－1，所以AQ ⊥BQ . 所以∠AQB ＝π2，即∠AQB 的大小为π2.②当直线l 与x 轴不垂直时，由题意可设直线AB 的方程为y ＝k (x ＋65)(k ≠0)． 由⎩⎪⎨⎪⎧y ＝k (x ＋65)，x 24＋y 2＝1，消去y 得(25＋100k 2)x 2＋240k 2x ＋144k 2－100＝0.因为点(－65，0)在椭圆C 的内部，显然Δ>0. ⎩⎪⎨⎪⎧x 1＋x 2＝－240k 225＋100k 2，x 1x 2＝144k 2－10025＋100k 2.因为QA →＝(x 1＋2，y 1)，QB →＝(x 2＋2，y 2)，y 1＝k (x 1＋65)，y 2＝k (x 2＋65)，所以QA →·QB →＝(x 1＋2)(x 2＋2)＋y 1y 2 ＝(x 1＋2)(x 2＋2)＋k (x 1＋65)·k (x 2＋65) ＝(1＋k 2)x 1x 2＋(2＋65k 2)(x 1＋x 2)＋4＋3625k 2＝(1＋k 2)144k 2－10025＋100k 2＋(2＋65k 2)(－240k 225＋100k 2)＋4＋3625k 2＝0. 所以QA →⊥QB →.所以△QAB 为直角三角形．假设存在直线l 使得△QAB 为等腰三角形，则|QA |＝|QB |. 如图，取AB 的中点M ，连接QM ，则QM ⊥AB .记点(－65，0)为N .因为x M ＝x 1＋x 22＝－120k 225＋100k 2＝－24k 25＋20k 2，所以y M ＝k (x M ＋65)＝6k5＋20k 2，即M (－24k 25＋20k 2，6k 5＋20k 2)．所以QM →＝(10＋16k 25＋20k 2，6k 5＋20k 2)，NM →＝(65＋20k 2，6k 5＋20k 2)． 所以QM →·NM →＝10＋16k 25＋20k 2×65＋20k 2＋6k 5＋20k 2×6k 5＋20k 2＝60＋132k 2(5＋20k 2)2≠0.所以QM →与NM →不垂直，即QM →与AB →不垂直，矛盾．所以假设不成立，故当直线l 与x 轴不垂直时，不存在直线l 使得△QAB 为等腰三角形．15．设椭圆M ：y 2a 2＋x 2b 2＝1(a >b >0)的离心率与双曲线x 2－y 2＝1的离心率互为倒数，且内切于圆x 2＋y 2＝4.(1)求椭圆M 的方程；(2)若直线y ＝2x ＋m 交椭圆于A 、B 两点，椭圆上一点P (1，2)，求△P AB 面积的最大值．解析 (1)双曲线的离心率为2，则椭圆的离心率为 e ＝c a ＝22，圆x 2＋y 2＝4的直径为4，则2a ＝4，得⎩⎪⎨⎪⎧ 2a ＝4，c a ＝22，b 2＝a 2－c 2⇒⎩⎨⎧a ＝2，c ＝2，b ＝ 2.所求椭圆M 的方程为y 24＋x 22＝1. (2)直线AB 的直线方程为y ＝2x ＋m . 由⎩⎪⎨⎪⎧y ＝2x ＋m ，x 22＋y 24＝1，得4x 2＋22mx ＋m 2－4＝0.由Δ＝(22m )2－16(m 2－4)>0，得－22<m <2 2. ∵x 1＋x 2＝－22m ，x 1x 2＝m 2－44.∴|AB |＝1＋2|x 1－x 2|＝3·(x 1＋x 2)2－4x 1x 2 ＝3·12m 2－m 2＋4＝ 3 4－m 22.又P 到AB 的距离为d ＝|m |3. 则S △ABC ＝12|AB |d ＝12 3 4－m 22|m |3＝12m 2(4－m 22)＝122m 2(8－m 2)≤122·m 2＋(8－m 2)2＝2，当且仅当m ＝±2∈(－22，22)取等号． ∴(S △ABC )max ＝ 2.16．设椭圆C ：x 2＋2y 2＝2b 2(常数b >0)的左，右焦点分别为F 1，F 2，M ，N 是直线l ：x ＝2b 上的两个动点，F 1M →·F 2N →＝0.(1)若|F 1M →|＝|F 2N →|＝25，求b 的值； (2)求|MN |的最小值．解析 设M (2b ，y 1)，N (b ，y 2)， 则F 1M →＝(3b ，y 1)，F 2N →＝(b ，y 2)． 由F 1M →·F 2N →＝0，得y 1y 2＝－3b 2.① (1)由|F 1M →|＝|F 2N →|＝25，得(3b )2＋y 21＝2 5.②b 2＋y 22＝2 5.③由①、②、③三式，消去y 1，y 2，并求得b ＝ 2. (2)易求椭圆C 的标准方程为x 24＋y 22＝1.方法一 |MN |2＝(y 1－y 2)2＝y 21＋y 22－2y 1y 2≥－2y 1y 2－2y 1y 2＝－4y 1y 2＝12b 2，所以，当且仅当y 1＝－y 2＝3b 或y 2＝－y 1＝3b ，|MN |取最小值23b . 方法二 |MN |2＝(y 1－y 2)2＝y 21＋9b 4y 21＋6b 2≥12b 2，所以，当且仅当y 1＝－y 2＝3b 或y 2＝－y 1＝3b 时，|MN |取最小值23b . 17．(2013·武汉)如图，DP ⊥x 轴，点M 在DP 的延长线上，且|DM |＝2|DP |.当点P 在圆x 2＋y 2＝1上运动时．(1)求点M 的轨迹C 的方程；(2)过点T (0，t )作圆x 2＋y 2＝1的切线l 交曲线C 于A ，B 两点，求△AOB 面积S 的最大值和相应的点T 的坐标．解析 (1)设点M 的坐标为(x ，y )，点P 的坐标为(x 0，y 0)，则x ＝x 0，y ＝2y 0，所以x 0＝x ，y 0＝y 2.①因为P (x 0，y 0)在圆x 2＋y 2＝1上，所以x 20＋y 20＝1.②将①代入②，得点M 的轨迹C 的方程为x 2＋y 24＝1.(2)由题意知，|t |≥1.当t ＝1时，切线l 的方程为y ＝1，点A 、B 的坐标分别为(－32，1)、(32，1)，此时|AB |＝3，当t ＝－1时，同理可得|AB |＝3；当|t |>1时，设切线l 的方程为y ＝kx ＋t ，k ∈R.由⎩⎪⎨⎪⎧y ＝kx ＋t ，x 2＋y 24＝1，得(4＋k 2)x 2＋2ktx ＋t 2－4＝0.③设A ，B 两点的坐标分别为(x 1，y 1)，(x 2，y 2)，则由③得 x 1＋x 2＝－2kt 4＋k 2，x 1x 2＝t 2－44＋k 2.又由l 与圆x 2＋y 2＝1相切，得|t |k 2＋1＝1，即t 2＝k 2＋1.所以|AB |＝(x 2－x 1)2＋(y 2－y 1)2 ＝(1＋k 2)[4k 2t 2(4＋k 2)2－4(t 2－4)4＋k 2]＝43|t |t 2＋3.因为|AB |＝43|t |t 2＋3＝43|t |＋3|t |≤2，且当t ＝±3时，|AB |＝2，所以|AB |的最大值为2.依题意，圆心O 到直线AB 的距离为圆x 2＋y 2＝1的半径，所以△AOB 面积S ＝12|AB |×1≤1，当且仅当t ＝±3时，△AOB 面积S 的最大值为1，相应的T 的坐标为(0，－3)或(0，3)．18．已知焦点在y 轴上的椭圆C 1：y 2a 2＋x 2b 2＝1经过A (1,0)点，且离心率为32. (1)求椭圆C 1的方程；(2)过抛物线C 2：y ＝x 2＋h (h ∈R)上P 点的切线与椭圆C 1交于两点M 、N ，记线段MN 与P A 的中点分别为G 、H ，当GH 与y 轴平行时，求h 的最小值．解析 (1)由题意可得⎩⎪⎨⎪⎧1b 2＝1，c a ＝32，a 2＝b 2＋c 2.解得a ＝2，b ＝1，所以椭圆C 1的方程为x 2＋y 24＝1.(2)设P (t ，t 2＋h )，由y ′＝2x ，抛物线C 2在点P 处的切线的斜率为k ＝y ′|x ＝t ＝2t ，所以MN 的方程为y ＝2tx －t 2＋h .代入椭圆方程得4x 2＋(2tx －t 2＋h )2－4＝0， 化简得4(1＋t 2)x 2－4t (t 2－h )x ＋(t 2－h )2－4＝0. 又MN 与椭圆C 1有两个交点， 故Δ＝16[－t 4－2(h ＋2)t 2－h 2＋4]>0.①设M (x 1，y 1)，N (x 2，y 2)，MN 中点横坐标为x 0，则x 0＝x 1＋x 22＝t (t 2－h )2(1＋t 2).设线段P A 的中点横坐标为x 3＝1＋t2. 由已知得x 0＝x 3，即t (t 2－h )2(1＋t 2)＝1＋t2.②显然t ≠0，h ＝－(t ＋1t ＋1)．③当t >0时，t ＋1t ≥2，当且仅当t ＝1时取得等号，此时h ≤－3不符合①式，故舍去；当t <0时，(－t )＋(－1t )≥2，当且仅当t ＝－1时取得等号，此时h ≥1，满足①式．综上，h 的最小值为1.19．已知△ABC 中，点A 、B 的坐标分别为(－2，0)，B (2，0)，点C 在x 轴上方．(1)若点C 坐标为(2，1)，求以A 、B 为焦点且经过点C 的椭圆的方程； (2)过点P (m,0)作倾斜角为34π的直线l 交(1)中曲线于M 、N 两点，若点Q (1,0)恰在以线段MN 为直径的圆上，求实数m 的值．解析 (1)设椭圆方程为x 2a 2＋y 2b 2＝1，c ＝2，2a ＝|AC |＋|BC |＝4，b ＝2，所以椭圆方程为x 24＋y 22＝1.(2)直线l 的方程为y ＝－(x －m )，令M (x 1，y 1)，N (x 2，y 2)，联立方程解得 3x 2－4mx ＋2m 2－4＝0，⎩⎪⎨⎪⎧x 1＋x 2＝4m3，x 1x 2＝2m 2－43若Q 恰在以MN 为直径的圆上，则y 1x 1－1·y 2x 2－1＝－1，即m 2＋1－(m ＋1)(x 1＋x 2)＋2x 1x 2＝0,3m 2－4m －5＝0，解得m ＝2±193.20．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，其中左焦点F (－2,0)． (1)求椭圆C 的方程；(2)若直线y ＝x ＋m 与椭圆C 交于不同的两点A ，B ，且线段AB 的中点M 关于直线y ＝x ＋1的对称点在圆x 2＋y 2＝1上，求m 的值．解析(1)⎩⎨⎧c a ＝22，c ＝2⇒x 28＋y 24＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，M (x 3，y 3)，V (x 4，y 4)． 由⎩⎪⎨⎪⎧x 28＋y 24＝1，y ＝x ＋m⇒3x 2＋4mx ＋2m 2－8＝0.∴Δ＝96－8m 2>0⇒－23<m <2 3. ∴x 3＝x 1＋x 22＝－2m 3，y 3＝x 3＋m ＝m3.又⎩⎪⎨⎪⎧y 3＋y 42＝x 3＋x 42＋1，y 4－y 3x 4－x 3＝－1⇒⎩⎪⎨⎪⎧x 4＝m3－1，y 4＝1－2m 3，在x 2＋y 2＝1上．∴(m 3－1)2＋(1－2m 3)2＝1⇒m 29－2m 3＋4m 21－4m 3＋1＝0. ∴5m 2－18m ＋9＝0⇒(5m －3)(m －3)＝0. ∴m ＝35或m ＝3经检验成立． ∴m ＝35或m ＝3.21．(2012·浙江宁波市期末)已知抛物线C ：x 2＝2py (p >0)的焦点为F ，抛物线上一点A 的横坐标为x 1(x 1>0)，过点A 作抛物线C 的切线l 1交x 轴于点D ，交y 轴于点Q ，交直线l ：y ＝p2于点M ，当|FD |＝2时，∠AFD ＝60°.(1)求证：△AFQ 为等腰三角形，并求抛物线C 的方程；(2)若B 位于y 轴左侧的抛物线C 上，过点B 作抛物线C 的切线l 2交直线l 1于点P ，交直线l 于点N ，求△PMN 面积的最小值，并求取到最小值时的x 1的值．解析 (1)设A (x 1，y 1)，则切线AD 的方程为y ＝x 1p x －x 212p .所以D (x 12，0)，Q (0，－y 1)，|FQ |＝p 2＋y 1，|F A |＝p2＋y 1，所以|FQ |＝|F A |. 所以△AFQ 为等腰三角形， 且D 为AQ 中点，所以DF ⊥AQ . ∵|DF |＝2，∠AFD ＝60°，∴∠QFD ＝60°，p 2＝1，得p ＝2，抛物线方程为x 2＝4y . (2)设B (x 2，y 2)(x 2<0)，则B 处的切线方程为y ＝x 22x －x 224. 由⎩⎪⎨⎪⎧y ＝x 12x －x 214，y ＝x 22x －x 224⇒P (x 1＋x 22，x 1x 24)，⎩⎪⎨⎪⎧y ＝x 12x －x 214，y ＝1⇒M (x 12＋2x 1，1)．同理N (x 22＋2x 2，1)，所以面积S ＝12(x 12＋2x 1－x 22－2x 2)·(1－x 1x 24)＝(x 2－x 1)(4－x 1x 2)216x 1x 2.①设AB 的方程为y ＝kx ＋b ，则b >0. 由⎩⎨⎧ y ＝kx ＋b ，x 2＝4y ⇒x 2－4kx －4b ＝0， 得⎩⎨⎧x 1＋x 2＝4k ，x 1x 2＝－4b ，代入①得 S ＝16k 2＋16b (4＋4b )264b ＝(1＋b )2k 2＋b b ，使面积最小，则k ＝0，得到S ＝(1＋b )2b b.② 令b ＝t ，②得S (t )＝(1＋t 2)2t ＝t 3＋2t ＋1t ，S ′(t )＝(3t 2－1)(t 2＋1)t 2，∴当t ∈(0，33)时S (t )单调递减；当t ∈(33，＋∞)时S (t )单调递增． ∴当t ＝33时，S 取最小值为1639，此时b ＝t 2＝13，k ＝0， ∴y 1＝13即x 1＝233. 22.如图，已知M (m ，m 2)、N (n ，n 2)是抛物线C ：y ＝x 2上的两个不同的点，且m 2＋n 2＝1，m ＋n ≠0，直线l 是线段MN 的垂直平分线，设椭圆E 的方程为x 22＋y 2a ＝1(a >0，a ≠2)．(1)当M 、N 在C 上移动时，求直线l 的斜率k 的取值范围；(2)已知直线l 与抛物线C 交于A 、B 两点，与椭圆E 交于P 、Q 两点，设线段AB 的中点为R ，线段QP 的中点为S ，若OR →·OS →＝0，求椭圆E 的离心率的取值范围．解析 (1)由题意知，直线MN 的斜率k MN ＝m 2－n 2m －n ＝m ＋n .又l ⊥MN ，m ＋n ≠0，∴直线l 的斜率k ＝－1m ＋n. ∵m 2＋n 2＝1，由m 2＋n 2≥2mn ，得2(m 2＋n 2)≥(m ＋n )2， 即2≥(m ＋n )2(当m ＝n 时，等号成立)，∴|m ＋n |≤ 2. ∵M 、N 是不同的两点，即m ≠n ，∴0<|m ＋n |< 2. ∴|k |>22，即k <－22或k >22.(2)由题意易得，线段MN 的中点坐标为(m ＋n 2，m 2＋n 22)． ∵直线l 是线段MN 的垂直平分线， ∴直线l 的方程为y －m 2＋n 22＝k (x －m ＋n2)． 又∵m 2＋n 2＝1，k ＝－1m ＋n ，∴直线l 的方程为y ＝kx ＋1.将直线l 的方程代入抛物线方程和椭圆方程并分别整理，得 x 2－kx －1＝0， ①(a ＋2k 2)x 2＋4kx ＋2－2a ＝0. ② 易知方程①的判别式Δ1＝k 2＋4>0， 方程②的判别式Δ2＝8a (2k 2＋a －1)．由(1)易知k 2>12，且a >0，∴2k 2＋a －1>a >0，∴Δ2>0恒成立．设A (x A ，y A )，B (x B ，y B )，P (x P ，y P )，Q (x Q ，y Q )，则x A ＋x B ＝k ，y A ＋y B ＝kx A ＋1＋kx B ＋1＝k (x A ＋x B )＋2＝k 2＋2.∴线段AB 的中点R 的坐标为(k 2，k 22＋1)． 又x P ＋x Q ＝－4ka ＋2k 2，y P ＋y Q＝kx P ＋1＋kx Q ＋1 ＝k (x P ＋x Q )＋2＝2aa ＋2k 2.第 31 页 共 31 页 ∴线段QP 的中点S 的坐标为(－2k a ＋2k 2，a a ＋2k 2)．∴OR →＝(k 2，k 22＋1)，OS →＝(－2k a ＋2k 2，a a ＋2k 2)，由OR →·OS →＝0， 得－k 2＋a (k 22＋1)a ＋2k 2＝0，即－k 2＋a (k 22＋1)＝0.∴a ＝2k 2k 2＋2.∵k 2>12，∴a ＝2k 2k 2＋2＝21＋2k 2>25，a ＝2k 2k 2＋2＝2－4k 2＋2<2.∴25<a <2.由题易知，椭圆E 的离心率e ＝2－a 2，∴a ＝2－2e 2，∴25<2－2e 2<2，∴0<e 2<45，∴0<e <255.∴椭圆E 的离心率的取值范围是(0，255)．。

高考数学一轮复习---正弦定理和余弦定理(二)考点一 有关三角形面积的计算例、(1)(△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，已知b ＝7，c ＝4，cos B ＝34，则△ABC 的面积等于( )A ．37 B.372 C ．9 D.92(2)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .若△ABC 的面积为34(a 2＋c 2－b 2)，则B ＝________. 变式练习1.(变条件)本例(1)的条件变为：若c ＝4，sin C ＝2sin A ，sin B ＝154，则S △ABC ＝________. 2.(变结论)本例(2)的条件不变，则C 为钝角时，ca 的取值范围是________．3．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，(2b －a )cos C ＝c cos A .(1)求角C 的大小；(2)若c ＝3，△ABC 的面积S ＝433，求△ABC 的周长．[解题技法]1．求三角形面积的方法(1)若三角形中已知一个角(角的大小或该角的正、余弦值)，结合题意求解这个角的两边或该角的两边之积，代入公式求面积．(2)若已知三角形的三边，可先求其一个角的余弦值，再求其正弦值，代入公式求面积．总之，结合图形恰当选择面积公式是解题的关键． 2．已知三角形面积求边、角的方法(1)若求角，就寻求夹这个角的两边的关系，利用面积公式列方程求解． (2)若求边，就寻求与该边(或两边)有关联的角，利用面积公式列方程求解．考点二 平面图形中的计算问题例、如图，在平面四边形ABCD 中，∠ABC ＝3π4，AB ⊥AD ，AB ＝1.(1)若AC ＝5，求△ABC 的面积； (2)若∠ADC ＝π6，CD ＝4，求sin ∠CAD .[解题技法]与平面图形有关的解三角形问题的关键及思路：求解平面图形中的计算问题，关键是梳理条件和所求问题的类型，然后将数据化归到三角形中，利用正弦定理或余弦定理建立已知和所求的关系．具体解题思路如下：(1)把所提供的平面图形拆分成若干个三角形，然后在各个三角形内利用正弦、余弦定理求解； (2)寻找各个三角形之间的联系，交叉使用公共条件，求出结果． 跟踪训练1.如图，在△ABC 中，D 是边AC 上的点，且AB ＝AD,2AB ＝3BD ，BC ＝2BD ，则sin C 的值为________．2.如图，在平面四边形ABCD 中，DA ⊥AB ，DE ＝1，EC ＝7，EA ＝2，∠ADC ＝2π3，且∠CBE ，∠BEC ，∠BCE 成等差数列．(1)求sin ∠CED ； (2)求BE 的长．考点三 三角形中的最值、范围问题例、(1)在△ABC 中，内角A ，B ，C 对应的边分别为a ，b ，c ，A ≠π2，sin C ＋sin(B －A )＝2sin 2A ，则角A的取值范围为( ) A.]6,0(πB.]4,0(πC.]4,6[ππD.]3,6[ππ (2)已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且cos 2A ＋cos 2B ＝2cos 2C ，则cos C 的最小值为( ) A.32 B.22 C.12 D ．－12[解题技法]1．三角形中的最值、范围问题的解题策略解与三角形中边角有关的量的取值范围时，主要是利用已知条件和有关定理，将所求的量用三角形的某个内角或某条边表示出来，结合三角形边角取值范围等求解即可．2．求解三角形中的最值、范围问题的注意点(1)涉及求范围的问题，一定要搞清已知变量的范围，利用已知的范围进行求解， 已知边的范围求角的范围时可以利用余弦定理进行转化．(2)注意题目中的隐含条件，如A ＋B ＋C ＝π，0<A <π，b －c <a <b ＋c ，三角形中大边对大角等． 跟踪训练1．在钝角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，B 为钝角，若a cos A ＝b sin A ，则sin A ＋sin C 的最大值为( )A. 2B.98 C ．1 D.782．在△ABC 中，已知c ＝2，若sin 2A ＋sin 2B －sin A sin B ＝sin 2C ，则a ＋b 的取值范围为________． 3．已知在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且cos B b ＋cos C c ＝sin A3sin C.(1)求b 的值；(2)若cos B ＋3sin B ＝2，求△ABC 面积的最大值．考点四 解三角形与三角函数的综合应用 考法(一) 正、余弦定理与三角恒等变换例、在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知b sin A ＝ac os ⎪⎭⎫⎝⎛-6πB . (1)求角B 的大小；(2)设a ＝2，c ＝3，求b 和sin(2A －B )的值．考法(二) 正、余弦定理与三角函数的性质 例、已知函数f (x )＝c os 2x ＋3sin(π－x )c os(π＋x )－12.(1)求函数f (x )在[0，π]上的单调递减区间；(2)在锐角△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知f (A )＝－1，a ＝2，b sin C ＝a sin A ，求△ABC 的面积． 跟踪训练1.在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，(2a －c )cos B －b cos C ＝0. (1)求角B 的大小；(2)设函数f (x )＝2sin x cos x cos B －32cos 2x ，求函数f (x )的最大值及当f (x )取得最大值时x 的值．课后作业1．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，cos 2A ＝sin A ，bc ＝2，则△ABC 的面积为( ) A.12 B.14C ．1D ．2 2．在△ABC 中，a ，b ，c 分别是角A ，B ，C 所对的边，若(2a ＋c )cos B ＋b cos C ＝0，则角B 的大小为( ) A.π6 B.π3 C.2π3 D.5π63．在锐角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若sin A ＝223，a ＝3，S △ABC ＝22，则b 的值为( )A ．6B ．3C ．2D ．2或34．在△ABC 中，已知AB ＝2，AC ＝5，t a n ∠BAC ＝－3，则BC 边上的高等于( ) A ．1 B.2 C. 3 D ．25．已知a ，b ，c 分别是△ABC 的内角A ，B ，C 的对边，且a sin B ＝3b cos A ，当b ＋c ＝4时，△ABC 面积的最大值为( ) A.33 B.32C.3 D ．23 6．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若bc ＝1，b ＋2c cos A ＝0，则当角B 取得最大值时，△ABC 的周长为( )A ．2＋ 3B ．2＋2C ．3D ．3＋2 7．在△ABC 中，B ＝120°，AC ＝7，AB ＝5，则△ABC 的面积为________．8．在△ABC 中，三个内角A ，B ，C 的对边分别为a ，b ，c ，若 12b cos A ＝sin B ，且a ＝23，b ＋c ＝6，则△ABC 的面积为________．9．已知在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，∠BAC ＝π2，点D 在边BC 上，AD ＝1，且BD＝2DC ，∠BAD ＝2∠DAC ，则sin Bsin C＝________.10．如图所示，在△ABC 中，C ＝π3，BC ＝4，点D 在边AC 上，AD ＝DB ，DE ⊥AB ，E 为垂足，若DE ＝22，则cos A ＝________.11．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知c (1＋cos B )＝b (2－cos C )．(1)求证：2b ＝a ＋c ；(2)若B ＝π3，△ABC 的面积为43，求b .12．在△ABC 中，AC ＝6，cos B ＝45，C ＝π4.(1)求AB 的长； (2)求c os ⎪⎭⎫⎝⎛-6πA 的值．提高训练1．在锐角三角形ABC中，角A，B，C的对边分别为a，b，c，若B＝2A，则2ba的取值范围是()A．(2，2)B．(2，6)C．(2，3)D．(6，4)2．△ABC的三个内角A，B，C所对的边分别为a，b，c，a sin A sin B＋bc os2A＝2a，则角A的取值范围是________．3．如图，在平面四边形ABCD中，AB⊥BC，AB＝2，BD＝5，∠BCD＝2∠ABD，△ABD的面积为2.(1)求AD的长；(2)求△CBD的面积．。

2014届高三数学理科单元过关自测(九)（ 数列、不等式、数学归纳法）一、选择题：1、不等式2210x x -->的解集是（ ）A ．），（121- B.），（∞+1 C ．），（），（∞+∞-21 D ．），（），（∞+-∞-121 2.下列命题中正确的是 ( )A.xx y 1+=的最小值是2 B.x x y x sin 2sin ),,0(+=∈π的最小值是22C.4522++=x x y 的最小值是2 D.+∈R x ,x x y 432--=的最大值是342-3．设S n 是等差数列{a n }的前n 项和，若35a a ＝95，则59S S ＝( )．A ．1B ．－1C ．2D ．21 4.已知数列{}n a 的前n 项和29n S n n =-，第k 项满足58k a <<,则k =( )A. 9B. 8C. 7D. 65、 对任何实数x ，若不等式12x x k +-->恒成立，则实数k 的取值范围为 ( )(A)k<3(B)k<-3(C)k ≤3(D) k ≤-36、已知平面直角坐标系xOy 上的区域D 由不等式组0222x y x y⎧≤≤⎪≤⎨⎪≤⎩给定，若(),M x y 为D 上的动点，点A 的坐标为()2,1，则z OM OA =⋅的最大值为（ ）A ．3B ．4C ．32D ．427、已知),2(241321...2111N n n n n n ∈≥>+++++过程中，由"1"""+==k n k n 变到时，不等式左边的变化是（ ）A ．)1(21++k B ．11221121+-++++k k k C ．11221+-++k k D ．)1(21121++++k k 8、如果c bx x x f ++=2)(对于任意实数t 都有)3()3(t f t f -=+，那么（ ）A .)4()1()3(f f f <<B .)4()3()1(f f f <<C .)1()4()3(f f f <<D .)1()3()4(f f f <<班别： 姓名： 学号： 成绩：一、选择题答案1 2 3 4 5 6 7 8二、填空题9. 不等式1|31|≥-+x x 的解集是 . 10. 已知递增的等差数列{}n a 满足21321,4a a a ==-，则_____n a =11、已知变量x ，y 满足约束条件30111x y x y -+≥⎧⎪-≤≤⎨⎪≥⎩则z x y =+的最大值是________。