铁道车辆轮对结构与轮轨接触几何关系 (1)
- 格式:ppt
- 大小:7.25 MB
- 文档页数:94
轮轨接触几何参数轮轨接触几何参数(wheel-rail contact geometry parameters)由轮轨接触几何关系所确定的轮对和钢轨上的一系列几何量。
主要包括下述11种参数。
车轮名义宜径由于车轮踏面具有斜度,各处直径是不相同的,根据规左,车辆在离轮缘内侧面70mm处(车辆)或73mm处(机车)测量得到的直径为剑义直径,该圆称为滚动圆。
车轮名义直径的大小影响机车车辆的性能。
中国客车标准轮径为915mm,货车标准轮径为 840mm,内燃机车标准轮径为1050mm,电力机车标准轮径为1250mm。
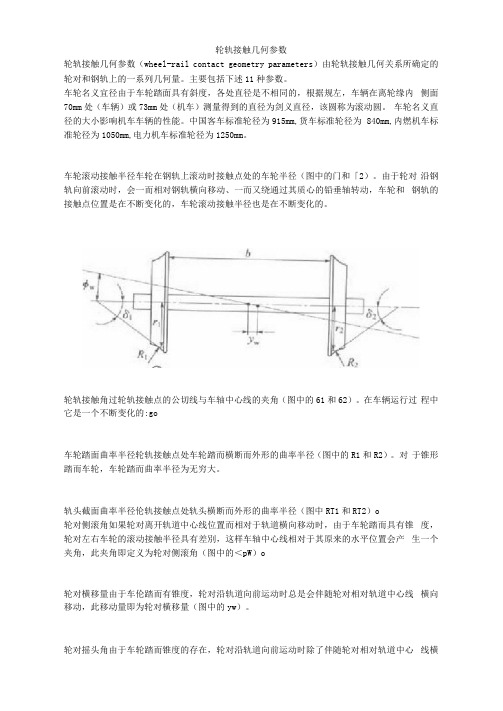
车轮滚动接触半径车轮在钢轨上滚动时接触点处的车轮半径(图中的门和「2)。
由于轮对沿钢轨向前滚动时,会一而相对钢轨横向移动、一而又绕通过其质心的铅垂轴转动,车轮和钢轨的接触点位置是在不断变化的,车轮滚动接触半径也是在不断变化的。
轮轨接触角过轮轨接触点的公切线与车轴中心线的夹角(图中的61和62)。
在车辆运行过程中它是一个不断变化的:go车轮踏面曲率半径轮轨接触点处车轮踏而横断而外形的曲率半径(图中的R1和R2)。
对于锥形踏而车轮,车轮踏而曲率半径为无穷大。
轨头截面曲率半径伦轨接触点处轨头横断而外形的曲率半径(图中RT1和RT2)o轮对侧滚角如果轮对离开轨道中心线位置而相对于轨道横向移动时,由于车轮踏而具有锥度,轮对左右车轮的滚动接触半径具有差別,这样车轴中心线相对于其原来的水平位置会产生一个夹角,此夹角即定义为轮对侧滚角(图中的<pW)o轮对横移量由于车伦踏而有锥度,轮对沿轨道向前运动时总是会伴随轮对相对轨道中心线横向移动,此移动量即为轮对横移量(图中的yw)。
轮对摇头角由于车轮踏而锥度的存在,轮对沿轨道向前运动时除了伴随轮对相对轨道中心线横向移动外,轮对还会绕通过其质心的铅垂轴转动,转动的角度即为轮对摇头角。
轮缘内侧距轮对两轮缘的内侧而间的距离即为轮缘内侧距(图中的b),对于标准轨距,轮缘内侧距为(1 353+2) mm<>轨距两根钢轨头部内侧间与轨道中心线相垂直的水平距离,并规左在轨顶下16mm处测崑世界上大部分国家均采用1435mm的标准轨距,即准轨。

轮轨接触⼏何关系轮轨接触⼏何关系班级:学号:姓名:轮轨接触⼏何关系是轮轨关系研究的基本内容,它不仅关系到车辆的动⼒学性能,也关系到轮轨之间的磨耗。
其研究结果可以⽤于横向稳定性计算、随机响应计算及动态曲线通过计算等,还可以⽤于轨道⼏何参数和轮轨外形的合理选择。
选择合适的轮轨⼏何,不仅可以改善车辆的动⼒学性能,还能降低轮轨间的磨耗,减少制造和维修成本,提⾼车辆的可靠性,延长车轮的使⽤寿命。
本⽂采⽤Simpack软件模拟轮轨接触,选⽤的车轮踏⾯为S1002,轨头为CHN_60。
1. S1002踏⾯外形S1002外形轮廓由车轮踏⾯作⽤区域之外的倒⾓、外侧斜度区域A、踏⾯区域B和C、踏⾯外形轮廓与轮廓外部区域的连接区域D、70o轮缘⾓长度区域E和轮缘区域F、G、H构成。
其中,外侧斜度区域A的斜度值可从6.5%⾄15%;踏⾯区域B和C由两段凹凸⽅向不同的⾼次曲线构成;连接区域D为⼀段半径为13mm的圆弧;70o轮缘⾓长度区域E为⼀条切线段;当车轮直径≥760mm时,轮缘⾼度h为28mm,轮缘区域F、G、H分别由半径为30mm、12mm和20.5mm的三段圆弧构成。
随着轮缘厚度的变化,轮缘及其踏⾯的连接区域也随之变化。
S1002踏⾯外形如图1-1所⽰。
图1-1 S1002踏⾯外形2. CHN_60轨⾯形状CHN_60钢轨顶⾯采⽤80-300-80的复合圆弧,具有与车轮踏⾯相适应的外形,能改善轮轨接触条件,提⾼抵抗压陷的能⼒;同时具有⾜够的⽀承⾯积,以备磨耗。
CHN_60踏⾯外形如图2-1所⽰。
图2-1 CHN_60轨⾯截⾯形状3. 轮轨⼏何关系参数轮轨⼏何关系重要参数有:车轮和钢轨型⾯、轨距、轨底坡、轮缘内侧距、名义滚动圆距轮对中⼼距离和车轮名义直径。
其⼏何关系平⾯图(见图3-1)和影响轮轨接触⼏何关系参数的平⾯图(图3-2)如下所⽰。
图3-1 轮轨接触⼏何关系平⾯图图3-2 影响轮轨接触⼏何关系平⾯图4. 轮轨接触⼏何关系的特征参数在机车车辆动⼒学研究中,除了要计算处接触点位置和相应参数值,另外,还要研究和动⼒学性能直接相关的轮轨关系特征参数,它们分别是:等效锥度、等效接触⾓、轮对重⼒刚度和重⼒⾓刚度。



轮轨接触几何关系探讨卜庆萌指导教师姚林泉摘要: 轮轨接触几何关系在高速、安全的轨道交通中具有重要的作用。
本文根据我国使用的三种主要车轮踏面的轮廓线,采用对其一、二阶导函数比较分析的方法研究它们的光滑度。
同时考察不同规格钢轨的光滑度以及与各车轮踏面相配合的结果。
从轮轨几何光滑接触的角度,指出了较优的车轮踏面,较优的轮轨配合以及几何优化原则。
关键字:轮轨关系,接触几何,车轮踏面,钢轨Abstract: The geometric relation of wheel-rail contact plays an important part in fast and safety rail transportation. Based on the three main Chinese wheels, we work out the first and second derivative of the contours in order to compare their smoothness. Also we research the smoothness of different rails and the effect to work in different wheels. From the aspect of that wheel and rail contact in smoothness, the better interface, the better coupling of wheel-rail and the principle of geometric optimization are shown.Keywords: wheel-rail relation,contact geometry,wheel treads,rail1 引言随着铁路列车运行速度、运载重量和运输密度的大幅度提高,机车车辆与轨道结构之间的相互作用引发的问题更加严重,也更趋复杂。

第三节轮轨接触几何关系及滚动理论轨道车辆沿钢轨运行,其运行性能与轮轨接触几何关系和轮轨之间的相互作用有着密切的关系。
同时,由于轮轨的原始外形不同和运用中形状的变化,轮轨之间的接触几何关系和接触状态也是不同和变化的。
米用车轮轴承、滚动是车辆获取导向、驱动或制动力的主要方式,轨道车辆中地铁、轻轨常采用钢轮钢轨方式,而独轨、新交通系统及部分地铁则采用充气轮胎走行在硬质导向路面上。
车轮与导轨间的滚动接触关系决定了它们间的作用力、变形和相对运动。
因此滚动接触直接影响城市轨道车辆的性能、安全、磨耗与使用寿命。
一轮轨接触参数和接触状态当车辆沿轨道运行时,为了避免车轮轮缘与钢轨侧面经常接触和便于车辆通过曲线,左右车轮的轮缘外侧距离小于轨距,因此轮对可以相对轨道作横向位移和摇头角位移。
在不同的横向位移和摇头角位移的条件下,左右轮轨之间的接触点有不同位置。
于是轮轨之间的接触参数也出现变化。
对车辆运行中动力学性能影响较大的轮轨接触几何参数如下(图5一8): 1左轮和右轮实际滚动半径r L ,r R。
当轮对为刚性轮对,轮对绕其中心线转动时,各部分的转速是一致的,车轮滚动半径大,在同样的转角下行走距离长。
同一轮对左右车轮滚动半径越大,左右车轮滚动时走行距离差就加大,车轮滚动半径的大小也影响轮轨接触力。
2左轮和右轮在轮轨接触点处的踏面曲率半径和3左轨相石轨在稚轨接触点处的矶头截曲曲率半径和轮轨接触点处的曲率半径大小将会影响轮轨实际接触斑的大小、形状和轮轨的接触应力。
4左轮和右轮在接触点处的接触角s:和6R,即轮轨接触点处的轮轨公切面与轮对中心。
线之间的夹角。
轮轨接触角的大小影响轮轨之间的法向力和切向力在垂向和水平方向分量的大小。
5轮对侧滚角小w。
轮对侧滚角会引起转向架的侧滚和车体侧滚。
6.轮对中心上下位移Z w。
该量的变化会引起转向架和车体的垂向位移。
研究轮轨接触关系时应特别注意轮轨间的接触状态。
车轮与钢轨之间的接触状态可能有两种,即一点接触和两点接触(图5一9),轮对相对轨道的移动量不大时,一般出现车轮踏面与钢轨顶面相接触,通常为“一点接触”;当轮对相对轨道的横移和摇头角位移量超过一定范围,根据不同轮轨形状特点可能引起车轮踏面和轮缘同时与钢轨顶面和侧面接触,即所谓“两点接触”。
轮轨关系轨道车辆和线路的作用问题是铁路轮轨接触式运输的基本问题。
发展重载运输必须解决好轮轨之间的动力作用,努力减轻重载列车与线路的动态作用。
但由于轮轨关系自身的复杂性,目前的研究理论和模型仍然基于一些假设[1]:1)法向接触满足Hertz 接触条件;2)轮轨接触副视为弹性半空间;3) 接触表面是理想光滑连续的,而接触表面之间的 “第三介质 ,’ 如水、油和其它污染物的影响被忽略;4) 轮轨接触斑以外边界支撑和约束条件对轮轨接触行为的影响被忽略;5) 高速轮轨滚动接触时的惯性力被忽略;6) 不考虑温度的影响。
上述几点假设是不符合实际但是理论的前提。
轮轨关系的主要研究内容为轮轨接触几何的确定和轮轨滚动接触理论的应用。
实际接触参数计算和列解微分方程的过程可简述如下:在某一瞬时位置确定轮轨接触点是关键,之后就可以在确定了接触点的基础上利用几何推导出各个重要的接触几何参数,如左右轮/轨在接触点的接触角L δ、R δ,左右轨在接触点处的钢轨顶面曲率半径RR ρ、RL ρ,左右轮在接触点处的踏面曲率半径WR ρ、WL ρ,左右轮实际滚动半径R r 、L r ,轮轨接触时的侧滚角k θ,轮对中心的上下位移k z ,其中变量为轮对相对轨道的横移量和摇头角w y 、w ψ。
利用已求得的接触参数和Hertz 接触理论公式计算出接触椭圆的长短半轴,从而确定轮轨接触斑。
然后利用接触椭圆的长短半轴长和查表得到的kalker 系数及材料常数计算得到蠕滑系数,之后再通过实际速度和纯滚动速度计算出蠕滑率,将二者带入蠕滑力公式求得蠕滑力。
最后就可以列出含有蠕滑力,悬挂力,惯性力的运动微分方程,利用计算机求解得到位移、速度、加速度和相关模态值。
最初进行轮轨接触几何关系研究并确定接触参数的实用方法有两种:一种是圆弧形截面模型,一种是任意截面模型。
前者可直观的用数学解析的方法确定其几何关系,后者是数值方法,需编程实现。
前者在综述中提到;现重点论述后者,它是一种通用性很强的求解轮轨接触几何的数值方法。