212 光的衍射(二)
- 格式:doc
- 大小:207.00 KB
- 文档页数:3


高中物理:光学-光的衍射光的衍射是光学中的经典知识点,其在多个领域都有着广泛的应用,例如显微镜、天文望远镜等。
本文将详细介绍光的衍射的基本概念、衍射定理、夫琅禾费衍射以及常见的实验方法。
一、光的衍射的基本概念光的衍射是指光通过一个孔或者通过物体表面的缝隙后,光波会扩散成为一组新的光波,这种现象被称为光的衍射。
在光的衍射中,光波会形成一些明暗交替的区域,这些区域被称为衍射图样,其形状和孔或者缝隙的大小和形状有关。
二、衍射定理衍射定理是光学中最重要的定理之一,它是描述从一个孔或者一个光源丝的发射的光经过另一个孔或者缝隙后产生的光的波前的变化情况。
衍射定理可以用来计算衍射图案的形状,以及通过使用光的衍射图案来确定物体的大小和形状。
衍射定理的公式如下所示:sinθ = nλ/d其中,θ是衍射角,n是衍射序数,λ是光的波长,d是孔或者缝隙的宽度。
三、夫琅禾费衍射夫琅禾费衍射是一种典型的衍射现象,它是一种发生在单缝或双缝上的衍射现象。
夫琅禾费衍射的衍射图样是一组纵向的亮暗条纹。
夫琅禾费衍射的公式如下所示:dsinθ = nλ其中,d是缝隙的大小,θ是衍射角,n是衍射序数,λ是光的波长。
四、实验方法实验方法是研究光的衍射现象的重要手段。
常见的光的衍射实验方法包括单缝衍射实验、双缝干涉实验、格点衍射实验等。
(1)单缝衍射实验单缝衍射实验是研究光的衍射现象的最简单的实验方法之一,它可以通过一个狭窄的孔洞使光波扩散成为一个圆形的波前来观察光的衍射现象。
(2)双缝干涉实验双缝干涉实验是研究光的干涉现象的重要实验方法,它可以通过两个狭缝使光波扩散成为一组具有干涉现象的亮暗条纹。
(3)格点衍射实验格点衍射实验是一种研究光的衍射现象的实验方法,它可以通过一个光栅来使光波扩散成为一组具有规律的亮暗条纹。
五、练习题1. 一束波长为500nm的光穿过一个宽度为0.3mm的单缝后,经过距离1m的观察屏时,其衍射图样的第五个主极大的位置距离中心线的距离是多少?参考答案:0.30mm2. 光通过一组双缝(缝距为0.1mm,缝宽为0.05mm),在距离屏幕40cm处出现了一组亮暗条纹。


高中物理光的衍射知识点复习光学衍射现象是光在传播过程中出现的一种波动状态。
这部分内容在《光学》中比较抽象,学生学习起来比较困难。
下面店铺给大家带来高中物理光的衍射知识点,希望对你有帮助。
高中物理光的衍射知识点(1)光的衍射现象光绕过障碍物偏离直线传播路径而进入阴影区里的现象,叫光的衍射。
光的衍射和光的干涉一样证明了光具有波动性。
小孔或障碍物的尺寸比光波的波长小,或者跟波长差不多时,光才能发生明显的衍射现象。
(2)衍射现象的特点:①光束在衍射屏上的某一方位受到限制,则远处屏幕上的衍射强度就沿该方向扩展开来。
②若光孔线度越小,光束受限制得越厉害,则衍射范围越加弥漫。
理论上表明光孔横向线度与衍射发散角Δ之间存在反比关系。
(3)产生条件由于光的波长很短,只有十分之几微米,通常物体都比它大得多,所以当光射向一个针孔、一条狭缝、一根细丝时,可以清楚地看到光的衍射。
用单色光照射时效果好一些,如果用复色光,则看到的衍射图案是彩色的。
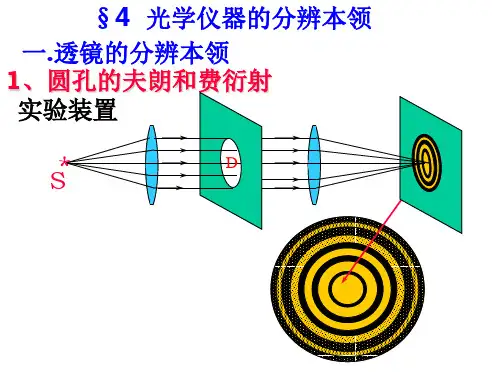
(3)衍射图样①单缝衍射:中央为亮条纹,向两侧有明暗相间的条纹,但间距和亮度不同.白光衍射时,中央仍为白光,最靠近中央的是紫光,最远离中央的是红光.②圆孔衍射:明暗相间的不等距圆环.③泊松亮斑:光照射到一个半径很小的圆板后,在圆板的阴影中心出现的亮斑,这是光能发生衍射的有力证据之一。
(4)衍射应用光的衍射决定光学仪器的分辨本领。
气体或液体中的大量悬浮粒子对光的散射,衍射也起重要的作用。
在现代光学乃至现代物理学和科学技术中,光的衍射得到了越来越广泛的应用。
衍射应用大致可以概括为以下四个方面:①衍射用于光谱分析。
如衍射光栅光谱仪。
②衍射用于结构分析。
衍射图样对精细结构有一种相当敏感的“放大”作用,故而利用图样分析结构,如X射线结构学。
③衍射成像。
在相干光成像系统中,引进两次衍射成像概念,由此发展成为空间滤波技术和光学信息处理。
光瞳衍射导出成像仪器的分辨本领。
④衍射再现波阵面。
这是全息术原理中的重要一步。



光的衍射(二)
1 用含有波长1λ、2λ的复色光作光栅衍射实验,先后两次实验用了A 、B 两块光栅常数d 相同、总刻痕数B A N N ≠的光栅,测得两组一级光谱(如图所示),则[ ]。
A .21;λλ><
B A N N
B .21;λλ>>B A N N
C .21;λλ<<B A N N
D .21;λλ<>B A N N
答:[D ]
解:由光栅方程λθm d =sin ,同一级光栅衍射光谱,波长越大,衍射角越大,由图21λλ<。
由光栅的色分辨本领mN d R ==λ
λ,同一级光栅衍射光谱,光栅总刻痕数越多,光栅色分辨本领越高,能分辨的波长差越小,由图B A N N >。
2.某确定波长的光垂直入射一光栅,屏幕上只能看到0级和l 级主极大,要想在屏幕上观察到更高级次的衍射主极大,应该[]。
A .减小光栅与观察屏之间的距离
B .增大光栅与观察屏之间的距离
C .换一个光栅常数较小的光栅
D .换一个光栅常数较大的光栅
答:[D ]
解:由光栅方程λθm d =sin 可知,屏幕上2级以上衍射主极大,是因为2级衍射角已经大于0
90。
为了减小2级以上衍射主极大的衍射角,靠改变光栅与观察屏之间的距离无济于事,在波长确定的情况下,只能换一个光栅常数较大的光栅。
3.波长为nm 500的单色光以030的倾角入射到光栅上,已知光栅常数m d μ1.2=、透光 缝宽m a μ7.0=,求:所有能看到的谱线级次。
解:斜入射光栅方程为 λθθm d =-)sin (sin 0
所以,各级衍射角满足
0sin /sin θλθ+=d m
由于能够在屏幕上观察到的衍射主极大的衍射角必须满足
009090+<<-θ
因此,能够在屏幕上观察到的衍射主极大的级次必须满足
15.02100
500sin /0<+=+m
d m θλ 由此,解得 3.6;1.2-><-+m m
所以,能够在屏幕上观察到的衍射主极大的级次最高为
6;2-==-+m m
又因-3和-6缺级,
所以能看见2、1、0、-1、-2、-4、-5等7条谱线。
4 复色光由波长为nm 6001=λ与nm 4002=λ的单色光组成,垂直入射到光栅上,测得屏幕上距离中央明文中心cm 5处1λ的m 级谱线与2λ的1+m 谱线重合,若会聚透镜的焦距cm f 50=,求:(1)m 的值:(2)光栅常数d 。
解:(1)不同波长的光的不同级次的衍射光谱线在屏幕上重合,说明它们的衍射角相同
nm
m m nm
m m d 400)1()1(600sin 21⨯+=+=⨯==λλθ
由此,解得1λ的级次为2=m 。
(2)nm m d 1200
sin 1==λθ,所以 nm nm nm nm d 12050
/51200tan 1200sin 1200==≈=θθ 5 一块光栅,每毫米有400条刻痕,用白光(波长范围为nm nm 750~400)垂直照射,问: 可以测到多少级不重叠的完整光谱?
解:白光中,最长波长nm 750=+λ,最短波长nm 400=-λ,由光栅方程,得到
++=λθm d m s i n ,--++=λθ)1(sin 1m d m
题中“谱线不重叠”,即要求-++<1m m θθ,所以
-++<λλ)1(m m
由此,得到不重叠的级次满足
14.1400
750400=-=-<-+-
λλλm 因此,只有第1 级谱线是不重叠的完整光谱。
6 nm 11.0=λ的X 射线射向岩盐晶面,测得第1级亮纹的掠射角为05.11,求:
(1)岩盐晶体这一方向上的品格常数d ;
(2)当换另一束X 射线时,测得第1级亮纹出现在掠射角为0
5.17的方向上,求该射线的波长。
解:(1)X 射线衍射主极大满足布拉格公式 ),3,2,1(sin 2 ==Φk k d λ
由此可以解得岩盐晶体这一方向上的品格常数
nm k d 276.05
.11sin 211.01sin 20=⨯⨯=Φ=λ (2)再由X 射线衍射主极大满足布拉格公式,得到另一束X 射线的波长
nm k d 166.01
5.17sin 275.02sin 20
=⨯⨯=Φ=λ 7 用晶格常数nm d 275.0=的晶体,作X 射线衍射实验,若射线包含nm nm 130.0~095.0波带中的各种波长,(1)当掠射角015=ϕ,问是否可以测得衍射极大?(2)
045=ϕ呢?
解:X 射线衍射主极大满足布拉格公式为 ),3,2,1(sin 2 ==k k d λϕ
(1)当掠射角015=ϕ时,有
k
k d 0
15sin 275.02sin 2⨯⨯==ϕλ 1=k ,nm 142.0=λ:2=k ,nm 071.0=λ
都不在nm nm 130.0~095.0范围内,k 为其他值,也不会有在此范围内的波长了,所以在掠射角0
15=ϕ方向上,不可能测得衍射极大。
(2)当掠射角045=ϕ时,有 k
k d 0
45sin 275.02sin 2⨯⨯==ϕλ 3=k ,nm 1296.0=λ;4=k ,nm 097.0=λ
在所定的波长范围内。
8 解释布拉格公式λαm d =sin 2、光栅衍射公式λθm d =sin 中α、θ的含意,说明两式中的d 有什么不同。
答:λαm d =si n 2中的α是X 射线对晶体表面的掠射角(=90-入射角);而λθm sin d =中的θ是光栅衍射中光与透镜光轴之间的夹角。
光栅中d 是光栅常数,即透光狭缝高度与遮光狭缝高度的和;而布拉格公式中的d ,是晶体中相邻两层晶体原子之间的距离,即晶格常数。