当前位置：文档之家 › 试井模型及典型曲线形态

试井模型及典型曲线形态

  • 格式：ppt
  • 大小：1.69 MB
  • 文档页数：53

下载文档原格式

  / 53

合集下载

线性复合油气藏试井解释模型及典型曲线分析

线性复合油气藏试井解释模型及典型曲线分析

线性复合油气藏试井解释模型及典型曲线分析罗建新;张烈辉;赵玉龙;刘启国【摘要】对于河道沉积环境所形成的条带状油气藏,储层物性的平面分布往往表现出较强的不连续性,呈现出线性组合的特征.在对这类油气藏的压力恢复和压力降落测试数据进行试井解释时,需要考虑其特殊性.根据表皮效应和井筒储集效应,通过建立外边界封闭线性复合油气藏试井解释模型,并结合拉普拉斯变换、有限傅里叶余弦变换以及正交变换法对该模型进行求解.利用Stehfest数值反演算法以及计算机编程技术编制了计算程序,绘制了线性复合油气藏的井底无因次压力典型曲线,并对各个流动阶段以及各种参数对曲线形态的影响进行了分析.该研究丰富了现代试井解释模型,对该类油气藏试井资料的解释具有指导作用.【期刊名称】《长江大学学报（自然版）理工卷》【年(卷),期】2011(008)002【总页数】3页(P65-67)【关键词】线形复合油藏;渗流模型;试井解释;典型曲线【作者】罗建新;张烈辉;赵玉龙;刘启国【作者单位】油气藏地质及开发工程国家重点实验室(西南石油大学),四川成都610500;油气藏地质及开发工程国家重点实验室(西南石油大学),四川成都610500;油气藏地质及开发工程国家重点实验室(西南石油大学),四川成都610500;油气藏地质及开发工程国家重点实验室(西南石油大学),四川成都610500【正文语种】中文【中图分类】TE353贾永禄[1，2]等人建立了均质多重不等厚地层试井分析模型，并对样板曲线进行了分析；向开理[3]、田冷[4]和何维署[5]等对径向复合油气藏进行过研究。

但是针对条带状油藏的不稳定渗流模型的相关研究较少。

为此，笔者建立了线性复合油气藏渗流物理模型，利用数学物理方法，对模型进行了求解，并利用计算机编程技术绘制了该类油气藏的压力典型曲线，并对各个流动阶段以及各种参数对曲线形态的影响进行了分析。

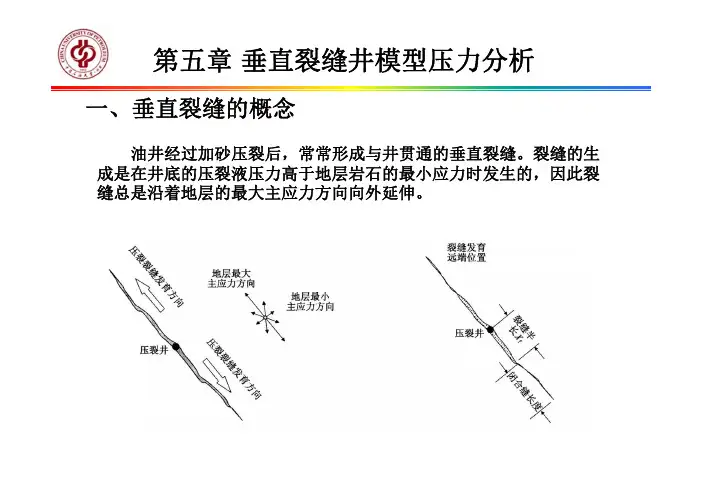
复合矩形油藏示意图如图1所示，其边界均封闭，油藏被分为左右2部分(Ⅰ区和Ⅱ区)，其孔隙度和渗透率均不相同，Ⅰ区中任意位(xw,yw)有一口垂直井，以定产量qsc进行生产。

第十一讲-垂直裂缝井的试井曲线分析

第十一讲-垂直裂缝井的试井曲线分析

大型压裂后，压力恢复测试一口油井 测试 大型压裂后，压力恢复测试一口油井,测试 资料整理表现形式: 资料整理表现形式 （1）MDH法 ） 法 续流段较长， 续流段较长， 压力恢复缓慢
大型压裂后， 大型压裂后，测试资料整理表现形式
（2）
井储效应所显示的直线段
（3） 3
综合图8-14、 15、 16可以 看出图8－14出现的直线不 是MDH半对数直线，而是 垂直裂缝的反应
压裂 所谓压裂就是利用水力作用， 所谓压裂就是利用水力作用，使油层形成裂缝 的一种方法，又称油层水力压裂。 的一种方法，又称油层水力压裂。油层压裂工艺过 程是用压裂车， 程是用压裂车，把高压大排量具有一定粘度的液体 挤入油层，当把油层压出许多裂缝后， 挤入油层，当把油层压出许多裂缝后，加入支撑剂 如石英砂等)充填进裂缝，提高油层的渗透能力， (如石英砂等)充填进裂缝，提高油层的渗透能力， 以增加注水量(注水井)或产油量(油井) 以增加注水量(注水井)或产油量(油井)。常用的压 裂液有水基压裂液、油基压裂液、乳状压裂液、 裂液有水基压裂液、油基压裂液、乳状压裂液、泡 沫压裂液及酸基压裂液5种基本类型。 沫压裂液及酸基压裂液5种基本类型。
油井酸化处理 酸化的目的是使酸液大体沿油井径向渗入地 从而在酸液的作用下扩大孔隙空间， 层，从而在酸液的作用下扩大孔隙空间，溶解空 间内的颗粒堵塞物， 间内的颗粒堵塞物，消除井筒附近使地层渗透率 降低的不良影响，达到增产效果。 降低的不良影响，达到增产效果。 压裂酸化 在足以压开地层形成裂缝或张开地层原有裂 缝的压力下对地层挤酸的酸处理工艺称为压裂酸 化。压裂酸化主要用于堵塞范围较深或者低渗透 区的油气井。 区的油气井。
c．地层内的线性流动： 地层内的线性流动：
在多孔介质内的流体靠地层与流体 的弹性膨胀， 线性流动方式 的弹性膨胀，以线性流动方式 流入裂缝， (c)所示 所示。 流入裂缝，如图 (c)所示。

试井模型简介

试井模型简介

外围地层变差 存在不渗透边界 外围地层变好 地层部分射开
定压的外边界（油层有活跃的边底水） 双重介质地层或双渗地层的过渡流
试井分析模式图
模式图指具备典型特征的双对数分析图。它代表着某一类均质的或非 均质的地层，加上地层外围某种特定外边界条件，再加上某一类特定的 井身结构或某一类完井井底条件，以及井筒对于流动过程的影响，经过 各种组合后所表现出的动态特征情况。 常见的地层类型有：均质地层，双重介质地层，双渗地层等。 储层外边界条件有：不同的边界形状－－直线形，直线组合形，圆形， 封闭矩形，以及其它复杂形状，等等；不同的边界性质 ――不渗透边界， 定压边界（对于油井），半渗透边界，等等。 储层的平面分布状态：Kh值和φ值分布状态，流体分布状态。
e
M-15
井储 C 表皮 S 复杂组系性裂缝
B D C
a c b
a-b 续流段 b-c A 区径向流段 c-d 边界反映段 d-e B、C 等外区供气段
M-16
均质地层 井储 C 表皮 S 水平井
d b a c
e
a-b 续流段 b-c 垂向径向流段 c-d 线性流段 d-e 拟径向流段
均质地层和均质地层不稳定试井曲线特征
现代试井分析模型简介
油气井试井常用的分析图
3 类常用的分析图： 压力、产量与时间关系的直角坐标图； 压降曲线、压力恢复曲线的半对数图（单对数图）； 不稳定试井曲线压力和压力导数的双对数分析图（log-log图）。
压力、产量 /时间的直角坐标图又称为压力、产量历史图。它包含了一口油 （气）井生产过程的全部信息，只有在试井分析中预测得到的理论模型压力与 之拟合一致，才能确认解释结果的正确性。 半对数图产生于20世纪50年代，是试井分析技术的第一次突破，奠定了现代 试井方法中常规分析方法的基础，目前仍然广泛应用。 压力和压力导数双对数，以及双对数图版拟合分析法产生于 20 世纪 70-80 年 代，它是现代试井分析方法的基础，适用于各类地层和各种完井条件，可以分

中国石油大学(北京)现代试井分析-第五章 垂直裂缝井模型压力分析

中国石油大学(北京)现代试井分析-第五章 垂直裂缝井模型压力分析

S
2rw S ln xf
二、无限导流垂直裂缝模型 2、常规试井分析方法
2.12 103 qB Kt lg p 1.512 2 C x Kh t f
pwf p1h
m 2.12 10 q B Kh
3
2.12 103 q B K mh
CDf
C 2 Ct hx 2 f
二、无限导流垂直裂缝模型 3、典型曲线拟合分析方法 纯井筒储集阶段 裂缝线性流阶段 径向流动阶段
pD
t Df CDf
pD t Df
dpD p' D dt Df 2 t Df
pD 0.5 ln t Df 2.2
dpD 0.5 p' D dt Df t Df
S
二、无限导流垂直裂缝模型 2、常规试井分析方法
由 得
pD 0.5ln t De 0.80907
pD 0.5(ln t Df 2.2)
0.5ln t Df 2.2 0.5ln t De 0.80907
2 x2 4 . 0186 r f we
x f 2rwe 2rwe
3
3.6k 1 xf Ct t Df t 拟合
t Df PD q B k 1.842 10 h P t
3
拟合
C 2 Ct hx ( CDf )拟合
2 f
2rw S ln xf
无限导流 垂直裂缝
3、常规试井分析方法 （1）双线性流
2.45 pD K fDW 4 t Df
fD
6.2163 10 3 qB 4 t p h k f W 4 ct k

04第4章 试井解释模型20131018

04第4章 试井解释模型20131018
5
类别 内边界模型 储层模型
外边界模型 流体模型 流量模型
学
位
模型
Modern well test
第四章、试井解释模型及现代试井解释方法
4.1 试井解释模型
4.3 现代试井解释方法
学
4.2 从系统分析看试井解释
位
6
Modern well test
4.2 从系统分析看试井解释
位
油藏
输入信号 产量变化
学
位
17
Modern well test
现代试井解释方法
现代试井解释方法的重要手段之 一是解释图版拟合，或称为样板曲线 解释图版拟合 拟合（Type Curve Match）。 通过图版拟合，可以得到关于油 藏及油井类型、流动阶段等多方面的 信息，还可以算出K、S、C等参数。
18
学
位
Modern well test
Modern well test
学
第四章 试井解释模型及现代 试井解释方法
1
位
Modern well test
第四章、试井解释模型及现代试井解释方法
4.1 试井解释模型
4.3 现代试井解释方法
学
4.2 从系统分析看试井解释
位
2
Modern well test
4.1 试井解释模型
油气藏在岩石类型、物理性质、埋藏深浅、 压力大小、流体种类和组分等方面都各不相同。但 在试井过程中，所呈现的性态却是有限的。 这是因为油气藏只不过像一个精度不太高的反 应器，只当输出讯号的差别足够大时，地层的差异 才能显现出来，试井才能探测得到。此外，所有各 种性态都只由若干个基本“部分”或“部件”组成。具 体来说，试井解释模型由基本模型、内边界条件和 外边界条件三大部分组成，每一大部分在测试的不 同时间起着支配作用。显然，要想得心应手地选择 试井解释模型，就得对组成解释模型的所有各个基 本“部分”或“阶段”，以及它们的特征有清楚的了解 。

试井模型简介ppt课件

试井模型简介ppt课件

均质地层
井储 C 表皮 S 水平井
封闭边界（定容地层）
封闭边界（定容地层）
导流能力很强的压裂裂缝（线性流） 单方向发育的裂缝系统
有限导流压裂裂缝（双线性流） 外围地层变差 存在不渗透边界 外围地层变好 地层部分射开
定压的外边界（油层有活跃的边底水）
双重介质地层或双渗地层的过渡流
试井分析模式图
模式图指具备典型特征的双对数分析图。它代表着某一类均质的或非 均质的地层，加上地层外围某种特定外边界条件，再加上某一类特定的 井身结构或某一类完井井底条件，以及井筒对于流动过程的影响，经过 各种组合后所表现出的动态特征情况。
单一直线不渗透边界
M-10
均质地层
井储 C 表皮 S 直线夹角不渗透边界
M-11
均质地层
井储 C 表皮 S 近方形封闭边界
精品课件
模式图
参数及特征
a-b 续流段
d
e
b-c 内区径向流段
a
b
c
c-d 过渡流段 d-e 外区径向流段
a-b 续流段
b-c 内区径向流段
b
c
c-d 过渡流段
a
d
e
d-e 外区径向流段
M-2
井储 C 表皮 S
裂缝和总系统两个径向流
双重介质地层
M-3
井储 C 表皮 S
只有总系统径向流
均质地层
M-4
井储 C 裂缝表皮 Sf
无限导流垂直裂缝
均质地层
M-5
井储 C 裂缝表皮 Sf
有限导流垂直裂缝
均质地层
M-6
井储 C 表皮 S
地层部分射开
精品课件
模式图
参数及特征

最新试井标准曲线模板

最新试井标准曲线模板

M大于1时，D的变 化规律与二者之间 差值大小有关
0.01 0.01 0.1 1 10 Time [hr] 100 1000
Sensitivity to D: p-p@dt=0 and derivative [MPa] vs dt [hr]
复合地层半对数直线分析
2.4 35 Slope Intercept Slope Intercept k.h k Skin Mob. Ratio Intersection X Interface 0.718339 MPa 35.1063 MPa 0.357738 MPa 34.4751 MPa 299 md.m 32.7 md -0.135 0.498 -1.7506 352 m
均质无限大地层井储系数C的影响关系
0.005 m3/ MPa 0.01 m3/ MPa 0.1 m3/ MPa 0.230592 m3/ MPa (current) 0.5 m3/ MPa 0.9 m3/ MPa 1.2 m3/ MPa
1
0.1
自左至右，井储系数逐渐增大，测试出现径 向流的时间也随之增大
均质无限大地层表皮系数S的影响关系
-5 -4 -2 0 (current) 2 4 8 15
自下而上表皮 系数S逐渐增大
10
1
表明表皮系数S的大小
0.1
0.01 1E-3
0.01
0.1
1 Time [hr]
10
100
1000
Sensitivity to Skin: p-p@dt=0 and derivative [MPa] vs dt [hr]
系统径向流
1
此凹陷的跨度及开始时间 与窜流系数相关
0.1
此凹陷深度表示了 储能系数的大小

实用现代试井解释模型

实用现代试井解释模型
1 tD pD = [ln + 0.80907 + ln( CDe 2 s )] 2 CD
1 pD = [ln t D + 0.80907 + 2 S ] 2
p′ = D
dpD tD 1 CD tD ⋅ = ⋅ = 0.5 d( tD / CD ) CD 2 tD CD
Copyright: luopei ,Chongqing University of Science and Technology
pwD = pwDi + pwDb
存在外边界影响的 井底压力 无限大油藏 井底压力 边界影响产生的 井底压力
Copyright: luopei ,Chongqing University of Science and Technology
厚德 博学 砺志 笃行 三、 几种常见边界的压力特征
1. 一条直线封闭边界
厚德 博学 砺志 笃行 （四）均质无限大油藏压力压力特征
101 100
10-1
m =1
10-3 10-2 10-1 100
p′ = 0.5 D
101 102
10-2 10-4
tD
均质无限大油藏压力和压力导数曲线的基本特征
Copyright: luopei ,Chongqing University of Science and Technology
1
2
3 4 5
k = 50mD
k = 100mD
储层渗透率对半对数曲线特征的影响
Copyright: luopei ,Chongqing University of Science and Technology
厚德 博学 砺志 笃行
25 P (MPa) 20 15 10 5 0 10-4 10-3 10-2 10-1 100 101 102 t (hr)

试井解释基础知识理论

试井解释基础知识理论
坐标表示（tp+△t)/△t,这样的半对数曲线就 称为霍纳曲线。 MDH曲线：即以直角坐标表示关井井底压力Pws(△t),对数坐 标表示关井时间△t,这样的半对数曲线就称为MDH 曲线。
利用压力恢复曲线可以计算油层渗透率k、表皮系数S以及油层外推压
力等。
13.井筒储集效应和储集系数
在油井开井阶段和刚关井时，由于流体自身的压缩性， 都存在续流影响，这就是“井筒储集效应”。
几种特定流动的压力导数特征斜率值
9.段塞流
在钻柱(DST)测试中，打开井底阀以后，随着地层 流体的产出，测试管柱的液面不断上升。对于自喷能量 差的地层，液面达到井口之前，流动即停止，从而形成 自动关井。这种流动称为“段塞流”。
10.探测半径
当一口井以产量q生产时，井底压力开始下降，压力波不断向地层内部传播， “压降漏斗”不断扩大和加深，在任何时刻ti,都总有那么一个距离ri,在油层中 与生产井距离超过的ri地方，压降仍为0(严格地说，该地方压降仍然非常小，只 是无法探测出来而已).这个距离就称为“探测半径”。
试井解释基本模型 及其特征曲线
一、均质油藏
1、物理模型
✓流体为单相微可压缩液体，储层中达到径向流； ✓忽略毛管力和重力； ✓油井测试前地层各处的压力均匀； ✓地层各向同性，均匀等厚。
井
k
2、数学模型
渗流方程： 2p1pCt p
r2 rr 3.6k t
边界条件： p|t0 pi
p|rpi
rp rrrw
实际上油井一开井总要受到实际上油井一开井总要受到井筒储集和表皮效应或者其他因素的影井筒储集和表皮效应或者其他因素的影响这时虽然也是向着井筒流动但是响这时虽然也是向着井筒流动但是尚未形成径向流的等压面这一阶段称尚未形成径向流的等压面这一阶段称为为早期段早期段在生产影响达到油藏边在生产影响达到油藏边界以后此时因受边界影响不呈平面径界以后此时因受边界影响不呈平面径向流这一阶段称为向流这一阶段称为晚期段晚期段真正真正称为径向流的只是它们之间的一段时间称为径向流的只是它们之间的一段时间即即中期段中期段长庆油田公司第二采油厂2

试井曲线分析应用课件

试井曲线分析应用课件

05
试井曲线分析软件介绍
软件功能介绍
数据导入导出
支持多种数据格式，方便用户导入和导出数 据。
数据分析
支持对数据进行统计分析、趋势分析等。
曲线拟合
提供多种曲线拟合算法，满足不同类型数据 的拟合需求。
结果可视化
提供丰富的图表类型，方便用户对结果进行 可视化展示。
软件操作流程
数据导入
将数据导入软件中 。
目的
试井的目的是为了获取地层参数 、确定地层产能、评估油气藏类 型和特征，以及了解井筒和地层 之间的相互关系。
试井曲线的类型
01
02
03
压力曲线
压力曲线是试井过程中记 录的压力随时间的变化曲 线，可以反映地层压力和 产能的变化。
流量曲线
流量曲线是试井过程中记 录的流量随时间的变化曲 线，可以反映地层流体的 流动特性和产能。
评估油气藏类型
通过试井曲线分析，可以评估油气藏的类型和特征，如构 造油气藏、岩性油气藏等，为后续的开发方案制定提供依 据。
提高采收率
通过试井曲线分析，可以了解油气藏的流动特性和生产潜 力，为制定合理的采收率提供依据，提高油气藏的经济效 益。
02
试井曲线分析方法
径向流分析
总结词
径向流分析是试井曲线分析中的一种基本方法，用于描述地层中流体流动的径 向分布。
环境监测
用于分析环境参数的变化趋势，评估环境质量状 况和预测未来变化趋势。
THANKS
感谢观看
详细描述
径向流分析基于地层中流体流动的径向分布模型，通过分析试井曲线数据，可 以确定地层的渗透率和孔隙度等参数，进而评估地层的生产能力和开发潜力。
线性流分析
总结词

水平井试井分析模型

水平井试井分析模型

一符号说明和无量纲量字符说明英文符号：B = 流体积系数；C = 井筒存储系数（m3/MPa）；c t = 总压缩系数（1/MPa）；h = 有效层厚（m）；I j(v) = j阶第一类修正Bessel函数；k j = j方向渗透率（μm2），j = h、v；K j(v) = j阶第二类修正Bessel函数；L = 水平井筒半长（m）；P = 压力（MPa)；△P = 压差（MPa)；q = 产量（m3/d）；r w = 水平井筒半径（m）；Skin = 表皮因子；s = Laplace变换量；t = 时间（hour）；x、y = 坐标；x e、y e = 外边界距离（m）；z = 坐标；z w = 水平井垂向位置，m；希腊符号：μ =流体粘度（mPa·s）；φ = 孔隙度；ηj = j方向扩散系数，定义为ηj = k j /φμc tj；下标：D = 无量纲；w = 井壁；i = 初始状态；eD = 无量纲外边界无量纲量定义采用中国SI 单位制，定义如下无量纲量群： 无量纲压力：Bq P P h k P i j D μ310842.1)(-⨯-=；xy h m f j ,,,=；xy h k k =表皮压力降：i h si S hk B q P μ310842.1-⨯=∆，β,,z m i =无量纲时间：2wh D r tt η=，h v i c k ti i ,==φμη无量纲井筒存储系数：22wt D hr c CC πφ=，22L r C C wD DL = 无量纲Fair 变井筒存储参数： φφC q u B kh C D 310842.1-⨯=，βφμβ26.3wt D r c k = 无量纲坐标：L x x D =，L y y D =，L r r D =，h zz D =，hz z w wD = 无量纲井筒半长：h v D k k hL L =；v h weD k k r h h =；⎪⎪⎭⎫ ⎝⎛+=vhwe we k k r r 12 无量纲渗透边界补给系数： ()1/-=e fd fdr r k k LB无量纲双孔介质参数：λα=r k k wm f 2；mt ft h c h c )()(φφω=二 试井分析理论模型由于试井分析模型较多，本章将分类介绍主要模型。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

19/64
2014-6-25
曲线特征：
有最大值， 表示污染井
100 II III
0.5水 平线
10
I
P WD , P WD '
1
第Ⅰ段双对数和导数合二为一 ，呈45°的直线，表明续流段 的影响。
0.1
0.01 0.1 1 10 100 1000 10000 100000 1000000 10000000
2
1
内区
外区
无限大复合油藏试井曲线特征
100 I II III IV V
PWD ,PWD '
流动系数和储容 系数减小的复合 储层
10
1
0.1
0.01 0.1
1

100
1000
10000
100000
1000000 10000000
水平线, 内区渗 流
P WD
t D /C D
18 16 14 12 10 8 6 4 2 0 0.1 1 10 100 1000 10000 100000 1000000 10000000 I II III IV V
0.5M12 水平线, 外区渗 流
m2
m1
m2/m1 =M12
t D /C D
无限大复合油藏试井曲线特征
流动系数和储容系数减小的复合储层
无限大复合油藏试井曲线特征
1000 I 100 II III IV V
P WD , P WD '
10
1 内区水 平段 1/2斜率
0.1
流动系数 增大
0.01
0.01 0.1 1 10 100
t D /C D
kf
km
23/64
2014-6-25
24/64
2014-6-25
三、主要研究成果
2、油藏模型
（2）双孔模型
双孔介质响应一般出现在天然裂性储层、层间渗透率差别 较大的多层储层和沿储层厚度方向渗透率变化较大的单层储层 中。由此可见，双重介质模型解释出的高渗透系统（用下标1或 f表示）的渗透率Kf也就是整个储层渗透率参数K。 如果多层储层可分作渗透率明显不同的高渗透层组和低渗 透层组，并且每组中各层渗透率差异不很大，则可使用双孔储 层模型进行解释。
t D /C D
P WD
第Ⅱ段为过渡段，导数出现峰 值后向下倾斜，峰的高低取决 于 CDe2 S 的大小， CDe2 S 越 大，峰值越高。
第Ⅲ段出现导数水平段，为径 向流段。
14 12 10 8 6 4 2 0 0.1 1 10 100 1000 10000 100000 1000000 10000000 I+II III
0.01 0.1 1 10 100 1000 10000 100000 1000000 10000000
t D /C D
14 I 12 10 8 △P II III IV
PWD
6 4 2 0 0.1 1 10 100 1000 10000 100000 1000000 10000000
t D /C D
15/64
2014-6-25
1、井筒模型
（5）部分射开
曲率受 线为部 也 分 会 射 发。开 生此的 变外影 化受响 。纵 压 向力 渗导 透数 率曲 的线 影表 响现 导为 数斜
-1/2 ,
,
16/64
2014-6-25
三、主要研究成果
（6）水平井
1、井筒模型
井筒储集效应结束后，会出现 早期径向流段，压力导数为一 条直线；然后出现线性流，压 力导数表现为一条斜率为 0.5的 直线段；后期出现系统径向流 段，压力导数为0.5一条直线。
t D /C D
20/64
2014-6-25
100 II III
10
I
P WD , P WD '
1
0.1
0.01
0.01 0.1 1 10 100 1000 10000 100000 1000000 10000000
t D /C D
无最大值， 表示措施井
21/64
2014-6-25
三、主要研究成果
31/64
2014-6-25
三、主要研究成果
2、油藏模型
（3）双层窜流油藏
双层窜流油藏导数曲线中期反映流体的窜流特征，受参数κ、λ、ω 影响， 在λ、ω不变时，κ 越大，导数曲线越下凹。
32/64
2014-6-25
三、主要研究成果
2、油藏模型
（4）径向复合油藏
径向复合油藏是由径向上两个渗透性差异较大的区域组成的油藏，如 图所示。储层改造，如酸化、压裂、调剖堵水等措施都可能造成这种 情况。
25/64
2014-6-25
2、油藏模型
（2）双孔模型
储容比：
f Cf f C f m Cm
＝1----纯裂缝油藏（基质岩块无孔隙的裂缝性 油藏）为均质储层响应
＝0----常规的粒间孔隙油藏，为均质储层响应
0＜＜1----双孔隙裂缝性油藏
一般：=0.001~0.3
26/64
因裂缝具有无限大的渗透率，沿裂缝无压力降。流体一旦从地层流入裂缝，将 瞬时流入井筒。所以，对无限导流垂直裂缝的油藏，缝中的流动不存在。
1 井
筒
模 型 地层线性流动 拟径向流动
11/64
2014-6-25
1、井筒模型
（3）无限导流
对于无限导流模型的均质油藏，压力导数曲线表现出斜率为0. 5的直线段，后期压力 导数表现为0.5的水平线；受井筒储存系数 C影响，C越大，双对数曲线越靠右，反之 靠左。
2014-6-25
前
言
现代试井解释技术----是根据各种试井模型的数学
模型算出不同参数下的无量纲井底压力随无量纲时间的变化曲 线，并绘制在双对数坐标图上，称为理论图版或样板曲线。因 为不同的试井模型具有不同的曲线特征，再看实测曲线符合哪 类试井模型的曲线特征，就选哪类试井模型的理论图版进行拟 合，拟合的结果也就确定了该实测曲线对应的油藏的参数。 因此，试井解释模型及典型曲线特征是试井解释技术的重 要内容。
储层模型
外边界模型
7/64
2014-6-25
1、井筒模型
（1）井筒储存 +表皮污染
对于定井储模型，污染系数S越大，双对数曲线开口越大，反之开口越小。
8/64
2014-6-25
1、井筒模型
（2）变井+表皮
受井筒储存系数 C的影响，试井早期曲线发生变异，C变大时，曲线偏离45°线 向右偏移，反之向左；此外曲线形态还具有压力导数曲线超越压力线的特征。
17/64
2014-6-25
2、油藏模型
（1）均质模型 均质模型是指地层中只有一种介质， 均匀分布在地层中。
k
18/64
2014-6-25
2、油藏模型
（1）均质模型
均质油藏是目前最常见的一种地层类型，对于我 国东部地区第三系的大部分砂岩地层，均呈现出均质 油藏的特征。某些具有天然裂缝的碳酸盐岩地层，当 裂缝发育均匀时，常常也表现出均质油藏的特征。
6/64
2014-6-25
3、试井解释模型的组成
类别 内边界模型 模型 井储+表皮、变井储、压裂井、 部分射开、斜井和水平井等 均质、双孔介质、双渗介质、三重介质、多重介质、复合模型 （包括径向复合和单向线性复合）、多重复合模型（包括径 向复合和单向线性复合）和分形介质模型 定压边界、变压边界（升压或降压）、不渗透边界（一条直线 断层或多条直线断层）、封闭储层、半渗透（泄漏）断层和 高渗透断层 等 流体模型 流量模型 油井、气井、凝析气井、水井、单相流、多相流、非达西流等 恒流量、变流量
2014-6-25
三、主要研究成果
2、油藏模型
（3）双层窜流油藏
双渗介质是由渗透
率相差相当大的两种 介 质 构 成 的， 与 双 孔 介 质 不 同 的是 ， 两 种 介 质 中 的 流体 都 可 以 直接流入井筒。
K1， h1, S K2， h2, S
K1
K2
30/64
2014-6-25
三、主要研究成果
2、油藏模型
（2）双孔模型
双孔介质是指不同孔隙度和渗透率的
两种均质介质间的相互作用。两种介质可 以是均匀分布的，也可以是分离的，但只 有一种介质（高渗透系统）允许生产流体 通过并流入井底，而另一种介质（低渗透 系统）只起着源的作用。
22/64
2014-6-25
三、主要研究成果
2、油藏模型
（2）双孔模型
流体的流动：
1
井
筒 模 型
早期线性流
拟径向流
14/64
2014-6-25
1、井筒模型
（4）有限导流
对于有限导流垂直裂缝模型，在井筒储集效应和表皮影响段，压力导数曲线表现出斜 率为1的直线段；中期为有限导流垂直裂缝影响的特征曲线，压力导数曲线表现出斜 率为0.25的直线段；晚期为均质油藏特征，压力导数曲线为0.5的水平线。
2、油藏模型
（3）双层窜流油藏
●双渗介质可在层间渗透率差别不大的多层储层中和 基岩与裂缝中的流体都可同时流到井筒中的裂缝储层中见 到。 ●双渗介质的压力导致曲线形状，一般是介于双孔介 质的不稳定流动和拟稳定流动模型响应之间的一种动态， 其实测资料在两种双孔模型的典型曲线上都不能得到很好 的拟合。 ●双渗介质模型的解是介于均质储层模型和双孔介质 （介质间拟稳定流）模型的解之间。双渗介质的特性参数 κ比较小时（κ＜0.6,其压力导数曲线接近于均质储层的 曲线，它相当于达到了总系统径向流的特性，当κ=1时， 其压力导数特征曲线就成为双孔介质模型的曲线。
1/64
2014-6-25