高中数学 5.3.3《循环语句》教案 苏教版必修3
- 格式:doc
- 大小:98.47 KB
- 文档页数:7


江苏省射阳县盘湾中学高中数学 1.3基本算法语句循环语句教
案苏教版必修3
教学目标:正确理解循环语句的概念,并掌握其结构;会应用循环语句编写程序.进一步提高逻辑思维能力
教学重点:两种循环语句的表示方法、结构和用法,用循环语句表示算法.
教学难点:理解循环语句的表示方法、结构和用法,会编写程序中的循环语句.
教学过程
一、问题情境
⨯⨯⨯⨯⨯的一个算法,并画出流程图.
问题:设计计算135799
二、学生活动
探究:
1、算法:
2、流程图:
对于以上算法过程,我们能否用条件语句来实现?
三、建构数学
1.循环语句:
(1)“For”语句:
(2)“While”语句:
说明:
用循环语句表示上述算法:
四、数学运用
例1.(1)用算法语句表示:计算自然数1+2+3+…+10的和。
(2)试用算法语句表示:寻找满足1+2+3+…+_________>2013的最小整数的算法.
小结:
例2.抛掷一枚硬币时,既可能出现正面,也可能出现反面,预先作出确定的判断是不可能的,但是假如硬币质量均匀,那么当抛掷次数很多时,出现正面的频率应接近50%.试设计一个循环语句模拟抛掷硬币的过程,并计算抛掷中出现正面的频率.
小结:
练习:书P24 2、3
五、回顾小结:
知识:思想方法:
六、课外作业:
书P25 5、6、7。

引入新课问题:设计计算997531⨯⨯⨯⨯⨯ 的一个算法.(1)用当循环语句描述这一算法过程. (2)将上述算法改写为直到型循环.例题剖析抛掷一枚硬币时,既可能出现正面,也可能出现反面,预先作出确定的判断是不可能的,但是假如硬币的质量均匀,那么当抛掷次数很多时,出现正面的频 率应接近于%50,试设计一个循环语句模拟抛掷硬币的过程,并计算抛掷中出 现正面的频率.例1巩固练习1.用流程图给出计算54321++++的一个算法,试用循环语句描述这一算法过程.2.2000年我国人口数约为13亿,如果每年的人口自然增长率为‰15,那么多少年后我国人口数将达到或超过15亿?这个问题可通过循环方式计算完成,即每一次在原有的基础上增加‰15,直到达到或超过15亿,再记下循环次数.试用循环语句表示这一过程.3.,,2,3,5,8,13, 这一列数的规律是:第一、第二个数是,从第三个数起,每个数是其前两个数的和.试用循环语句描述计算这列数中第二十个数的算法.课堂小结理解并掌握循环语句的格式和作用;会写一般的循环语句;能用循环语句进行编程.课后训练班级:高二( )班 姓名:____________一 基础题1.算法中实现循环结构的语句叫 .2.“For ”语句的一般形式是: “While ”语句的一般形式是: ; ; ; ; ; .(第3题图①) (第3题图②)(第4题图)3.在上面的两个伪代码中,①的运行结果为 ,②的运行结果为 . 4.根据如图所示的伪代码,可知道输出的结果S 为 . 二 提高题5.输入三个数a ,b ,c ,如果这三个数能作为一个三角形的三边长, 那么输出)(21c b a ++,否则提示重新输入,试用算法语句表示上述过程.0←i 0S ← While 20≤S i S S +← 1+←i i End while int Pr i End 0←i0S ← While 20≤S 1+←i i i S S +← End while int Pr iEnd 1←Ihile W 8<I2+←I I32+←I S End while int Pr S End6.设计一个计算10019914131211++++++的算法,并画出流程图,写出伪代码.7.青年歌手大奖赛有10名选手参加,并请了12名评委.为了减少极端分数的影响,通常去掉一个最高分和一个最低分后再求平均分.请用算法语句表示:输入12名评委所打的分数)1221( =,,, i a i ,用函数)(1221a a a Max ,,, 和)(1221a a a Min ,,, 分别求出)1221( =,,, i a i 中的最大值和最小值,最后输出该歌手的成绩.。
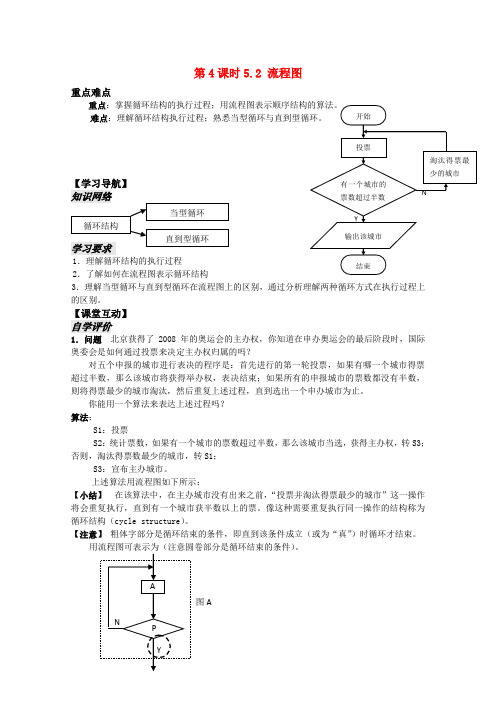
第4课时5.2 流程图重点难点重点难点1.理解循环结构的执行过程 2.了解如何在流程图表示循环结构3.理解当型循环与直到型循环在流程图上的区别,通过分析理解两种循环方式在执行过程上的区别。
【课堂互动】自学评价1.问题 北京获得了2008年的奥运会的主办权,你知道在申办奥运会的最后阶段时,国际奥委会是如何通过投票来决定主办权归属的吗?对五个申报的城市进行表决的程序是:首先进行的第一轮投票,如果有哪一个城市得票超过半数,那么该城市将获得举办权,表决结束;如果所有的申报城市的票数都没有半数,则将得票最少的城市淘汰,然后重复上述过程,直到选出一个申办城市为止。
你能用一个算法来表达上述过程吗?算法:S1:投票S2:统计票数,如果有一个城市的票数超过半数,那么该城市当选,获得主办权,转S3;否则,淘汰得票数最少的城市,转S1;S3:宣布主办城市。
上述算法用流程图如下所示:【小结】 在该算法中,在主办城市没有出来之前,“投票并淘汰得票最少的城市”这一操作将会重复执行,直到有一个城市获半数以上的票。
像这种需要重复执行同一操作的结构称为循环结构(cycle structure )。
【注意】 粗体字部分是循环结束的条件,即直到该条件成立(或为“真”)时循环才结束。
图A2. 写出求12345⨯⨯⨯⨯值的一个算法。
算法一:S1 先求12⨯,得到2;S2 将S1得到的结果再乘3,得到6;S3 将S2得到的结果再乘4,得到24;S4 将S3得到的结果再乘5,得到最后的结果120。
;【思考】如果一直乘到100,上述算法有何弊端,有通用性吗?算法二:S1 设一个变量T←1;S2 设另一个变量为i←2;S3 T←T×i { 将T×i的结果仍放在变量T中 };S4 i←i+1 {i的值增加1};S5 如果i不大于5,转S3,否则输出T,算法结束。
【比较】算法二与算法一相比有何优越性?这个方法可以在条件限制中加入任意的值来,比如1234100⨯⨯⨯⨯⨯也可以用同样的程序来执行,只要修改一下限制条件即可。

总 课 题 基本算法语句 总课时 第 8 课时 分 课 题循环语句分课时第 3 课时教学目标学习循环语句的一般格式,掌握循环语句的作用,并能进行最简单的编程;理解并掌握循环语句在机算机程序语言中的作用,掌握两种循环语句应用的实例:数列求和、求积;培养学生的探索问题、分析问题和解决问题的能力,培养学生思维的严谨性和条理性. 重点难点让学生理解并掌握循环语句的格式和作用;能写出一般的循环语句;能将循环语句用与简单的编程中.引入新课问题:设计计算997531⨯⨯⨯⨯⨯ 的一个算法.(1)用当循环语句描述这一算法过程. (2)将上述算法改写为直到型循环.例题剖析抛掷一枚硬币时,既可能出现正面,也可能出现反面,预先作出确定的判断是不可能的,但是假如硬币的质量均匀,那么当抛掷次数很多时,出现正面的频 率应接近于%50,试设计一个循环语句模拟抛掷硬币的过程,并计算抛掷中出 现正面的频率.巩固练习1.用流程图给出计算54321++++的一个算法,试用循环语句描述这一算法过程.例115,那么多少年后我国2.2000年我国人口数约为13亿,如果每年的人口自然增长率为‰人口数将达到或超过15亿?这个问题可通过循环方式计算完成,即每一次在原有的基础上15,直到达到或超过15亿,再记下循环次数.试用循环语句表示这一过程.增加‰3.1,1,2,3,5,8,13, 这一列数的规律是:第一、第二个数是1,从第三个数起,每个数是其前两个数的和.试用循环语句描述计算这列数中第二十个数的算法.课堂小结理解并掌握循环语句的格式和作用;会写一般的循环语句;能用循环语句进行编程.课后训练班级:高二()班姓名:____________ 一基础题1.算法中实现循环结构的语句叫.2.“For ”语句的一般形式是: “While ”语句的一般形式是: ; ; ; ; ; .(第3题图①) (第3题图②)(第4题图)3.在上面的两个伪代码中,①的运行结果为 ,②的运行结果为 . 4.根据如图所示的伪代码,可知道输出的结果S 为 . 二 提高题5.输入三个数a ,b ,c ,如果这三个数能作为一个三角形的三边长, 那么输出)(21c b a ++,否则提示重新输入,试用算法语句表示上述过程.6.设计一个计算100199********++++++ 的算法,并画出流程图,写出伪代码.0←i 0S ← While 20≤S i S S +← 1+←i i End while int Pr i End 0←i 0S ←While 20≤S1+←i ii S S +←End whileint Pr iEnd1←Ihile W 8<I2+←I I32+←I S End while int Pr S End7.青年歌手大奖赛有10名选手参加,并请了12名评委.为了减少极端分数的影响,通常去掉一个最高分和一个最低分后再求平均分.请用算法语句表示:输入12名评委所打的分数)1221(=,,,iai ,用函数)(1221aaaMax,,,和)(1221aaaMin,,,分别求出)1221(=,,,iai中的最大值和最小值,最后输出该歌手的成绩.。

1.3.3循环语句(While语句与Do语句)学习目标:了解循环语句的结构特征,掌握循环语句的具体应用。
学习重点:While语句与Do语句的表示方法,结构和用法。
学习难点:将具体问题的流程图转化为程序语句的过程,当型循环和直到型循环的格式与逻辑的区别与联系。
学习过程:一.复习回顾:(1)赋值语句:(2)输入语句:(3)输出语句:(4)条件语句:(5)循环结构特征图:当型循环:直到型循环:二.问题引入:设计计算2×4×6×8×…×100的一个算法,并画出流程图.解: 算法如下:(当型)当型语句如下:(直到型)直到型语句:三、总结归纳:循环语句:(当型语句): (直到型语句):While p Do循环体 循环体End while Until pEnd Do四.例题讲解:例1.分别使用当型循环和直到型循环设计求 1+2+3+…+n >2006 的最小正整数n 的伪代码,并画出流程图.解:例2.下列伪代码实现的是什么运算?S ←0a ←1i ←1While i ≤101S ←S +a ×ia ←a ×(-1)i ← i +2End WhilePrint S答案:五.课堂小结:当型循环直到型循环当型循环语句伪代码格式:While P Do循环体循环体 End While Until PEnd Do 六.课后作业1.编写程序,计算自然数1+2+3+……+99+100的和。
2.下列伪代码实现的什么算法?S←0i ←0While i≤99i←i+1S←S+iEnd whilePrint S。
数学:1.3.3《循环语句》教案(苏教版必修3)第9课时1.3.3循环语句(While语句与Do语句)教学目标:了解循环语句的结构特征,掌握循环语句的具体应用。
教学重点:While语句与Do语句的表示方法,结构和用法。
教学难点:将具体问题的流程图转化为程序语句的过程,当型循环和直到型循环的格式与逻辑的区别与联系。
教学过程:一.复习回顾:(1)赋值语句: 变量←表达式或变量或常数.(2)输入语句: Read a,b(3)输出语句: Print a,b(4)条件语句: If A ThenBElseCEnd If(5)循环结构特征图:当型循环直到型循环二.问题引入:设计计算2×4×6×8× ×100的一个算法,并画出流程图.解: 算法如下:(当型)当型语句如下:S1 T ← 1;T←1S2 I ← 1;I ←1S3 若I≤50,则转S4,While I≤50否则转S6;T←T×2IS4 T ← T×2I;I←I+1S5 I ← I+1,转S3;End whileS6 输出T.Print T(直到型)直到型语句:S1 T ← 1;T←1S2 I ← 1;I←1S3 T ← T×2I;DoS4 I ← I+1 ;T←T×2IS5 若I50,则转S6,I←I+1否则转S3;Until I50S6 输出T.End DoPrint T三、总结归纳:循环语句:(当型语句):(直到型语句):While pDo循环体循环体End whileUntil pEnd Do四.例题讲解:例1.分别使用当型循环和直到型循环设计求 1+2+3+...+n>2006的最小正整数n的伪代码,并画出流程图.解:使用当型循环语句设计如下:S←0n←1While S≤2006S←S+nn←n+1End whilen←n-1Print n 使用直到循环语句:S←0n←1DoS←S+nn←n+1EndDon←n-1Print n例2.下列伪代码实现的是什么运算?S←0a←1i←1While i≤101S←S+a×ia←a×(-1)i ← i+2End WhilePrint S答案:1-3+5-7+9-...+101五.课堂小结:当型循环直到型循环当型循环语句伪代码格式:直到型循环语句伪代码格式:While PDo循环体循环体End WhileUntil PEnd Do六.课后作业1.编写程序,计算自然数1+2+3+......+99+100的和。
第9课时5.3 基本算法语句
重点难点
重点:正确理解循环语句的概念,并掌握其结构;会应用循环语句编写程序;并能进行简单的综合应用。
难点:理解循环语句的表示方法、结构和用法;会编写程序中的循环语句. 【学习导航】
知识网络
循环语句→当型循环语句⎩⎨⎧语句
语句for while
学习要求
1.正确理解循环语句的概念,并掌握其结构;会应用循环语句编写程序;并能进行简单的综合应用。
2.理解并掌握循环语句在计算机程序语言中的作用,掌握两种循环语句应用的实例:数列求和、求积。
【课堂互动】
自学评价
1.问题:
设计计算997531⨯⨯⨯⨯⨯Λ的一个算法。
【分析】将上述表达式看成49个乘法,用公式表示为:
S ←S ×I
S 初始为1,I 为1,将每次的乘积都赋予S ,I 从1到99,每次增加2,公式S ←S ×I 会被重复执行,这种执行过程可用循环结构表示。
算法一:
S1 S ←1;
S2 I ←1;
S3 I ←I+2;
S4 S ←S ×I ;
S5 如果I 小于99,那么转S3;
S6 输出S
上述算法用流程图表示如下:
【说明】算法一是先执行后判断的直到型循环结构,常用“Do ”语句表示,我们不再学习。
算法二:
S1 S←1;
S2 I←1;
S3 当I不大于99时转S4,否则转S6;S4 S←S×I;
S5 I←I+2;
S6 输出S
【说明】算法二可以理解为:当I>99时, 才循环执行S4和S5两步,这种先判断后执行的循环结构我们称为当型循环,常用“While”语句和“For”语句表示,其中“While语句”可以
用伪代码表示为:
S←1
I←1
While I≤99
S ←S ×I
I ←I+2
End While
Print S
由此可见,同一个问题可以用不同的循环方式来解决,直到型循环和当型循环的控制条件是不同的,请注意流程图中判断分支的流向条件。
在算法二的伪代码中,可以看成I 从1到99,每次增加2,用For 语句写成I From 1 To 99 Step 2,“Step 2”意为I 每次增加2。
写成一般形式为:
注意黑体字部分是For 循环语句的关键词,在“For ”和“End For ”之间的步骤称为循环体,如果省略“Step 2”,那么循环时I 的值默认增加1。
上述问题用For 循环语句的伪代码可以表示为:
S ←1
Print S
【总结】当循环的次数确定时,我们通常用For 循环语句,而当循环的次数不确定时,我们通常用While 循环语句,这两种语句都是前测试语句,即先判断后执行。
若初始条件不成立,则一次也不执行循环体中的内容,任何一种需要重复处理的问题都可以用这种前测试循环来实现。
【经典范例】
例1 分别用While 语句和For 语句写出求1+2+3+…+100的和的一个算法。
【解】用伪代码表示为:
S ←0
Print S
或:
S ←0
Print S
【注意】在累加的算法中,S 的初始值一般设为0,在累乘的算法中,S 的初始值一般设为1,为什么?
例2 问题:将前面的问题改为
⨯⨯⨯⨯⨯Λ7531 >1
0000,那么,如何寻找满足条件的最小整数呢?请用伪代码写出一个算法。
【分析】这个问题中,因为不知道循环需要进行的次数,所以不能用For 循环语句。
【解】算法:
S1 S ←1;
S2 I ←1;
S3 如果S ≤10000,那么I ←I+2,S ←S ×I ,重复S3;
S4 输出I 。
上述算法可以理解为:当S ≤10000时,循环执行S3。
伪代码如下:
S ←1;
I ←1
Print I
在“For ”语句中,I 的变化是通过“Step ”设置的,在程序运行时自动改变,所以循环体中没有如“I ←I+2”这样的语句,而在“While ”语句中,则需要手工编写如“I ←I+2”这样的代码以控制程序的运行,避免出现“死循环”。
例3 抛掷一枚硬币时,既可能出现正面,也可能出现反面,预先做出确定的判断是不可能的,但是假如硬币的质量均匀,那么当抛掷次数很多时,出现正、反面的机率都应接近于50%,试设计一个循环语句模拟抛掷硬币的过程,并计算抛掷中出现正面的机率。
分析:抛掷硬币的过程实际上是一个不断重复的地做同一件事情的过程,这样的过程我们可以通过循环语句模拟。
在程序语言中,有一个随机函数“Rnd ”,它能产生0与1之间的随机数,这样,我们可以用大于0.5的随机数表示出现正面,不大于0.5的随机数表示出现反面,
【解】用伪代码表示为:
S ←0 {求累计和,初始值设为0}
Read n
For I From 1 To n
If Rnd>0.5 Then S
←S+1
End For
Print 出现正面的频率为n
s {单行条件语句不需要结束标志“End If ”}
追踪训练
1.下面的伪代码中,“For ”语句的循环体是__________________________.
【解】循环体是
S←2S+3,
If S>20 Then
S←S -20
End If
2.我们曾研究过问题++++Λ321 >2 004,试用“While ”语句描述这一问题的算法过程。
【解】
S ←0
I ←1 While S ≤2004
S ←S+I
I ←I+1
End While
Print I
3.2000年我国人口数约为13亿,如果每年的人口自然增长率为15‰,那么多少年后我国人口数将达到或超过15亿?
这个问题可通过循环方式计算完成,即每一次在原有的基础上增加15‰,直到达到或超过15亿,再记下循环次数,试用循环语句表示这一过程。
【解】
s ←1300000000
i ←0
while s ≤1500000000
s ←s ×(1+0.015)
i ←i+1
End While
Print i
4. 1,1,2,3,5,8,13,…这一列数的规律是:第1、第2个数是1,从第3个数起,该数是其前面2个数之和,试用循环语句描述计算这列数中前20个数之和的算法.
【解】
a ←1
b ←1
S ←2
For n From 3 To 20
c ←a+b
S ←S+c
a ←b
b ←c
End For
Print S
第9课时基本算法语句(3) 分层训练
1、下列程序框中,出口可以有两个流向的是()
A.起止框 B.输入输出框
C.处理框 D.判断框
2、下面程序运行结果是。
3、下面程序运行结果是。
4、下面算法实现的功能是。
思考•运用
5、将下列问题的算法用伪代码中的“for ”语句表示(写在下面的框中).
6、试用算法语句表示:
使22221232006n ++++>L 成立的最小正整数的算法过程.
解:
7、读入80个自然数,统计出其中偶数的个数,用伪代码表示解决这个问题的算法过程. 解:。