上海市闵行区23校2015年七年级上期中联考数学试卷及答案(沪科版)

2022-2023学年上海市闵行区部分学校七年级（上）期中数学试卷注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上，写在试卷上无效．3.考试结束后，本试卷和答题卡一并交回．一、选择题（本大题共6小题，共12分）1.下列代数式2213,,23,,0,14x y a x x x a +---中，单项式有（）A.1个B.2个C.3个D.4个【答案】B【解析】【分析】根据单项式定义即可得出答案.【详解】根据单项式定义可知，题目中是单项式的有：-a ，0，共两个，故答案为B.【点睛】本题考查的是单项式的定义：①数字或字母的乘积；②单个的数字或字母也是单项式.2.在下列运算中，计算正确的是（）A.326a a a ⋅= B.52(a a = C.2242a a a += D.2224()ab a b =【答案】D【解析】【分析】根据同底数幂的乘法，幂的乘方与积的乘方，合并同类项逐项进行判断即可．【详解】解：A ．325a a a ⋅=，因此选项A 不符合题意；B ．236()a a =，因此选项B 不符合题意；C ．2222a a a +=，因此选项C 不符合题意；D ．2224ab a b =（），因此选项D 符合题意；故选：D ．【点睛】本题考查同底数幂的乘法，幂的乘方与积的乘方以及合并同类项，掌握同底数幂的乘法的计算法则，幂的乘方与积的乘方的运算性质以及合并同类项法则是正确判断的前提．3.在下列代数式中，表示“m 的3倍与n 的和的平方”的是（）A.223m n + B.22(3)m n + C.23()m n + D.2(3)m n +【答案】D【解析】【分析】先表示出m 的3倍，然后表示m 的3倍与n 的和，最后再表示平方，从而列出代数式．【详解】解：表示“m 的3倍与n 的和的平方”的是2(3)m n +，故选：D ．【点睛】本题考查列代数式，理解文字叙述中的计算顺序是解题关键．4.下列整式乘法能用平方差公式计算的是（）A.()()22a b a b +- B.()()22b a a b ---C.()()22a b a b +-- D.()()22a b b a --【答案】B【解析】【分析】根据平方差公式对各选项分别进行判断．【详解】解：A 、()()22a b a b +-不能用平方差公式计算，故此选项不符合题意；B 、22(2)(2)(2)(2)4b a a b a b a b a b ---=-+=-，故此选项符合题意；C 、2(2)(2)(2)a b a b a b +--=-+D 、2(2)(2)(2)a b b a a b --=--，故此选项不符合题意．故选：B ．【点睛】本题主要考查了平方差公式，解题的关键是熟练掌握平方差公式：22()()a b a b a b +-=-．5.如果多项式1x -与多项式2x ax b +-相乘，乘积不含一次项以及二次项，那么a ,b 的值分别是（）A.1,1;B.1,-1;C.-1,-1;D.-1,1;【答案】B【解析】【分析】根据多项式乘法法则，先将两个多项式相乘得出结果，再根据结果不含一次项和二次项，说明一次项系数和二次项系数为0，从而建立关于a 、b 的方程，即可求解.【详解】()()21+--x x ax b =322+---+x ax bx x ax b=()()321+--++x a x a b x b∵乘积不含一次项以及二次项∴10a -=，()=0-+a b 解得=1a ，1b =-故选B .【点睛】本题考查多项式乘法，除了掌握多项式乘法公式外，本题还需要掌握乘积不含一次项以及二次项即一次项系数和二次项系数为0.6.如图是按规律排列的一组图形的前四个，观察图形：那么第8个图形中的点的数量为（）A.47B.48C.49D.50【答案】C【解析】【分析】根据前三个图形的变化规律即可写出第n 个图形点的数量，根据所得规律即可写出第8个图形中点的个数．第一个图形中，一共有61+（）个点，第二个图形中，一共有621⨯+（）个点，第三个图形中，一共有631⨯+（）个点，⋯第n 个图形中，一共有61n +（）个点．∴第8个图形中，一共有68149⨯+=（）个点．故选：C ．【点睛】本题考查了图形的变化类，解决本题的关键是寻找规律．二、填空题（本大题共12小题，共24分）7.单项式23a bc -的次数是______．【答案】4【解析】【分析】根据单项式次数的定义来求解．单项式中所有字母的指数和叫做这个单项式的次数．【详解】解：根据单项式定义得：单项式23a bc -的次数是2114++=．故答案为：4．【点睛】本题考查单项式的知识，确定单项式的系数和次数时，把一个单项式分解成数字因数和字母因式的积，是找准单项式的系数和次数的关键．8.把多项式3221223x y y xy x -+-按照字母x 升幂排列：______．【答案】2231223y xy x x y -+-+【解析】【分析】先分清多项式的各项：32x y ，213y -，2xy ，2x -；再按升幂排列的定义排列．【详解】解：把多项式3221223x y y xy x -+-按照字母x 的升幂排列是：2231223y xy x x y -+-+．故答案为：223122.3y xy x x y -+-+【点睛】考查了多项式的定义，解答此题必须熟悉降幂排列的定义：我们把一个多项式的各项按照某个字母的指数从大到小或从小到大的顺序排列称为按这个字母的降幂或升幂排列．9.计算：3212a b ⎛⎫-= ⎪⎝⎭______．【答案】6318a b -【解析】【分析】根据幂的乘方和积的乘方法则计算．【详解】解：32631128a b a b ⎛⎫-=- ⎪⎝⎭，故答案为：6318a b -．【点睛】本题考查了幂的乘方和积的乘方，解题的关键是掌握运算法则．10.已知单项式13n x y -与2212m x y +-是同类项，则mn =______．【答案】3【解析】【分析】根据同类项的定义（所含字母相同，相同字母的指数相同）列出方程12n -=，23m +=，求出n ，m 的值，再代入代数式计算即可．【详解】解：∵13n x y -与2212m x y +-是同类项，∴12n -=，32m =+，∴3n =，1m =，∴3mn =．故答案为：3．【点睛】此题主要考查了同类项的定义、代数式求值、方程思想应用，理解掌握同类项的定义是解题关键．11.一个多项式减去242x x --得到21x -，那么这个多项式为______．【答案】25x x -+-【解析】【分析】根据一个多项式减去242x x --得到21x -，可知这个多项式为：22(42)(1)x x x --+-，然后计算即可．【详解】解：∵一个多项式减去242x x --得到21x -，∴这个多项式为：22(42)(1)x x x --+-22421x x x =--+-25x x =-+-，故答案为：25x x -+-．【点睛】本题考查整式的加减，解答本题的关键是明确去括号和合并同类项的方法．12.计算：()()3121a a +-=______．【答案】261a a --【解析】【分析】利用多项式乘多项式的运算法则对所求的式子进行运算即可．【详解】解：()()3121a a +-26321a a a =-+-261a a =--．故答案为：261a a --．【点睛】本题主要考查多项式乘多项式，解答的关键是熟练运用多项式乘多项式的运算法则．13.若x 2－2mx ＋9是一个完全平方式，则m 的值为______；【答案】±3【解析】【分析】本题考查完全平方公式的灵活应用，这里首末两项是x 和3的平方，那么中间项为加上或减去x 和3的乘积的2倍．【详解】∵x 2-2mx+9是一个完全平方式，∴-2m=±6，解得：m=±3．故答案为±3．【点睛】本题主要考查完全平方公式，属于基础题，关键是根据两平方项确定出这两个数，再根据乘积二倍项求解．14.一种计算机每秒可做8410⨯次运算，它工作3310⨯秒运算的次数为______（用科学记数法表示）【答案】121.210⨯【解析】【分析】根据题意列出代数式，再根据单项式的乘法法则以及同底数幂的乘法的性质进行计算即可．【详解】解：计算机工作3310⨯秒运算的次数为：83(410)(310)⨯⨯⨯83(43)(1010)=⨯⨯⨯111210=⨯121.210=⨯．故答案为：121.210⨯．【点睛】此题考查了科学记数法，单项式的乘法法则以及同底数幂的乘法的性质，解题的关键是熟练掌握以上知识点．15.不等式()2(2)1x x x ->-的解集是______．【答案】43x <##113x <【解析】【分析】把已知不等式两边展开，变形得3>4x --，即可解得不等式解集．【详解】解：()2(2)1x x x ->-2244>x x x x-+-4>4x x -+-3>4x --解得43x <，故答案为：43x <．【点睛】本题考查解一元一次不等式，解题的关键是把已知的不等式化简变形和掌握不等式的性质．16.计算：128184⎛⎫-⨯= ⎪⎝⎭__．【答案】1【解析】【分析】利用积的乘方公式逆用简便计算即可．【详解】1281()84-⨯24241()22=⨯241(2)2=⨯241=1=．故答案为：1．【点睛】本题主要考查积的乘方，能够熟练逆运用积的乘方公式是解题关键17.我们生活中有两种日常温度计量单位，一种是摄氏度c t ，一种是华氏度F t ，它们可以用公式9325F c t t =+相互换算，那么华氏212度相当于______摄氏度．【答案】100【解析】【分析】把212F t =代入公式9325F c t t =+中得：9322125c t +=，然后进行计算即可解答．【详解】解：把212F t =代入公式9325F c t t =+中得：9322125c t +=，解得：100c t =，故答案为：100．【点睛】本题考查了解一元一次方程，熟练掌握解一元一次方程的步骤是解题的关键．18.规定：对于两个一元多项式（含字母x ）来说，当未知数x 任取同一个数值时，如果它们所得的值都是相等的，那么就称这两个一元多项式恒等．例如：若两个一元多项式2x +与(ax b a +、b 是常数)是恒等的，那么1a =，2b =；如果多项式()3231a b x x +++与231102a b x x -++（a 、b 是常数）恒等，那么b a 的值是______．【答案】14##0.25【解析】【分析】根据多项式恒等的条件列方程组求解．【详解】解：由题意可得1032a b a b +=⎧⎪⎨-=⎪⎩，解得82a b =⎧⎨=⎩，∴8214b a ==．故答案为：14．【点睛】本题考查解二元一次方程组，理解恒等多项式的条件列出符合题意的二元一次方程组，掌握解二元一次方程组的步骤是解题关键．三、解答题（本大题共10小题，共64分）19.计算：232332(23())x x x x x -++- ．【答案】64x -【解析】【分析】先进行幂的运算，再合并同类项即可．【详解】解：232332(23())x x x x x -++- ＝66683x x x -++＝64x -．【点睛】本题考查了幂的运算，解题关键是熟记幂的运算法则，准确进行计算．20.计算：222433311()45312a b ab ab a b ⎛⎫---+ ⎪⎝⎭．【答案】34115a b -【解析】【分析】先算乘方，再根据多项式乘单项式法则算乘法，最后合并同类项即可．【详解】解：原式2222433311()()45912a b ab a b a b =--+433443111121512a b a b a b =--+34115a b =-．【点睛】本题考查了整式的混合运算的应用，注意：运算顺序（有乘方先算乘方，再算乘除，最后算加减，有括号先算括号里面的）．21.计算：()()25454(43)m m m +---．【答案】2162432m m +-【解析】【详解】解：原式()()2222544249m m m =---+22251616249m m m =--+-2162432m m =+-．【点睛】本题考查整式的运算，解题的关键是掌握平方差公式和完全平方公式．22.用乘法公式计算：50.249.8⨯．【答案】2499.96【解析】【分析】根据平方差公式进行解答便可．【详解】解：50.249.8⨯(500.2)(500.2)=+⨯-22500.2=-25000.04=-2499.96=．【点睛】本题考查了有理数乘法，平方差公式，灵活应用平方差公式是解题的关键．23.计算：()()2323x y z x y z -++-．【答案】222496x y yz z -+-【解析】【分析】先利用括号里面各项的关系进行重新组合，再根据平方差与完全平方公式进行计算便可．【详解】解：()()2323x y z x y z -++-=()()[23][23]x z y x z y +---=()()2223x z y --222496x y yz z =-+-．【点睛】本题考查多项式乘多项式、平方差公式和完全平方公式，关键是熟记平方差公式，完全平方公式．24.若整式211422x xy ⎛⎫-+ ⎪⎝⎭减去某个多项式的差是22233x xy -+-，求这个多项式．【答案】27113612x xy -+【解析】【分析】根据题意，可以列出算式22112242233x xy x xy ⎛⎫⎛⎫-+--+- ⎪ ⎝⎭⎝⎭，然后去括号，合并同类项即可．【详解】解：22112242233x xy x xy ⎛⎫⎛⎫-+--+- ⎪ ⎪⎝⎭⎝⎭22112224233x x xy xy =+-+-+27113612x xy =-+即这个多项式为27113612x xy -+．【点睛】本题考查整式的加减，解答本题的关键是明确去括号法则和合并同类项的方法．25.解方程：()()()()56731212x x x x -+=-+-．【答案】43x =-【解析】【分析】先去括号，再移项合并得到2432x -=，然后把x 的系数化为1即可．．【详解】解：去括号得2267303563212x x x x x x +--=+---，移项得730323512x x x x --+=--，合并得2432x -=，系数化为1得43x =-．【点睛】本题考查了解一元一次方程：熟练掌握解一元一次方程的一般步骤是解决问题的关键．26.已知：221x x +=，将()()()()2(1)3331x x x x x --+----先化简，再求它的值．【答案】2211x x +-，10-【解析】【分析】根据完全平方公式、多项式乘多项式可以将题目中的式子展开，然后合并同类项，再根据221x x +=，整体代入化简后的式子计算即可．【详解】解：()()()()2(1)3331x x x x x --+----22212933x x x x x x =-+-+-++-2211x x =+-，当221x x +=时，原式11110=-=-．【点睛】本题考查整式的混合运算，熟练掌握运算法则是解答本题的关键．27.某超市“十一黄金周”进行促销活动期间，前六天的总营业额为450万元，第七天的营业额是前六天总营业额的12%．（1）求该超市“十一黄金周”这七天的总营业．（2）若该超市7月份的营业额为a 万元，8、9月份营业额的月增长率相同，且增长率均为x ，那么7、8、9三个月的营业额一共有多少万元？（用含字母a 、x 的代数式表示，并化简）【答案】（1）504万元（2）()233a ax ax++万元【解析】【分析】（1）根据该超市去年“十一黄金周”这七天的总营业额=前六天的总营业额+第七天的营业额，即可求出结论；（2）根据8月份的营业额7=月份的营业额()1x ⨯+，9月份的营业额8=月份的营业额()1x ⨯+，即可求解．【小问1详解】45045012504+⨯=％（万元）答：该超市去年“十一黄金周”这七天的总营业额为504万元．【小问2详解】由题意得：8月份的营业额为()1a x +万元9月份的营业额为()21a x +万元所以()()()221133a a x a x a ax ax ++++=++万元答：7、8、9三个月的营业额一共有()233a ax ax ++万元．【点睛】本题考查了列代数式、增长率问题等知识点，属于常见的应用题，难度不大．解题的关键是理解平均增长率和营业额的关系，即若变化前的量为a ，增长率为x ，则经过两次变化后的数量关系为()21a x ⨯±．28.如图，已知正方形ABCD 的边长为a ，正方形BEFG 的边长为()<b b a ，点G 在边BC 上，点E 在边AB 的延长线上，DE 交边BC 于点.H 连接FH 、DF ．（1）填空：用a ，b 表示ADE V 的面积ADE S = ______（写出化简后结果）；（2）用a ，b 表示DHF △的面积，并化简；（3）如图2，若点M 是线段AE 的中点，连接MC 、MF 、CF ，试比较MFC △的面积和DHF △的面积的大小（写出过程）．【答案】（1）21122a ab +（2）22111222ab b b +-，12ab （3）MFC DHFS S >【解析】【分析】（1）直接根据三角形的面积公式12AE AD ⋅计算即可；（2）延长DC 交EF 延长线于Q ，先由正方形的性质得EF BE b ==，DQ a b =+，再由DHF DEF HEF S S S =- ，即可得出答案；（3）延长DC 交EF 延长线于Q ，先由正方形的性质得AD CD a ==，EF BE CQ b ===，AE a b =+，QF QE EF BC EF a b =-=-=-，则122a b AM EM AE +===，再由矩形面积、三角形面积和梯形面积公式进行解答即可，由214MFC DHF S S a b -=- （），b a <，即可得出结论．．【详解】解：2111112222ADE S AE AD a b a a ab =⋅=+⋅=+ （）（），故答案为：21122a ab +；2（）延长DC 交EF 延长线于Q ，如图1所示：则四边形AEQD 、四边形CGFQ 都为长方形，正方形ABCD 的边长为a ，正方形BEFG 的边长为b ，EF BE b ∴==，DQ a b =+，221111111122222222DHF DEF HEF S S S EF DQ EF BE b a b b b ab b b ab ∴=-=⋅-⋅=⋅+-⋅=+-= （）；3（）延长DC 交EF 延长线于Q ，如图2所示：则四边形AEQD 、四边形CGFQ 、四边形BCQE 都为长方形，正方形ABCD 的边长为a ，正方形BEFG 的边长为b ，AD CD a ∴==，EF BE CQ b ===，AE a b ∴=+，QF QE EF BC EF a b =-=-=-，点M 是线段AE 的中点，122a b AM EM AE +∴===， 四边形ABCD 是正方形，∴四边形AMCD 是直角梯形，MCF CQF MEF AEQD AMCDS S S S S ∴=--- 长方形梯形111222AD AE CQ QF EM EF AM CD AD =⋅-⋅-⋅-+⋅（）11122222a b a b a a b b a b b a a ++=⋅+-⋅--⨯⋅-+⋅（）（）（）2222111131224444a ab ab b ab b a ab =+-+----221144a b =+2214a b =+（）；2214MFC S a b =+ （），12DHF S ab = ，22222111124244MFC DHF S S a b ab a ab b a b ∴-=+-=-+=- （）（）（），b a < ，2104a b ∴->（），0MFC DHF S S ∴-> ，MFC DHF S S ∴> ．【点睛】本题是四边形综合题目，考查了正方形的性质、长方形的性质、三角形面积以及梯形面积公式等知识；熟练掌握正方形和长方形的性质，熟记三角形面积公式和梯形面积公式是解题的关键．第15页/共15页。

2024-2025学年上海市闵行区19校联考七年级（上）期中数学试卷一、选择题：本题共6小题，每小题2分，共12分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.下列说法正确的是( )A. 2不是单项式B. x−32是一次式C. x−32的一次项系数是1 D. x+13是单项式2.下列等式一定成立的是( )A. a3+a4=a7B. x3⋅(−x)2=x6C. 8a3−(2a)3=6a3D. (−a3)4=a123.找规律：a，4a3，9a5，16a7，⋯，若n为正整数，第n个单项式是( )A. 2n a n+2B. n2a n+1C. n2a n+2D. n2a2n−14.下列多项式中，不能用平方差公式计算的是( )A. (a+1)(−a+1)B. (a+b)(b−a)C. (−a+b)(a−b)D. (a+b)(a−b)5.如果A、B都是关于x的单项式，且A⋅B是一个八次单项式，A−B是一个五次多项式，那么A+B的次数( )A. 一定是五次B. 一定是八次C. 一定是三次D. 无法确定6.如图，下列代数式中，表示图形面积错误的是( )A. (x+1)2−12B. (x+1)2−x2C. x(x+2)D. x(x+1)+x二、填空题：本题共12小题，每小题2分，共24分。

7.x(x≠0)的倒数减去y的平方，可以用代数式表示为______．8.单项式−x2y5的系数是______．9.将−2x5y5−3xy4−3y+12x2y3按字母x的升幂排列是______．10.计算：(−13a2b)3=______．11.计算：(2a−b)(a+3b)=______．12.计算：(−4)2025×(0.25)2024=______．13.已知单项式−2ab 3与4a n b m +1是同类项，则m +n = ______．14.若多项式2xy 2+4kxy−6x 2y +xy−1不含xy 项，则k = ______．15.当我们购买硬盘时，制造商通常采用十进制单位标注产品容量.数据的存储单位一般用KB 、MB 、GB 、TB⋯来表示，其中1MB =210KB ，1GB =210MB.一个硬盘的容量是900GB ，可用科学记数法表示为______MB ．16.已知关于x 的整式4x 2−kx +9是某个关于x 的整式的平方，那么k = ______．17.若x−1x =5，则(x +1x )2= ______⋅18.已知四边形ABCD 是长方形，以DC 为直径的A 半圆与AB 只有一个交点，且AD =a ，用含a 的代数式表示阴影部分面积为______．三、解答题：本题共10小题，共64分。

沪科版数学初一上学期模拟试卷(答案在后面)一、选择题（本大题有10小题，每小题3分，共30分）1、已知一个长方形的长是10厘米，宽是5厘米，求这个长方形的面积。

A、40平方厘米B、50平方厘米C、25平方厘米D、100平方厘米2、一个等腰三角形的底边长为8厘米，腰长为6厘米，求这个三角形的周长。

A、18厘米B、20厘米C、24厘米D、26厘米3、下列哪个数是平方数？A. 2B. 3C. 4D. 54、一个长方形的长是8厘米，宽是5厘米，那么这个长方形的面积是多少平方厘米？A. 13C. 33D. 355、下列数中，最接近于圆周率π的是（）A. 3.14B. 3.141C. 3.1416D. 3.141596、一个长方形的长是8厘米，宽是5厘米，那么它的周长是（）A. 17厘米B. 23厘米C. 18厘米D. 26厘米7、一个长方形的长是10cm，宽是6cm，那么这个长方形的周长是多少平方厘米？选项：A、60cm²B、30cm²C、56cm²D、40cm²8、下列哪个数是负数？选项：A、-5C、-10D、09、（1）一个几何图形的周长是12厘米，如果这个图形是正方形，那么它的面积是（）A. 9平方厘米B. 16平方厘米C. 36平方厘米D. 64平方厘米（2）一个长方形的长是6厘米，宽是4厘米，那么这个长方形的对角线长度是（）A. 10厘米B. 12厘米C. 8厘米D. 5厘米二、填空题（本大题有5小题，每小题3分，共15分）1、一个长方形的长是6厘米，宽是3厘米，那么这个长方形的面积是______ 平方厘米。

2、若直角三角形的两个直角边分别为3厘米和4厘米，则该直角三角形的斜边长度是 ______ 厘米。

3、若一个等腰三角形的底边长为6厘米，腰长为8厘米，则该三角形的面积是 ____ 平方厘米。

4、小华在计算一道一元一次方程时，错误地将未知数x的系数乘以了2，得到的方程为2x - 5 = 3，求出小华得到的解x’后，若将其代入原方程x + 3 = 7，求小华得到的解x’在原方程中的情况。

2022-2023学年上海市闵行区七年级（上）期中数学试卷一、选择题（共6小题，每小题3分，满分18分）. 1．（3分）下列各式中，是代数式的有( ) ①23xy ；②2r π；③2S r π=；④b ；⑤512+>；⑥2ab． A ．3个B ．4个C ．5个D ．6个2．（3分）下列运算正确的是( ) A ．235235x x x += B ．33(2)6x x -=-C ．222()x y x y +=+D ．2(32)(23)49x x x +-=-3．（3分）当2x =时，整式31ax bx +-的值等于19-，那么当2x =-时，整式31ax bx +-的值为( ) A ．19B ．19-C ．17D ．17-4．（3分）如果A 、B 都是关于x 的单项式，且A B ⋅是一个九次单项式，A B +是一个五次多项式，那么A B -的次数( ) A ．一定是九次B ．一定是五次C ．一定是四次D ．无法确定5．（3分）如果(1)(3)x x a ++的乘积中不含x 的一次项，则a 为( ) A ．3B ．3-C ．13D ．13-6．（3分）某商店经销一批衬衣，每件进价为a 元，零售价比进价高%m ，后因市场变化，该商店把零售价调整为原来零售价的%n 出售．那么调整后每件衬衣的零售价是( ) A ．(1%)(1%)a m n +-元 B ．%(1%)am n -元 C ．(1%)%a m n +元D ．(1%%)a m n +元二、填空题（本大题共12小题，每小题2分，满分24分） 7．（2分）“a 的平方的倒数减去12的差”用代数式表示为： ． 8．（2分）单项式2237xy π-的系数是 ．次数是 ．9．（2分）把多项式323274x x y y xy -+-按x 的升幂排列为 ．10．（2分）如果单项式312a b x y +与25b x y 的和仍是单项式，则a b -的值为 ．11．（2分）如果整式2274a ab b +-加上一个多项式得2a ab -，那么所加上的多项式是 ．12．（2分）计算：2()x x -⋅-= ． 13．（2分）计算：226(31)3m m m --= ．14．（2分）计算：1281()84-⨯= ．15．（2分）如果代数式2238a b -++的值为1，那么代数式2462a b -+的值等于 ． 16．（2分）如果3m a =，12n a =，那么32m n a += ． 17．（2分）已知6x y +=，7xy =，那么22(3)(3)x y x y +++的值为 ．18．（2分）观察等式：232342222:22222+=-++=-；2345222222+++=-，⋯已知按一定规律排列的一组数：502、512、522、⋯、992、1002，若502a =，则用含a 的式子表示这组数的和是 ．三、简答题（本大题共6题，每题5分，满分30分） 19．（5分）计算：232233()()()x x x x --⋅--⋅-． 20．（5分）计算：(23)(23)a b a b -++-． 21．（5分）计算：2(23)(32)(23)x y x y x y -+--． 22．（5分）利用公式计算：21001999997⨯-． 23．（5分）计算：22(32)(32)a b a b -+．24．（5分）计算：2481632(21)(21)(21)(21)(21)+⨯+⨯+⨯+⨯+（结果用幂的形式表示）． 四、解答题（本大题共4题，第25题6分，第26、27题每题7分，第28题8分，满分28分）25．（6分）已知代数式22321A x xy y =++-，212B x xy x =-+-．（1）如果x ，y 满足2(1)|2|0x y ++-=，求2A B -的值； （2）如果2A B -的值与x 的取值无关，求y 的值． 26．（7分）已知2510m m --=，求22125m m m -+的值． 27．（7分）如图，正方形ABCD 与正方形CEFG 的面积之差是6，求阴影部分的面积．28．（8分）阅读材料：在学习多项式乘以多项式时，我们知道1(4)(25)(36)2x x x ++-的结果是一个多项式，并且最高次项为：312332x x x x ⋅⋅=，常数项为：45(6)120⨯⨯-=-．那么一次项是多少呢？要解决这个问题，就是要确定该一次项的系数．通过观察，我们发现：一次项系数就是：15(6)2(6)434532⨯⨯-+⨯-⨯+⨯⨯=-，即一次项为3x -． 参考材料中用到的方法，解决下列问题：（1）计算(2)(31)(53)x x x ++-所得多项式的一次项系数为 ．（2）如果计算22(1)(3)(21)x x x x a x ++-+-所得多项式不含一次项，求a 的值； （3）如果202220222021202001220212022(1)x a x a x a x a x a +=+++⋯++，求2021a 的值．参考答案一、选择题（本大题共6小题，每小题3分，满分18分） 1．（3分）下列各式中，是代数式的有( ) ①23xy ；②2r π；③2S r π=；④b ；⑤512+>；⑥2ab． A ．3个B ．4个C ．5个D ．6个 解：由代数式的定义可知，是代数式的有：①23xy ；②2r π；④b ；⑥2ab，共4个． 故选：B ．2．（3分）下列运算正确的是( ) A ．235235x x x += B ．33(2)6x x -=-C ．222()x y x y +=+D ．2(32)(23)49x x x +-=-解：A 选项，22x 与33x 不是同类项，不能合并，故该选项计算错误，不符合题意； B 选项，原式38x =-，故该选项计算错误，不符合题意；C 选项，原式222x xy y =++，故该选项计算错误，不符合题意；D 选项，原式2222(3)49x x =-=-，故该选项计算正确，符合题意；故选：D ．3．（3分）当2x =时，整式31ax bx +-的值等于19-，那么当2x =-时，整式31ax bx +-的值为( ) A ．19B ．19-C ．17D ．17-解：当2x =时，整式31ax bx +-的值为19-， 82119a b ∴+-=-，即8218a b +=-，则当2x =-时，原式82118117a b =---=-=． 故选：C ．4．（3分）如果A 、B 都是关于x 的单项式，且A B ⋅是一个九次单项式，A B +是一个五次多项式，那么A B -的次数( ) A ．一定是九次 B ．一定是五次C ．一定是四次D ．无法确定解：A B ⋅是一个九次单项式，A B +是一个五次多项式，∴单项式A 、B 一个是5次单项式，一个是4次单项式，A B ∴-的次数是5次．故选：B ．5．（3分）如果(1)(3)x x a ++的乘积中不含x 的一次项，则a 为( ) A ．3B ．3-C ．13D ．13-解：(1)(3)x x a ++， 233x ax x a =+++，23(3)x a x a =+++， 乘积中不含x 的一次项， 30a ∴+=，解得：3a =-， 故选：B ．6．（3分）某商店经销一批衬衣，每件进价为a 元，零售价比进价高%m ，后因市场变化，该商店把零售价调整为原来零售价的%n 出售．那么调整后每件衬衣的零售价是( ) A ．(1%)(1%)a m n +-元 B ．%(1%)am n -元 C ．(1%)%a m n +元D ．(1%%)a m n +元解：每件进价为a 元，零售价比进价高%m ，∴零售价为：(1%)a m +元，要零售价调整为原来零售价的%n 出售． ∴调整后每件衬衣的零售价是：(1%)%a m n +元．故选：C ．二、填空题（本大题共12小题，每小题2分，满分24分）7．（2分）“a 的平方的倒数减去12- 解：“a 的平方的倒数减去12的差”用代数式表示为：2112a -， 故答案为：2112a -． 8．（2分）单项式2237xy π-的系数是 97π- ．次数是 ．解：单项式2237xy π-的系数是97π-，次数是3．故答案为：97π-，3．9．（2分）把多项式323274x x y y xy -+-按x 的升幂排列为 322347y xy x y x --+ ．解：多项式323274x x y y xy -+-的各项为3x ，27x y -，3y ，24xy -， 按x 的升幂排列为：322347y xy x y x --+． 故答案为：322347y xy x y x --+．10．（2分）如果单项式312a b x y +与25b x y 的和仍是单项式，则a b -的值为 4- ．解：单项式312a b x y +与25b x y 的和仍是单项式，∴312a b x y +与25b x y 是同类项， 2a b ∴+=，3b =，解得：1a =-，3b =， ∴原式134=--=-，故答案为：4-．11．（2分）如果整式2274a ab b +-加上一个多项式得2a ab -，那么所加上的多项式是 2265a ab b --+ ．解：由题意可得，所加上的多项式是：222(74)a ab a ab b --+- 22274a ab a ab b =---+ 2265a ab b =--+．故答案为：2265a ab b --+．12．（2分）计算：2()x x -⋅-= 3x - ． 解：223()x x x x x -⋅-=-⋅=-． 故答案为：3x -．13．（2分）计算：226(31)3m m m --= 321846m m m -- ．解：226(31)3m m m --22636613m m m m m =⋅-⋅-⨯321846m m m =--．故答案为：321846m m m --．14．（2分）计算：1281()84-⨯= 1 ．解：1281()84-⨯24241()22=⨯ 241(2)2=⨯ 241=1=．故答案为：1．15．（2分）如果代数式2238a b -++的值为1，那么代数式2462a b -+的值等于 16 ． 解：2238a b -++的值为1， 22381a b ∴-++=， 2237a b ∴-+=-， 2462a b ∴-+22(23)2a b =--++ 2(7)2=-⨯-+ 142=+16=故答案为：16．16．（2分）如果3m a =，12n a =，那么32m n a + 解：当3m a =，12n a =时， 32m n a + 32m n a a =⨯32()()m n a a =⨯ 3213()2=⨯1274=⨯274=．故答案为：274． 17．（2分）已知6x y +=，7xy =，那么22(3)(3)x y x y +++的值为 304 ． 解：原式22229669x xy y x xy y =+++++22101210x xy y =++ 2210()12x y xy =++ 210()8x y xy =+-，当6x y +=，7xy =，原式210687304=⨯-⨯=． 故答案为：304．18．（2分）观察等式：232342222:22222+=-++=-；2345222222+++=-，⋯已知按一定规律排列的一组数：502、512、522、⋯、992、1002，若502a =，则用含a 的式子表示这组数的和是 22a a - ． 解：232222+=-；23422222++=-； 2345222222+++=-；⋯231222222n n +∴+++⋯+=-， 5051529910022222∴+++⋯++231002349(2222)(2222)=+++⋯+-+++⋯+ 10150(22)(22)=---1015022=-，502a =，10150222(2)22a ∴==， ∴原式22a a =-．故答案为：22a a -．三、简答题（本大题共6题，每题5分，满分30分） 19．（5分）计算：232233()()()x x x x --⋅--⋅-．解：232233()()()x x x x --⋅--⋅-649()()x x x x =--⋅-⋅- 1010x x =+ 102x =．20．（5分）计算：(23)(23)a b a b -++-． 解：(23)(23)a b a b -++- [(23)][(23)]a b a b =--+-22(23)a b =-- 224129a b b =-+-．21．（5分）计算：2(23)(32)(23)x y x y x y -+--． 解：原式624962(421292)x xy xy y x xy y =+----+ 62562421292x xy y x xy y =---+- 227152x xy y =+-．22．（5分）利用公式计算：21001999997⨯-． 解：（3）21001999997⨯-2(10001)(10001)(10003)=+⨯--- 2210001100060009=--+- 600010=-5990=．23．（5分）计算：22(32)(32)a b a b -+． 解：原式2[(32)(32)]a b a b =-+222[(3)(2)]a b =- 222(94)a b =-4224817216a a b b =-+．24．（5分）计算：2481632(21)(21)(21)(21)(21)+⨯+⨯+⨯+⨯+（结果用幂的形式表示）． 解：原式224816321(21)(21)(21)(21)(21)(21)3=⨯-⨯+⨯+⨯+⨯+⨯+44816321(21)(21)(21)(21)(21)3=⨯-⨯+⨯+⨯+⨯+ 8816321(21)(21)(21)(21)3=⨯-⨯+⨯+⨯+ 1616321(21)(21)(21)3=⨯-⨯+⨯+ 32321(21)(21)3=⨯-⨯+ 641(21)3=⨯-． 四、解答题（本大题共4题，第25题6分，第26、27题每题7分，第28题8分，满分28分）25．（6分）已知代数式22321A x xy y =++-，212B x xy x =-+-．（1）如果x ，y 满足2(1)|2|0x y ++-=，求2A B -的值； （2）如果2A B -的值与x 的取值无关，求y 的值． 解：（1）原式221(2321)2()2x xy y x xy x =++---+-2223212221x xy y x xy x =++--+-+ 522xy x y =-+，由题意可知：10x +=，20y -=， 1x ∴=-，2y =，原式5(1)22(1)22=⨯-⨯-⨯-+⨯ 1024=-++ 4=-．（2）原式(52)2y x y =-+， 令520y -=， 25y ∴=． 26．（7分）已知2510m m --=，求22125m m m -+的值． 解：2510m m --=， 251m m ∴-=，15m m-=， 21()25m m∴-=，221225m m ∴+-=， 22127m m ∴+=， ∴22125m m m -+ 22215m m m m =-++127=+28=． 27．（7分）如图，正方形ABCD 与正方形CEFG 的面积之差是6，求阴影部分的面积．解：设正方形ABCD 与正方形CEFG 的边长分别为a 和b ，由题意得：226b a -=．由图形可得：()2111222S a b a b ab ⎛⎫=-+- ⎪⎝⎭阴 2211112222ab a b ab =-+- 221()2b a =- 162=⨯ 3=．故阴影部分的面积为3．28．（8分）阅读材料：在学习多项式乘以多项式时，我们知道1(4)(25)(36)2x x x ++-的结果是一个多项式，并且最高次项为：312332x x x x ⋅⋅=，常数项为：45(6)120⨯⨯-=-．那么一次项是多少呢？ 要解决这个问题，就是要确定该一次项的系数．通过观察，我们发现：一次项系数就是：15(6)2(6)434532⨯⨯-+⨯-⨯+⨯⨯=-，即一次项为3x -．参考材料中用到的方法，解决下列问题：（1）计算(2)(31)(53)x x x ++-所得多项式的一次项系数为 11- ．（2）如果计算22(1)(3)(21)x x x x a x ++-+-所得多项式不含一次项，求a 的值；（3）如果202220222021202001220212022(1)x a x a x a x a x a +=+++⋯++，求2021a 的值． 解：（1）一次项系数为11(3)23(3)21511⨯⨯-+⨯⨯-+⨯⨯=-， 故答案为：11-；（2）根据题意，得一次项系数1(1)(3)1(1)210a a ⨯⨯-+-⨯⨯-+⨯⨯=， 解得3a =-；（3）2022(1)x +的一次项系数为202212022⨯=， 20212022a ∴=．。

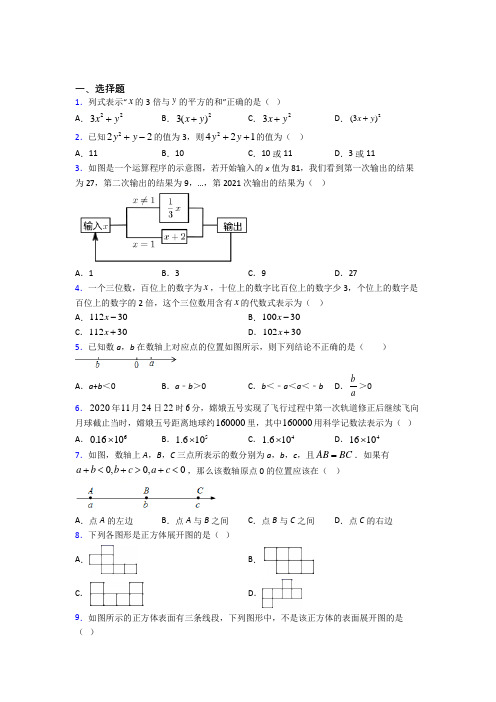
一、选择题1．列式表示“x 的3倍与y 的平方的和”正确的是（ ） A ．223+x y B ．23()x y + C ．23x y + D ．2(3)x y + 2．已知222y y +-的值为3，则2421y y ++的值为（ ）A ．11B ．10C ．10或11D ．3或11 3．如图是一个运算程序的示意图，若开始输入的x 值为81，我们看到第一次输出的结果为27，第二次输出的结果为9，…，第2021次输出的结果为（ ）A ．1B ．3C ．9D ．274．一个三位数，百位上的数字为x ，十位上的数字比百位上的数字少3，个位上的数字是百位上的数字的2倍，这个三位数用含有x 的代数式表示为（ ）A ．11230x -B ．10030x -C ．11230x +D ．10230x +5．已知数a ，b 在数轴上对应点的位置如图所示，则下列结论不正确的是（ ）A ．a +b ＜0B ．a ﹣b ＞0C ．b ＜﹣a ＜a ＜﹣bD ．b a＞0 6．2020年11月24日22时6分，嫦娥五号实现了飞行过程中第一次轨道修正后继续飞向月球截止当时，嫦娥五号距离地球约160000里，其中160000用科学记数法表示为（ ） A ．601610⨯. B ．51.610⨯ C ．41.610⨯ D ．41610⨯ 7．如图，数轴上A ，B ，C 三点所表示的数分别为a ，b ，c ，且AB BC =．如果有0,0,0a b b c a c +<+>+<，那么该数轴原点0的位置应该在（ ）A ．点A 的左边B ．点A 与B 之间C ．点B 与C 之间D ．点C 的右边 8．下列各图形是正方体展开图的是（ ）A ．B ．C ．D ．9．如图所示的正方体表面有三条线段，下列图形中，不是该正方体的表面展开图的是（ ）A ．B ．C ．D ．10．把图中的硬纸片沿虚线折起来，便可成为一个正方体，这个正方体的2号平面的对面是（ ）A ．3号面B ．4号面C ．5号面D ．6号面 11．对于有理数a ，b ，有以下四个判断：①若a b =，则b a ≥；②若a b >，则a ＞b ；③若a b =，则a b =；④若a b <，则a b <．其中错误的判定个数是（ ） A ．4个 B ．3个 C ．2个 D ．1个12．如图是一个正方体的平面展开图，若将展开图折叠成正方体后，相对面上所标的两个数相等，则a ﹣b ﹣c 的值为（ ）A ．2B ．﹣2C ．4D ．﹣4二、填空题13．下列图形都是由同样大小的实心圆点按一定规律组成的，其中第①个图形一共有5个实心圆点，第②个图形一共有8个实心圆点，第③个图形一共有11个实心圆点，…，按此规 律排列下去，第n 个图形中实心圆点的个数为________．14．按如图所示的程序计算，若开始输入的x 的值为16，我们发现第1次得到的结果为8，第2次得到的结果为4，……，请你探索第2021次得到的结果为________．15．若a ，b 互为相反数，c ，d 互为倒数，且b ≠0，则（a +b ）2019+（cd ）2020+（a b ）2021的值为_____． 16．“数形结合”思想在数轴上得到充分体现，如在数轴上表示数5和2-的两点之间的距离，可列式表示为()52--，或25--；表示数x 和3-的两点之间的距离可列式表示为()33x x --=+．已知31239x x y y ++-+++-=，则x y +的最大值为______．17．已知数轴上A 、B 两点所对应的数分别是1和3，P 为数轴上任意一点，对应的数为x ．（1）则A 、B 两点之间的距离为________；（2）式子|1||3||2017||2019|x x x x -+-++-+-的最小值为________． 18．用一个平面去截正方体（如图），下列关于截面（截出的面）形状的结论： ①可能是锐角三角形；②可能是钝角三角形；③可能是长方形；④可能是梯形．其中正确结论的是______（填序号）.19．一个正方体的表面展开图如图所示，这个正方体的每一个面上都填有一个数字，且各相对面上所填的数字互为倒数，则()x yz 的值为___.20．一个正方体的六个面上分别标有1、2、3、4、5、6，根据图中从各个方向看到的数字，解答下面的问题：“？”处的数字是_____．三、解答题21．先化简，再求值：232222231(2)(4)(8+4)2xy x y x y xy x y x y ⎡⎤+--+-⎢⎥⎣⎦，其中112x y =-=，． 22．先化简，再求值（1）已知()2a 1b-20++=，求()()2222225a -b 2a -b -5a -3b -ab + （2）已知a 2＋5ab ＝76，3b 2＋2ab ＝51，求代数式a 2＋11ab ＋9b 2的值．23．计算：（1）（﹣5.5）+（﹣3.2）﹣（﹣2.5）﹣4.8；（2）12(2)8(2)()9()23-+÷-⨯--⨯-； （3）32431(2)()()3|1|323-÷-⨯--⨯--． 24．若a ，b 是整数且满足：|1||1|1a b -++=，求-a b 的值． 25．某种包装盒的形状及相关尺寸如图所示(单位:cm).(1)请你画出沿长为3 cm 的棱将这个包装盒剪开的平面展开图,并标出相应的尺寸(接头处忽略不计);(2)计算这个包装盒的表面积.26．一个由若干小正方体堆成的几何体，它的主视图和左视图如图①所示（1）这个几何体可以是图②甲、乙、丙中的______；（2）这个几何体最多由______个小正方体构成，最少由______个小正方体构成．请在图③中画出符合最少情况的一个俯视图．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】认真阅读，列式分三步：第一步计算x的3倍，第二步计算y的平方，第三步计算前两步的和即可．【详解】∵x的3倍为3x，y的平方为2y，∴x的3倍与y的平方的和为：2，3x y故选C．【点睛】本题考查了代数式的布列，准确理解题意，找准分布计算与整体计算是解题的关键．2．A解析：A【分析】观察题中的两个代数式可以发现2（2y2+y）=4y2+2y，因此可整体求出4y2+2y的值，然后整体代入即可求出所求的结果．【详解】解：∵2y2+y-2的值为3，∴2y2+y-2=3，∴2y2+y=5，∴2（2y2+y）=4y2+2y=10，∴4y2+2y+1=11．故选：A．【点睛】代数式中的字母表示的数没有明确告知，而是隐含在题设中，首先应从题设中获取代数式4y2+2y的值，然后利用“整体代入法”求代数式的值．3．B解析：B【分析】分别求出第一次输出27，第二次输出9，第三次输出3，第四次输出1，第五次输出3，第六次输出1，由此可得，从第三次开始，每两次一个循环．【详解】解：由题可知，第一次输出27，第二次输出9，第三次输出3，第四次输出1，第五次输出3，第六次输出1，由此可得，从第三次开始，每两次一个循环，()20212210091-÷=， 第2021次输出结果与第3次输出结果一样， 第2021次输出的结果为3，故选：B ．【点睛】 本题考查数字的变化规律，找到循环规律是解题的关键．4．A解析：A【分析】先分别用x 表示十位上和个位上的数字，再利用十位制列出代数式、计算整式的加减即可得．【详解】由题意得：十位上的数字为3x -，个位上的数字为2x ，则这个三位数用含有x 的代数式表示为10010(3)211230x x x x +-+=-， 故选：A ．【点睛】本题考查了列代数式、整式的加减，依据题意，正确得出十位上和个位上的数字是解题关键．5．D解析：D【分析】根据数轴上a 、b 的位置结合有理数的运算法则即可判断．【详解】解：由数轴可知：b ＜0＜a ，|b |＞|a |，∴﹣b ＞a ，∴a +b ＜0，a ﹣b ＞0，b a＜0，b ＜﹣a ＜0＜a ＜﹣b ． 故选：D ．【点睛】本题考查数轴的定义，解题的关键是正确理解数轴与有理数之间的关系，本题属于基础题型． 6．B解析：B【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数，确定a 和n 即可．【详解】解：160000用科学记数法表示为：5160000 1.610=⨯，故选：B ．【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．．7．C解析：C【分析】根据各个选项的情况，去分析a ，b ，c 三个数的正负，判断选项的正确性．【详解】解：若原点在点A 左边，则0a >、0b >、0c >，就不满足0a b +<，故A 选项错误； 若原点在点A 与点B 之间，则0a <、0b >、0c >，且a c <，就不满足0a c +<，故B 选项错误；若原点在点B 与点C 之间，则0a <、0b <、0c >，条件都可以满足，故C 选项正确； 若原点在点C 右边，则0a <、0b <、0c <，就不满足0b c +>，故D 选项错误． 故选：C ．【点睛】本题考查数轴，解题的关键是根据数轴上点的位置判断式子的正负．8．D解析：D【解析】【分析】根据正方体展开图的11种形式对各选项分析判断即可得解．【详解】A 、不是正方体展开图，故选项错误；B 、有田字格，不是正方体展开图，故选项错误；C 、是凹字形，不是正方体展开图，故选项错误；D 、1﹣4﹣1型，是正方体展开图，故选项正确．故选D ．【点睛】本题考查了正方体的展开图，熟记展开图的11种形式是解题的关键，利用不是正方体展开图的“一线不过四、田凹应弃之”（即不能出现同一行有多于4个正方形的情况，不能出现田字形、凹字形的情况）判断也可．9．D解析：D【解析】【分析】由平面图形的折叠及正方体的展开图解题．【详解】不是该正方体的展开图的是选项D ，故选D ．本题考查了几何体的展开图，解题时勿忘记四棱柱的特征及正方体展开图的各种情形． 10．C解析：C【分析】折成正方体，分析相对面，再作答．【详解】解：折成正方体后1和3相对，4和6相对，2和5相对．故选：C ．【点睛】本题考查了正方体的空间图形，熟练掌握是解题的关键．11．B解析：B【分析】根据绝对值的性质依次判断即可．【详解】解：①若a b =，则，b a =±且0b ≥，所以b a ≥，正确；②若2,5a b ==-时，a b >，但a ＜b ，原说法错误；③若a b =，则a b =±，原说法错误；④若2,5a b ==-时，a b <，但a b >，原说法错误；故选：B ．【点睛】本题考查了绝对值的定义及其相关性质．牢记以下规律：（1）|a|=-a 时，a≤0；（2）|a|=a 时，a≥0；（3）任何一个非0的数的绝对值都是正数．12．A解析：A【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形确定出相对面，再根据相对面上的数字相等，求出a 、b 、c ，然后代入代数式进行计算即可得解．【详解】正方体的表面展开图，相对的面之间一定相隔一个正方形，“a ”与“﹣1”是相对面，“b ”与“﹣5”是相对面，“c ”与“2”是相对面，∵相对面上的两个数相等，∴a ＝﹣1，b ＝﹣5，c ＝2，∴a ﹣b ﹣c ＝﹣1+5﹣2＝2．【点睛】本题考查了正方体的表面展开图，熟知正方体的表面展开图中相对的面之间一定相隔一个正方形式解决问题的关键.二、填空题13．【分析】根据已知图形中实心圆点的个数得出规律：第n个图形中实心圆点的个数为2n+n+2据此求解可得【详解】解：∵第①个图形中实心圆点的个数5＝2×1+3第②个图形中实心圆点的个数8＝2×2+4第③个解析：32n+【分析】根据已知图形中实心圆点的个数得出规律：第n个图形中实心圆点的个数为2n+n+2，据此求解可得．【详解】解：∵第①个图形中实心圆点的个数5＝2×1+3，第②个图形中实心圆点的个数8＝2×2+4，第③个图形中实心圆点的个数11＝2×3+5，……∴第n个图形中实心圆点的个数为2×n+n+2＝32n+，故答案为：32n+．【点睛】本题主要考查图形的变化规律，解题的关键是根据已知图形得出第n个图形中实心圆点的个数为2n+n+2的规律．14．6【分析】把x＝16代入程序中计算以此类推得到一般性规律求出第2021次得到的结果即可【详解】解：第1次得到的结果为16×＝8第2次得到的结果为8×＝4第3次得到的结果为4×＝2第4次得到的结果为2解析：6【分析】把x＝16代入程序中计算，以此类推得到一般性规律，求出第2021次得到的结果即可．【详解】解：第1次得到的结果为16×12＝8，第2次得到的结果为8×12＝4，第3次得到的结果为4×12＝2，第4次得到的结果为2×12＝1，第5次得到的结果为1+5＝6，第6次得到的结果为6×12＝3，第7次得到的结果为3＋5＝8，第8次得到的结果为8×12=4，第9次得到的结果为4×12＝2，第10次得到的结果为2×12＝1，第11次的到的结果为1＋5＝6，第12次得到的结果为6×12＝3，……∴结果是8，4，2，1，6，3六个为周期循环，∵2021÷6＝335…5，∴第2021次得到的结果为6，故答案为：6．【点睛】此题考查了数字的变化规律、代数式求值，由题意得出规律是解本题的关键．15．0【分析】根据ab互为相反数cd互为倒数且b≠0可以得到a+b＝0cd＝1＝﹣1从而可以计算出所求式子的值【详解】解：∵ab互为相反数cd互为倒数且b≠0∴a+b＝0cd＝1＝﹣1∴（a+b）201解析：0【分析】根据a，b互为相反数，c，d互为倒数，且b≠0，可以得到a+b＝0，cd＝1，ab＝﹣1，从而可以计算出所求式子的值．【详解】解：∵a，b互为相反数，c，d互为倒数，且b≠0，∴a+b＝0，cd＝1，ab＝﹣1，∴（a+b）2019+（cd）2020+（ab）2021＝02019+12020+（﹣1）2021＝0+1+（﹣1）＝0，故答案为：0．【点睛】本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法．16．4【分析】根据题意分别得到和的最小值结合得到=4=5根据x和y的范围得到x+y 的最大值【详解】解：由题意可得：表示x 与-3的距离和x 与1的距离之和表示y 与-2的距离和y 与3的距离之和∴当-3≤x≤1解析：4【分析】 根据题意分别得到31x x ++-和23y y ++-的最小值，结合31239x x y y ++-+++-=得到31x x ++-=4，23y y ++-=5，根据x 和y 的范围得到x+y 的最大值．【详解】解：由题意可得：31x x ++-表示x 与-3的距离和x 与1的距离之和，23y y ++-表示y 与-2的距离和y 与3的距离之和，∴当-3≤x≤1时，31x x ++-有最小值，且为1-（-3）=4，当-2≤x≤3时，23y y ++-有最小值，且为3-（-2）=5， ∵31239x x y y ++-+++-=， ∴31x x ++-=4，23y y ++-=5，∴x+y 的最大值为：1+3=4，故答案为：4．【点睛】本题考查了数轴上两点之间的距离，绝对值的意义，，用几何方法借助数轴来求解，数形结合是解答此题的关键．17．2；【分析】（1）根据两点间的距离公式解题即可；（2）由绝对值的几何意义表示数x 到数的距离要使式子取得最小值则应找到与最小数和最大数距离相等的x 的值即可解题【详解】（1）两点之间的距离为3-1=2故解析：2； 510050．【分析】（1）根据两点间的距离公式解题即可；（2）由绝对值的几何意义，||x a -表示数x 到数a 的距离，要使式子取得最小值，则应找到与最小数和最大数距离相等的x 的值，即可解题．【详解】（1）A 、B 两点之间的距离为3-1=2，故答案为：2；（2）由已知条件可知，||x a -表示数x 到数a 的距离，只有当x 到1的距离等于x 到2019的距离时，式子即可取最小值，∴当1201910102x +==时，|1||3||2017||2019|x x x x -+-++-+-取最小值，最小值为：|10101||10103||10102017||10102019|-+-++-+-=1009+1007+1005+1+1++1005+1007+1009=2(1009+1007+1005+1)⨯(10091)505=22+⨯⨯ 510050=【点睛】本题考查数轴、绝对值、两点间的距离等知识，是重要考点，难度一般，掌握相关知识是解题关键．18．①③④19．18- 20．1三、解答题21．233xy x y -；14-【分析】原式去括号合并得到最简结果，把x 与y 的值代入计算即可求出值．【详解】 解：232222231(2)(4)(8+4)2xy x y x y xy x y x y ⎡⎤+--+-⎢⎥⎣⎦ 232222231=24(8+4)2xy x y x y xy x y x y +-+-- 232222232442xy x y x y xy x y x y =+-++-233xy x y =- 当112x y =-=，时，原式3111=3(1)(1)424⨯-⨯--⨯=-． 【点睛】此题考查了整式的加减-化简求值，熟练掌握运算法则是解本题的关键．22．（1）2a²-ab ，4；（2）229【分析】（1）根据绝对值和偶次方的非负性分别求出a 、b ，根据整式的加减运算法则把原式化简，代入求值即可得出答案；（2）先将a 2＋11ab ＋9b 2化为与a 2＋5ab 和3b 2＋2ab 相关的式子再将值代入即可得出答案．【详解】（1）解：()()2222225a -b 2a -b -5a -3b -ab + =5a²-b²+2a²-2b²-5a²+3b²-ab=2a²-ab∵|a+1|+（b-2）²=0∴|a+1|=0，（b-2）²=0解得a=-1 ，b=2代入2a²-ab得2×（-1）²-（-1）×2=4（2）解：∵3b²+2ab=51∴3（3b²+2ab ）=9b²+6ab=51×3=153又a²+5ab=76∴a²+11ab+9b²=a²+5ab+（9b²+6ab ）=229．【点睛】本题考查了整式的化简求值、非负数的性质，熟练掌握整式的加减运算是解题的关键． 23．（1）﹣11；（2）6；（3）﹣21【分析】（1）根据有理数的加减法可以解答本题；（2）根据有理数的乘除法和加减法可以解答本题；（3）根据有理数的乘方、有理数的乘除法和加减法可以解答本题．【详解】解：（1）（﹣5.5）+（﹣3.2）﹣（﹣2.5）﹣4.8＝（﹣5.5）+（﹣3.2）+2.5+（﹣4.8）＝[（﹣5.5）+2.5]+[（﹣3.2）+（﹣4.8）]＝（﹣3）+（﹣8）＝﹣11；（2）12(2)8(2)()9()23-+÷-⨯--⨯-＝（﹣2）+（﹣4）×（﹣12）+6 ＝（﹣2）+2+6＝6；（3）32431(2)()()3|1|323-÷-⨯--⨯--＝（﹣8）×（﹣34）×（﹣32）﹣9×43 ＝﹣9﹣12＝﹣21．【点睛】本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法．24．1或3．【分析】根据数轴上两点间的距离及绝对值的意义，结合题意确定a 与b 的值，然后代入求解．【详解】解：|1|a -表示数轴上表示a 的点与1的距离，|1|b +表示数轴上表示b 的点与-1的距离 又∵|1||1|1a b -++=且a ，b 是整数∴|1|0|1|1a =b -+=，或|1|1|1|0a =b -+=， 由此解得：当a=2，b=-1时，2(1)3a b -=--=；当a=0，b=-1时，0(1)1a b -=--=；当a=1，b=0时，101a b -=-=；当a=1，b=-2时，1(2)3a b -=--=；综上，-a b 的值为1或3．【点睛】本题考查绝对值的意义及有理数的减法运算，正确理解题意，采用数形结合思想解题是关键．25．（1）详见解析；（2）22.【分析】(1)根据长方体的展开图的特点以及沿长为3厘米的棱剪开这两个知识点画出图形即可；(2)根据上面画出的展开图求出每个长方形的面积，再加起来计算出结果即可.【详解】(1)如图所示(只要画出一个正确的即可).(2)包装盒的表面积:2×(2×1+2×3+1×3)=22(cm 2).【点睛】本题考查的是几何体的展开图，解决此类问题要知道长方体的展开图的特点.26．（1）乙、丙；（2）9、7．【解析】【分析】（1）结合主视图和左视图对甲、乙、丙逐一判断可得；（2）根据“俯视图打地基，主视图疯狂盖，左视图拆违章”判断可得．【详解】（1）这个几何体可以是图②甲、乙、丙中的乙、丙，故答案为：乙、丙；（2）这个几何体最多由9个小正方体构成，最少由7个小正方体构成．最少情况的一个俯视图如下：故答案为：9、7．【点睛】本题主要考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，主视图疯狂盖，左视图拆违章”就更容易得到答案．。

2014-2015学年上海市闵行区九校联考七年级（上）期末数学试卷一、选择题（本大题共6题，每题2分，满分12分）1．（2分）下列计算中正确的是（）A．﹣23•（﹣2）0=0 B．（﹣2x2y3）3=6x6y9C．（3m+n）•（﹣n+3m）=9m2﹣n2D．（﹣a）3÷（﹣a）=﹣a22．（2分）分式有意义，则（）A．x≠2 B．x≠﹣1 C．x≠2或x≠﹣1 D．x≠2且x≠﹣13．（2分）下列六个图形中既是轴对称图形，又是中心对称图形的有（）个线段、等边三角形、正方形、等腰梯形、圆、平行四边形．A．2个 B．3个 C．4个 D．5个4．（2分）把分式的a，b都扩大到原来的3倍，则分式的值（）A．扩大到原来的9倍B．扩大到原来的3倍C．不变D．缩小到原来的5．（2分）三个连续奇数，中间一个是k，则这三个数的积为（）A．k3﹣4k B．8k3﹣8k C．4k3﹣k D．8k3﹣2k6．（2分）已知a+b=4，ab=2，那么a2+b2的值是（）A．12 B．14 C．16 D．18二、填空题（本大题共12题，每题2分，满分24分）7．（2分）计算：2x•（﹣x）3=．8．（2分）计算：=．9．（2分）计算：（3a6b3﹣6ab5）÷（﹣3ab3）=．10．（2分）当x时，分式的值为0．11．（2分）因式分解：x2y﹣5xy+6y=．12．（2分）分解因式：a2﹣b2﹣2a+1=．13．（2分）将代数式2﹣1（x﹣y）﹣3表示成只含有正整数指数幂的形式为．14．（2分）已知：1纳米=0.00000001米，那么308纳米用科学记数法表示为米．15．（2分）如图，将△ABC沿CB方向平移3cm到△A′B′C′的位置，若BC=5cm，则B′C=cm．16．（2分）如图，把△ABC（其中∠ABC=60°）绕点B顺时针旋转得到△A′BC′，使得A′，B，C在同一直线上，那么这个旋转角的度数=．17．（2分）关于x的方程有增根，则a的值为．18．（2分）如图是用棋子摆成的“上”字，如果按照这样的规律继续摆下去，那么第n个“上”字需用枚棋子．三、简答题（本大题共7题，每题6分，满分42分）19．（6分）计算：÷2a．20．（6分）计算：．21．（6分）计算：．22．（6分）因式分解：18a2﹣50（a+b）2．23．（6分）分解因式：（a2﹣4a）2﹣8（a2﹣4a+6）24．（6分）解方程：．25．（6分）先化简，再求值：，其中x=﹣2．四、解答题（本大题共3题，第26、27每题7分，28题8分，满分22分）26．（7分）如图，已知△ABC、直线l及点A2．（1）请画出与△ABC关于直线l对称的△A1B1C1；（2）如果点A1与A2点关于某点成中心对称，请标出这个对称中心O，并画出与△A1B1C1关于点O成中心对称的△A2B2C2．[不写画法，保留画图痕迹]．27．（7分）甲、乙两人共同录入一份文件，甲需要录1800个字，乙需要录2000个字，已知乙的工作效率比甲高25%，完成上述任务的时间比甲少5min，甲、乙两人各花多少时间完成任务．28．（8分）如图，在直角三角形ABC中，∠B=90°，点M、N分别在边BA、BC 上，且BM=BN．（1）画出直角三角形ABC关于直线MN对称的三角形A′B′C′；（2）如果AB=a，BC=b，BM=x，用a、b、x的代数式分别表示三角形AMA'的面积S1和四边形AA′C′C的面积S，并化简．2014-2015学年上海市闵行区九校联考七年级（上）期末数学试卷参考答案与试题解析一、选择题（本大题共6题，每题2分，满分12分）1．（2分）下列计算中正确的是（）A．﹣23•（﹣2）0=0 B．（﹣2x2y3）3=6x6y9C．（3m+n）•（﹣n+3m）=9m2﹣n2D．（﹣a）3÷（﹣a）=﹣a2【解答】解：A、原式=﹣8×1=﹣8，错误；B、原式=﹣8x6y9，错误；C、原式=9m2﹣n2，正确；D、原式=（﹣a）2=a2，错误，故选C2．（2分）分式有意义，则（）A．x≠2 B．x≠﹣1 C．x≠2或x≠﹣1 D．x≠2且x≠﹣1【解答】解：由题意得：x2﹣x﹣2≠0，（x﹣2）（x+1）≠0，解得：x≠2或﹣1，故选：C．3．（2分）下列六个图形中既是轴对称图形，又是中心对称图形的有（）个线段、等边三角形、正方形、等腰梯形、圆、平行四边形．A．2个 B．3个 C．4个 D．5个【解答】解：线段、正方形、圆既是轴对称图形，又是中心对称图形，故选：B．4．（2分）把分式的a，b都扩大到原来的3倍，则分式的值（）A．扩大到原来的9倍B．扩大到原来的3倍C．不变D．缩小到原来的【解答】解：∵=，∴分式的值不变，故选C．5．（2分）三个连续奇数，中间一个是k，则这三个数的积为（）A．k3﹣4k B．8k3﹣8k C．4k3﹣k D．8k3﹣2k【解答】解：∵三个连续奇数，中间一个是k，∴较小的为：k﹣2，较大的奇数为：k+2，故这三个数的积为：k（k﹣2）（k+2）=k3﹣4k．故选：A．6．（2分）（2010秋•浦东新区校级期末）已知a+b=4，ab=2，那么a2+b2的值是（）A．12 B．14 C．16 D．18【解答】解：∵（a+b）2=a2+b2+2ab=16，即a2+b2+4=16，∴a2+b2=12．故选A．二、填空题（本大题共12题，每题2分，满分24分）7．（2分）计算：2x•（﹣x）3=﹣2x4．【解答】解：原式=2x•（﹣x3）=﹣2x4，故答案为：﹣2x48．（2分）计算：=4x2﹣2xy+y2．【解答】解：=4x2﹣2xy+y2，故答案为：4x2﹣2xy+y2．9．（2分）计算：（3a6b3﹣6ab5）÷（﹣3ab3）=﹣a5+2b2．【解答】解：原式=3a6b3÷（﹣3ab3）﹣6ab5÷（﹣3ab3）=﹣a5+2b2．故答案为：﹣a5+2b2．10．（2分）当x=﹣2时，分式的值为0．【解答】解：由题意，得4﹣x2=0，且3x﹣6≠0，解得x=﹣2，故答案为：=﹣2．11．（2分）因式分解：x2y﹣5xy+6y=y（x﹣2）（x﹣3）．【解答】解：原式=y（x2﹣5x+6）=y（x﹣2）（x﹣3），故答案为：y（x﹣2）（x﹣3）12．（2分）（2003•上海）分解因式：a2﹣b2﹣2a+1=（a+b﹣1）（a﹣b﹣1）．【解答】解：a2﹣b2﹣2a+1，=a2﹣2a+1﹣b2，=（a﹣1）2﹣b2，=（a+b﹣1）（a﹣b﹣1）．13．（2分）将代数式2﹣1（x﹣y）﹣3表示成只含有正整数指数幂的形式为．【解答】解：2﹣1（x﹣y）﹣3=，故答案为：14．（2分）已知：1纳米=0.00000001米，那么308纳米用科学记数法表示为 3.08×10﹣7米．【解答】解：308纳米用科学记数法表示为3.08×10﹣7米，故答案为：3.08×10﹣7．15．（2分）如图，将△ABC沿CB方向平移3cm到△A′B′C′的位置，若BC=5cm，则B′C=8cm．【解答】解：∵将△ABC沿CB方向平移3cm到△A′B′C′的位置，∴BB′=3cm，∵BC=5cm，∴B′C=BB′+BC=8cm．故答案为8．16．（2分）如图，把△ABC（其中∠ABC=60°）绕点B顺时针旋转得到△A′BC′，使得A′，B，C在同一直线上，那么这个旋转角的度数=120°．【解答】解：由旋转的性质得：∠A′BC′=∠ABC=60°，∴∠ABC′=180°﹣60°﹣60°=60°，∴∠ABA′=60°+60°=120°；即这个旋转角的度数为120°，故答案为：120°．17．（2分）关于x的方程有增根，则a的值为2．【解答】解：方程两边都乘（x﹣2），得x+x﹣2=a，即a=2x﹣2．分式方程的增根是x=2，∵原方程增根为x=2，∴把x=2代入整式方程，得a=2，故答案为：2．18．（2分）如图是用棋子摆成的“上”字，如果按照这样的规律继续摆下去，那么第n个“上”字需用（4n+2）枚棋子．【解答】解：∵第一个“上”字需用6枚棋子，第二个“上”字需用10枚棋子，第三个“上”字需用14枚棋子，∴依次多4个，∴第n个“上”字需用（4n+2）枚棋子．故答案为：（4n+2）．三、简答题（本大题共7题，每题6分，满分42分）19．（6分）（2005秋•上海期末）计算：÷2a．【解答】解：原式=（4a2﹣4ab+b2+4ab﹣b2）÷2a=4a2÷2a=2a．20．（6分）计算：．【解答】解：=[+]×=．21．（6分）计算：．【解答】解：原式=（）×（﹣）÷a4b4=a4b2×（﹣）÷a4b4=﹣a3b4÷a4b4=﹣．22．（6分）因式分解：18a2﹣50（a+b）2．【解答】解：原式=2[9a2﹣25（a+b）2]=2[3a+5（a+b）][3a﹣5（a+b）]=﹣2（8a+5b）（2a+5b）23．（6分）分解因式：（a2﹣4a）2﹣8（a2﹣4a+6）【解答】解：原式=（a2﹣4a）2﹣8（a2﹣4a）﹣48=（a2﹣4a+4）（a2﹣4a﹣12）=（a﹣2）2（a﹣6）（a+2）．24．（6分）解方程：．【解答】解：方程两边乘以（x+2）（x﹣2）得：1﹣x（x﹣2）=﹣（x+2）（x﹣2），解得：x=1.5，检验：x=1.5时，（x+2）（x﹣2）≠0，x=1.5是原方程的解：因此，原方程的解为x=1.5．25．（6分）先化简，再求值：，其中x=﹣2．【解答】解：原式=•=•=x+3，当x=﹣2时，原式=﹣2+3=1．四、解答题（本大题共3题，第26、27每题7分，28题8分，满分22分）26．（7分）如图，已知△ABC、直线l及点A2．（1）请画出与△ABC关于直线l对称的△A1B1C1；（2）如果点A1与A2点关于某点成中心对称，请标出这个对称中心O，并画出与△A1B1C1关于点O成中心对称的△A2B2C2．[不写画法，保留画图痕迹]．【解答】解：（1）如图，△A1B1C1即为所求；（2）如图，点O即为旋转中心，△A2B2C2即为所求．27．（7分）甲、乙两人共同录入一份文件，甲需要录1800个字，乙需要录2000个字，已知乙的工作效率比甲高25%，完成上述任务的时间比甲少5min，甲、乙两人各花多少时间完成任务．【解答】解：设甲每小时打字x个，则：﹣=，解得：x=2400个/小时，经检验x=2400是原方程的解．甲完成任务需要时间为=小时，即50分钟，乙完成任务需要50﹣5=45分钟，答：甲完成任务需要50分钟，乙完成任务需要45分钟．28．（8分）（2008秋•浦东新区期末）如图，在直角三角形ABC中，∠B=90°，点M、N分别在边BA、BC上，且BM=BN．（1）画出直角三角形ABC关于直线MN对称的三角形A′B′C′；（2）如果AB=a，BC=b，BM=x，用a、b、x的代数式分别表示三角形AMA'的面积S1和四边形AA′C′C的面积S，并化简．【解答】解：（1）△A′B′C′如图所示；（2）∵∠B=90°，BM=BN，∴△BMN是等腰直角三角形，∴△AMA′是等腰直角三角形，∴△AMA'的面积S1=（a﹣x）2=a2﹣ax+x2；四边形AA′C′C的面积S=△AMA′的面积+△CNC′的面积+△ABC的面积+△A′B′C′的面积﹣正方形BNB′M的面积，=（a﹣x）2+（b﹣x）2+ab+ab﹣x2，=a2+b2﹣ax﹣bx+ab．参与本试卷答题和审题的老师有：sks；王学峰；知足长乐；gbl210；zhjh；神龙杉；梁宝华；2300680618；MMCH；HLing；家有儿女；sjzx；gsls；lantin；caicl；zjx111；CJX；733599；星期八（排名不分先后）hu2017年3月9日。

一、选择题1．对于多项式534ax bx ++，当1x =时，它的值等于5，那么当1x =-时，它的值为（ ） A ．5-B ．5C ．3-D ．32．如图所示的数码叫“莱布尼茨调和三角形”，它们是由整数的倒数组成的，第n 行有n 个数，且两端的数均为1n，每个数是它下一行左右相邻两数的和，则第8行第3个数（从左往右数）为（ ）A ．160B ．1168C ．1252D ．12803．有依次排列的3个数：3，9，6，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，3-，6，这称为第一次操作：做第二次同样的操作后也可产生一个新数串：3，3，6，3．9，12-，3-，9，6，继续依次操作下去，问：从数串3，9，6开始操作第200次以后所产生的那个新数串的所有数之和是（ ） A ．600B ．618C ．680D ．7184．如图是由“○”组成的龟图，则第10个龟图中“○”的个数是（ ）A ．77B ．90C ．95D ．1165．如图，数轴上A ，B ，C 三点所表示的数分别为a ，b ，c ，且AB BC =．如果有0,0,0a b b c a c +<+>+<，那么该数轴原点0的位置应该在（ ）A ．点A 的左边B ．点A 与B 之间C ．点B 与C 之间D ．点C 的右边6．某地一天早晨的气温是2-℃，中午温度上升了12℃，半夜又下降了8℃，则半夜的气温是（）-℃B．6-℃C．2℃D．6℃A．107．如图是由5个大小相同的正方体组成的几何体，则该几何体从正面看得到的平面图形是（）A．B．C．D．8．如图所示的几何体的俯视图是（）A．B．C．D．9．如图是由几个相同的小正方体组成的立体图形的俯视图，图上的数字表示该位置上小正方体的个数，这个立体图形的左视图是（）A．B．C．D．10．下列各图经过折叠能围成一个正方体的是（）A．B．C．D ．11．有理数p ，q ，r ，s 在数轴上的对应点的位置如图所示．若10p r -=，12p s -=，9q s -=，则q r -的值是（ ）A ．5B ．6C ．7D ．1012．辽宁男篮夺冠后，从4月21日至24日各类媒体关于“辽篮CBA 夺冠”的相关文章达到810000篇，将数据810000用科学记数法表示为（ ） A ．40.8110⨯B ．50.8110⨯C ．48.110⨯D ．58.110⨯二、填空题13．两堆棋子，将第一堆的3个棋子移动到第二堆之后，现在第二堆的棋子数是第一堆棋子数的3倍，设第一堆原有m 个棋子，则第二堆的棋子原有_______个． 14．如图所示，将形状大小完全相同的“”按照一定的规律摆成下列图形：第1幅图中“”的个数为1a ，第2幅图中“”的个数为2a ，第3幅图中“”的个数为3a ，…，以此类推．（1）按照图中规律，5a =____________； （2）12320201111a a a a ++++=____________．15．面对2020年突如其来的新冠疫情，党和国家及时采取“严防严控”措施，并对新冠患者全部免费治疗，据统计共投入约21亿元资金，21亿用科学记数法表示为______． 16．如图，是北京S1线地铁的分布示意图，其中桥户营、四道桥、金安桥、苹果园四站在同一条直线上．如果在图中以正东为正方向建立数轴，桥户营站、苹果园站表示的数分别是4-，2，那么金安桥站表示的数是___________．17．国家统计局刚刚发布数据，初步核算，2020年全年国内生产总值为1015986亿元，将1015986科学记数法可以表示为___．18．某班数学活动小组的同学用纸板制作长方体包装盒，其平面展开图和相关尺寸如下，其中阴影部分为内部粘贴角料，（单位：mm ）.则此长方体包装盒的体积是___________.19．正方体切去一块，可得到如图几何体，这个几何体有______条棱．20．如图，若要使图中平面展开图折叠成正方体后，相对面上两个数字之和为6，则x ﹣y=________ ．三、解答题21．已知A ＝2x 2﹣6ax+3，B ＝﹣7x 2﹣8x ﹣1，按要求完成下列各小题． （1）当a ＝﹣2时，求A ﹣3B 的结果．（2）若A+B 的结果中不存在含x 的一次项，求a 的值．22．有一块长为m 米，宽为n 米的长方形ABCD 布料（AB DC =，AD BC =，90A B C D ∠=∠=∠=∠=︒），14EC DG DH BC ===，13CF CD =，某裁缝师傅在长方形布料的右上角和右下角分别剪下一个如图所示的扇形和一个小长方形．（1）请用含m 、n 的式子表示剩余布料的面积；（2）若该布料每平方米32元，当9m =，6n =时，求（1）中剩余布料的总价为多少元？（π取3，结果保留整数）23．如图，已知数轴上A 、B 两点所表示的数分别为﹣2和6 （1）求线段AB 的长；（2）已知点P 为数轴上点A 左侧的一个动点，且M 为PA 的中点，N 为PB 的中点．请你画出图形，并探究MN 的长度是否发生改变？若不变，求出线段MN 的长；若改变，请说明理由．24．计算（1）()()43526⨯--⨯-+； （2）()2202011336⎡⎤--⨯--⎣⎦．25．图中所示是一个由小正方体搭成的几何体的俯视图，小正方体中的数字表示该位置的小正方体的个数，请分别画出该几何体的主视图和左视图．26．在水平的桌面上，由若干个完全相同棱长为10cm 的小正方体堆成一个几何体，如图所示．（1）请你在方格纸中分别画出这个几何体的主视图、左视图和俯视图；（2）若现在手头还有一些相同的小正方体，如果保持这个几何体的左视图和俯视图不变，在这个几何体上最多可以添加多少个小正方体？（3）若给该几何体露在外面的面喷上红漆（不含几何体的底面），则需要喷漆的面积是多少cm2？【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】把x=1代入多项式ax5+bx3+4=5，得a+b=1，把x=-1代入ax5+bx3+4得原式=-a-b+4=-(a+b)+4，根据前面的结果即可求出最后的值．【详解】解：把x=1代入多项式ax5+bx3+4=5，得a+b+4=5，即a+b=1，把x=-1代入ax5+bx3+4得，原式=-a-b+4=-(a+b)+4=3．∴多项式ax5+bx3+4当x=-1时的值为3．故选：D．【点睛】本题考查了代数式的求值，解题时要利用x的值是1或-1的特点，代入原式，将（a+b）作为一个整体来看待．2．B解析：B 【分析】根据给出的数据可得：第n行的第三个数等于112n n--的结果再乘11n-，再把n的值代入即可得出答案．【详解】解：根据给出的数据可得：第n行的第三个数等于112n n--的结果再乘11n-，则第8行第3个数（从左往右数）为1111 82881168⎛⎫-⨯=⎪--⎝⎭；故选：B．【点睛】本题考查与实数运算相关的规律题，通过阅读题意归纳总结有关规律再运算是解题关键．3．B解析：B【分析】首先具体地算出每一次操作以后所产生的那个新数串的所有数之和，从中发现规律，进而得出操作第200次以后所产生的那个新数串的所有数之和．【详解】解：设A=3，B=9，C=6，操作第n次以后所产生的那个新数串的所有数之和为S n．n=1时，S1=A+（B-A）+B+（C-B）+C=B+2C=（A+B+C）+1×（C-A），n=2时，S2=A+（B-2A）+（B-A）+A+B+（C-2B）+（C-B）+B+C=-A+B+3C=（A+B+C）+2×（C-A），…故n=200时，S200=（A+B+C）+200×（C-A）=-199A+B+201C=-199×3+9+201×6=618，故选：B．【点睛】本题考查找规律-数字的变化，本题中理解每一次操作的方法是前提，得出每一次操作以后所产生的那个新数串的所有数之和的规律是关键．4．C解析：C【分析】先求出第1、2、3、4个图中“○”的个数，再归纳类推出一般规律，由此即可得出答案．【详解】观察图可知，第1个图中“○”的个数是5510=+⨯，第2个图中“○”的个数是7521=+⨯，第3个图中“○”的个数是11532=+⨯，第4个图中“○”的个数是17543=+⨯，归纳类推得：第n 个图中“○”的个数是5(1)n n +-，其中n 为正整数， 则第10个图中“○”的个数是510995+⨯=， 故选：C ． 【点睛】本题考查了用代数式表示图形的规律，依据已知图形，正确归纳类推出一般规律是解题关键．5．C解析：C 【分析】根据各个选项的情况，去分析a ，b ，c 三个数的正负，判断选项的正确性． 【详解】解：若原点在点A 左边，则0a >、0b >、0c >，就不满足0a b +<，故A 选项错误； 若原点在点A 与点B 之间，则0a <、0b >、0c >，且a c <，就不满足0a c +<，故B 选项错误；若原点在点B 与点C 之间，则0a <、0b <、0c >，条件都可以满足，故C 选项正确； 若原点在点C 右边，则0a <、0b <、0c <，就不满足0b c +>，故D 选项错误． 故选：C ． 【点睛】本题考查数轴，解题的关键是根据数轴上点的位置判断式子的正负．6．C解析：C 【分析】温度上升是加法，温度下降是减法，据此列式计算即可． 【详解】由题意得：-2+12-8=2（℃）， 故选：C ． 【点睛】此题考查有理数加减法解决实际问题，正确理解上升与下降的含义列算式计算是解题的关键．7．A解析：A 【解析】 【分析】从正面看到的图叫做主视图，从左面看到的图叫做左视图，从上面看到的图叫做俯视图．根据图中正方体摆放的位置判定则可． 【详解】从正面看，主视图有三列，正方体的数量分别是2、1、1． 故选A ．【点睛】本题考查了三种视图中的主视图，比较简单．8．C解析：C【解析】【分析】根据从上面看得到的图形是俯视图，可得俯视图．【详解】从上面看是三个等长的矩形，符合题意的是C，故选C．【点睛】本题考查了简单组合体的三视图，从上面看得到的图形是俯视图．9．A解析：A【解析】【分析】根据从左边看得到的图形是左视图，可得答案．【详解】该几何体的左视图为故选A．【点睛】本题考查了简单组合体的三视图，从左边看得到的图形是左视图．10．D解析：D【分析】直接根据平面图形的折叠状况逐项判定即可．【详解】解：A、折叠后第一行两个面无法折起来，不能折成正方体；B、折叠后缺少上、下两个底面，不能折成正方体；C、折叠后有两个面重合，不能折成个正方体；D、可以折叠成一个正方体．故答案为D．【点睛】本题主要考查了展开图折叠成几何体，掌握平面图形的折叠和较好的空间想象能力是解答本题的关键．11．C解析：C【分析】根据绝对值的几何意义，将|p−r|＝10，|p−s|＝12，|q−s|＝9转化为两点间的距离，进而可得q、r两点间的距离，即可得答案．【详解】解：根据绝对值的几何意义，由|p−r|＝10，|p−s|＝12，|q−s|＝9得：|p−q|＝|p−s|－|q−s|＝3，|r−s|＝|p−s|－|p−r|＝2∴|q−r|＝|p−s|－|p−q|－|r−s|＝12－3－2＝7．故选：C．【点睛】本题考查了绝对值的几何意义，解题的关键是运用数形结合的数学思想表示出数轴上两点间的距离．12．D解析：D【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．【详解】810000=5，8.110故选：D．【点睛】此题考察科学记数法，注意n的值的确定方法，当原数大于10时，n等于原数的整数数位减1，按此方法即可正确求解．二、填空题13．3m-12【分析】第一堆的3个棋子移动后有（m-3）个表示出第二堆的数量然后减去3即可【详解】解：第一堆原有m个棋子移动后有（m-3）个则它的三倍为3（m-3）即第二堆的现有棋子为3（m-3）第二堆解析：3m-12【分析】第一堆的3个棋子移动后有（m-3）个，表示出第二堆的数量，然后减去3即可．【详解】解：第一堆原有m个棋子，移动后有（m-3）个，则它的三倍为3（m-3），即第二堆的现有棋子为3（m-3），第二堆的棋子原有棋子为：3（m-3）-3=（3m-12）个．【点睛】本题考查了列代数式和整式计算，解题关键是依据问题中与数量有关的词语，列出代数式，并进行计算．14．30；【分析】（1）先根据已知图形得出an ＝n （n ＋1）进而即可得到的值；（2）利用裂项化简可得答案【详解】（1）解：由图形知a1＝1×2a2＝2×3a3＝3×4…∴an ＝n （n ＋1）∴a5=5×6解析：30；20202021 【分析】（1）先根据已知图形得出a n ＝n （n ＋1），进而即可得到5a 的值；（2）利用111(1)1n n n n =-++裂项化简，可得答案． 【详解】（1）解：由图形知a 1＝1×2，a 2＝2×3，a 3＝3×4，…，∴a n ＝n （n ＋1），∴a 5=5×6=30，故答案是：30；（2）12320201111a a a a ++++ =111112233420202021++++⨯⨯⨯⨯ =1111111112342021232020-+-+-++- =112021- =20202021， 故答案是：20202021． 【点睛】本题主要考查图形的变化规律，解题的关键是根据已知图形得出a n ＝n （n ＋1）及111(1)1n n n n =-++． 15．【分析】科学记数法的表示形式为a×10n 的形式其中1≤|a|＜10继而用此形式来表示此数即可；【详解】∵21亿=2100000000∴故答案为：【点睛】本题考查了科学记数法的表示形式正确掌握科学记数解析：92.110⨯【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，继而用此形式来表示此数即可；【详解】∵21亿=2100000000∴92100000000=2.110⨯ ，故答案为：92.110⨯ ．【点睛】本题考查了科学记数法的表示形式，正确掌握科学记数法的表示形式是解题的关键． 16．0【分析】由桥户营站苹果园站表示的数分别是2计算出两点之间的距离为6求出一个单位长度表示的数是2即可得到答案【详解】∵桥户营站苹果园站表示的数分别是2∴桥户营站与苹果园站的距离是2-（-4）=6∵桥解析：0【分析】由桥户营站、苹果园站表示的数分别是4-，2，计算出两点之间的距离为6，求出一个单位长度表示的数是2，即可得到答案．【详解】∵桥户营站、苹果园站表示的数分别是4-，2，∴桥户营站与苹果园站的距离是2-（-4）=6，∵桥户营站与苹果园站之间共有三个单位长度，∴每个单位长度表示632÷=，∴金安桥表示的数是2-2=0，故答案为：0．【点睛】此题考查数轴上两点之间的距离，数轴上点的平移规律，有理数的加减法计算，掌握数轴上两点之间的距离公式是解题的关键．17．【分析】科学记数法的表示形式为a×10n 的形式其中1≤|a|＜10n 为整数确定n 的值时要看把原数变成a 时小数点移动了多少位n 的绝对值与小数点移动的位数相同当原数绝对值＞1时n 是正数；当原数的绝对值＜解析：61.01598610⨯【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数．【详解】1015986=61.01598610⨯，故答案为：61.01598610⨯．【点睛】此题考察科学记数法，注意n 的值的确定方法，当原数大于10时，n 等于原数的整数数位减1，按此方法即可正确求解．18．3182000mm19．1220．-10三、解答题21．（1）23x 2+36x+6；（2）a ＝﹣43 【分析】（1）先去括号，然后合并同类项，再把a ＝﹣2代入计算即可求解；（2）先代入计算，合并同类项后，根据A+B 结果中不含x 的一次项，得到6a+8＝0，解方程即可求解．【详解】解：（1）∵A ＝2x 2﹣6ax+3，B ＝﹣7x 2﹣8x ﹣1，a ＝﹣2，∴A ﹣3B ，＝2x 2﹣6ax+3+21x 2+24x+3，＝23x 2+（24﹣6a ）x+6，＝23x 2+36x+6；（2）∵A ＝2x 2﹣6ax+3，B ＝﹣7x 2﹣8x ﹣1，∴A+B ＝2x 2﹣6ax+3﹣7x 2﹣8x ﹣1＝﹣5x 2﹣（6a+8）x+2，由A+B 结果中不含x 的一次项，得到6a+8＝0，解得：a ＝﹣43． 【点睛】本题主要考查了整式化简求值，准确计算是解题的关键． 22．（1）2111264mn m π-平方米；（2）1462元 【分析】（1）用大长方形ABCD 的面积减去扇形和小长方形的面积即可；（2）将m=9，n=6代入，再乘以32即可得解．【详解】解：（1）∵长方形ABCD 的长为m ，宽为n ，即BC=m ，AB=n ， ∴144m EC D H G D BC ====，133n CF CD ==， ∴剩余布料的面积=214443m m n mn π⎛⎫-⨯-⨯ ⎪⎝⎭=2111264mn m π-平方米； （2）∵9m =，6n =，该布料每平方米32元， ∴211321264mn m π⎛⎫-⨯ ⎪⎝⎭=2119693321264⎛⎫⨯⨯⨯-⨯ ⎪⎝⎭=1462元，∴剩余布料的总价为1462元．【点睛】本题考查了列代数式，代数式求值，解题的关键是正确表示出剩余布料的面积． 23．（1）8；（2）见解析；MN 的长度不会发生改变，线段MN ＝4．【分析】（1）数轴上两点之间的距离等于较大数与较小数的差；（2）根据中点的意义，利用线段的和差可得出答案．【详解】解：（1）AB ＝|﹣2﹣6|＝8，答：AB 的长为8；（2）MN 的长度不会发生改变，线段MN ＝4，理由如下：如图，因为M 为PA 的中点，N 为PB 的中点，所以MA ＝MP ＝12PA ，NP ＝NB ＝12PB ， 所以MN ＝NP ﹣MP ＝12PB ﹣12PA ＝12（PB ﹣PA ） ＝12AB ＝12×8 ＝4．【点睛】本题考查了数轴上两点之间的距离，数轴上线段中点的意义，熟练掌握两点间距离计算方法，灵活运用中点的意义是解题的关键．24．（1）4；（2）0【分析】（1）根据有理数混合运算法则和顺序计算即可；（2）根据有理数混合运算法则和顺序计算即可．【详解】解：（1）原式()12106=-++()26=-+4=．（2）原式()11396=--⨯-()1166=--⨯- 110=-+=．【点睛】本题考查了有理数的混合运算，解题关键是熟练运用有理数运算法则，掌握正确的运算顺序．25．见解析【解析】【分析】根据题意可得，主视图有3列，每列小正方形数目分别为3，2，1；左视图有3列，每列小正方形数目分别为2，3，2，依此画出图形即可．【详解】如图所示：【点睛】本题考查了实物体的三视图．在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．26．（1）答案见解析；（2）3个；（3）3200cm 2【分析】（1）根据物体形状即可画出主视图、左视图和俯视图；（2）保持俯视图和左视图不变，可往第二列前面的几何体上放2个小正方体，后面的几何体上放1个小正方体；（3）利用几何体的形状求出其表面积即可，注意不含底面.【详解】解：（1）这个几何体的主视．．图和左视．．图如图：（2）保持俯视图和左视图不变，可往第二列前面的几何体上放2个小正方体，后面的几何体上放1个小正方体，故最多可再添加3个正方体，故答案为：3；（3）1010⨯⨯[（6+6）2⨯+6+2]=3200cm 2答：需要喷漆的面积是3200cm 2.【点睛】本题考查了三视图的画法．主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形；注意看到的用实线表示，看不到的用虚线表示．注意涂色面积指组成几何体的外表面积．。