中北大学机械电子工程信号与系统实验报告

信号与系统测试实训报告信号与系统测试实训报告一、引言在信号与系统的学习过程中，理论知识的掌握是非常重要的，但是对于学生来说，实际操作和实验测试同样重要。

本报告旨在总结信号与系统测试实训的过程、方法和结果，并对实训中遇到的问题进行分析和解决。

二、实验目的本次实验主要目的是通过使用各种仪器设备和软件工具，对不同类型的信号进行测试和分析，验证信号与系统理论知识，并培养学生动手能力和问题解决能力。

三、实验设备和软件1. 实验设备：- 函数发生器：用于产生各种类型的基本信号。

- 示波器：用于观测信号波形和频谱。

- 模拟滤波器：用于对信号进行滤波处理。

- 数字示波器：用于观测高频数字信号。

- 电脑：用于运行软件工具。

2. 软件工具：- MATLAB：用于信号处理与分析。

- Simulink：用于模拟系统响应。

四、实验步骤及结果1. 实验一：基本周期信号测试首先使用函数发生器产生正弦、方波、三角波等基本周期信号，然后用示波器观测信号波形，并通过MATLAB进行频谱分析。

实验结果显示，正弦信号的频谱主要集中在一个频率上，而方波和三角波的频谱则包含了多个谐波分量。

2. 实验二：连续时间系统测试使用函数发生器产生输入信号，经过模拟滤波器后，用示波器观测输出信号，并通过MATLAB进行系统响应分析。

实验结果显示，滤波器对输入信号进行了平滑处理，并且系统响应与理论预期相符。

3. 实验三：离散时间系统测试使用函数发生器产生离散时间序列输入信号，经过数字滤波器后，用数字示波器观测输出信号，并通过MATLAB进行系统响应分析。

实验结果显示，数字滤波器对输入信号进行了去噪处理，并且系统响应与理论预期相符。

五、实验问题与解决1. 问题一：示波器观测到的信号与理论预期不符。

解决方法：首先检查示波器的设置是否正确，并确保连接线路无误。

检查函数发生器的输出是否稳定和准确。

检查示波器通道的控制参数是否正确设置。

2. 问题二：MATLAB频谱分析结果不准确。

工业大学校区《信号与系统》课程实验报告专业班级学生《信号与系统》课程实验报告一实验名称一阶系统的阶跃响应姓名系院专业班级学号实验日期指导教师成绩一、实验目的1．熟悉一阶系统的无源和有源电路；2．研究一阶系统时间常数T的变化对系统性能的影响；3．研究一阶系统的零点对系统响应的影响。

二、实验原理1．无零点的一阶系统无零点一阶系统的有源和无源电路图如图2-1的(a)和(b)所示。

它们的传递函数均为：10.2s1G(s)＝+(a) 有源(b) 无源图2-1 无零点一阶系统有源、无源电路图2．有零点的一阶系统(|Z|<|P|)图2-2的(a)和(b)分别为有零点一阶系统的有源和无源电路图，它们的传递函数为：10.2s1)0.2(sG(s)++=，⎪⎪⎪⎪⎭⎫⎝⎛++=S611S161G(s）(a) 有源(b) 无源图2-2 有零点(|Z|<|P|)一阶系统有源、无源电路图3．有零点的一阶系统(|Z|>|P|)图2-3的(a)和(b)分别为有零点一阶系统的有源和无源电路图，它们的传递函数为：1s10.1sG(s)＝++(a) 有源(b) 无源图2-3 有零点(|Z|>|P|)一阶系统有源、无源电路图三、实验步骤1．打开THKSS-A/B/C/D/E型信号与系统实验箱，将实验模块SS02插入实验箱的固定孔中，利用该模块上的单元组成图2-1(a)(或(b))所示的一阶系统模拟电路。

2．实验线路检查无误后，打开实验箱右侧总电源开关。

3．将“阶跃信号发生器”的输出拨到“正输出”，按下“阶跃按键”按钮，调节电位器RP1，使之输出电压幅值为1V，并将“阶跃信号发生器”的“输出”端与电路的输入端“Ui”相连，电路的输出端“Uo”接到双踪示波器的输入端，然后用示波器观测系统的阶跃响应，并由曲线实测一阶系统的时间常数T。

4．再依次利用实验模块上相关的单元分别组成图2-2(a)(或(b))、2-3(a)(或(b))所示的一阶系统模拟电路，重复实验步骤3，观察并记录实验曲线。

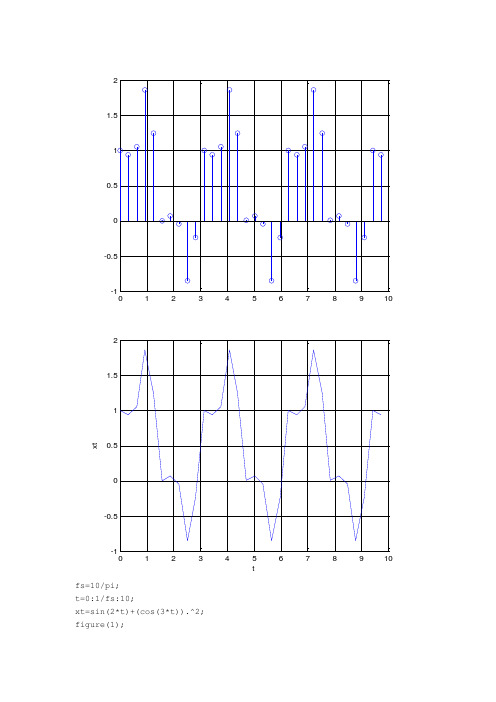
fs=10/pi; t=0:1/fs:10;xt=sin(2*t)+(cos(3*t)).^2; figure(1);012345678910012345678910-1-0.50.511.52tx tstem(t,xt);grid onfigure(2);plot(t,xt);grid onxlabel('t')ylabel('xt')012345678910fs=100/pi; t=0:1/fs:10;xt=sin(2*t)+(cos(3*t)).^2; figure(1); stem(t,xt,'*') grid on figure(2); plot(t,xt); grid on xlabel('t') ylabel('xt')012345678910-1-0.50.511.52tx tclear; close all ; dt=0.01; dw=0.1; t=-10:dt:10; w=-4*pi:dw:4*pi; x=sin(2*t)+cos(3*t).^2; X=x*exp(-j*t'*w)*dt; A=abs(X); plot(w,A);-15-10-551015012345678910请输入系统方程左面y 的系数[1 1 25] 请输入系统方程右面x 的系数[1 0]请输入系统方程左面y 的系数[1 1] 请输入系统方程右面x 的系数[1 -1]5100.51Magnitude responseFrequency in rad/sec 0510-2-1012Phase responseFrequency in rad/sec5100.51Real part of frequency responseFrequency in rad/sec510-0.50.5Imaginary part of frequency response Frequency in rad/sec5101111Magnitude responseFrequency in rad/sec 051001234Phase responseFrequency in rad/sec510-1-0.500.51Real part of frequency responseFrequency in rad/sec5100.51Imaginary part of frequency response Frequency in rad/sec请输入系统方程左面y 的系数[1 10 48 148 306 401 262] 请输入系统方程右面x 的系数[262]程序如下：clear alla=input('请输入系统方程左面y 的系数'); b=input('请输入系统方程右面x 的系数'); [H,w]=freqs(b,a); Hm=abs(H); phai=angle(H); Hr=real(H); Hi=imag(H); subplot(221)plot(w,Hm),grid on ,title('Magnitude response'),xlabel('Frequency in rad/sec') subplot(223)plot(w,phai),grid on ,title('Phase response'),xlabel('Frequency in rad/sec') subplot(222)plot(w,Hr),grid on ,title('Real part of frequency response'),xlabel('Frequency in rad/sec') subplot(224)plot(w,Hi),grid on , title('Imaginary part of frequency response'),xlabel('Frequency in rad/sec')51000.51Magnitude responseFrequency in rad/sec 0510-4-2024Phase responseFrequency in rad/sec510-1-0.500.51Real part of frequency responseFrequency in rad/sec510-1-0.500.51Imaginary part of frequency response Frequency in rad/secclear; close all ; dt=0.01; t=0:dt:100; x=sin(t)+sin(8*t); b=[262];a=[1 10 48 148 306 401 262]; sys=tf(b,a); h=impulse(sys,t); y=lsim(sys,x,t); subplot(321);plot(t,x); subplot(323);plot(t,h); subplot(325);plot(t,y); dw=0.1;w=-4*pi:dw:4*pi; X=x*exp(-j*t'*w)*dt; A=abs(X);[H,w]=freqs(b,a,w); Hm=abs(H); B=A.*Hm;subplot(322);plot(w,A); subplot(324);plot(w,Hm); subplot(326);plot(w,B);050100-202050100-0.500.51050100-101-20-10010200102030-20-10102000.51-20-1010200102030。

信号与系统实验报告好啦，今天咱们来聊聊信号与系统实验报告。

这话题有点儿“高大上”，但咱们不妨来点轻松的，把它聊得有趣一些。

先说说信号是什么。

信号其实就是一种信息传递的方式，可能是声音，可能是光，甚至是你手机屏幕上刷过的每一条消息。

简单来说，信号就是承载着信息的载体。

你看，像咱们日常生活中，电台广播，手机接收到的短信，甚至你家电视里放的广告，它们都是信号的一种表现形式。

啊，听起来有点儿复杂吧？其实不难，就像你一收到朋友发来的微信，手机屏幕上跳出来的就是一个信号。

信号怎么才能“正常工作”呢？这就得说到“系统”了。

系统呢，说白了就是一套能够处理信号的工具。

你想啊，信号如果没有一个合适的“平台”去接收、传递和处理，那就变得一团乱麻了。

就像是你给朋友发了个短信，但他手机坏了，信号接收不进去，结果信息就白发了。

系统在这里就相当于是一个“修理工”，它能让信号顺利通过、准确无误地到达目的地。

接下来说说我们在实验中的“主角”——信号与系统。

你看，实验嘛，往往让我们有点“心慌慌”。

不过，信号与系统的实验其实有点像玩拼图。

你得先弄清楚信号的各种“形状”，然后用系统去“加工处理”，让它变得符合要求。

比如，咱们常用的模拟信号，它是一个连续的过程，类似于咱们生活中的声音一样，是没有间断的。

而数字信号呢，就像你手机屏幕上的数字，离散的，断断续续的。

每种信号都有自己独特的“脾气”，你得了解它们的特点，才能搭配合适的系统。

你要是觉得这些实验有点儿复杂，那就来点儿幽默的比喻吧。

信号就像是你的朋友说的话，而系统就是你听的耳朵。

朋友说话的声音，可能因为距离远近，语速快慢，甚至音量的大小而有所不同。

系统就得根据这些变化去处理，比如调节音量、清晰度，甚至过滤掉不必要的噪声。

你想想，假如你能在嘈杂的环境下清楚地听到朋友的声音，那就是系统给你提供的帮助。

信号与系统的实验，就是在这种“听”和“说”之间找到平衡点。

咱们得说说实验中的一些基本工具了。

信号与系统实验报告目录1. 内容概要 (2)1.1 研究背景 (3)1.2 研究目的 (4)1.3 研究意义 (4)2. 实验原理 (5)2.1 信号与系统基本概念 (7)2.2 信号的分类与表示 (8)2.3 系统的分类与表示 (9)2.4 信号与系统的运算法则 (11)3. 实验内容及步骤 (12)3.1 实验一 (13)3.1.1 实验目的 (14)3.1.2 实验仪器和设备 (15)3.1.4 实验数据记录与分析 (16)3.2 实验二 (16)3.2.1 实验目的 (17)3.2.2 实验仪器和设备 (18)3.2.3 实验步骤 (19)3.2.4 实验数据记录与分析 (19)3.3 实验三 (20)3.3.1 实验目的 (21)3.3.2 实验仪器和设备 (22)3.3.3 实验步骤 (23)3.3.4 实验数据记录与分析 (24)3.4 实验四 (26)3.4.1 实验目的 (27)3.4.2 实验仪器和设备 (27)3.4.4 实验数据记录与分析 (29)4. 结果与讨论 (29)4.1 实验结果汇总 (31)4.2 结果分析与讨论 (32)4.3 结果与理论知识的对比与验证 (33)1. 内容概要本实验报告旨在总结和回顾在信号与系统课程中所进行的实验内容，通过实践操作加深对理论知识的理解和应用能力。

实验涵盖了信号分析、信号处理方法以及系统响应等多个方面。

实验一：信号的基本特性与运算。

学生掌握了信号的表示方法，包括连续时间信号和离散时间信号，以及信号的基本运算规则，如加法、减法、乘法和除法。

实验二：信号的时间域分析。

在本实验中，学生学习了信号的波形变换、信号的卷积以及信号的频谱分析等基本概念和方法，利用MATLAB工具进行了实际的信号处理。

实验三：系统的时域分析。

学生了解了线性时不变系统的动态响应特性，包括零状态响应、阶跃响应以及脉冲响应，并学会了利用MATLAB进行系统响应的计算和分析。

信号与系统实验报告5信号与系统实验报告5引言信号与系统是电子工程领域中的重要学科，它研究信号的产生、传输和处理过程，以及系统对信号的响应和影响。

在本次实验中，我们将探索信号与系统的一些基本概念和实际应用。

一、信号的分类与特性信号是信息的载体，可以是连续的或离散的。

根据信号的性质，我们可以将其分为模拟信号和数字信号。

模拟信号是连续变化的，可以用连续函数表示；而数字信号是离散的，以数字的形式表示。

在实验中，我们使用了示波器观察了不同类型的信号。

通过观察信号的波形、频谱和功率谱密度等特性，我们能够了解信号的频率、幅度和相位等信息。

二、系统的响应与特性系统是对信号进行处理或传输的装置或环境。

系统可以是线性的或非线性的，可以是时不变的或时变的。

在实验中，我们使用了滤波器作为系统模型来研究系统的响应和特性。

通过改变滤波器的截止频率，我们观察到不同频率的信号在系统中的响应差异。

我们还通过调整系统参数，如增益和相位延迟，来研究系统的线性性质和时不变性质。

三、信号与系统的应用信号与系统在现实生活中有着广泛的应用。

在通信领域，我们可以利用信号与系统的知识来设计和优化无线电、光纤通信和卫星通信等系统。

在音频处理领域，我们可以利用信号与系统的方法来实现音频的降噪、音效增强和语音识别等功能。

此外，信号与系统在图像处理、生物医学工程和控制系统等领域也有着重要的应用。

通过对信号的采集、处理和分析，我们能够从中提取有用的信息，并对系统进行建模和控制。

结论通过本次实验，我们深入了解了信号与系统的基本概念和实际应用。

我们学习了信号的分类与特性，系统的响应与特性，以及信号与系统在各个领域的应用。

这些知识不仅对我们理解和应用电子工程学科具有重要意义，也为我们今后的学习和研究提供了坚实的基础。

信号与系统是一门复杂而又有趣的学科，它涉及了数学、物理和工程等多个领域的知识。

通过不断学习和实践，我们能够更好地理解和应用信号与系统的理论，为解决实际问题提供有效的方法和工具。

信号系统实验报告信号系统实验报告引言信号系统是电子工程中的重要组成部分，它对于信息的传输和处理起着关键作用。

在本次实验中，我们将通过实际操作和测量来探索信号系统的性质和特点。

本报告将详细介绍实验的目的、原理、实验步骤和结果，以及对实验结果的分析和讨论。

实验目的本次实验的主要目的是研究信号系统的频率响应特性和线性时不变系统的特性。

通过测量和分析信号在系统中的传输和处理过程，我们可以了解信号系统的频率响应、幅频特性和相频特性，以及信号在系统中的失真情况。

实验原理1. 频率响应特性频率响应是指信号系统对不同频率信号的传输和处理能力。

通过输入不同频率的正弦信号，我们可以测量输出信号的幅度和相位，从而绘制出信号系统的幅频特性曲线和相频特性曲线。

2. 线性时不变系统特性线性时不变系统具有两个重要特性：线性性和时不变性。

线性性意味着系统对输入信号的响应是线性的，即输入信号的线性组合会导致输出信号的线性组合。

时不变性意味着系统的性质不随时间变化而改变，即系统对于不同时间的相同输入信号会有相同的输出响应。

实验步骤1. 准备工作在进行实验之前，我们需要准备好实验所需的设备和材料，包括信号发生器、示波器、电阻、电容等。

2. 测量频率响应特性首先，我们将信号发生器的输出连接到信号系统的输入端，然后将示波器的输入连接到信号系统的输出端。

接下来，我们通过改变信号发生器的频率，测量并记录示波器上的输出信号的幅度和相位。

最后，我们可以绘制出信号系统的幅频特性曲线和相频特性曲线。

3. 测量线性时不变系统特性为了测量线性时不变系统的特性，我们需要输入不同的信号，并观察输出信号的响应。

通过输入正弦信号、方波信号和脉冲信号，我们可以观察到信号系统对不同类型信号的响应特点，并判断系统是否具有线性性和时不变性。

实验结果通过实验测量和分析，我们得到了信号系统的频率响应特性曲线和线性时不变系统的特性。

在频率响应特性曲线中，我们可以观察到系统对不同频率信号的传输和处理能力。

实验一常用信号的观察一、任务与目标1. 了解常用信号的波形和特点。

2. 了解相应信号的参数。

3. 学习函数发生器和示波器的使用。

二、实验过程1．接通函数发生器的电源。

2．调节函数发生器选择不同的频率的正弦波、方波、三角波、锯齿波及组合函数波形，用示波器观察输出波形的变化。

三、实验报告为幅值)(x为时间，y100Hz 4V 正弦波y=2sin(628x-π/2)第1 页共32 页100Hz 4V 方波y=2 t=(2n-1)x*0.0025~(2n+1)x*0.0025 x为奇y=-2 t=(2n-1)x*0.0025~(2n+1)x*0.0025 x为偶100Hz 4V 锯齿波100Hz 4V 三角波由50Hz的正弦波和100Hz正弦波组合的波形y=0.2sin(628x)+0.1sin(314x)实验二零输入、零状态及完全响应一、实验目标1．通过实验，进一步了解系统的零输入响应、零状态响应和完全响应的原理。

2．学习实验电路方案的设计方法——本实验中采用用模拟电路实现线性系统零输入响应、零状态响应和完全响应的实验方案。

二、原理分析实验指导书P4三、实验过程1、接通电源；2、闭合K2，给电容充电，断开K2闭合K3，观察零输入响应曲线；3、电容放电完成后，断开K3，闭合K1，观察零状态响应曲线；4、断开K1，闭合K3，再次让电容放电，放电完成后断开K3闭合K2，在电容电压稳定于5V后断开K2，闭合K1，观察完全响应曲线。

四、实验报告上图为零输入响应、零状态响应和完全响应曲线。

五、实验思考题系统零输入响应的稳定性与零状态响应的稳定性是否相同？为什么？答：相同。

因为系统零输入响应和零状态响应稳定的充分必要条件都是系统传递函数的全部极点si(i=1,2,3,…,n)，完全位于s平面的左半平面。

实验五无源与有源滤波器一、实验原理实验指导书P14二、实验目的1．了解无源和有源滤波器的种类、基本结构及其特性；2．分析和对比无源和有源滤波器的滤波特性；3．掌握无源和有源滤波器参数的设计方法。