2017年全国卷3文科数学精彩试题及参考问题详解

实用文档文案大全绝密★启用前2017年普通高等学校招生全国统一考试文科数学本试卷共5页，满分150分。

考生注意：1．答卷前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，监考员将试题卷和答题卡一并交回。

一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A=??|2xx?，B=??|320xx??，则A．AB=3|2xx??????? B．AB??C．AB3|2xx???????? D．AB=R2．为评估一种农作物的种植效果，选了n块地作试验田.这n块地的亩产量（单位：kg）分别为x1，x2，…，x n，下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是A．x1，x2，…，x n的平均数 B．x1，x2，…，x n的标准差C．x1，x2，…，x n的最大值 D．x1，x2，…，x n的中位数3．下列各式的运算结果为纯虚数的是A．i(1+i)2 B．i2(1-i)C．(1+i)2 D．i(1+i)4．如图，正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是A14 Bπ8C12 Dπ 4实用文档文案大全5．已知F是双曲线C：x2-23y=1的右焦点，P是C上一点，且PF与x 轴垂直，点A的坐标是(1,3).则△APF的面积为A13 B1 2 C2 3 D3 26．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直接AB与平面MNQ不平行的是7．设x，y满足约束条件33,1,0,xyxyy??????????则z=x+y的最大值为A．0 B．1 C．2 D．38．.函数sin21cosxyx??的部分图像大致为9．已知函数()lnln(2)fxxx???，则A．()fx在（0,2）单调递增 B．()fx在（0,2）单调递减C．y=()fx的图像关于直线x=1对称 D．y=()fx的图像关于点（1,0）对称实用文档文案大全10．如图是为了求出满足321000nn??的最小偶数n，那么在和两个空白框中，可以分别填入A．A>1000和n=n+1 B．A>1000和n=n+2 C．A≤1000和n=n+1 D．A≤1000和n=n+211．△ABC的内角A、B、C的对边分别为a、b、c。

绝密★启封前2017全国卷Ⅲ高考压轴卷文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

注意事项： 1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2.第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。

3.考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

） 1．已知全集,U R =且{}{}2|12,|680,A x x B x x x =->=-+<则()U C A B 等于（A ）[1,4)- （B ）(2,3] （C ）(2,3) （D ）(1,4)-2.已知133iz i-=+（i 为虚数单位），则z 的共轭复数的虚部为（ ） (A)i - (B)i (C)1- (D)13袋中有五张卡片，其中红色卡片三张，标号分别为1,2,3，蓝色卡片两张，标号分别为1,2，从以上五张卡片中任取两张，则这两张卡片颜色不同且标号之和不小于4的概率为（A ）110 （B ）310 （C ）25 （D ）7104.在射击训练中，某战士射击了两次，设命题p 是“第一次射击击中目标”，命题q 是“第二次射击击中目标”，则命题“两次射击中至少有一次没有击中目标”为真命题的充要条件是（） A ．()()p q ⌝∨⌝为真命题 B ．()p q ∨⌝为真命题 C. ()()p q ⌝∧⌝为真命题 D ．p q ∨为真命题5.设n S 是等差数列{}n a 的前n 项和，若65911a a =，则119SS ＝（） （A ）1（B ）1- （C ）2（D ）12正视图侧视图6.榫卯(sŭn măo)是我国古代工匠极为精巧的发明，它是在两个构件上采用凹凸部位相结合的一种连接方式．我国的北京紫禁城、山西悬空寺、福建宁德的廊桥等建筑都用到了榫卯结构．如图所示是一种榫卯构件中榫的三视图，其表面积为（A ）1224+π （B ）1220+π（C ）1420+π（D ）1424+π7. 已知函数()cos()sin 4f x x x π=+⋅, 则函数()f x 的图象AA. 关于直线8x π=对称 B.关于点直线(,84π-对称 C. 最小正周期为T=2π D. 在区间(0,)8π上为减函数8. 下面左图是某学习小组学生数学考试成绩的茎叶图，1号到16号同学的成绩依次为1A 、2A 、……、16A ，右图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图.那么该算法流程图输出的结果是A. 6B. 10C. 91D. 92676981367929415861031114输入 16,,A 90iA 否9.正方体1111ABCD A B C D -中，,E F 分别是1,AD DD 的中点，4AB =,则过,,B E F 的平面截该正方体所得的截面周长为（A ）（B ）（C ）（D ）10．已知()f x 是定义在R 上的奇函数，且0x >时，()ln 1f x x x =-+，则函数()()x g x f x e =-（e 为自然对数的底数）的零点个数是（）A. 0B. 1C. 2D. 311.等差数列{}n a 前n 项和为n S ，已知510071007(1)2017(1)1a a ---=510111011(1)2017(1)1a a ---=-，则A ．2017100710112017,S a a =>B ．2017100710112017,S a a =->C ．2017100710112017,S a a =<D ．2017100710112017,S a a =-<12. 若(,0)F c 是双曲线22221(0)x y a b a b-=>>的右焦点，过F 作该双曲线一条渐近线的垂线与两条渐近线交于,A B 两点，O 为坐标原点,OAB ∆的面积为2127a ,则该双曲线的离心率e =A. 53B. 43C. 54D. 85第Ⅱ卷注意事项：须用黑色墨水签字笔在答题卡上作答。

绝密★启封前2017全国卷Ⅲ高考压轴卷文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

注意事项： 1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2.第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。

3.考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

） 1．已知全集,U R =且{}{}2|12,|680,A x x B x x x =->=-+<则()U C A B 等于（A ）[1,4)- （B ）(2,3] （C ）(2,3) （D ）(1,4)-2.已知133iz i-=+（i 为虚数单位），则z 的共轭复数的虚部为（ ） (A)i - (B)i (C)1- (D)13袋中有五张卡片，其中红色卡片三张，标号分别为1,2,3，蓝色卡片两张，标号分别为1,2，从以上五张卡片中任取两张，则这两张卡片颜色不同且标号之和不小于4的概率为（A ）110 （B ）310 （C ）25 （D ）7104.在射击训练中，某战士射击了两次，设命题p 是“第一次射击击中目标”，命题q 是“第二次射击击中目标”，则命题“两次射击中至少有一次没有击中目标”为真命题的充要条件是（） A ．()()p q ⌝∨⌝为真命题 B ．()p q ∨⌝为真命题 C. ()()p q ⌝∧⌝为真命题 D ．p q ∨为真命题5.设n S 是等差数列{}n a 的前n 项和，若65911a a =，则119SS ＝（） （A ）1（B ）1- （C ）2（D ）12正视图侧视图6.榫卯(sŭn măo)是我国古代工匠极为精巧的发明，它是在两个构件上采用凹凸部位相结合的一种连接方式．我国的北京紫禁城、山西悬空寺、福建宁德的廊桥等建筑都用到了榫卯结构．如图所示是一种榫卯构件中榫的三视图，其表面积为（A ）1224+π （B ）1220+π（C ）1420+π（D ）1424+π7. 已知函数()cos()sin 4f x x x π=+⋅, 则函数()f x 的图象AA. 关于直线8x π=对称 B. 关于点直线2(,)8π对称 C. 最小正周期为T=2π D. 在区间(0,)8π上为减函数 8. 下面左图是某学习小组学生数学考试成绩的茎叶图，1号到16号同学的成绩依次为1A 、2A 、……、16A ，右图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图.那么该算法流程图输出的结果是A. 6B. 10C. 91D. 92676981367929415861031114开始输入 12316,,,,A A A A 0,1n i ==输出n 结束1i i =+1n n =+90iA 是是否否16i ≤9.正方体1111ABCD A BC D -中，,E F 分别是1,AD DD 的中点，4AB =,则过,,B E F 的平面截该正方体所得的截面周长为（A ）3225（B ）6225（C ）（D ）10．已知()f x 是定义在R 上的奇函数，且0x >时，()ln 1f x x x =-+，则函数()()x g x f x e =-（e 为自然对数的底数）的零点个数是（） A. 0B. 1C. 2D. 311.等差数列{}n a 前n 项和为n S ，已知510071007(1)2017(1)1a a ---=510111011(1)2017(1)1a a ---=-，则A ．2017100710112017,S a a =>B ．2017100710112017,S a a =->C ．2017100710112017,S a a =<D ．2017100710112017,S a a =-<12. 若(,0)F c 是双曲线22221(0)x y a b a b-=>>的右焦点，过F 作该双曲线一条渐近线的垂线与两条渐近线交于,A B 两点，O 为坐标原点,OAB ∆的面积为2127a ,则该双曲线的离心率e = A. 53 B. 43 C. 54 D. 85第Ⅱ卷注意事项：须用黑色墨水签字笔在答题卡上作答。

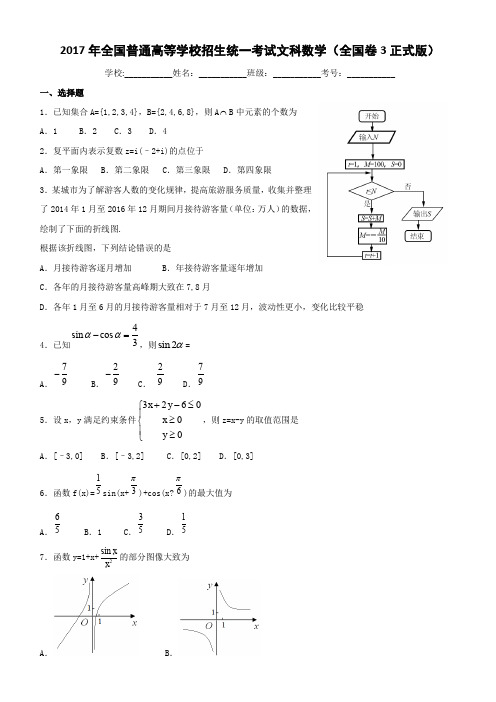
2017年全国普通高等学校招生统一考试文科数学（全国卷3正式版）学校:___________姓名：___________班级：___________考号：___________一、选择题1．已知集合A={1,2,3,4}，B={2,4,6,8}，则A⋂B中元素的个数为A．1 B．2 C．3 D．42．复平面内表示复数z=i(–2+i)的点位于A．第一象限 B．第二象限 C．第三象限 D．第四象限3．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图.根据该折线图，下列结论错误的是A．月接待游客逐月增加 B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7,8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳5．设x，y满足约束条件3260x yxy+-≤⎧⎪≥⎨⎪≥⎩，则z=x-y的取值范围是A．[–3,0] B．[–3,2] C．[0,2] D．[0,3]A． B．C ．D ．8．执行下面的程序框图，为使输出S 的值小于91，则输入的正整数N 的最小值为A ．5B ．4C ．3D ．29．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为10．在正方体1111ABCD A B C D -中，E 为棱CD 的中点，则A ．11A E DC ⊥B ．1A E BD ⊥C ．11A E BC ⊥D ．1AE AC ⊥20bx ay ab -+=相切，则C 的离心率为12．已知函数211()2()x x f x x x a ee --+=-++有唯一零点，则a=二、填空题三、解答题17．（12分）设数列{}n a 满足123(21)2n a a n a n +++-=.18．（12分）某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：以最高气温位于各区间的频率代替最高气温位于该区间的概率。

标准文档实用文案2016年全国高考文科数学试题（全国卷3）第Ⅰ卷一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设集合{0,2,4,6,8,10},{4,8}AB??，则BC A= （A）{48}，（B）{026}，，（C）{02610}，，，（D）{0246810}，，，，，（2）若43i z??，则||zz= （A）1 （B）1?（C）43+i55（D）43i55?（3）已知向量BA?=（12，32），BC?=（32，12），则∠ABC=（A）30°（B）45°（C）60°（D）120°（4）某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃，B点表示四月的平均最低气温约为5℃.下面叙述不正确的是（A）各月的平均最低气温都在0℃以上（B）七月的平均温差比一月的平均温差大（C）三月和十一月的平均最高气温基本相同（D）平均最高气温高于20℃的月份有5个（5）小敏打开计算机时，忘记了开机密码的前两位，只记得第一位是M，I,N中的一个字母，第二位是1,2,3,4,5中的一个数字，则小敏输入一次密码能够成功开机的概率是（A）815（B）18（C）115（D）130（6）若1tan3??，则cos2θ=（A）45?（B）15?（C）15（D）45（7）已知31323425,3,2???cba则(A)cab?? (B) cba?? (C)acb??(D) bac??（8）执行右面的程序框图，如果输入的a=4，b=6，那么输出的n=（A）3 （B）4 （C）5 （D）6标准文档实用文案（9）在△ABC中，BCB，4??边上的高等于BC31，则Asin= (A)310(B)1010(C)55(D)31010（10）如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为（A）18365?（B）54185?（C）90 （D）81（11）在封闭的直三棱柱ABC－A1B1C1内有一个体积为V的球.若AB⊥BC，AB=6，BC=8，AA1=3，则V的最大值是（A）4π（B）9π2（C）6π（D）32π3（12）已知O为坐标原点，F是椭圆C：22221(0)xyabab????的左焦点，A，B分别为C的左，右顶点.P为C上一点，且PF⊥x轴.过点A的直线l与线段PF交于点M，与y轴交于点E.若直线BM经过OE的中点，则C的离心率为（A）13（B）12（C）23（D）34第II卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题，每个试题考生都必须作答.第(22)题~第(24)题为选考题，考生根据要求作答. 二、填空题：本大题共4小题，每小题5分（13）设yx,满足约束条件210,210,1,xyxyx????????????则532???yxz的最小值为______. （14）函数xxycossin??的图像可由函数xysin2?的图像至少向右平移______个单位长度得到.（15）已知直线063:???yxl与圆1222??yx交于A、B两点，过A、B分别作l的垂线与x轴交于C、D两点，则|CD|=______.（16）已知f(x)为偶函数，当0x?时，1()x fxex????，则曲线y= f(x)在点(1,2)处的切线方程式_________.三.解答题：解答应写出文字说明，证明过程或演算步骤.（17）（本小题满分12分）已知各项都为正数的数列??n a满足11a?，211(21)20nnnn aaaa??????.（I）求23,aa；（II）求??n a的通项公式.标准文档实用文案（18）（本小题满分12分）下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图.注：年份代码1–7分别对应年份2008–2014.（Ⅰ）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；（Ⅱ）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量. 附注：参考数据：719.32ii y???，7140.17iii ty???，721()0.55ii yy????，≈2.646.参考公式：12211()()()(yy)niiinniiii ttyyrtt???????????，回归方程ya bt??中斜率和截距的最小二乘估计公式分别为：??，=.aybt?121()()()niiinii ttyybtt??????（19）（本小题满分12分）如图，四棱锥P-ABCD中，PA⊥地面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点. （I）证明MN∥平面PAB; （II）求四面体N-BCM的体积.标准文档实用文案（20）（本小题满分12分）已知抛物线C：y2=2x的焦点为F，平行于x轴的两条直线l1，l2分别交C于A，B两点，交C的准线于P，Q两点.（Ⅰ）若F在线段AB上，R是PQ的中点，证明AR∥FQ；（Ⅱ）若△PQF的面积是△ABF的面积的两倍，求AB中点的轨迹方程. （21）（本小题满分12分）设函数()ln1fxxx???. （I）讨论()fx的单调性；（II）证明当(1,)x???时，11lnxxx???；（III）设1c?，证明当(0,1)x?时，1(1)x cxc???.请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号（22）（本小题满分10分）选修4—1：几何证明选讲如图，⊙O中的中点为P，弦PC，PD分别交AB于E，F两点。

绝密★启用前2017年普通高等学校招生全国统一考试（全国卷2）文科数学注意事项：1.答题前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 设集合{1,2,3},{2,3,4}A B ==，则AB =A. {}123,4，，B. {}123，，C. {}234，，D. {}134，，2. (1)(2)i i ++=A.1i -B. 13i +C. 3i +D.33i +3. 函数()sin(2)3f x x π=+的最小正周期为A.4πB.2πC. πD.2π4. 设非零向量a ，b 满足+=-b b a a 则A. a ⊥bB. =b aC. a ∥bD. >b a5. 若1a >，则双曲线2221x y a-=的离心率的取值范围是A. +∞）B. ）C. （1D. 12（，）6. 如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为A. 90πB. 63πC. 42πD. 36π7. 设,x y 满足约束条件2+330233030x y x y y -≤⎧⎪-+≥⎨⎪+≥⎩。

则2z x y =+ 的最小值是 A. -15B.-9C. 1 D 98. 函数2()ln(28)f x x x =-- 的单调递增区间是A.(-∞,-2)B. (-∞,-1)C.(1, +∞)D. (4, +∞)9. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩，老师说，你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩，看后甲对大家说：我还是不知道我的成绩，根据以上信息，则 A. 乙可以知道两人的成绩 B. 丁可能知道两人的成绩 C. 乙、丁可以知道对方的成绩D. 乙、丁可以知道自己的成绩10. 执行右面的程序框图，如果输入的1a =-，则输出的S=A.2B.3C.4D.511. 从分别写有1,2,3,4,5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为A.110B.15C.310D.2512. 过抛物线2:4C y x =的焦点FC 于点M （M 在x 轴上方），l 为C 的准线，点N 在l 上且MN l ⊥，则M 到直线NF 的距离为A.B.C.D.二、填空题，本题共4小题，每小题5分，共20分.13. 函数()2cos sin f x x x =+的最大值为 .14. 已知函数()f x 是定义在R 上的奇函数，当(,0)x ∈-∞时，32()2f x x x =+，则(2)f =15. 长方体的长、宽、高分别为3，2，1，其顶点都在球O 的球面上，则球O 的表面积为16. ABC ∆的内角,,A B C 的对边分别为,,a b c ，若2cos cos cos b B a C c A =+，则B =三、解答题：共70分。

2017年全国卷3数学摘要：1.2017年全国卷三数学试题概述2.试题特点及难点分析3.解题策略与技巧4.典型题目解析5.备考建议正文：一、2017年全国卷三数学试题概述2017年全国卷三数学试题整体难度适中，试题结构保持稳定。

试题涵盖了高中数学的基础知识，注重考查考生的基本数学素养和解决问题的能力。

试题充分体现了数学学科的特点，注重知识之间的联系和应用。

二、试题特点及难点分析1.试题特点：（1）注重基础，强调通性通法；（2）突出能力考查，注重数学应用；（3）题目设置灵活，具有创新性；（4）试卷结构合理，难度梯度适中。

2.难点分析：（1）函数与导数：函数的性质、导数的计算与应用；（2）三角函数：三角函数的图像与性质、三角恒等变换；（3）概率与统计：概率的计算、统计量的应用；（4）解析几何：直线与圆的位置关系、圆锥曲线的综合问题。

三、解题策略与技巧1.熟悉基础知识，掌握基本方法；2.审题要细，明确题目要求；3.善于转化，灵活运用公式定理；4.控制计算量，注重解题效率；5.遇难题不慌，善于分析归纳。

四、典型题目解析1.函数与导数：解析函数的性质，求解导数不等式，利用导数研究函数的极值和最值；2.三角函数：求解三角方程，化简三角表达式，应用三角函数解决实际问题；3.概率与统计：计算概率，求解随机变量的问题，分析统计数据，解决实际统计问题；4.解析几何：求解直线、圆的位置关系，分析圆锥曲线的基本性质，解决综合问题。

五、备考建议1.系统复习，强化基础知识；2.多做练习，提高解题能力；3.分析总结，掌握解题技巧；4.调整心态，适应考试节奏；5.关注历年真题，模拟考试。

通过以上分析，相信大家对2017年全国卷三数学试题有了更深入的了解。

绝密★启用前2017年普通高等学校招生全国统一考试（新课标Ⅲ）文科数学注意事项：1．答题前，考生务必将自己的姓名、准考证填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A={1,2,3,4}，B={2,4,6,8}，则AB中元素的个数为?A．1B．2C．3D．42．复平面内表示复数z=i(–2+i)的点位于A．第一象限 B．第二象限 C．第三象限 D．第四象限3．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图.根据该折线图，下列结论错误的是A．月接待游客逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7,8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4????cossin?2sin= 4．已知，则3．7227??． D C．． B． A99993x?2y?6?0??x?0yzxxy-，则5．设=，的取值范围是满足约束条件??y?0?A．[–3,0] B．[–3,2] C．[0,2] D．[0,3]??1fxxx?)的最大值为+6．函数)+cos(()=sin( 536316D．． C．A． B1555x sin xy +的部分图像大致为7．函数=1+2x． AB．． DC．SN的最小值为，则输入的正整数．执行下面的程序框图，为使输出的值小于9182．D 3．C 4．B 5．A．9．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为πππ3π D． CA．． B．442ABCD?ABCD ECD的中点，则中，为棱10．在正方体1111AE⊥DCAE⊥BCAEE⊥BD⊥ACA．．B A．C． D 11111122yx??1abCAAAA 为直径的圆与直线11．已知椭圆：>0）的左、右顶点分别为，且以线段，（，>212122abbx?ay?2ab?0C的离心率为相切，则1236D．． CA．． B 3333?xx?12?1)?eex?2x?a(f(x)?a=有唯一零点，则12．已知函数111? DB．．1C．A．223二、填空题：本题共4小题，每小题5分，共20分。

2017高考全国3数学试卷及解析在2017年的高考中，数学科目一直是学生们最为关注和重视的科目之一。

而在全国3卷中，数学试卷的难度和题型也备受关注。

本文将对2017年全国3卷的数学试卷及其解析进行详细探讨，以帮助读者更好地理解题目和解题思路。

一、选择题部分选择题部分是数学试卷的基础部分，它占据了试卷的相对较大比例。

在2017年的全国3卷中，选择题的难度相对较高，涵盖了各个知识点。

其中包括代数、几何、概率与统计等相关知识。

在解题过程中，考生需要熟练掌握各个知识点的定义和解题技巧，以便正确选择答案。

二、填空题部分填空题部分是考察考生对知识点记忆和理解的一种方式。

在2017年的全国3卷中，填空题的数量也较为可观。

这些题目主要考察了代数运算、函数、数列等知识点。

在解答填空题时，考生需要注意运算的顺序和符号的使用，以避免出现计算错误。

三、解答题部分解答题部分是数学试卷中的重头戏，也是考察考生分析问题和解决问题能力的关键环节。

在2017年的全国3卷中，解答题的难度较大，需要考生有较为扎实的数学基础和一定的思维能力。

解答题的题型有多种多样，包括证明、计算、综合等。

在解答这些题目时，考生需要理清思路，合理运用所学知识，遵循解题的规则和步骤，以确保答案的正确性。

四、解析部分解析部分是数学试卷的附加部分，它用来解答考生在做题过程中可能出现的疑惑。

在2017年的全国3卷中，解析部分对每道题目都进行了详细的解释和解答过程。

通过阅读解析部分，考生可以更加全面地了解每道题目的解题思路和答案的推导过程，从而更好地掌握数学知识。

总结起来，2017年全国3卷的数学试卷在难度和题型上都给考生带来了一定的挑战。

考生在备考时需要全面复习各个知识点，熟练掌握解题技巧，注重解题过程的规范性和准确性。

同时，对于难题和解题过程中的疑惑，考生可以通过阅读解析部分来获得更好的理解和解答。

相信通过认真的备考和复习，考生们一定能够在数学考试中取得令人满意的成绩。

2017年全国高考文科数学试题及答案-全国卷3(2)(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017年全国高考文科数学试题及答案-全国卷3(2)(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017年全国高考文科数学试题及答案-全国卷3(2)(word版可编辑修改)的全部内容。

2017年普通高等学校招生全国统一考试文科数学注意事项：1．答题前,考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动,用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上.写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题:本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

1．已知集合A={1,2,3,4}，B={2,4，6，8},则AB中元素的个数为A．1 B．2 C．3 D．4【答案】B【解析】由题意可得：。

本题选择B选项.2．复平面内表示复数z=i(–2+i)的点位于A．第一象限 B．第二象限 C．第三象限 D．第四象限【答案】B【解析】由题意：.本题选择B选项.3．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人)的数据，绘制了下面的折线图.根据该折线图,下列结论错误的是A．月接待游客逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7，8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳【答案】A【解析】由折线图,7月份后月接待游客量减少，A错误；本题选择A选项。