第十章输出反馈与状态反馈

格式：ppt
大小：365.00 KB
文档页数：50

下载文档原格式

输出反馈极点配置ppt

停止
Step5.对{A,B}，任意指定n个实部为负期望闭环特征
值 {1*，*2，，*n1 }，按多输入情形极点配置算法，计
算 p n 镇定状态反馈矩阵K，计算停止。
三、状态反馈动态解耦
1、系统和假定
(1)受控系统为方系统，即输入变量和输出变量具有相同个数，即p＝q 。
(2)控制规律取为“状态反馈”结合“输入变换”形式，
yˆi (s) gii (s)vˆi (s)，i 1,2,..., p
三、状态反馈动态解耦
3、系统的结构特征量（结构特性指数 & 结构特性向量）
一、输出反馈极点配置
3、输出反馈极点配置结论3【输出反馈极点配置】对完全能控和完全能观测n维 LTI受控系统，设 rankB p，rankC q ，采用输出反馈：U v FY ，可对数目为 min{n,p q 1} 的闭环系统极点进行“任意接近”式配置，即使其可任意地接近任给的期望极点位置。
又由于 (s) 0 (s) 0 的根为开环传递函数：
c(sI A)1b (s) / (s)
的极点与零点。
再由根轨迹法可知，闭环极点只能分布于以开环极点为起点、开环零点与无穷远为终点，当输出反馈系数f 0 和
f 0 - 时在复平面上导出的一组根轨迹线段上，而不能位于根轨迹以外。
1*，*2，，*n
确定一个反馈矩阵F，使输出反馈闭环系统：
X (A BFC)X Bv Y CX
的所有特征值实现期望配置，即有： i (A BFC) *i，i 1,2,..., n
一、输出反馈极点配置
2、输出反馈局限性
结论1【输出反馈局限性】对完全能控的连续时间LTI受控系统，采用输出反馈一般不能任意配置系统全部极点

输出反馈

C H
T
T

(5-15)
(5-15）是一个q个未知量，n个方程的方程组，而是任意的n维向量，它由所期望的极点所决定。
方程（5-15）对任意的有解，显然要求 C 是n×n可逆方阵。
一般来说当q<n 时，对于任意，（5-15）无解。
对于给定的，方程（5-15）有解的条件是它们相容，亦即当C的秩为q时，q个方程的唯一解应满足剩下的n-q个方程。这时，这n-q个等式给出了加在
用静态输出反馈配置极点首先研究单输入多输出的系统，以说明用静态输出反馈配置极点时所遇到的困难，而这些困难是用全部状态变量作反馈时所未遇到的。一个单输入多输出系统动态方程为
Ax bu x y Cx
（5-11）
(5-12)
u=Hy+v
联合（5-11）和（5-12）可得闭环系统的动态方程为
i
i , i 0 使得扰动后的S非奇异，由于 C 的秩为q，
这总是可以做到的。式（5-17）给出了H的一个明显表达式，并且 i H i 是给定的 1 , 2 ,, q 的函数， i S非奇异，则可精确地使闭环如果所给的能使
全维状态观测器及其设计
状态观测器状态估计器状态重构
^
2n阶复合系统：
. x . A ^ L HC x
y C
Bk x B ^ v A Bk HC L x B
x 0 ^ x
ˆ x x ( A Hc )( x x ) L 由(1)-(2):
3. 分离定理： . cx 原系统 x Ax Bu y ^ 引入状态反馈： u v k x
x Ax Bk x Bv, y cx . ^ ^ ^ 全维观测器：

状态反馈与输出反馈

概述(6/标一般定义为关于状态x(t)和输入的积分型优化型性能指标一般定义为关于状态和输入u(t)的积分型和输入性能指标函数或关于末态x(t 的末值型性能指标函数的末值型性能指标函数。性能指标函数或关于末态 f)的末值型性能指标函数。而综合的任务,就是要确定使性能指标函数取极值的控制而综合的任务就是要确定使性能指标函数取极值的控制规律,即最优控制律即最优控制律。规律即最优控制律。相应地性能指标函数值则称为最优性能。相应地性能指标函数值则称为最优性能。
概述(2/12) 概述(2/12)
一般情况下,控制理论发展与控制系统设计的追求目标一般情况下控制理论发展与控制系统设计的追求目标为解析的反馈控制作用规律(反馈控制律反馈控制律)。为解析的反馈控制作用规律反馈控制律。对复杂的动力学被控系统,在解析反馈控制规律难于对复杂的动力学被控系统在解析反馈控制规律难于求解的情形下,需要求系统的数值反馈控制规律或外求解的情形下需要求系统的数值反馈控制规律或外部输入函数的数值解序列(开环控制输入开环控制输入)。部输入函数的数值解序列开环控制输入。系统综合首先需要确定关于系统运动形式，或关于系统运系统综合首先需要确定关于系统运动形式，动动态过程和目标的某些特征的性能指标函数,然后据此确动动态过程和目标的某些特征的性能指标函数然后据此确定控制规律。定控制规律。综合问题的性能指标函数可分为优化型和非优化型性能指标, 指标两者差别在于: 两者差别在于
概述(12/12) 概述(12/12)
下面,本章将就这些系统综合的主要问题如下面本章将就这些系统综合的主要问题,如本章将就这些系统综合的主要问题极点配置、极点配置、镇定、镇定、解耦与观测器问题, 观测器问题基于状态反馈理论作细致讨论。基于状态反馈理论作细致讨论。

第十章输出反馈及状态反馈课件

➢而该对偶系统可以视为是系统 (AT, CT, BT)经输出反馈阵为HT构成的闭环反馈系统;
✓由于输出反馈不改变系统的可控性，因此闭环系统 H(A-BHC, B, C)的状态可观性等价于其对偶系统 (AT, CT, BT)的状态可控性;
➢又由对偶性原理有，系统 (AT, CT, BT)的状态可控性等价于其对偶系统 (A, B, C)的状态可观性。
Ø 闭环系统的状态可控性和可观性
Ø 状态反馈镇定
口由于线性定常离散系统状态空间模型以及可控性判据的类同性，因此本节讨论的概念和方法也可推广到线性定常离散系统的状态反馈和输出反馈系统的分析和设计问题。
10.1.1 状态反馈的描述式
口对线性定常连续系统 (A, B, C)，若取系统的状态变量来构成反馈，则所得到的闭环控制系统称为状态反馈系统。 Ø 状态反馈闭环系统的系统结构可如图10-1所示
✓将一个 MIMO 系统通过反馈控制实现一个输入只控制一个输出的系统综合问题称为系统解耦(System decoupling)问题。
v 系统解耦对于高维复杂系统尤为重要。 ✓使系统的输出y(t) 无静差地跟踪一个外部信号y0(t)
作为性能指标，相应的综合问题称为跟踪(Tracking) 问题。
7
口优化型性能指标一般定义为关于状态 x(t) 和输入 u(t) 的积分型性能指标函数或关于末态 x(tf) 的末值型性能指标函数。 Ø 而综合的任务，就是要确定使性能指标函数取极值的控制规律，即最优控制(Optimal control)问题。 Ø 相应地性能指标函数值则称为最优性能。
➢另一方面，从状态空间模型的输出方程可以看出，输出反馈可视为状态反馈的一个特例。
✓因此，采用状态反馈应能达到更高的性能。

状态反馈和输出反馈（精品）

5．1 线性反馈控制系统的基本结构及其特性在现代控制理论中，控制系统的基本结构和经典控制理论一样，仍然是由受控对象和反馈控制器两部分构成的闭环系统。

不过在经典理论中习惯于采用输出反馈，而在现代控制理论中则更多地采用状态反馈。

由于状态反馈能提供更丰富的状态信息和可供选择的自由度，因而使系统容易获得更为优异的性能。

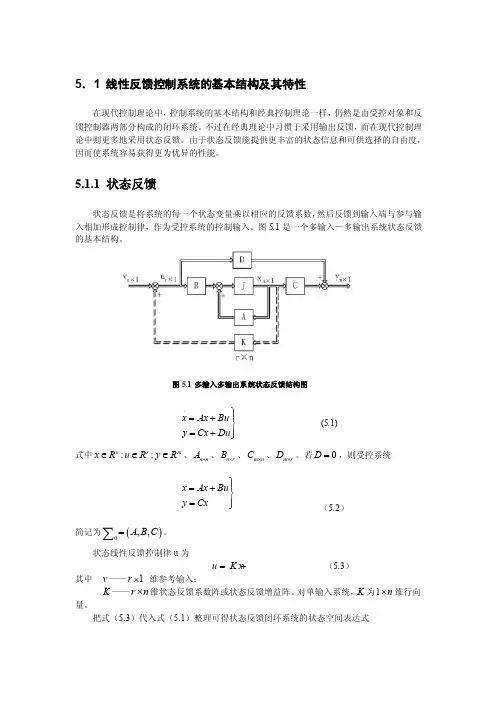
5.1.1 状态反馈状态反馈是将系统的每一个状态变量乘以相应的反馈系数，然后反馈到输入端与参与输入相加形成控制律，作为受控系统的控制输入。

图5.1是一个多输入—多输出系统状态反馈的基本结构。

图5.1 多输入多输出系统状态反馈结构图.x Ax Bu y Cx Du ⎫⎪=+⎬=+⎪⎭ (5.1) 式中n x R ∈;r u R ∈;m y R ∈、n n A ⨯、n r B ⨯、m n C ⨯、m r D ⨯。

若0D =，则受控系统.x Ax Bu y Cx ⎫⎪=+⎬=⎪⎭ （5.2）简记为()0,,A B C =∑。

状态线性反馈控制律u 为u K xv =+ （5.3）其中 v ——1r ⨯ 维参考输入；K ——r n ⨯维状态反馈系数阵或状态反馈增益阵。

对单输入系统，K 为1n ⨯维行向量。

把式（5.3）代入式（5.1）整理可得状态反馈闭环系统的状态空间表达式.()()x A BK x Bv y C DK x Dv ⎫⎪=++⎬=++⎪⎭（5.4）若0D =，则.()x A BK x Bv y Cx ⎫⎪=++⎬=⎪⎭ （5.5）简记为[](),,hA BKBC =+∑。

闭环系统的传递函数矩阵[]1()()k W s C sI A BK B -=-+ （5.6）比较开环系统()0,,A B C =∑与闭环系统[](),,hA BKBC =+∑可见，状态反馈阵K 的引入，并不增加系统的维数，但可通过K 的选择自由地改变闭环系统的特征值，从而使系统获得所要求的性能。

5.1.2 输出反馈输出反馈是采用输出矢量Y 构成线性反馈律。

现代控制理论基础总复习

第二章线性系统的数学描述数学模型可以有许多不同的形式，较常见的有三种：第一种是：把系统的输入量和输出量之间的关系用数学方式表达出来，称之为输入输出描述，或外部描述；第二种是：不仅可以描述系统输入、输出之间的关系，而且还可以描述系统的内部特性，称之为状态空间描述或内部描述；第三种是：用比较直观的方块图（结构图）和信号流图模型进行描述。

910 2.1 线性系统的时域数学模型()(1)(2)121()()()()()n n n n n c t a c t a c t a c t a c t ---+++++()(1)(2)0121()()()()()m m m m m b r t b r t b r t b r t b r t ---=+++++ (2.1) 式中，()r t 和()c t 分别是系统的输入信号和输出信号，()()n c t 为()c t 对时间t 的n 阶导数；i a (1,2,)i n =和j b (0,1,)j m =是由系统的结构参数决定的系数。

2.2 传递函数11m n b s a s --++++++11 式中1011()m m m m M s b s b s b s b --=++++1011()nn n n N s a s a s a s a --=++++()M s 和()N s 分别称为传递函数()G s 的分子多项式和分母多项式。

2.5 线性系统的状态空间描述A Buy C du =+⎧⎨=+⎩x x x(2.3) 2.5.2 状态空间表达式与传递函数的关系1()()G s C sI A B D -=-+(2.4)12 2.5.3 状态空间表达式的建立情形一：线性微分方程中不含输入的导数项，传递函数没有零点()(1)11n n n n y a y a y a y u --++++= (2.5)情形二线性微分方程含有输入的导数(不超过3阶)，传递函数有零点 ()(1)()(1)11011n n n n n n n n y a y a y a y b u b u b u b u ----++++=++++ (2.6) 1011111()()n n n nn n n nb s b s b s b Y s U s s a s a s a ----++++=++++(2.7)13 Chp.9 状态空间系统响应、可控性与可观性9.1 线性定常系统的响应已知线性定常连续系统状态方程的一般形式为0()()(), (0)t A t B t =+=x x u x x(2.8) 状态变量的初始值为0x ，控制作用为()t u 。

东电考研大纲841、842、843、844、845、846

（1）841 自动控制原理一、考试形式与试卷结构1、试卷满分及考试时间试卷满分为150分，考试时间为180分钟2、考试方式考试方式为闭卷、笔试3、试卷的题型结构选择填空题，分析计算题，综合设计题二、考察的知识及范围第一章自动控制系统导论内容：（1）自动控制系统的一般性概念和基本工作原理；（2）反馈控制系统的基本组成、分类及对控制系统的基本要求；（3）《自动控制原理》课程研究的主要内容及其发展现状。

重点掌握：自动控制系统的一般性概念和基本工作原理；反馈控制系统的基本组成、分类及对控制系统的基本要求第二章控制系统的数学模型内容：（1）复数和复变函数的基本概念，拉普拉斯变换和拉普拉斯反变换；（2）控制系统研究中几种主要数学模型：微分方程、传递函数和频率特性的内在联系；（3）典型环节的数学模型；（4）常见电气系统和一般机械系统的数学建模；（5）方块图的化简法则；（6）利用梅逊公式求取系统的传递函数。

重点掌握：传递函数的概念、结构图的建立与等效变换、梅逊公式第三章自动控制系统的时域分析内容：（1）系统阶跃响应性能指标；（2）一阶、二阶系统阶跃响应的特点及一阶、二阶系统动态性能；（3）高阶系统动态性能（4）线性系统稳定的充要条件；（5）利用劳斯判剧判别系统的稳定性；（6）稳态误差的定义；（7）稳态误差系数的求取及减小或消除系统稳态误差的方法；重点掌握：稳定性、稳态误差、系统阶跃响应的特点及动态性能与系统参数间的关系等有关概念，有关的计算方法。

第四章根轨迹法内容：（1）根轨迹的定义、幅值和相角条件；（2）根轨迹的绘制法则；（3）利用根轨迹分析系统的特性。

重点掌握：根轨迹的绘制方法，利用根轨迹分析系统的特性。

第五章线性系统的频域分析法内容：（1）频率特性的定义、求法及性质；（2）线性系统极坐标图画法；Nyquist图稳定判据的应用；（3）线性系统伯德图的画法；最小相位系统的定义及性质；（4）利用Bode图求取系统稳态误差；增益裕量和相位裕量的定义、物理意义和求取；重点掌握：正确理解频率响应、频率特性的概念及特点，明确频率特性的物理意义；熟练掌握运用奈奎斯特稳定判据和对数频率判据判定系统稳定性的方法；熟练掌握计算稳定裕度的方法。

现代控制理论 5-1 状态反馈和输出反馈

e 输出—状态微分 ⎧x& = (A − HC)x + Bv
反馈闭环系统 ⎩⎨y = Cx
ca u(t) B
x& (t )
x(t )
y(t )
∫
C
y A
输出
tc H
输入
定理9-3：输出至参考输入反馈的引入不改变系统的可控性与可观测性。
ae 输出至参考输入反馈系统可控（可观测）
的充分必要件是被控系统可控（可观测）。
12
输出—状态微分反馈 x& = (A − HC)x + Bu
u(t )
e B
x& (t )
x(t )
y(t )
∫
C
aA
cH
三种反馈的共同点
前页
y 不增加新的状态变量，系统开环、闭环同维； tc 反馈增益阵都是常数矩阵，反馈为线性变换。
二、反馈结构对系统性能的影响
1，可控可观性
e状态反馈定理 9-1 a输出—状态微分反馈定理 9-2 c 输出—参考输入反馈定理 9-3
ap×1 参考输入 c控制量： u = v − Fy
q ×1 输出
p ×1
p × q 实反馈增益矩阵
y 输出—参考输入 ⎧x& = (A − BFC)x + Bv
tc 反馈闭环系统 ⎩⎨y = Cx
例题
9
控制量： u = v − Fy
e 输出—参考输入 ⎧x& = (A − BFC)x + Bv
反馈闭环系统 ⎩⎨y = Cx
c⎡ 0 1 0 ⎤
A
=
⎢ ⎢
0
0
1
⎥ ⎥
y ⎢⎣− 20 − 29 −10⎥⎦

先进控制技术试卷A答案

南阳理工学院电子与电气工程系2009—2010学年第一学期期末考试卷课程名称先进控制技术试卷编号 A 考试方式开卷满分分值 100分一、填空题（每空1分，共10分）。

1、系统的输出是指能从外部量测到的来自系统的信息。

2、动态方程包括状态方程和输出方程。

3、性能指标J 是个标量。

4、从训练的角度而言，神经网络可分为有监督训练与无监督训练。

5、若某系统处在最优控制下，则其性能指标取极值。

6、神经网络的训练是应用一系列输入向量，通过预先确定的过程（算法）调整网络的权值来实现的。

7、线性系统在t 0时刻可控的充要条件是该系统的可控的格拉姆矩阵为非奇异矩阵。

8、状态变量是确定动力学系统状态的最小一组变量。

9、若在系统的状态空间表达式中，f 和g 均是线性函数，则称系统为线性系统。

10、状态调节器的基本任务是：当系统状态偏离系统平衡状态时，寻求一个控制，在消耗能量不大的条件下使状态向量的各分量趋于零。

二、选择题（每题3分，共15分）。

11、若系统能从0(t )x α= 转移到(t )0f x =，则下列说法正确的 ( B )。

A 、α为t 0时刻可达； B 、 α为t 0时刻可控；C 、 α为t 0时刻可观；D 、 α为t 0时刻可构。

12、关于神经网络的特性，下列说法错误的是（ D ）。

A 、自学习能力； B 、容错能力； C 、并行处理能力； D 、以上说法都不对。

13、关于知识表示方法应该有的性质，下列说法错误的是（ D ）。

A 、表达充分 B 、推理有效 C 、有效获取知识 D 、便于记忆。

14、关于最优控制，下列说法正确的是（ C ）。

A 、控制过程中所用时间最少；B 、控制过程能量消耗最少；C 、性能指标取极值；D 、以上说法都不对。

15、关于设计模型参考自适应控制系统核心问题，下列说法正确的是( B ) 。

A 、选择好参考模型；B 、如何设计好自适应调整率；C 、 A 和B 都正确；D 、以上说法都不对。

状态反馈与闭环极点配置极点配置条件

u B
x
x
y
∫
C
A
H
-
B
∫
C
实际系统基于准确模型，且
A
没有考虑扰动
代入 ye C xe
25
附1：存在扰动时的状态误差
u B
x
x
dy
∫
C
A
H
-
B
∫
C
A
代入 ye C xe d
存在扰动时，不能使状态误差→0
26
附2：存在模型失配时的状态误差
u B'
x
x
y
∫
C'
A'
H
-
B
∫
C
A
存在模型失配时，不能使状态误差→0
2
一、状态反馈与输出反馈
1. 状态反馈
u B -
x
xy
∫
C
A
闭环传函？状态
K
方程？
加入状态反馈后的系统结构图
3
综合的手段：改变 K 阵的参数综合的目的：改变系统矩阵，从而改变系统的特性
注：状态反馈通常只用系数阵即可满足要求，一般不需要采用动态环节
4
2. 输出反馈
u B -
x
xy
∫

35
闭环传递函数的不变性
闭环传递函数等同于直接状态反馈的情况；观测器的引入不影响闭环传递函数
注：分离性原理和传函的不变性都基于精确模型 36
仿真例：系统的状态空间表达式同前面例
（1）要求状态观测器的特征值为（2）通过状态反馈将系统的闭环极点配置为
（3）仿真验证观测状态对实际状态的跟踪情况，
27
状态观测器的等价结构

现代控制理论基础复习资料_普通用卷

现代控制理论基础课程一单选题 (共30题，总分值30分 )1. 已知，则该系统是（）（1 分）A. 能控不能观的B. 能控能观的C. 不能控能观的D. 不能控不能观的2. 下面关于线性连续定常系统的最小实现说法中( )是不正确的。

（1 分）A. 最小实现的维数是唯一的。

B. 最小实现的方式是不唯的，有无数个。

C. 最小实现的系统是能观且能控的。

D. 最小实现的系统是稳定的。

3. 下面关于连续线性时不变系统的能控性与能观性说法正确的是（）（1 分）A. 能控且能观的状态空间描述一定对应着某些传递函数阵的最小实现。

B. 能控性是指存在受限控制使系统由任意初态转移到零状态的能力。

C. 能观性表征的是状态反映输出的能力。

D. 对控制输入的确定性扰动影响线性系统的能控性，不影响能观性。

4. 下面关于线性非奇异变换说法错误的是（）（1 分）A. 非奇异变换阵P是同一个线性空间两组不同基之间的过渡矩阵。

B. 对于线性定常系统，线性非奇异变换不改变系统的特征值。

C. 对于线性定常系统，线性非奇异变换不改变系统的传递函数。

D. 对于线性定常系统，线性非奇异变换不改变系统的状态空间描述。

5. 线性定常系统的状态转移矩阵，其逆是（）（1 分）A.B.C.D.6. 下面关于系统Lyapunov稳定性说法正确的是（）（1 分）A. 系统Lyapunov稳定性是针对平衡点的，只要一个平衡点稳定，其他平衡点也稳定。

B. 通过克拉索夫斯基法一定可以构造出稳定系统的Lyapunov函数。

C. Lyapunov第二法只可以判定一般系统的稳定性，判定线性系统稳定性，只可以采用Lyapunov方程。

D. 线性系统Lyapunov局部稳定等价于全局稳定性。

7. 线性SISO定常系统，输出渐近稳定的充要条件是（）（1 分）A. 其不可简约的传递函数的全部极点位于s的左半平面。

B. 矩阵A的特征值均具有负实部。

C. 其不可简约的传递函数的全部极点位于s的右半平面。

状态反馈和状态观测器1

1 6)(s
12)
s3
1 18s 2
72s
综合指标为： % 5%；tS 0.5s，ep 0,试用状态反馈实现上述指标。
解：将极点配置为一对主导极点和一个非主导极点；根据二阶
系统的性能指标，求出 0.707，n 10。取 0.707，n 10
则，主导极点为：
s1，2 0.707 j7.07
状态反馈闭环系统的状态空间表达式为
x (A BK )x Br
y Cx
简记为 K (A BK ), B,C。该系统的闭环传递函数阵为
GK (s) CsI (A BK ) 1 B
经过状态反馈后，系数矩阵C和B没有变化，仅仅是系统矩阵A发生了变
化，变成了 (A BK )。也就是说状态反馈矩阵K的引入，没有增加新的状态
证明：假定开环系统能控，A，b可为能控标准形
0 1 0 0
A
0
0
1
0
1
a0
a1
a
n
1
K K0 K1 Kn1
0 0 则 bK K0 K1
0
K
n
1
0
b
0
1
0
10
0
[A bK]
0
01
1
(a0 K0 ) (a1 K1)
(an1 Kn1)
sn rn1sn1 r0 0
实际系统与希望系统的特征方程的系数应当相一致。
3、状态反馈阵K的计算步骤 1）判断A，b能控性 2）写出实际的闭环特征方程（传递阵的分母为0的方程）
SI [A bK] 0
3）根据要配置的特征根，写出希望的特征方程
f (s) (s 1)(s n ) 0
4）对应实际的与希望的特征方程，求出K。

状态反馈相对于输出反馈的优越性是显而易见的系统的任

证明令定理5-9的证明中A22的维数为零，即可证明本定理。这个定理相当于（A，B，C）的极点用
状态反馈可任意配置的对偶形式。
证完。
三、单输入单输出系统的状态观测器
对单输入、单输出系统，若(A, b, c) 可观测，状态观测器的极点配置问题可按以下步骤来解决：
1 . 记 d e t ( s I A ） s n a 1 s n 1 a n 1 s a n 。
1 . A 阵的特征多项式为 s 3 5 s 2 8 s 4 0 ;
2.根据以上介绍的变换阵，有
8 51110 4 2 1 1 1 1 P 5 1 0 121 4 3 1 ,P 1 1 10
1 0 0 144 1 1 0 1 2 4
因原系统（A, c)可观测，对其作等价变换后有
2021/5/1
17
0 1 x 1
y 0 0
an n
an
1
n 1
x u
1 a1 1
A
b
0 1x
2 .对 ( A , b , c )构造状态观测器：
xˆ ( A g c ) xˆ bu gy，得到
c
Agc
x ˆ A x ˆ B u G ( y C x ˆ ) 根据前面的分析：
x(A G C )x A A A 1 2 1 1A 0 2 2 G G G 1 2 C [C 10 ]
有x A A 2 11 1 G G 1 2 C C 1 1 A 0 22 x
因为
(A1T1,C1T )
0 1 1
1 (a1g1)
g
若给定了n个希望的极点s1,s2, ,sn ,则有
f (s) sn a1sn1 an1s an

状态反馈与闭环极点配置条件-自动控制原理

A
BK HC
BK
x xˆ
BB r
y C
0
x xˆ
引入线性变换
x xe
In I n
0 x In xˆ
得
x x e
A
BK 0
A
BK HC
x xe
B 0
r
y C
0
x xe
35
极点配置的分离性原理
带状态观测器的状态反馈系统的特征多项式为
det sI
s 0 0 1 1 0 1
det 0
s
0 1
1
0
0
k1
k2
k3
0 0 s 0 1 3 0
s3 ( k1 3 )s2 ( k2 2k1 2 )s ( k3 3k2 3k1 6 )
而系统希望的特征多项式为
f * ( s ) ( s 1 )( s 2 )( s 3 ) s3 5s2 17 s 13 令 f * ( s ) f ( s ) 得 k1 8, k2 35, k3 136
1 2 3 1
15
解：状态反馈系统的特征多项式为
f ( s ) det[ sI A BK ] s3 ( k1 3 )s2 ( k2 2k1 2 )s ( k3 3k2 3k1 6 ) 而系统希望的特征多项式为 f * ( s ) ( s 1 )3 s3 3s2 3s 1
1
( s 3 )( s 1.414 )( s 1.414 )
有反馈时 x ( A BK )x Br , X ( s ) G f ( s )U ( s ),
Gf
(
s
)
(
sI
A
BK
)1 B
1
(

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

而综合的任务，就是要确定使性能指标函数取极值的控制规律，即最优控制(Optimal control)问题。
相应地性能指标函数值则称为最优性能。
8
系统综合问题，无论是对优化型还是非优化型性能指标函数, 首先存在 2 个主要问题。
一个是控制的存在性问题，即所谓可综合条件、控制规律存在条件。
Ch.10 线性反馈系统的时间域综合
1
目
概述
录
10.1 输出反馈与状态反馈
10.2 极点配置问题 10.3 状态重构与状态观测器设计 10.4 最优控制问题概论* 10.5 系统解耦* 10.6 跟踪问题*
概
述
系统综合(system synthesis)是系统分析(analysis)的逆问题。
输出反馈不改变状态可观性。
根据对偶性原理和输出反馈不改变状态可控性的结论，可对上述结论证明如下:
证明过程图解输出反馈闭环系统 H(A-BHC,B,C) 的状态可观性对偶原理对偶系统 H T ( AT C T H T BT , C T , BT ) 的状态可控性
?
需证明的结论
12
这样，基于理想模型综合得到的控制器，运用于实际系统中所构成的闭环控制系统，对这些建模误差
和参数摄动是否具有良好的抗干扰性(不敏感性)，是否使系统保持稳定，是否使系统达到或接近预期的性能指标成为控制系统实现的关键问题。该问题称为系统鲁棒性(robustness)问题。
基于提高系统鲁棒性的控制综合方法也称为鲁棒控制(robust control)方法。
状态反馈闭环系统可以简记为 K(A- BK, B, C), 其传递函数阵为: GK(s) = C(sI-A+BK)-1B
10.1.2 输出反馈的描述式
与状态反馈有何不同?
对线性定常连续系统(A,B,C), 若取系统的输出变量来构成反馈，则所得到的闭环控制系统称为输出反馈控制系统。输出反馈控制系统的结构图如图10-2所示。
系统分析是对已知系统结构和参数, 以及确定好系统的外部输入(系统激励)下, 对系统运动进行定性分析如可控性、可观性、稳定性等和定量运动规律分析的探讨
如系统运动轨迹、系统的性能品质指标等。
而系统综合问题为已知系统系统结构和参数，以及所期望的系统运动形式或关于系统运动动态过程和目标的某
State feedback and output feedback
控制理论最基本的任务是，对给定的被控系统设计能满足所期望的性能指标的闭环控制系统，即寻找反馈控制律。状态反馈和输出反馈是控制系统设计中两种主要的反馈策略，其意义分别为将观测到的状态和输出取作反馈量以构成反馈律，实现对系统的闭环控制，以达到期望的
17
重点！
本节讨论的主要问题：
基本概念: 状态反馈、输出反馈
基本性质: 反馈闭环系统的可控性和可观性本节的讲授顺序为:
状态反馈的描述式
输出反馈的描述式闭环系统的状态可控性和可观性状态反馈镇定由于线性定常离散系统状态空间模型以及可控性判据的类同
性，因此本节讨论的概念和方法也可推广到线性定常离散系统的状态反馈和输出反馈系统的分析和设计问题。
由于由状态变量所得到的关于系统动静态的信息比输出
变量提供的信息更丰富、更全面。
因此，若用状态来构成反馈控制律，与用输出反馈构成的反馈控制律相比，则设计反馈律有更大的可选择的范围，而闭环系统能达到更佳的性能。另一方面，从状态空间模型的输出方程可以看出，输出反馈可视为状态反馈的一个特例。因此，采用状态反馈应能达到更高的性能。
品质指标(如过渡过程的快速性、超调量、周期性等)，在很大程度上是由闭环系统的极点位置所决定的。
6
因此，在进行系统设计时，设法使闭环系统的极点位于 s 平面上的一组合理的、具有所期望
的性能品质指标的期望极点上，可以有效地改善系统的性能品质指标。
将一个 MIMO 系统通过反馈控制实现一个输入只
13
下面，本章将就这些系统综合的主要问题，如
状态反馈与输出反馈（10.1节）
极点配置（10.2节）
基于观测器的设计（10.3节）
最优控制* （10.4节）
系统解耦* （10.5节）
跟踪问题* （10.6节）进行细致讨论。
14
10.1 输出反馈与状态反馈
15
状态反馈与输出反馈
显然, 只有对可综合的问题，控制命题才成立，才
有必要去求解控制规律。
对不可综合的问题，可以考虑修正性能指标函数，或改变被控系统的机理、结构或参数，以使系统可综合条件成立。
9
另一个是如何求解控制规律, 即构造求解控制律的解析求解方法或计算机数值算法。
利用这些算法，对满足可综合条件的系统，可确定
v + u B + + A H 开环系统 x'

x C
y
图10-2 输出反馈系统的结构图
22
输出反馈闭环系统的状态空间模型可描述如下: 开环系统状态空间模型和输出反馈律分别为
x Ax Bu y Cx u Hy v
其中 H 为 rm 维的实矩阵，称为输出反馈矩阵。
反之，则不然。
由此也可知，状态反馈可以达到比输出反馈更好的控制品质，更佳的性能。
10.1.3 闭环系统的状态可控性和可观性
对于由状态反馈和输出反馈构成的闭环系统，其状态可控/可观性是进行反馈律设计和闭环系统分析时所关注的问题。下面分别讨论两种闭环系统的状态可控性 state controllability 状态可观性 state observability
控制一个输出的系统综合问题称为系统解耦(System decoupling)问题。
系统解耦对于高维复杂系统尤为重要。使系统的输出 y(t) 无静差地跟踪一个外部信号 y0(t) 作为性能指标，相应的综合问题称为跟踪(Tracking) 问题。
7
优化型性能指标一般定义为关于状态 x(t) 和输入 u(t) 的积分型性能指标函数或关于末态 x(tf) 的末值型性能指标函数。
10.1.1 状态反馈的描述式
对线性定常连续系统 (A, B, C)，若取系统的状态变量来构
成反馈，则所得到的闭环控制系统称为状态反馈系统。
状态反馈闭环系统的系统结构可如图10-1所示
v + u B + + A K 开环系统 x'

x C
y
图10-1 状态反馈系统的结构图
19
状态反馈闭环系统的状态空间模型可描述如下: 设开环系统状态空间模型和状态反馈律分别记为
对系统的性能指标要求。
在经典控制理论中用传递函数描述系统，只能由系统的输出变量来构成反馈律，即输出反馈。
在现代控制理论的状态空间分析方法中，多考虑采用状态变量来构成反馈律，即状态反馈。
16
之所以采用状态变量来构成反馈律，是因为状态空间分
析中所采用的模型为状态空间模型，其状态变程，则可得如下输出反馈闭环控制系统的状态空间模型:
x ( A BHC ) x Bv y Cx
输出反馈闭环系统可简记为H(A-BHC,B,C)，其传递函数阵为:
GH(s)=C(sI-A+BHC)-1B
由状态反馈和输出反馈的闭环控制系统状态空间模型可知，输出反馈其实可以视为当 K = HC 时的状态反馈。因此，在进行系统分析时，输出反馈可以看作状态反馈的一种特例。
5
对于非优化型性能指标，按照对闭环系统期望的运动形式从不同的角度去规定性能，可以有多种提法和形式。
常用的非优化型性能指标提法有以下几种
以系统渐近稳定作为性能指标，相应的综合问题称为镇定(Stabilization)问题。
以一组期望的闭环系统极点位置或极点凸约束区域 (空间)为性能指标，相应的综合问题为极点配置。对线性定常系统，系统的稳定性和各种性能的
这就需要基于状态观测理论，根据系统模型，利用直接测量到的输入输出信息来构造或重构状态变量信息。
相应的理论问题称为状态重构(state-reconstruction)问题, 即基于观测器的设计(observer based design)问题。
11
2. 建模误差和参数摄动问题
对系统综合问题，首先需建立一个描述系统动力学特性的数学模型。
4
优化型和非优化型性能指标的差别在于: 优化性能指标是一类极值型指标，综合的目的
是使该性能指标函数取极小(极大)；
而非优化型性能指标是一类由不等式及等式约束的性能指标凸空间，一般只要求解的控制规律对应的性能指标到达该凸空间即可。对优化型性能指标，需要函数优化理论和泛函理论求解控制规律；而对非优化型性能指标一般存在解析方法求解控制规律，如极点配置(Pole assignment)方法。
上式即表明状态反馈不改变系统的状态可控性。
由于输出反馈可视为状态反馈在 K=HC 时的特例，故输出反馈也不改变系统的状态可控性。
2. 闭环系统的状态可观性
对被控系统 (A, B, C) 有如下结论: 采用输出反馈构成的闭环系统 H (A-BHC, B, C) 后状态可观性不变，即
并且，系统分析与综合都是建立在模型基础上的。正如在第 2 章所述，系统模型是理想与现实，精确描述与简化描述的折中，任何模型都会有建模误差。
此外，由于系统本身的复杂性及其所处环境的复杂性，系统的动力学特性会产生缓慢变化。
这种变化在一定程度上可视为系统模型的参数摄动（parametric perturbations）。