(完整版)机械原理课后全部习题答案

第2章 机构的结构分析(P29)2-12：图a 所示为一小型压力机。

图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O 连续转动。

在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C 轴上下摆动。

同时，又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。

最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。

试绘制其机构运动简图，并计算自由度。

解：分析机构的组成：此机构由偏心轮1’（与齿轮1固结）、连杆2、滑杆3、摆杆4、齿轮5、滚子6、滑块7、冲头8和机架9组成。

偏心轮1’与机架9、连杆2与滑杆3、滑杆3与摆杆4、摆杆4与滚子6、齿轮5与机架9、滑块7与冲头8均组成转动副，滑杆3与机架9、摆杆4与滑块7、冲头8与机架9均组成移动副，齿轮1与齿轮5、凸轮(槽)5与滚子6组成高副。

故解法一：7=n 9=l p 2=h p12927323=-⨯-⨯=--=h l p p n F解法二：8=n 10=l p 2=h p 局部自由度1='F11210283)2(3=--⨯-⨯='-'-+-=F p p p n F h l(P30) 2-17：试计算如图所示各机构的自由度。

图a 、d 为齿轮-连杆组合机构；图b 为凸轮-连杆组合机构（图中在D 处为铰接在一起的两个滑块）；图c 为一精压机机构。

并问在图d 所示机构中，齿轮3与5和齿条7与齿轮5的啮合高副所提供的约束数目是否相同？为什么？解： a) 4=n 5=l p 1=h p11524323=-⨯-⨯=--=h l p p n Fb) 5=n 6=l p 2=h p12625323=-⨯-⨯=--=h l p p n F12625323=-⨯-⨯=--=h l p p n Fc) 5=n 7=l p 0=h p10725323=-⨯-⨯=--=h l p p n Fd) 6=n 7=l p 3=h p13726323=-⨯-⨯=--=h l p p n F(C 可看做是转块和导块,有1个移动副和1个转动副)齿轮3与齿轮5的啮合为高副（因两齿轮中心距己被约束，故应为单侧接触）将提供1个约束。

[标签:标题]篇一：机械原理(西工大第七版)课后答案2-7章精选第二章题2-2 图a所示为一小型压力机。

图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O 连续转动。

在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C 轴上下摆动。

同时，又通过偏心轮1’、连杆2、滑杆3使C轴上下移动。

最后通过在摆杆4的叉槽中的滑块7和铰链G使冲头8实现冲压运动。

试绘制其机构运动简图，并计算自由度。

解：分析机构的组成：此机构由偏心轮1’（与齿轮1固结）、连杆2、滑杆3、摆杆4、齿轮5、滚子6、滑块7、冲头8和机架9组成。

偏心轮1’与机架9、连杆2与滑杆3、滑杆3与摆杆4、摆杆4与滚子6、齿轮5与机架9、滑块7与冲头8均组成转动副，滑杆3与机架9、摆杆4与滑块7、冲头8与机架9均组成移动副，齿轮1与齿轮5、凸轮(槽)5与滚子6组成高副。

故解法一：n?7 pl?9ph?2可绕固定轴心C转动的圆柱4中滑动。

当偏心轮1按图示方向连续转动时，可将设备中的空气按图示空气流动方向从阀5中排出，从而形成真空。

由于外环2与泵腔6有一小间隙，故可抽含有微小尘埃的气体。

试绘制其机构的运动简图，并计算其自由度。

解：1)取比例尺,绘制机构运动简图。

(如图题2-3所示)４ＡF?3n?2pl?ph?3?7?2?9?2?1解法二：n?8 pl?10 ph?2 局部自由度题2-32) n?3 pl?4 ph?0F??1F?3n?2pl?ph?3?3?2?4?0?1题2-4 使绘制图a所示仿人手型机械手的食指机构的F?3n?(2pl?ph?p?)?F??3?8?2?10?2?11题2-3如图a所示为一新型偏心轮滑阀式真空泵。

其偏心轮1绕固定轴A转动，与外环2固连在一起的滑阀3在机构运动简图（以手指8作为相对固定的机架），并计算其自由度。

解：1)取比例尺,绘制机构运动简图。

(如图2-4所示)2) n?7 pl?10 ph?0F?3n?2pl?ph?3?7?2?10?0?13题2-4题2-5 图a所示是为高位截肢的人所设计的一种假肢膝关节机构，该机构能保持人行走的稳定性。

机械原理第三版课后答案1. 机械原理基础知识。

1.1 什么是机械原理？机械原理是研究机械运动规律和力学性能的科学，它是工程学的基础学科之一。

通过机械原理的研究，可以揭示机械系统的运动规律和力学性能，为机械设计和工程实践提供理论依据。

1.2 机械原理的基本概念。

机械原理涉及的基本概念包括力、力的作用点、力的方向、力的大小、力的合成、力的分解、平行力的平衡条件、力的偶力、力的力矩、力的力矩平衡条件等。

这些基本概念是理解机械原理的基础，对于解决机械系统的运动和力学问题具有重要意义。

2. 机械原理的应用。

2.1 机械原理在机械设计中的应用。

在机械设计中，机械原理可以用来分析和计算机械系统的运动规律和力学性能，为机械产品的设计提供理论依据。

比如，通过机械原理可以确定机械零件的尺寸、结构和材料，使得机械产品具有良好的运动性能和工作效率。

2.2 机械原理在工程实践中的应用。

在工程实践中，机械原理可以用来分析和解决机械系统的故障和问题，指导工程师进行维修和改进。

比如，通过机械原理可以判断机械系统是否处于平衡状态，分析机械系统的运动轨迹和受力情况，为工程实践提供技术支持。

3. 机械原理的发展趋势。

3.1 数值模拟技术在机械原理中的应用。

随着计算机技术的发展，数值模拟技术在机械原理中得到了广泛应用。

通过数值模拟技术，可以对复杂的机械系统进行模拟和分析，为机械设计和工程实践提供更精确的数据和方法。

3.2 智能化技术在机械原理中的应用。

智能化技术在机械原理中的应用也越来越广泛。

通过智能化技术，可以实现机械系统的自动化控制和优化设计，提高机械产品的性能和可靠性。

4. 结语。

机械原理是工程学的基础学科，它对于理解和应用机械系统具有重要意义。

在未来的发展中，机械原理将会与计算机技术和智能化技术相结合，为机械设计和工程实践带来新的发展机遇。

希望大家能够认真学习机械原理，不断提高自己的理论水平和实践能力，为机械工程事业做出更大的贡献。

机械原理第九版课后题答案1. 多杆杆机构1.题目：一个三杆杆机构可构成一个正运动副吗？答案：一个三杆杆机构可以构成一个正运动副，只需要其中两个杆满足以下条件即可：–杆的长度之和大于第三个杆的长度。

–两个杆的长度之差小于第三个杆的长度。

2.题目：判定一个六杆机构能否构成一个运动副。

答案：判定一个六杆机构能否构成一个运动副，可以有两种方法：1.根据杆的数目和自由度之间的关系，自由度即为杆数减去2。

•六杆机构的自由度为6-2=4，而运动副的自由度为1，因此六杆机构不能构成一个运动副。

2.根据六杆机构的几何特性，判定它是否为运动副，如判断杆的长度是否满足某些条件。

3.题目：一个六杆机构有一个杆为固定杆，其他杆均可任意旋转，是否可以构成一个四杆机构？答案：一个六杆机构有一个杆为固定杆，其他杆均可任意旋转，可以构成一个四杆机构。

由于固定杆不会运动，因此可以将它从机构中去掉，这样剩下的五杆就构成了一个四杆机构。

2. 齿轮传动4.题目：两个齿轮的模数分别为4和6，齿数分别为24和36，求它们的传动比。

答案：传动比可以通过齿轮的齿数比和模数比来计算。

传动比等于从驱动齿轮到被动齿轮的转速比，即被动齿轮的齿数除以驱动齿轮的齿数。

传动比 = 36 / 24 = 1.55.题目：一个齿轮传动系统，输入齿轮的转速为2000 rpm，输出齿轮的齿数为40。

如果两个齿轮的模数相等，求输出齿轮的转速。

答案：齿轮传动系统的转速比等于被动齿轮的齿数除以驱动齿轮的齿数。

假设输入齿轮的转速为N1，输出齿轮的转速为N2，输入齿轮的齿数为Z1，输出齿轮的齿数为Z2，则有公式：转速比 = N2 / N1 = Z2 / Z1在本题中，已知N1 = 2000 rpm，Z2 = 40，且两个齿轮的模数相等，即Z1 = Z2，所以有：N2 / 2000 = 40 / 40N2 = 2000 rpm6.题目：一个齿轮传动系统中，输入齿轮的齿数为20，传动比为4，求输出齿轮的齿数。

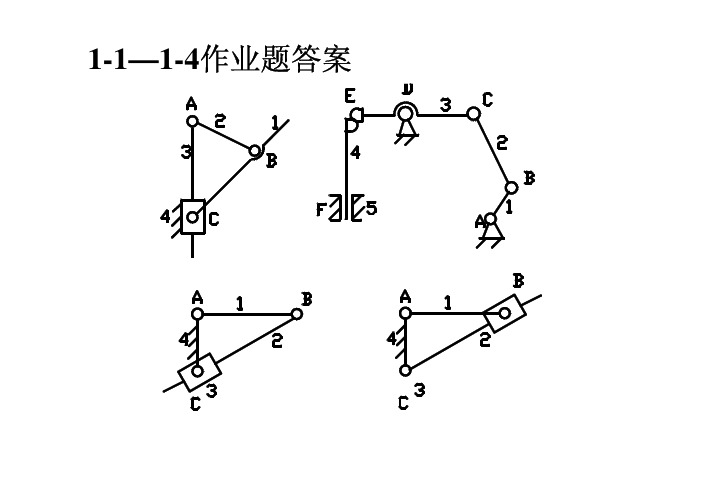
2-8解：（1）取μ= m/mml作机构位置图如（a)图（2）求v、ω、列矢量方程式取μ,作速度（b)图v（3）求a、α列矢量方程式作加速度（c)图题5-8解αa1=arccos(rb/ra1)=arccos[(z1cosα)/(z1+2ha*)] =31°46′O1 α PN2B2N1αa2=26°14′10″B1P=B1N1-N1PB1 PbⅠ=mz1/2·cosα(tgαa1- tgα′)=11.39mm B2P=12.72mm B1B2=24.11mm 作用弧CD=B1B2cosα′=25.66mm 作用角 ϕ 1 =CD/r1′=25.66/47.5=30°58 ′αⅡO2εα=B1B2/Pb=1.63题5-12解N 1 N 2 = 2 N 1 P = 2r sin α N 1 N 2 2r sin α ∴ tgα a = = = 2tgα = 0.7279 O1 N 1 r cos α 3′ α a = 36° 9″ rb r cos α z cos α 又 cos α a = = = * ra r + ha z + 2ha* 2ha cos α ∴z = = 12.323 cos α − cos α aO1 α ra rb (B2) αa P rb ra αa α O2 N1(B1) N2∴不根切，z最少为13题5-13解h m − xm = MN* aMN = PN sinα = OPsin2 α mz 2 = sin α 2* az 2 x = h − sin α 2x=1-35/2 sin 20° =-1.0471 or x=(17-35)/17=-1.05882题5-15解解题思路： 1.设计题，主要确定尺寸 r 、ra、r f 、rb 2.变位齿轮传动设计步骤：由 a 、 a ′、 α → α ′ → x Σ → x 1、 x 2 ← x min ← 据 z = 12 z Σ、 α 、 α ′ → y 、 x Σ → ∆ y 计算： r 、 ra、 r f 、 rb 3 .验证 s a < 0 .2 m 、 ε α ≥ 1题5-15解1.选择传动类型 2. 求 α ′和 x Σα ′ = arccos(m a = ( z1 + z 2 ) = 120mm < a ′ 2a cos α ) = 29 ° 5 0 ′ 2 8 ′′ a′x∑( z 1 + z 2 )( inv α ′ − inv α ) = = 1 . 2505 2 tg α17 − 12 z1 = z2 = 12 < 17,∴ x1.2 > = 0.2941 17 ∴ x1 = x2 = x∑ / 2 = 1.2505/ 2 = 0.62533.分配 x 1 和 x 24.求y和∆y y = (a ′ − a ) / m = (130 − 120) / 10 = 1; ∆y = x ∑ − y = 0.2505 mz 1.2 = 60mm 5.r1.2 = 2 * ra 1.2 = r1.2 + ( ha + x1.2 − ∆y )m = 73.75mm* r f 1.2 = r1.2 − ( ha + c * − x1.2 )m = 53.75mmmz 1.2 rb1.2 = cos α = 56.38mm 2 6.验算sa 和ε α ′23 s = (π / 2 + 2 x1.2 tgα )m = 20.26mm ;α a 1.2 = arccos(rb1.2 / ra 1.2 ) = 40°8 ″ sa 1.2 = s ra 1.2 − 2ra 1.2 ( invα a 1.2 − invα ) r1.2 73.75 − 2 × 73.75(0.142715 − 0.014904) = 6.05mm > 0.2m 60= 20.26 ×题5-15解1 [ z1 ( tgα a 1 − tgα ′ ) + z 2 ( tgα a 2 − tgα ′ )] εα = 2π 1 = z1 ( tgα a 1 − tgα ′ ) = 1.03π题5-16解 用等变位修复，小正变位；大负变位* * ∆d a 2 = d 2 + 2( ha + x 2 )m − ( d 2 + 2ha m ) = 2 x 2 m则 x 2 = ∆d a 2 / 2m = −1 而 x1 = − x 2 = 1d 1 = 96mm ; d 2 = 384mm ; d a 1 = 112mm ; d a 2 = 384mm ; d f 1 = 94mm ; d f 2 = 366mm ; d b1 = 90.21mm ; d b 2 = 360.84mm ; a ′ = a = 240mm .验算sa 和ε α d b1 α a 1 = arccos( ) = 36°21′; d a1α a 2 = 20° sa 1 = πm / 2 • d a 1 / d 1 − d a 1 ( invα a 1 − invα )= 1.02mm > 0.2m sa 2 ↑ 不验算 1 εα = [ z1 ( tgα a 1 − tgα ) + z 2 ( tgα a 2 − tgα )] 2π = 1.42mn (1 ) a ′ = a 12 = ( z3 + z4 ) 34 2 cos β ∴ cos β = 0 . 79412 , β = 37 ° 25 ′ 41 ″ m n z3 ( 2 )d 3 = m t z 3 = = 45 .33 mm ; d 4 = m t z 4 = 90 .67 mm ; cos β* d f 3 = d 3 − 2 ( han + c * ) m = 40 .33 mm ; d f 4 = 85 .67 mm ; * d a 3 = d 3 + 2 han m = 49 .33 mm ; d a 4 = 94 .67 mm tg α t = tg α n / cos β = 0 .4583 ; α t′ = α t = 24 ° 37 ′ 25 ″题5-20解d b 3 = d 3 cos α t = 41 .21 mm ; d b 4 = 82 . 42 mmα at 3 = arccos( d b 3 / d a 3 ) = 33 ° 20 ′ 35 ″; α at 4 = 29 ° 28 ′ 16 ″ εγ = εα + ε β= 3 . 118 1 = [ z 3 ( tg α at 3 − tg α t ) + z 4 ( tg α at 4 − tg α t )] 2π。

机械原理习题及答案 Prepared on 22 November 2020第二章 平面机构的结构分析 2-1 绘制图示机构的运动简图。

2-3 计算图示机构的自由度，并指出复合铰链、局部自由度和虚约束。

解：(a) C 处为复合铰链。

7,n =p h =0，p l =10。

自由度 323721001W l h F n p p =--=⨯-⨯-=。

(b) B 处为局部自由度，应消除。

3n =， p h =2，p l =2自由度 323323121W l h F n p p =--=⨯-⨯-⨯=。

(c) B 、D 处为局部自由度，应消除。

3n =， p h =2，p l =2。

自由度 323323121W l h F n p p =--=⨯-⨯-⨯=。

(d) CH 或DG 、J 处为虚约束，B 处为局部自由度，应消除。

6n =，p h =1，p l =8。

自由度 32362811W l h F n p p =--=⨯-⨯-=。

(e) 由于采用对称结构，其中一边的双联齿轮构成虚约束，在连接的轴颈处，外壳与支架处的连接构成一个虚约束转动副,双联齿轮与外壳一边构成虚约束。

其中的一边为复合铰链。

其中4n =，p h =2，p l =4。

自由度 32342422W l h F n p p =--=⨯-⨯-=。

(f) 其中，8n =，p h =0，p l =11。

自由度 323821102W l h F n p p =--=⨯-⨯-=。

(g) ① 当未刹车时，6n =，p h =0，p l =8，刹车机构自由度为② 当闸瓦之一刹紧车轮时，5n =，p h =0，p l =7，刹车机构自由度为③ 当两个闸瓦同时刹紧车轮时，4n =，p h =0，p l =6，刹车机构自由度为2-3 判断图示机构是否有确定的运动，若否，提出修改方案。

分析 (a) 要分析其运动是否实现设计意图，就要计算机构自由度，不难求出该机构自由度为零，即机构不能动。

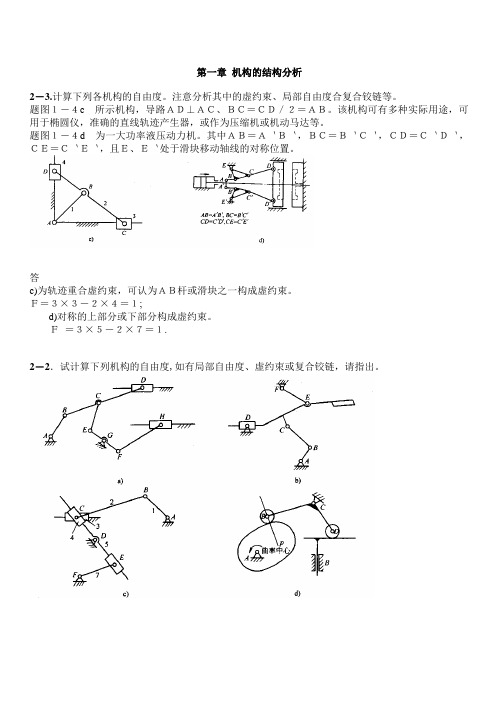
第一章机构的结构分析2－3.计算下列各机构的自由度。

注意分析其中的虚约束、局部自由度合复合铰链等。

题图１－４c所示机构，导路ＡＤ⊥ＡＣ、ＢＣ＝ＣＤ／２＝ＡＢ。

该机构可有多种实际用途，可用于椭圆仪，准确的直线轨迹产生器，或作为压缩机或机动马达等。

题图１－４d为一大功率液压动力机。

其中ＡＢ＝Ａ｀Ｂ｀，ＢＣ＝Ｂ｀Ｃ｀，ＣＤ＝Ｃ｀Ｄ｀，ＣＥ＝Ｃ｀Ｅ｀，且Ｅ、Ｅ｀处于滑块移动轴线的对称位置。

答c)为轨迹重合虚约束，可认为ＡＢ杆或滑块之一构成虚约束。

Ｆ＝３×３－２×４＝１;d)对称的上部分或下部分构成虚约束。

Ｆ＝３×５－２×７＝１.2－2．试计算下列机构的自由度,如有局部自由度、虚约束或复合铰链，请指出。

e）答案：a)Ｆ＝３×７－２×１０＝１．注意其中的Ｃ、Ｇ、Ｄ、Ｈ点并不是复合铰链。

b)Ｆ＝３×５－２×７＝１C）Ｆ＝３×７－２×１０＝１其中Ｃ点为复合铰链，分别由2、３、４构件在Ｃ点构成复合铰。

d)Ｆ＝３×３－２×３－２＝１或者Ｆ＝３×５－２×５－２－２＝１其中Ｂ、Ｄ处的滚子具有局部自由度。

(e) F=3×9－2×12－1－1=1或者：F=3×8－2×11－1=1（注意：BCD组成的三角形为一个构件）其中B点为局部自由度2-3试计算如图所示各平面高副机构的自由度,如有局部自由度、虚约束或复合铰链，请指出。

答：C点为局部自由度，E、F其中一点为虚约束。

F= 3×5－2×6－1－1=1或者：F=3×4－2×5－1=1第三章平面连杆机构及其分析与设计3－1．试求题图所示各机构在图示位置时全部瞬心的位置．答案：瞬心P 12在A 点 瞬心P 23、 P 24均在B 点 瞬心P 34在C 点 P 14、 P 13均在垂直导路的无 瞬心P 23、 P 13均在B 点 穷远处 瞬心P 14、 P 24均在D 点3-5在图示的齿轮-连杆组合机构中，试用瞬心法求齿轮1与齿轮3的传动比31/ωω。