机械原理 第四章练习题(答案)

图4-11所示为起重机机构，当摇杆CD 摇动时，连杆BC上悬挂重物的M点作近似 的水平直线移动，从而避免了重物平移时 因不必要的升降而发生的事故(shìgù)和能量的 损耗。
第三十四页，共八十八页。
图4-11 起重 机起重 机构 (qǐ zhònɡ)
(qǐ zhònɡ)
第三十五页，共八十八页。
两摇杆长度相等的双摇杆机构，称为(chēnɡ wéi)等腰梯形机构。
C2D，摆角为；而当曲柄顺时针再转过 角度2=180-时，摇杆由C2D摆回C1D，其
摆角仍然是 。虽然摇杆来回摆动的摆角
相同，但对应的曲柄转角不等(12);当
曲柄匀速转动时,对应的时间也不等(t1>t2)， 从而反映了摇杆往复摆动的快慢不同。
第十五页，共八十八页。
令摇杆自C1D摆至C2D为工作行程， 这时铰链C的平均速度是v1=C1C2/t1；摆 杆自C2D摆回至C1D为空回行程，这时C 点的平均速度是v2=C1C2/t2，v1<v2，表明
第四十二页，共八十八页。
上述关系说明：曲柄存在(cúnzài)的必要条件： （1） 在曲柄(qūbǐng)摇杆机构中，曲柄(qūbǐng)是最 短杆； （2） 最短杆与最长杆长度之和小于或等
于(děngyú)其余两杆长度之和。
第四十三页，共八十八页。
如何得到不同(bù tónɡ)类型的铰链四杆机构？ 根据(gēnjù)以上分析可知：
即机构处于压力角=90（传力角=0）的
位置时，驱动力的有效力为0。此力对A点 不产生力矩，因此不能使曲柄转动。机构 的这种位置称为死点。
第二十五页，共八十八页。
死点(sǐ diǎn)会使机构的从动件出现卡死或运 动不确定的现象。可以利用回转机构的惯性 或添加辅助机构来克服。如家用缝纫机中的 脚踏机构，图4-3a。

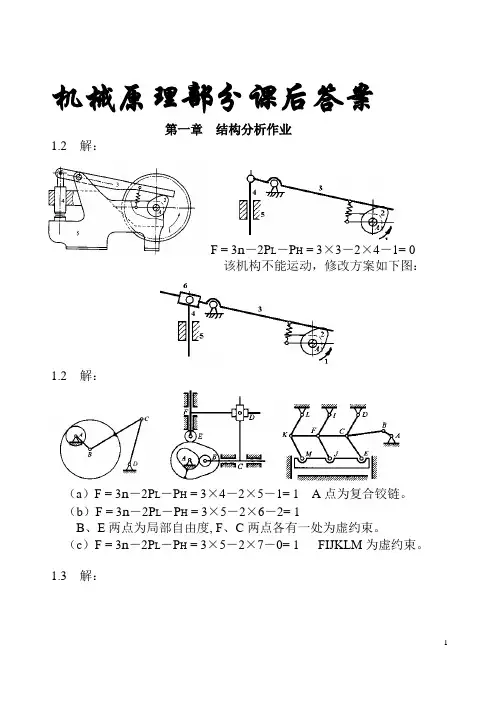
机械原理部分课后答案第一章结构分析作业1.2 解：F = 3n－2P L－P H = 3×3－2×4－1= 0该机构不能运动，修改方案如下图：1.2 解：（a）F = 3n－2P L－P H = 3×4－2×5－1= 1 A点为复合铰链。

（b）F = 3n－2P L－P H = 3×5－2×6－2= 1B、E两点为局部自由度, F、C两点各有一处为虚约束。

（c）F = 3n－2P L－P H = 3×5－2×7－0= 1 FIJKLM为虚约束。

1.3 解：F = 3n－2P L－P H = 3×7－2×10－0= 11）以构件2为原动件，则结构由8－7、6－5、4－3三个Ⅱ级杆组组成，故机构为Ⅱ级机构(图a)。

2）以构件4为原动件，则结构由8－7、6－5、2－3三个Ⅱ级杆组组成，故机构为Ⅱ级机构(图b)。

3）以构件8为原动件，则结构由2－3－4－5一个Ⅲ级杆组和6－7一个Ⅱ级杆组组成，故机构为Ⅲ级机构(图c)。

(a) (b) (c)第二章 运动分析作业2.1 解：机构的瞬心如图所示。

2.2 解：取mmmm l /5=μ作机构位置图如下图所示。

1.求D 点的速度V D13P D V V =而 25241314==P P AE V V E D ，所以 s mm V V E D /14425241502524=⨯==2. 求ω1s rad l V AE E /25.11201501===ω3. 求ω2因 98382412141212==P P P P ωω ，所以s rad /46.0983825.1983812=⨯==ωω 4. 求C 点的速度V Csmm C P V l C /2.10154446.0242=⨯⨯=⨯⨯=μω2.3 解：取mmmm l /1=μ作机构位置图如下图a 所示。

1. 求B 2点的速度V B2V B2 =ω1×L AB =10×30= 300 mm/s 2.求B 3点的速度V B3V B3 ＝ V B2 ＋ V B3B2大小 ？ ω1×L AB ？ 方向 ⊥BC ⊥AB ∥BC 取mm s mm v /10=μ作速度多边形如下图b 所示，由图量得：mmpb 223= ，所以smm pb V v B /270102733=⨯=⨯=μ由图a 量得：BC=123 mm , 则mmBC l l BC 1231123=⨯=⨯=μ3. 求D 点和E 点的速度V D 、V E利用速度影像在速度多边形，过p 点作⊥CE ，过b 3点作⊥BE ，得到e 点；过e 点作⊥pb 3，得到d 点 , 由图量得：mmpd 15=，mmpe 17=，所以smm pd V v D /1501015=⨯=⨯=μ ， smm pe V v E /1701017=⨯=⨯=μ；smm b b V v B B /17010173223=⨯=⨯=μ4. 求ω3s rad l V BC B /2.212327033===ω5. 求n B a 222212/30003010smm l a AB n B =⨯=⨯=ω6. 求3B aa B3 ＝ a B3n ＋ a B3t ＝ a B2 ＋ a B3B2k ＋ a B3B2τ 大小 ω32L BC ω12L AB 2ω3V B3B2 ？方向 B →C ⊥BC B →A ⊥BC ∥BC 22233/5951232.2s mm l a BC n B =⨯=⨯=ω223323/11882702.222s mm V a B B k B B =⨯⨯=⨯=ω取mm s mm a 2/50=μ作速度多边形如上图c 所示，由图量得：mmb 23'3=π ，mmb n 20'33=,所以233/11505023's mm b a a B =⨯=⨯=μπ2333/10005020's mm b n a at B =⨯=⨯=μ7. 求3α233/13.81231000s rad l a BC tB ===α8. 求D 点和E 点的加速度a D 、a E利用加速度影像在加速度多边形，作e b 3'π∆∽CBE ∆, 即 BE eb CE e CB b 33''==ππ，得到e 点；过e 点作⊥3'b π，得到d 点 , 由图量得：mme 16=π，mmd 13=π，所以2/6505013s mm d a a D =⨯=⨯=μπ ，2/8005016s mm e a a E =⨯=⨯=μπ 。

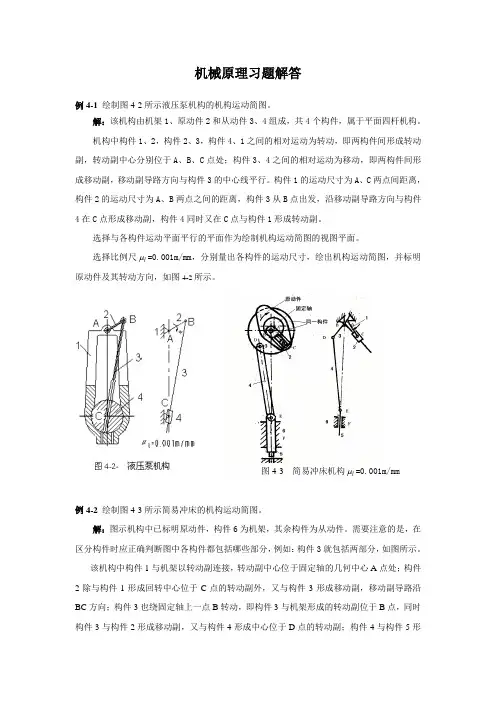
机械原理习题解答例4-1 绘制图4-2所示液压泵机构的机构运动简图。

解：该机构由机架1、原动件2和从动件3、4组成，共4个构件，属于平面四杆机构。

机构中构件1、2，构件2、3，构件4、1之间的相对运动为转动，即两构件间形成转动副，转动副中心分别位于A 、B 、C 点处；构件3、4之间的相对运动为移动，即两构件间形成移动副，移动副导路方向与构件3的中心线平行。

构件1的运动尺寸为A 、C 两点间距离，构件2的运动尺寸为A 、B 两点之间的距离，构件3从B 点出发，沿移动副导路方向与构件4在C 点形成移动副，构件4同时又在C 点与构件1形成转动副。

选择与各构件运动平面平行的平面作为绘制机构运动简图的视图平面。

选择比例尺l μ=0.001m/mm ，分别量出各构件的运动尺寸，绘出机构运动简图，并标明原动件及其转动方向，如图4-2所示。

例4-2 绘制图4-3所示简易冲床的机构运动简图。

解：图示机构中已标明原动件，构件6为机架，其余构件为从动件。

需要注意的是，在区分构件时应正确判断图中各构件都包括哪些部分，例如：构件3就包括两部分，如图所示。

该机构中构件1与机架以转动副连接，转动副中心位于固定轴的几何中心A 点处；构件2除与构件1形成回转中心位于C 点的转动副外，又与构件3形成移动副，移动副导路沿BC 方向；构件3也绕固定轴上一点B 转动，即构件3与机架形成的转动副位于B 点，同时构件3与构件2形成移动副，又与构件4形成中心位于D 点的转动副；构件4与构件5形图4-3 简易冲床机构l μ=0.001m/mm成中心位于E 点的转动副；构件5与机架6形成沿垂直方向的移动副。

该机构属于平面机构，因此选择与各构件运动平面平行的平面作为绘制机构运动简图的视图平面。

选择比例尺l μ=0.001m/mm ，量出各构件的运动尺寸，绘出机构运动简图，并标明原动件及其转动方向，如图4-3所示。

4-3 题4-３图为外科手术用剪刀。

第一章单元测试1、单选题：机械原理课程的研究对象是什么 ( ) 。

选项：A:机器B:构件C:机构D:机器和机构答案: 【机器和机构】2、单选题：下列关于机器和机构的关系描述中，正确的是 ( ) 。

选项：A:机器包含机构B:机构包含机器C:都有可能D:二者没有关系答案: 【机器包含机构】3、判断题：脚踏自行车既属于机构的范畴，又属于机器的范畴。

（）选项：A:对B:错答案: 【错】4、判断题：机械是机器和机构的总称。

（）选项：A:对B:错答案: 【对】5、判断题：常见的机构有带传动机构、齿轮传动机构、凸轮机构和连杆机构等。

（）选项：A:错B:对答案: 【对】6、判断题：机构是用来传递与变换运动和力的可动装置。

（）选项：A:对B:错答案: 【对】7、判断题：脚踏缝纫机是一种机器。

（）选项：A:对B:错答案: 【错】8、判断题：机器都是由各种机构组合而成的。

（）选项：A:错B:对答案: 【对】9、判断题：能够用来变换或传递能量的装置是机构。

（）选项：A:对B:错答案: 【错】10、判断题：机械原理课程的研究内容是有关机械的基本理论问题。

（）选项：A:错B:对答案: 【对】第二章单元测试1、单选题：平面运动副按其接触特性，就可以分成为（）。

选项：A:转动副与移动副B:低副与高副C:转动副与高副D:移动副与高副答案: 【低副与高副】2、单选题：由机械原理知识可知，电动自行车应属于 ( )选项：A:专用零件B:机构C:通用零件D:机器答案: 【机器】3、单选题：两构件通过点或线接触组成的运动副称为 ( )选项：A:高副B:移动副C:回转副D:低副答案: 【高副】4、单选题：将机构运动简图按实际长度放大一倍绘制，选用的长度比例尺应是 ( )选项：A:0.002m/mmB:0.005m/mmC:0.0002m/mmD:0.0005m/mm答案: 【0.0005m/mm】5、单选题：计算机构自由度时，如果没去除局部自由度，那么机构自由度的计算结果将会（）选项：A:增大B:减小C:都有可能D:不变答案: 【增大】6、判断题：构件是机构或机器中独立运动的单元体，也是机械原理研究的对象。

1.选择题
(8)凸轮机构若发生自锁，则其原因是______ 。 B A. 驱动力矩不够 B. 压力角太大 C. 基圆半径太小 (9)对于平底直动从动件盘形凸轮机构，移动导路的平移_____ C 。 A. 会改变从动件运动规律 B. 会影响机构压力角的大小 C. 不会影响从动件运动规律和机构压力角的大小
解： (1)凸轮偏心距。利用速度瞬心 ，几何 中心O即为速度瞬心p，可得ν=eω，求 得e=25mm。 90° k V （ 2 ）凸轮转过 90°时，从动件在 K 点 接触，其压力角为αk。 e/sinαk =R/sinθ；
hk
αk
α max
θ
(P) h F
当θ=90°时，αk达到最大值。
αk=arcsin(e/R)=30°
解： 具体解法如图（b）所示。
例6 ：图示为一直动推杆盘形凸轮机构。若一直凸轮 基圆半径r0，推杆的运动规律s=S(δ)，为使设计出的 凸轮机构受力状态良好，试结合凸轮机构压力角的计 算公式说明应采用哪些措施?
S,V, a 是确定的
推程
r0
O
ω
B
B
S
B
α
S0 δ
S δSS0α1O’ e O ω
O
（3）凸轮转过90°时，从动件的位移 为 h K。
（ 4 ）从动件在 F 点接触时为最大位移， 即行程为h，此时αF=0。
αF=0
例2 图（a）所示对心直动尖底从动件偏心圆盘凸轮机构，O为凸轮几何中心， O1为凸轮转动中心，直线AC⊥BD,O1O=OA/2，圆盘半径R=OA=60mm。（1） 根据图（a）及上述条件确定基圆半径r0，行程h， C点压力角αC和D点接触时的 压力角αD，位移hD；（2）若偏心圆盘凸轮几何尺寸不变，仅将从动件由尖底改 为滚子，见图（b）,滚子半径rr=10mm。试问，上述参数r0，h，αc，和hD，αD是 否改变？对于有改变的参数试分析其增大还是减小？

机械原理典型例题（第四章） ——连杆机构
2011.10
例1：铰链四杆机构，LBC=500，LCD=350， ：铰链四杆机构， ， ， LAD=300，AD为机架。问： 为机架。 ， 为机架 为曲柄， （1）若为曲柄摇杆机构，且AB为曲柄，求LAB的最 ）若为曲柄摇杆机构， 为曲柄 的最小值；（ ；（3） 大值；（ ；（2）若为双曲柄机构， 大值；（ ）若为双曲柄机构，求LAB的最小值；（ ） 若为双摇杆机构， 的取值范围。 若为双摇杆机构，求LAB的取值范围。 (1)曲柄摇杆机构： 曲柄摇杆机构： 曲柄摇杆机构 AB为曲柄，LAB=Lmin 为曲柄， 为曲柄 满足杆长条件L 满足杆长条件 AB+LBC≦LCD+LAD (2)双曲柄机构： 双曲柄机构： 双曲柄机构 AD杆为最短，LAD=Lmin ， 杆为最短， 杆为最短 满足杆长条件 ①Lmax=LBC， LAB<LBC， LAD+LBC≦LAB+LCD ②Lmax=LAB，LAB>LBC LAD+LAB≦LBC+LCD
1.选择题 选择题: 选择题
(6)对于 型曲柄摇杆机构，摇杆慢行程摆动方向与曲柄转向 A 对于I型曲柄摇杆机构 摇杆慢行程摆动方向与曲柄转向_____。 对于 型曲柄摇杆机构， 。 A. 相同 B.相反 相反 (7)对于 型曲柄摇杆机构，最小传动角出现在曲柄与机架 B 对于II 对于 型曲柄摇杆机构，最小传动角出现在曲柄与机架______ 共线位置。 共线位置。 A. 重叠 B. 拉直 (8)曲柄摇杆机构 曲柄摇杆机构________存在急回特性。 存在急回特性。 曲柄摇杆机构 存在急回特性 B A . 一定 B. 不一定 C. 一定不 (9)平面四杆机构所含移动副的个数最多为 B 平面四杆机构所含移动副的个数最多为________。 平面四杆机构所含移动副的个数最多为 。 A. 一个 B. 两个

pR12 M A
1ω O
ω 21
2
ω 23
3 pR32
B
P
4
2）确定ω21、ω23 的方向（如图）
pR12
A
ω 21
ω
M 1O
ω 23
2
3
B 4
P PR32
3）判断总反力应切于 A、B 处摩擦圆的上方还是下方（如图）
O
ω
1M
PR1
A
ω 21
2
ω 23
3 P
B 4 PR32
2.在图示曲柄滑块机构中 ，曲柄 1 在驱动力矩 M1 作用下等速转动。设已知各转动副的轴颈半径 r=10mm，当量摩擦系数 fv = 0.15 ，移动副中的滑块摩擦系数 f = 0.15 ，lAB = 100 mm，lBC = 350 mm。 各构件的质量和转动惯量忽略不计。当 M1 = 20 Nm 时，试求机构在图示位置所能克服的有效阻力 F3 及
uuur aBt 1 = 1× 55×102 = 5.5 m s2
uuuuur
ak B 2 B1
=
2
×10
×
0.55
=
11m
s2
uur a3
=
µα
.l p 'b2 '
=
0.2 ×
60
=
12
m
s2
4.已 知 图 所 示 的 机 构 的 尺 寸 及 ω 1＝
1rad/s，试用图解法求ω3，a3,vD和 aD。
FR 21 Q
=
sin(π + ϕ ) 2
sin(π − α − 2ϕ )
2
FR 21
=
sin 98.53° sin 12.94°

解：（1）、画出各 低副总反力的
R32 φ R43
3
Q β
方向；
4
R23 2
α1
(2)、画力平衡图
R21NBiblioteka 4 R41 NP R21 R41 0 P
R12
R23 R43 Q 0
R21
R41
构件1
6、在图示连杆机构中，已知：驱动力P沿NN方向向上指，移动副 的摩擦角φ已知（自定），图中各转动副的摩擦圆已知（如图）， 要求（1）、画出各低副总反力的方向（15）；
5、图示为一曲柄滑块块机构的某个位置，Ｐ为作用在活塞上的力， 转动副Ａ、Ｂ及C上所画的虚线小圆为摩擦圆，试决定在此位置 时作用在各构件上的作用力的真实方向（10）。
①、判断二力杆受力情况 ②、相对运动方向判断
ω23 3 ω34
③、运动副中总反力方向
4
4
R23
v R14
R34 3 R32
4
R43 R12
（2）、画出构件1、3之力平衡图
解：（1）、画出各 低副总反力的 方向；
R32
R302
3
4
(2)、画力平衡图
φ R43
Q β
R23 2
α
R21
1
R102 R12
P R21 R41 0 R23 R43 Q 0
Q R43
R23
构件2
NP 4 R41 N
填空题（每2分）
1、机构的静力分析是在 低速、轻型 条件下的力分析，而动态静力分析是 在 高速、重型 条件下的力分析。
2、两运动副的材料一定时，当量摩擦系数取决于 材料接触面接触情况
判断题（每2分）
2、当量摩擦系数fv与实际摩擦系数f 不同，是因为两物体接触面几何形状改 变，从而引起摩擦系数改变（ ）

补充题
1 如图所示，楔块机构中，已知γ ＝β ＝60°，Q＝1000N 格接触面摩擦系数 f＝0.15，如 Q 为 有效阻力，试求所需的驱动力 F。
解:对机构进行受力分析,并作出力三角形如图。 对楔块 1，
F F R 21 F R 31 0
由正弦定理有
sin(60o 2） sin(90o ） F FR 21
7-11 某内燃机的曲柄输出力矩 Md 随曲柄转角ψ 的变化曲线如图所示，其运动周期ψ T＝π ，曲 柄的平均转速 nm＝620r/min。当用该内燃机驱动一阻抗力为常数的机械时，如果要求其运转不均匀 系数δ ＝0.01。试求 1） 曲柄的最大转速 nmax 和相应的曲柄转角位置 φmax； 2） 装在曲轴上的飞轮转动惯量 JF（不计其余构件的转动惯量） 。
FR12
A ω 21 1 M 4 O 2 ω 23
ω
B F
3
FR32
解：上图构件 2 依然受压力。因在转动副 A 处 2、1 之间的夹角∠OAB 逐渐减小，故相对角速 度ω 21 沿顺时针方向，又因 2 受压力，故 FR12 应切于摩擦圆的下方；在转动副 B 处，2、3 之间的夹 角∠OBA 逐渐减小，故相对角速度ω 23 沿逆时针方向， FR32 应切于摩擦圆的下方。 4 O M 1 FR12 B
2
解法 3 根据运动副的自锁条件确定。 由于工件被夹紧后 P 力就被撤消，故楔块 3 的受力如图 b 所示，楔块 3 就如同一个受到 R23（此时为 驱动力）作用而沿水平面移动的滑块。故只要 R23 作用在摩擦角 φ 之内，楔块 3 即发生自锁。 R23 与垂直方向之间的夹角是 α-φ,要使 R23 作用在摩擦角 φ 之内,即
解：该系统的总效率为

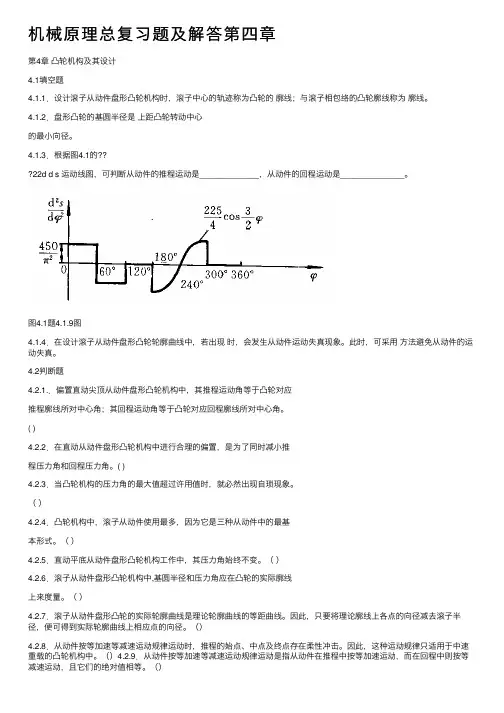
机械原理总复习题及解答第四章第4章凸轮机构及其设计4.1填空题4.1.1．设计滚⼦从动件盘形凸轮机构时，滚⼦中⼼的轨迹称为凸轮的廓线；与滚⼦相包络的凸轮廓线称为廓线。

4.1.2．盘形凸轮的基圆半径是上距凸轮转动中⼼的最⼩向径。

4.1.3．根据图4.1的??22d d s 运动线图，可判断从动件的推程运动是_____________，从动件的回程运动是______________。

图4.1题4.1.9图4.1.4．在设计滚⼦从动件盘形凸轮轮廓曲线中，若出现时，会发⽣从动件运动失真现象。

此时，可采⽤⽅法避免从动件的运动失真。

4.2判断题4.2.1.．偏置直动尖顶从动件盘形凸轮机构中，其推程运动⾓等于凸轮对应推程廓线所对中⼼⾓；其回程运动⾓等于凸轮对应回程廓线所对中⼼⾓。

( )4.2.2．在直动从动件盘形凸轮机构中进⾏合理的偏置，是为了同时减⼩推程压⼒⾓和回程压⼒⾓。

( )4.2.3．当凸轮机构的压⼒⾓的最⼤值超过许⽤值时，就必然出现⾃琐现象。

（）4.2.4．凸轮机构中，滚⼦从动件使⽤最多，因为它是三种从动件中的最基本形式。

（）4.2.5．直动平底从动件盘形凸轮机构⼯作中，其压⼒⾓始终不变。

（）4.2.6．滚⼦从动件盘形凸轮机构中,基圆半径和压⼒⾓应在凸轮的实际廓线上来度量。

（）4.2.7．滚⼦从动件盘形凸轮的实际轮廓曲线是理论轮廓曲线的等距曲线。

因此，只要将理论廓线上各点的向径减去滚⼦半径，便可得到实际轮廓曲线上相应点的向径。

（）4.2.8．从动件按等加速等减速运动规律运动时，推程的始点、中点及终点存在柔性冲击。

因此，这种运动规律只适⽤于中速重载的凸轮机构中。

（）4.2.9．从动件按等加速等减速运动规律运动是指从动件在推程中按等加速运动，⽽在回程中则按等减速运动，且它们的绝对值相等。

（）4.2.10．从动件按等速运动规律运动时，推程起始点存在刚性冲击，因此常⽤于低速的凸轮机构中。

（）4.2.11．在对⼼直动尖顶从动件盘形凸轮机构中，当从动件按等速运动规律运动时，对应的凸轮廓线是⼀条阿⽶德螺旋线。

题应注意的问题： • 解6-2题应注意的问题： 分解后的质径积的方向仍与原矢径方向一致， 1.分解后的质径积的方向仍与原矢径方向一致， 2.质径积分解公式： 质径积分解公式：
l I 面 W =mr : I L L−l I 面 WI = m I : I r L
式 ： −质 到 面 距 中 l 心 II 的 离 L−两 衡 之 距 平 面 间 离
F =3n−(2P + P ) l h =3×4−(2×5+1 =1 )
∴自由度为1，修改方 自由度为1 案能实现设计意图
习题解
3
2-2题 题
法： 1 F =3 −(2P + P ) −F1 n l h =3×8−(2× 0+2 −1=1 1 ) F1 局 自 度 为 部 由
法： 2 F =3 −(2P + P ) n l h =3×7−(2×9+2 =1 )
31
6 -2 作
解：根据动平衡条件有
m1r+ 2m2r22/3 +m3r32/3 +mbIrbI2=0
平衡基面I：mbI=5.7Kg，θbI=5.820 平衡基面I ， 同理平衡基面II： 同理平衡基面II：mbII=7063Kg，θbI=146.470 II ，
习题解
32
基面I质径积多边形： 基面I质径积多边形：
习题解
4
2-6题 题
虚约束数计算图
法： 1 虚 束 P' = 2P1 −3n1 = 2*10−3*6 = 2 约 ： L
∴F =3n−(2pl + ph −P' ) =3×11−(2×17−2) =1
法： 2 F =3n−2pl =3×5−2×7 =1

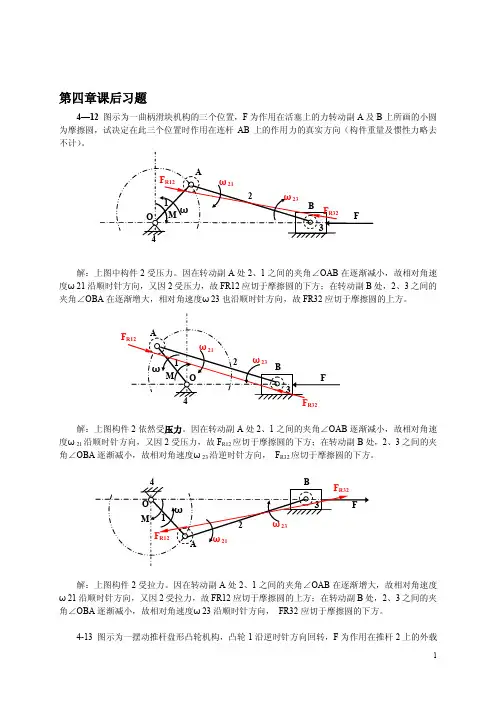
机械原理第四章答案【篇一：西北工业大学机械原理课后答案第4章】（a） (b)(c)解：(a)作铆钉机的机构运动简图及受力见下图（a）由构件3的力平衡条件有：fr?fr43?fr23?0?fr41?fd?0由构件1的力平衡条件有：fr21按上面两式作力的多边形见图（b）得??frfd?cot?（b）作压力机的机构运动简图及受力图见（c）由滑块5的力平衡条件有：?r65由构件2的力平衡条件有：r42 ?r45?0?r32?r12?0 其中 r42?r54按上面两式作力的多边形见图（d），得??gft(c) 对a点取矩时有 fr?a?fd?b ??其中a、b为fr、fd两力距离a 点的力臂。

??gftfdfr43rgdr41(a)(b)(d)解：1) 选定比例尺,?l?0.005绘制机构运动简图。

(图(a) )2）运动分析：以比例尺?v作速度多边形，如图 (b) 以比例尺?a作加速度多边形如图4-1 (c)ac??apc?23.44s2?210as2??aps2s2t?ancac2b?2???51502slbc?lbc3) 确定惯性力活塞3：fi3??m3as3??g3gac?3767(n) 方向与pc相反。

连杆2：fi32??m2as2??g2相反。

as2?5357(n) 方向与p?s2mi2??js2?2?218.8(n?m) （顺时针）总惯性力：fi?2?fi2?5357(n)lh2?mi2i2?0.04(m) (图(a) )(b)(c)解：1）求图a所示导轨副的当量摩擦系数fv，把重量g分解为g 左，g右g左?l2lg ， g右?1g ， fvg?ff左?ff右l1?l2l1?l2l?f??2??l1??fv??l1?l2l?f??2??l1??g??l1?l22）求图b所示转动副的摩擦圆半径?支反力fr左?l2lg ，fr右?1g l1?l2l1?l2假设支撑的左右两端均只在下半周上近似均匀接触。

机械原理习题集答案第一章：机械运动学1. 问题：简述平面运动的基本概念。

答案：平面运动是指物体在平面内的运动，其轨迹可以是直线或曲线。

在平面运动中，物体的每一个点都在同一平面内移动。

2. 问题：什么是四杆机构的运动规律？答案：四杆机构是最基本的机械机构之一，其运动规律取决于杆的长度和连接方式。

常见的四杆机构有双曲柄机构、曲柄滑块机构等。

第二章：机械动力学1. 问题：牛顿运动定律在机械设计中的应用是什么？答案：牛顿运动定律是描述物体运动的基本定律，包括惯性定律、力的作用与反作用定律和作用力与加速度的关系。

在机械设计中，这些定律用于预测和计算机械系统的运动状态和受力情况。

2. 问题：简述达朗贝尔原理。

答案：达朗贝尔原理是动力学中的一个基本原理，它指出在没有外力作用的系统中，系统内各部分的动量守恒。

在机械设计中，这一原理常用于分析和计算机械系统的动态平衡。

第三章：机构设计与分析1. 问题：什么是机构的自由度？答案：机构的自由度是指在没有约束的情况下，机构能够独立进行的运动的数量。

自由度的计算公式为：\( F = 3n - 2j - h \)，其中\( n \)是机构中杆件的数量，\( j \)是铰链的数量，\( h \)是高副的数量。

2. 问题：如何确定一个机构的运动类型？答案：确定机构的运动类型需要分析机构的几何形状和连接方式。

例如，如果机构中存在曲柄和滑块，它可能是一个曲柄滑块机构，其运动类型为往复直线运动。

第四章：机械结构设计1. 问题：机械结构设计中需要考虑哪些因素？答案：在机械结构设计中，需要考虑的因素包括材料的选择、强度和刚度的计算、尺寸的确定、成本控制、维护的便利性等。

2. 问题：什么是疲劳强度？答案：疲劳强度是指材料在反复加载和卸载过程中抵抗断裂的能力。

在机械结构设计中，需要考虑疲劳强度以确保结构的可靠性和耐久性。

第五章：机械传动1. 问题：什么是齿轮传动？答案：齿轮传动是一种利用齿轮啮合来传递运动和动力的机械传动方式。

《机械原理》第四章课后答案（孙恒版）回复关键词：机械原理即可获取其他章节答案资源第4章平面机构的力分析4-1何谓机构的动态静力分析?对机构进行动态静力分析的步骤如何?答: (1) 动态静力分析是指将惯性力视为一般外力加于相应构件上，再按静力学方法进行分析的过程。

(2)对机构进行动态静力学分析的步骤如下:①对机构作运动分析以确定在所要求位置时各构件的角加速度和质心加速度，求各构件的惯性力;②对机构进行拆分杆组，如有高副，应先进行高副低代;③从外力全部已知的构件组开始分析，逐步推算出未知构件;④对机构进行动态静力计算，求出运动副反力和平衡力的变化规律。

⑤如需考虑摩擦，可采用逐次逼近的方法。

4-2何谓质量代换法?进行质量代换的目的何在?动代换和静代换各应满足什么条件?各有何优缺点?静代换两代换点与构件质心不在一直线上可以吗?答: (1) 质量代换法是指为了简化构件惯性力的确定，把构件的质量按一定条件用集中于构件上某个选定点的假想集中质量来代替的方法。

(2)进行质量代换的目的简化惯性力的确定，代换后只需求各集中质量的惯性力，而无需求惯性力偶矩。

(3)动代换和静代换应满足的条件①动代换满足的条件:a.代换前后构件的质量不变;b.代换前后构件的质心位置不变;c.代换前后构件对质心轴的转动惯量不变。

②静动代换满足的条件:a.代换前后构件的质量不变;b.代换前后构件的质心位置不变。

采(4)动代换和静代换的优缺点①动代换的优缺点:a.优点代换后，构件的惯性力和惯性力偶都不会发生改变;b.缺点其代换点的位置不能随意选择，则会给工程计算带来不便。

②静代换的优缺点:a.优点代换后，构件的惯性力和惯性力偶都不会发生改变;b.缺点其代换点的位置不能随意选择，则会给工程计算带来不便。

②静代换的优缺点:a.优点两个代换点位置均可以任意选取，引起的误差能被一-般工程接受，常为工程上所采纳;b.缺点代换后，构件的惯性力偶会产生- -定误差。

第二章平面机构的结构分析题2-1 图a 所示为一简易冲床的初拟设计方案。

设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。

试绘出其机构运动简图（各尺寸由图上量取），分析是否能实现设计意图，并提出修改方案。

解：1)取比例尺,绘制机构运动简图。

(图2-1a) 2)要分析是否能实现设计意图,首先要计算机构的自由度。

尽管此机构有4个活动件，但齿轮1和凸轮2是固装在轴A 上，只能作为一个活动件，故3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数，此简易冲床不能运动，即不能实现设计意图。

分析：因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。

故需增加构件的自由度。

3)提出修改方案：可以在机构的适当位置增加一个活动构件和一个低副，或用一个高副来代替一个低副。

(1) 在构件3、4之间加一连杆及一个转动副(图2-1b)。

(2) 在构件3、4之间加一滑块及一个移动副(图2-1c)。

(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。

11(c)题2-1(d)54364(a)5325215436426(b)321讨论：增加机构自由度的方法一般是在适当位置上添加一个构件（相当于增加3个自由度）和1个低副（相当于引入2个约束），如图2-1（b ）（c ）所示，这样就相当于给机构增加了一个自由度。

用一个高副代替一个低副也可以增加机构自由度，如图2-1（d ）所示。

题2-2 图a 所示为一小型压力机。

图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O 连续转动。

在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C 轴上下摆动。

同时，又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。

最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。

第一章机构的组成和结构1-1 试画出图示平面机构的运动简图，并计算其自由度。

F＝3×3－2×4＝1 F＝3×3－2×4＝1F＝3×3－2×4＝1 F＝3×3－2×4＝11-2 计算图示平面机构的自由度。

将其中高副化为低副。

确定机构所含杆组的数目和级别，以及机构的级别。

（机构中的原动件用圆弧箭头表示。

）F＝3×7－2×10＝1 F＝3×7－2×10＝1含3个Ⅱ级杆组：6-7，4-5，2-3。

含3个Ⅱ级杆组：6-7，4-5，2-3。

该机构为Ⅱ级机构构件2、3、4连接处为复合铰链。

该机构为Ⅱ级机构F＝3×4－2×5－1＝1 F＝3×3－2×3－2＝1F＝3×5－2×7＝1（高副低代后） F＝3×5－2×7＝1（高副低代后）含1个Ⅲ级杆组：2-3-4-5。

含2个Ⅱ级杆组： 4-5，2-3。

该机构为Ⅲ级机构构件2、3、4连接处为复合铰链。

该机构为Ⅱ级机构F＝3×8－2×11－1＝1 F＝3×6－2×8－1＝1F＝3×9－2×13＝1（高副低代后）F＝3×7－2×10＝1（高副低代后）含4个Ⅱ级杆组：8-6，5-7，4-3，2-11。

含1个Ⅱ级杆组6-7。

该机构为Ⅱ级机构含1个Ⅲ级杆组2-3-4-5。

第二章 连 杆 机 构2-1 在左下图所示凸轮机构中，已知r = 50mm ，l OA =22mm ，l AC =80mm,︒=901ϕ，凸轮1的等角速度ω1=10rad/s ，逆时针方向转动。

试用瞬心法求从动件2的角速度ω2。

解：如右图，先观察得出瞬心P 13和P 23为两个铰链中心。

再求瞬心P 12：根据三心定理，P 12应在P 13与P 23的连线上，另外根据瞬心法，P 12应在过B 点垂直于构件2的直线上，过B 点和凸轮中心O 作直线并延长，与P 13、P 23连线的交点即为P 12。

4-2如图4-40所示，设已知四杆机构各构件的长度为a=300mm，b=600mm，c=450mm，d=500mm。

试问：（1）当取d为机架时，是否有曲柄存在，此时为什么机构？（2）若各杆长度不变，能否获得双曲柄机构和双摇杆机构？如何获得？（3）若a、b、c三杆长度不变，取杆d为机架，要获得曲柄摇杆机构，d的取值范围应为何值？解：（1）b为最长杆，a为最短杆满足杆长条件。

故机构有整转副。

且a为连架杆，故机构有曲柄存在，为曲柄摇杆机构。

（2）选择a杆为机架可以得到双曲柄机构。

选择c杆为机架可以得到双摇杆机构。

（3）若d为最长杆，则若b为最短杆，则故当时机构为曲柄摇杆机构。

4-5在如图4-41所示的连杆机构中，已知各构件的尺寸为：lAB=160mm，lBC=260mm，lCD=200mm，lAD=80mm，构件AB为原动件，沿顺时针方向匀速回转，试确定：（1）四杆机构ABCD的类型；（2）该机构的最小传动角γmin；（3）滑块F的行程速比系数K。

解：（1）lAD为最短杆，且为机架。

故该机构为双曲柄机构。

（2）故最小传动角γmin=13.33°。

（3）作图可知，极限位置时，曲柄位置的极位夹角θ=43°。

γγ+--=+--=⨯⨯=︒+-+=+-+=⨯⨯=︒222'222222''222()arccos 2260200(80160) arccos 2260200 13.33()arccos 2260200(80160) arccos 2260200 61.26BC CD AD AB BC CD BC CD AD AB BC CD4-6试设计一翻料四杆机构，其连杆机构BC=400mm ，连杆的两个位置关系如图4-22所示，要求机架AD 与B1C1平行，且在其下相距350mm 。

解：图解过程如图所示可得：AB=372.24mm ，CD=358.19mm ，AD=202.40mm 。