南京航空航天大学结构力学课后习题答案

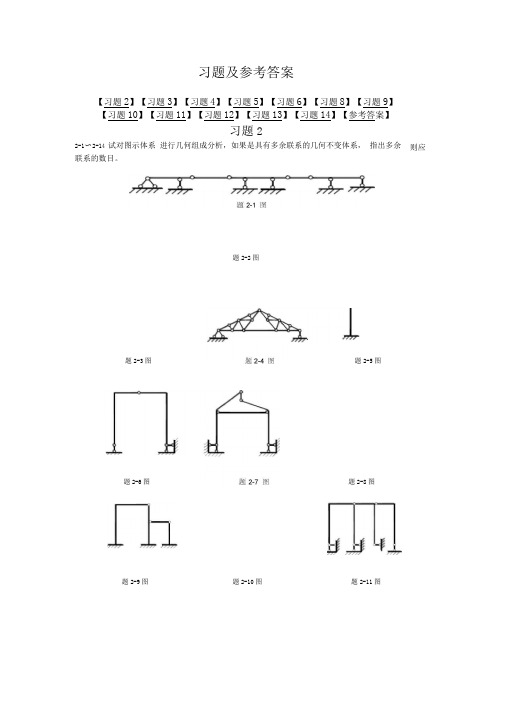
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1〜2-14 试对图示体系进行几何组成分析，如果是具有多余联系的几何不变体系，指出多余则应联系的数目。

题2-2图题2-3图题2-5图题2-6图题2-8图题2-9图题2-10图题2-11图题4-1图4-2 作图示刚架的M 图。

3-1 试作图示多跨静定梁的M 及Q 图。

习题(a)1.5m 1 2m I2.5m | 1.5m l 4.5m题3-1(b)3-2 试不计算反力而绘出梁的M 图。

4m40kN(a) 5kN/mM(b )4-1 作图示刚架的M 、Q 、N 图。

2kN /m2kN • m (a)2kN 题3-2习题4(b ) (c )4-3 4-4 4-54m(a)(d)作图示三铰刚架的M图。

M=4Pa2a(b)4kN4m 4m(c)珂10kN/m4m(e)题4-2图CE0.5m ]m2J 0.5m7mB7m(a)题4-3作图示刚架的M图。

(a)I 盒lUlUUW已知结构的M图，试绘出荷载。

10kN/m1.5m题4-4图urm*~ G3mC7.35m 7.35m(b)m6Nn m220kN40kN/m4m(b)C_PaPaPaa4-6 检查下列刚架的M图，并予以改正。

5-15-2 题4-5图(b)P(d)(e) (f)(c)题4-6图习题5图示抛物线三铰拱轴线方程4 f1kN/mx)x，(h)试求D截面的内力。

20kN10m题5-1图K15m j 5ml=30m带拉杆拱，拱轴线方程 y ，求截面的弯矩。

题5-3图习题66-1 判定图示桁架中的零杆。

6-2 6-3 6-4 6-5 用结点法计算图示桁架中各杆内力。

(b) (c)m题6-2用截面法计算图示桁架中指定各杆的内力。

3m [ 3m3m I 3m题6-3试求图示组合结构中各链杆的轴力并作受弯杆件的用适宜方法求桁架中指定杆内力。

7-1 图示为各种形式的薄壁梁剖面，设缘条（集中面积）承受正应力，壁板只受剪切，求： （1）剖面各点对x 轴的静矩S x ； （2）剖面对x 轴的惯性矩； （3）剖面的弯心位置。

（a ）解：剖面关于x 轴对称，x 轴是中心主轴。

（1）剖面各点对x 轴的静矩22121fHH f S S x x =⋅==- fH H f fH S x =⋅+=-2232 2243fHH f fH S x=⋅-=- （2）剖面对x 轴的惯性矩22)2(4fH H f J x == （3）剖面的弯心位置结构关于x 轴对称，弯心必在x 轴上 取点3为力矩中心，则：2)2(11241b b H fH fHd S J X s x x-=⋅⋅-⋅==⎰ρ 即剖面弯心位于2b x -=处（1）剖面各点对x 轴的静矩12233445563()28837828711828117()82873()828x x x x x H H S f fH H S fH f fH H S fH f fHH S fH f fH H S fH f fH -----=⋅-==+⋅==+⋅==+⋅-==+⋅-= 剪流沿1-2-3-4-5-6方向为正（2）剖面对x 轴的惯性矩2222412[()2()]28232x i i H H H J f y f f fH ==⋅-+⋅=∑ （3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在3-4杆左侧，距3-4杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和3-4杆交点处取矩，则1223455608228y H H H HQ X q b q b q b q b ----⋅-⋅⋅-⋅⋅-⋅⋅-⋅⋅= （1） 又知y x y xQ q S J =则（1）式可化为12234556131()822841x x x x x bH bH bH bH X S S S S b J ----=⋅+⋅+⋅+⋅=即结构弯心在x 轴上3-4杆左侧3141b 处题7-1b 图（1）剖面各点对x 轴的静矩12322545651221221122221()221()22x x x x x H S f fH H S f fH H S fH fH f H S f fHH S f fH-----=⋅==⋅==++⋅=⋅-=-=⋅-=- 剪流方向如图（2）剖面对x 轴的惯性矩22224()22()222x i i H HJ f y f f fH ==⋅+⋅⋅=∑（3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在2-5杆左侧，距2-5杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点 的合力矩为零现对x 轴和2-5杆交点处取矩，则12234556022222222y b H b H b H b HQ X q q q q ----⋅+⋅⋅-⋅⋅+⋅⋅-⋅⋅= （1）又知y x y xQ q S J =则（1）式可化为122345561()04444x x x xx bH bH bH bH X S S S S J ----=-⋅+⋅-⋅+⋅= 即结构弯心在x 轴上与2-5杆相交处题7-1c 图（1）剖面各点对x 轴的静矩x S fR =（2）剖面对x 轴的惯性矩222x i i J f y fR ==∑（3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上11Rx x xs X S ds fR ds J J πρρ=⋅=⋅⎰⎰（1）其中ρ为承受剪流的面积到x 轴的距离，取极坐标θ，记上缘条处0θ=，逆时针方向为正，则cos R ρθ=，代入（1）式得11cos cos 0RxxX fR R ds fR R Rd J J ππθθθ=⋅=⋅⋅=⎰⎰即剖面弯心在两缘条中心连线与x 轴的交点处题7-1d 图（1）剖面各点对x 轴的静矩122343355667871099714452424144515244225722227522221()441()44152()424x x x x x x x x x H S f fH fH H S f fHH S f fHH S fH fH f fHH S fH f fHH S fH f fHH S f fHH S f fHH S fH f fH---------=⋅==+⋅==⋅==++⋅==+⋅==-⋅==⋅-=-=⋅-=-=-+⋅-=- 剪流方向如图（2）剖面对x 轴的惯性矩2222134()62()224x i i H H J f y f f fH ==⋅+⋅⋅=∑ （3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在5-6杆右侧，距5-6杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和5-6杆交点处取矩，则1223433567()42422y H H H H HQ X q a b q a q b q b q b -----⋅-⋅⋅+-⋅⋅-⋅⋅-⋅⋅-⋅⋅ 7879910()0424H H Hq b q a q a b ----⋅⋅-⋅⋅-⋅⋅+= （1） 又知y x y xQ q S J =代入（1）式可得11(2)26X a b =+ 即结构弯心在x 轴上5-6杆右侧11(2)26a b +处 题7-1e 图7-2 题7－2图所示薄壁梁剖面，缘条承受正应力，其截面积为22cm f =。

复习思考题1结构动力计算与静力计算的区别是什么？答：区别是动力计算考虑的力系中包括惯性力，考虑的平衡是瞬时平衡。

2动力学中体系的自由度与几何组成分析中体系的自由度的概念有什么不同？动力学中体系的自由度如何确定？答：动力学中体系的自由度是确定全部质点与某一时刻的位置所需要的独立的几何参变量的数目。

几何组成分析中体系是指体系运动时可以独立变化的几何参数的个数，动力学中体系的自由度的确定，采用附加链杆法，即加入最少数量的链杆限制钢架上所有质点的位置，则该刚架的自由度数目等于所加入链杆数目。

4建立振动微分方程有哪两种基本方法？两种方法的物理意义是什么？答：是刚度法和柔度法。

物理意义，刚度法是动力平衡方法，柔度法是位置协调。

5在建立振动微分方程时，若考虑重力的影响，动位移方程有无变化？答：无变化，因为振动本身不考虑重力，动位移是从平衡位置算起的。

6为什么说自振频率和自振周期是结构的固有性质？它与结构的哪些因素有关？答：因为自振频率和自振周期跟体系是否振动无关，跟质量大小，质量分布，结构形式，结构跨度，材料，截面形式等有关。

7阻尼对结构的自振频率和振幅有什么影响？什么是临界阻尼系数？答：影响，（1）在阻尼比§<0.2的情况下，阻尼对自振频率的影响不大，可以忽略。

（2）由于阻尼的影响，振幅随时间而逐渐衰减，阻尼比§值越大，则衰减速度越快。

当阻尼比§<1时，体系在自由反应中是会引起振动的，而当阻尼增大到阻尼比§=1时，体系在自由度振动中即不再引起振动，这时的阻尼系数成为临界阻尼系数。

9在计算简谐荷载作用下体系的振幅时，在什么情况下阻尼的影响最大？答：在共振情况下阻尼的影响最大。

10何谓动力系数？动力系数与哪些因素有关？在什么情况下动力系数为负值？为负值的物理意义是什么？动力系数为考虑阻尼时的放大系数Ud ；动力系数Ud不仅与Ѳ和w 的比值有关，而且还与阻尼比§有关；无阻尼的动力系数可以为负值；物理意义为表现出共振现象。

第三章能量原理（习题解答）3-1写出下列弹性元件的应变能和余应变能的表达式。

（a ）等轴力杆；（b ）弯曲梁；（c ）纯剪矩形板。

解：（a ）等轴力杆 应变能 余应变能其中L 为杆的长度，f 为杆的截面积，△为杆的变形量，E 为材料的弹性模量。

（b ） 弯曲梁 应变能 余应变能（c ） 纯剪矩形板 应变能 余应变能3-2求图3-2所示桁架的应变能及应变余能，应力一应变之间的关系式为 (a) E (b)E,_解：取节点2进行受力分析，如图3-2a 所示 根据平衡条件，有U BdV fl dV联立（1）、（2）、（3）、（4）,得到桁架的应变能为 联立（1）、（2）、（3）、（5）,得到桁架的余应变能为(a ) E 时N 1 cos45 N 3COS 45N 1 si n45 N 3 sin 45PN 1p1BN1、2N巳P N 1 1f 13N 3f 3N ±3N 31Ef 1Ef 3 U v AdVfld(1)(2)(3) (4) (5)Nj 联立（1）、（2）、（4）、（6）,得到桁架的应变能为 联立（1）、（2）、（5）、（6）,得到桁架的应变能为3-3 一种假想的材料遵循如下二维的应力一应变规律 其中E 、G 和 是材料常数。

导出用这种材料做成的二维物体的应变能密度解：应变能密度 余应变能密度 总应变能密度 而 所以应变能密度为3-4试用虚位移原理或最小位能原理确定题3-4图所示平面桁架的节点 o的位置和各杆内力。

各杆材料相同，弹性常数为 E 。

P 1 104N ，P 2 5 103 N ，各杆截面积 f 1 1.5cm 2， f 2. 2cm 2，o-2 杆:系统位能 令 0,则——0，—— 0 ,从而：uv解得由N 旦^ ，得l3-5 试用最小位能原理导出承受均布载荷 q 的弯曲等截面梁（图3-5）的 平衡方程式。

解：由教科书例3-2知 悬臂梁的边界条件为： 在 x 0 处，w 0， dw 0dx在x l 处，剪力Q 0，弯矩M 0 又知u z 业（直法线假设）dx(b )3cm 2。

7-1 图示为各种形式的薄壁梁剖面，设缘条（集中面积）承受正应力，壁板只受剪切，求： （1）剖面各点对x 轴的静矩S x ； （2）剖面对x 轴的惯性矩； （3）剖面的弯心位置。

（a ）解：剖面关于x 轴对称，x 轴是中心主轴。

（1）剖面各点对x 轴的静矩22121fHH f S S x x =⋅==- fH H f fH S x =⋅+=-2232 2243fHH f fH S x=⋅-=- （2）剖面对x 轴的惯性矩22)2(4fH H f J x == （3）剖面的弯心位置结构关于x 轴对称，弯心必在x 轴上 取点3为力矩中心，则：2)2(11241b b H fH fHd S J X s x x-=⋅⋅-⋅==⎰ρ 即剖面弯心位于2b x -=处（1）剖面各点对x 轴的静矩12233445563()28837828711828117()82873()828x x x x x H H S f fH H S fH f fH H S fH f fHH S fH f fH H S fH f fH -----=⋅-==+⋅==+⋅==+⋅-==+⋅-= 剪流沿1-2-3-4-5-6方向为正（2）剖面对x 轴的惯性矩2222412[()2()]28232x i i H H H J f y f f fH ==⋅-+⋅=∑ （3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在3-4杆左侧，距3-4杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和3-4杆交点处取矩，则1223455608228y H H H HQ X q b q b q b q b ----⋅-⋅⋅-⋅⋅-⋅⋅-⋅⋅= （1） 又知y x y xQ q S J =则（1）式可化为12234556131()822841x x x x x bH bH bH bH X S S S S b J ----=⋅+⋅+⋅+⋅=即结构弯心在x 轴上3-4杆左侧3141b 处题7-1b 图（1）剖面各点对x 轴的静矩12322545651221221122221()221()22x x x x x H S f fH H S f fH H S fH fH f H S f fHH S f fH-----=⋅==⋅==++⋅=⋅-=-=⋅-=- 剪流方向如图（2）剖面对x 轴的惯性矩22224()22()222x i i H HJ f y f f fH ==⋅+⋅⋅=∑（3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在2-5杆左侧，距2-5杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点 的合力矩为零现对x 轴和2-5杆交点处取矩，则12234556022222222y b H b H b H b HQ X q q q q ----⋅+⋅⋅-⋅⋅+⋅⋅-⋅⋅= （1）又知y x y xQ q S J =则（1）式可化为122345561()04444x x x xx bH bH bH bH X S S S S J ----=-⋅+⋅-⋅+⋅= 即结构弯心在x 轴上与2-5杆相交处题7-1c 图（1）剖面各点对x 轴的静矩x S fR =（2）剖面对x 轴的惯性矩222x i i J f y fR ==∑（3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上11Rx x xs X S ds fR ds J J πρρ=⋅=⋅⎰⎰（1）其中ρ为承受剪流的面积到x 轴的距离，取极坐标θ，记上缘条处0θ=，逆时针方向为正，则cos R ρθ=，代入（1）式得11cos cos 0RxxX fR R ds fR R Rd J J ππθθθ=⋅=⋅⋅=⎰⎰即剖面弯心在两缘条中心连线与x 轴的交点处题7-1d 图（1）剖面各点对x 轴的静矩122343355667871099714452424144515244225722227522221()441()44152()424x x x x x x x x x H S f fH fH H S f fHH S f fHH S fH fH f fHH S fH f fHH S fH f fHH S f fHH S f fHH S fH f fH---------=⋅==+⋅==⋅==++⋅==+⋅==-⋅==⋅-=-=⋅-=-=-+⋅-=- 剪流方向如图（2）剖面对x 轴的惯性矩2222134()62()224x i i H H J f y f f fH ==⋅+⋅⋅=∑ （3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在5-6杆右侧，距5-6杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和5-6杆交点处取矩，则1223433567()42422y H H H H HQ X q a b q a q b q b q b -----⋅-⋅⋅+-⋅⋅-⋅⋅-⋅⋅-⋅⋅ 7879910()0424H H Hq b q a q a b ----⋅⋅-⋅⋅-⋅⋅+= （1） 又知y x y xQ q S J =代入（1）式可得11(2)26X a b =+ 即结构弯心在x 轴上5-6杆右侧11(2)26a b +处 题7-1e 图7-2 题7－2图所示薄壁梁剖面，缘条承受正应力，其截面积为22cm f =。

6－1 题6－1图所示平面桁架，各杆Ef 相同，求在载荷P 作用下桁架各杆的内力。

解：(1)解除约束：系统静不定度为K=1,故解除1-2杆的约束， 代之以约束力X 1，如图6-1a 所示。

（2）内力分析：求<<P>>状态下的内力N p 、 单位状态<<1>> 下的内力N 1，内力分别如图6-1b,6-1c 所示。

（3）求典型方程中的影响系数δ11和载荷系数△1PEfdEf l N i i )223(2111+===∑ δ EfPdEf l N N i i P P 2111-===∆∑（4）求解多余约束力X 1:由典型方程01111=∆+P X δ解得：PP d EfEf Pd X P 172.0)223()223(22/1111≈-=+=∆-=δ（5）用叠加原理11X N N N P +=求出各杆的内力PN N P N N P N N P N )12(;)222(;)22(;)223(45342414251312-==-==-==-=6-2 题6-2图所示平面桁架，杆长AD=DC=BC=1m,AC 杆和BD 杆的截面积A AC =A BD =200mm 2，A AD =A DC =A BC =150mm 2， 各杆材料均相同，E ＝200KN/mm 2，当C 点受垂直载荷P ＝100KN 作用时，求该结构各杆的内力。

解：（1）解除约束：系统静不定度为K=1,故解除CD 杆的约束， 代之以约束力X 1，如图6-2a 所示。

（2）内力分析：求<<P>>状态下的内力N p 、 单位状态<<1>>下的内力N 1，内力分别如图6-2b,6-2c 所示。

（3）求典型方程中的影响系数δ11和载荷系数△1P1150.0803342111≈+===∑ i i Ef l N δ4316.048093411-≈-===∆∑P Ef l N N i i P P （4）求解多余约束力X 1:由典型方程01111=∆+P X δ解得：755.3663437233480480934/1111≈--=+⨯--=∆-=P P X P δ（5）用叠加原理求出各杆的内力： 11X N N N P +=KN N C B 480.88=-KN N D B 252.3-=-748.46=-C A NKN N D A 877.1=-KN N D C 755.3=-如图6-2d 所示。

结构力学第2章习题及参考答案word文档，精心编排整理，均可修改你的满意，我的安心2第2章 习 题字体如需要请自己调整2-1 试判断图示桁架中的零杆。

2-1（a ）解 静定结构受局部平衡力作用，平衡力作用区域以外的构件均不受力。

所有零杆如图（a-1）所示。

2-1 (b)解 从A 点开始，可以依次判断AB 杆、BC 杆、CD 杆均为无结点荷载作用的结点单杆，都是零杆。

同理，从H 点开始，也可以依次判断HI 杆、IF 杆、FD 杆为零杆。

最后，DE 杆也变成了无结点荷载作用的结点D 的单杆，也是零杆。

所有零杆如图（b-1）所示。

(a-(a)(b)(b-32-1(c)解 该结构在竖向荷载下，水平反力为零。

因此，本题属对称结构承受对称荷载的情况。

AC 、FG 、EB 和ML 均为无结点荷载作用的结点单杆，都是零杆。

在NCP 三角形中，O 结点为“K ”结点，所以F N OG ＝－F N OH （a ）同理，G 、H 结点也为“K ”结点，故F N OG ＝－F N GH （b ） F N HG ＝－F N OH （c ）由式（a ）、（b ）和（c ）得(c-1)FN OG＝F N GH＝F N OH＝0同理，可判断在TRE三角形中FN SK＝F N KL＝F N SL＝0D结点也是“K”结点，且处于对称荷载作用下的对称轴上，故ID、JD杆都是零杆。

所有零杆如图（c-1）所示。

2-2试用结点法求图示桁架中的各杆轴力。

2-2(a)(a-33 3(a-33 345解 （1）判断零杆①二杆结点的情况。

N 、V 结点为无结点荷载作用的二杆结点，故NA 、NO 杆件和VI 、VU 杆件都是零杆；接着，O 、U 结点又变成无结点荷载作用的二杆结点，故OP 、OJ 、UT 、UM 杆件也是零杆。

②结点单杆的情况。

BJ 、DK 、QK 、RE 、HM 、SL 、LF 杆件均为无结点荷载作用的结点单杆，都是零杆；接着，JC 、CK 、GM 、LG 杆件又变成了无结点荷载作用的结点单杆，也都是零杆。

第二章 薄板的弯曲（习题解答）2-1 写出2-1图所示矩形薄板的边界条件。

OA 为简支边，并作用有分布的弯矩M 。

BC 边为固支边，OC 边为简支边。

AB 边为自由边。

解：OA 边：M x w D y w u x w D M w x x x x x -=∂∂-=∂∂+∂∂-======0220222200)(0；OC 边：0)(00220222200=∂∂-=∂∂+∂∂-======y y y y y y wD x w u y w D M w ；BC 边：00=∂∂===ax a x xww ；AB 边：0)(2222=∂∂+∂∂-===b y by yx wu y w D M0])2([)(2333=∂∂∂-+∂∂-=∂∂+==by by yx y y x w u y w D xM Q2-2 如图2-2所示，矩形薄板OA 边和OC 边为简支边，AB 和BC 为自由边，在点B 受向下的横向集中力P 。

试证w mxy =可作为该薄板的解答，并确定常数m 、内力及边界处反力。

解：mxy w =满足平衡微分方程0/4==∇D q wOC 边上：0)(0022220＝；==∂∂+∂∂-=y y x wu y w D wOA 边上：0)(0022220＝；==∂∂+∂∂-=x x y wu x w D wAB 边上：0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==by b y y x wu y w D x w u y w D ；BC 边上：0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==ax a x y x wu x w D y w u x w D ；在B 点上：P m u D y x wu D by a x -=--=∂∂∂--==)1(2)()1(2,2)1(2u D Pm -=⇒所以)1(2u D Pxyw -=0)(2222=∂∂+∂∂-=y wu x w D M x ；0)(2222=∂∂+∂∂-=x w u y w D M y ；2)1(2P y x w u D M xy-=∂∂∂--= ；02=∇∂∂-=w xD Q x ；02=∇∂∂-=w y D Q y P R R P y x wu D R O C AA ==-=∂∂∂--=；)()1(222-3 如图2-3所示，半椭圆形薄板，直线边界为简支边，曲线边界ACB 为固支边，承受横向载荷0q=q xa 。

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】「习题11】【习题12】【习题13】【习题14】【参考答衆】习题22-1〜2-14试对图示体系进行儿何组成分析，如果是只有多余联系的儿何不变体系，则应指出多余联系的数目。

d5∑° X 厂^τ"βH题2-2图ΓΛ题2-3图题2-5图题2-6图题2-1图H 2-9 图题2-10图题2-11图题2-12图题2-13图习题3试作图示多跨挣定梁的M及Q图。

(a) (b)题3-1图3-2试不计算反力而绘出梁的M图。

题3-2图习题44-1作图示刚架的M、Q、N图。

40fcN 40kN20kNm4-2作图示刚架的M图。

2OkN m SkN mSkXm 40fcN题4-1图4-3作图示三狡刚架的M图。

4-4作图示刚架的M图。

AEmJnIAr lD1题4-2图4-5己知结构的M图•试绘出荷载。

题4-4图3IOkNnlJ^1.5mC(a)题4-3日6erIB9 9题5-1图5-2带拉杆拱，拱轴线方程y= il(l-χ)χ,求截面K 的弯矩。

题5-2图5-3试求图示带拉杆的半圆三狡拱截面K 的内力・4-6检査F 列刚架的M 图，并予以改正。

题4-5图ω∙I ∣ULL∏ ∏ ⅛)题4-6图习题5图示抛物纟戈三铁拱轴线方程y = ff(l-x)x ，试求D 截面的内力。

IkNm15m [ 5m [ ICm 1=3OmC题5-3图习题6 6-1判定图示桁架中的零杆。

题6-1图6-2用结点法计算图示桁架中各杆内力。

(a) FGH月Λ4x4m=16m题6-2图6-3用截面法计算图示桁架中指定各杆的内力。

40kN题6-3图6-4试求图示组介结构中齐链杆的轴力并作受弯杆件的Q图。

2m ] 2m ]lm]lπ⅝] 2m [题6-4图6-5用适宜方法求桁架中指定杆内力。

题6-6图习题88-1试作图示悬臂梁的反力V B 、MB 及内力Q C 、MC 的影响线。