城中区一中2018-2019学年高三上学期11月月考数学试卷含答案

上城区第一中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 函数f （x ）=x 2﹣x ﹣2，x ∈[﹣5，5]，在定义域内任取一点x 0，使f （x 0）≤0的概率是（ ）A．B ．C ．D．2． 执行如图所示的程序框图，若输入的分别为0，1，则输出的（）A ．4B ．16C ．27D ．363． 若a ＞b ，则下列不等式正确的是（ ）A ．B ．a 3＞b 3C ．a 2＞b 2D ．a ＞|b|4． 已知tanx=，则sin 2（+x ）=（ ）A ．B ．C ．D ．5． 设双曲线焦点在y 轴上，两条渐近线为，则该双曲线离心率e=（）A ．5B ．C ．D ．6． 已知函数f （x ）的图象如图，则它的一个可能的解析式为（）A ．y=2B ．y=log 3（x+1）C ．y=4﹣D ．y=班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________7． 已知函数f （x ）=x （1+a|x|）．设关于x 的不等式f （x+a ）＜f （x ）的解集为A ，若，则实数a 的取值范围是（ ）A ．B ．C ．D ．8． 设F 1，F 2分别是椭圆+=1（a ＞b ＞0）的左、右焦点，过F 2的直线交椭圆于P ，Q 两点，若∠F 1PQ=60°，|PF 1|=|PQ|，则椭圆的离心率为（ ）A ．B ．C ．D ．9． 数列{a n }满足a n+2=2a n+1﹣a n ，且a 2014，a 2016是函数f （x ）=+6x ﹣1的极值点，则log 2（a 2000+a 2012+a 2018+a 2030）的值是（ ）A ．2B ．3C ．4D ．510．已知函数，关于的方程（）有3个相异的实数根，则的()x e f x x=x 2()2()10f x af x a -+-=a R Îa 取值范围是（）A ．B ．C ．D ．21(,)21e e -+¥-21(,)21e e --¥-21(0,21e e --2121e e ìü-ïïí-ïïîþ【命题意图】本题考查函数和方程、导数的应用等基础知识，意在考查数形结合思想、综合分析问题解决问题的能力．11．抛物线y=﹣8x 2的准线方程是（ ）A．y=B ．y=2C ．x=D ．y=﹣212．设m ，n 是正整数，多项式（1﹣2x ）m +（1﹣5x ）n 中含x 一次项的系数为﹣16，则含x 2项的系数是（ ）A ．﹣13B ．6C ．79D ．37二、填空题13．已知函数的一条对称轴方程为，则函数的最大值为21()sin cos sin 2f x a x x x =-+6x π=()f x ___________．【命题意图】本题考查三角变换、三角函数的对称性与最值，意在考查逻辑思维能力、运算求解能力、转化思想与方程思想．14．若与共线，则y= ．15．已知实数x ，y 满足，则目标函数z=x ﹣3y 的最大值为 16．【2017-2018第一学期东台安丰中学高三第一次月考】函数的单调递增区间为__________．()2ln f x x x =-17．设函数，其中[x]表示不超过x 的最大整数．若方程f （x ）=ax 有三个不同的实数根，则实数a 的取值范围是 ． 18．若点p （1，1）为圆（x ﹣3）2+y 2=9的弦MN 的中点，则弦MN 所在直线方程为　三、解答题19．在四棱锥E ﹣ABCD 中，底面ABCD 是边长为1的正方形，AC 与BD 交于点O ，EC ⊥底面ABCD ，F 为BE 的中点．（Ⅰ）求证：DE ∥平面ACF ；（Ⅱ）求证：BD ⊥AE．20．（本小题满分12分）如图，在直二面角中，四边形是矩形，，，是以为直角顶C AB E --ABEF 2=AB 32=AF ABC ∆A 点的等腰直角三角形，点是线段上的一点，．P BF 3=PF （1）证明：面；⊥FB PAC （2）求异面直线与所成角的余弦值．PC AB PCABEF21．设点P的坐标为（x﹣3，y﹣2）．（1）在一个盒子中，放有标号为1，2，3的三张卡片，现在从盒子中随机取出一张卡片，记下标号后把卡片放回盒中，再从盒子中随机取出一张卡片记下标号，记先后两次抽取卡片的标号分别为x、y，求点P在第二象限的概率；（2）若利用计算机随机在区间上先后取两个数分别记为x、y，求点P在第三象限的概率．22．已知数列{a n}满足a1=，a n+1=a n+，数列{b n}满足b n=（Ⅰ）证明：b n∈（0，1）（Ⅱ）证明：=（Ⅲ）证明：对任意正整数n有a n．23．（本小题满分12分）2014年7月16日，中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》，报告显示：我国网3.32络购物用户已达亿．为了了解网购者一次性购物金额情况，某统计部门随机抽查了6月1日这一天1000.4名网购者的网购情况，得到如下数据统计表．已知网购金额在2000元以上（不含2000元）的频率为．（Ⅰ）确定，，，的值；x y p q （Ⅱ）为进一步了解网购金额的多少是否与网龄有关，对这100名网购者调查显示：购物金额在2000元以上的网购者中网龄3年以上的有35人，购物金额在2000元以下（含2000元）的网购者中网龄不足3年的有20人．①请将列联表补充完整；网龄3年以上网龄不足3年合计购物金额在2000元以上35购物金额在2000元以下20合计100②并据此列联表判断，是否有%的把握认为网购金额超过2000元与网龄在三年以上有关？97.5参考数据：()2k P K ≥0.150.100.050.0250.0100.0050.001k2.0722.7063.8415.0246.6357.87910.828（参考公式：，其中）()()()()()22n ad bc a b c d a c b d -K =++++n a b c d =+++24．已知椭圆E 的长轴的一个端点是抛物线y 2=4x 的焦点，离心率是．（1）求椭圆E 的标准方程；（2）已知动直线y=k （x+1）与椭圆E 相交于A 、B 两点，且在x 轴上存在点M ，使得与k 的取值无关，试求点M 的坐标．上城区第一中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题1．【答案】C【解析】解：∵f（x）≤0⇔x2﹣x﹣2≤0⇔﹣1≤x≤2，∴f（x0）≤0⇔﹣1≤x0≤2，即x0∈[﹣1，2]，∵在定义域内任取一点x0，∴x0∈[﹣5，5]，∴使f（x0）≤0的概率P==故选C【点评】本题考查了几何概型的意义和求法，将此类概率转化为长度、面积、体积等之比，是解决问题的关键　2．【答案】D【解析】【知识点】算法和程序框图【试题解析】A=0，S=1，k=1，A=1，S=1，否；k=3，A=4，S=4，否；k=5，A=9，S=36，是，则输出的36。

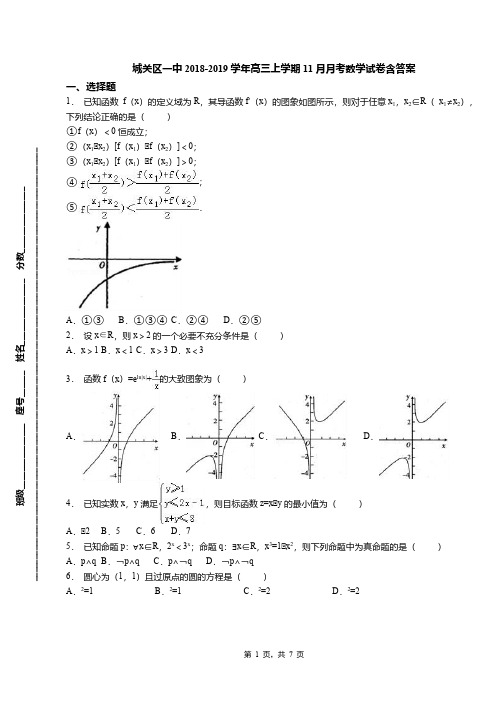
城关区一中2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 已知函数 f （x ）的定义域为R ，其导函数f ′（x ）的图象如图所示，则对于任意x 1，x 2∈R （ x 1≠x 2），下列结论正确的是（ ）①f （x ）＜0恒成立；②（x 1﹣x 2）[f （x 1）﹣f （x 2）]＜0；③（x 1﹣x 2）[f （x 1）﹣f （x 2）]＞0；④；⑤．A ．①③B ．①③④C ．②④D ．②⑤2． 设x ∈R ，则x ＞2的一个必要不充分条件是（ ）A ．x ＞1B ．x ＜1C ．x ＞3D ．x ＜33． 函数f （x ）=e ln|x|+的大致图象为（）A ．B ．C ．D ．4． 已知实数x ，y 满足，则目标函数z=x ﹣y 的最小值为（ ）A ．﹣2B ．5C ．6D ．75． 已知命题p ：∀x ∈R ，2x ＜3x ；命题q ：∃x ∈R ，x 3=1﹣x 2，则下列命题中为真命题的是（ ）A ．p ∧qB ．￢p ∧qC ．p ∧￢qD ．￢p ∧￢q6． 圆心为（1，1）且过原点的圆的方程是（）A ．2=1B ．2=1C ．2=2D ．2=2班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________7． 现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张，从中任取3张，要求取出的这些卡片不能是同一种颜色，且红色卡片至多1张，不同取法的种数为（ ）A ．232B ．252C ．472D ．4848． 已知e 是自然对数的底数，函数f （x ）=e x +x ﹣2的零点为a ，函数g （x ）=lnx+x ﹣2的零点为b ，则下列不等式中成立的是（ ）A ．a ＜1＜b B ．a ＜b ＜1C ．1＜a ＜bD ．b ＜1＜a9． 已知，，其中是虚数单位，则的虚部为（ ）i z 311-=i z +=32i 21z z A ．B ．C ．D ．1-54i -i 54【命题意图】本题考查复数及共轭复数的概念，复数除法的运算法则，主要突出对知识的基础性考查，属于容易题.10的倾斜角为（ ）10y -+=A ．B ．C ．D ．150o120o60o30o11．两座灯塔A 和B 与海洋观察站C 的距离都等于a km ，灯塔A 在观察站C 的北偏东20°，灯塔B 在观察站C 的南偏东40°，则灯塔A 与灯塔B 的距离为（ ）A ．akmB ．akm C ．2akmD ． akm12．已知函数有两个零点，则实数的取值范围是（ ）1()1x f x ae x a -=+--a A ．B ．C ．D ．[1,1]-[0,1]{1}(0,1]-U {1}[0,1)-U 二、填空题13．曲线y ＝x 2＋3x 在点（－1，－2）处的切线与曲线y ＝ax ＋ln x 相切，则a ＝________．14．数列{ a n }中，a 1＝2，a n ＋1＝a n ＋c （c 为常数），{a n }的前10项和为S 10＝200，则c ＝________．15．函数y=lgx 的定义域为 ．16．如图，正方形的边长为1，它是水平放置的一个平面图形的直观图，则原图的''''O A B C cm 周长为．1111]17．已知f （x ）＝x （e x ＋a e －x ）为偶函数，则a ＝________．18．抛物线的准线与双曲线的两条渐近线所围成的三角形面积为__________三、解答题19．已知函数f （x ）=|2x ﹣a|+|x ﹣1|．（1）当a=3时，求不等式f （x ）≥2的解集；（2）若f （x ）≥5﹣x 对∀x ∈R 恒成立，求实数a 的取值范围．20．设函数f （x ）=|x ﹣a|﹣2|x ﹣1|．（Ⅰ）当a=3时，解不等式f （x ）≥1；（Ⅱ）若f （x ）﹣|2x ﹣5|≤0对任意的x ∈[1，2]恒成立，求实数a 的取值范围．21．（本小题满分12分）某校高二奥赛班名学生的物理测评成绩（满分120分）分布直方图如下，已知分数在100-110的学生N 数有21人.（1）求总人数和分数在110-115分的人数；N （2）现准备从分数在110-115的名学生（女生占）中任选3人，求其中恰好含有一名女生的概率；13（3）为了分析某个学生的学习状态，对其下一阶段的学生提供指导性建议，对他前7次考试的数学成绩（满分150分），物理成绩进行分析，下面是该生7次考试的成绩.y 数学888311792108100112物理949110896104101106已知该生的物理成绩与数学成绩是线性相关的，若该生的数学成绩达到130分，请你估计他的物理y 成绩大约是多少？附：对于一组数据，……，其回归线的斜率和截距的最小二乘估计分11(,)u v 22(,)u v (,)n n u v v u αβ=+别为：，.^121()()niii nii u u v v u u β==--=-∑∑^^a v u β=-22．为了了解湖南各景点在大众中的熟知度，随机对15～65岁的人群抽样了n人，回答问题“湖南省有哪几个著名的旅游景点？”统计结果如下图表．组号分组回答正确的人数回答正确的人数占本组的频率第1组[15，25）a0.5第2组[25，35）18x第3组[35，45）b0.9第4组[45，55）90.36第5组[55，65]3y（Ⅰ）分别求出a，b，x，y的值；（Ⅱ）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，求第2，3，4组每组各抽取多少人？（Ⅲ）在（Ⅱ）抽取的6人中随机抽取2人，求所抽取的人中恰好没有第3组人的概率．23．某单位为了了解用电量y度与气温x℃之间的关系，随机统计了某4天的用电量与当天气温．气温（℃）141286用电量（度）22263438（1）求线性回归方程；（）（2）根据（1）的回归方程估计当气温为10℃时的用电量．附：回归直线的斜率和截距的最小二乘法估计公式分别为：=，=﹣．　24．某电脑公司有6名产品推销员，其工作年限与年推销金额的数据如表：推销员编号12345工作年限x/年35679推销金额y/万元23345（1）以工作年限为自变量x，推销金额为因变量y，作出散点图；（2）求年推销金额y关于工作年限x的线性回归方程；（3）若第6名推销员的工作年限为11年，试估计他的年推销金额．城关区一中2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题题号12345678910答案D A CABDCABC题号1112答案DD二、填空题13．14．15．　{x|x ＞0}　． 16．8cm 17．18．三、解答题19． 20．21．（1），；（2）；（3）.60N =6n =815P =11522． 23． 24．。

城区高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 如果定义在R 上的函数)(x f 满足：对于任意21x x ≠，都有)()(2211x f x x f x +)()(1221x f x x f x +>，则称)(x f 为“H 函数”．给出下列函数：①13++-=x x y ；②)cos sin (23x x x y --=；③1+=x e y ；④⎩⎨⎧=≠=00||ln x x x y ，其中“H 函数”的个数是（ ）A ．4B ．3C ．2D ．12． 已知定义在区间[0，2]上的函数y=f （x ）的图象如图所示，则y=f （2﹣x ）的图象为（ ）A． B． C． D．3． 若等式（2x ﹣1）2014=a 0+a 1x+a 2x 2+…+a 2014x 2014对于一切实数x 都成立，则a 0+1+a 2+…+a 2014=（ ）A． B． C． D ．04． 下列说法正确的是（ ）A.圆锥的侧面展开图是一个等腰三角形；B.棱柱即是两个底面全等且其余各面都是矩形的多面体；C.任何一个棱台都可以补一个棱锥使他们组成一个新的棱锥；D.通过圆台侧面上的一点，有无数条母线.5． 若动点A ，B 分别在直线l 1：x+y ﹣7=0和l 2：x+y ﹣5=0上移动，则AB 的中点M 到原点的距离的最小值为（ ） A ．3B ．2C ．3D ．46． 已知直线mx ﹣y+1=0交抛物线y=x 2于A 、B 两点，则△AOB （ ）A ．为直角三角形B ．为锐角三角形C ．为钝角三角形D ．前三种形状都有可能7． 在正方体ABCD ﹣A 1B 1C 1D 1中，点E ，F 分别是棱AB ，BB 1的中点，则异面直线EF 和BC 1所成的角是（ ）班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A ．60°B ．45°C ．90°D ．120°8． “p q ∨为真”是“p ⌝为假”的（ ）条件A ．充分不必要B ．必要不充分C ．充要D ．既不充分也不必要 9． 随机变量x 1～N （2，1），x 2～N （4，1），若P （x 1＜3）=P （x 2≥a ），则a=（ ） A ．1 B ．2 C ．3 D ．410．下列各组函数中，表示同一函数的是（ ）A 、()f x =x 与()f x =2x xB 、()1f x x =- 与()f x =C 、()f x x =与()f x = D 、()f x x =与2()f x =11．已知α，β为锐角△ABC 的两个内角，x ∈R ，f （x ）=（）|x ﹣2|+（）|x ﹣2|，则关于x 的不等式f （2x ﹣1）﹣f （x+1）＞0的解集为（ ）A ．（﹣∞，）∪（2，+∞）B ．（，2）C ．（﹣∞，﹣）∪（2，+∞）D ．（﹣，2）12．在ABC ∆中，222sin sin sin sin sin A B C B C ≤+-，则A 的取值范围是（ ）1111] A ．(0,]6πB ．[,)6ππ C. (0,]3π D ．[,)3ππ 二、填空题13．若正方形P 1P 2P 3P 4的边长为1，集合M={x|x=且i ，j ∈{1，2，3，4}}，则对于下列命题：①当i=1，j=3时，x=2； ②当i=3，j=1时，x=0；③当x=1时，（i ，j ）有4种不同取值； ④当x=﹣1时，（i ，j ）有2种不同取值； ⑤M 中的元素之和为0．其中正确的结论序号为 ．（填上所有正确结论的序号）14．某高中共有学生1000名，其中高一年级共有学生380人，高二年级男生有180人.如果在全 校学生中抽取1名学生，抽到高二年级女生的概率为19.0，先采用分层抽样（按年级分层）在全校抽取 100人，则应在高三年级中抽取的人数等于 .15．如图，在三棱锥P ABC -中，PA PB PC ==，PA PB ⊥，PA PC ⊥，PBC △为等边三角形，则PC 与平面ABC 所成角的正弦值为______________.【命题意图】本题考查空间直线与平面所成角的概念与计算方法，意在考查学生空间想象能力和计算能力． 16．图中的三个直角三角形是一个体积为20的几何体的三视图，则h =__________.17．运行如图所示的程序框图后，输出的结果是18．已知一组数据1x ，2x ，3x ，4x ，5x 的方差是2，另一组数据1ax ，2ax ，3ax ，4ax ，5ax （0a >）的标准差是a = ．三、解答题19．（本小题满分12分）设函数()()2741201x x f x a a a --=->≠且.（1）当a =()0f x <的解集； （2）当[]01x ∈，时，()0f x <恒成立，求实数的取值范围．20．为了预防流感，某学校对教室用药熏消毒法进行消毒．已知药物释放过程中，室内每立方米空气中的含药量y （毫克）与时间t （小时）成正比；药物释放完毕后，y 与t 的函数关系式为1()16t ay -=（a 为常数），如图所示．据图中提供的信息，回答下列问题：（1）写出从药物释放开始，每立方米空气中的含药量y （毫克）与时间t （小时）之间的函数关系式； （2）据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室。

城区实验中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 曲线y=在点（1，﹣1）处的切线方程为（ ）A ．y=x ﹣2B ．y=﹣3x+2C ．y=2x ﹣3D ．y=﹣2x+12． 如果定义在R 上的函数)(x f 满足：对于任意21x x ≠，都有)()(2211x f x x f x +)()(1221x f x x f x +>，则称)(x f 为“H 函数”．给出下列函数：①13++-=x x y ；②)cos sin (23x x x y --=；③1+=x e y ；④⎩⎨⎧=≠=000||ln x x x y ，其中“H 函数”的个数是（ ）A ．4B ．3C ．2D ．13． 下列函数中，既是偶函数又在(0,)+∞单调递增的函数是（ ）A ．3y x =B ． 21y x =-+C ．||1y x =+D ．2x y -=4． 已知 m 、n 是两条不重合的直线，α、β、γ是三个互不重合的平面，则下列命题中 正确的是（ ） A ．若 m ∥α，n ∥α，则 m ∥n B ．若α⊥γ，β⊥γ，则 α∥βC ．若m ⊥α，n ⊥α，则 m ∥nD ．若 m ∥α，m ∥β，则 α∥β5． 在《张邱建算经》中有一道题：“今有女子不善织布，逐日所织的布比同数递减，初日织五尺， 末一日织一尺，计织三十日”，由此推断，该女子到第10日时，大约已经完成三十日织布总量的（ ） A ．33% B ．49% C ．62% D ．88% 6． 已知函数f （x ）=lnx+2x ﹣6，则它的零点所在的区间为（ ） A ．（0，1） B ．（1，2） C ．（2，3） D ．（3，4） 7． 如图，已知平面=，．是直线上的两点，是平面内的两点，且，，，．是平面上的一动点，且有，则四棱锥体积的最大值是（ ）A ．B ．C ．D ．8． 已知a ＞b ＞0，那么下列不等式成立的是（ ）A ．﹣a ＞﹣bB ．a+c ＜b+cC ．（﹣a ）2＞（﹣b ）2D．9． 如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别为（ ）班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A．10 13 B．12.5 12 C．12.5 13 D．10 1510．已知圆C：x2+y2﹣2x=1，直线l：y=k（x﹣1）+1，则l与C的位置关系是（）A．一定相离 B．一定相切C．相交且一定不过圆心D．相交且可能过圆心11．（m+1）x2﹣（m﹣1）x+3（m﹣1）＜0对一切实数x恒成立，则实数m的取值范围是（）A．（1，+∞）B．（﹣∞，﹣1）C．D．12．已知曲线C1：y=e x上一点A（x1，y1），曲线C2：y=1+ln（x﹣m）（m＞0）上一点B（x2，y2），当y1=y2时，对于任意x1，x2，都有|AB|≥e恒成立，则m的最小值为（）A．1 B．C．e﹣1 D．e+1二、填空题13．不等式的解集为．14．已知f（x）=，若不等式f（x﹣2）≥f（x）对一切x∈R恒成立，则a的最大值为．15．设a抛掷一枚骰子得到的点数，则方程x2+ax+a=0有两个不等实数根的概率为．16．平面内两定点M（0，一2）和N（0,2），动点P（x，y）满足，动点P的轨迹为曲线E，给出以下命题：①∃m，使曲线E过坐标原点；②对∀m，曲线E与x轴有三个交点；③曲线E只关于y轴对称，但不关于x轴对称；④若P、M、N三点不共线，则△PMN周长的最小值为＋4;⑤曲线E上与M,N不共线的任意一点G关于原点对称的另外一点为H，则四边形GMHN的面积不大于m。

上城区一中2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 设函数f （x ）=则不等式f （x ）＞f （1）的解集是（ ）A ．（﹣3，1）∪（3，+∞）B ．（﹣3，1）∪（2，+∞）C ．（﹣1，1）∪（3，+∞）D ．（﹣∞，﹣3）∪（1，3）2． 如图F 1、F 2是椭圆C 1：+y 2=1与双曲线C 2的公共焦点，A 、B 分别是C 1、C 2在第二、四象限的公共点，若四边形AF 1BF 2为矩形，则C 2的离心率是（ ）A ．B ．C ．D ．3． 若复数z 满足iz=2+4i ，则在复平面内，z 对应的点的坐标是（ ） A ．（2，4） B ．（2，﹣4）C ．（4，﹣2）D ．（4，2）4． 已知回归直线的斜率的估计值是1.23，样本点的中心为（4，5），则回归直线的方程是（ ）A ． =1.23x+4B ． =1.23x ﹣0.08C ． =1.23x+0.8D ． =1.23x+0.08 5． 在ABC ∆中，22tan sin tan sin A B B A =，那么ABC ∆一定是（ ）A ．锐角三角形B ．直角三角形C ．等腰三角形D ．等腰三角形或直角三角形6． 已知幂函数y=f （x ）的图象过点（，），则f （2）的值为（ ）A ．B ．﹣C ．2D ．﹣27． 执行如图所示的程序框图，若输出的S=88，则判断框内应填入的条件是（ ）班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A．k＞7 B．k＞6 C．k＞5 D．k＞48．5名运动员争夺3项比赛冠军（每项比赛无并列冠军），获得冠军的可能种数为（）A．35B．C．D．539．已知a＞b＞0，那么下列不等式成立的是（）A．﹣a＞﹣b B．a+c＜b+c C．（﹣a）2＞（﹣b）2D．10．在10201511xx⎛⎫++⎪⎝⎭的展开式中，含2x项的系数为（）（A）10（B ）30（C）45（D）12011．设a=lge，b=（lge）2，c=lg，则（）A．a＞b＞c B．c＞a＞b C．a＞c＞b D．c＞b＞a12．设函数的集合，平面上点的集合，则在同一直角坐标系中，P中函数的图象恰好经过Q中两个点的函数的个数是A4B6C8D10二、填空题13．设S n 是数列{a n }的前n 项和，且a 1=﹣1， =S n ．则数列{a n }的通项公式a n = ．14．意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…其中从第三个数起，每一个数都等于他前面两个数的和．该数列是一个非常美丽、和谐的数列，有很多奇妙的属性．比如：随着数列项数的增加，前一项与后一项之比越逼近黄金分割0.6180339887…．人们称该数列{a n }为“斐波那契数列”．若把该数列{a n }的每一项除以4所得的余数按相对应的顺序组成新数列{b n }，在数列{b n }中第2016项的值是 ．15．【泰州中学2018届高三10月月考】设函数()f x '是奇函数()f x 的导函数，()10f -=，当0x >时，()()0xf x f x -<'，则使得()0f x >成立的x 的取值范围是__________．16．函数y=sin 2x ﹣2sinx 的值域是y ∈ ．17．由曲线y=2x 2，直线y=﹣4x ﹣2，直线x=1围成的封闭图形的面积为 ．18．抛物线y=4x 2的焦点坐标是 ．三、解答题19．已知函数f （x ）=，求不等式f （x ）＜4的解集．20．如图，在四棱锥P ﹣ABCD 中，平面PAD ⊥平面ABCD ，AB=AD ，∠BAD=60°，E 、F 分别是AP 、AD 的中点，求证：（1）直线EF ∥平面PCD ； （2）平面BEF ⊥平面PAD ．21．△ABC 的三个内角A 、B 、C 所对的边分别为a 、b 、c ，asinAsinB+bcos 2A=a ．（Ⅰ）求；（Ⅱ）若c 2=b 2+a 2，求B ．22．（本小题满分12分）某超市销售一种蔬菜，根据以往情况，得到每天销售量的频率分布直方图如下：（Ⅰ）求频率分布直方图中的a 的值，并估计每天销售量的中位数；（Ⅱ）这种蔬菜每天进货当天必须销售，否则只能作为垃圾处理．每售出1千克蔬菜获利4元，未售出的蔬菜，每千克亏损2元．假设同一组中的每个数据可用该组区间的中点值代替，估计当超市每天的进货量为75千克时获利的平均值．23．已知斜率为1的直线l 经过抛物线y 2=2px （p ＞0）的焦点F ，且与抛物线相交于A ，B 两点，|AB|=4．（I ）求p 的值；（II ）若经过点D （﹣2，﹣1），斜率为k 的直线m 与抛物线有两个不同的公共点，求k 的取值范围．千克24．已知函数f（x）=log a（x2+2），若f（5）=3；（1）求a的值；（2）求的值；（3）解不等式f（x）＜f（x+2）．上城区一中2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题13． ．14． 0 ．15．()(),10,1-∞-⋃ 16． [﹣1，3] ．17． ．18． ．三、解答题19． 20． 21．22．（本小题满分12分）解：本题考查频率分布直方图，以及根据频率分布直方图估计中位数与平均数． （Ⅰ）由(0.0050.0150.020.025)101a ++++⨯=得0.035a = （3分）每天销售量的中位数为0.15701074.30.35+⨯=千克 （6分） （Ⅱ）若当天的销售量为[50,60)，则超市获利554202180⨯-⨯=元；若当天的销售量为[60,70)，则超市获利654102240⨯-⨯=元； 若当天的销售量为[70,100)，则超市获利754300⨯=元， （10分） ∴获利的平均值为0.151800.22400.65300270⨯+⨯+⨯=元. （12分） 23．24．。

城区高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 给出下列命题：①在区间（0，+∞）上，函数y=x ﹣1，y=，y=（x ﹣1）2，y=x 3中有三个是增函数；②若log m 3＜log n 3＜0，则0＜n ＜m ＜1；③若函数f （x ）是奇函数，则f （x ﹣1）的图象关于点A （1，0）对称；④若函数f （x ）=3x ﹣2x ﹣3，则方程f （x ）=0有2个实数根．其中假命题的个数为（ ）A ．1B ．2C ．3D ．42． 下列函数中，与函数的奇偶性、单调性相同的是（ ）()3x xe ef x --=A ．B ．C ． D．(ln y x =+2y x =tan y x =xy e =3． 袋内分别有红、白、黑球3，2，1个，从中任取2个，则互斥而不对立的两个事件是（ ）A ．至少有一个白球；都是白球B ．至少有一个白球；至少有一个红球C ．恰有一个白球；一个白球一个黑球D ．至少有一个白球；红、黑球各一个4． 设m ，n 表示两条不同的直线，α、β表示两个不同的平面，则下列命题中不正确的是（ ）A ．m ⊥α，m ⊥β，则α∥βB ．m ∥n ，m ⊥α，则n ⊥αC ．m ⊥α，n ⊥α，则m ∥nD ．m ∥α，α∩β=n ，则m ∥n5． （m+1）x 2﹣（m ﹣1）x+3（m ﹣1）＜0对一切实数x 恒成立，则实数m 的取值范围是（ ）A ．（1，+∞）B ．（﹣∞，﹣1）C ．D ．　6． 已知曲线的焦点为，过点的直线与曲线交于两点，且，则2:4C y x =F F C ,P Q 20FP FQ +=u u u r u u u r r OPQ ∆的面积等于（）A ．B ．CD7． 双曲线4x 2+ty 2﹣4t=0的虚轴长等于（ ）A ．B ．﹣2tC ．D ．48． 已知命题和命题，若为真命题，则下面结论正确的是（ ）p p q ∧A ．是真命题B ．是真命题C ．是真命题D ．是真命题p ⌝q ⌝p q ∨()()p q ⌝∨⌝9． 已知命题“如果﹣1≤a ≤1，那么关于x 的不等式（a 2﹣4）x 2+（a+2）x ﹣1≥0的解集为∅”，它的逆命题、否命题、逆否命题及原命题中是假命题的共有（ ）A ．0个B ．1个C ．2个D ．4个班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________10．已知直线x+ay ﹣1=0是圆C ：x 2+y 2﹣4x ﹣2y+1=0的对称轴，过点A （﹣4，a ）作圆C 的一条切线，切点为B ，则|AB|=（ ）A ．2B ．6C ．4D ．211．下列函数中，在其定义域内既是奇函数又是减函数的是（）A ．y=|x|（x ∈R ）B ．y=（x ≠0）C ．y=x （x ∈R ）D ．y=﹣x 3（x ∈R ）12．关于函数，下列说法错误的是（ ）2()ln f x x x=+（A ）是的极小值点2x =()f x （ B ） 函数有且只有1个零点 ()y f x x =- （C ）存在正实数，使得恒成立k ()f x kx >（D ）对任意两个正实数，且，若，则12,x x 21x x >12()()f x f x =124x x +>二、填空题13．已知点A （2，0），点B （0，3），点C 在圆x 2+y 2=1上，当△ABC 的面积最小时，点C 的坐标为 ．　14．设不等式组表示的平面区域为M ，若直线l ：y=k （x+2）上存在区域M 内的点，则k 的取值范围是 ．15．将一枚质地均匀的骰子先后抛掷两次，若第一次朝上一面的点数为a ，第二次朝上一面的点数为b ，则函数y=ax 2﹣2bx+1在（﹣∞，2]上为减函数的概率是 ．16．函数y=lgx 的定义域为 ．17．如图是函数y=f （x ）的导函数y=f ′（x ）的图象，对此图象，有如下结论：①在区间（﹣2，1）内f （x ）是增函数；②在区间（1，3）内f （x ）是减函数；③在x=2时，f （x ）取得极大值；④在x=3时，f （x ）取得极小值．其中正确的是 ．18．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若△ABC 不是直角三角形，则下列命题正确的是 （写出所有正确命题的编号）①tanA•tanB•tanC=tanA+tanB+tanC②tanA+tanB+tanC的最小值为3③tanA，tanB，tanC中存在两个数互为倒数④若tanA：tanB：tanC=1：2：3，则A=45°⑤当tanB﹣1=时，则sin2C≥sinA•sinB．三、解答题19．如图所示，已知在四边形ABCD中，AD⊥CD，AD=5，AB=7，BD=8，∠BCD=135°．（1）求∠BDA的大小（2）求BC的长．20．已知等差数列{a n}的首项为a，公差为b，且不等式log2（ax2﹣3x+6）＞2的解集为{x|x＜1或x＞b}．（Ⅰ）求数列{a n}的通项公式及前n项和S n公式；（Ⅱ）求数列{}的前n项和T n．21．已知函数的图象在y轴右侧的第一个最大值点和最小值点分别为（π，2）和（4π，﹣2）．（1）试求f（x）的解析式；（2）将y=f（x）图象上所有点的横坐标缩短到原来的（纵坐标不变），然后再将新的图象向轴正方向平移个单位，得到函数y=g（x）的图象．写出函数y=g（x）的解析式．22．如图，AB 是⊙O 的直径，AC 是弦，∠BAC 的平分线AD 交⊙O 于点D ，DE ⊥AC ，交AC 的延长线于点E ，OE 交AD 于点F ．（1）求证：DE 是⊙O 的切线．（2）若，求的值．23．（本小题满分12分）数列满足：，，且.{}n b 122n n b b +=+1n n n b a a +=-122,4a a ==（1）求数列的通项公式；{}n b （2）求数列的前项和.{}n a n S 24．已知函数f （x ）=ax 2﹣2lnx ．（Ⅰ）若f （x ）在x=e 处取得极值，求a 的值；（Ⅱ）若x ∈（0，e]，求f （x ）的单调区间；（Ⅲ）设a＞，g（x）=﹣5+ln，∃x1，x2∈（0，e]，使得|f（x1）﹣g（x2）|＜9成立，求a的取值范围．城区高级中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题题号12345678910答案A A DDCCCCCB题号1112答案DC二、填空题13．　（，）　．14． ． 15．　　．16．　{x|x ＞0}　．17．　③　．18．　①④⑤　三、解答题19． 20． 21． 22．23．（1）；（2）．122n n b +=-222(4)n n S n n +=-++24．。

城区高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 在△ABC 中，sinB+sin （A ﹣B ）=sinC 是sinA=的（）A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既不充分也非必要条件2． 复数是虚数单位）的虚部为（ ）i iiz (21+=A ．B ．C ．D ．1-i -i 22【命题意图】本题考查复数的运算和概念等基础知识，意在考查基本运算能力．3． 设a ，b ∈R ，i 为虚数单位，若＝3＋b i ，则a －b 为（ ）2＋a i1＋iA ．3B ．2C ．1D ．04． 如图，四面体OABC 的三条棱OA ，OB ，OC 两两垂直，OA=OB=2，OC=3，D 为四面体OABC 外一点．给出下列命题．①不存在点D ，使四面体ABCD 有三个面是直角三角形②不存在点D ，使四面体ABCD 是正三棱锥③存在点D ，使CD 与AB 垂直并且相等④存在无数个点D ，使点O 在四面体ABCD 的外接球面上其中真命题的序号是（ ）A ．①②B ．②③C ．③D ．③④5． 已知双曲线的方程为﹣=1，则双曲线的离心率为（ ）A ．B ．C ．或D ．或6． 命题“存在实数x ，使x ＞1”的否定是（ ）A ．对任意实数x ，都有x ＞1B ．不存在实数x ，使x ≤1C ．对任意实数x ，都有x ≤1D ．存在实数x ，使x ≤17． 下列函数在（0，+∞）上是增函数的是（ ）A ．B ．y=﹣2x+5C ．y=lnxD ．y=8． 利用计算机在区间（0，1）上产生随机数a ，则不等式ln （3a ﹣1）＜0成立的概率是（ ）A ．B ．C ．D ．班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________9． 若函数则的值为（ ）1,0,()(2),0,x x f x f x x +≥⎧=⎨+<⎩(3)f -A ．5B ．C ．D ．21-7-10．已知向量=（1，1，0），=（﹣1，0，2）且k+与2﹣互相垂直，则k 的值是（ ）A ．1B ．C ．D ．11．已知是虚数单位，若复数在复平面内对应的点在第四象限，则实数的值可以是（ ）22aiZ i+=+A ．-2 B ．1C ．2D ．312．函数f （x ）=ax 2+2（a ﹣1）x+2在区间（﹣∞，4]上为减函数，则a 的取值范围为（）A ．0＜a ≤B ．0≤a ≤C ．0＜a ＜D ．a ＞二、填空题13．【2017-2018学年度第一学期如皋市高三年级第一次联考】已知函数()211{52128lnx x xf x m x mx x +>=-++≤，，，，若有三个零点，则实数m 的取值范围是________．()()g x f x m =-14．若函数为奇函数，则___________．63e ()()32ex x bf x x a =-∈R ab =【命题意图】本题考查函数的奇偶性，意在考查方程思想与计算能力．15．若实数x ，y 满足x 2+y 2﹣2x+4y=0，则x ﹣2y 的最大值为 ．16．一个正四棱台，其上、下底面均为正方形，边长分别为2cm 和4cm ,侧棱长为2cm ,则其表面积为__________2cm .17．数列{a n }是等差数列，a 4=7，S 7= ．18．在中，已知角的对边分别为，且，则角ABC ∆C B A ,,c b a ,,B c C b a sin cos +=B 为.三、解答题19．已知函数f （x ）=x 2﹣mx 在[1，+∞）上是单调函数．（1）求实数m 的取值范围；（2）设向量，求满足不等式的α的取值范围．20．已知f（x）=log3（1+x）﹣log3（1﹣x）．（1）判断函数f（x）的奇偶性，并加以证明；（2）已知函数g（x）=log，当x∈[，]时，不等式f（x）≥g（x）有解，求k的取值范围．21．如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，H是CF的中点．（1）求证：AC⊥平面BDEF；（2）求二面角H﹣BD﹣C的大小．22．已知p：，q：x2﹣（a2+1）x+a2＜0，若p是q的必要不充分条件，求实数a的取值范围．23．已知函数f （x ）=（log 2x ﹣2）（log 4x ﹣）（1）当x ∈[2，4]时，求该函数的值域；（2）若f （x ）＞mlog 2x 对于x ∈[4，16]恒成立，求m 的取值范围．24．（本小题满分12分）已知函数．1()ln (42)()f x m x m x m x=+-+∈R （1）时，求函数的单调区间；当2m >()f x （2）设，不等式对任意的恒成立，求实数的[],1,3t s ∈|()()|(ln 3)(2)2ln 3f t f s a m -<+--()4,6m ∈a 取值范围．【命题意图】本题考查函数单调性与导数的关系、不等式的性质与解法等基础知识，意在考查逻辑思维能力、等价转化能力、分析与解决问题的能力、运算求解能力．城区高级中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题题号12345678910答案A A D C C C C D111]D题号1112答案A B二、填空题13．7 14⎛⎤ ⎥⎝⎦，14．2016 15．1016．20 17．4918．4π三、解答题19．20．21．22．23．24．。

城区高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 已知||=3，||=1，与的夹角为，那么|﹣4|等于（）A ．2B ．C ．D ．132． 已知实数x ，y 满足a x ＜a y （0＜a ＜1），则下列关系式恒成立的是（ ）A ．B ．ln （x 2+1）＞ln （y 2+1）C ．x 3＞y 3D ．sinx ＞siny 3． 如图，四面体OABC 的三条棱OA ，OB ，OC 两两垂直，OA=OB=2，OC=3，D 为四面体OABC 外一点．给出下列命题．①不存在点D ，使四面体ABCD 有三个面是直角三角形②不存在点D ，使四面体ABCD 是正三棱锥③存在点D ，使CD 与AB 垂直并且相等④存在无数个点D ，使点O 在四面体ABCD 的外接球面上其中真命题的序号是（ ）A ．①②B ．②③C ．③D ．③④4． sin45°sin105°+sin45°sin15°=（ ）A ．0B ．C ．D ．15． 已知抛物线的焦点为，，点是抛物线上的动点，则当的值最小时，24y x =F (1,0)A -P ||||PF PA PAF ∆的面积为（ ）B. C.D. 24【命题意图】本题考查抛物线的概念与几何性质，考查学生逻辑推理能力和基本运算能力.6． 设方程|x 2+3x ﹣3|=a 的解的个数为m ，则m 不可能等于（ ）A ．1B ．2C ．3D ．47． 在△ABC 中，C=60°，AB=，AB 边上的高为，则AC+BC 等于（）A ．B ．5C ．3D ．8． 已知直线l ⊥平面α，直线m ⊂平面β，有下面四个命题：（1）α∥β⇒l ⊥m ，（2）α⊥β⇒l ∥m ，班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________（3）l ∥m ⇒α⊥β，（4）l ⊥m ⇒α∥β，其中正确命题是（）A ．（1）与（2）B ．（1）与（3）C ．（2）与（4）D ．（3）与（4）　9． 在等差数列中，，公差，为的前项和.若向量，，{}n a 11a =0d ≠n S {}n a n 13(,)m a a u r =133(,)n a a r=-且，则的最小值为（ ）0m n u r r ×=2163n n S a ++A ．B．C ．D ．432-92【命题意图】本题考查等差数列的性质，等差数列的前项和，向量的数量积，基本不等式等基础知识，意在n 考查学生的学生运算能力，观察分析，解决问题的能力．10．常用以下方法求函数y=[f （x ）]g （x ）的导数：先两边同取以e 为底的对数（e ≈2.71828…，为自然对数的底数）得lny=g （x ）lnf （x ），再两边同时求导，得•y ′=g ′（x ）lnf （x ）+g （x ）•[lnf （x ）]′，即y ′=[f （x ）]g （x ）{g ′（x ）lnf （x ）+g （x ）•[lnf （x ）]′}．运用此方法可以求函数h （x ）=x x （x ＞0）的导函数．据此可以判断下列各函数值中最小的是（ ）A ．h （）B ．h （）C ．h （）D ．h （）11．已知命题“如果﹣1≤a ≤1，那么关于x 的不等式（a 2﹣4）x 2+（a+2）x ﹣1≥0的解集为∅”，它的逆命题、否命题、逆否命题及原命题中是假命题的共有（ ）A ．0个B ．1个C ．2个D ．4个12．已知等比数列{a n }的前n 项和为S n ，若=4，则=（）A ．3B ．4C ．D ．13二、填空题13．如图，在棱长为的正方体中，点分别是棱的中点,是侧1111D ABC A B C D -,E F 1,BC CC P 面内一点，若平行于平面,则线段长度的取值范围是_________.11BCC B 1AP AEF 1A P 14．圆上的点（2，1）关于直线x+y=0的对称点仍在圆上，且圆与直线x ﹣y+1=0相交所得的弦长为，则圆的方程为 ．15．已知过球面上 ,,A B C 三点的截面和球心的距离是球半径的一半，且2AB BC CA ===，则球表面积是_________.16．设函数，其中[x]表示不超过x的最大整数．若方程f（x）=ax有三个不同的实数根，则实数a的取值范围是 ．17．某高中共有学生1000名，其中高一年级共有学生380人，高二年级男生有180人.如果在全19.0校学生中抽取1名学生，抽到高二年级女生的概率为，先采用分层抽样（按年级分层）在全校抽取100人，则应在高三年级中抽取的人数等于.18．以抛物线y2=20x的焦点为圆心，且与双曲线：的两条渐近线都相切的圆的方程为 ．三、解答题19．已知函数f（x）=．（1）求函数f（x）的最小正周期及单调递减区间；（2）当时，求f（x）的最大值，并求此时对应的x的值．20．已知函数f（x）=ax2+lnx（a∈R）．（1）当a=时，求f（x）在区间[1，e]上的最大值和最小值；（2）如果函数g（x），f1（x），f2（x），在公共定义域D上，满足f1（x）＜g（x）＜f2（x），那么就称g （x）为f1（x），f2（x）的“活动函数”．已知函数+2ax．若在区间（1，+∞）上，函数f（x）是f1（x），f2（x）的“活动函数”，求a的取值范围．21．如图，⊙O的半径为6，线段AB与⊙相交于点C、D，AC=4，∠BOD=∠A，OB与⊙O相交于点．（1）求BD 长；（2）当CE ⊥OD 时，求证：AO=AD ．22．已知定义域为R 的函数f （x ）=是奇函数．（Ⅰ）求b 的值；（Ⅱ）判断函数f （x ）的单调性；（Ⅲ）若对任意的t ∈R ，不等式f （t 2﹣2t ）+f （2t 2﹣k ）＜0恒成立，求k 的取值范围．　23．（本小题满分10分）已知函数.()|||2|f x x a x =++-（1）当时，求不等式的解集；3a =-()3f x ≥（2）若的解集包含，求的取值范围.()|4|f x x ≤-[1,2]24．（本小题满分13分）在四棱锥中，底面是直角梯形，，，．P ABCD -ABCD //AB DC 2ABC π∠=AD =33AB DC ==（Ⅰ）在棱上确定一点，使得平面；PB E //CE PAD （Ⅱ）若，，求直线与平面所成角的大小．PA PD ==PB PC =PA PBC ABCDP城区高级中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题题号12345678910答案C C DCBADBAB题号1112答案CD二、填空题13．14．　（x ﹣1）2+（y+1）2=5　．15．649π16．　（﹣1，﹣]∪[，）　． 17．2518．　（x ﹣5）2+y 2=9　．三、解答题19．20． 21． 22．23．（1）或；（2）.{|1x x ≤8}x ≥[3,0]-24．。

中山区第一中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 已知集合，，则（ ）{2,1,0,1,2,3}A =--{|||3,}B y y x x A ==-∈A B =I A ．B ．C ．D ．{2,1,0}--{1,0,1,2}-{2,1,0}--{1,,0,1}-【命题意图】本题考查集合的交集运算，意在考查计算能力．2． ，分别为双曲线（，）的左、右焦点，点在双曲线上，满足，1F 2F 22221x y a b-=a 0b >P 120PF PF ⋅=u u u r u u u u r 若，则该双曲线的离心率为（ ）12PF F∆C.D.1+1+【命题意图】本题考查双曲线的几何性质，直角三角形内切圆半径与外接圆半径的计算等基础知识，意在考查基本运算能力及推理能力．3． 下列图象中，不能作为函数y=f （x ）的图象的是（）A ．B ．C ．D ．4． 高一新生军训时，经过两天的打靶训练，甲每射击10次可以击中9次，乙每射击9次可以击中8次．甲、乙两人射击同一目标（甲、乙两人互不影响），现各射击一次，目标被击中的概率为（ ）A ．B ．C ．D ．5． 设n S 是等比数列{}n a 的前项和，425S S =，则此数列的公比q =（ ）A ．-2或-1B ．1或2C.1±或2D ．2±或-16． 在函数y=中，若f （x ）=1，则x 的值是（）A ．1B ．1或C ．±1D ．7． 设集合，，则（）{}|||2A x R x =∈≤{}|10B x Z x =∈-≥A B =I 班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A. B. C. D. {}|12x x <≤{}|21x x -≤≤{}2,1,1,2--{}1,2【命题意图】本题考查集合的概念，集合的运算等基础知识，属送分题．8． 命题“∀a ∈R ，函数y=π”是增函数的否定是（ ）A ．“∀a ∈R ，函数y=π”是减函数B ．“∀a ∈R ，函数y=π”不是增函数C ．“∃a ∈R ，函数y=π”不是增函数D ．“∃a ∈R ，函数y=π”是减函数9． 若关于x 的方程x 3﹣x 2﹣x+a=0（a ∈R ）有三个实根x 1，x 2，x 3，且满足x 1＜x 2＜x 3，则a 的取值范围为（）A ．a ＞B ．﹣＜a ＜1C ．a ＜﹣1D ．a ＞﹣110．若关于的不等式的解集为或，则的取值为（ ）2043x ax x +>++31x -<<-2x >A ． B ． C ．D ．1212-2-11．抛物线E ：y 2=2px （p ＞0）的焦点为F ，点A （0，2），若线段AF 的中点B 在抛物线上，则|BF|=（）A ．B ．C ．D ．12．设,,a b c R ∈，且a b >，则（ ）A ．ac bc >B ．11a b< C ．22a b >D ．33a b>二、填空题13．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，sinA ，sinB ，sinC 依次成等比数列，c=2a 且•=24，则△ABC 的面积是 ．14．已知，，则的值为．1sin cos 3αα+=(0,)απ∈sin cos 7sin 12ααπ-15．在4次独立重复试验中，随机事件A 恰好发生1次的概率不大于其恰好发生两次的概率，则事件A 在一次试验中发生的概率P 的取值范围是 ．16．已知i 是虚数单位，复数的模为 ．　17．若圆与双曲线C ：的渐近线相切，则_____；双曲线C 的渐近线方程是____．18．如图，是一回形图，其回形通道的宽和OB 1的长均为1，回形线与射线OA 交于A 1，A 2，A 3，…，若从点O 到点A 3的回形线为第1圈（长为7），从点A 3到点A 2的回形线为第2圈，从点A 2到点A 3的回形线为第3圈…依此类推，第8圈的长为 ．三、解答题19．函数f （x ）=sin 2x+sinxcosx ．（1）求函数f （x ）的递增区间；（2）当x ∈[0，]时，求f （x ）的值域．20．（本小题满分12分）已知函数，数列满足：，（）.21()x f x x +={}n a 12a =11n n a f a +⎛⎫= ⎪⎝⎭N n *∈（1）求数列的通项公式；{}n a （2）设数列的前项和为，求数列的前项和.{}n a n n S 1n S ⎧⎫⎨⎬⎩⎭n n T 【命题意图】本题主要考查等差数列的概念，通项公式的求法，裂项求和公式，以及运算求解能力.21．已知f （）=﹣x ﹣1．（1）求f （x ）；（2）求f （x ）在区间[2，6]上的最大值和最小值．　22．（本题满分12分）为了了解某地区心肺疾病是否与性别有关，在某医院随机地对入院的50人进行了问卷调查，得到了如下的列联表：22⨯患心肺疾病患心肺疾病合计男20525女101525合计302050（1）用分层抽样的方法在患心肺疾病的人群中抽6人，其中男性抽多少人？（2）在上述抽取的6人中选2人，求恰有一名女性的概率.（3）为了研究心肺疾病是否与性别有关，请计算出统计量，判断心肺疾病与性别是否有关？2K 下面的临界值表供参考：)(2k K P ≥15.010.005.0025.0010.0005.0001.0k 2.0722.7063.841 5.024 6.6357.879828.10（参考公式：，其中）))()()(()(22d b c a d c b a bc ad n K ++++-=d c b a n +++=23．在等比数列{a n }中，a 3=﹣12，前3项和S 3=﹣9，求公比q ．24．（本小题满分10分）选修4-5：不等式选讲设函数．()5f x x a x =-+（1）当时，求不等式的解集；1a =-()53f x x ≤+（2）若时有，求的取值范围．1x ≥-()0f x ≥a中山区第一中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题1． 【答案】C【解析】当时，，所以，故选C ．{2,1,0,1,2,3}x ∈--||3{3,2,1,0}y x =-∈---A B =I {2,1,0}--2． 【答案】D【解析】∵，∴，即为直角三角形，∴，120PF PF ⋅=u u u r u u u u r12PF PF ⊥12PF F ∆222212124PF PF F F c +==，则，12||2PF PF a -=222221212122()4()PF PF PF PF PF PF c a ⋅=+--=-.所以内切圆半径2222121212()()484PF PF PF PF PF PF c a +=-+⋅=-12PF F ∆，外接圆半径.由题意，得，整理，得12122PF PF F F r c +-==-R c =c -=，∴双曲线的离心率，故选D.2()4ca=+1e =+3． 【答案】B【解析】解：根据函数的定义可知，对应定义域内的任意变量x 只能有唯一的y 与x 对应，选项B 中，当x ＞0时，有两个不同的y 和x 对应，所以不满足y 值的唯一性．所以B 不能作为函数图象．故选B ．【点评】本题主要考查函数图象的识别，利用函数的定义是解决本题的关键，注意函数的三个条件：非空数集，定义域内x 的任意性，x 对应y 值的唯一性．　4． 【答案】 D 【解析】【解答】解：由题意可得，甲射中的概率为，乙射中的概率为，故两人都击不中的概率为（1﹣）（1﹣）=，故目标被击中的概率为1﹣=，故选：D ．【点评】本题主要考查相互独立事件的概率乘法公式，所求的事件的概率与它的对立事件的概率之间的关系，属于基础题．5． 【答案】D 【解析】试题分析：当公比1-=q 时，0524==S S ，成立.当1-≠q 时，24,S S 都不等于，所以42224==-q S S S , 2±=∴q ,故选D.考点：等比数列的性质.6． 【答案】C【解析】解：∵函数y=中，f （x ）=1，∴当x ≤﹣1时，x+2=1，解得x=﹣1；当﹣1＜x ＜2时，x 2=1，解得x=1或x=﹣1（舍）；当x ≥2时，2x=1，解得x=（舍）．综上得x=±1故选：C ．　7． 【答案】D 【解析】由绝对值的定义及，得，则，所以，故选D.||2x ≤22x -≤≤{}|22A x x =-≤≤{}1,2A B =I 8． 【答案】C【解析】解：因为全称命题的否定是特称命题，所以，命题“∀a ∈R ，函数y=π”是增函数的否定是：“∃a ∈R ，函数y=π”不是增函数．故选：C ．【点评】本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．　9． 【答案】B【解析】解：由x 3﹣x 2﹣x+a=0得﹣a=x 3﹣x 2﹣x ，设f （x ）=x 3﹣x 2﹣x ，则函数的导数f ′（x ）=3x 2﹣2x ﹣1，由f ′（x ）＞0得x ＞1或x ＜﹣，此时函数单调递增，由f ′（x ）＜0得﹣＜x ＜1，此时函数单调递减，即函数在x=1时，取得极小值f （1）=1﹣1﹣1=﹣1，在x=﹣时，函数取得极大值f （﹣）=（﹣）3﹣（﹣）2﹣（﹣）=，要使方程x 3﹣x 2﹣x+a=0（a ∈R ）有三个实根x 1，x 2，x 3，则﹣1＜﹣a ＜，即﹣＜a ＜1，故选：B ．【点评】本题主要考查导数的应用，构造函数，求函数的导数，利用导数求出函数的极值是解决本题的关键．　10．【答案】D 【解析】试题分析：由题意得，根据不等式与方程的关系可知，不等式解集的端点就是对应的方程的根，可得方程，解得，其对应的根分别为，所以，故选2043x ax x +=++3,1,x x x a =-=-=-3,1,2x x x =-=-=2a =-D.考点：不等式与方程的关系.11．【答案】D【解析】解：依题意可知F 坐标为（，0）∴B 的坐标为（，1）代入抛物线方程得=1，解得p=，∴抛物线准线方程为x=﹣，所以点B 到抛物线准线的距离为=，则B 到该抛物线焦点的距离为．故选D ．　12．【答案】D 【解析】考点：不等式的恒等变换.二、填空题13．【答案】　4　．【解析】解：∵sinA ，sinB ，sinC 依次成等比数列，∴sin 2B=sinAsinC ，由正弦定理可得：b 2=ac ，∵c=2a ，可得：b=a ，∴cosB===，可得：sinB==，∵•=24，可得：accosB=ac=24，解得：ac=32，∴S △ABC =acsinB==4．故答案为：4．14．【解析】,7sinsin sin cos cos sin 12434343πππππππ⎛⎫=+=+ ⎪⎝⎭Q =,sin cos 7sin 12ααπ-∴==考点：1、同角三角函数之间的关系；2、两角和的正弦公式.15．【答案】　[]　．【解析】解：由题设知C 41p （1﹣p ）3≤C 42p 2（1﹣p ）2，解得p ，∵0≤p ≤1，∴，故答案为：[]．　16．【答案】 ．【解析】解：∵复数==i ﹣1的模为=．故答案为：．【点评】本题考查了复数的运算法则、模的计算公式，属于基础题．　17．【答案】，【解析】【知识点】圆的标准方程与一般方程双曲线【试题解析】双曲线的渐近线方程为：圆的圆心为（2，0），半径为1．因为相切，所以所以双曲线C 的渐近线方程是：故答案为：，18．【答案】　63　．【解析】解：∵第一圈长为：1+1+2+2+1=7第二圈长为：2+3+4+4+2=15第三圈长为：3+5+6+6+3=23…第n 圈长为：n+（2n ﹣1）+2n+2n+n=8n ﹣1故n=8时，第8圈的长为63，故答案为：63．【点评】本题主要考查了归纳推理，解答的一般步骤是：先通过观察第1，2，3，…圈的长的情况发现某些相同性质，再从相同性质中推出一个明确表达的一般性结论，最后将一般性结论再用于特殊情形．　三、解答题19．【答案】 【解析】解：（1）…（2分）令解得…f （x ）的递增区间为…（6分）（2）∵，∴…（8分）∴，∴…（10分）∴f （x ）的值域是…（12分）【点评】本题考查两角和与差的三角函数，二倍角公式的应用，三角函数的最值，考查计算能力．　20．【答案】【解析】（1）∵，∴. 211()2x f x x x +==+11()2n n na f a a +==+即，所以数列是以首项为2，公差为2的等差数列，12n n a a +-={}n a∴. （5分）1(1)22(1)2n a a n d n n =+-=+-=（2）∵数列是等差数列，{}n a ∴，1()(22)(1)22n n a a n n nS n n ++===+∴. （8分）1111(1)1n S n n n n ==-++∴1231111n n T S S S S =++++L 11111111()(((1223341n n =-+-+-++-+L . （12分）111n =-+1nn =+21．【答案】【解析】解：（1）令t=，则x=，∴f （t ）=，∴f （x ）=（x ≠1）…（2）任取x 1，x 2∈[2，6]，且x 1＜x 2，f （x 1）﹣f （x 2）=﹣=，∵2≤x 1＜x 2≤6，∴（x 1﹣1）（x 2﹣1）＞0，2（x 2﹣x 1）＞0，∴f （x 1）﹣f （x 2）＞0，∴f （x ）在[2，6]上单调递减，…∴当x=2时，f （x ）max =2，当x=6时，f （x ）min =…　22．【答案】【解析】【命题意图】本题综合考查统计中的相关分析、概率中的古典概型，突出了统计和概率知识的交汇，对归纳、分析推理的能力有一定要求，属于中等难度.第 11 页，共 11页23．【答案】【解析】解：由已知可得方程组，第二式除以第一式得=，整理可得q 2+4q+4=0，解得q=﹣2．24．【答案】【解析】（1）当时，不等式，1a =-()53f x x ≤+ ∴，5315x x x ≤+++∴，∴．13x +≤24x -≤≤∴不等式的解集为．()53f x x ≤+[4,2]-（2）若时，有，1x ≥-()0f x ≥ ∴，即，50x a x -+≥5x a x -≥-∴，或，∴，或，5x a x -≥-5x a x -≤6a x ≤4a x ≥-∵，∴，，∴，或．1x ≥-66x ≥-44x -≤6a ≤-4a ≥∴的取值范围是．a (,6][4,)-∞-+∞U。