递归最小二(RLS)自适应均衡算法

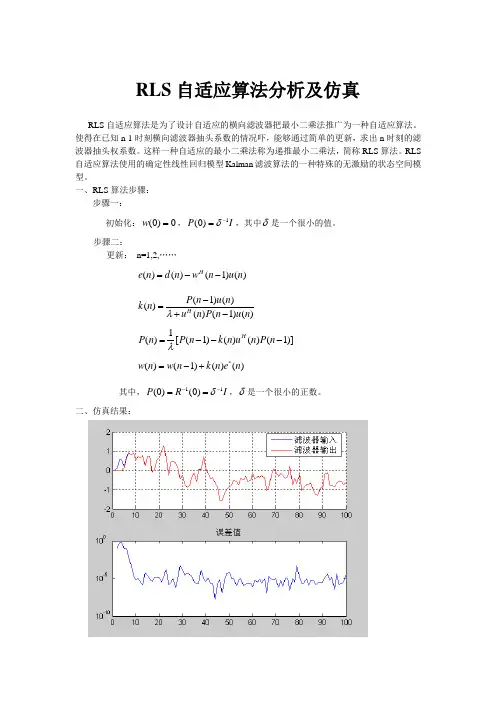
RLS 自适应算法分析及仿真RLS 自适应算法是为了设计自适应的横向滤波器把最小二乘法推广为一种自适应算法。

使得在已知n-1时刻横向滤波器抽头系数的情况吓，能够通过简单的更新，求出n 时刻的滤波器抽头权系数。

这样一种自适应的最小二乘法称为递推最小二乘法，简称RLS 算法。

RLS 自适应算法使用的确定性线性回归模型Kalman 滤波算法的一种特殊的无激励的状态空间模型。

一、RLS 算法步骤：步骤一：初始化：(0)0w =，1(0)P I δ-=，其中δ是一个很小的值。

步骤二：更新： n=1,2,……()()(1)()H e n d n w n u n =--(1)()()()(1)()H P n u n k n u n P n u n λ-=+- 1()[(1)()()(1)]H P n P n k n u n P n λ=---*()(1)()()w n w n k n e n =-+其中，11(0)(0)P R I δ--==，δ是一个很小的正数。

二、仿真结果：从上图可以看出RLS滤波的跟踪性能是比较好的，滤波器的输入与输出在初始值之后几乎重合。

由于RLS存在自适应更新过程，因此其效果比LMS更好。

由下图可以看出，其RLS算法误差是具有收敛性的，收敛结果与δ密切相关，δ在取值为1的时候严重影响RLS算法的收敛速度及结果。

三、仿真程序：clear allclcM=5;%权系数个数N=100;%数据点数n=1:N;wn=0.36*randn(1,N);vn=randn(1,N);d(1)=0;for n=2:Nd(n)=0.8*d(n-1)+wn(n); %期望响应enduu=d+vn;w=zeros(M,1);P=0.05*eye(M,M);q=0.1; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%for n=M:N;u=uu(n:-1:n-M+1)' ;e(n)=d(n)-w'*u;k=P*u*inv(q+u'*P*u);P=(1/q)*(P-k*u'*P);w=w+k*e(n);out(n)=w'*u;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%subplot(211)t=1:N;hold on;plot(d(t));hold on;plot(out(t),'r');grid onlegend('滤波器输入','滤波器输出')subplot(212)semilogy(abs(out-d));title('误差值')。

前言自适应信号处理的理论和技术经过40 多年的发展和完善,已逐渐成为人们常用的语音去噪技术。

我们知道, 在目前的移动通信领域中, 克服多径干扰, 提高通信质量是一个非常重要的问题, 特别是当信道特性不固定时, 这个问题就尤为突出, 而自适应滤波器的出现, 则完美的解决了这个问题。

另外语音识别技术很难从实验室走向真正应用很大程度上受制于应用环境下的噪声。

自适应滤波的原理就是利用前一时刻己获得的滤波参数等结果, 自动地调节现时刻的滤波参数, 从而达到最优化滤波。

自适应滤波具有很强的自学习、自跟踪能力, 适用于平稳和非平稳随机信号的检测和估计。

自适应滤波一般包括3个模块：滤波结构、性能判据和自适应算法。

其中, 自适应滤波算法一直是人们的研究热点, 包括线性自适应算法和非线性自适应算法, 非线性自适应算法具有更强的信号处理能力, 但计算比较复杂, 实际应用最多的仍然是线性自适应滤波算法。

线性自适应滤波算法的种类很多, 有RLS自适应滤波算法、LMS自适应滤波算法、变换域自适应滤波算法、仿射投影算法、共扼梯度算法等[1]。

其中最小均方(Least Mean Square,LMS)算法和递归最小二乘(Recursive Least Square,RLS)算法就是两种典型的自适应滤波算法, 它们都具有很高的工程应有价值。

本文正是想通过这一与我们生活相关的问题, 对简单的噪声进行消除, 更加深刻地了解这两种算法。

我们主要分析了下LMS算法和RLS算法的基本原理, 以及用程序实现了用两种算法自适应消除信号中的噪声。

通过对这两种典型自适应滤波算法的性能特点进行分析及仿真实现, 给出了这两种算法性能的综合评价。

1 绪论自适应噪声抵消( Adaptive Noise Cancelling, ANC) 技术是自适应信号处理的一个应用分支, 年提出, 经过三十多年的丰富和扩充, 现在已经应用到了很多领域, 比如车载免提通话设备, 房间或无线通讯中的回声抵消( AdaptiveEcho Cancelling, AEC) , 在母体上检测胎儿心音, 机载电子干扰机收发隔离等, 都是用自适应干扰抵消的办法消除混入接收信号中的其他声音信号。

MIMO均衡算法（CMALMSRLS）原理介绍MIMO（Multiple Input Multiple Output）均衡算法是用来解决多输入多输出通信系统中的信号干扰问题的一种方法。

MIMO系统是一种通过在发送和接收端使用多个天线来提高通信性能的技术，它可以同时传输多个信号流，从而提高了系统的传输容量和可靠性。

MIMO均衡算法主要有三种：CMA（Constant Modulus Algorithm）、LMS（Least Mean Square Algorithm）和RLS（Recursive Least Square Algorithm）。

下面将对这三种算法的原理进行详细介绍。

1.CMA算法原理：CMA算法是一种基于判决反馈的盲均衡算法，主要用于消除通信系统中的多径干扰。

其原理基于一种常数模型，即假设接收信号的样本具有常数模量。

CMA算法通过最小化误差信号的功率来估计多径信道，从而实现均衡。

算法的核心思想是根据判决反馈，通过调整均衡器的参数来最小化误差信号的功率。

2.LMS算法原理：LMS算法是一种基于梯度下降法的自适应均衡算法，其主要特点是简单易理解、计算速度快。

LMS算法通过最小化接收信号与期望信号之间的误差来更新均衡器的权重。

算法的核心思想是根据误差信号和输入信号之间的相关性来更新均衡器的参数，从而逐步优化均衡器的性能。

3.RLS算法原理：RLS算法是一种基于递推最小二乘法的自适应均衡算法，其主要特点是收敛速度快、抗干扰性能好。

RLS算法通过最小化误差的均方值来更新均衡器的权重。

算法的核心思想是根据输入信号和误差信号之间的相关性来更新均衡器的参数，从而实现均衡。

相比于LMS算法，RLS算法的计算复杂度较高，但是收敛速度更快，适用于信道条件变化频繁的情况。

总而言之，MIMO均衡算法通过调整均衡器的权重来消除多输入多输出通信系统中的信号干扰，从而提高通信系统的性能。

CMA算法是一种基于判决反馈的盲均衡算法，LMS算法是一种基于梯度下降法的自适应均衡算法，RLS算法是一种基于递推最小二乘法的自适应均衡算法。

4 递归最小二乘自适应算法及仿真4.1 引言最小二乘(RLS)法是一种典型的有效的数据处理方法。

由著名学者高斯在1795年提出，他认为，根据所获得的观测数据来推断未知参数时，未知参数最可能的值是这样一个数据，即它使各项实际观测值和计算值之间的差的平方乘以度量其精度的数值以后的和为最小。

这就是著名的最小二乘法。

前面所研究的自适应滤波算法根据的最佳准则为最小均方误差准则。

自适应算法的目标在于，使滤波器输出与需要信号的误差的平方的统计平均值最小。

这个准则根据输入数据的长期统计特性寻求最佳滤波。

然而，我们通常己知的仅是一组数据，因而只能对长期统计特性进行估计或近似。

LMS 算法、格形梯度算法都是这样。

而最小二乘算法就是能直接根据一组数据寻求最佳解。

换句话说，根据最小均方误差准则得到的是对一类数据的最佳滤波器，而根据最小二乘法得到的是对一组已知数据的最佳滤波器。

对同一类数据来说，最小均方误差准则对不同的数据组导出同样的“最佳”滤波器;而最小二乘法对不同的数据组导出不同的“最佳”滤波器。

因而常说最小二乘法导出的最佳滤波器是“精确”的。

递推最小二乘法(R 璐)是最小二乘法的一类快速算法。

4.2 递推最小二乘（RLS ）算法递推最小二乘(RLS)算法是一种在自适应迭代的每一步都要求最优的迭代算法，滤波器输出信号法，滤波器输出信号()y n 等于输入信号()x n 与冲激响应序列()i w n 的卷积和，即()()()11Mk k y n w n x n k ==*-+∑ K 1,2,...,n N = (4.1)误差信号()()()e n d n y n =-。

由此可以得到自适应横向滤波器按最小均方准则设 计的代价函数()()()()2211N N i i J n e n d i y i ====-⎡⎤⎣⎦∑∑ （4.2） 式中()d i 与()y i 分别为自适应滤波器的期望相应于输出信号。

()e i 为误差信号。

LMS 和RLS 算法应用及仿真分析摘要：本文采用MATLAB 软件对LMS 和RLS 两种自适应均衡算法在回波抵消器中的应用进行仿真，分析收敛步长μ、抽头w 、遗忘因子λ 等参数对回波抵消器性能的影响，并对两种算法下的性能做出比较。

关键词：LMS ；RLS ；自适应；回波抵消1 引言进入90 年代后期，通过网络拨打长途电话即IP 电话开始盛行，由于发话端到受话端的延迟达100ms 以上，而人耳对大于50ms 的回声就能辨别出来，因此IP 电话的回声严重影响通话效果。

如何消除回声成为非常重要的问题，回波抵消器就是一个自适应辨识系统，它通过特定的算法辨识未知的目标系统，即回声路径。

本文采用LMS 和RLS 算法实现回波抵消，并对收敛步长μ、抽头w 、遗忘因子λ 等相关参数对回波抵消性能的影响进行了仿真分析，从而为一种通用的回波抵消技术的实际应用提供理论参考。

回波抵消算法原理图如图1 所示。

图1 回波抵消算法原理图 2 LMS 和RLS 算法概述最陡下降法（LMS ）和递归最小二乘算法（RLS ）是自适应滤波最常用，也是最基本的两种算法。

下面分别对LMS 和RLS 两种算法原理做简单介绍。

2.1 LMS 算法设J(n)是n 时刻均方误差，J(n+1)是n+1 时刻的均方误差，W(n)、W(n+1)分别是n 、n+1时刻M 维抽头权向量011()[()()...()]T M W n w n w n w n -= (1)为使J(n+1)<J(n) (2)W(n)必须按J(n)的负方向变化即(1)()W n W n J μ→→→+=-∇ (μ>0) (3)最后以U (n )*e (n )瞬时值代替统计平均，得到抽头权向量迭代式 *(1)()()()W n W n U n e n μ→→+=- (4)式中U(n)式n 时刻的输入向量[u(n) u(n-1) u(n-2)···u(n-M+1)]。

可取滤波器的实际输入d*(i)作为期望响应d(i)。 将误差代入代价函数得到加权误差平方和的完整表达式
J (n) | d (i) w (n) * u(i) |
ni H i 0
n
2
RLS算法基本原理
• 抽头权向量取的是n时刻的w(n)而不是i时 刻的w(i). • i<=n时刻，
1 H
k (n)
1
w 又由： (n)
R (n)r(n) P(n)r(n)
H H
P(n 1)r (n 1) 1d * (n)[P(n 1)u (n) w(n 1) d * (n)k (n) k (n)u H (n) w(n 1) 化简得：w(n) w(n - 1) k(n)e (n)
故代价函数J(n)比J(n)^更合理。
RLS算法基本原理
• 为了使代价函数取得最小值, 可通过对权向量求导
J ( n) 0 w
解得： R(n)w(n) r (n) w(n) R1 (n)r (n) 其中： R(n) niu(i)u H (i)
i 0 n
（公式1） （公式2）
RLS自适应算法基本原理
刘庆杰 信号与信息处理
目录：
★RLS算法基本原理 ★RLS算法性能分析
★RLS算法的特点 ★RLS算法简单应用
RLS算法基本原理
通用自适应滤波器的基本原理
u n
输入信号
线性滤波器
滤波器参数
yn
输出信号
d n
期望响应
性能评价 自适应方法
en
误差
Wnew (n) Wold (n 1) W (n) （校正项）
r (n) ni u(i)d * (i)

河南工业大学信息科学与工程学院
4.2 矩阵求逆引理
设A和B是两个M×M正定阵，它们之间的关系为 是两个M
A = B−1 +CD−1CH
(4-14)
其中，D 其中，D是N×M正定阵，C是M×N矩阵。根据矩阵求 正定阵，C 逆引理，可将A 逆引理，可将A的逆矩阵表示为
A−1 = B− B (D+CH B )−1CH B C C
u(i) =[u(i), u(i −1 L (i −M +1 T ), u )]
(4-3)
式中W 式中W（n）是n时刻抽头权向量，定义为 ）是n
w(n) =[ω0(n),ω (n),L ωM−1(n)]T , 1
(4-4)
注意，在代价函数 ξ(n) 定义的观测区间１≤i ≤n内，横向 定义的观测区间１≤ ≤n内，横向 滤波器的抽头权值保持不变． 式（4 式（4-1）中的加权因子β(n,i) 满足如下关系 0< β(n,i)≤1 i=1,2,…n (4-5)
y(i) = wH (n)u(i)
2)正则化项 2)正则化项
δλ w(n) =δλ w (n)w(n)
n 2 n H
式中δ是一个正实数，称为正则化参数．除了因子 δλ 外， 正则化项只取决于抽头权向w(n).将这一项包含在代价函 数中，以便通过平滑作用来稳定递归最小二乘问题的解。
n
河南工业大学信息科学与工程学院
^
^ 2
λ
2
^
形式，其中 F(w)是由RLS滤波器实现的输入输出映射关 系，D是差分算子。式（4-7）的正则化项通常用在RLS滤 波器设计中。
河南工业大学信息科学与工程学院
4.1.2 正则方程的变形
将式（4 将式（4-7）展开并进行整理，我们发现，在代价函数 δ(n)中增加正则化项 δλ w ) ，相当于将抽头输入向量 (n)中增加正则化项 (n

RLS和LMS自适应算法分析RLS (Recursive Least Squares) 和 LMS (Least Mean Squares) 是两种常见的自适应滤波算法。

它们在信号处理、通信系统和自适应控制等领域得到广泛应用。

本文将对这两种算法进行分析比较。

首先，我们来看看RLS算法。

RLS算法使用最小均方误差准则来自适应调整滤波器系数。

它利用递归方式计算出均方误差的最小值。

RLS算法基于Wiener-Hopf方程，通过解析方法来计算最优系数。

这种方法计算量较大，但是提供了更好的性能。

RLS算法根据观测数据和期望输出之间的误差信号来不断调整滤波器的权重，并且在递归过程中更新这些权重。

相比于LMS算法，RLS算法具有更快的收敛速度和更高的精度。

但是，RLS 算法也存在一些问题，比如计算复杂度高、存储要求大以及对噪声和系统不确定性敏感。

接下来，我们来看看LMS算法。

LMS算法是一种基于随机梯度下降的自适应算法。

在LMS算法中，滤波器的系数通过逐步调整以减小误差标准差。

LMS算法利用误差信号和输入信号之间的乘积来更新滤波器系数。

这种算法简单易于实现，计算复杂度低，并且对存储要求不高。

LMS算法适用于非平稳环境下的自适应滤波问题。

然而，LMS算法的收敛速度较慢，需要一定的迭代次数才能达到最优解，而且对于高阶滤波器，可能存在稳定性问题。

此外，LMS算法对输入信号的统计特性有一定的要求。

综上所述，RLS算法和LMS算法都是常见的自适应滤波算法，它们在不同的应用领域有不同的适用性和特点。

RLS算法在计算复杂度和存储要求上较高，但是具有更快的收敛速度和更高的精度。

LMS算法计算复杂度低，存储要求小，但是收敛速度较慢。

一般情况下，对于较小的系统和较简单的滤波器，可以使用LMS算法，而对于复杂的系统和高阶滤波器，可以使用RLS算法。

在实际应用中，需要根据具体的要求和约束来选择合适的算法。

此外，还可以根据实时计算需求和系统资源限制等因素，对RLS 和LMS算法进行优化和改进，如考虑快速RLS算法和正则化LMS算法等。

采用小波变换改进递归最小二乘（RLS）算法作者：肖伟来源：《科学导报·科学工程与电力》2019年第22期【摘 ;要】自适应滤波是信号处理的重要基础，近年来发展速度很快，在各个领域取得了广泛的应用。

尽管使用用于白噪声输入的RLS算法获得快速初始自适应收敛速率，但是对于彩色输入信号观察到慢收敛。

在本文中，我们推导出一种新的比例型RLS算法，该算法采用小波变换和稀疏自适应子滤波器，数字网络回波消除器应用的仿真结果说明了当采用该方法时所提出的收敛性改善。

【关键词】自适应滤波;RLS算法;小波变换;收敛性众所周知，当系数的数量非常大时，自适应滤波算法的收敛变慢。

然而，在诸如数字网络和声学回声消除器的许多应用中，被建模的系统具有稀疏脉冲响应，即，其大多数系数具有小幅度。

传统的自适应技术，例如最小均方（LMS）和递归最小二乘（RLS）算法，没有考虑这种系统的稀疏特性。

为了改善这些应用的收敛性，最近提出了采用小波变换改进递归最小二乘（RLS）算法，它采用各个步长来更新不同的系数。

对于具有较大幅度的系数，适应步长变得更大，导致最重要系数的更快收敛。

RLS（递推最小二乘法）算法的关键是用二乘方的时间平均的最小化锯带最小均方准则，并按时间进行迭代计算。

对于非平稳信号的自适应处理，最合适的方法是采用最小二乘自适应滤波器。

它使误差的总能量最小。

RLS算法的优点是收敛速度快，其收敛性能与输入信号的频谱特性无关，但其缺点是计算复杂度很高，对于N阶的滤波器，RLS算法的计算量为O（N2）[1，2]为了对非平稳信号进行跟踪，RLS算法引入了数加权遗忘因子λ。

该遗忘因子的引入，使RLS算法能够对非平稳信号进行跟踪。

由于设计简单、性能最佳，其中RLS滤波器具有稳定的自适应行为而且算法简单，收敛性能良好。

这里讨论RLS算法收敛特性两个方面的问题：一是从均值的意义上讨论的收敛性;二是从均方值的意义上讨论误差的收敛性。

为了讨论进行这样的讨论，必须对输入过程的类别作出规定。

RLS算法的研究引言：RLS（Recursive Least Squares，递归最小二乘）算法是一种最小二乘滤波算法，是现代统计学和估计理论中的重要工具之一、它通过递归更新模型参数来最小化预测误差的平方和，被广泛应用于信号处理、自适应滤波、通信系统、控制系统等领域。

本文将对RLS算法的研究进行探讨，从算法原理、性能评价、改进方法等方面进行详细讨论。

一、算法原理：y(n)=h^T(n)x(n)其中h^T(n)表示h(n)的转置。

我们的目标是通过观测到的输入输出信号对滤波器的脉冲响应进行估计。

RLS算法通过迭代的方式更新滤波器的参数估计值。

假设初始时刻滤波器的参数估计为h(0)，观测到的输入信号为x(n)（n为离散时间），输出信号为y(n)，预测误差为e(n)=d(n)-y(n)，其中d(n)为对应的期望输出信号。

我们可以定义滤波器的误差函数J(h)为：J(h)=E{e^2(n)}其中E{}表示期望运算。

RLS算法的基本思想是通过最小化误差函数J(h)，得到滤波器的最优参数估计。

二、性能评价：1.收敛性：RLS算法在迭代过程中是否能够收敛是一项重要的性能指标。

理想情况下，算法应该能够在有限的迭代次数内收敛。

2.计算复杂度：算法的计算复杂度是衡量其实用性的重要指标。

由于RLS算法涉及到矩阵运算，因此其计算复杂度较高。

3.稳定性：算法的稳定性是指在存在噪声的情况下，算法能够保持良好的性能。

对于RLS算法来说，稳定性指的是滤波器参数估计值是否能够跟随信号的变化。

三、改进方法：1.快速RLS算法：由于RLS算法的计算复杂度较高，因此研究者们提出了一系列的快速RLS算法以降低计算复杂度。

其中一种常用的方法是QR分解法，通过将系数矩阵进行QR分解，可以减少乘法运算的次数，从而提高算法的运行效率。

2.递归RLS算法：递归RLS算法是一种改进的RLS算法，通过递归的方式更新滤波器的参数估计值。

相比于传统的RLS算法，递归RLS算法具有更快的收敛速度和更低的计算复杂度。

LMS与RLS算法程序LMS（最小均方）和RLS（递推最小二乘）是两种常见的自适应滤波算法，在信号处理和通信系统中被广泛应用。

本文将介绍LMS和RLS的基本理论原理，并给出相应的算法程序。

1.LMS算法LMS算法是一种最简单的自适应滤波算法，其基本原理是通过调整滤波器的权值，使得输出信号与期望信号的均方误差最小化。

LMS算法每次迭代都根据误差进行权值更新，可通过以下步骤实现：步骤1:初始化滤波器的权值w(n)=0；步骤2:输入一个样本x(n)；步骤3:计算滤波器的输出y(n)=w(n)^T*x(n)；步骤4:计算误差e(n)=d(n)-y(n)，其中d(n)为期望输出；步骤5:更新滤波器权值w(n+1)=w(n)+μ*e(n)*x(n)，其中μ为步长参数；步骤6:返回步骤2下面是一个简单的LMS算法的Python代码示例：```pythonimport numpy as npdef LMS(x, d, mu, iterations):N = len(x)w = np.zeros(N) # 初始化滤波器权值y = np.zeros(N) # 存储输出信号e = np.zeros(N) # 存储误差信号for n in range(iterations):y[n] = np.dot(w, x[n]) # 计算输出信号e[n]=d[n]-y[n]#计算误差信号w = w + mu * e[n] * x[n] # 更新权值return y, e, w#测试x = np.array([[1, 2, 3, 4, 5], [2, 3, 4, 5, 6]]) # 输入信号d = np.array([4, 7, 10, 13, 16]) # 期望输出mu = 0.01 # 步长参数iterations = len(x[0]) # 迭代次数y, e, w = LMS(x, d, mu, iterations)print("输出信号:", y)print("误差信号:", e)print("滤波器权值:", w)```2.RLS算法RLS算法是一种快速收敛的自适应滤波算法，它通过递推计算得到滤波器的权值更新，以减小均方误差。

敛性能及稳定性 。
关键词 ： 自适应滤波 ； 最小均方 ； 递 归最 小二 乘 ＭＡ Ｔ Ｌ Ａ Ｂ
一
、
引 言
失调噪 声 。干扰 噪声越大 ， 则 引起 的失调
另一方面 ， 可以将
） 视作为
自适 应滤波器是 近 ３ ０ 年来 发展起 来 噪声就越大。 减小步长因子产可降低自适 的关于信 号处理 方法和技 术的滤波 器 ， 其 应滤波算法的稳态失调 ， 提高算法的收敛 设计 方法对滤波器的性能影 响很 大 。 维纳 精度 。
技术成果展示
＾ 技 术 协 作 信 息
２ Ｓ自适应方法的性能分析
孕 兵／ 广东电网有限责任公司梅州供电局
摘 要： 自适应滤波算法广泛应用于系统辨识、 回声抵消、 语音去噪声、 通信中的信道均衡、 阵列波速形成等。在一些信号和噪 声特性无法预知或他们是 随时 间变化 的情况下 ， 通过 自 适应 滤波算法调整 滤波器 系数 ， 使得 滤波器的特性 随信 号和噪 声的变化 而
号特征 先验知识 基础上 的。然 而 ， 在 实际
Ｌ Ｍ Ｓ 算法的判据是最小均方误差 ， 即 号 （ ） 未知 ， 故ｊ ７ （ ） 是不 可观测 的或无
应用 中常 常无法 得到信号特 征先验 知识 ， 理想信号 （ ） 与滤波器输 出． ｙ ）之差
在这种情 况下 ， 自适应 滤波器 能够得 到较 （ ） 的平方值的期望值最小 ， 并且根据这 可观测 的 ， 它与 阪复误差 的关系 为 ： 好的滤波性能 。当输入 信号的统计特 『 生 未 个判据来修改权系数 ＿ Ｈ 】 ＝ ｌ （ ） 由此产生的算 知 ，或者输 入信号 的统计特 陆变化 时 ， 自 法称为最小均方算法（ Ｌ Ｍ Ｓ ） 。绝大多数对

自适应滤波LMS算法及RLS算法及其仿真1.引言2.自适应滤波LMS算法LMS（Least Mean Square）算法是一种最小均方误差准则的自适应滤波算法。

其基本原理是通过不断调整滤波器的权值，使得输出信号的均方误差最小化。

LMS算法的迭代公式可以表示为：w(n+1)=w(n)+μ*e(n)*x(n)其中，w(n)为滤波器的权值向量，μ为步长因子，e(n)为误差信号，x(n)为输入信号。

通过迭代更新权值，LMS算法逐渐收敛，实现了自适应滤波。

3.RLS算法RLS（Recursive Least Square）算法是一种递归最小二乘法的自适应滤波算法。

相比于LMS算法，RLS算法具有更好的收敛性能和适应性。

RLS算法基于最小二乘准则，通过递归式地计算滤波器权值矩阵，不断优化滤波器的性能。

迭代公式可以表示为：P(n)=(P(n-1)-P(n-1)*x(n)*x(n)'*P(n-1)/(λ+x(n)'*P(n-1)*x(n))) K(n)=P(n)*x(n)/(λ+x(n)'*P(n)*x(n))w(n+1)=w(n)+K(n)*e(n)其中，P(n)为滤波器的协方差矩阵，K(n)为最优权值，λ为遗忘因子（用于控制算法的收敛速度），e(n)为误差信号。

4.仿真实验为了验证LMS算法和RLS算法的性能，我们进行了一组仿真实验。

假设输入信号为一个正弦信号，噪声为高斯白噪声。

我们分别使用LMS和RLS算法对输入信号进行自适应滤波，比较其输出信号和原始信号的均方误差。

在仿真中，我们设置了相同的滤波器长度和步长因子，比较LMS和RLS算法的收敛速度和输出质量。

实验结果表明，相对于LMS算法，RLS 算法在相同条件下具有更快的收敛速度和更低的均方误差。

这验证了RLS 算法在自适应滤波中的优越性。

5.结论本文介绍了自适应滤波LMS算法和RLS算法的原理及其在仿真中的应用。

实验结果表明，相对于LMS算法，RLS算法具有更好的收敛性能和适应性。

基于RLS算法实现自适应均衡器的MATLAB仿真1. 实验目的用RLS算法实现自适应均衡器，画出一次实验的误差平方的收敛曲线，给出最后设计滤波器系数。

一次实验的训练序列长度为500。

进行20次独立实验，画出误差平方的收敛曲线。

2. 实验原理自适应均衡器的工作过程包含两个阶段，一是训练过程，二是跟踪过程。

在训练过程中，发送端向接收机发射一组已知的固定长度训练序列，接收机根据训练序列设定滤波器的参数，使检测误码率最小。

典型的训练序列是伪随机二进制信号或一个固定的波形信号序列，紧跟在训练序列后面的是用户消息码元序列。

接收机的自适应均衡器采用递归算法估计信道特性，调整滤波器参数，补偿信道特性失真，训练序列的选择应满足接收机均衡器在最恶劣的信道条件下也能实现滤波器参数调整图1自适应均衡试验框图如图1所示，系统中使用两个独立的随机数发生器，一个用xn来表示，用来测试信道。

另一个用v(n)来表示，用来模拟接收器中加性白噪声的影响。

序列xn是xn=1的Bernoulli2序列，随变量xn具有零均值和单位方差。

第二个序列v(n)具有零均值，其方差v由实验中需要的信噪比决定。

均衡器有11个抽头。

3. MATLAB仿真1. RLS法1次实验clear;N=500;db=25;sh1=sqrt(10^(-db/10));u=;m=*sh1^2;error_s=0;for loop=1:1w=zeros(1,11)';p=1/m*eye(11,11);V=sh1*randn(1,N );Z=randn(1,N);x=sign(Z);for n=3:N;M(n)=*x(n)+*x(n-1)+*x(n-2);endz=M+V;for n=8:N;d(n)=x(n-7);endfor n=11:N;z1=[z(n) z(n-1) z(n-2) z(n-3) z(n-4) z(n-5) z(n-6) z(n-7) z(n-8) z(n-9) z(n-10)]';k=u^(-1).*p*z1./(1+u^(-1).*z1'*p*z1);e(n)=d(n)-w'*z1;w=w+k.*conj(e(n));p=u^(-1).*p-u^(-1).*k*z1'*p;y(n)=w'*z1;e1(n)=d(n)-w'*z1;enderror_s=error_s+e.^2;endwerror_s=error_s./1;n=1:N;plot(n,error_s);xlabel('n (忘却因子u=1;DB=25时)');ylabel('误差');title('RLS法1次实验误差平方的均值曲线 ');2. RLS法20次实验clear;N=500;db=25;sh1=sqrt(10^(-db/10));u=;m=*sh1^2;error_s=0;for loop=1:20w=zeros(1,11)';p=1/m*eye(11,11);V=sh1*randn(1,N );Z=randn(1,N);x=sign(Z);for n=3:N;M(n)=*x(n)+*x(n-1)+*x(n-2);endz=M+V;for n=8:N;d(n)=x(n-7);endfor n=11:N;z1=[z(n) z(n-1) z(n-2) z(n-3) z(n-4) z(n-5) z(n-6) z(n-7) z(n-8) z(n-9) z(n-10)]';k=u^(-1).*p*z1./(1+u^(-1).*z1'*p*z1);e(n)=d(n)-w'*z1;w=w+k.*conj(e(n));p=u^(-1).*p-u^(-1).*k*z1'*p;y(n)=w'*z1;e1(n)=d(n)-w'*z1;enderror_s=error_s+e.^2;endwerror_s=error_s./20;n=1:N;plot(n,error_s);xlabel('n (忘却因子u=1;DB=25时)');ylabel('误差');title('RLS法20次实验误差平方的均值曲线 ');4. 实验结果图2图3。

自适应均衡rls算法仿真流程下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!自适应均衡 RLS 算法仿真流程。

1. 数据准备。

收集输入和输出信号序列，并将其转换为时域或频域表示。

RLS算法自适应去噪RLS算法（Recursive Least Square Algorithm）是一种经典的自适应滤波算法，常用于信号处理领域中的去噪。

它通过不断地更新权重系数来适应输入信号的动态变化，从而实现有效的信号去噪。

RLS算法的基本原理是利用最小二乘法，通过最小化输入信号与期望输出信号之间的误差来求解权重系数。

具体来说，算法会根据当前输入信号的状态，预测下一时刻的输出信号，并与实际输出信号进行比较，计算误差。

然后，利用这个误差和输入信号的相关性，更新权重系数，使得误差最小化。

1.初始化：设置初始权重系数向量w，并设置初始协方差矩阵P。

2.输入信号预测：利用当前的权重系数向量w，对当前时刻的输入信号进行预测，得到预测输出。

3.误差计算：将预测输出与实际输出信号进行比较，计算误差。

4.协方差更新：根据当前的协方差矩阵P、输入信号的自相关矩阵和下一时刻预测误差的方差，利用递推公式更新协方差矩阵。

5.权重系数更新：根据当前的协方差矩阵P、输入信号和误差，利用递推公式更新权重系数向量w。

6.返回第2步，重复执行，直到达到预设的终止条件。

然而，RLS算法也存在一些局限性。

首先，算法的计算复杂度较高，尤其是在处理大规模信号时。

其次，算法对误差的估计非常敏感，使得在高噪声环境下容易受到误差的影响。

最后，算法对输入信号的统计特性有一定的要求，如果输入信号的统计特性与算法假设的模型不匹配，可能会导致性能下降。

综上所述，RLS算法作为一种经典的自适应滤波算法，在信号处理领域中的去噪应用具有重要的实际意义。

它通过动态更新权重系数，能够适应输入信号的变化，并对噪声进行有效的抑制。

然而，算法的高计算复杂度和对统计特性的要求限制了其在一些场景下的应用。

因此，在实际应用中，需要根据具体问题和需求，结合算法的特点和局限性，进行综合考量，选择合适的去噪算法。

递归最小二乘算法及性能仿真RLS Algorithm and Its Performance Simulation[摘要] 自适应滤波理论和技术是统计信号处理和非平稳随机信号处理的主要内容，它具有维纳滤波和卡尔曼滤波的最佳滤波性能，而且不需要先验知识的初始条件，所以，自适应滤波器不但可以用来检测确定性信号，也可以用来检测平稳的或非平稳的随机过程。

本文详细阐述了递归最小二乘算法的基本理论，研究了自适应滤波的原理和方法，并讨论了LMS和RLS的优劣性。

主要内容概括如下：RLS算法的主要优点是收敛速度快，且对自相关矩阵特征值的分散性不敏感，其缺点是计算量比较大。

LMS算法具有计算量小、易于实现等优点，缺点是收敛速度慢。

重点研究了LMS自适应算法和递归最小二乘算法，给出了它们具体的推导过程和基本原理，并对其性能进行了简单分析。

利用MATLAB仿真软件，在信道均衡实验中对比了上述两种算法的性能，验证了变递归最小二乘算法的优良性能。

[关键词] 递归最小二乘；自适应滤波；LMS算法；MATLAB仿真[Abstract]Adaptive filter theory and techniques of statistical signal processing and non-stationary random signal processing main content, which has Wiener filtering and Kalman filtering the best filtering performance, and does not require prior knowledge of initial conditions, therefore, adaptive filter not only can be used to detect deterministic signals can also be used to detect stationary or nonstationary stochastic process.This paper describes the basic theory of recursive least squares algorithm to study the principles and methods of adaptive filtering, and discussed the merits of LMS and RLS. Mainly be summarized as follows:The main advantage of RLS algorithm is fast convergence, and the eigenvalue of the autocorrelation matrix is not sensitive to the dispersion, the drawback is larger than calculated. LMS algorithm has a computation, easy implementation, convergence speed is slow.Focus of the LMS adaptive algorithm and recursive least squares algorithm, given their specific process and the basic principle of derivation, and its performance is also analyzed.Using MATLAB simulation software, channel equalization experiment compared the performance of these two algorithms, recursive least squares algorithm with variable verified the excellent performance.[Keywords] RLS Algorithm; Adaptive Filtering; LMS algorithm; MATLAB simulation.目录目录................................................................... I II1 绪论 (1)1.1 自适应信号处理的国内外发展现状 (1)1.2 自适应信号处理技术的应用 (2)1.3 本文的主要研究内容及工作安排 (2)2 自适应滤波的原理与算法 (4)2.1 自适应滤波的原理 (4)2.2 自适应滤波算法 (5)2.3 自适应滤波的特征 (6)2.4 自适应滤波器的应用 (7)3 LMS自适应算法 (8)3.1 最小均方算法的结构和运算概述 (8)3.1 最速下降概述 (9)3.3 LMS自适应滤波算法 (12)4 递归最小二乘自适应算法及仿真 (15)4.1 引言 (15)4.2 递推最小二乘（RLS）算法 (15)4.3 递推最小二乘算法性能分析 (18)5 结论与展望 (21)5.1 总结 (21)5.2 展望 (21)致谢 (22)参考文献 (23)烟台大学毕业论文1 绪论自适应信号处理是近40年来发展起来的信号处理领域一个新的分支。