当前位置：文档之家 › 习题-第三章直线与平面、平面与平面的相对位置

习题-第三章直线与平面、平面与平面的相对位置

  • 格式：ppt
  • 大小：2.11 MB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

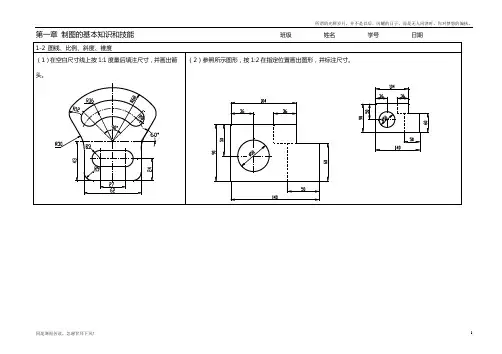
(新)机械制图习题集答案(供参考)

(新)机械制图习题集答案(供参考)

第一章制图的基本知识和技能班级姓名学号日期
第一章制图的基本知识和技能班级姓名学号日期
第一章制图的基本知识和技能班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第三章正投影法的基本原理班级姓名学号日期
第四章变换投影面法班级姓名学号日期
第四章变换投影面法班级姓名学号日期
第四章变换投影面法班级姓名学号日期
第五章基本体的三视图班级姓名学号日期
第五章基本体的三视图班级姓名学号日期
第五章基本体的三视图班级姓名学号日期
第五章基本体的三视图班级姓名学号日期
第五章基本体的三视图班级姓名学号日期
第五章基本体的三视图班级姓名学号日期
第五章基本体的三视图班级姓名学号日期。

工程制图 2.5 直线与平面、平面与平面的相对位置

工程制图 2.5 直线与平面、平面与平面的相对位置
●
通过重影点判别可见性。
●
例：求直线MN与平面ABC的交点K，并判别可见性。
b B K A m m a
2 ●
●
n
a
1(2)
●
k ●
c c
●
N
C
M 2
m
c
1 a
n H
k 1 b
b k
n
2、直线为特殊位置
m b k a n b k● 2 m(n)
● ●
c
●
1(2)
●
c
●
kHale Waihona Puke 1(2) A N Cb
k m (n) c H
●
c
a
a
1
3、一般位置直线与一般位置平面相交
一般位置直线与一般位置平面相交
辅助平面法：过直线作一特殊位置的平面， 先求两平面的交线， 再求交线与已知直线的交点， 此交点即为直线与平面的交点。
PV a’ d’ m’ k’ c’ n’ e’ d n c
1、平面为特殊位置 例：求直线MN与平面ABC的交点K，并判别可见性。 空间及投影分析 b n 平面ABC是一铅垂面， 其水平投影积聚成一条直 k 1(2) 线，该直线与mn的交点即 a ● 为K点的水平投影。 c m 作 图 ① 求交点 m ●2 c ② 判别可见性 ● 由水平投影可知，KN b k 1 a n 段在平面前，故正面投 影上kn为可见。
有无数解
b
n a
●
mc
例2：过M点作一正平线MN平行于平面 ABC。
b cm
●
n
a
a b
c
唯一解
●
m
n
例 3
不平行

机械制图(工程图学)第三章 直线与平面、平面与平面

机械制图(工程图学)第三章 直线与平面、平面与平面
b' e' d' a' a' c' f' X e b c 2 1 a d a d a d 1 X e b c 2 f' X e b c c' f' a' c' e' 2' 1' d' 1' d' b' e' 2' b'
f
f
f
(a)
(b) (c) 图3-12铅垂面与一般位置平面相交 铅垂面与一般位置平面相交
南京师范大学xws 17
3.3垂直问题 垂直问题
3.3.1直线与平面垂直 直线与平面垂直
垂直于平面的直线被称为该平面的垂线或法线，解题时的关键是在投影图 中如何定出法线的方向。 直线与平面垂直，则直线垂直平面上的任意直线（过垂足或不过垂足）。 反之，如直线垂直于平面上的任意两条相交直线，则直线垂直于该平面。
b' b' b' 1' 1' c' e(f) a' a' a' k' e'(f') c' k' 1' e'(f') 2' c'
X f b
X X f g c k a h e (a) e a b 1 c k h 1(2) c f g b 1
a
e (b) 图3-11铅垂线与一般位置平面相交 铅垂线与一般位置平面相交
f' d' n' m' c' a' k' e' X e k n a m b d 图3-5两平面平ቤተ መጻሕፍቲ ባይዱ的投影图 两平面平行的投影图 f c

第三章 平面与直线 平面与平面面的位置关系

第三章 平面与直线 平面与平面面的位置关系

n
b b m
n
a
c n b ● m(n) c
32
a
四、两平面的相对位置
⒈ 两平面平行
⑴ 若一平面上的两相交 直线分别平行于另一 平面上的两相交直线， 则这两平面相互平行。
⑵ 若两投影面垂直面相 互平行，则它们具有 积聚性的那组投影必 相互平行。
a
c a d f e f b c d e f
用线上 取点法
● ●
② 判别可见性 n 由水平投影可知， KN段在平面前，故正 还可通过重影点判别可见性。 面投影上kn为可见。12
k 1 b
⑵ 直线为特殊位置
b k a b k● 2 m(n ) ●
● ●
m
空间及投影分析
c
●
直线MN为铅垂线，其水 平投影积聚成一个点，故交点 K的水平投影也积聚在该点上。
b 如何判别？
可通过正面投影 直观地进行判别。
例：求两平面的交线 MN并判别可见性。
⑴ a
d
a d
●
b m(n)
●
e
f
c d
a
b m(n) e ●
f c
●
n
e c d
f
a
●
e n c f
m
●
m
b
b
同面的异侧，异面的同侧可见性相反。
16
⑵
d′ a′
b′
n′
●
e′
a
b
b
e e
f
c
a d b d′ b′ e′ a
c
f a′ h′
c′
f′
h(f) b d(e) c 34
3.一般位置直线与一般位置平面相交

直线与平面、两平面的相对位置

直线与平面、两平面的相对位置
如果两个平面内的两条相交直线互相垂直，那么这两个平面互相垂直。
THANKS
感谢观看
04
直线与平面、两平面相对位置的性质
和定理
直线与平面垂直的性质和定理
直线与平面垂直的性质
如果一条直线垂直于一个平面，那么这 条直线上的任意一点到平面的距离都相 等。
VS
直线与平面垂直的定理
如果一条直线与平面内的两条相交直线都 垂直，那么这条直线与这个平面垂直。
直线与平面平行的性质和定理
直线与平面平行的性质
在构建过程中，需要充分考虑直线与平面的关系，以及两平 面之间的相对位置，以确保所构建的几何形状符合设计要求 。
建筑设计中的应用
在建筑设计中，直线与平面、两平面 的相对位置关系具有重要意义。通过 合理利用这些关系，可以设计出具有 独特美感和实用性的建筑作品。
例如，可以利用直线与平面的垂直关 系设计出高耸入云的摩天大楼，利用 两平面之间的角度关系创造出独特的 建筑造型。
直线与平面相交
总结词
当直线与平面有一个公共点时，直线 与平面相交。
详细描述
直线与平面相交意味着直线和平面在 某一点相遇。这个点是直线和平面的 唯一公共点。
直线与平面垂直
总结词
当直线的方向向量与平面的法向量平行时，直线与平面垂直。
详细描述
直线与平面垂直意味着直线与平面中的所有线段都垂直。在这种情况下，直线要么完全位于平面上，要么与平面 相交于一点。
应用
在几何学、物理学和工程学中，两平面垂直 的情况也经常出现，例如建筑物的墙与地面 、电路板上的线路与基板等。
03
直线与平面、两平面相对位置的应用
空间几何形状的构建
空间几何形状的构建是直线与平面、两平面相对位置在实际 应用中的重要体现。通过利用这些相对位置关系，可以构建 出各种复杂的空间几何形状，如球体、立方体、圆柱体等。

机械制图第三章 几何元素间的相对位置关系

机械制图第三章 几何元素间的相对位置关系

二、点的投影变换规律
1．点的一次变换 2．点的投影变换规律 3．点的两次变换
1．点的一次变换
V1⊥H,投影轴为O1X1
a1′ax1⊥o1x1， aax1⊥o1x1， a1′ax1=a′ax
V1 a1
ax
ax1
X1
V1 a1
a1
aa1′⊥o1x1
2． 点的投影变换规律
（1） 点的新投影和不变投影的连线，必垂直于新投影轴。
c
a
k
k a
c
n
[例题9] 试过定点K作特殊位置平面的法线。
h
h
h
h
（a）
h
（b）
h
（c）
[例题10] 试求定点A到一般位置直线EF的距离。
分析
过已知点A作平面垂直于已知直线EF，并交于点K，连接AK，
AK即为所求直线的投影，在由直角三角形求出实长。
A
E
K
F
作图
2
f 2 k
a2 b2
b1
V1
a1
X1
作图过程
把一般位置直线变为投影面垂直线 a2 b2
[例题2] 求点C到直线AB的距离（例题11）
提示
作图过程
作图
a1 c1
k1 b1
k'
b'2 k'2
a'2
c'2
距离
k
[例题3] 求两直线AB与CD的公垂线 。
b 1
2
1
2
c2
22
12
c'1
2'1
d'1
d2
平行，则该直线与该平面平行。
直线与平面平行

3 平面的投影及直线、平面的相对位置

3 平面的投影及直线、平面的相对位置
m n c b b n c
10
m
a
11
(2) 平面上取点
面上取点的方法：
首先面上取线
先找出过此点而又在平面内的一条直线作为 辅助线，然后再在该直线上确定点的位置。
例1：已知K点在平面ABC上，求K点的水平投影。
b b c
X
●
d c d c
k ● a
X
k
a
a
k
●
b
a
●
b c
c ●
● a
● ● a
c ●
● a ● ●
●
c
●
●
c
● a ●
●
c
d
● a
X
b ● b a
● ●
X
b ●b a●
●
X
b ●b
●
c
a●
●
●
X
b ●b a●
●
b ●b
X a●
●
d c
c
c
c
不在同一 直线上的 三个点
直线及 线外一 点
两平行 直线
两相交 直线
平面 图形
Байду номын сангаас
2
2. 迹线表示法
平面倾斜投影面——投影类似原平面
2.三面体系中平面的投影特性
特 殊 位 置 平 面
投影面垂直面
垂直于某一投影面而 与其余两投影面倾斜
正垂面（垂直于V，倾斜H、V） 侧垂面（垂直于W，倾斜H、V） 铅垂面（垂直于Ｈ，倾斜H、V) 正平面（//Ｖ，垂直于H、W）
投影面平行面
平行某一投影面而与 其余两投影面垂直
6
⑵ 投影面平行面
a b

直线与平面平面与平面的相对位置

直线与平面平面与平面的相对位置
解题过程： ①过b’作b’d’∥e’f’，求出db； ②检验bd是否与ef平行，
结论：平行
平面与平面的相对位置有:平行、相交和垂直三 种情况
二. 平面与平面平行
判定定理： 若一平面上的一对相交直线分别与另一平面上的
一对相交直线互相平行，则二平面平行。
E
D F
B A
C
若属于一平面的相交两直线对应平行于属于另一平面的相交两直 线，则此两平面平行
连接d’k’，延长后交
c’f’ 于m’点；
2）由m’ 得m，连 接dm与ab交得k；
3）根据重影点Ⅰ、 Ⅱ判别可见性。
3. 一般位置线与一般位置面相交
〖例〗如图所示，求作直线MN和平面△ABC的交 点K，并判别投影的可见性。
作图步骤：
1）在V面投影图中 标出直线MN与AC、 AB的重影点1’、2’。
〖例〗已知空 间点M和平面ABCD 的两面投影,求作 过M点垂直于平面 ABCD的垂线MN的 投影
作图步骤：
1）作a’1’∥OX轴，求
得1’ 和1，过点m作a1
的垂线。
2）作a2∥OX轴，由2 得2’，过m’作a’2’的垂 线m’n’。
3）由n’得n点，将 m’n’和mn画成粗实线。
2．特殊位置的直线与平面垂直
2）由1’、2’ 得1、 2，连接12与mn交得 点k。
3）由k得k’。
4）根据重影点Ⅳ、 Ⅴ判别可见性。
二. 平面与平面相交
M
K
L
F
N
两平面的交线是一条直线，这条直线为两平面所共有
平面与平面相交的问题，主要是求交线和判别 可见性的问题。
1．两特殊位置平面相交
投影面垂直面相交： 两个平面的投影均积聚为直线，若两直线相交， 则空间两平面相交，交点即为两平面交线。（交 点必为该投影面垂直线）

§3-2 相交问题--线面相交

§3-2 相交问题--线面相交

k'
顶 Kr
/ az
ar
FCT
J
E
特殊位置直线投影有积聚性
___
直线与平面的交点属于直线和平面
B
交点的投影一定与直线的积聚性投影 重合
a
b

画法儿何及凯披制约
§3-2相交问题
例9求EF直线与AABC的交点。
画法儿何及凯披制约
§3-2相交问题
例9求EF直线与AABC的交点。
直线EF为铅垂线，水平投影有积聚 性。 直线与平面的交点K属于直线和平面， 所以交点的水平投影k可以先确定。
§3-2相交问题
画法兀何及机*惘 例8求DE 直线与AABC的交点。
§3-2相交问题
三角形ABC为正垂面，正投
影积聚。
直线与平面的交点K属于直线和
平面，所以交点的正投影k，可
以 确定。 利用线上定点的方法可以求出交
点的水平投影k。
利用重影点判定直线的可见性。
画法儿何及凯披制约
§3-2相交问题
2.特殊位置I三直线与一般位置平面相交
， 利用面上定点的方法可以求出交点的
正面投影k 。 判定直线的可见性。
J) w)
交点特性： 1. 直线与平面的共有点; 2. 直线可见性的分界点。
画法儿何及凯披制约
§3-2相交问题
1. 一般位置直线与特殊位置
直线与平面的交点属于直线 和平面共有 特殊位置平面投影有积聚性 交点的投影一定与平面的积聚 性投影重合
%) F F 圣
画法兀何及机*惘 例8求DE 直线与AABC的交点。
画法丿L•阿及以若訊J登I
第三章直线与平面、平面与平面的相对
位置
第三章直蠡一与平所平而与平而 的和対放置

中南大学远程教育《画法几何及工程制图》期末考试复习题及参考答案

中南大学远程教育《画法几何及工程制图》期末考试复习题及参考答案

《画法几何及工程制图》作业参考答案（一）第一章1-1.练习长仿宋字。

[p78](自行完成)1-2.数字和字母练习（临摹“画法几何及工程制图”第十一章中的相关字体）。

[p81](自行完成)1-3.在A3幅面的图纸上，用1：1的比例按下列图形练习图线（不注尺寸），图名为“图线练习”。

[p83](自行完成)1-4.按给出的图样画徒手图。

[p85]（自行完成）第二章点、线、面投影2-1.根据点的空间位置，画出点的投影图。

[p1]（答案略）2-2.根据点到投影面的距离，画出点的三面投影图。

（答案略）ab”A AA BBB c ׳2-3.根据点的坐标，画出点的投影图和空间位置。

[p2]（答案略）2-4.根据点的两面投影求第三投影，并判定其相对位置。

[p3]b' bb”c' c” c ( a” ) ( )2-5.已知点B 在点A 的正上方10，点C 在点B 的正左方10，求A 、B 、C 的三面投影，并标明其可见性。

[p4]2-6.已知长方体的投影图，试判定棱线AB 、AC 、CD 与投影面的相对位置，并标明其侧面投影。

[p4]（答案见复习题）2-7.注出三棱锥SABC各棱线的水平和正面投影，并判定它们属于哪类直线。

[p5]（答案见复习题）2-8.求直线AB、CD和EF的第三投影。

[p6]2-9.分别求出直线CD和EF的实长及其倾角α和β。

[p7]2-10.已知直线AB与V面的倾角β=300，求其水平投影ab。

[p7]2-11.判定点K是否在直线AB上。

[p7] 提示：用点分线段成定比的方法判定b2-12.判定下列直线的相对位置（平行、相交、交叉）。

[p7]（答案见复习题）2-13.求点M到直线AB的距离。

[p8]2-14.求一距H面为20的水平线，与两交叉直线AB、CD相交。

[p8]2-15.判定两条交叉直线AB、CD对V、W面重影点的可见性。

[p8]2-16.试求两条直线AB、CD之间的距离。

工程制图-第三章-直线、平面的相对位置

工程制图-第三章-直线、平面的相对位置

直线、平面的相对位置本章讨论直线与平面、平面与平面的相对位置关系及其投影，包括以下内容：1)平行关系：直线与平面平行，两平面平行。

2)相交关系：直线与平面相交，两平面相交。

§1 平行关系1.1 直线与平面平行定理:若一直线平行于平面上的某一直线，则该直线与此平面必相互平行。

以，直线EF平行于ABC平面。

[例1]过已知点k ，作一条水平线平行于△ABC 平面。

步骤：1）在ABC 平面内作一水平线AD ； 2）过点K 作 KL ∥AD ； 3）直线KL即为所求。

d′d l′lk′k a′a b′e′bc X[例2]试判断:已知直线AB是否平行于四棱锥的侧表面SCF。

作图步骤：1）作c'm'∥a'b'；2）根据CM在平面SCF内，作出cm；3）由于cm不平行于ab，即在该平面内作不出与AB平行的直线，所以，直线AB不平行于四棱锥侧表面SCF。

1.2 平面与平面平行两平面相平行的条件是：如果一平面上的两条相交直线分别平行于另一平面上的两条相交直线，则此两平面平行。

所以：平面ABC 和平面DEF 相平行。

［例3］过点K作一平面，是其与平面ABC平行。

解：只要过K点作两条相交直线分别平行于△ABC的两条边，则这两条相交直线所确定的平面就是所求平面。

作图步骤：2）作KD∥AC(k'd'∥a'c',kd∥ac);a'cac'bb'k'kl'ld'dX1）作KL∥BC(k'l'∥b'c', kl∥bc); 3）平面KDL即为所求。

2.1 直线与平面相交2.1.1 利用积聚性求交点当平面或直线的投影有积聚性时，交点的两个投影中有一个可直接确定，另一个投影可用在直线上或平面上取点的方法求出。

⑴平面为特殊位置[例]求直线MN与平面ABC的交点K并判别可见性。

空间及投影分析平面ABC 是一正垂面，其V 投影积聚成一条直线，该直线与m'n'的交点即为K点的V 投影。

工程制图第3章答案

工程制图第3章答案

3．两直线交叉
交叉两直线各组同面投影不会都平行，特殊情况下可能有一两组 平行；其各组同面投影交点的连线与相应的投影轴不垂直，即不符合 点的投影规律。
重影点 反之，如果两直线的投影既不符合平行两直线的投影特性，也不 符合相交两直线的投影特性，则该两直线空间为交叉两直线。
4．两直线垂直
一般情况下，在投影图中不能确定空间两直线是否垂直， 但当直线处于特殊位置时可以直接从投影图中判断：
三、正投影的基本性质
1. 实形性
2．积聚性
∟
三、正投影的基本性质
3.类似性
4．平行性
三、正投影的基本性质
5．定比性
6．从属性
3-2 三视图的形成及其投影关系
一、 三视图的形成
1. 三投影面体系的建立
物体的一个投影不能确定空间物体的形状。
怎吗办？
建立三面投影体系
2．三视图的形成
主视图
左 视图
[例3-4] 已知点A(15,10,12)，求作点A的三面投影图。
作图步骤如下：
1.自原点O沿OX轴向左量取x=15,得点 ax 2.过ax作OX轴的垂线，在垂线上自ax向下量取y=10,得点A的水平投影a 向上量取z=12,得点A的正面投影a
3.根据点的投影规律，可由点的两个投影作出第三投影 a 。
★ 我们只讨论直线与平面中至少有一个处于特殊位置的情况。
[例3-11] 求一般位置直线MN与铅垂面ABC的交点 分析： 作图：
判可见性：
[例3-12] 求铅垂线MN与一般位置平面△ABC的交点 分析： 作图：
判可见性：
⒉ 两平面相交
两平面相交其交线为直线，交线是两平面的共 有线，同时交线上的点都是两平面的共有点。

哈工大画法几何与机械制图答案

哈工大画法几何与机械制图答案

习题 2-5 习题 2-9 习题 2-14 习题 2-18,19 习题 2-24,25 习题 2-29 习题 2-34,35
习题 2-6,7 习题 2-10,11 习题 2-15,16 习题 2-20,21 习题 2-26,27 习题 2-30,31 习题 2直线和平面
2-29 完成平面图形的第三投影，并判断属于何种位置平面。
一般位置平面
正垂面
侧垂面
铅垂面
水平面
侧平面
第二章 点、直线和平面
2-30 已知属于平面的点或直线的一个投影，求另一投影。 2-31 作出平面图形的另一投影。
第二章 点、直线和平面
2-32 过直线作平面（用迹线表示）。
2-33 完成下列个题。
第六章 立体
6-13 作出圆锥被截切后的另两个投影。 6-14 求带缺口圆柱的侧面投影。
第六章 立体
6-15 求带切口圆柱的侧面投影。
6-16 补全圆柱被截切后的正面投影和侧面投影。
第六章 立体
6-17 作出圆柱被挖切后的侧面投影。
6-18 作出圆柱管被切割后的水平投影和侧面投影。
第六章 立体
第三章 直线与平面、平面与平面的相对位置
3-19 求平行两直线 AB 、 CD 间的距离。
3-20 完成下题。
第三章 直线与平面、平面与平面的相对位置
3-21 以线段 AB 为底作等腰三角形，使定点 C 属于直线 3-22 以点 A 为顶点作等边 ABC ，使底边 BC 属于直线
MN 。
MN 。
第六章 立体
习题 6-1 习题 6-6 习题 6-11,12 习题 6-17,18 习题 6-23,24 习题 6-28 习题 6-31,32
习题 6-2,3 习题 6-7,8 习题 6-13,14 习题 6-19,20 习题 6-25,26 习题 6-29 习题 6-33,34

第三章线与面、面与面的相对位置习题

第三章线与面、面与面的相对位置习题

PH
a e
例题3 14 例题3-14：求两平面的交线，并判断可见性。
（2）利用线面交点法求交线 温故知新
m' n'
n m
全交
例题3 15 例题3-15：求两平面的交线，并判断可见性。
n'
m'
n m
例题3 15 例题3-15：求两平面的交线，并判断可见性。
n'
m'
n m
互交
（3）用辅助平面求两平面的交线
第三章 线与面、面与面的相对位置
§3-2 平面与平面的相对位置
一、两平面平行
如果平面内的两 条相交直线平行 于另一平面内的 两条相交直线， 则两平面互相平 行
例题3 11 例题3-11：过点A作一平面与平面DEFG平行
e' a' d' f'
X O
g'
f a d g
e
例题3 12 例题3-12：判定两平面是否平行。
c' d' e' b' d e c a b g a' g'
例题3 13 例题3-13：判定两正垂面是否平行。
d a' d e c a b b g
c' e'
g
二、两平面相交
交线——共有线
求交线的方法：
（1）利用积聚性求交线
b' f' k' l' e' a' a f k(l) e c d d' c' 两垂直面的交线是垂直线
Pv Qv l' k'
k
l
平面扩大后再交
思考题一 参与相交的两个平面都是特殊位 置时，其交线的投影如何求出？

道桥复习题

道桥复习题
3.斜二测图的轴向伸缩系数是D
（A）p=q=r=1（B）p=q=r=0.82（C）p=r=1,q=0.5（D）p=q=1,r=0.5
4.形体只在正平面上有圆、半圆、圆角时，作图简单的轴测图是B
（A）正等测（B）斜二测（C）正二测（D）前三者一样
5.平行于正面的正方形，对角线平行于X轴、Z轴，它的正等测图是D
12.平面的正面投影积聚为一条直线并与OX轴平行，该平面是B
（A）正平面（B）水平面（C）正垂面（D）铅垂面
13.能取到正垂线的平面是C
（A）铅垂面（B）一般位置平面（C）正垂面（D）侧垂面
14.在一般位置平面P内取一直线AB,已知ab∥OX轴,直线AB是B
（A）水平线（B）正平线（C）侧平线（D）侧垂线
（A）6个（B）5个（C）4个（D）3个
16.如图所示，两体相交所产生相贯线的特殊点有C
（A）8个（B）4个（C）5个（D）6个
第五单元轴测图（单项选择题）
1.获得正轴测图的投影方法是B
（A）中心投影法（B）正投影法（C）斜投影法（D）平行投影法
2.斜二测图的轴间角是C
（A）都是90（B）都是1200（C）900,1350,1350（D）900,900,1350
2.空间点A只有y坐标为零时，空间位置在D
（A）原点处（B）W面上（C）OX轴上（D）V面上
3.空间点A在点B的正左方，这两个点为B
（A）H面的重影点（B）W面的重影点（C）V面和W面的重影点（D）V面的重影点
4.下列几组点中，哪一组是W面上的重影点，并且A点为可见A
（A）A(5，10，8)、B(10，10，8)（B）A(10，10，8)、B(10，10，5)（C）A(10，30，-5)、B(8，30，-5)（D）A(10，30，8)、B(10，20，8)

机械工程图学习题集加详细解答 第3章

机械工程图学习题集加详细解答 第3章

第三章几何元素间相对位置
二、回答问题
1、属于平面的投影面平行线的投影特性？
答：具有投影面平行线的投影特性、满足直线从属于平面的几何特性、与相应的迹线平行。

2、空间两直线平行的投影特性是什么？
答：两直线空间平行同面投影也平行，空间长度之比等于各同面投影长度之比。

3、两直线垂直其投影特性是什么（即直角投影定理）？答：两直线互相垂直（相交垂直或交叉垂直），其中一条直线平行于某投影面时，则两条直线在该投影面中的投影仍互相垂直，即反映直角；反之，若两直线（相交或交叉）在同一投影面中的投影互相垂直（即反映直角），且其中一条直线平行于该投影面，则两直线空间必互相垂直。

二、回答问题
4、直线与平面垂直及两平面垂直的几何定理、投影特性
是什么？解决哪些问题？
答：
1）如果一条直线和一平面内两条相交直线都垂直，那么
这条直线垂直于该平面。

反之，如果一直线垂直于一平面，则必垂直于属于该平面的一切直线。

2）若一直线垂直于一平面，则包含这条直线的一切平面都垂直于该平面。

3）投影特性：两种垂直关系最终都归结为两直线的垂直
问题，应用两直线垂直的投影特性解决此类问题。

4）可以解决各种位置线与线、线与面、面与面的垂直问题。

§3-2 相交问题--线面相交

§3-2 相交问题--线面相交

第三章 直线与平面、平面与平面的相对位置
§3-2 相交问题
A 交点
K
P
B
直线与平面相交
§3－2 相交问题
B
M L
A
N
交线
C
平面与平面相交
一、直线与平面相交
A K
交点特性： 1. 直线与平面的共有点; 2. 直线可见性的分界点。
§3－2 相交问题
P B
§3－2 相交问题
1.一般位置直线与特殊位置平面相交
P
A PH
a
E
C
F
K
k
B
cb
直线与平面的交点属于直线 和平面 共有
特殊位置平面投影有积聚性
交点的投影一定与平面的积聚 性投影重合
例8 求DE直线与ABC的交点。
d
c b
a
e
X
d
c
a
be
§3－2 相交问题
例8 求DE直线与ABC的交点。
c
d
a
k
b
2 1
e
X
d
c
ak
(1)2
be
§3－2 相交问题
三角形ABC为正垂面，正投 影abc积聚。 直线与平面的交点K属于直线和 平面 ，所以交点的正投影k可以 确定。
例9 求EF直线与ABC的交点。
e
c
a
k d
(1) 2 b
f
c
a
k1 ef
d

2b
§3－2 相交问题
例9 求EF直线与ABC的交点。
直线EF为铅垂线，水平投影有积聚 性。
直线与平面的交点K属于直线和平面 ， 所以交点的水平投影k可以先确定。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a′
c′ m′ b c a m
a′
b
c′
否
22/2012 土木类
3-13
（1）
过点M作直线MN，与平面垂直。
（2） a′
p′ n′
m′
n′ b′ a n m n p b
m′
m
23/2012 土木类
3-14
（1） m′
过点A作直线平面，与直线MN垂直。
（2）
c′ a′
c′
n′
b′
n′
m a b c n
判别下列直线与平面、平面与平面是否垂直。
（2） p′ q′ p′ a′ b b′ （3） c′ s′ m′ m s c 是 n
n′
b′
b
p a 否 q 是 p
a
21/2012 土木类
3-12
（4）
判别下列直线与平面、平面与平面是否垂直。
b′ n′
（5） b′ d′ e′ g′ f′ d e n 是 a c f g h h′
g′ a′ c′ e′ g
a
e
b f c
26/2012 土木类
3-17 求点M到平面△ABC距离。
b′
c′ a′ m′ c a m b
27/2012 土木类
m′ m
b′ c
a′ a
b
n
24/2012 土木类
3-15
（1）
过直线MN作平面与平面△ABC垂直。
（2）
a′ b′ a′ n′ c′ a c a m n b c
m′
b′
m′
n′
b n m
c′
25/2012 土木类
3-16 已知平面△EFG与平面△ABC垂直，画全△EFG 的 水平投影。 f′ b′
c′
n′ a′ m′
b
c
n a
m b′
9/2012 土木类
3-7
过点M作直线与平面P、Q都平行。
m′
PV n′ q′
n q m
10/2012 土木类
3-8 过点M作平面与平面 ABC平行。
b′
e′ m′ f′ b e a′ c′
f m a
c
11/2012 土木类
3-9 已知平面ABC与平面DEFG平行,求平面 ABC的正面投影。
k′
n′
c′ c
b
PH m k
2
1 34 （ ） n
a
16/2012 土木类
3-11
（1）
求两平面的交线，并判别可见性。
q′ b′ m′ n′ a′
c′
c n
a
m
b
17/2012 土木类
3-11
（2）
求两平面的交线，并判别可见性。
b′ p′ m′ n′ a′ p a c n c′
m
b
18/2012 土木类
3-11
（3）
求两平面的交线，并判别可见性。
b′
n′ a′ p′ m′
c′
b
p
m n a c
19/2012 土木类
3-11
（4）
求两平面的交线，并判别可见性。
b′ （3′ e′ ）
4′ m′
1′ 2′
a′ d′
n′
f′ c′
3
e c
1 2） （
m 4
d
a
n
f
b
20/2012 土木类
3-12
（1） a′
n′ m′ c′ a′ c a n b
b′
m
6/2012 土木类
3-4
过直线作平面与已知直线平行。
a′ m′
b′
c′
n′
m
a
b
n
c
7/2012 土木类
3-5
过点M作平面与直线AB、CD都平行。
m′ e′ c′ b′ a′ f′ e m b c
d′afd8/2012 土木类3-6 已知线段MN=30mm,点N在点M之后，且线段 MN与△ABC平行，完成线段MN与△ABC的另一投影 。
b′
e′
c d a b AB与CDE 否
d e
d AB与CDE
b 是
4/2012 土木类
3-2
（1）
判别平面与平面是否平行。
a′ e′ c′ f′ d′ g′
（2）
p′
q′
b′
a
b
d
g q e
c
ABC与DEFG
f 否
p P面与Q面 否
5/2012 土木类
3-3
过点M作正平线与平面ABC平行，且使MN=25mm。
14/2012 土木类
3-10
求直线与平面的交点，并判别直线的可见性。
b′ m′ 2′ 1′ m a k′ 4′ n′ c c′
（3）
a′ PH
（3′） 3 k4
1 2 （）
n
b
15/2012 土木类
3-10
求直线与平面的交点，并判别直线的可见性。
b′
（ 1′ 2′） 3′ a′ 4′
（4）
m′
b′
a′ c′ d′ f′ e′ g′
c a b
e f
d
g
12/2012 土木类
3-10
求直线与平面的交点，并判别直线的可见性。
b′
m′ n′ ） （ k′ c′ n b k c a m
（1）
a′
13/2012 土木类
3-10
求直线与平面的交点，并判别直线的可见性。
b′
（2）
m′
k′
c′
a′ m k a n b c n′
1/2012 土木类
2/2012 土木类
重点、难点：
1. 平行关系判别、作图方法； 2. 垂直关系判别、作图方法（特 殊情况）； 3. 求交点、交线的作图方法，可
见性的判别（特殊情况）。
3/2012 土木类
3-1
（1）
判别直线与平面是否平行。
（2）
b′ a′ c′
d′
a′ c′ e′ c a
d′