特殊的平行四边形知识结构图

北师大版二年级（下册）数学第七单元：认识图形
认识角（角的初步认识）
知识点：
1．角是由一个顶点和两条直直的边组成的；
2．角的各部分名称、记法和读法；
3．能用角的符号（“∠”）表示角；
4．会比较角的大小。

了解角的大小与两边张口的大小有关，与边的长短无关；
5、能辨认直角、锐角和钝角。

长方形与正方形
知识点：
1.掌握长方形正方形的特征：长方形和正方形都有4条边，4个直角，长方形对边相等，正方形四条边都相等。

2.初步了解长方形、正方形之间的联系：正方形是特殊的长方形。

3.能在方格纸上画出长方形与正方形。

平行四边形
知识点：
1．直观认识平行四边形，知道平行四边形有四条边、四个角，对边相等。

2．初步了解长方形是特殊的平行四边形。

欣赏与设计
知识点：
1．进一步掌握已学过的图形，感受图形之美。

2．能用学过的图形在方格纸上设计图案，涂色时有一定规律性。

【下载后获高清版】初中八年级数学下必考点-平行四边形几何模型详解一、基础知识条件的组合搭配是解决几何综合题目的基本思路，在进行组合搭配中往往遇到一些常用的结构．可以通过补全图形，从而构造熟悉的结构：三角形的三线：底边上的中线、底边上的高线、顶角的角平分线.二、方法技能1．几何计算、证明的基本思考流程①标注条件，合理转化；②组合特征，分析结构；③由因导果，执果索因．2．特殊四边形中隐含条件①平行四边形中隐含条件：平行、中点；②菱形中隐含条件：平行、中点、角平分线、垂直；③矩形中隐含条件：平行、中点、垂直；④正方形中隐含条件：平行、中点、角平分线、垂直．3．四边形中常见几何结构举例①中点结构：直角+中点，平行+中点，多个中点；②旋转结构：等线段共点，对角互补；③弦图结构：外弦图，内弦图，等腰直角，三垂；④面积结构：三个“一半”，平行转化．三、典例精讲1．如图，在平行四边形ABCD 中，BC= 2AB ，CE⊥AB 于点E，F为AD的中点，若∠AEF = 54°，则∠B = ．【分析】（体会条件组合与搭配）方法一：①AB∥CD ，F为AD 的中点；→平行夹中点→延长证全等；②∠GCE = ∠CEB= 90°，F为AD的中点；→直角+中点→直角三角形斜边上的中线等于斜边的一半．∴易证△AFE≌△DFG (SAS) ，∴EF=FG∵∠GCE=∠CEB = 90°，∴EF=GF=CF∵BC=2AB ，∴FD=CD∵∠AEF=54°，∴∠FEC=∠FCE = 36°，∠CFD=∠FCD=∠G=54°∴∠B=∠CDF=180°-108°=72°方法二：F为AD的中点，取CE中点造梯形AECD 的中位线（构成△CEF 两线合一）∵∠AEF=54°，∴∠FEC=∠FCE=36°，∠CFD=∠FCD=54°∴∠B=∠CDF=180°-108°=72°方法三：∵CE⊥ AB 于点E ，∴取BC中点，构造直角三角形斜边上的中线等于斜边的一半又∵BC=2AB ，∴BG=EG=CG=CD=FD=AF ，∴AB∥FG∥CD ，∴∠GEF=∠GFE=∠AEF=54°，∠B=∠GEB=72°2．如图，在菱形ABCD中，∠A =110°，E 、F分别是边AB 、BC的中点，若EP⊥CD于点P ，则∠FPC= ．【分析】四边形ABCD是菱形，F分别是边BC的中点，构成平行夹中点→延长证△BEF≌△CGF(SAS)∴EF=FG=FP ，AE=BE=BF=FG（菱形的四边相等）∴∠B=70°,∠BFE=∠BEF=∠G=∠FPC=55°3．如图，在菱形ABCD中，AB=BD,点E，F分别在边AB，AD上，且AE=DF连接BF,与DE相交于点G，连接CG,与BD相交于点H ．则下列结论：①△AED≌△DFB；②∠BGD=120°其中正确的是．（填序号）【分析】①△AED≌△DFB（SAS），∴①正确②由△AED≌△DFB 得∠1 = ∠2 ，∴∠BGE=∠1+∠3=∠2+ ∠3 = 60°，∠BGD =120°∴②正确③∵∠BGD+∠BCD=120°+ 60°=180°（对角互补）,CD =CB（等线段共点C）∴可以考虑将△CDG绕点C逆时针旋转60°到△CBM ，也可将△CBG绕点C 顺时针旋转60°注意：辅助线的叙述与三点共线叙述一：将△CDG旋转到△CBM ，必须根据对角互补说明G、B、M三点在一条直线上；叙述二：延长GB至M ，使BM=DG（保证了G、B 、M 三点在一条直线上)，连接CM，此法只需要证明△CBM≌△CDG(SAS) ，从而证得△CGM是等边三角形.∴∴③正确4.（2019）如图，在△ABC中，∠ACB=90°，AC=BC=6，点D为BC的中点，点P是射线AD (与A重合)上的一个动点，则当△PBC为直角三角形时，AP 的长为 .【分析】∵点P是射线AD上的一点，且不与A重合，∴∠BCP=90°∵∠ACB=90°，AC=BC=6，点D为BC的中点，∴四、典型练习【思路分析】本题给出F为AD的中点，结合平行四边形提供的对边平行，故考虑“平行夹中点”，借助全等转移边、转移角．综上，其中一定正确的是①②④．【思路分析】本题给出AB=OB ，点E是OA的中点（等腰+中点构三线合一）∴连接BE得BE⊥ AC3．如图，在梯形ABCD中，AD∥BC ，点E在BC边上，AE=BE ，F是CD边的中点，且AF⊥AB ．若AD=2.7 ，AF=4，AB=6，则CE的长为．【思路分析】本题给出AD∥BC，F是CD边的中点，这是很典型的“平行夹中点”∴延长AF，BC交于点G ，易证△ADF≌△GCF，∴AF=FG=4 ，∵AF⊥AB ，∴由勾股定理可得BG=10．∵AE=BE ，∴∠B=∠2 ，∴∠B+∠G=∠1+∠2=90°，∴∠1=∠G ，AE=EG=BE=5，∴CE=5-2.7=2.3【思路分析】本题给出正方形内含有正方形结构，∴构造弦图易证：△ABC≌△GFB，△AOB≌△GOF得OA=OG，∠AOG=90°，AG=12 ，∴AC=GB=12+4=16【思路分析】本题给出ABCD是正方形，∠CED=90°，∴∠COD+∠CED=180°，∠ODE+∠OCE=180°构成对角互补，∵OC=OD ，构成等线段共点，∴可考虑将△ODE顺时针旋转90°∴将OE顺时针旋转90°到OF，连接CF，易证△ABC≌△GFB ，∴∠ODE=∠OCF，DE=CF，OE=OF6．如图，两个边长均为2的正方形重叠在一起，正方形OPQR的顶点O与正方形ABCD的中心重合．给出以下结论：①四边形OECF 的面积为1；②CE+CF=2；③OE+OF=2；④四边形OECF 的周长为4 ．其中正确的是．（填序号）【思路分析】本题给出正方形OPQR的顶点O与正方形ABCD的中心重合．方法一：∴∠EOF+∠ECF=90°+90°=180°（对角互补），连接OC、OD，△OEC与△OFD构成旋转型全等.方法二：∵∠EOF这个直角的两边不是水平线和铅垂线（称为斜直角），解决“斜直角”问题常用的方法就是“斜直角放正”（直角的两边由水平线和铅垂线构成），这种方法在直角坐标系中用得很多！∴作OG⊥BC于G，OH⊥CD于H ，易证△OGE≌△OHF，同样可得上述结论．【思路分析】∠AMF是斜直角，可考虑“斜直角放正”，得△AMG≌△BMF ，∴AG=FB，GM=FM∴四边形OGMF是正方形，OG=OF=3，AG=FB=1；△OAB≌△EBC（三垂全等），∴BE=OA=2，CE=OB=4，∴点C的坐标为（6,4）构造弦图可得：△OAB≌△EBC（三垂全等），△OME 是等腰直角三角形，∴OE=6, BE=OA=2 ,CE=OB=4 ,∴点C的坐标为（6，4）8．如图，正方形ABCD的面积为18，菱形AECF的面积为6，则菱形的边长为．【思路分析】本题给出正方形和菱形，他们的对角线都是互相垂直平分的，∴连接BD，AC9．如图，四边形ABCD和CEFG都是菱形，连接AG、GE、AE，若∠F=60°，EF=4，则△AEG的面积为．【思路分析】本题给出两个锐角为60°的菱形，∴连接AC，可得∠ACB=∠GEC=60°，∴AC∥BG，∴（构造平行线造等底等高，平行转移）10．如图，E是□ABCD内任一点，若□ABCD的面积为8，则图中阴影部分的面积为．【思路分析】过点E作AD的平行线交AB于G，交CD于F，利用平行转移得：11．如图，在边长为4的菱形ABCD中,∠B=60°，点E，F，G，H分别在边AB ，AD，DC，CB上，且AF=CH，BE=DG=2.P是直线EF，GH之间的任一点，连接PE，PF，PG，PH，则△PEF与△PGH的面积之和为 .【思路分析】由已知易证△AEF≌△CGH，△BEH≌△DGF，∴EF=GH，EH=FG∴四边形EFGH是平行四边形，∴由“三个一半，平行转化”知连接EG，过点P作EF的平行线因此12．如图，在平行四边形ABCD中，AB:BC=3:2，∠DAB=60°，点E在AB边上，且AE:EB=1:2，F为BC边的中点，过点D作DP⊥AF于点P，DQ⊥CE 于点Q，则DP:DQ的值为【思路分析】∵DQ⊥CE，DP⊥AF，由“三个一半”得(求两高之比，由面积公式转化为底边之反比) 由已知数据求得：五、重点提升【中点结构】【垂直结构】。

A B C DC平行四边形判定知识讲解一、知识结构：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧形分的四边形是平行四边对角线：对角线互相平的四边形是平行四边形角：两组对角分别相等四边形是平行四边形一组对边平行且相等的边形是平行四边形两组对边分别相等的四边形是平行四边形两组对边分别平行的四边平行四边形的判定 二、型例题讲解：例1、如图,AD=BC,要使四边形ABCD 是平行四边形,还需补充的一个条件是______ 分析：可以从边、角、对角线上分别考虑。

答案：不唯一：如，AB ＝CD ，AD ∥BC ，∠A ＋∠B ＝180°，∠C ＋∠D ＝180° 点评：本体起点低，入口宽，能够满足不同层次的同学。

例2、点A 、B 、C 、D 在同一平面内，从①AB ∥CD ②AB ＝CD ③BC ∥AD ④BC ＝AD 这四个条件中任选两个，使四边形ABCD 是平行四边形的选法有（ ）A.3种B.4种C.5种D.6种分析：可以用①分别与②、③、④组合，可以构成①②，①③两组正确命题；②与②④组合，可以构成②④一组正确命题；③与④组合，可以构成③④一组正确命题，因此，共有4组，故，选择B 。

答案：B点评：本题考查大家灵活掌握平行四边形判定方法和分类思想。

例3、下列条件中，能确定四边形ABCD 是平行四边形的是（ ）A. 对角线AC 平分BDB. ∠A=∠B, ∠C=∠DC. AB=AD, CB=CDD. AB=CD, AD=BC 分析：本体给出的条件有边、角、对角线，那我们就可以从边、角、对角线三个知识点来加以分析，利用排除法进行淘汰。

答案：D点评：只有熟练掌握其知识点，才能做出正确的选择。

例4、D 、E 、F 分别是△ABC 的边BC 、AB 、AC 上，且DE ∥AF ，DE ＝AF ，G 在FD 的延长线上，DG ＝DF ，试说明AG 和ED 互相平分分析：要想判断AG 和ED 互相平分，我们可以说明四边形ADGE 可以连接AD 、EG ，先证四边形AEDF 是平行四边形，再证四边形AEGD 解：连接AD 、EG ，因为，DE ∥AF ，DE ＝AF ，所以，四边形AEFD 是平行四边形（一组对边平行且相等的四边形是平行四边形） 所以，AE ∥DF ，AE=DF （平行四边形的一组对边平行且相等）又因为，DG ＝DF所以，AE=DG ，AE ∥DG所以，四边形AEGD 是平行四边形（一组对边平行且相等的四边形是平行四边形） 所以，AG 和ED 互相平分（平行四边形的对角线互相评分）点评：本题主要是考查平行四边形的判定与性质的运用，在使用的过程中要注意二者的O A BC DG H E F区别和联系。

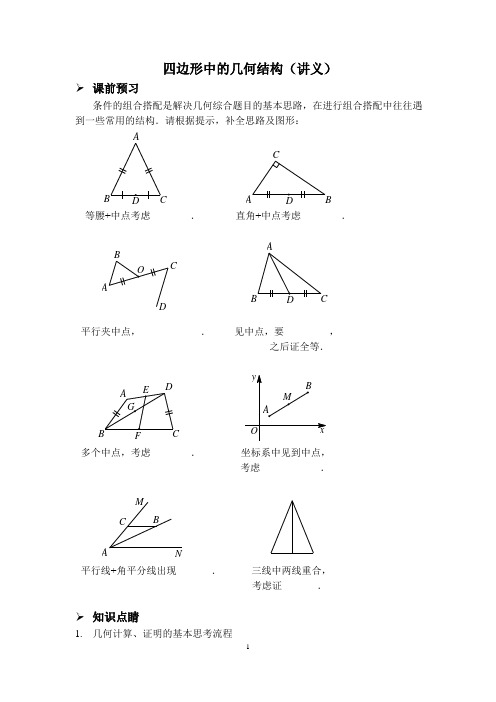
四边形中的几何结构（讲义）➢ 课前预习条件的组合搭配是解决几何综合题目的基本思路，在进行组合搭配中往往遇到一些常用的结构．请根据提示，补全思路及图形：等腰+中点考虑________． 直角+中点考虑________．C平行夹中点，____________． 见中点，要_________，_______之后证全等．多个中点，考虑________． 坐标系中见到中点，考虑____________．M NC BA平行线+角平分线出现_______． 三线中两线重合，考虑证_______．➢ 知识点睛1. 几何计算、证明的基本思考流程①标注条件，合理转化； ②组合特征，分析结构； ③由因导果，执果索因． 2. 特殊四边形中隐含条件①平行四边形中隐含条件：平行、中点；②菱形中隐含条件：平行、中点、角平分线、垂直； ③矩形中隐含条件：平行、中点、垂直；④正方形中隐含条件：平行、中点、角平分线、垂直． 3. 四边形中常见几何结构举例①中点结构：直角+中点，平行夹中点，多个中点； ②旋转结构：等线段共端点； ③弦图结构：外弦图，内弦图； ④面积结构：三个“一半”，平行转化．➢ 精讲精练1. 如图，在平行四边形ABCD 中，BC =2AB ，CE ⊥AB 于点E ，F 为AD 的中点，若∠AEF =54°，则∠B =__________．CDFBE AP A EB FDC第1题图 第2题图2. 如图，在菱形ABCD 中，∠A =110°，E ，F 分别是边AB ，BC 的中点，若EP⊥CD 于点P ，则∠FPC =__________．3. 如图，在四边形ABCD 中，∠ABC =∠ADC =90°，AD = CD ，DP ⊥AB 于点P ．若 四边形ABCD 的面积是16， 则DP 的长为__________．4. DC5. 接BF ，与DE 相交于点G ，连接CG ，与BD 相交于点H ．则下列结论：①△AED ≌△DFB ；②∠BGD =120°；③24BCDG S CG =四边形．其中正确的是__________．（填写序号）B E AF HCD G6. 已知，在平面直角坐标系中放置了5个如图所示的正方形，其中点B 1在y 轴上，点C 1，E 1，E 2，C 2，E 3，E 4，C 3均在x 轴上．若正方形A 1B 1C 1D 1的边长为1，∠B 1C 1O =60°，B 1C 1∥B 2C 2∥B 3C 3，则点A 3到x 轴的距离为___________．7. 如图，O ，在Rt △DCE中，∠CED ABCD 的面积为___________．EO DCBAPQFEABCD第7题图 第8题图8. 如图，在平行四边形ABCD 中，AB :BC =3:2，∠DAB =60°，点E 在AB 边上，且AE :EB =1:2，F 为BC 边的中点，过点D 作DP ⊥AF 于点P ，DQ ⊥CE 于点Q ，则DP :DQ 的值为__________．9. 如图，在边长为4的菱形ABCD 中，∠B =60°，点E ，G ，H ，F 分别在边AB ，BC ，CD ，AD 上，且AF =CG =1，BE =DH =2．P 是直线EF ，GH 之间的任一点，连接PE ，PF ，PG ，PH ，则△PEF 与△PGH 的面积之和为________________．D PFHCGBE A【参考答案】➢课前预习三线合一；斜边中线等于斜边的一半；延长证全等；倍长；倍长；中位线；中点坐标公式；等腰；等腰➢精讲精练1.72°2.55°3. 44.1 35.①②③6.7. 48.9.。

平行四边形的应用平行四边形是一种特殊的四边形，它的对边是平行的。

这种几何形状在现实生活中有着广泛的应用，涉及到建筑、设计、物理等各个领域。

本文将探讨平行四边形的一些应用，并举例说明其在实际情境中的应用价值。

一、建筑领域1. 平行四边形的解析几何应用平行四边形在建筑设计中的应用非常广泛。

在建筑平面图中，平行四边形用来表示建筑物的外形和内部空间的布局。

通过分析平行四边形的各个边长和角度，可以推测建筑物的结构、稳定性和美观性。

2. 平行四边形的结构应用平行四边形在建筑结构中也有其独特的应用。

例如，在桥梁设计中，通过将桥面视为平行四边形，可以确定桥梁的跨度和承重能力，确保桥梁的稳定性和安全性。

二、设计领域1. 平行四边形的比例应用在设计中，平行四边形的比例关系常常被用来实现视觉上的平衡和美感。

通过调整平行四边形的边长和角度，设计师可以创造出丰富的空间效果和流线型的外观。

这种设计技巧在建筑、室内设计和产品设计中都可以见到。

2. 平行四边形的色彩应用在平面设计和图形设计中，平行四边形的色彩应用也非常常见。

通过运用不同色彩的平行四边形，设计师可以创造出丰富的图案和层次感，增加设计作品的视觉吸引力和表达力。

三、物理领域1. 平行四边形的力学应用平行四边形在物理学中有着重要的应用。

例如，在力学和结构力学中，平行四边形的力学性质被用来描述物体的受力情况。

通过分析平行四边形的各个边和角的关系，可以推断物体受力情况及其稳定性。

2. 平行四边形的光学应用在光学领域中，平行四边形也有其独特的应用。

例如，在光线的反射和折射过程中，平行四边形的边界条件被用来描述光线的传播规律和位置变化。

这种应用有助于我们理解光的行为和光学相关的现象。

综上所述，平行四边形在建筑、设计和物理等领域中都有着广泛的应用。

通过分析和应用平行四边形的性质和特点，可以帮助人们更好地理解和解决实际问题。

因此，深入研究和应用平行四边形的知识对于相关领域的专业人士和学习者来说都是非常有价值的。

摘要随着课程改革不断推进，各地出现了各有特点的数学教材,教材的编写者有不同的思路，因此教材在各个方面也会存在一定的差异，同时不同版本的教材对比也有助于教师更好地教学与进行教学研究.通过对人教版、北师大版、苏科版中的“平行四边形”部分进行比较研究,从而帮助对该部分知识点的全面把握,以便更好地把握数学教材内容,优化教学设计.通过文献分析法、对比分析法、统计法、问卷调查法对不同版本初中数学教材从结构、引入、探究及习题设置进行了比较，从而发现三个版本教材的特色以及各自的异同点.通过对此课题的研究,提供一些有益的数学教学建议.关键词平行四边形教材对比人教版北师大版苏科版A comparative study on the set of knowledge points in different editionsof textbooks—— A case study of Parallelogram in junior middle schoolAbstract With the continuous advancement of the curriculum reform, mathematics textbooks with their own characteristics have appeared in various places. The compilers of the textbooks have different ideas, so there are certain differences in various aspects of the textbooks, at the same time, the comparison of different versions of teaching materials is helpful to teachers. This paper makes a comparative study of the "Parallelogram" section in the people s education press, the Beijing Normal University press and the Soviet section press, so as to help us grasp the knowledge points of this section in anall-round way, so as to better grasp the contents of the mathematics teaching materials and optimize the teaching design. Through literature analysis, Comparative Analysis, Statistics and Questionnaire survey, this paper compares the structure, Introduction, exploration and problem setting of different editions of junior middle school mathematics textbooks, thus discovered three edition teaching material's characteristic as well as respective similarities and differences. Through the research on this subject, some useful suggestions on mathematics teaching are provided.Key words Parallelogram textbook comparison People's Education Edition Beijing Normal University Edition Suke edition目录摘要 (II)Abstract (III)引言 (1)1绪论 (1)1.1问题的提出 (1)1.2国内外研究现状 (1)1.2.1国外研究概况 (1)1.2.2国内研究概况 (2)2研究对象、研究维度、研究思路与研究方法 (2)2.1研究对象 (2)2.2研究维度 (2)2.3研究思路 (2)2.4研究方法 (3)3平行四边形内容设置的比较研究 (3)3.1教材内容结构比较 (3)3.2引入的比较 (5)3.3探究活动的比较 (12)3.4习题的比较 (14)4初中不同版本数学教材比较的实证研究 (16)4.1问卷调查对象 (16)4.2问卷调查数据整理 (16)4.3问卷调查数据分析 (17)5结论 (17)5.1三个版本教材的横向比较 (17)5.2三个版本教材的纵向比较 (18)6建议 (18)6.1内容结构方面 (18)6.2引入方式方面 (18)6.3习题设置方面 (19)6.4探究活动方面 (19)结语 (20)参考文献 (21)致谢 (22)附录 (23)引言教育改革的核心是课程改革，课程改革促进了教材的优化 [1]P10.结合不同的地域特点和教育现状，国家支持相关部门编写不同特征的教材，不同教材的编写思路决定了教材在各个方面也会存在一定差异[2]P59-66.目前有很多专家学者对不同版本的初中数学教材进行了对比研究，很多一线教师也在关注不同教材下同一知识点的异同点.目前各种教材是怎样设计的，有什么样的优缺点、异同点，编写意图是什么?这些有待作进一步研究.在实际教学过程中应如何选用和使用教材是值得每一个基础教育工作者思考的问题.作为一名未来从事教育事业的毕业生，我结合自身学习的理论经验和实习期间的实践教学经验，对人民教育出版社[3]P41-67(以下简称人教版)、北京师范大学出版社[4]P135-140（以下简称北师版）、江苏风凰科学技术出版社[5]P56-90（以下简称苏科版）三个版本教材中“平行四边形”的内容进行比较研究，在研究过程中主要运用内容分析和统计分析法，并且结合一定的实践经验，通过对不同教材进行比较，希望可以深入的理解教材，找到不同之处，取长补短，对初中数学教材进行优化与反思.1绪论1.1问题的提出教科书是教师教和学生学的主要载体[6].现如今，越来越多的人去研究教材，新版本的初中数学教材有哪些特点，现在各种教材是怎样设计的，有什么样的优缺点、异同点?这些有待作进一步研究.平行四边形是四边形内容中的重要部分.它在教材中有着呈上启下的作用.研究发现，这部分研究较缺乏，因此，本文通过对三个版本初中数学教材中“平行四边形”部分进行对比研究,分析不同版本教材的特点.1.2 国内外研究现状现在对教材的研究较多，研究的方面也很多，作者搜集了大量的资料，通过分析整理，对国内外已有的教材对比研究现状进行了分析概括.1.2.1国外研究概况近年来，我国教育事业有了很大的发展，因为我们不断与国外教材进行比较研究，比较研究大多是对某一个具体的模块进行具体的分析比较，从而找出国内外教材之间的差异.2002年， Hoyles等学者，借助TIMSS这种手段对多国教材进行有针对性的比较，分析了这些国家的数学教科书与学生的成绩测试以及评价结果，对异同点进行了详细的比较[7]P61-P65；2006年，梁贯成等学者对日本、韩国等国家的教材进行了多方面比较，同时也对比了中澳数学教材中的价值观和中新数学教材的知识架构等等[8]P32-34；2007年，范良火等学者通过对三个国家的初中数学教材内容中的“问题解决步骤的呈现方式”进行比较，发现这三个国家在这方面的异同点，同时也提供了建议[9]P61-75；2013年，曹一鸣等人对不同国家初中数学的数与代数、统计与概率和图形与几何的整体布局进行了比较[10]P29-36。

平行四边形的性质平行四边形是几何学中常见的一个特殊四边形，具有独特的性质。

本文将围绕平行四边形的定义、性质和应用展开论述。

一、平行四边形的定义平行四边形是指具有两对对边分别平行的四边形。

简而言之，就是四条边两两平行的四边形。

除了具备四边形的性质外，平行四边形还有一些与其特有的性质。

二、平行四边形的性质1. 对边性质：平行四边形的两对对边分别相等，即对边相等。

2. 对角线性质：平行四边形的对角线相互平分，并且互相垂直。

3. 角性质：平行四边形的相邻内角互补，即和为180°。

4. 对边角性质：平行四边形的一对对边的内角互补，即和为180°。

5. 对边角关系：平行四边形的一对对边内角相等，另一对对边内角相等。

三、平行四边形的应用平行四边形的性质在实际应用中有着广泛的运用，以下是其中几个常见的应用场景：1. 建筑设计：在建筑设计中，平行四边形的概念可以用来确定建筑物的平面结构，如房屋的地基或屋顶的平面设计。

2. 图形设计：平行四边形的性质被广泛应用于图形设计中，例如设计图纸的布局、logo设计等。

3. 数学几何问题：在解决数学几何问题时，平行四边形的性质可以作为推理和证明的依据，在计算面积、角度等方面具有重要作用。

4. 物理学问题：在物理学中，平行四边形的性质可以用来解决力的平衡问题，如力的分解与合成等。

总结：平行四边形作为一个常见的特殊四边形，具有独特的性质，包括对边相等、对角线相互平分且互相垂直、相邻内角互补等。

这些性质在实际应用中有着广泛的运用，从建筑设计到数学几何问题，都能看到平行四边形的身影。

熟练掌握平行四边形的性质，将有助于我们更好地理解和运用几何知识。