2020年秋苏科版数学七年级上册期末满分突破专练：角的计算综合(二)

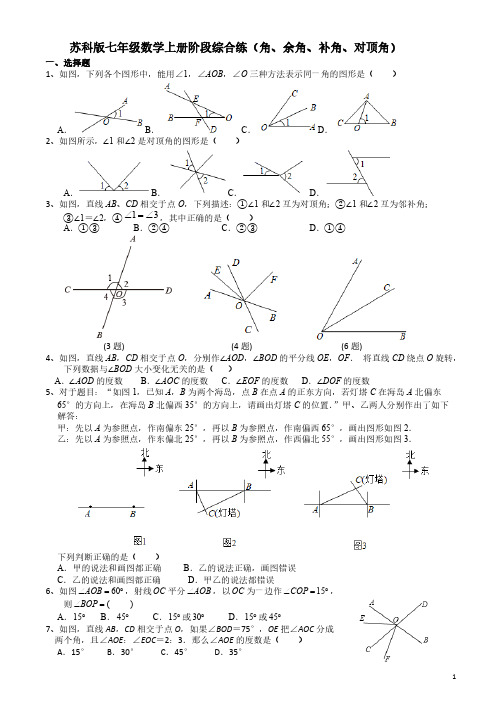
苏科版七年级数学上册阶段综合练（角、余角、补角、对顶角）一、选择题1、如图，下列各个图形中，能用∠1，∠AOB ，∠O 三种方法表示同一角的图形是（ ）A ．B ．C ．D ．2、如图所示，∠1和∠2是对顶角的图形是（ ）A ．B ．C ．D ．3、如图，直线AB 、CD 相交于点O ，下列描述：①∠1和∠2互为对顶角；②∠1和∠2互为邻补角；③∠1＝∠2，④，其中正确的是（ ）13∠=∠A ．①③B ．②④C ．②③D ．①④(3题) (4题) (6题)4、如图，直线AB ，CD 相交于点O ，分别作∠AOD ，∠BOD 的平分线OE ，OF ． 将直线CD 绕点O 旋转，下列数据与∠BOD 大小变化无关的是（ ）A ．∠AOD 的度数B ．∠AOC 的度数 C ．∠EOF 的度数D ．∠DOF 的度数5、对于题目：“如图1，已知A ，B 为两个海岛，点B 在点A 的正东方向，若灯塔C 在海岛A 北偏东65°的方向上，在海岛B 北偏西35°的方向上，请画出灯塔C 的位置．”甲、乙两人分别作出了如下解答：甲：先以A 为参照点，作南偏东25°，再以B 为参照点，作南偏西65°，画出图形如图2．乙：先以A 为参照点，作东偏北25°，再以B 为参照点，作西偏北55°，画出图形如图3．下列判断正确的是（ ）A ．甲的说法和画图都正确B ．乙的说法正确，画图错误C ．乙的说法和画图都正确D ．甲乙的说法都错误6、如图，射线平分，以为一边作，60AOB ∠=︒OC AOB ∠OC 15COP ∠=︒则 (BOP ∠=)A ． B ． C ．或 D ．或15︒45︒15︒30︒15︒45︒7、如图，直线AB ，CD 相交于点O ，如果∠BOD ＝75°，OE 把∠AOC 分成两个角，且∠AOE ：∠EOC ＝2：3．那么∠AOE 的度数是（ ）A ．15°B ．30°C ．45°D ．35°8、如图，直线AB ，CD 相交于点O ，OF 平分∠BOD ，OE 平分∠COF ，∠AOD ：∠BOF ＝4：1，则∠AOE ＝ ．(8题) (9题) (10题)9、如图，直线、相交于点，．下列说法不正确的是 AB CD O 90EOD ∠=︒()A ．B ．AOD BOC ∠=∠AOC AOE∠=∠C ．D ．90AOE BOD ∠+∠=︒180AOD BOD ∠+∠=︒10、如图，直线，相交于点，平分，且，则的度数是 AB CD O OA EOC ∠:2:9EOC EOB ∠∠=BOD ∠()A ．B ．C ．D ．15︒16︒18︒20︒二、填空题11、已知和，画一个角使它等于，画法如下：1∠2∠12∠+∠（1）画______________．AOB ∠=（2）以点O 为顶点，为始边，在的__________作；则．OB AOB ∠2BOC ∠=∠12AOC ∠=∠+∠12、若与是对顶角，的补角是，则的余角的度为 ．α∠β∠α∠100︒β∠13、如图，钟表上显示的时间是，此时，时针与分针的夹角是_________12:20(13题) (14题) (16题)14、如图所示：直线与相交于O ，已知，是的平分线，AB CD 130∠=︒OE BOC ∠则的度数为________．2∠15、平面内，已知，，平分，平分，则 ．90AOB ∠=︒20BOC ∠=︒OE AOB ∠OF BOC ∠EOF ∠=16、如图，直线、相交于点，射线平分，．若，AB CD O OM AOC ∠90MON ∠=︒50BON ∠=︒则的度数为 ．BOD ∠17、如图，∠AOB ＝∠AOC ＝90°，∠DOE ＝90°，OF 平分∠AOD ，∠AOE ＝36°，则∠BOF 的度数＝______．(17题) (18题)18、如图，，相交于点，，有以下结论：AB CD O 90BOE ∠=︒①与互为余角； ②与互为余角； ③；AOC ∠COE ∠BOD ∠COE ∠AOC BOD ∠=∠④与互为补角； ⑤与互为补角； ⑥COE ∠DOE ∠AOC ∠DOE ∠AOC COE∠=∠其中错误的有 （填序号）．三、解答题19、计算：（1）； （2）； （3）； （4）．32175342427︒'''+︒'''90361215︒-︒'''2512355︒'''⨯536︒÷20、完成推理填空：如图，直线AB 、CD 相交于O ，∠EOC ＝90°，OF 是∠AOE 的角平分线，∠COF ＝34°，求∠BOD 的度数．其中一种解题过程如下：请在括号中注明根据，在横线上补全步骤．解：∵∠EOC ＝90°，∠COF ＝34° （ ）∴∠EOF ＝ °又∵OF 是∠AOE 的角平分线 （ ）∴∠AOF ═ ＝56° （ ）∴∠AOC ＝∠ ﹣∠ ＝ °∴∠BOD ＝∠AOC ＝ °（ ）21、如图，已知直线，相交于点，平分，平分．若，AB CD O OE BOD ∠OF COE ∠100AOD ∠=︒求：（1）的度数；EOD ∠（2）的度数．AOF ∠22、如图，直线AB ，CD 相交于点O ，∠AOC ＝120°，OE 平分∠BOC ．（1）求∠BOE 的度数；（2）若OF 把∠AOE 分成两个角，且∠AOF ：∠EOF ＝2：3，判断OA 是否平分∠DOF ？并说明理由．23、如图，为直线上一点，，平分．O AB 90DOE ∠=︒OF BOD ∠（1）若，则 ；20AOE ∠=︒BOF ∠=（2）若是的5倍，求度数．BOF ∠AOE ∠AOE ∠24、已知点是直线上一点，，是的平分线．O AB 60COE ∠=︒OF AOE ∠（1）如图1，当时，求的度数；80BOE ∠=︒COF ∠（2）当和射线在如图2所示的位置，且题目条件不变时．COE ∠OF ①求与之间的数量关系；COF ∠AOE ∠②直接写出的值．2BOE COF ∠-∠25、如图①，直角三角板的直角顶点在直线上，，是三角板的两条直角边，射线是O AB OC OD OE 的平分线．AOD ∠（1）当时，求的度数；50AOE ∠=︒BOD ∠（2）当时，求的度数；30COE ∠=︒BOD ∠（3）当时，则 （用含的式子表示）；COE α∠=BOD ∠=α（4）当三角板绕点逆时针旋转到图②位置时，，其它条件不变，则 O COE α∠=BOD ∠=（用含 的式子表示）．α26、已知直线和相交于，为锐角．AB CD O AOC ∠（1）填空：如图1图中有___________对相等的角（平角除外）分别是_____________________，判断的依据是_____________________（2）如图2，作，平分，求的度数．90COE ∠=︒OF COB ∠AOF EOF ∠-∠（3）在（2）的条件下，，计算的度数．:2:5AOC COF ∠∠=DOF ∠答案一、选择题1、如图，下列各个图形中，能用∠1，∠AOB，∠O三种方法表示同一角的图形是（ ）A．B．C．D．【解题思路】根据角的表示方法判断即可．【解答过程】解：A、图形中的∠1，能用∠AOB表示，但不能用∠O表示，本选项不符合题意；B、图形中的∠1，能用∠AOB，∠O表示，本选项符合题意；C、图形中的∠1，能用∠AOB表示，但不能用∠O表示，本选项不符合题意；D、图形中的∠1，能用∠AOB表示，但不能用∠O表示，本选项不符合题意；故选：B．2、如图所示，∠1和∠2是对顶角的图形是（ ）A．B．C．D．【答案】B【分析】根据对顶角的定义，对顶角：有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角，据此即可求解．【详解】解：对顶角：有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，满足条件的只有B ．故选：B ．3、如图，直线AB 、CD 相交于点O ，下列描述：①∠1和∠2互为对顶角；②∠1和∠2互为邻补角；③∠1＝∠2，④，其中正确的是（ ）13∠=∠A ．①③B ．②④C ．②③D ．①④【答案】B【分析】根据对顶角和邻补角的定义逐个判断即可得．【详解】解：和不是对顶角，互为邻补角，则①错误，②正确；1∠2∠，但和不一定相等，则③错误；12180∠+∠=︒1∠2∠由对顶角相等得：，则④正确；13∠=∠综上，正确的是②④，故选：B ．4、如图，直线AB ，CD 相交于点O ，分别作∠AOD ，∠BOD 的平分线OE ，OF ． 将直线CD 绕点O 旋转，下列数据与∠BOD 大小变化无关的是（ ）A ．∠AOD 的度数B ．∠AOC 的度数 C ．∠EOF 的度数D ．∠DOF 的度数【答案】C【分析】由角平分线性质解得，根据对角线性质、平角性质解得，90EOF ∠=︒180AOD BOD ∠=︒-∠，据此解题．1,2AOC BOD DOF BOD∠=∠∠=∠【详解】解： OE ，OF 平分∠AOD ，∠BOD 11,22AOE EOD AOD DOF FOB BOD∴∠=∠=∠∠=∠=∠180AOD BOD ∠+∠=︒ 111()90222EOD DOF AOD BOD AOD BOD ∴∠+∠=∠+∠=∠+∠=︒90EOF ∴∠=︒180AOD BOD∴∠=︒-∠1,2AOC BOD DOF BOD∴∠=∠∠=∠都与∠BOD 大小变化有关，只有∠EOF 的度数与∠BOD 大小变化无关，故选：C ．5、对于题目：“如图1，已知A ，B 为两个海岛，点B 在点A 的正东方向，若灯塔C 在海岛A 北偏东65°的方向上，在海岛B 北偏西35°的方向上，请画出灯塔C 的位置．”甲、乙两人分别作出了如下解答：甲：先以A 为参照点，作南偏东25°，再以B 为参照点，作南偏西65°，画出图形如图2．乙：先以A 为参照点，作东偏北25°，再以B 为参照点，作西偏北55°，画出图形如图3．下列判断正确的是（ ）A ．甲的说法和画图都正确B ．乙的说法正确，画图错误C ．乙的说法和画图都正确D ．甲乙的说法都错误【解题思路】根据方向角定义即可进行判断．【解答过程】解：根据方向角定义可知：灯塔C 在海岛A 北偏东65°的方向上，在海岛B 北偏西35°的方向上，画出灯塔C 的位置如图3．故选：D ．6、如图，射线平分，以为一边作，则 60AOB ∠=︒OC AOB ∠OC 15COP ∠=︒(BOP ∠=)A ．B ．C ．或D ．或15︒45︒15︒30︒15︒45︒【分析】根据，射线平分，可得，分在内，在60AOB ∠=︒OC AOB ∠30BOC ∠=︒OP BOC ∠OP 内，两种情况讨论求解即可．AOC ∠【解析】，射线平分，60AOB ∠=︒ OC AOB ∠，1302AOC BOC AOB ∴∠=∠=∠=︒又15COP ∠=︒①当在内，OP BOC ∠，301515BOP BOC COP ∠=∠-∠=︒-︒=︒②当在内，OP AOC ∠，301545BOP BOC COP ∠=∠+∠=︒+︒=︒综上所述：或．15BOP ∠=︒45︒故选：．D7、如图，直线AB ，CD 相交于点O ，如果∠BOD ＝75°，OE 把∠AOC 分成两个角，且∠AOE ：∠EOC ＝2：3．那么∠AOE 的度数是（ ）A ．15°B ．30°C ．45°D ．35°【解析】∵∠BOD ＝75°，∴∠AOC ＝75°，∵∠AOE ：∠EOC ＝2：3，∴设∠AOE ＝2x °，∠EOC ＝3x °，则2x +3x ＝75，解得：x ＝15，∴∠AOE ＝30°，故选：B ．8、如图，直线AB ，CD 相交于点O ，OF 平分∠BOD ，OE 平分∠COF ，∠AOD ：∠BOF ＝4：1，则∠AOE ＝ ．【分析】根据角平分线的定义得出∠BOD ＝2∠BOF ，∠BOF ＝∠DOF ，根据∠AOD ：∠BOF ＝4：1求出∠AOD ：∠BOD ＝4：2，根据邻补角互补求出∠AOD ＝120°，∠BOD ＝60°，求出∠AOC ＝60°，根据角平分线定义求出∠COE ，再求出答案即可．【解析】∵OF 平分∠BOD ，∴∠BOD ＝2∠BOF ，∠BOF ＝∠DOF ，∵∠AOD ：∠BOF ＝4：1，∴∠AOD ：∠BOD ＝4：2，∵∠AOD +∠BOD ＝180°，∴∠AOD ＝120°，∠BOD ＝60°，∴∠AOC ＝∠BOD ＝60°，∴∠BOF ＝∠DOF==30°， 6021∴∠COF ＝180°﹣∠DOF ＝150°，∵OE 平分∠COF ，∴∠COE=COF=，∠21 7515021=⨯∴∠AOE ＝∠AOC +∠COE ＝60°+75°＝135°，故答案为：135°．9、如图，直线、相交于点，．下列说法不正确的是 AB CD O 90EOD ∠=︒()A ．B ．AOD BOC∠=∠AOC AOE ∠=∠C ．D ．90AOE BOD ∠+∠=︒180AOD BOD ∠+∠=︒【分析】根据对顶角相等可得，不是的角平分线，因此和不一AOD BOC ∠=∠AO COE ∠AOC ∠AOE ∠定相等，根据，利用平角定义可得，根据邻补角互补可得90EOD ∠=︒90AOE BOD ∠+∠=︒180AOD BOD ∠+∠=︒【解析】、，说法正确；A AOD BOC ∠=∠、，说法错误；B AOC AOE ∠=∠、，说法正确；C 90AOE BOD ∠+∠=︒、，说法正确；D 180AOD BOD ∠+∠=︒故选：．B 10、如图，直线，相交于点，平分，且，则的度数是 AB CD O OA EOC ∠:2:9EOC EOB ∠∠=BOD ∠()A ．B ．C ．D ．15︒16︒18︒20︒【分析】根据角平分线的定义和对顶角的性质即可得到结论．【解析】设，，2EOC x ∠=9EOB x ∠=平分，OA EOC ∠，12AOE EOC x ∴∠=∠=根据题意得，解得，9180x x +=︒18x =︒，18EOA AOC x ∴∠=∠==︒，18BOD AOC ∴∠=∠=︒故选：．C 二、填空题11、已知和，画一个角使它等于，画法如下：1∠2∠12∠+∠（1）画______________．AOB ∠=（2）以点O 为顶点，为始边，在的__________作；则．OB AOB ∠2BOC ∠=∠12AOC ∠=∠+∠【答案】 外部1∠【分析】根据角的画法步骤，先画出∠AOB=∠1，再在∠AOB 的外部画出∠2，即可得到∠AOC【解析】画法详解:（1）画∠AOB=∠1．（2）以点O 为顶点，OB 为始边，在∠AOB 的外部作∠BOC=∠2；则∠AOC=∠1+∠2．故答案: （1）∠1 （2）外部12、若与是对顶角，的补角是，则的余角的度为 ．α∠β∠α∠100︒β∠【分析】根据补角定义可得的度数，再根据对顶角相等可得答案．α∠【解析】的补角为，α∠ 100︒，18010080α∴∠=︒-︒=︒与是对顶角，α∠ β∠，80βα∴∠=∠=︒的余角的度为，β∴∠10︒故答案为：．10︒13、如图，钟表上显示的时间是，此时，时针与分针的夹角是_________12:20【答案】110︒【分析】根据时针在钟面上每分钟转，分针每分钟转，然后分别求出时针、分针转过的角度，即可得到答0.5 6案．【详解】解：∵时针在钟面上每分钟转，分针每分钟转，0.5 6 ∴钟表上12时20分钟时，时针转过的角度为，分针转过的角度为，0.52010⨯= 620120⨯=所以时分针与时针的夹角为．12:2012010110-= 14、如图所示：直线与相交于O ，已知，是的平分线，AB CD 130∠=︒OE BOC ∠则的度数为________．2∠【答案】75°．【分析】由邻补角的定义可求得∠COB ＝150°，然后根据角平分线的定义可求得∠2．【详解】解：∵∠1+∠COB ＝180°，∠1＝30°，∴∠COB ＝180°﹣30°＝150°．∵OE 是∠BOC 的平分线，∴∠2＝ ∠COB ＝75°．12故答案为：75°．15、平面内，已知，，平分，平分，则 ．90AOB ∠=︒20BOC ∠=︒OE AOB ∠OF BOC ∠EOF ∠=【分析】分两种情况：当在内时；当在外时．根据角平分线的定义，角的和差进行OC AOB ∠OC AOB ∠解答便可．【解析】当在内时，如图1，OC AOB ∠；11119020352222EOF BOE BOF AOB BOC ∠=∠-∠=∠-∠=⨯︒-⨯︒=︒当在外时，如图2，OC AOB ∠，11119020552222EOF BOE BOF AOB BOC ∠=∠+∠=∠+∠=⨯︒+⨯︒=︒故答案为：或．35︒55︒16、如图，直线、相交于点，射线平分，．若，AB CD O OM AOC ∠90MON ∠=︒50BON ∠=︒则的度数为 ．BOD ∠【分析】首先根据余角的性质可得，再根据角平分线的性质可算出905040AOM ∠=︒-︒'=︒，再根据对顶角相等可得的度数，40280AOC ∠=︒⨯=︒BOD ∠【解析】．，90MON ∠=︒ 50BON ∠=︒，905040AOM ∴∠=︒-︒'=︒射线平分，OM AOC ∠，40280AOC ∴∠=︒⨯=︒．80BOD AOC ∴∠=∠=︒故答案为：．80︒17、如图，∠AOB ＝∠AOC ＝90°，∠DOE ＝90°，OF 平分∠AOD ，∠AOE ＝36°，则∠BOF 的度数＝______．【答案】63°【分析】先求出∠AOD ＝54°，再求出∠BOD 和∠DOF ，即可求出∠BOF ．【详解】解：∵∠DOE ＝90°，∠AOE ＝36°，∴∠AOD ＝90°﹣36°＝54°，∵∠AOB ＝90°，∴∠BOD ＝90°﹣54°＝36°，∵OF 平分∠AOD ，∴∠DOF ∠AOD ＝27°，12=∴∠BOF ＝36°+27°＝63°．18、如图，，相交于点，，有以下结论：AB CD O 90BOE ∠=︒①与互为余角； ②与互为余角；③；AOC ∠COE ∠BOD ∠COE ∠AOC BOD ∠=∠④与互为补角； ⑤与互为补角； ⑥COE ∠DOE ∠AOC ∠DOE ∠AOC COE∠=∠其中错误的有 （填序号）．【分析】根据垂线的定义、对顶角、邻补角的性质解答即可．【解析】，相交于点，，AB CD O 90BOE ∠=︒①与互为余角，正确；∴AOC ∠COE ∠②与互为余角，正确；BOD ∠COE ∠③，正确；AOC BOD ∠=∠④与互为补角，正确；COE ∠DOE ∠⑤设，则，，故与互为补角错误；30AOC ∠=︒120DOE ∠=︒180AOC DOE ∠+∠≠︒AOC ∠BOC DOE ∠=∠⑥，错误；AOC BOD COE ∠=∠≠∠故答案为：⑤⑥．三、解答题19、计算：（1）； （2）； （3）； （4）．32175342427︒'''+︒'''90361215︒-︒'''2512355︒'''⨯536︒÷【分析】（1）1度分，即，1分秒，即，依此计算加法；60=160︒='60=160'=''（2）1度分，即，1分秒，即，依此计算减法；60=160︒='60=160'=''（3）1度分，即，1分秒，即，依此计算乘法；60=160︒='60=160'=''（4）1度分，即，1分秒，即，依此计算除法．60=160︒='60=160'=''【解析】（1）原式；=︒'''=︒74596075（2）原式；=︒'''534745（3）原式；=︒'''=︒'''12560175126255（4）原式．850=︒'20、完成推理填空：如图，直线AB、CD相交于O，∠EOC＝90°，OF是∠AOE的角平分线，∠COF＝34°，求∠BOD的度数．其中一种解题过程如下：请在括号中注明根据，在横线上补全步骤．解：∵∠EOC＝90°，∠COF＝34°（ ）∴∠EOF＝ °又∵OF是∠AOE的角平分线（ ）∴∠AOF═ ＝56°（ ）∴∠AOC＝∠ ﹣∠ ＝ °∴∠BOD＝∠AOC＝ °（ ）【分析】利用角的和差关系和角平分线定义可得∠AOF的度数，然后利用垂垂线定义计算出∠AOC的度数，再根据对顶角相等可得∠BOD的度数．【解析】∵∠EOC＝90°，∠COF＝34°（已知），∴∠EOF＝56°，又∵OF是∠AOE的角平分线（已知），∴∠AOF ═∠EOF ＝56° （角平分线定义），∴∠AOC ＝∠AOF ﹣∠COF ＝22°，∴∠BOD ＝∠AOC ＝22°（对顶角相等）．故答案为：已知；56；已知；∠EOF ；角平分线定义；AOF ；COF ；22；22；对顶角相等．21、如图，已知直线，相交于点，平分，平分．若，AB CD O OE BOD ∠OF COE ∠100AOD ∠=︒求：（1）的度数；EOD ∠（2）的度数．AOF ∠【答案】（1）40°；（2）150°【分析】（1）根据邻补角的性质，可求出的度数，再根据角平分线的性质即可求出的度数，DOB ∠DOE ∠（2）根据邻补角的性质，可求出的度数，再根据角平分线的性质，求出，在根据对顶角COE ∠COF ∠的性质求出，即可求出的度数．AOC ∠AOF ∠【详解】（1）∵直线，相交于点，AB CD O ∴，180AOD BOD ∠+∠=︒∵，100AOD ∠=︒∴，18080BOD AOD ∠=-∠=°°∵平分，OE BOD ∠∴．1402DOE BOD ∠=∠=°（2）∵，180COE DOE ∠+∠=°∴，180140COE DOE ∠=-∠=°°∵平分，OF COE ∠∴，1702COF COE ∠=∠=°∵，80AOC BOD ∠=∠=︒∴．150AOF AOC COF ∠=∠+∠=°22、如图，直线AB ，CD 相交于点O ，∠AOC ＝120°，OE 平分∠BOC ．（1）求∠BOE 的度数；（2）若OF 把∠AOE 分成两个角，且∠AOF ：∠EOF ＝2：3，判断OA 是否平分∠DOF？并说明理由．【答案】（1）30°；（2）平分，理由见解析．【分析】（1）根据邻补角的概念求出，根据角平分线的定义计算，得到答案；BOC ∠（2）求出，根据题意分别求出，根据角平分线的定义证明即可．AOE ∠AOF EOF ∠∠、【详解】解：（1）∵∠AOC ＝120°，∴∠BOC ＝180°﹣120°＝60°，∵OE 平分∠BOC ，∴∠BOE ＝∠BOC ＝×60°＝30°；1212（2）OA 平分∠DOF ，理由如下：∵∠BOE ＝30°，∴∠AOE ＝180°﹣30°＝150°，∵∠AOF ：∠EOF ＝2：3，∴∠AOF ＝60°，∠EOF ＝90°，∵∠AOD ＝∠BOC ＝60°，∴∠AOD ＝∠AOF ，∴OA 平分∠DOF ．23、如图，为直线上一点，，平分．O AB 90DOE ∠=︒OF BOD ∠（1）若，则 ；20AOE ∠=︒BOF ∠=（2）若是的5倍，求度数．BOF ∠AOE ∠AOE ∠【分析】（1）根据互余、互补以及角平分线的定义可得答案；（2）由（1）的方法列出方程可求出答案．【解析】（1），，90DOE ∠=︒ 20AOE ∠=︒．902070AOD DOE AOE ∴∠=∠-∠=︒-︒=︒．180********BOD AOD ∴∠=︒-∠=︒-︒=︒平分．OF BOD ∠．∴111105522BOF BOD ∠=∠=⨯︒=︒故答案为：．55︒（2）设，AOE x ∠=则．5BOF x ∠=．90AOD x ∴∠=︒-．180(90)90BOD x x ∠=︒-︒-=︒+平分，OF BOD ∠．∴11(90)4522BOF x x ∠=︒+=︒+，∴14552x x ︒+=即9452x =︒，∴245109x =︒⨯=︒．10AOE ∴∠=︒24、已知点是直线上一点，，是的平分线．O AB 60COE ∠=︒OF AOE ∠（1）如图1，当时，求的度数；80BOE ∠=︒COF ∠（2）当和射线在如图2所示的位置，且题目条件不变时．COE ∠OF ①求与之间的数量关系；COF ∠AOE ∠②直接写出的值．2BOE COF ∠-∠【答案】（1）10°；（2）①；②60°1602COF AOE∠=︒-∠【分析】（1）利用角平分线的定义以及角的和差计算即可求解；（2）利用角平分线的定义以及角的和差列式即可；（3）利用邻补角的定义结合（2）的结论即可求解．【详解】解：（1）∵，，∴，．80BOE ∠=︒60COE ∠=︒40AOC ∠=︒100AOE ∠=︒∵是的平分线，∴，OF AOE ∠1502AOF AOE ∠=∠=︒∴；10COF AOF AOC ∠=∠-∠=︒（2）①∵是的平分线，∴，OF AOE ∠12EOF AOE∠=∠∴；1602COF COE EOF AOE∠=∠-∠=︒-∠②∵∠BOE=180-∠AOE ，︒∴∠BOE-2∠COF=180-∠AOE-2(60-∠AOE)=180-∠AOE-120+∠AOE ．︒︒12︒︒60=︒25、如图①，直角三角板的直角顶点在直线上，，是三角板的两条直角边，射线是O AB OC OD OE 的平分线．AOD ∠（1）当时，求的度数；50AOE ∠=︒BOD ∠（2）当时，求的度数；30COE ∠=︒BOD ∠（3）当时，则 （用含的式子表示）；COE α∠=BOD ∠=α（4）当三角板绕点逆时针旋转到图②位置时，，其它条件不变，则 O COE α∠=BOD ∠=（用含 的式子表示）．α【分析】（1）根据角平分线的定义先求出，再根据互补求出即可；AOD ∠BOD ∠（2）根据互余求出，再根据角平分线的定义求出，最后根据互补求出的答案；DOE ∠AOD ∠（3）由（2）的解题过程可得答案；（4）根据互余、互补、角平分线的定义可求出答案．【解析】（1）射线平分，，OE AOD ∠22250100AOD AOE DOE ∴∠=∠=∠=⨯︒=︒；180********BOD AOD ∴∠=︒-∠=︒-︒=︒（2），，，90COD ∠=︒ 30COE ∠=︒903060DOE ∴∠=︒-︒=︒又平分，，OE AOD ∠2260120AOD DOE ∴∠=∠=⨯︒=︒；180********BOD AOD ∴∠=︒-∠=︒-︒=︒（3），，，90COD ∠=︒ COE α∠=90DOE α∴∠=︒-又平分，，OE AOD ∠22(90)1802AOD DOE αα∴∠=∠=⨯︒-=︒-，180********BOD AOD αα∴∠=︒-∠=︒-︒+=故答案为：；2α（4）由图②得，，90DOE α∠=-︒平分，，OE AOD ∠22180AOD DOE α∴∠=∠=-︒，18018021803602BOD AOD αα∴∠=︒-∠=︒-+︒=︒-故答案为：．3602α︒-26、已知直线和相交于，为锐角．AB CD O AOC ∠（1）填空：如图1图中有___________对相等的角（平角除外）分别是_____________________，判断的依据是_____________________（2）如图2，作，平分，求的度数．90COE ∠=︒OF COB ∠AOF EOF ∠-∠（3）在（2）的条件下，，计算的度数．:2:5AOC COF ∠∠=DOF ∠【答案】（1）2，、，对顶角相等；（2）90°；（3）105°=COB AOD ∠∠=AOC BOD ∠∠【分析】（1）根据对顶角相等证明即可；（2）设，表示已知条件中的角推理计算即可；=AOC x ∠（3）结合（2）中的关系列方程即可求出x 的值，再由和互补求AOC COF ∠∠、DOF ∠COF ∠出．DOF ∠【详解】（1）根据对顶角相等可得图1中有2对相等的角（平角除外）分别是:，．=COB AOD ∠∠=AOC BOD ∠∠故答案为：2，、，对顶角相等；=COB AOD ∠∠=AOC BOD ∠∠（2）设°，则=AOC x ∠180BOC x ∠=︒-︒∵平分∴OF COB ∠11=9022COF BOC x ∠∠=︒-︒∴1==90+2AOF AOC COF x ∠∠+∠︒︒∵∴90COE ∠=︒1=2EOF COE COF x ∠∠-∠=︒∴；11=90+=9022AOF EOF x x ∠-∠-︒（3）∵:2:5AOC COF ∠∠=∴5=2AOC COF∠∠由（2）可知：，=AOC x ∠1=902COF x ∠︒-︒∴解得15=2(90)2x x ︒︒-︒30x =︒∴, ∴190=752COF x ∠=-︒180105DOF COF ∠=-∠=︒27。

2020年秋人教数学七年级上册期末满分突破专练：角的计算综合（三）1．如图，A，O，B三点在一条直线上，∠AOC＝3∠COD，OE平分∠BOD，∠COE＝80°，求∠COD的度数．2．如图，OC是∠AOB内一条射线，且∠AOC＜∠BOC，OE是∠AOB的平分线，OD是∠AOC的平分线，则：（1）若∠AOB＝108°，∠AOC＝36°，则OC是∠DOE平分线．请说明理由；（2）小明由第（1）题得出猜想：当∠AOB＝3∠AOC时，OC一定平分∠DOE．你觉得小明的猜想正确吗？若正确，请说明理由；若不正确，判断当∠AOB和∠AOC满足什么条件时OC一定平分∠DOE，并说明理由．3．如图，OC是∠AOB内的一条射线，OD、OE分别平分∠AOB、∠AOC．（1）若∠BOC＝80°，∠AOC＝40°，求∠DOE的度数；（2）若∠BOC＝α，∠AOC＝50°，求∠DOE的度数；（3）若∠BOC＝α，∠AOC＝β，试猜想∠DOE与α、β的数量关系并说明理由．4．已知O是直线AB上的一点，∠COD＝90°，OE平分∠BOC．（1）如图①，若∠AOC＝30°，∠DOE＝；（2）如图①，若∠AOC＝α，∠DOE＝；（用含α的代数式表示）；（3）将图①中的∠DOC绕顶点O顺时针旋转至图②的位置，其他条件不变，那么（2）中所求出的结论是否还成立，请说明理由．5．已知，点O为直线AB上一点，∠COD＝90°，OE是∠AOD的平分线．（1）如图1，若∠COE＝63°，求∠BOD的度数；（2）如图2，OF是∠BOC的平分线，求∠EOF的度数；（3）如图3，在（2）的条件下，OP是∠BOD的一条三等分线，∠DOP＝∠BOD，若∠AOC+∠DOF＝∠EOF，求∠FOP的度数．6．已知∠AOB＝90°，OC是一条可以绕点O转动的射线，ON平分∠AOC，OM平分∠BOC．（1）当射线OC转动到∠AOB的内部时，如图1，求∠MON的度数．（2）当射线OC转动到∠AOB的外时（90°＜∠BOC＜∠180°），如图2，∠MON的大小是否发生变化？变或者不变均说明理由．7．26、如图，∠AOB＝90°．∠BOC＝30°，OM平分∠AOC，ON平分∠BOC．（1）求∠MON的度数；（2）若∠BOC＝60°，其他条件不变，则∠MON＝；（3）若∠AOB＝α，其他条件不变，求∠MON的度数；（4）从上面的结果能看出什么规律？8．已知∠AOD＝160°，OB、OC、OM、ON是∠AOD内的射线．（1）如图1，若OM平分∠AOB，ON平分∠BOD．当OB绕点O在∠AOD内旋转时，求∠MON 的大小；（2）如图2，若∠BOC＝20°，OM平分∠AOC，ON平分∠BOD．当∠BOC绕点O在∠AOD 内旋转时，求∠MON的大小；（3）在（2）的条件下，若∠AOB＝10°，当∠BOC在∠AOD内绕着点O以2度/秒的速度逆时针旋转t秒时，∠AOM＝∠DON．求t的值．9．已知∠AOB＝90°，∠COD＝60°，按如图1所示摆放，将OA、OC边重合在直线MN上，OB、OD边在直线MN的两侧：（1）保持∠AOB不动，将∠COD绕点O旋转至如图2所示的位置，则①∠AOC+∠BOD＝；②∠BOC﹣∠AOD＝．（2）若∠COD按每分钟5°的速度绕点O逆时针方向旋转，∠AOB按每分钟2°的速度也绕点O逆时针方向旋转，OC旋转到射线ON上时都停止运动，设旋转t分钟，计算∠MOC ﹣∠AOD（用t的代数式表示）．（3）保持∠AOB不动，将∠COD绕点O逆时针方向旋转n°（n≤360），若射线OE平分∠AOC，射线OF平分∠BOD，求∠EOF的大小．10．如图，已知∠AOC＝∠BOD＝120°，∠BOC＝∠AOD．（1）求∠AOD的度数；（2）若射线OB绕点O以每秒旋转20°的速度顺时针旋转，同时射线OC以每秒旋转15°的速度逆时针旋转，设旋转的时间为t秒（0＜t＜6），试求当∠BOC＝20°时t的值；（3）若∠AOB绕点O以每秒旋转5°的速度逆时针旋转，同时∠COD绕点O以每秒旋转10°的速度逆时针旋转，设旋转的时间为t秒（0＜t＜18），OM平分∠AOC，ON平分∠BOD，在旋转的过程中，∠MON的度数是否发生改变？若不变，求出其值：若改变，说明理由．参考答案1．解：设∠COD＝x°，∵∠AOC＝3∠COD，∴∠AOC＝3x°，∠AOD＝4x°，∵OE平分∠BOD，∴∠BOE＝∠DOE＝（180°﹣∠AOD）＝（90°﹣2x）°，由∠COE＝∠COD+∠DOE得，x+90°﹣2x＝80°，∴x＝10°，即：∠COD＝10°．2．解：（1）∵OE是∠AOB的平分线，∠AOB＝108°，∴∠AOE＝∠BOE＝∠AOB＝×108°＝54°，∵∠AOC＝36°，∴∠COE＝54°﹣36°＝18°，∵OD是∠AOC的平分线，∠AOC＝36°，∴∠COD＝∠AOD＝∠AOC＝×36°＝18°，∴OC是∠DOE平分线；（2）正确，设∠AOC＝α，则∠AOB＝3α，∵OE平分∠AOB，∠AOB＝3α，∴∠AOE＝α，∵∠AOC＝α，∴∠COE＝α，∵OD是∠AOC的平分线，∴∠COD＝α＝∠COE，∴OC平分∠DOE．3．解：（1）∵OD、OE分别平分∠AOB、∠AOC，∠AOC＝40°，∴∠AOE＝∠EOC＝∠AOC＝20°，∠AOB＝2∠AOD＝2∠DOB，∵∠BOC＝∠BOD+∠COD＝∠AOD+∠COD，∴∠BOC＝∠AOC+2∠COD，即：80°＝40°+2∠COD，∴∠COD＝20°，∴∠DOE＝∠COD+∠COE＝20°+20°＝40°；（2）∵OD、OE分别平分∠AOB、∠AOC．∴∠AOE＝∠EOC＝∠AOC＝25°，∠AOB＝2∠AOD＝2∠DOB，∵∠BOC＝∠BOD+∠COD＝∠AOD+∠COD，∴∠BOC＝∠AOC+2∠COD，即：α＝50°+2∠COD，∴∠COD＝，∴∠DOE＝∠COD+∠COE＝+25°＝；（3），与β无关∵OD、OE分别平分∠AOB、∠AOC．∴∠AOE＝∠EOC＝∠AOC＝，∠AOB＝2∠AOD＝2∠DOB，∵∠BOC＝∠BOD+∠COD＝∠AOD+∠COD，∴∠BOC＝∠AOC+2∠COD，即：α＝β+2∠COD，∴∠COD＝，∴∠DOE＝∠COD+∠COE＝+＝；4．解：（1）∵∠AOC＝30°，∴∠BOC＝150°，∵OE平分∠BOC，∴∠COE＝75°，又∵∠COD＝90°，∴∠DOE＝90°﹣75°＝15°．故答案为：15°；（2）∵∠AOC＝α，∴∠BOC＝180°﹣α，∵OE平分∠BOC，∴∠COE＝90°﹣α，又∵∠COD＝90°，∴∠DOE＝90°﹣（90°﹣α）＝α．故答案为：α；（3）结论仍然成立，理由：∵∠AOC＝α，∴∠BOC＝180°﹣α，∵OE平分∠BOC，∴∠COE＝∠BOC＝90°﹣α，∴∠DOE＝90°﹣∠COE＝90°﹣（90°﹣α）＝α．5．解：（1）∵∠COD＝90°，∠COE＝63°，∴∠DOE＝∠COD﹣∠COE＝27°，∵OE是∠AOD的平分线，∴∠AOD＝2∠DOE＝54°，∴∠BOD＝180°﹣∠AOD＝180°﹣54°＝126°；答：∠BOD的度数为126°．（2）∵OE是∠AOD的平分线．∴∠AOE＝，∵OF是∠BOC的平分线，∴∠BOF＝∠COF＝＝，∴∠EOF＝180°﹣∠AOE﹣∠BOF＝∵∠AOC+∠BOD＝180°﹣90°＝90°，∴∠EOF＝×90°＝45°，答：∠EOF的度数为45°．（3）由（2）得∠EOF＝45°∵∠AOC+∠DOF＝∠EOF＝45°，∴∠DOF＝45°﹣∠AOC，又∵∠DOF＝∠COD﹣∠COF＝＝45°﹣∠BOD，∴45°﹣∠AOC＝45°﹣∠BOD，∴∠AOC＝∠BOD，∵∠AOC+∠BOD＝90°，∴∠AOC＝30°，∠BOD＝60°，∴∠DOF＝45°﹣30°＝15°，∵∠DOP＝∠BOD，∴∠DOP＝20°，∴∠FOP＝∠DOF+∠DOP＝15°+20°＝35°6．解：（1）如图1所示：∵ON平分∠AOC，∴∠CON＝，又∵OM平分∠BOC，∴∠COM＝，又∵∠AOB＝∠AOC+∠BOC＝90°，∴∠MON＝∠CON+∠COM＝＝＝45°；（2）∠MON的大小不变，如图2所示，理由如下：∵OM平分∠BOC，∴∠MOC＝，又∵ON平分∠AOC，∴∠AON＝，又∵∠MON＝∠AON+∠AOM，∴∠MON＝＝＝＝45°．7．解：（1）根据题意，得∵∠AOB＝90°，∠BOC＝30°，∴∠AOC＝∠AOB+∠BOC＝120°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC＝∠AOC＝60°，∠CON＝BOC＝15°，∴∠MON＝∠MOC﹣∠CON＝60°﹣15°＝45°．答：∠MON的度数为45°．（2）∠MON＝（150﹣60）＝45°．故答案为45°．（3）∵∠AOB＝α，∠BOC＝30°，∴∠AOC＝∠AOB+∠BOC＝α+30°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC＝∠AOC＝α+15°，∠CON＝BOC＝15°，∴∠MON＝∠MOC﹣∠CON＝+15°﹣15°＝．答：∠MON的度数为．（4）∠MON的度数始终是∠AOB的一半，与∠BOC的大小没有关系．8．解：（1）因为∠AOD＝160°，OM平分∠AOB，ON平分∠BOD，所以∠MOB＝∠AOB，∠BON＝∠BOD，即∠MON＝∠MOB+∠BON＝∠AOB∠BOD＝（∠AOB+∠BOD）＝∠AOD＝80°，答：∠MON的度数为80°；（2）因为OM平分∠AOC，ON平分∠BOD，所以∠MOC＝∠AOC，∠BON＝∠BOD，射线OC在OB左侧时，如图：∠MON＝∠MOC+∠BON﹣∠BOC＝∠AOC∠BOD﹣∠BOC＝（∠AOC+∠BOD）﹣∠BOC＝（∠AOD+∠BOC）﹣∠BOC＝×180°﹣20°＝70°；答：∠MON的度数为70°．（3）∵射线OB从OA逆时针以2°每秒的速度旋转t秒，∠COB＝20°，∴根据（2）中，得∠AOC＝∠AOB+∠COB＝2t°+10°+20°＝2t°+30°．∵射线OM平分∠AOC，∴∠AOM＝∠AOC＝t°+15°．∵∠BOD＝∠AOD﹣∠BOA，∠AOD＝160°，∴∠BOD＝150°﹣2t°．∵射线ON平分∠BOD，∴∠DON＝∠BOD＝75°﹣t°．又∵∠AOM：∠DON＝2：3，∴（t+15）：（75﹣t）＝2：3，解得t＝21．答：t的值为21秒．9．解：（1）①∠AOC+∠BOD＝∠AOC+∠AOD+∠AOB＝∠COD+∠AOB＝60°+90°＝150°；②∠BOC﹣∠AOD＝（∠AOB﹣∠AOC）﹣（∠COD﹣∠AOC）＝∠AOB﹣∠AOC﹣∠COD+∠AOC＝∠AOB﹣∠COD＝90°﹣60°＝30°；故答案为：150°、30°；（2）设运动时间为t秒，0＜t≤36，∠MOC＝（5t）°，①0＜t≤20时，OD与OA相遇前，∠AOD＝（60+2t﹣5t）°＝（60﹣3t）°，∴∠MOC﹣∠AOD＝（8t﹣60）°；②20＜t≤36时，OD与OA相遇后，∠AOD＝[5t﹣（60+2t）]°＝（3t﹣60）°，∴∠MOC﹣∠AOD＝（2t+60）°；（3）设OC绕点O逆时针旋转n°，则OD也绕点O逆时针旋转n°，①0＜n°≤150°时，如图4，射线OE、OF在射线OB同侧，在直线MN同侧，∵∠BOF＝[90°﹣（n﹣60°）]＝（150﹣n）°，∠BOE＝（90﹣n）°＝（180﹣n）°，∴∠EOF＝∠BOE﹣∠BOF＝15°；②150°＜n°≤180°时，如图5，射线OE、OF在射线OB异侧，在直线MN同侧，∵°，∠BOE＝（90﹣n）°＝（180﹣n）°，∴∠EOF＝∠BOE+∠BOF＝15°；③180°＜n°≤330°时，如图6，射线OE、OF在射线OB异侧，在直线MN异侧，∵°，°，∴∠EOF＝∠DOF+∠COD+∠COE＝165°；④330°＜n°≤360°时，如图7，射线OE、OF在射线OB同侧，在直线MN异侧，∵∠DOF＝[360﹣（n﹣150）]°＝（510﹣n）°，°，∴∠EOF＝∠DOF﹣∠COD﹣∠COE＝15°；综上，∠EOF＝15°或165°．10．解：如图所示：（1）设∠AOD＝5x°，∵∠BOC＝∠AOD∴∠BOC＝•5x°＝3x°又∵∠AOC＝∠AOB+∠BOC，∠BOD＝∠DOC+∠BOC，∠AOD＝∠AOB+∠BOC+∠DOC，∴∠AOC+∠BOD＝∠AOD+∠BOC，又∵∠AOC＝∠BOD＝120°，∴5x+3x＝240解得：x＝30°∴∠AOD＝150°；（2）∵∠AOD＝150°，∠BOC＝∠AOD，∴∠BOC＝90°，①若线段OB、OC重合前相差20°，则有：20t+15t+20＝90，解得：t＝2，②若线段OB、OC重合后相差20°，则有：20t+15t﹣90＝20解得：，又∵0＜t＜6，∴t＝2或t＝；（3）∠MON的度数不会发生改变，∠MON＝30°，理由如下：∵旋转t秒后，∠AOD＝150°﹣5t°，∠AOC＝120°﹣5t°，∠BOD＝120°﹣5t°∵OM、ON分别平分∠AOC、∠BOD∴∠AOM＝∠AOC＝，∠DON＝＝∴∠MON＝∠AOD﹣∠AOM﹣∠DON＝150°﹣5t°﹣﹣＝30°．。

2020年秋人教数学七年级上册期末满分突破专练：角的计算综合（二）1．如图所示，∠AOB是平角，OM、ON分别是∠AOC、∠BOD的平分线．（1）当∠BOC＝140°时，求∠AOM的度数；（2）当∠AOC＝30°，∠BOD＝60°时，求∠MON的度数；（3）当∠COD＝x度时，则∠MON＝度．（请直接写出答案）2．如图所示，OC是∠AOD的平分线，OE是∠BOD的平分线，∠EOC＝65°，∠DOC＝25°，求∠AOB的度数．3．如图，已知射线OC在∠AOB内，OM和ON分别平分∠AOC和∠BOC．（1）若∠AOC＝50°，∠BOC＝30°，求∠MON的度数．（2）探究∠MON与∠AOB的数量关系．4．如图，已知A、O、B三点在一条直线上，OC平分∠AOD，∠AOC+∠EOB＝90°．（1）求∠COE的度数；（2）判断∠DOE和∠EOB之间有怎样的关系，并说明理由．5．填空，完成下列说理过程．如图，点A、O、B在同一条直线上，OD，OE分别平分∠AOC和∠BOC．（1）求∠DOE的度数；（2）如果∠COD＝65°，求∠AOE的度数．解：（1）如图，因为OD是∠AOC的平分线，所以∠COD＝∠AOC因为OE是∠BOC的平分线，所以∠COE＝所以∠DOE＝∠COD+ ＝（∠AOC+∠BOC）＝∠AOB＝°（2）由（1）可知∠DOE＝90°因为∠COD＝65°所以＝∠COD＝65°则：∠AOE＝∠AOD+ ＝°6．如图，O为直线AB上一点，∠BOE＝80°，直线CD经过点O．（1）如图1，若OC平分∠AOE，求∠AOD的度数；（2）如图2，若∠BOC＝2∠AOC，OE平分∠COF，求∠COF的度数．7．已知，∠AOB＝80°，作射线OC，再分别作∠AOC和∠BOC的平分线OD、OE．（1）如图①，当∠BOC＝60°时，求∠DOE的度数；（2）如图②，当射线OC在∠AOB内绕O点旋转时，∠DOE的大小是否发生变化，说明理由；（3）当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时，画出图形，请直接写出相应的∠DOE的度数（不必写出过程）．8．如图，已知∠AOB＝2∠BOC，∠BOC＝24°，∠COD＝40°，OE是∠AOD的平分线，求∠EOB 的度数．9．已知OM是∠AOB的平分线，ON是∠BOC的平分线．（1）若射线OC在∠AOB的外部（图1），∠AOB＝50，∠BOC＝30°，求∠MON的度数；（2）若射线OC在∠AOB的外部（图1），∠AOC＝80°，求∠MON的度数；（3）若射线OC在∠AOB的内部（图2），∠AOC＝80°，求∠MON的度数．10．如图，已知∠AOC＝90°，∠AOE＝138°，OD平分∠COE，∠BOD＝2∠AOB，求∠BOC的度数．参考答案1．解：（1）∵∠AOB是平角，∴∠AOC+∠COB＝180°，∵∠BOC＝140°，∴∠AOC＝180°﹣140°＝40°，∵OM是∠AOC的平分线．∴∠AOM＝40°÷2＝20°，（2）∵∠AOB是平角，∴∠AOB＝180°，∵OM、ON分别是∠AOC、∠BOD的平分线，∴∠AOM＝∠COM＝∠AOC÷2，∠BON＝∠DON＝∠BOD，∵∠AOC＝30°，∠BOD＝60°，∴∠AOM＝30°÷2＝15°，∠BON＝60°÷2＝30°，∴∠MON＝180°﹣15°﹣30°＝135°，（3）当∠COD＝x度时，则∠MON＝90°+x．由（1）的方法得，∠MON＝∠MOC+∠COD+∠DON＝∠AOC+∠BOD+∠COD＝（180°﹣∠COD）+∠COD＝90°+x．故答案为：（90+x），2．解：如图所示：∵∠EOC＝∠DOE+∠DOC，∠EOC＝65°，∠DOC＝25°，∴∠DOE＝65°﹣25°＝40°，∵OC是∠AOD的平分线，∠BOD＝2∠EOD＝2×40°＝80°，同理可得：∠AOD＝50°又∵∠AOB＝∠AOD+∠BOD∴∠AOB＝130°．3．解：（1）∵OM，ON分别平分∠AOC、∠BOC，∴．∵∠AOC＝50°，∠BOC＝30°，∴∠COM＝25°，∠CON＝15°，∴∠MON＝∠COM+∠CON＝25°+15°＝40°．（2）∵OM和ON分别平分∠AOC和∠BOC，∴，∴＝即：．4．解：（1）∵A、O、B三点在一条直线上，∠AOC+∠EOB＝90°，∴∠COE＝180°﹣（∠AOC+∠EOB）＝180°﹣90°＝90°；（2）∠DOE＝∠EOB，理由如下：∵OC平分∠AOD，∴∠AOC＝∠COD，由（1）得∠COE＝90°，即∠COD+∠DOE＝90°，∴∠AOC+∠DOE＝90°，∵∠AOC+∠EOB＝90°，∴∠DOE＝∠EOB．5．解：（1）如图，因为OD是∠AOC的平分线，所以∠COD＝∠AOC，因为OE是∠BOC的平分线，所以∠COE＝∠BOC，所以∠DOE＝∠COD+∠COE＝（∠AOC+∠BOC）＝∠AOB＝90°，（2）由（1）可知∠DOE＝90°，因为∠COD＝65°，所以∠AOD＝∠COD＝65°，则：∠AOE＝∠AOD+∠DOE＝155°．故答案为：∠BOC，∠COE，90，∠AOD，∠DOE，155．6．解：（1）∵O为直线AB上一点，∠BOE＝80°，∴∠AOE＝100°，∵OC平分∠AOE，∴∠AOC＝∠AOE＝50°，∴∠AOD＝180°﹣∠AOC＝130°；（2）∵∠BOC＝2∠AOC，O为直线AB上一点，∴∠AOC＝60°，∠BOC＝120°，∴∠BOE＝80°，∴∠COE＝180°﹣∠AOC﹣∠BOE＝180°﹣60°﹣80°＝40°，∵OE平分∠COF，∴∠EOF＝∠COE＝40°，∴∠COF＝∠COE+∠EOF＝80°．7．解：（1）∵OD、OE分别是∠AOC和∠BOC的平分线．∴∠AOD＝∠COD＝∠AOC＝（∠AOB﹣∠BOC）＝（80°﹣60°）＝10°，∠BOE＝∠COE＝∠BOC＝×60°＝30°，∴∠DOE＝∠DOC+∠COE＝10°+30°＝40°；（2）∠DOE的大小是不发生变化，理由如下：∵OD、OE分别是∠AOC和∠BOC的平分线．∴∠AOD＝∠COD＝∠AOC＝（∠AOB﹣∠BOC），∠BOE＝∠COE＝∠BOC，∴∠DOE＝∠DOC+∠COE＝（∠AOB﹣∠BOC）﹣∠BOC＝∠AOB＝40°；（3）如图所示，40°或140°；①如图1，∠DOE＝∠COD﹣∠COE＝∠AOC﹣∠BOC＝∠AOB＝×80°＝40°；②如图2，∠DOE＝∠COE﹣∠COD＝∠BOC﹣∠AOC＝∠AOB＝×80°＝40°；③如图3，∠DOE＝∠COD+∠COE＝∠AOC+∠BOC＝（∠AOC+∠BOC）＝（360°﹣∠AOB）＝（360°﹣80°）＝140°，综上所述，∠DOE的度数为40°或140°，答：∠DOE的度数为40°或140°．8．解：∵∠AOB＝2∠BOC，∠BOC＝24°，∴∠AOB＝48°，∵∠COD＝40°，∴∠AOD＝112°，∵OE是∠AOD的平分线，∴∠AOE＝56°，∴∠EOB＝56°﹣48°＝8°．故∠EOB的度数是8°．9．解：（1）∵OM是∠AOB的平分线，ON是∠BOC的平分线，∠AOB＝50°，∠BOC＝30°，∴∠BOM＝∠AOB＝×50°＝25°，∠BON＝∠COB＝×30°＝15°，∴∠MON＝∠BOM+∠BON＝25°﹣15°＝40°；（2）∵OM是∠AOB的平分线，ON是∠BOC的平分线，∴∠BOM＝∠AOB，∠BON＝∠COB，∴∠MON＝∠BOM+∠BON＝∠AOB+∠COB＝（∠AOB+∠BOC）＝∠AOC，∵∠AOC＝80°，∴∠MON＝∠AOC＝，（3））∵OM是∠AOB的平分线，ON是∠BOC的平分线，∴∠MOB＝∠AOB，∠BON＝∠BOC，∴∠MON＝∠MOB﹣∠BON＝∠AOB﹣∠BOC＝（∠AOB﹣∠BOC）＝∠AOC＝×80°＝40°．10．解：∵∠AOC＝90°，∠AOE＝138°，∴∠COE＝∠AOE﹣∠AOC＝138°﹣90°＝48°，∵OD平分∠COE，∴∠COD＝∠DOE＝∠COE＝24°，设∠BOC＝x°，则∠AOB＝（90﹣x）°，又∵∠BOD＝2∠AOB，∴x+24＝2（90﹣x），解得，x＝52，即∠BOC＝52°。

(完整版)苏教版七年级上册数学期末复习题型训练及试卷含答案最新版(word 版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)苏教版七年级上册数学期末复习题型训练及试卷含答案最新版(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)苏教版七年级上册数学期末复习题型训练及试卷含答案最新版(word版可编辑修改)的全部内容。

＋名学生，其中男生人数占．我国是一个严重缺水的国家，大家应倍加珍惜水资源，节约用水。

据测试，拧不紧的水龙毫升。

小明同学在洗手后B20x30将某种电器打折销售,如果按标价的六折出售52元，问：，最多能打几折？38元 84元（1）一个暖瓶与一个水杯分别是多少元?（2）甲、乙两家商场同时出售同样的暖瓶和水杯，为了迎接新年，两家商场都在搞促销活动，甲商场规定：这两种商品都打九折；乙商场规定:买一个暖瓶赠送一个水杯。

若某单位想要买4个暖瓶和15个水杯，请问选择哪家商场购买更合算，并说明理由。

１4。

我国某部边防军小分队成一列在野外行军,通讯员在队伍中,数了一下他前后的人数，发现前面人数是后面的两倍，他往前超了6位战士,发现前面的人数和后面的人数一样。

(1)这列队伍一共有多少名战士?(2)这列队伍要过一座320米的大桥，为安全起见,相邻两个战士保持相同的一定间距,行军速度为5米/秒，从第一位战士刚上桥到全体通过大桥用了100秒时间，请问相邻两个战士间距离为多少米（不考虑战士身材的大小)？15．2011年扬州某学校组织七年级（1)班学生于清明节上午七时乘客车沿淮江高速公路前往距离扬州140千米的淮安楚州“爱国主义教育基地"周恩来纪念馆参观学习，车速是每小时60千米。

2020年秋人教数学七年级上册期末满分突破专练：角的计算综合（四）1．已知D为直线AB上的一点，∠COE是直角，OF平分∠AOE．（1）如图1，若∠COF＝18°，则∠B0E＝；若∠COF＝m°，则∠BOE＝；∠BOE与∠COF的数量关系为．（2）当射线OE绕点O逆时针旋转到如图2的位量时，（1）中∠BOE与∠COF的数量关系是否仍然成立？如成立，请写出关系式并写出推理过程；如不成立，请说明理由．（3）在图3中，若∠COF＝70°，在∠BOE的内部是否存在一条射线OD，使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半？若存在，请求出∠BOD的度数；若不存在，请说明理由．2．完成下列填空：（1）如图1，∠AOB为直角，∠AOC＝62°，且OM平分∠BOC，ON平分∠AOC，求∠MON 的度数．（2）如图2，∠AOB＝40°，∠AOC＝58°，且OM平分∠BOC，ON平分∠AOC．直接写出∠MON的度数．解：（1）因为∠AOB＝90°，∠AOC＝62°，所以∠BOC＝°；因为∠AOC＝62°，OM平分∠BOC，所以∠＝∠BOC＝°；因为∠AOC＝62°，ON平分∠AOC，所以∠＝∠AOC＝°；所以∠MON＝°；（2）∠MON＝°．3．根据阅读材料，回答问题．材料：如图所示，有公共端点（O）的两条射线组成的图形叫做角（∠AOB）．如果一条射线（OC）把一个角（∠AOB）分成两个相等的角（∠AOC和∠BOC），这条射线（OC）叫做这个角的平分线．这时，∠AOC＝∠BOC＝∠AOB（或2∠AOC＝2∠BOC＝∠AOB）．问题：平面内一定点A在直线MN的上方，点O为直线MN上一动点，作射线OA，OP，OA′．当点O在直线MN上运动时，始终保持∠MOP＝90°，∠AOP＝∠A′OP，将射线OA绕点O顺时针旋转60°得到射线OB．（1）如图1，当点O运动到使点A在射线OP的左侧时，若OB平分∠A′OP，求∠AOP的度数；（2）当点O运动到使点A在射线OP的左侧，∠AOM＝3∠A′OB时，求∠AOP的值；（3）当点O运动到某一时刻时，∠A′OB＝150°，直接写出此时∠BOP的度数．4．如图，∠AOB＝92°，∠AOC＝28°，且OM平分∠BOC，ON平分∠AOC．（1）求∠MON的度数；（2）若∠AOB＝α，其他条件不变，求∠MON的度数．5．已知，在∠AOB内部作射线OC，OD平分∠BOC，∠AOD+∠COD＝120°．（1）如图1，求∠AOB的度数；（2）如图2，在∠AOB的外部和∠BOD的内部分别作射线OE、OF，已知∠COD＝2∠BOF+∠BOE，求证：OF平分∠DOE；（3）如图3，在（2）的条件下，在∠COD内部作射线OM，当∠BOM＝4∠COM，∠BOE＝∠AOC时，求∠MOF的度数．6．如图1，点O为直线AB上一点，过点O作射线OC，将一直角的直角顶点放在点O处，即∠MON，反向延长射线ON，得到射线OD．（1）当∠MON的位置如图（1）所示时，使∠NOB＝20°，若∠BOC＝120°，求∠COD的度数．（2）当∠MON的位置如图（2）所示时，使一边OM在∠BOC的内部，且恰好平分∠BOC，问：射线ON的反向延长线OD是否平分∠AOC？请说明理由；注意：不能用问题（1）中的条件（3）当∠MON的位置如图（3）所示时，射线ON在∠AOC的内部，若∠BOC＝120°．试探究∠AOM与∠NOC之间的数量关系，不需要证明，直接写出结论．7．如图，O是直线CE上一点，以O为顶点作∠AOB＝90°，且OA，OB位于直线CE两侧，OB平分∠COD．（1）①当∠AOC＝50°时，求∠DOE的度数：②当∠AOC＝70°时，则∠DOE的度数为．（2）通过（1）的计算，请你猜想∠AOC和∠DOE的数量关系，并说明理由．8．如图，点A、O、B在同一直线上，OC平分∠AOB，若∠COD＝35°（1）求∠BOD的度数；（2）若OE平分∠BOD，求∠AOE的度数．9．已知：∠AOB＝140°，OC，OM，ON是∠AOB内的射线．（1）如图1所示，若OM平分∠BOC，ON平分∠AOC，求∠MON的度数：（2）如图2所示，OD也是∠AOB内的射线，∠COD＝15°，ON平分∠AOD，OM平分∠BOC．当∠COD绕点O在∠AOB内旋转时，∠MON的位置也会变化但大小保持不变，请求出∠MON 的大小；（3）在（2）的条件下，以∠AOC＝20°为起始位置（如图3），当∠COD在∠AOB内绕点O以每秒3°的速度逆时针旋转t秒，若∠AON：∠BOM＝19：12，求t的值．10．在同一平面内已知∠AOB＝150°，∠COD＝90°，OE平分∠BOD．（1）当∠COD的位置如图1所示时，且∠EOC＝35°，求∠AOD的度数；（2）当∠COD的位置如图2所示时，作∠AOC的角平分线OF，求∠EOF的度数；（3）当∠COD的位置如图3所示时，若∠AOC与∠BOD互补，请你过点O作射线OM，使得∠COM为∠AOC的余角，并求出∠MOE的度数．（题中的角都是小于平角的角）参考答案1．解：（1）∵∠COE是直角，∠COF＝18°，∴∠EOF＝90°﹣18°＝72°，∵OF平分∠AOE，∴∠AOE＝2∠EOF＝144°，∴∠BOE＝180°﹣144°＝36°．若∠COF＝m°，∴∠EOF＝90°﹣m°，∴∠AOE＝2∠EOF＝180°﹣2m°，∴∠BOE＝180°﹣（180°﹣2m°）＝2m°，则∠BOE＝2∠COF．故答案为36°、2m°、∠BOE＝2∠COF．（2）∠BOE与∠COF的数量关系仍然成立．理由如下：设∠COF＝m°，如图2，∴∠EOF＝90°﹣m°，∴∠AOE＝2∠EOF＝180°﹣2m°，∴∠BOE＝180°﹣（180°﹣2m°）＝2m°，则∠BOE＝2∠COF．（3）存在．理由如下：如图3，∠COF＝70°，∴∠BOE＝2×70°＝140°，∴∠EOF＝∠AOF＝90°﹣70°＝20°，∵2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半，∴2∠BOD+20°＝（140°﹣∠BOD），∴∠BOD＝20°．答：∠BOD的度数为20°．2．解：（1）∵∠AOB＝90°，∠AOC＝62°，∴∠BOC＝∠AOB+AOC＝90°+62°＝152°；∵∠BOC＝152°，OM平分∠BOC，∴∠MOC＝＝×152°＝76°，∵∠AOC＝62°，ON平分∠AOC，∴∠NOC＝＝31°，∴∠MON＝∠MOC﹣∠NOC＝45°；故答案为：①152°②MOC③76 ④NOC⑤31°⑥45，（2）∠MON＝20°，∵∠AOB＝40°，∠AOC＝58°，∴∠BOC＝∠AOB+AOC＝40°+58°＝98°；∵∠BOC＝98°，OM平分∠BOC，∴∠MOC＝＝×98°＝49°，∵∠AOC＝58°，ON平分∠AOC，∴∠NOC＝＝29°，∴∠MON＝∠MOC﹣∠NOC＝49°﹣29°＝20°；故答案为：20．3．解：（1）设∠AOP的度数为x，由题意可知：∠A′OP＝x，∠POB＝60°﹣x因为OB平分∠A′OP，所以2∠POB＝∠A′OP，所以2（60°﹣x）＝x解得，x＝40．答：∠AOP的度数为40°．（2）①如图2，当射线OB在∠A′OP内部时，设∠AOP的度数为y，由题意可知：∠A′OP＝y，∠POB＝60°﹣y，∵∠MOP＝90°，∴∠AOM＝90°﹣y，∵∠AOM＝3∠A′OB，∴∠A′OB＝（90°﹣y），∵∠A′OB+∠POB＝∠A′OP，∴（90°﹣y）+（60°﹣y）＝y，解得，y＝；②如图3，当射线OB在∠A′OP外部时，设∠AOP的度数为y，由题意可知：∠A′OP＝y，∠POB＝60°﹣y，∵∠MOP＝90°，∴∠AOM＝90°﹣y，∵∠AOM＝3∠A′OB，∴∠A′OB＝（90°﹣y），∵∠AOP+∠A′OP+∠A′OB＝60°，∴y+y+（90°﹣y）＝60°，解得，y＝18°．答；∠AOP的值为或18°．（3）如图4，当∠A′OB＝150°时，由图可得：∠A′OA＝∠A′OB﹣∠AOB＝150°﹣60°＝90°，又∵∠AOP＝∠A′OP，∴∠AOP＝45°，∴∠BOP＝60°+45°＝105°；如图5，当∠A′OB＝150°时，由图可得：∠A′OA＝360°﹣150°﹣60°＝150°，又∵∠AOP＝∠A′OP，∴∠AOP＝75°，∴∠BOP＝60°+75°＝135°；当射线OP在MN下面时，∠BOP＝75°或45°．综上所述：∠BOP的度数为105°或135°或75°或45°．4．解：（1）∵∠AOB＝92°，∠AOC＝28°，∴∠BOC＝92°+28°＝120°，∵OM平分∠BOC，ON平分∠AOC．∴∠BOM＝∠COM＝∠BOC＝60°，∠CON＝∠AON＝∠AOC＝14°∴∠MON＝∠COM﹣∠CON＝60°﹣14°＝46°；（2）∵OM平分∠BOC，ON平分∠AOC．∴∠BOM＝∠COM＝∠BOC＝（∠AOB+∠AOC），∠CON＝∠AON＝∠AOC，∴∠MON＝∠COM﹣∠CON＝（∠AOB+∠AOC）﹣∠AOC＝∠AOB＝α．5．（1）解：∵OD平分∠BOC，∴∠BOD＝∠COD，∵∠AOD+∠COD＝120°，∴∠AOD+∠BOD＝120°，即∠AOB＝120°；（2）证明：∵OD平分∠BOC，∴∠BOD＝∠COD，∵∠COD＝2∠BOF+∠BOE，∴∠BOD＝2∠BOF+∠BOE，∴∠DOF＝∠BOD﹣∠BOF＝2∠BOF+∠BOE﹣∠BOF＝∠BOF+∠BOE＝∠EOF，∴OF平分∠DOE；（3）解：设∠AOC＝10α，则∠BOE＝11α，∵∠AOB＝120°，∴∠BOC＝∠AOB﹣∠AOC＝120°﹣10α，∵OD平分∠BOC，∴∠COD＝∠BOD＝∠BOC＝60°﹣5α，∵∠BOM＝4∠COM，∴∠COM＝∠BOC＝（120°﹣10α）＝24°﹣2α，∴∠DOM＝∠COD﹣∠COM＝（60°﹣5α）﹣（24°﹣2α）＝36°﹣3α，∴∠DOE＝∠BOD+∠BOE＝（60°﹣5α）+11α＝60°+6α，∵OF平分∠DOE，∴∠DOF＝∠DOE＝（60°+6α）＝30°+3α，∴∠MOF＝∠DOM+∠DOF＝（36°﹣3α）+（30°+3α）＝66°．6．解：（1）∵∠AOB＝180°，∠NOB＝20°，∠BOC＝120°，∴∠COD＝∠AOB﹣∠NOB﹣∠BOC＝180°﹣20°﹣120°＝40°，∴∠COD为40°；（2）OD平分∠AOC，理由如下：∵∠MON＝90°，∴∠DOM＝180°﹣∠MON＝180°﹣90°＝90°，∴∠DOC+∠MOC＝∠MOB+∠BON＝90°，∵OM平分∠BOC，∴∠MOC＝∠MOB，∴∠DOC＝∠BON，∵∠BON+∠AON＝∠AON+∠AOD＝180°∴∠BON＝∠AOD，又∵∠BON＝∠COD，∴∠COD＝∠AOD，∴OD平分∠AOC；（3）∵∠BOC＝120°，∴∠AOC＝180°﹣∠BOC＝60°，∵∠MON＝90°，∴∠MON﹣∠AOC＝30°，∴（∠MON﹣∠AON）﹣（∠AOC﹣∠AON）＝30°，即∠AOM﹣∠NOC＝30°．7．解：（1）①∵∠AOB＝90°，∠AOC＝50°，∴∠BOC＝90°﹣50°＝40°，∵OB平分∠COD，∴∠BOC＝∠BOD＝40°，∴∠DOE＝180°﹣40°﹣40°＝100°；②∵∠AOB＝90°，∠AOC＝70°，∴∠BOC＝90°﹣70°＝20°，∵OB平分∠COD，∴∠BOC＝∠BOD＝20°，∴∠DOE＝180°﹣20°﹣20°＝140°；（2）∠DOE＝2∠AOC，理由如下：∵∠AOB＝90°，∴∠BOC＝90°﹣∠AOC，∵OB平分∠COD，∴∠BOC＝∠BOD＝90°﹣∠AOC，∴∠DOE＝180°﹣2∠BOC＝180°﹣2（90°﹣∠AOC）＝2∠AOC．8．解：如图所示：（1）∵OC平分∠AOB，∠AOB＝180°∴∠AOC＝∠BOC＝90°又∵∠COD＝35°，∠BOC＝∠BOD+∠COD，∴∠BOD＝90°﹣35o＝55o（2）∵OE平分∠BOD，∴∠DOE＝∠EOB，又∵∠BOD＝55°，∴∠DOE＝＝＝27.5°又∵∠AOE＝∠AOC+∠COD+∠DOE，∴∠AOE＝90°+35°+27.5°＝152.5°9．解：（1）∵ON平分∠AOC，OM平分∠BOC，∴∠CON＝∠AOC，∠COM＝∠BOC∠MON＝∠CON+∠COM＝（∠AOC+∠BOC）＝∠AOB又∠AOB＝140°∴∠MON＝70°答：∠MON的度数为70°．（2）∵OM平分∠BOC，ON平分∠AOD，∴∠COM＝∠BOC，∠DON＝∠AOD即∠MON＝∠COM+∠DON﹣∠COD＝∠BOC+∠AOD﹣∠COD＝（∠BOC+∠AOD）﹣∠COD．＝（∠BOC+∠AOC+∠COD）﹣∠COD＝（∠AOB+∠COD）﹣∠COD＝（140°+15°）﹣15°＝62.5°答：∠MON的度数为62.5°．（3）∠AON＝（20°+3t+15°），∠BOM＝（140°﹣20°﹣3t）又∠AON：∠BOM＝19：12，12（35°+3t）＝19（120°﹣3t）得t＝20答：t的值为20．10．解：（1）∵∠COD＝90°，∠EOC＝35°，∴∠EOD＝55°，∵OE平分∠BOD，∴∠BOD＝2∠EOD＝110°，∴∠AOD＝∠AOB﹣∠BOD＝40°；（2）∵∠AOB＝150°，∠COD＝90°，∴∠AOC+∠BOD＝360°﹣150°﹣90°＝120°，∵OF平分∠AOC，OE平分∠BOD，∴∠COF＝AOC，∠DOE＝BOD，∴∠COF+∠DOE＝60°，∴∠EOF＝60°+90°＝150°；（3）设∠AOC＝α，∵∠AOB＝150°，∠COD＝90°，∴∠AOD＝90°﹣α，∠BOC＝150°﹣α，∵∠AOC与∠BOD互补，∴∠AOC+∠BOD＝180°，∴∠AOD+∠BOC＝180°，∴90°﹣α+150°﹣α＝180°，∴α＝30°，即∠AOC＝30°，∴∠BOD＝150°，∵OE平分∠BOD，∴∠DOE＝∠BOE＝75°，如图3，∵∠COM为∠AOC的余角，∴∠COM＝60°，∴∠DOM＝30°，∴∠MOE＝∠MOD+∠DOE＝30°+75°＝105°，如备用图，∵∠COM为∠AOC的余角，∴∠COM＝60°，∠BOM＝60°，∴∠MOE＝∠BOM+∠BOE＝60°+75°＝135°；综上所述，∠MOE的度数为105°或135°．。

苏科版数学七年级上册期末满分突破专练：数轴类动点综合题（三）1．如图，点A、B都在数轴上，O为原点．（1）点B表示的数是；（2）若点B以每秒2个单位长度的速度沿数轴向右运动，则2秒后点B表示的数是；（3）若点A、B分别以每秒1个单位长度、3个单位长度的速度沿数轴向右运动，而点O不动，t秒后，A、B、O三个点中有一个点是另外两个点为端点的线段的中点，求t 的值．2．如图，在一条不完整的数轴上从左到右有点A，B，C，D，其中点A与点B之间距离为3，点B与点C之间距离为2，点C与点D之间距离为1．设点A，B，C，D所对应数的和为w．（1）若点C为数轴的原点．请你写出点A、B、D所对应的数，并计算w的值；（2）若点C与数轴原点的距离为2020时，求w的值；（3）若点C与数轴原点的距离为a（a＞0）时，求w的值．3．如图，数轴的单位长度为1．（1）如果点A，D表示的数互为相反数，那么点B表示的数是多少？（2）如果点B，D表示的数互为相反数，那么图中表示的四个点中，哪一点表示的数的绝对值最大？为什么？（3）当点B为原点时，若存在一点M到A的距离是点M到D的距离的2倍，则点M 所表示的数是．4．如图所示，一个点从数轴上的原点开始，先向右移动2个单位长度，再向左移动5个单位长度，可以看到终点表示是﹣3，已知A、B是数轴上的点，请参照如图并思考，完成下列各题．（1）如果点A表示的数﹣1，将点A向右移动4个单位长度，那么终点B表示的数是．A、B两点间的距离是．（2）如果点A表示的数2，将点A向左移动6个单位长度，再向右移动3个单位长度，那么终点B表示的数是．A、B两点间的距离是．（3）如果点A表示的数m，将点A向右移动n个单位长度，再向左移动p个单位长度，那么请你猜想终点B表示的数是．A、B两点间的距离是．5．“幸福是奋斗出来的”，在数轴上，若C到A的距离刚好是3，则C点叫做A的“幸福点”，若C到A、B的距离之和为6，则C叫做A、B的“幸福中心”（1）如图1，点A表示的数为﹣1，则A的幸福点C所表示的数应该是；（2）如图2，M、N为数轴上两点，点M所表示的数为4，点N所表示的数为﹣2，点C就是M、N的幸福中心，则C所表示的数可以是（填一个即可）；（3）如图3，A、B、P为数轴上三点，点A所表示的数为﹣1，点B所表示的数为4，点P所表示的数为8，现有一只电子蚂蚁从点P出发，以2个单位每秒的速度向左运动，当经过多少秒时，电子蚂蚁是A和B的幸福中心？6．一辆货车从货场A出发，向西走了1.5千米到达批发部B，接着向东走了2千米到达商场C，又向东走了4.5千米到达超市D，最后回到货场．（1）用一个单位长度表示1千米，向东为正方向，以货场为原点，画出数轴并在数轴上标明A，B，C，D的位置．（2）超市D距货场A多远？（3）货车一共行驶了多少千米？7．如图所示，在数轴上有三个点，A，B，C，它们所表示的数分别为﹣3、﹣2、2，试回答下列问题．（1）A，C两点间的距离是；（2）若E点与B点的距离是8，则E点表示的数是；（3）若将数轴折叠，使A点与C点重合，则点B与数表示的点重合．8．阅读理解，完成下列各题定义：已知A、B、C为数轴上任意三点，若点C到A的距离是它到点B的距离的2倍，则称点C是[A，B]的2倍点．例如：如图1，点C是[A，B]的2倍点，点D不是[A，B]的2倍点，但点D是[B，A]的2倍点，根据这个定义解决下面问题：（1）在图1中，点A是的2倍点，点B是的2倍点；（选用A、B、C、D表示，不能添加其他字母）；（2）如图2，M、N为数轴上两点，点M表示的数是﹣2，点N表示的数是4，若点E 是[M，N]的2倍点，则点E表示的数是；（3）若P、Q为数轴上两点，点P在点Q的左侧，且PQ＝m，一动点H从点Q出发，以每秒2个单位长度的速度沿数轴向左运动，设运动时间为t秒，求当t为何值时，点H恰好是P和Q两点的2倍点？（用含m的代数式表示）9．如图所示，一个点从数轴上的原点开始，先向右移动3个单位长度，再向左移动5个单位长度，可以发现终点表示的数是﹣2，已知点A，B是数轴上的点，请参照图并思考，完成下列各题．（1）如果点A表示数﹣3，将点A向右移动7个单位长度，那么终点B表示的数是，A、B两点间的距离是；（2）如果点A表示数3，将点A向左移动7个单位长度，再向右移动5个单位长度，那么终点B表示的数是，A、B两点间的距离为；（3）如果点A表示数﹣4，将点A向右移动168个单位长度，再向左移动256个单位长度，那么终点B表示的数是，A、B两点间的距离为．（4）一般地，如果A点表示的数为m，将A点向右移动n个单位长度，再向左移动p 个单位长度，那么，请你猜想终点B表示的数是，A、B两点间的距离是．10．如图，已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）数轴上点B表示的数是，点P表示的数是（用含t的代数式表示）；（2）动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发．求：①当点P运动多少秒时，点P与点Q相遇？②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？参考答案1．解：（1）点B表示的数是﹣4；（2）2秒后点B表示的数是﹣4+2×2＝0；（3）①当点O是线段AB的中点时，OB＝OA，4﹣3t＝2+t，解得t＝0.5；②当点B是线段OA的中点时，OA＝2OB，2+t＝2（3t﹣4），解得t＝2；③当点A是线段OB的中点时，OB＝2 OA，3t﹣4＝2（2+t），解得t＝8．综上所述，符合条件的t的值是0.5，2或8．故答案为：﹣4；0．2．解：（1）若点C为数轴的原点，即C点表示的数为0，∵点C与点D之间距离为1，∴D点对应的数为1，∵点B与点C之间距离为2，∴B点对应的数为﹣2，∵点A与点B之间距离为3，∴A点表示的数为﹣5，∴w＝﹣5+（﹣2）+1＝﹣6；（2）点C与数轴原点的距离为2020时，即C点对应的数为2020或﹣2020，当C点对应的数为2020，∴D点表示的数为2020+1＝2021，B点对应的数为2020﹣2＝2018，A点表示的数为2018﹣3＝2015，∴w＝2021+2018+2020+2015＝8074；当C点对应的数为﹣2020，∴D点表示的数为﹣2020+1＝﹣2019，B点对应的数为﹣2020﹣2＝﹣2022，A点表示的数为﹣2022﹣3＝﹣2025，∴w＝﹣2025﹣2022﹣2020﹣2025＝﹣8086；即w的值为8074或﹣8086；（3）若点C与数轴原点的距离为a（a＞0），即C点对应的数为a或﹣a，当C点对应的数为a，∴D点表示的数为a+1，B点对应的数为a﹣2，A点表示的数为a﹣2﹣3＝a﹣5，∴w＝a﹣5+a﹣2+a+a+1＝4a﹣6；当C点对应的数为﹣a，∴D点表示的数为﹣a+1，B点对应的数为﹣a﹣2，A点表示的数为﹣a﹣2﹣3＝﹣a﹣5，∴w＝﹣a﹣5﹣a﹣2﹣a﹣a+1＝﹣4a﹣6；即w的值为﹣4a﹣6或4a﹣6．3．解：（1）点B表示的数是﹣1；（2）当B，D表示的数互为相反数时，A表示﹣4，B表示﹣2，C表示1，D表示2，所以点A表示的数的绝对值最大．点A的绝对值是4最大．（3）2或10．设M的坐标为x．当M在A的左侧时，﹣2﹣x＝2（4﹣x），解得x＝10（舍去）当M在AD之间时，x+2＝2（4﹣x），解得x＝2当M在点D右侧时，x+2＝2（x﹣4），解得x＝10故答案为：①点M在AD之间时，点M的数是2②点M在D点右边时点M表示数为10．4．解：（1）终点B表示：﹣1+4＝3，A、B间的距离是4；（2）终点B表示：2﹣6+3＝﹣1，A、B间的距离是2﹣（﹣1）＝2+1＝3；（3）终点B表示：m+n﹣p，A、B两点间的距离是|m+n﹣p﹣m|＝|n﹣p|．故答案为：（1）3，4；（2）﹣1，3；（3）m+n﹣p，|n﹣p|．5．解：（1）A的幸福点C所表示的数应该是﹣1﹣3＝﹣4或﹣1+3＝2；（2）∵4﹣（﹣2）＝6，∴M，N之间的所有数都是M，N的幸福中心．故C所表示的数可以是﹣2或﹣1或0或1或2或3或4（答案不唯一）；（3）设经过x秒时，电子蚂蚁是A和B的幸福中心，依题意有①8﹣2x﹣4+（8﹣2x+1）＝6，解得x＝1.75；②4﹣（8﹣2x）+[﹣1﹣（8﹣2x）]＝6，解得x＝4.75．故当经过1.75秒或4.75秒时，电子蚂蚁是A和B的幸福中心．6．解：（1）如图所示：；（2）∵D点表示5千米，∴超市D距货场A为5千米；（3）货车一共行驶了：1.5+2+4.5+5＝13（千米）．答：货车一共行驶了13千米．7．解：（1）A，C两点间的距离是2+3＝5；（2）设E表示的数是x，则|x+2|＝8，则x＝6，﹣10．（3）A与C重合，则对称点表示的数是：﹣0.5，则点B与表示1的点重合．故答案是：5；6或﹣10；1．8．解：（1）∵CA＝2，DA＝1，CA＝2DA∴点A是[C，D]的2倍点∵BD＝2，BC＝1，BD＝2BC∴点B是[D，C]的2倍点．故答案为：[C，D][D，C]（2）∵NM＝4﹣（﹣2）＝6当点E在线段MN上又∵点E是[M，N]的2倍点∴EM＝MN＝4∴点E表示的数是2当点E在点N右侧∴EM＝2NE∴MN＝NE＝6∴ME＝12∴点E表示的数是10．故答案为：2或10；（3 ）∵PQ＝m，PH＝m﹣2t，∴HQ＝2t又∵点H恰好是P和Q两点的2倍点∴点H是[P，Q]的2倍点或点H是[Q，P]的2倍点∴PH＝2HQ或HQ＝2PH即：2×2t＝m﹣2t或2t＝2（m﹣2t）或2t＝2（2t﹣m），解得t＝m或t＝m或t＝m所以，当t＝m或t＝m或t＝m时，点H恰好是P和Q两点的2倍点．9．解：（1）如果点A表示数﹣3，将点A向右移动7个单位长度，那么终点B表示的数是4，A，B两点间的距离是7．（2）如果点A表示数3，将A点向左移动7个单位长度，再向右移动5个单位长度，那么终点B表示的数是1，A，B两点间的距离为2．（3）如果点A表示数﹣4，将A点向右移动168个单位长度，再向左移动256个单位长度，那么终点B表示的数是﹣92，A，B两点间的距离是88．（4）一般地，如果A点表示的数为m，将A点向右移动n个单位长度，再向左移动p 个单位长度，那么，终点B表示的数是m+n﹣p，A，B两点间的距离为|n﹣p|．故答案为：（1）4，7；（2）1，2；（3）﹣92，88；（4）m+n﹣p，|n﹣p|．10．解：（1）∵数轴上点A表示的数为6，∴OA＝6，则OB＝AB﹣OA＝4，点B在原点左边，∴数轴上点B所表示的数为﹣4；点P运动t秒的长度为6t，∵动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，∴P所表示的数为：6﹣6t；（2）①点P运动t秒时追上点R，根据题意得6t＝10+4t，解得t＝5，答：当点P运动5秒时，点P与点Q相遇；②设当点P运动a秒时，点P与点Q间的距离为8个单位长度，当P不超过Q，则10+4a﹣6a＝8，解得a＝1；当P超过Q，则10+4a+8＝6a，解得a＝9；答：当点P运动1或9秒时，点P与点Q间的距离为8个单位长度．。

-苏科版七年级数学上册（角的计算 ）专题复习一、选择题1、当时钟指向上午10：10分，时针与分针的夹角是多少度（ ）A ．115°B ．120°C ．105°D ．90° 2、已知6032'α∠=︒，则的余角是A ．2928'︒B ．2968'︒C ．11928'︒D ．11968'︒ 3、已知∠1和∠2互为余角，且∠2与∠3互补，∠1＝60°，则∠3为（ ）A ．120°B ．60°C ．30°D ．150°4、已知∠α和∠β互补，且∠α＞∠β，则有下列式子：①90°﹣∠β；②∠α﹣90°；③21（∠α+∠β）④21（∠α﹣∠β）；⑤21（∠α﹣90°），其中，表示∠β的余角的式子有（ ） A ．4个B ．3个C ．2个D ．1个 5、如图，直线AB ，CD 相交于点O ，∠COE 是直角，OF 平分∠AOD ，若∠BOE ＝40°，则∠AOF 的度数是( ) A ．65° B ．60° C ．50° D ．40°(5题) (6题) (7题) (8题)6、如图，直线AB ，CD 交于点O ，射线OM 平分∠AOC ，若∠AOC ＝76°，则∠BOM 等于（）A ．38°B ．104°C ．142°D ．144°7、如图，点O 在直线DB 上，已知∠1＝20°，∠AOC ＝90°，则∠2的度数为（ ）A ．150°B ．120°C ．110°D ．100°8、O 为直线AB 上一点，OC OD ⊥，若140∠=︒，则2∠=（）A ．30°B ．40°C ．50°D ．60°9、如图，将一张长方形纸片的角A 、E 分别沿着BC 、BD 折叠，点A 落在A '处，点E 落在边BA '上的E '处，则∠CBD的度数是（ ）A ．85°B ．90°C ．95°D ．100°(9题) (10题) (12题)10、某教科局提出开展“三有课堂”，某中学在一节体现“三有课堂”公开展示课上，李老师展示一幅图，条件是：C为直线AB 上一点，∠DCE 为直角，CF 平分∠ACD ，CH 平分∠BCD ，CG 平分∠BCE ，各个小组经过讨论后得到以下结论：①∠ACF 与∠BCH 互余 ②∠FCG 与∠HCG 互补 ③∠ECF 与∠GCH 互补 ④∠ACD ﹣∠BCE ＝90°，聪明的你认为哪些组的结论是正确的，正确的有（ ）个．A ．1B ．2C ．3D ．4二、填空题11、35.15°＝ ° ′ ″；12°15′36″＝ °．12、如图，已知∠AOB ＝40°，∠AOC ＝90°，OD 平分∠BOC ，则∠AOD 的度数是 ．13、已知OC 平分∠AOB ，若∠AOB ＝70°，∠COD ＝10°，则∠AOD 的度数为 ．14、已知，在同一平面内，∠AOB ＝30°，射线OC 在∠AOB 的外部，OD 平分∠AOC ，若∠BOD ＝40°，则∠AOC 度数为 ．15、如图，把一张长方形纸片沿AB 折叠后，若∠1＝50°，则∠2的度数为______．(15题) (16题) (17题)16、如图,将长方形纸片ABCD 的∠C 沿着GF 折叠(点F 在BC 上,不与B,C 重合),使点C 落在长方形内部的点E 处,若FH 平分∠BFE,则∠GFH 的度数是____.17、将一副三角板如图放置，若20AOD ∠=，则BOC ∠的大小为______．18、如图所示，直线AB ，CD ，EF 交于点O ，OG 平分∠BOF ，且CD ∠EF ，若∠AOE = 70°，则∠DOG = ________ .(18题) (19题)19、如图，直线与相交于点,60O AOC ∠=，一直角三角尺的直角顶点与点重合，平分AOC ∠，现将三角尺EOF 以每秒3的速度绕点O 顺时针旋转，同时直线CD 也以每秒9的速度绕点O 顺时针旋转，设运动时间为t 秒（040t ≤≤），当CD 平分EOF ∠时，t 的值为（ ）A ．2.5B ．30C ．2.5或30D ．2.5或32.5三、解答题20、如图，点O 在直线AB 上，OE 、OD 分别是∠AOC 、∠BOC 的平分线．（1）∠AOE 的补角是∠ ；（2）若∠BOC ＝62°，求∠COD 的度数；（3）射线OD 与OE 之间有什么特殊的位置关系？为什么？21、如图，直线AB 、CD 相交于点O ，已知∠AOC ＝75°，∠BOE ：∠DOE ＝2：3．（1）求∠BOE 的度数；（2）若OF 平分∠AOE ，∠AOC 与∠AOF 相等吗？为什么？22、如图，已知直线AB ，CD 相交于点O ，∠BOE ＝90°．（1）若∠BOD ＝40°，求∠COE 的度数；（2）若∠AOC ：∠BOC ＝3：7，求∠DOE 的度数．23、如图，直线AB，CD交于点O，OE平分∠COB，OF是∠EOD的角平分线．（1）说明：∠AOD＝2∠COE；（2）若∠AOC＝50°，求∠EOF的度数；（3）若∠BOF＝15°，求∠AOC的度数．24、如图，OC是∠AOD的平分线，OE是∠BOD的平分线．（1）若∠AOB＝120°，则∠COE是多少度？（2）如果∠BOC＝3∠AOD，∠EOD﹣∠COD＝30°，那么∠BOE是多少度？25、如图，在同一平面内，∠AOB＝150°，∠COD＝90°，OE平分∠BOD．（1）当∠COD的位置如图1所示时，若∠COE＝25°，则∠AOD＝；（2）当∠COD的位置如图2所示时，若∠AOE＝90°，则∠AOD＝；（3）当∠COD的位置如图3所示时，若∠BOE＝∠AOC，求∠AOD的度数．26、如图1，已知∠AOB ＝150°，∠COE 与∠EOD 互余，OE 平分∠AOD ．（1）在图1中，若∠COE ＝32°，则∠DOE ＝ ；∠BOD ＝ ；（2）在图1中，设∠COE ＝α，∠BOD ＝β，请探索α与β之间的数量关系；（3）在已知条件不变的前提下，当∠COD 绕点O 逆时针转动到如图2的位置时，（2）中α与β的数量关系是否仍然成立？若成立，请说明理由；若不成立，直接写出α与β的数量关系．27、【阅读理解】射线OC 是∠AOB 内部的一条射线，若∠COA =21∠BOC ，则我们称射线OC 是射线OA 的伴随线．例如，如图1，∠AOB ＝60°，∠AOC ＝∠COD ＝∠BOD ＝20°，则∠AOC =21∠BOC ，称射线OC 是射线OA 的伴随线；同时，由于∠BOD=21∠AOD ，称射线OD 是射线OB 的伴随线． 【知识运用】（1）如图2，∠AOB ＝120°，射线OM 是射线OA 的伴随线，则∠AOM ＝ °，若∠AOB 的度数是α，射线ON 是射线OB 的伴随线，射线OC 是∠AOB 的平分线，则∠NOC的度数是 ．（用含α的代数式表示）（2）如图3，如∠AOB ＝180°，射线OC 与射线OA 重合，并绕点O 以每秒3°的速度逆时针旋转，射线OD 与射线OB 重合，并绕点O 以每秒5°的速度顺时针旋转，当射线OD 与射线OA 重合时，运动停止．∠是否存在某个时刻t （秒），使得∠COD 的度数是20°，若存在，求出t 的值，若不存在，请说明理由．∠当t 为多少秒时，射线OC 、OD 、OA 中恰好有一条射线是其余两条射线的伴随线．（答案）一、选择题1、当时钟指向上午10：10分，时针与分针的夹角是多少度（ ）A ．115°B ．120°C ．105°D ．90°【解答】解：时钟指向上午10：10分，时针与分针相距3+6050=623份， 时钟指向上午10：10分，时针与分针的夹角是多少度30°×623=115°， 或时针与分针的夹角是120°﹣10×（21）°＝115°； 故选：A ．2、已知6032'α∠=︒，则的余角是A ．2928'︒B ．2968'︒C ．11928'︒D ．11968'︒【解析】的余角为，故选A ．3、已知∠1和∠2互为余角，且∠2与∠3互补，∠1＝60°，则∠3为（ ）A ．120°B ．60°C ．30°D ．150°【解答】解：∠∠1和∠2互为余角，∠1＝60°，∠∠2＝90°﹣∠1＝90°﹣60°＝30°， ∠∠2与∠3互补，∠∠3＝180°﹣∠2＝180°﹣30°＝150°．故选：D ．4、已知∠α和∠β互补，且∠α＞∠β，则有下列式子：∠90°﹣∠β；∠∠α﹣90°；∠21（∠α+∠β）∠21（∠α﹣∠β）；∠21（∠α﹣90°），其中，表示∠β的余角的式子有（ ） A ．4个 B ．3个 C ．2个 D ．1个【解答】解：∠∠α与∠β互补，∠∠β＝180°﹣∠α，∠α＝180°﹣∠β，∠90°﹣∠β表示∠β的余角，∠∠正确；∠α﹣90°＝180°﹣∠β﹣90°＝90°﹣∠β，∠∠正确；180°﹣∠α＝∠β，∠∠错误；21（∠α﹣∠β）=21（180°﹣∠β﹣∠β）＝90°﹣∠β，∠∠正确，∠错误． 故表示∠β的余角的式子有3个．故选：B ．α∠α∠9060322928︒-︒'=︒'A ．65°B ．60°C ．50°D ．40°【解析】由余角的性质，得∠BOD=90°-∠BOE=90°-40°=50°，由邻补角的性质，得∠AOD=180°-∠BOD=180°-50°=130°，由角平分线的性质，得∠AOF=12∠AOD=12×130°=65°，故答案为65°．6、如图，直线AB ，CD 交于点O ，射线OM 平分∠AOC ，若∠AOC ＝76°，则∠BOM 等于（）A ．38°B ．104°C ．142°D ．144°【解析】∠∠AOC ＝76°，射线OM 平分∠AOC ，∠∠AOM=12∠AOC=12×76°=38°，∠∠BOM=180°−∠AOM=180°−38°=142°，故选C.7、如图，点O 在直线DB 上，已知∠1＝20°，∠AOC ＝90°，则∠2的度数为（ ）A ．150°B ．120°C ．110°D ．100°【解答】解：∠∠AOC ＝90°，∠1＝20°，∠∠BOC ＝90°﹣20°＝70°，又∠点O 在直线DB 上，∠∠2＝180°﹣70°＝110°．故选：C ．8、O 为直线AB 上一点，OC OD ⊥，若140∠=︒，则2∠=（）A ．30°B ．40°C ．50°D ．60°【解析】解：∠OC∠OD ，∠∠COD=90°，∠∠1=40°，∠∠2=180°-∠COD -∠1=180°-90°-40°=50°．故选：C ．9、如图，将一张长方形纸片的角A 、E 分别沿着BC 、BD 折叠，点A 落在A '处，点E 落在边BA '上的E '处，则∠CBD的度数是（ ）A ．85°B ．90°C ．95°D ．100°【解析】根据折叠的性质可得：∠ABC =∠A′BC ，∠EBD =∠E′BD ，∠∠ABC +∠A′BC +∠E′BD +∠EBD =180°，∠2∠A′BC +2∠E′BD =180°．∠∠A′BC +∠E′BD =90°．∠∠CBD =90°．故选B ．10、某教科局提出开展“三有课堂”，某中学在一节体现“三有课堂”公开展示课上，李老师展示一幅图，条件是：C为直线AB 上一点，∠DCE 为直角，CF 平分∠ACD ，CH 平分∠BCD ，CG 平分∠BCE ，各个小组经过讨论后得到以下结论：∠∠ACF 与∠BCH 互余 ∠∠FCG 与∠HCG 互补 ∠∠ECF 与∠GCH 互补 ∠∠ACD ﹣∠BCE ＝90°，聪明的你认为哪些组的结论是正确的，正确的有（ ）个．A ．1B ．2C ．3D ．4【解析】∠CF 平分∠ACD ，CH 平分∠BCD ，CG 平分∠BCE ，∠∠ACF ＝∠FCD =21∠ACD ，∠DCH ＝∠HCB =21∠DCB ，∠BCG ＝∠ECG =21∠BCE ，∠∠ACB ＝180°，∠DCE ＝90°，∠∠FCH ＝90°，∠HCG ＝45°，∠FCG ＝135°∠∠ACF +∠BCH ＝90°，∠FCG +∠HCG ＝180°，故∠∠正确，∠∠ECF ＝∠DCE +∠FCD ＝90°+∠FCD ，∠FCD +∠DCH ＝90°，∠∠ECF +∠DCH ＝180°，∠∠ACD ﹣∠BCE ＝180°﹣∠DCB ﹣∠BCE ＝90°，故∠正确．故选C ．二、填空题11、35.15°＝ ° ′ ″；12°15′36″＝ °．【解答】解：∠0.15°＝9′，∠35.15°＝35°9′；∠36″＝0.6′，15.6′＝0.26°，∠12°15′36″＝12.26°，故答案为：35，9，0；12.26．12、如图，已知∠AOB ＝40°，∠AOC ＝90°，OD 平分∠BOC ，则∠AOD 的度数是 ．解：∵∠AOB ＝40°，∠AOC ＝90°,∴∠BOC ＝40°+90°＝130°∵OD 平分∠BOC,∴∠BOD ＝65°∴∠AOD ＝∠BOD ﹣∠AOB ＝65°﹣40°＝25°．故答案为25°．13、已知OC 平分∠AOB ，若∠AOB ＝70°，∠COD ＝10°，则∠AOD 的度数为 ．【解析】（1）若射线OD 在OC 的下方时，如图1所示：∠OC 平分∠AOB ，∠∠AOC=21ÐAOB ，又∠∠AOB ＝70°，∠∠AOC=21×70=35°，又∠∠AOC ＝∠COD +∠AOD ，∠COD ＝10°，∠∠AOD ＝35°﹣10°＝25°；（2）若射线OD 在OC 的上方时，如图2所示：同（1）可得：∠AOC ＝35°，又∠∠AOD ＝∠AOC +∠COD ，∠∠AOD ＝35°+10°＝45°；综合所述∠AOD 的度数为25°或45°，故答案为25°或45°．14、已知，在同一平面内，∠AOB＝30°，射线OC在∠AOB的外部，OD平分∠AOC，若∠BOD＝40°，则∠AOC度数为．【解答】解：有两种情况，∠如图1所示，∠AOD＝∠AOB+∠BOD＝30°+40°＝70°，∠OD平分∠AOC，∠∠AOC＝2∠AOD＝2×70°＝140°；∠如图2所示，∠AOD＝∠BOD﹣∠AOB＝40°﹣30°＝10°，∠OD平分∠AOC，∠∠AOC＝2∠AOD＝2×10°＝20°．综上所述，∠AOC度数为140°或20°．故答案为：140°或20°15、如图，把一张长方形纸片沿AB折叠后，若∠1＝50°，则∠2的度数为______．【解析】∠把一张长方形纸片沿AB折叠，∠∠2=∠3，∠∠1+∠2+∠3=180°，∠1=50°，∠∠2=（180°-∠1） 2=65°.16、如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部的点E处,若FH平分∠BFE,则∠GFH的度数是____.【解析】∠将长方形纸片ABCD 的角C 沿着GF 折叠（点F 在BC 上，不与B ，C 重合），使点C 落在长方形内部点E 处，∠∠CFG=∠EFG=12∠CFE ， ∠FH 平分∠BFE ，∠∠HFE=12∠BFE ， ∠∠GFH=∠GFE+∠HFE=12（∠CFE+∠BFE ）=12×180°=90°，故答案为：90°． 17、将一副三角板如图放置，若20AOD ∠=，则BOC ∠的大小为______．解：∠∠AOD=20°，∠COD=∠AOB=90°，∠∠COA=∠BOD=90°﹣20°=70°，∠∠BOC=∠COA+∠AOD+∠BOD=70°+20°+70°=160°，故答案为160°．18、如图所示，直线AB ，CD ，EF 交于点O ，OG 平分∠BOF ，且CD ∠EF ，若∠AOE = 70°，则∠DOG = ____55_____ .19、如图，直线AB 与CD 相交于点,60O AOC ∠=，一直角三角尺EOF 的直角顶点与点O 重合，OE 平分AOC ∠，现将三角尺EOF 以每秒3的速度绕点O 顺时针旋转，同时直线CD 也以每秒9的速度绕点O 顺时针旋转，设运动时间为t 秒（040t ≤≤），当CD 平分EOF ∠时，t 的值为（ ）A ．2.5B ．30C ．2.5或30D ．2.5或32.5【解析】解：分两种情况：∠如图OC 平分EOF ∠时，45AOE ∠=︒，即930345t t +︒-=︒，解得 2.5t =； ∠如图OC 平分EOF ∠时，45COE ∠=︒，即9150345t t -︒-=︒，解得32.5t =．综上所述，当CD 平分EOF ∠时，t 的值为2.5或32.5．故选：D ．三、解答题20、如图，点O 在直线AB 上，OE 、OD 分别是∠AOC 、∠BOC 的平分线． （1）∠AOE 的补角是∠ ； （2）若∠BOC ＝62°，求∠COD 的度数；（3）射线OD 与OE 之间有什么特殊的位置关系？为什么？【解答】解：（1）∠点O 在直线AB 上，∠∠AOE 的补角是∠BOE ；故答案为：BOE ；（2）∠OD 是∠BOC 的平分线，∠ÐCOD=21ÐBOC=21×62 =31． （3）OD ∠OE ．∠OE 、OD 分别是∠AOC 、∠BOC 的平分线， ∠ÐCOE=21ÐAOC,ÐCOD=21ÐBOC ． ∠ÐDOE=ÐCOE+ÐCOD=21ÐAOC+21ÐBOC=21ÐAOB=90, ∠OD ∠OE ．21、如图，直线AB、CD相交于点O，已知∠AOC＝75°，∠BOE：∠DOE＝2：3．（1）求∠BOE的度数；（2）若OF平分∠AOE，∠AOC与∠AOF相等吗？为什么？【解答】解：（1）设∠BOE＝2x，则∠EOD＝3x，∠BOD＝∠AOC＝75°，∠2x+3x＝75°，解得x＝15°，则2x＝30°，3x＝45°，∠∠BOE＝30°；（2）∠∠BOE＝30°，∠∠AOE＝150°，∠OF平分∠AOE，∠∠AOF＝75°，∠∠AOC＝∠AOF．22、如图，已知直线AB，CD相交于点O，∠BOE＝90°．（1）若∠BOD＝40°，求∠COE的度数；（2）若∠AOC：∠BOC＝3：7，求∠DOE的度数．【解答】解：（1）∠∠BOE＝90°，∠BOD＝40°，∠∠AOE＝90°，∠AOC＝∠BOD＝40°，则∠COE＝90°﹣40°＝50°；（2）∠∠AOC：∠BOC＝3：7，∠设∠AOC＝3x，则∠BOC＝7x，∠∠AOC+∠BOC＝180°，∠3x+7x＝180°，解得：x＝18°，∠∠AOC＝54°，∠∠BOD＝∠AOC，∠∠BOD＝54°，∠∠DOE＝∠BOE+∠BOD＝90°+54°＝144°．23、如图，直线AB ，CD 交于点O ，OE 平分∠COB ，OF 是∠EOD 的角平分线． （1）说明：∠AOD ＝2∠COE ；（2）若∠AOC ＝50°，求∠EOF 的度数； （3）若∠BOF ＝15°，求∠AOC 的度数．【解答】解：（1）∠OE 平分∠COB ，∠∠COE =21∠COB ， ∠∠AOD ＝∠COB ，∠∠AOD ＝2∠COE ；（2）∠∠AOC ＝50°，∠∠BOC ＝180°﹣50°＝130°，∠∠EOC =21∠BOC ＝65°， ∠∠DOE ＝180°﹣∠EOC ＝180°﹣65°＝115°， ∠OF 平分∠DOE ，∠∠EOF =21∠DOC ＝57.5°； （3）设∠AOC ＝∠BOD ＝α，则∠DOF ＝α+15°，∠∠EOF ＝∠DOF ＝α+15°，∠∠EOB ＝∠EOF +∠BOF ＝α+30°，∠∠COB ＝2∠EOB ＝2α+60°， 而∠COB +∠BOD ＝180°，即，3α+60°＝180°， 解得，α＝40°，即，∠AOC ＝40°．24、如图，OC 是∠AOD 的平分线，OE 是∠BOD 的平分线．（1）若∠AOB ＝120°，则∠COE 是多少度？（2）如果∠BOC ＝3∠AOD ，∠EOD ﹣∠COD ＝30°，那么∠BOE 是多少度？【解答】解：（1）∠OC 是∠AOD 的平分线，∠∠AOC ＝∠DOC ．∠OE 是∠BOD 的平分线，∠∠BOE ＝∠DOE ，所以ÐCOE=21ÐAOB= 60． （2）设∠BOE 的度数为x ，则∠DOE 的度数也为x ．∠∠EOD ﹣∠COD ＝30°，∠∠COD ＝∠AOC ＝x ﹣30°， ∠∠AOD ＝2∠AOC ＝2（x ﹣30°）．∠∠BOC ＝3∠AOD ，∠可列方程为x +x +x ﹣30°＝3×2（x ﹣30°），解得x ＝50°，即∠BOE 的度数为50°．25、如图，在同一平面内，∠AOB ＝150°，∠COD ＝90°，OE 平分∠BOD ． （1）当∠COD 的位置如图1所示时，若∠COE ＝25°，则∠AOD ＝ ； （2）当∠COD 的位置如图2所示时，若∠AOE ＝90°，则∠AOD ＝ ； （3）当∠COD 的位置如图3所示时，若∠BOE ＝∠AOC ，求∠AOD 的度数．解：（1）∵∠COD ＝90°，∠COE ＝25°，∴∠EOD ＝65°，∵OE 平分∠BOD ，∴∠BOD ＝2∠EOD ＝130°，∴∠AOD ＝∠AOB ﹣∠BOD ＝20°； 故答案为：20°（2）∵∠AOE ＝90°，∴∠AOD +∠DOE ＝90°，∵OE 平分∠BOD ，∴∠DOC ＝∠BOE ，∴∠AOD +∠BOE ＝90°，∴∠AOD ＝∠BOC ， ∵∠AOD +∠COD +∠BOC ＝∠AOB ＝150°，∴2∠AOD ＝150°﹣90°＝60°， ∴∠AOD ＝30°．故答案为：30°（3）因为OE 平分∠BOD, 所以∠BOE ＝∠DOE因为∠BOE ＝∠AOC, 所以∠BOD ＝5∠AOC因为∠COD ＝90°，所以∠AOD +∠AOC ＝90° 设∠AOC ＝x ，则∠AOD ＝90°﹣x ，∠BOD ＝5x ，因为∠AOD +∠BOD +∠AOB ＝360°,所以90°﹣x +5x +150°＝360°，解得：x ＝30°，所以∠AOD ＝90°﹣x ＝90°﹣30°＝60°，即∠AOD 的度数是60°．26、如图1，已知∠AOB ＝150°，∠COE 与∠EOD 互余，OE 平分∠AOD ． （1）在图1中，若∠COE ＝32°，则∠DOE ＝ ；∠BOD ＝ ； （2）在图1中，设∠COE ＝α，∠BOD ＝β，请探索α与β之间的数量关系；（3）在已知条件不变的前提下，当∠COD 绕点O 逆时针转动到如图2的位置时，（2）中α与β的数量关系是否仍然成立？若成立，请说明理由；若不成立，直接写出α与β的数量关系．【解答】解：（1）∠∠COE 与∠EOD 互余，∠∠DOE ＝90°﹣∠COE ＝90°﹣32°＝58°，∠OE 平分∠AOD ，∠∠AOD ＝2∠DOE ＝2×58°＝116°， ∠∠BOD ＝∠AOB ﹣∠AOD ＝150°﹣116°＝34°；故答案为：58°，34°；（2）∠∠COE 与∠EOD 互余，∠∠DOE ＝90°﹣∠COE ＝90°﹣α，∠OE 平分∠AOD ，∠∠AOD ＝2∠DOE ＝2（90°﹣α），∠∠AOB ＝150°，∠BOD ＝β，∠2（90°﹣α）+β＝150°，整理得，2α﹣β＝30°； （3））∠∠COE 与∠EOD 互余，∠∠DOE ＝90°﹣∠COE ＝90°﹣α，∠OE 平分∠AOD ，∠∠AOD ＝2∠DOE ＝2（90°﹣α）， ∠∠AOB ＝150°，∠BOD ＝β，∠2（90°﹣α）﹣150°＝β， 整理得2α+β＝30°．27、【阅读理解】射线OC 是∠AOB 内部的一条射线，若∠COA =21∠BOC ，则我们称射线OC 是射线OA 的伴随线．例如，如图1，∠AOB ＝60°，∠AOC ＝∠COD ＝∠BOD ＝20°，则∠AOC =21∠BOC ，称射线OC 是射线OA 的伴随线；同时，由于∠BOD=21∠AOD ，称射线OD 是射线OB 的伴随线．【知识运用】（1）如图2，∠AOB ＝120°，射线OM 是射线OA 的伴随线，则∠AOM ＝ °，若∠AOB 的度数是α，射线ON 是射线OB 的伴随线，射线OC 是∠AOB 的平分线，则∠NOC的度数是 ．（用含α的代数式表示）（2）如图3，如∠AOB ＝180°，射线OC 与射线OA 重合，并绕点O 以每秒3°的速度逆时针旋转，射线OD 与射线OB 重合，并绕点O 以每秒5°的速度顺时针旋转，当射线OD 与射线OA 重合时，运动停止．∠是否存在某个时刻t （秒），使得∠COD 的度数是20°，若存在，求出t 的值，若不存在，请说明理由．∠当t 为多少秒时，射线OC 、OD 、OA 中恰好有一条射线是其余两条射线的伴随线．【解答】解：（1）40°，6a； （2）射线OD 与OA 重合时，t =5180=36（秒） ∠当∠COD 的度数是20°时，有两种可能：若在相遇之前，则180﹣5t ﹣3t ＝20，∠t ＝20； 若在相遇之后，则5t +3t ﹣180＝20，∠t ＝25；所以，综上所述，当t ＝20秒或25秒时，∠COD 的度数是20°． ∠相遇之前：（i ）如图1，OC 是OA 的伴随线时，则∠AOC =21∠COD 即 3t =21（180﹣5t ﹣3t ）,∠t =790 （ii ）如图2，OC 是OD 的伴随线时，则∠COD =21∠AOC 即180﹣5t ﹣3t =21×3t, ∠t =19360 相遇之后：（iii ）如图3，OD 是OC 的伴随线时，则∠COD =21∠AOD 即5t +3t ﹣180=21（180﹣5t ）,∠t =7180 （iv ）如图4，OD 是OA 的伴随线时，则∠AOD =21∠COD 即180﹣5t =21（3t +5t ﹣180）∠t ＝30 综上所述，当t =790，19360，7180，30时，OC 、OD 、OA 中恰好有一条射线是其余两条射线的伴随线．。

七上期末复习压轴题---角的旋转（难题）训练一、计算题1.如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC=120∘.将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．(1)将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC.问：此时直线ON是否平分∠AOC?请说明理由．(2)将图1中的三角板绕点O以每秒6∘的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为_____(直接写出结果)．(3)将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，求∠AOM−∠NOC的度数．2.如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC=120∘.将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．(1)将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC.问：此时直线ON是否平分∠AOC?请说明理由．(2)将图1中的三角板绕点O以每秒6∘的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为_____(直接写出结果)．(3)将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，求∠AOM−∠NOC的度数．3.如图1，点O是直线AB上的一点．(1)如图1，当∠AOD是直角，3∠AOC=∠BOD，求∠COD的度数；(2)在(1)中∠COD绕着点O顺时针旋转(OD与OB重合即停止)，如图2，OE、OF分别平分∠AOC、∠BOD，则在旋转过程中∠EOF的大小是否变化？若不变，求出∠EOF的大小；若改变，说明理由；(3)在图1中，∠AOD=90°，∠AOC=30°，线段OC、OD绕着点O顺时针旋转，速度分别为每秒20°和每秒10°(当．OD．．重合时旋转都停止．．．．．．．．)，OM、ON分别平．．与．OB分∠BOC、∠BOD，多少秒时∠COM=∠BON(直接写出答案，不必写出过程)．二、解答题4.如图1，已知∠AOC=2∠BOC，∠AOC的余角比∠BOC小30°(1)求∠COB的度数(2)经过点O作射线OD，使得∠AOC=4∠AOD，求∠BOD的度数(3)如图2，在∠AOB的内部作∠EOF，OM、ON分别为∠AOE和∠BOF的平分线，当∠EOF绕点O在∠AOB的内部转动时，请写出∠AOB、∠EOF、∠MON之间的数量关系，并说明理由。

七上期末难点复习专题二角动点问题题型一 不涉及速度的角的旋转例1、已知∠AOB ＝100°，∠COD ＝40°，OE 平分∠AOC ，OF 平分 ∠BOD （本题中的角均为大于0°且小于180°的角）. （1）如图1，当OB 、OC 重合时，求∠EOF 的度数；（2）当∠COD 从图1所示位置绕点O 顺时针旋转n °（0＜n ＜90）时，∠AOE －∠BOF 的值是否为定值？若是定值，求出∠AOE －∠BOF 的值；若不是，请说明理由；（3）当∠COD 从图1所示位置绕点O 顺时针旋转n °（0＜n ＜180）时，满足∠AOD ＋∠EOF ＝6∠COD ,则n ＝.例2、已知：O 为直线AB 上的一点，射线OA 表示正北方向，射线OC 在北偏东m °的方向， 射线OE 在南偏东n °的方向，射线OF 平分∠AOE ，且2m ＋2n ＝180°. （1）如图1，∠COE ＝，∠COF 和∠BOE 之间的数量关系为.（2）若将∠COE 绕点O 旋转至图2的位置，射线OF 仍然平分∠AOE 时，试问（1）中 ∠COF 和∠BOE 之间的数量关系是否发生变化？若不发生变化，请你加以说明，若发生变化，请你什么理由；（3）若将∠COE 绕点O 旋转至图3的位置，射线OF 仍然平分∠AOE 时,2∠COF ＋∠BOE ＝.备用图1备用图2图1O OOABBADB (C )AEF北西南东O图1图3图2O O F EA BCF EA B CCBA EF例3、如图，线段OA 绕点O 逆时针旋转一周，满足∠EOF 始终在∠AOB 的内部且∠EOF ＝58°，线段OM 、ON 分别为∠AOE 和∠BOF 的平分线，在旋转过程中，∠MON 的最大值是.题型二 涉及速度的角的旋转例4、如图1，点O 为直线AB 上一点，过O 点作射线OC ，使∠AOC ：∠BOC ＝1:3，将一直角△MON 的直角顶点放在点O 处，边OM 在射线OB 上，另一边ON 在直线AB 的下方，绕点O 逆时针旋转△MON ，其中旋转的角度为a （0＜ a ＜360°）.（1）如图2逆时针旋转图1中的直角△MON ，使得ON 落在射线OB 上，此时a 为度；（2）若直角△MON 绕点O 按每秒5°的速度逆时针旋转，当直角△MON 的直角边ON 所在直线恰好平分∠AOC 时，求此时直角△MON 绕点O 的旋转时间t 的值.（3）若直角△MON 绕点O 按每秒5°的速度逆时针旋转，当直角△MON 的直角边ON 所在直线恰好平分∠AOC 时，求此时直角△MON 绕点O 的旋转时间t 的值.例5、如图1，O 为直线AB 上一点，过O 作射线OC ，∠AOC ＝30°，将一直角三角板（∠M ＝30°）的直角顶点放在点O 处，一边ON 在射线OA 上，另一边OM 与OC 都在直线AB 上方. （1）将图1中的三角板绕点O 以每秒3°的速度沿顺时针方向旋转一周. ①如图2，经过t 秒后，OM 恰好平分∠BOC ，求此时t 的值； ②此时ON 是否平分∠AOC ？请说明理由.O A B CO O O 图1图2图3N M A BC N M A B C NM A B C（2）在（1）的条件下，若在三角板开始转动的同时，射线OC 也绕O 点以每秒6°的速度沿顺时针方向旋转一周.如图3，那么经过多长时间OC 平分∠MOB ？请画图并说明理由.（3）在（2）的条件下，从旋转开始经过多长时间OC 平分∠MOB ？请画图并说明理由.例6、已知：如图1，∠AOB 和∠COD 共顶点O ，OB 和OD 重合，OM 为∠AOD 的平分线，ON 为∠BOC 的平分线，∠AOB ＝α,∠COD ＝β.（1）如图2，若α＝90°，β＝30°，则∠MON ＝ ； （2）如图3，若∠COD 绕O 逆时针旋转，且∠BOD ＝γ，求∠MON ；（3）如图4，2α=β，∠COD 绕O 逆时针旋转，转速为3°/秒，∠AOB 绕O 同时逆时针旋转，转速为1°/秒，（转到OC 与OA 共线时停止运动），且OE 平分∠BOD ，以下两个结论：①COEAOD∠∠的值不变； ②AOD COE ∠-∠的值不变，其中只有一个结论准确，请判断正确的结论，并说明理由.综合题型例1、如图1，点O 为直线AB 上一点，过点O 作射线OC ，使∠BOC=120°.将一直角三角板的直角顶点放在点O 处，一边OM 在射线OB 上，另一边ON 在直线AB 的下方.（1）将图1中的三角板绕点O 逆时针旋转至图2，使一边OM 在∠BOC 的内部，且恰好平分∠BOC ，问：直线ON 是否平分∠AOC ？请说明理由；CB A M N CB A M M NC BA NO O O 图1图2图3（D ）图3图2图1DCBAEN M CB AMN D C B AOOO图4N MAB C （D ）（2）将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为多少？（直接写出结果）；（3）将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，请探究：在旋转过程中，①∠AO M﹣∠NO C②∠AO M+∠NO C哪个值是不变的，哪一个值是变化的？若不变，请求出这个定值，若变化，请求出值的变化范围。

与角平分线+余角补角有关的计算1．如图，O 是直线AB 上一点，OC 为任意一条射线，OD 平分∠BOC ，OE 平分∠AOC ．(1)图中∠AOD 的补角是 ；∠BOD 的余角是 ．(2)已知∠COD ＝40°，求∠COE 的度数．2．如图，点O 在直线AB 上，CO ⊥AB ，∠2﹣∠1＝34°，OE 是∠AOD 的平分线，OF ⊥OE ．(1)求∠AOE 的度数．(2)找出图中与∠BOF 互补的角，并求出∠BOF 补角的度数．3．90MON ∠=︒，点A ，B 分别在OM 、ON 上运动(不与点O 重合)．(1)如图①，AE 、BE 分别是BAO ∠和ABO ∠的平分线，随着点A 、点B 的运动，当AO=BO 时AEB ∠= ︒；(2)如图②，若BC 是ABN ∠的平分线，BC 的反向延长线与OAB ∠的平分线交于点D ，随着点A ，B 的运动D ∠的大小会变吗？如果不会，求D ∠的度数；如果会，请说明理由；(3)如图③，延长MO 至Q ，延长BA 至G ，已知BAO ∠，OAG ∠的平分线与BOQ ∠的平分线及其延长线相交于点E 、F ，在AEF 中，如果有一个角是另一个角的3倍，求ABO ∠的度数．4．点O 为直线AB 上一点，过点O 作射线OC ，使∠AOC =120°, 一直角三角板的直角顶点放在点O处．(1)如图1，将三角板DOE的一边OD与射线OB重合时，则∠COD=∠COE；(2)如图2，将图1中的三角板DOE绕点O逆时针旋转一定角度，当OC恰好是∠BOE的角平分线时，求∠COD的度数；(3)将图1中的三角尺DOE绕点O逆时针旋转旋转一周，设旋转的角度为α度，在旋转的过程中，能否使∠AOE=3∠COD？若能，求出α的度数；若不能，说明理由.⊥．5．如图，直线AB与CD相交于点O，OE是∠COB的平分线，OE OF(1)若2∠=∠，求∠AOD的度数；COF COE(2)试判断OF是否平分∠AOC，并说明理由．6．如图1，已知射线OB在∠AOC内，若满足∠BOC+∠AOC＝180°，则称射线OB为∠BOC与∠AOC的“互补线”．(1)如图2，已知点O是直线AD上一点，射线OB、OC在直线AD同侧，且射线OC平分∠BOD．试说明：射线OB为∠BOC与∠AOC的“互补线”；(2)如图3，已知直线AB、CD相交于点O，射线OE为∠BOC与∠BOE的“互补线”，若∠AOD＝136°，求∠DOE的度数；(3)如图4，已知射线OB为∠BOC与∠AOC的“互补线”，且射线OE、OF分别平分∠AOC、∠BOC，试判断∠BOC +∠EOF 的度数是否为定值，若为定值，求出定值的度数；若不为定值，请说明理由． 7．如图，AOC ∠与BOC ∠互为补角，BOC ∠与BOD ∠互为余角，且4BOC BOD ∠=∠．(1)求BOC ∠的度数；(2)若OE 平分AOC ∠，求∠BOE 的度数．8．若A 、O 、B 三点共线，40BOC ∠=︒，将一个三角板的直角顶点放在点O 处（注：90DOE ∠=︒，30EDO ∠=︒）．(1)如图1，使三角板的长直角边OD 在射线OB 上，则COE ∠=____________°；(2)将图1中的三角板DOE 绕点O 以每秒2°的速度按逆时针方向旋转到图2位置，此时14COD AOE ∠=∠，求运动时间t 的值； (3)将图2中的三角板DOE 再绕点O 以每秒5°的速度按顺时针转方向旋转一周，经过t 秒后，直线OC 恰好平分DOE ∠，求t 的值．9．如图，直线AB ，CD 相交于点O ，OF ⊥CD ，OE 平分∠BOC ．(1)若∠BOE ＝60°，求∠DOE 的度数；(2)若∠BOD ：∠BOE ＝2：3，求∠AOF 的度数．10．已知：射线OC 在AOB ∠的内部，:9:1AOC BOC ∠∠=，2COD COB ∠=∠，OE 平分AOD ∠．(1)如图，若点A ，O ，B 在同一条直线上，OD 是AOC ∠内部的一条射线，请根据题意补全图形，并求COE ∠的度数；(2)若()016BOC αα∠=︒<<︒，直接写出COE ∠的度数（用含α的代数式表示）．11．如图（1），直线AB 、CD 相交于点O ，直角三角板EOF 边OF 落在射线OB 上，将三角板EOF 绕点O 逆时针旋转180°．(1)如图（2），设AOE n ∠=︒，当OF 平分BOD ∠时，求DOF ∠（用n 表示）(2)若40AOC ∠=︒，①如图（3），将三角板EOF 旋转，使OE 落在AOC ∠内部，试确定COE ∠与BOF ∠的数量关系，并说明理由．②若三角板EOF 从初始位置开始，每秒旋转5°，旋转时间为t ，当AOE ∠与DOF ∠互余时，求t 的值．12．如图，直线AB 、CD 相交于点O ，AB CD ⊥，90EOF ∠=︒．(1)若30COE ∠=︒，则BOF ∠= __________．(2)从（1）的时刻开始，若将EOF ∠绕O 以每秒15的速度逆时针旋转一周，求运动多少秒时，直线AB 平分EOF ∠．(3)从（1）的时刻开始，若将EOF ∠绕O 点逆时针旋转一周，如果射线OP 是COE ∠的角平分线，请直接写出此过程中AOP ∠与BOF ∠的数量关系．（不考虑OE 与AB 、CD 重合的情况）13．如图，直线AB 与CD 相交于点O ，OE 是∠COB 的平分线，OE ⊥OF ．（1）图中∠BOE 的补角是 ；（2）若∠COF =2∠COE ，求△BOE 的度数；（3）试判断 OF 是否平分∠AOC ，请说明理由．14．如图，直线AB ，CD ，EF 相交于点O ，OG ⊥C D ．（1）已知∠AOC ＝38°12'，求∠BOG 的度数；（2）如果OC 是∠AOE 的平分线，那么OG 是∠EOB 的平分线吗？说明理由．15．已知直线AB和CD交于点O，∠AOC＝α，∠BOE＝90°，OF平分∠AOD．（1）当α＝30°时，则∠EOC＝_________°；∠FOD＝_________°．（2）当α＝60°时，射线OE′从OE开始以12°/秒的速度绕点O逆时针转动，同时射线OF′从OF开始以8°/秒的速度绕点O顺时针转动，当射线OE′转动一周时射线OF′也停止转动，求经过多少秒射线OE′与射线OF′第一次重合？（3）在（2）的条件下，射线OE′在转动一周的过程中，当∠E′OF′＝90°时，请直接写出射线OE′转动的时间为_________秒．答案与解析1．如图，O是直线AB上一点，OC为任意一条射线，OD平分∠BOC，OE平分∠AOC．(1)图中∠AOD的补角是；∠BOD的余角是．(2)已知∠COD＝40°，求∠COE的度数．(1)求∠AOE的度数．(2)找出图中与∠BOF互补的角，并求出∠BOF补角的度数．∴∠AOF ＝∠EOF ﹣∠AOE ＝21°．【点睛】本题考查垂线的定义，角的和差关系，角平分线的定义，补角的定义，熟练掌握这些知识点是解题关键．3．90MON ∠=︒，点A ，B 分别在OM 、ON 上运动(不与点O 重合)．(1)如图①，AE 、BE 分别是BAO ∠和ABO ∠的平分线，随着点A 、点B 的运动，当AO=BO 时AEB ∠= ︒；(2)如图②，若BC 是ABN ∠的平分线，BC 的反向延长线与OAB ∠的平分线交于点D ，随着点A ，B 的运动D ∠的大小会变吗？如果不会，求D ∠的度数；如果会，请说明理由；(3)如图③，延长MO 至Q ，延长BA 至G ，已知BAO ∠，OAG ∠的平分线与BOQ ∠的平分线及其延长线相交于点E 、F ，在AEF 中，如果有一个角是另一个角的3倍，求ABO ∠的度数．放在点O 处．(1)如图1，将三角板DOE 的一边OD 与射线OB 重合时，则∠COD = ∠COE ；(2)如图2，将图1中的三角板DOE 绕点O 逆时针旋转一定角度，当OC 恰好是∠BOE 的角平分线时，求∠COD 的度数；(3)将图1中的三角尺DOE 绕点O 逆时针旋转旋转一周，设旋转的角度为α度，在旋转的过程中，能否使∠AOE =3∠COD ？若能，求出α的度数；若不能，说明理由. 【答案】(1)2(2)30(3)45︒或67.5︒【分析】（1）由邻补角和余角的定义求出两个角，即可得出结论；（2）由角平分线的定义可得60COE BOC ∠=∠=︒，再根据90DOE ∠=︒，从而可求解；（3）分两种情况讨论：①OC 是BOC ∠内；②OC 在BOC ∠外，分析清楚角关系求解即可．（1）解：120AOC ∠=︒，OD 与射线OB 重合，18060COD AOC ∴∠=︒-∠=︒，90DOE ∠=︒，906030COE ∴∠=︒-︒=︒，2COD COE ∴∠=∠，故答案为：2；解：由（1）得，60BOC ∠=︒，OC 是∠BOE 的角平分线，60COE BOC ∴∠=∠=︒，90DOE ∠=︒，906030COD ∴∠=︒-︒=︒； （3）解：能，①当OD 是BOC ∠内时，有： 60COD α∠=︒-，18090AOE DOE αα∠=︒-∠-=︒-，则903(60)αα︒-=︒-，解得：45α=︒；②当OD 在BOC ∠外时，有：60COD α∠=-︒，90AOE α∠=︒-，则903(60)αα︒-=-︒，解得：67.5α=︒．综上所述，α的度数为45︒或67.5︒．【点睛】本题主要考查三角形的内角和定理，余角和补角，解题的关键是结合图形分析清楚角与角之间的关系．5．如图，直线AB 与CD 相交于点O ，OE 是∠COB 的平分线，OE OF ⊥．(1)若2COF COE ∠=∠，求∠AOD 的度数；(2)试判断OF 是否平分∠AOC ，并说明理由．【答案】(1)60︒(2)证明见解析【分析】（1）根据垂直的定义先求解,COE 再利用角平分线的定义求解,BOC ∠ 结合对顶角的定义可得答案；（2）由垂直的定义及补角的性质可得结论．解：∵OE ⊥OF ，∴∠EOF =90°，即∠COF +∠COE =90°，∵∠COF =2∠COE ，∴∠COF =60°，∠COE =30°，∵OE 是∠COB 的平分线，∴∠COB =2∠COE =60°．∴∠AOD =∠COB =60°．(2)解：OF 平分∠AOC ，理由如下：∵OE ⊥OF ，∴∠EOF =90°，即∠COF +∠COE =90°，∠AOF +∠BOE =90°，∵OE 是∠COB 的平分线，∴∠EOB =∠COE ，∴∠AOF =∠COF ，即OF 平分∠AOC ．【点睛】本题考查的是角平分线的定义、垂直的定义、余角与补角，掌握它们的概念与性质是解决此题关键．6．如图1，已知射线OB 在∠AOC 内，若满足∠BOC +∠AOC ＝180°，则称射线OB 为∠BOC 与∠AOC 的“互补线”．(1)如图2，已知点O 是直线AD 上一点，射线OB 、OC 在直线AD 同侧，且射线OC 平分∠BOD ．试说明：射线OB 为∠BOC 与∠AOC 的“互补线”；(2)如图3，已知直线AB 、CD 相交于点O ，射线OE 为∠BOC 与∠BOE 的“互补线”，若∠AOD ＝136°，求∠DOE 的度数；(3)如图4，已知射线OB 为∠BOC 与∠AOC 的“互补线”，且射线OE 、OF 分别平分∠AOC 、∠BOC ，试判断∠BOC +∠EOF 的度数是否为定值，若为定值，求出定值的度数；若不为定值，请说明理由．【答案】(1)见解析(2)88︒(3)90EOF BOC ∠+∠=︒证明：OC ∠+∠AOC∴∠+∠AOC∴射线OB （2）射线OE ∴BOC∠BOC∠∠=AODCOB∴∠=∴∠=BOE∴∠BOD∴∠DOE （3）射线OB 射线(1)求BOC∠的度数；(2)若OE平分AOC∠，求∠BOE的度数．∠=︒）．30EDO(1)如图1，使三角板的长直角边OD 在射线OB 上，则COE ∠=____________°；(2)将图1中的三角板DOE 绕点O 以每秒2°的速度按逆时针方向旋转到图2位置，此时14COD AOE ∠=∠，求运动时间t 的值； (3)将图2中的三角板DOE 再绕点O 以每秒5°的速度按顺时针转方向旋转一周，经过t 秒后，直线OC 恰好平分DOE ∠，求t 的值．经过t秒后，∠EOE=5t此时有：5t-10º-45º=180º，(1)若∠BOE＝60°，求∠DOE的度数；(2)若∠BOD：∠BOE＝2：3，求∠AOF的度数．(1)如图，若点A ，O ，B 在同一条直线上，OD 是AOC ∠内部的一条射线，请根据题意补全图形，并求COE ∠的度数；(2)若()016BOC αα∠=︒<<︒，直接写出COE ∠的度数（用含α的代数式表示）．∵点A，O，B在同一条直线上，∠的外部时，如图，当射线OD在AOC【点睛】本题是有关角的计算，考查了角平分线的定义、平角定义以及角的和差倍分，注意板EOF绕点O逆时针旋转180°．(1)如图（2），设AOE n ∠=︒，当OF 平分BOD ∠时，求DOF ∠（用n 表示）(2)若40AOC ∠=︒，①如图（3），将三角板EOF 旋转，使OE 落在AOC ∠内部，试确定COE ∠与BOF ∠的数量关系，并说明理由．②若三角板EOF 从初始位置开始，每秒旋转5°，旋转时间为t ，当AOE ∠与DOF ∠互余时，求t 的值． 【答案】(1)90DOF n ∠=︒-︒(2)①130COE BOF ∠+∠=︒，理由见解析；②4秒或22秒【分析】（1）利用角的和差关系求解,BOF ∠ 再利用角平分线的含义求解DOF ∠即可；（2）①设∠=COE β，再利用角的和差关系依次求解40AOE β∠=︒-， 50AOF β∠=︒+，130BOF β∠=︒-， 从而可得答案；②由题意得：OE 与OA 重合是第18秒，OF 与OD 重合是第8秒，停止是36秒．再分三种情况讨论：如图，当08t <<时 905AOE t ∠=︒-，405DOF t ∠=︒-，如图，当818t <<时 905AOE t ∠=︒-，540DOF t ∠=-︒，如图，当1836t <<时，590AOE t ∠=-︒，540DOF t ∠=-︒，再利用互余列方程解方程即可.（1）解：180,90,,AOB EOF AOE n∴ 18090BOF EOF AOE n ∠=︒-∠-∠=︒-︒∵OF 平分BOD ∠∴90DOF BOF n ∠=∠=︒-︒（2）解：①设∠=COE β，则40AOE β∠=︒-，∴()904050AOF ββ∠=︒-︒-=︒+∴()180********BOF AOF ββ∠=︒-∠=︒-︒+=︒-，∴130COE BOF ∠+∠=︒②由题意得：OE 与OA 重合是第18秒，OF 与OD 重合是第8秒，停止是36秒． 如图，当08t <<时 905AOE t ∠=︒-，405DOF t ∠=︒-，则90540590t t -+-=，∴4t =如图，当818t <<时 905AOE t ∠=︒-，540DOF t ∠=-︒，则90554090t t -+-=，方程无解，不成立如图，当1836t <<时，590AOE t ∠=-︒，540DOF t ∠=-︒，则59054090t t -+-=，∴22t =综上所述4t =秒或22秒【点睛】本题考查的是角的和差运算，角平分线的定义，角的动态定义的理解，互为余角的含义，清晰的分类讨论是解本题的关键.12．如图，直线AB 、CD 相交于点O ，AB CD ⊥，90EOF ∠=︒．(1)若30COE ∠=︒，则BOF ∠= __________．(2)从（1）的时刻开始，若将EOF ∠绕O 以每秒15的速度逆时针旋转一周，求运动多少秒时，直线AB 平分EOF ∠．(3)从（1）的时刻开始，若将EOF ∠绕O 点逆时针旋转一周，如果射线OP 是COE ∠的角平分线，请直接写出此过程中AOP ∠与BOF ∠的数量关系．（不考虑OE 与AB 、CD 重合的情况）情况二（3）∠的角平分线，∵∠COE=∠BOF，射线OP是COE1∠的角平分线，∵∠COE=90°+∠BOE=∠BOF，射线OP是COE11（1）图中∠BOE的补角是；（2）若∠COF=2∠COE，求△BOE的度数；（3）试判断OF是否平分∠AOC，请说明理由．（3）OF平分∠AOC，∵OE是∠COB的平分线，OE⊥OF．∴∠BOE＝∠COE，∠COE＋∠COF＝90°，∵∠BOE＋∠EOC＋∠COF＋∠FOA＝180°，∴∠COE＋∠FOA＝90°，∴∠FOA＝∠COF，即，OF平分∠AOC．【点睛】考查互为余角、互为补角、角平分线的意义，解题的关键是熟知：如果两角之和等于180°，那么这两个角互为补角.其中一个角叫做另一个角的补角；如果两个角的和是直角，那么称这两个角“互为余角”，简称“互余”，也可以说其中一个角是另一个角的余角．14．如图，直线AB，CD，EF相交于点O，OG⊥C D．（1）已知∠AOC＝38°12'，求∠BOG的度数；（2）如果OC是∠AOE的平分线，那么OG是∠EOB的平分线吗？说明理由．【答案】（1）51°48′；（2）OG是∠EOB的平分线，理由见解析【分析】（1）根据互为余角的意义和对顶角的性质，可得∠AOC＝∠BOD＝38°12′，进而求出∠BOG；（2）求出∠EOG＝∠BOG即可．【详解】解：（1）∵OG⊥C D．∴∠GOC＝∠GOD＝90°，∵∠AOC＝∠BOD＝38°12′，∴∠BOG＝90°﹣38°12′＝51°48′，（2）OG是∠EOB的平分线，理由：∵OC是∠AOE的平分线，∴∠AOC＝∠COE＝∠DOF＝∠BOD，∵∠COE+∠EOG＝∠BOG+∠BOD＝90°，∴∠EOG＝∠BOG，即：OG平分∠BOE．【点睛】本题主要考查角平分线的定义及余角，熟练掌握角平分线的定义及余角是解题的关键．15．已知直线AB和CD交于点O，∠AOC＝α，∠BOE＝90°，OF平分∠AOD．（1）当α＝30°时，则∠EOC＝_________°；∠FOD＝_________°．（2）当α＝60°时，射线OE′从OE开始以12°/秒的速度绕点O逆时针转动，同时射线OF′从OF开始以8°/秒的速度绕点O顺时针转动，当射线OE′转动一周时射线OF′也停止转动，求经过多少秒射线OE′与射线OF′第一次重合？（3）在（2）的条件下，射线OE′在转动一周的过程中，当∠E′OF′＝90°时，请直接写出射线OE′转动的时间为_________秒．。