三角函数的周期与频率

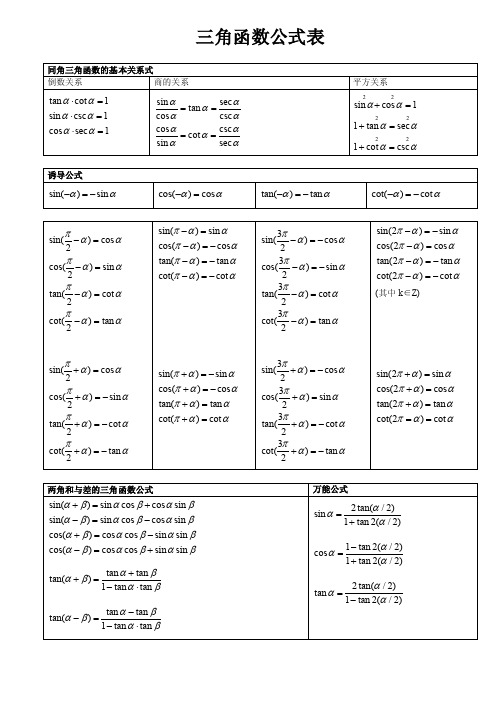
三角函数公‎式表物理量计算公式备注速度υ= S / t1m / s = 3.6 Km / h声速υ= 340m / s光速C = 3×108 m /s密度ρ= m / V 1 g / c m3 = 103 Kg / m3合力 F = F1 - F2F = F1 + F2 F1、F2在同一直线线上且方向相反F1、F2在同一直线线上且方向相同压强p = F / Sp =ρg h p = F / S适用于固、液、气p =ρg h适用于竖直固体柱p =ρg h可直接计算液体压强1标准大气压= 76 cmHg柱= 1.01×105 Pa = 10.3 m水柱浮力①F浮= G – F②漂浮、悬浮：F浮= G③F浮= G排=ρ液g V排④据浮沉条件判浮力大小（1）判断物体是否受浮力（2）根据物体浮沉条件判断物体处于什么状态（3）找出合适的公式计算浮力物体浮沉条件（前提：物体浸没在液体中且只受浮力和重力）：①F浮＞G（ρ液＞ρ物）上浮至漂浮②F浮=G（ρ液=ρ物）悬浮③F浮＜G（ρ液＜ρ物）下沉杠杆平衡条件F1 L1 = F2 L 2 杠杆平衡条件也叫杠杆原理滑轮组 F = G / nF =（G动+ G物）/ nSF = n SG 理想滑轮组忽略轮轴间的摩擦n：作用在动滑轮上绳子股数功W = F S = P t 1J = 1N•m = 1W•s功率P = W / t = Fυ1KW = 103 W，1MW = 103KW有用功W有用= G h（竖直提升）= F S（水平移动）= W总– W额=ηW总额外功W额= W总– W有= G动h（忽略轮轴间摩擦）= f L（斜面）总功W总= W有用+ W额= F S = W有用/ η机械效率η= W有用/ W总η=G /（n F）= G物/（G物+ G动）定义式适用于动滑轮、滑轮组中考物理所有的公式特点或原理串联电路并联电路时间：t t=t1=t2 t=t1=t2电流：I I = I 1= I 2 I = I 1+ I 2电压：U U = U 1+ U 2 U = U 1= U 2电荷量：Q电Q电= Q电1= Q电2 Q电= Q电1+ Q电2电阻：R R = R 1= R 2 1/R=1/R1+1/R2 [R=R1R2/(R1+R2)]电功：W W = W 1+ W 2 W = W 1+ W 2电功率：P P = P 1+ P 2 P = P 1+ P 2电热：Q热Q热= Q热1+ Q热 2 Q热= Q热1+ Q热 2物理量（单位）公式备注公式的变形速度V（m/S）v= S：路程/t：时间重力G（N）G=mg m：质量g：9.8N/kg或者10N/kg密度ρ（kg/m3）ρ=m：质量V：体积合力F合（N）方向相同：F合=F1+F2方向相反：F合=F1—F2 方向相反时，F1>F2浮力F浮(N) F浮=G物—G视G视：物体在液体的重力浮力F浮(N) F浮=G物此公式只适用物体漂浮或悬浮浮力F浮(N) F浮=G排=m排g=ρ液gV排G排：排开液体的重力m排：排开液体的质量ρ液：液体的密度V排：排开液体的体积(即浸入液体中的体积)杠杆的平衡条件F1L1= F2L2 F1：动力 L1：动力臂F2：阻力 L2：阻力臂定滑轮F=G物S=h F：绳子自由端受到的拉力G物：物体的重力S：绳子自由端移动的距离h：物体升高的距离动滑轮F= （G物+G轮）S=2 h G物：物体的重力G轮：动滑轮的重力滑轮组F= （G物+G轮）S=n h n：通过动滑轮绳子的段数机械功W（J）W=Fs F：力s：在力的方向上移动的距离有用功W有总功W总W有=G物hW总=Fs 适用滑轮组竖直放置时机械效率η= ×100%功率P（w）P=W：功t：时间压强p（Pa）P=F：压力S：受力面积液体压强p（Pa）P=ρgh ρ：液体的密度h：深度（从液面到所求点的竖直距离）热量Q（J）Q=cm△t c：物质的比热容 m：质量△t：温度的变化值燃料燃烧放出的热量Q（J）Q=mq m：质量q：热值常用的物理公式与重要知识点一．物理公式单位）公式备注公式的变形串联电路电流I（A）I=I1=I2=…… 电流处处相等串联电路电压U（V）U=U1+U2+…… 串联电路起分压作用串联电路电阻R（Ω）R=R1+R2+……并联电路电流I（A）I=I1+I2+…… 干路电流等于各支路电流之和（分流）并联电路电压U（V）U=U1=U2=……并联电路电阻R（Ω）= + +……欧姆定律I=电路中的电流与电压成正比，与电阻成反比电流定义式I=Q：电荷量（库仑）t：时间（S）电功W（J）W=UIt=Pt U：电压 I：电流t：时间 P：电功率电功率P=UI=I2R=U2/R U:电压 I：电流R：电阻电磁波波速与波长、频率的关系C=λν C：波速（电磁波的波速是不变的，等于3×108m/s）λ：波长ν：频率二．知识点1．需要记住的几个数值：a．声音在空气中的传播速度：340m/s b光在真空或空气中的传播速度：3×108m/sc．水的密度：1.0×103kg/m3 d．水的比热容：4.2×103J/（kg•℃）e．一节干电池的电压：1.5V f．家庭电路的电压：220Vg．安全电压：不高于36V2．密度、比热容、热值它们是物质的特性，同一种物质这三个物理量的值一般不改变。

函数周期性结论总结函数周期性是数学中的一个重要概念，它在解决各种实际问题中起到了重要的作用。

在本文中，我将对函数周期性的结论做一个总结，以便对读者有更清晰的认识。

以下是我对函数周期性的总结：1. 周期性定义在数学中，一个函数被称为具有周期性，当且仅当存在一个正数T，使得对于每一个x值都有f(x+T) = f(x)成立。

其中，T被称为函数的周期。

2. 常见函数的周期性2.1 三角函数的周期性三角函数是一类具有周期性的函数。

常见的三角函数有正弦函数和余弦函数。

正弦函数的周期为2π，即sin(x+2π) = sin(x)；余弦函数的周期也为2π，即cos(x+2π) = cos(x)。

这意味着在一个周期内，正弦函数和余弦函数的值会周期性地重复。

2.2 指数函数的周期性指数函数也具有周期性。

以自然对数为底的指数函数具有周期为2πi的形式，即e^(x+2πi) = e^x。

其中，i是虚数单位。

这意味着在一个周期内，指数函数的值也会周期性地重复。

3. 周期性性质3.1 零点的周期性如果一个函数的周期为T，那么对于任意一个零点x0，它的周期性可以表示为x0 + Tn，其中n为任意整数。

这意味着函数的零点也具有周期性，每隔一个周期就会出现一个零点。

3.2 值域的周期性如果一个函数具有周期T，那么对于函数值f(x)来说，它的周期性可以表示为f(x+T) = f(x)。

这意味着函数的值域也具有周期性，每隔一个周期就会重复一次。

4. 应用举例函数周期性在各个领域都有广泛的应用。

举几个例子来说明：4.1 电力系统在电力系统中，交流电的变化是具有周期性的。

电压和电流随着时间呈周期性变化，周期性的特点使得电力系统能够稳定地运行。

4.2 信号处理在信号处理领域，周期性信号的分析和处理是很重要的。

通过对周期信号的分析，可以准确地获取信号的频率和振幅等信息。

4.3 声音与音乐声音和音乐是具有周期性的。

乐器的音调是具有周期性的，音乐也是以一定的节拍和律动来展现周期性。

三角函数的图像与性质先将y ＝sin x 的图象上各点的横坐标变为原来的ω1倍(ω＞0)，再沿x 轴向左(ϕ＞0)或向右(ϕ＜0＝平移ωϕ||个单位，便得y ＝sin(ωx ＋ϕ)的图象。

5．由y ＝A sin(ωx ＋ϕ)的图象求其函数式：给出图象确定解析式y =A sin （ωx +ϕ）的题型，有时从寻找“五点”中的第一零点（－ωϕ，0）作为突破口，要从图象的升降情况找准．．第一个零点的位置。

6．对称轴与对称中心：sin y x =的对称轴为2x k ππ=+，对称中心为(,0) k k Z π∈；cos y x =的对称轴为x k π=，对称中心为2(,0)k ππ+；对于sin()y A x ωφ=+和cos()y A x ωφ=+来说，对称中心与零点相联系，对称轴与最值点联系。

7．求三角函数的单调区间：一般先将函数式化为基本三角函数的标准式，要特别注意A 、ω的正负利用单调性三角函数大小一般要化为同名函数,并且在同一单调区间；8．求三角函数的周期的常用方法：经过恒等变形化成“sin()y A x ωφ=+、cos()y A x ωφ=+”的形式，在利用周期公式，另外还有图像法和定义法。

9．五点法作y =A sin （ωx +ϕ）的简图： 五点取法是设x =ωx +ϕ，由x 取0、2π、π、2π3、2π来求相应的x 值及对应的y 值，再描点作图。

二．典例分析考点一：三角函数的定义域与值域典题导入(1)(2013·湛江调研)函数y ＝lg(sin x )＋cos x －12的定义域为________．(2)函数y ＝sin 2x ＋sin x －1的值域为( )A ． B.⎣⎢⎡⎦⎥⎤－54，－1 C.⎣⎢⎡⎦⎥⎤－54，1D.⎣⎢⎡⎦⎥⎤－1，54(1)要使函数有意义必须有⎩⎪⎨⎪⎧sin x >0，cos x －12≥0，即⎩⎪⎨⎪⎧sin x >0，cos x ≥12，解得⎩⎪⎨⎪⎧2k π<x <π＋2k π，－π3＋2k π≤x ≤π3＋2k π(k ∈Z )，∴2k π<x ≤π3＋2k π，k ∈Z ，∴函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π<x ≤π3＋2k π，k ∈Z .(2)y ＝sin 2x ＋sin x －1，令sin x ＝t ，则有y ＝t 2＋t －1，t ∈，画出函数图象如图所示，从图象可以看出，当t ＝－12及t ＝1时，函数取最值，代入y ＝t 2＋t －1可得y ∈⎣⎢⎡⎦⎥⎤－54，1.(1)⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π<x ≤π3＋2k π，k ∈Z (2)C若本例(2)中x ∈⎣⎢⎡⎦⎥⎤0，π2，试求其值域．解：令t ＝sin x ，则t ∈．∴y ＝t 2＋t －1＝⎝ ⎛⎭⎪⎫t ＋122－54.∴y ∈．∴函数的值域为．由题悟法1．求三角函数定义域实际上是解简单的三角不等式，常借助三角函数线或三角函数图象来求解．2．求解涉及三角函数的值域(最值)的题目一般常用以下方法： (1)利用sin x 、cos x 的值域；(2)形式复杂的函数应化为y ＝A sin(ωx ＋φ)＋k 的形式逐步分析ωx ＋φ的范围，根据正弦函数单调性写出函数的值域(如本例以题试法(2))；(3)换元法：把sin x 或cos x 看作一个整体，可化为求函数在给定区间上的值域(最值)问题(如例1(2))．以题试法1． (1)函数y ＝2＋log 12x ＋tan x 的定义域为________．(2)(2012·山西考前适应性训练)函数f (x )＝3sin ⎝ ⎛⎭⎪⎫2x －π6在区间⎣⎢⎡⎦⎥⎤0，π2上的值域为( )A.⎣⎢⎡⎦⎥⎤－32，32B.⎣⎢⎡⎦⎥⎤－32，3C.⎣⎢⎡⎦⎥⎤－332，332D.⎣⎢⎡⎦⎥⎤－332，3解析：(1)要使函数有意义则⎩⎪⎨⎪⎧2＋log 12x ≥0，x >0，tan x ≥0，x ≠k π＋π2，k ∈Z ⇒⎩⎪⎨⎪⎧0<x ≤4，k π≤x <k π＋π2k ∈Z .利用数轴可得 函数的定义域是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪0<x <π2，或π≤x ≤4.(2)当x ∈⎣⎢⎡⎦⎥⎤0，π2时，2x －π6∈⎣⎢⎡⎦⎥⎤－π6，5π6，sin ⎝ ⎛⎭⎪⎫2x －π6∈⎣⎢⎡⎦⎥⎤－12，1，故3sin ⎝ ⎛⎭⎪⎫2x －π6∈⎣⎢⎡⎦⎥⎤－32，3即此时函数f (x )的值域是⎣⎢⎡⎦⎥⎤－32，3. 答案：(1)⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪0<x <π2，或π≤x ≤4 (2)B考点二：三角函数的单调性典题导入(2012·华南师大附中模拟)已知函数y ＝sin ⎝ ⎛⎭⎪⎫π3－2x ，求：(1)函数的周期；(2)求函数在上的单调递减区间．由y ＝sin ⎝ ⎛⎭⎪⎫π3－2x 可化为y ＝－sin ⎝ ⎛⎭⎪⎫2x －π3. (1)周期T ＝2πω＝2π2＝π.(2)令2k π－π2≤2x －π3≤2k π＋π2，k ∈Z ，得k π－π12≤x ≤k π＋5π12，k ∈Z .所以x ∈R 时，y ＝sin ⎝⎛⎭⎪⎫π3－2x 的减区间为⎣⎢⎡⎦⎥⎤k π－π12，k π＋5π12，k ∈Z .从而x ∈时， y ＝sin ⎝ ⎛⎭⎪⎫π3－2x 的减区间为⎣⎢⎡⎦⎥⎤－π，－7π12，⎣⎢⎡⎦⎥⎤－π12，0.由题悟法求三角函数的单调区间时应注意以下几点：(1)形如y ＝A sin(ωx ＋φ)(A >0，ω>0)的函数的单调区间，基本思路是把ωx ＋φ看作是一个整体，由－π2＋2k π≤ωx ＋φ≤π2＋2k π(k ∈Z )求得函数的增区间，由π2＋2k π≤ωx ＋φ≤3π2＋2k π(k ∈Z )求得函数的减区间．(2)形如y ＝A sin(－ωx ＋φ)(A >0，ω>0)的函数，可先利用诱导公式把x 的系数变为正数，得到y ＝－A sin(ωx －φ)，由－π2＋2k π≤ωx －φ≤π2＋2k π(k ∈Z )得到函数的减区间，由π2＋2k π≤ωx －φ≤3π2＋2k π(k ∈Z )得到函数的增区间．(3)对于y ＝A cos(ωx ＋φ)，y ＝A tan(ωx ＋φ)等，函数的单调区间求法与y ＝A sin(ωx ＋φ)类似．以题试法2．(1)函数y ＝|tan x |的增区间为________．(2)已知函数f (x )＝sin x ＋3cos x ，设a ＝f ⎝ ⎛⎭⎪⎫π7，b ＝f ⎝ ⎛⎭⎪⎫π6，c ＝f ⎝ ⎛⎭⎪⎫π3，则a ，b ，c的大小关系是( )A ．a <b <cB ．c <a <bC ．b <a <cD ．b <c <a解析：(1)作出y ＝|tan x |的图象，观察图象可知，y ＝|tan x |的增区间是⎣⎢⎡⎭⎪⎫k π，k π＋π2，k ∈Z . (2)f (x )＝sin x ＋3cos x ＝2sin ⎝ ⎛⎭⎪⎫x ＋π3，因为函数f (x )在⎣⎢⎡⎦⎥⎤0，π6上单调递增，所以f ⎝ ⎛⎭⎪⎫π7<f ⎝ ⎛⎭⎪⎫π6，而c ＝f ⎝ ⎛⎭⎪⎫π3＝2sin2π3＝2sin π3＝f (0)<f ⎝ ⎛⎭⎪⎫π7， 所以c <a <b .答案：(1)⎣⎢⎡⎭⎪⎫k π，k π＋π2，k ∈Z (2)B考点三：三角函数的周期性与奇偶性典题导入(2012·广州调研)已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋3π2(x ∈R )，给出下面四个命题：①函数f (x )的最小正周期为π；②函数f (x )是偶函数；③函数f (x )的图象关于直线x ＝π4对称；④函数f (x )在区间⎣⎢⎡⎦⎥⎤0，π2上是增函数．其中正确命题的个数是( )A ．1B ．2C ．3D ．4函数f (x )＝sin ⎝⎛⎭⎪⎫2x ＋3π2＝－cos 2x ，则其最小正周期为π，故①正确；易知函数f (x )是偶函数，②正确；由f (x )＝－cos 2x 的图象可知，函数f (x )的图象不关于直线x ＝π4对称，③错误；由f (x )的图象易知函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上是增函数，故④正确．综上可知，选C.C由题悟法1．三角函数的奇偶性的判断技巧首先要对函数的解析式进行恒等变换，再根据定义、诱导公式去判断所求三角函数的奇偶性；也可以根据图象做判断．2．求三角函数周期的方法 (1)利用周期函数的定义；(2)利用公式：y ＝A sin(ωx ＋φ)和y ＝A cos(ωx ＋φ)的最小正周期为2π|ω|，y ＝tan(ωx ＋φ)的最小正周期为π|ω|； (3)利用图象． 3．三角函数的对称性正、余弦函数的图象既是中心对称图形，又是轴对称图形．正切函数的图象只是中心对称图形，应熟记它们的对称轴和对称中心，并注意数形结合思想的应用．以题试法3．(1)(2013·青岛模拟)下列函数中，周期为π，且在⎣⎢⎡⎦⎥⎤π4，π2上为减函数的是( ) A ．y ＝sin ⎝⎛⎭⎪⎫2x ＋π2 B ．y ＝cos ⎝⎛⎭⎪⎫2x ＋π2C ．y ＝sin ⎝⎛⎭⎪⎫x ＋π2D ．y ＝cos ⎝⎛⎭⎪⎫x ＋π2(2)(2012·遵义模拟)若函数f (x )＝sin ax ＋cos ax (a >0)的最小正周期为1，则它的图象的一个对称中心为( )A.⎝ ⎛⎭⎪⎫－π8，0B ．(0,0)C.⎝ ⎛⎭⎪⎫－18，0D.⎝ ⎛⎭⎪⎫18，0 解析：(1)选A 对于选项A ，注意到y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π2＝cos 2x 的周期为π，且在⎣⎢⎡⎦⎥⎤π4，π2上是减函数．(2)选C 由条件得f (x )＝2sin ⎝ ⎛⎭⎪⎫ax ＋π4，又函数的最小正周期为1，故2πa ＝1，∴a＝2π，故f (x )＝2sin ⎝ ⎛⎭⎪⎫2πx ＋π4.将x ＝－18代入得函数值为0.板书设计 三角函数的图像与性质1．正弦函数、余弦函数、正切函数的图像2．三角函数的单调区间3．函数Bx A y ++=)sin(ϕω），（其中00>>ωA 4．对称轴与对称中心 5．五点法作图教学三角函数的图像与性质是三角函数的重点知识之一，复习时，要让学生熟练记忆三角函数的图。

高一数学三角函数知识整理一、正弦函数 图像函数y=sin x 的定义域，值域，奇偶性，单调性，周期性 1、 函数y=sin x 的定义域是R ，值域为[-1，1] 2、 当x ∈{x| x=22k ππ+,k ∈Z}时，y 有最大值为1，当x ∈{x|x=322k ππ+,k ∈Z}时，y 有最小值为-13、 函数y=sin x 的图像关于原点对称是奇函数，可以根据sin(-x)=-sinx 证明。

对称中心为（k π，0）对称轴为x=k π+2π(k ∈Z)。

4、在[22k ππ-，22k ππ+]k ∈Z 上单调递增，在[22k ππ+，322k ππ+]k∈Z 上单调递减。

5、函数y=sin x 的周期为2k π（k ∈Z 且k ≠0），最小正周期为2π 注意有界性：sin 1x ≤ 二、余弦函数 图像函数y=cosx 的定义域，值域，奇偶性，单调性，周期性 1、 函数y=cos x 的定义域是实数集R ，值域是[-1，1]2、 当x ∈{x | x=2k π，k ∈Z}时y 有最大值为1，当x ∈{x | x=2k π+π,k∈Z}时，y 有最小值为-1。

3、 函数y=cosx 关于y 轴对称是偶函数，可以通过诱导公式cos(-x)=cosx 证明。

对称中心[2k ππ+，0]，对称轴为x= k π4、 在[2k ππ-，2k π]上单调递增，在[2k π，2k ππ+]上单调递减。

5、 函数y=cosx 的周期为2k π（k ∈Z 且k ≠0）最小正周期为2π。

注意有界性：cos 1x ≤ 三、正切函数 图像函数y=tanx 定义域，值域，奇偶性，单调性，周期性1、 y=tan x 的定义域是{x| x ∈R 且x ≠2k ππ+,k ∈Z}。

因为定义域不连贯，所以当有题目说该函数在定义域上怎么怎么样是错误的（同样用于其它所有函数）。

值域是一切实数R2、 y=tan x 的定义域关于原点对称是奇函数，根据诱导公式且tan(-x)=-tan x 可以证明。

第一部分 集合1．理解集合中元素的意义．．．．．是解决集合问题的关键：元素是函数关系中自变量的取值？还是因变量的取值？还是曲线上的点？… ； 2．数形结合．．．．是解集合问题的常用方法：解题时要尽可能地借助数轴、直角坐标系或韦恩图等工具，将抽象的代数问题具体化、形象化、直观化，然后利用数形结合的思想方法解决； 3．（1）含n 个元素的集合的子集数为2n ,真子集数为2n －1；非空真子集的数为2n －2；（2）;B B A A B A B A =⇔=⇔⊆ 注意：讨论的时候不要遗忘了φ=A 的情况。

4．φ是任何集合的子集，是任何非空集合的真子集。

第二部分 函数与导数1．映射：注意 ①第一个集合中的元素必须有象；②一对一，或多对一。

2．函数值域的求法：①分析法 ；②配方法 ；③判别式法 ；④利用函数单调性 ；⑤换元法 ；⑥利用均值不等式2222b a b a ab +≤+≤； ⑦利用数形结合或几何意义（斜率、距离、绝对值的意义等）；⑧利用函数有界性（xa 、x sin 、x cos 等）；⑨导数法 3．复合函数的有关问题 （1）复合函数定义域求法：① 若f(x)的定义域为［a ，b ］,则复合函数f[g(x)]的定义域由不等式a≤g(x)≤b 解出② 若f[g(x)]的定义域为[a,b],求 f(x)的定义域，相当于x ∈[a,b]时，求g(x)的值域。

（2）复合函数单调性的判定：①首先将原函数)]([x g f y =分解为基本函数：内函数)(x g u =与外函数)(u f y =；②分别研究内、外函数在各自定义域内的单调性；③根据“同性则增，异性则减”来判断原函数在其定义域内的单调性。

4．分段函数：值域（最值）、单调性、图象等问题，先分段解决，再下结论。

5．函数的奇偶性⑴函数的定义域关于原点对称是函数具有奇偶性的必要条件．．．．； ⑵)(x f 是奇函数⇔f(－x)=－f(x)；)(x f 是偶函数⇔f(－x)= f(x) ⑶奇函数)(x f 在原点有定义，则0)0(=f ；⑷在关于原点对称的单调区间内：奇函数有相同的单调性，偶函数有相反的单调性；⑸若所给函数的解析式较为复杂，应先等价变形，再判断其奇偶性； 6．函数的单调性 ⑴单调性的定义：①)(x f 在区间M 上是增函数,,21M x x ∈∀⇔当21x x <时有12()()f x f x <；②)(x f 在区间M 上是减函数,,21M x x ∈∀⇔当21x x <时有12()()f x f x >；⑵单调性的判定① 定义法：一般要将式子)()(21x f x f -化为几个因式作积或作商的形式，以利于判断符号； ②导数法（见导数部分）；③复合函数法；④图像法。

三角函数图像公式w和T的关系
三角函数中w是简谐振动的角频率，w=2兀/T，三角函数的图象的伸缩多少由w决定；W是角频率。

是描述物体振动快慢的物理量，与振动系统的固有属性有关，常用符号ω表示。

在国际单位制中，角频率的单位是弧度/秒(rad/s)。

三角函数y=ASin(wX+Q)的最小正周期T和w的关系为T=2兀
/lw|；三角函数y=Acos(wX十+Q)的最小正周期T=2兀/|w|，特别注意的三角函数y=Atan(wX+Q)的最小正周期T=兀/丨w丨，在用周期公式时最易错的是认为三个公式没区别，条件中若没有w>0而不加绝对值，将公式变形知周期可求w。

T=2π/w 所以有w=2π/T, 即w与T成反比；
wT=2π可由此看出w, 比如T=π,则w=2 T=4π,则w=1/2。

三角函数的关系与应用三角函数是数学中的重要概念，它们在几何学、物理学、工程学等领域中有广泛的应用。

本文将探讨三角函数之间的关系以及它们在实际问题中的应用。

一、三角函数的定义与关系1. 正弦函数（sine function）是一个周期函数，它的定义域是实数集，值域是[-1, 1]。

正弦函数的图像是一条连续的曲线，它在每个周期内都有一段上升和一段下降。

2. 余弦函数（cosine function）也是一个周期函数，它的定义域和值域与正弦函数相同。

余弦函数的图像与正弦函数的图像非常相似，只是相位有所不同。

3. 正切函数（tangent function）是一个无穷函数，它的定义域是实数集，值域是整个实数集。

正切函数的图像是一条连续的曲线，它在每个周期内都有一个渐近线。

这三个函数之间有一些重要的关系。

首先，正弦函数和余弦函数是互补的，即sin(x) = cos(π/2 - x)，cos(x) = sin(π/2 - x)。

其次，正切函数可以用正弦函数和余弦函数表示，即tan(x) = sin(x) / cos(x)。

二、三角函数的应用1. 几何学中的应用三角函数在几何学中有广泛的应用。

例如，我们可以利用正弦定理和余弦定理来计算三角形的边长和角度。

正弦定理表明，在一个三角形中，三条边的比值与对应的正弦值成比例。

余弦定理则可以用来计算三角形的边长，它表明一个三角形的边长与对应的余弦值的平方成反比。

2. 物理学中的应用三角函数在物理学中也有重要的应用。

例如，我们可以利用正弦函数来描述波动的性质。

正弦函数可以用来表示周期性的波动，例如声波和光波。

正弦函数的振幅可以表示波的强度，而频率则表示波的周期。

另外，三角函数还可以用来描述旋转运动的性质，例如物体绕轴旋转的角速度。

3. 工程学中的应用在工程学中，三角函数也有广泛的应用。

例如，我们可以利用正弦函数来描述交流电的变化。

交流电的电压和电流都是周期性变化的，它们可以用正弦函数来表示。