第01讲 集合的概念与运算(学生版) 备战2021年新高考数学微专题讲义

『高考复习|学与练』『汇总归纳·备战高考』高考复习·学与练专题1.1 集合【考纲要求】1.了解集合的含义，体会元素与集合的属于关系；能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题；2.理解集合之间包含与相等的含义，能识别给定集合的子集；在具体情境中了解全集与空集的含义；3.理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集；理解在给定集合中一个子集的补集的含义，会求给定子集的补集；能使用韦恩(Venn)图表达集合间的基本关系及集合的基本运算。

4.培养学生数学抽象、逻辑推理、数学运算、直观想象能力。

【知识清单】1．集合与元素(1)集合元素的三个特征：确定性、互异性、无序性．(2)元素与集合的关系是属于或不属于关系，用符号∈或∉表示．(3)集合的表示法：列举法、描述法、图示法．(4)常见数集的记法【特别提醒】N为自然数集(即非负整数集)，包含0，而N*和N＋的含义是一样的，表示正整数集，不包含0.2．集合间的基本关系A B(或B A)3.集合的基本运算【特别提醒】1．非常规性表示常用数集{x|x＝2(n－1)，n∈Z}为偶数集，{x|x＝4n±1，n∈Z}为奇数集等．2．集合子集的个数若有限集A中有n个元素，则A的子集有2n个，真子集有2n－1个. 3．集合的运算性质(1)并集的性质：A∪∅＝A；A∪A＝A；A∪B＝B∪A；A∪B＝A⇔B⊆A.(2)交集的性质：A∩∅＝∅；A∩A＝A；A∩B＝B∩A；A∩B＝A⇔A⊆B.(3)补集的性质：A∪(∁U A)＝U；A∩(∁U A)＝∅；∁U (∁U A)＝A；∁U (A∩B)＝(∁U A)∪(∁U B)；∁U (A∪B)＝(∁U A)∩(∁U B)．4．区间及有关概念(1)一般区间的表示．设a，b∈R，且a<b，规定如下：(2)【特别提醒】(1)关注实心点、空心圈：用数轴表示区间时，用实心点表示包括在区间内的端点，用空心圈表示不包括在区间内的端点．(2)区分开和闭：在用区间表示集合时，开和闭不能混淆．(3)正确理解“∞”：“∞”是一个趋向符号，不是一个数，它表示数的变化趋势．以“－∞”和“＋∞”为区间的一端时，这一端点必须用小括号．【考点梳理】考点一 集合的基本概念【典例1】（2020·山西忻州一中模拟）设集合A ＝{0，1，2，3}，B ＝{x |－x ∈A ，1－x ∉A }，则集合B 中元素的个数为( ) A ．1 B ．2 C ．3D ．4【典例2】(2018课标II 理2)已知集合(){}22,3,,A x y xy x y =+≤∈∈Z Z ，则A 中元素的个数为（ ）A ．9B ．8C ．5D ．4【规律方法】与集合中的元素有关的问题的三种求解策略(1)研究一个用描述法表示的集合时，首先要看集合中的代表元素，然后再看元素的限制条件. (2)根据元素与集合的关系求参数时要注意检验集合中的元素是否满足互异性. (3)集合中的元素与方程有关时注意一次方程和一元二次方程的区别.【变式探究】(2018豫南九校联考一)已知集合{}1,2A =，则集合(){,|,}B x y x A y A =∈∈中元素的个数为（ ）A ．1B ．2C ．3D ．4 【领悟技法】与集合元素有关问题的思路：（1）确定集合的元素是什么，即确定这个集合是数集还是点集． （2）看这些元素满足什么限制条件．（3）根据限制条件列式求参数的值或确定集合元素的个数，但要注意检验集合是否满足元素的互异性 考点二：集合间的基本关系【典例3】（2012·湖北省高考真题（文））已知集合{}{}2|320,,|05,A x x x x R B x x x N =-+=∈=<<∈，则满足条件A C B ⊆⊆的集合C 的个数为（ ）。

2021年高考数学一轮复习专题1.1 集合的概念及其基本运算（讲）文（含解析）【课前小测摸底细】1.【课本典型习题，P12第3题】设集合，，求，．【答案】当时，，；当时，，；当时，则，；当，，时，，．2. 【xx高考天津，文1】已知全集,集合,集合,则集合（）(A) (B) (C) (D)【答案】B【解析】,,则,故选B.3. 【湖北省武汉市xx届高三9月调研测试1】设集合，，，则中元素的个数为（）A．3 B．4 C．5 D．6【答案】B.4.【基础经典试题】集合，集合，则等于( )A． B． C． D．5.【改编自xx年江西卷理科】若集合，则集合中的元素的非空子集个数为( )A．7 B．6 C．5 D．4【答案】A【解析】由已知得，集合＝，所以其非空子集个数为，故选A．【考点深度剖析】高考对集合知识的考查要求较低，均是以小题的形式进行考查，一般难度不大，要求考生熟练掌握与集合有关的基础知识．纵观近几年的高考试题，主要考查以下两个方面：一是考查具体集合的关系判断和集合的运算．解决这类问题的关键在于正确理解集合中元素所具有属性的含义，弄清集合中元素所具有的形式以及集合中含有哪些元素．二是考查抽象集合的关系判断以及运算．【经典例题精析】考点1 集合的概念【1-1】若，集合，求的值________．【答案】2【解析】由可知，则只能，则有以下对应关系：①或0,,1,a bb aba⎧⎪+=⎪=⎨⎪⎪=⎩②由①得符合题意；②无解．∴．【1-2】已知集合A＝{x|x2＋mx＋4＝0}为空集，则实数m的取值范围是( )A．(－4，4) B．[－4，4] C．(－2，2) D．[－2，2]【答案】A【解析】依题意知一元二次方程无解，所以，解得．故选A．【1-3】已知A＝{a＋2，(a＋1)2，a2＋3a＋3}，若1∈A，则实数a构成的集合B的元素个数是( ) A．0 B．1 C．2 D．3【课本回眸】1、集合的含义：某些指定的对象集在一起就成为一个总体，这个总体就叫集合，其中每一个对象叫元素。

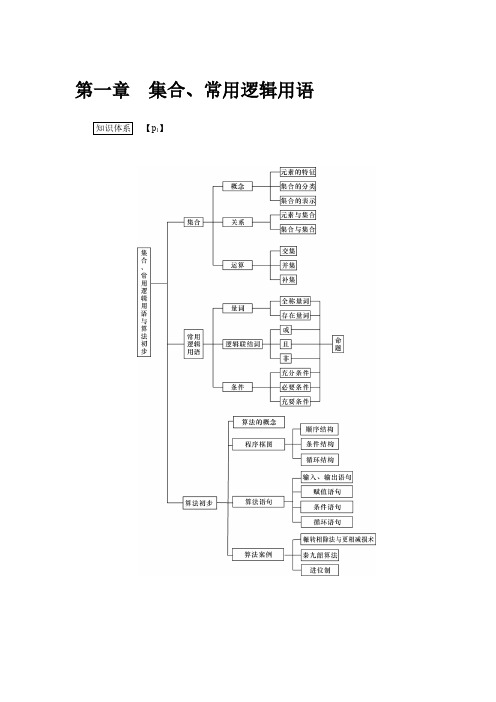
第一章集合、常用逻辑用语知识体系【p1】第1讲集合及其运算夯实基础【p2】【学习目标】1．了解集合的含义、元素与集合的“属于”关系，能用自然语言、图形语言、集合语言(列举法或描述法)来描述不同的具体问题，理解集合中元素的互异性；2．理解集合之间包含和相等的含义，能识别给定集合的子集，了解在具体情境中全集与空集的含义；3．理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集，理解在给定集合中一个子集的补集的含义，会求给定子集的补集；4．能使用韦恩(Venn)图表达集合间的关系与运算．【基础检测】1．已知集合M＝{0，1}，则下列关系式中，正确的是()A．{0}∈M B．{0}∉M C．0∈M D．0⊆M2．已知集合A＝{x|－1＜x＜3}，B＝{x|x>2}，则A∪B＝()A．(－1，3) B．(2，3)C．(－1，＋∞) D．(2，＋∞)3．设集合A＝{x|x2－3x>0}，B＝{x||x|<2}，则A∩B＝()A．(－2，0) B．(－2，3) C．(0，2) D．(2，3)4．已知集合A＝{0，1}，B＝{－1，0，a＋3}，若A⊆B，则a的值为()A．－2 B．－1 C．0 D．15．已知全集U＝R，集合A＝{x|x2－x－6<0}，B＝{1，2，3，4}，则Venn图中阴影部分所表示的集合是()A．{1，2} B．{2，3} C．{3，4} D．{2，3，4}【知识要点】1．集合的含义与表示(1)一般地，我们把研究对象统称为__元素__，把一些元素组成的总体叫__集合__，简称为集．(2)集合中的元素的三个特征：__确定性__、__互异性__、__无序性__．(3)集合的表示方法有：__列举法__、__描述法__、__图示法__、__区间法__．(4)集合中元素与集合的关系分为属于与不属于两种，分别用“__∈__”与“__∉__”来表示．(5)常用的数集：自然数集N；正整数集N*(或N＋)；整数集Z；有理数集Q；实数集R.2．集合之间的关系(1)一般地，对于两个集合A，B，如果集合A中任意一个元素__都是__集合B中的元素，我们就说这两个集合有__包含__关系，称集合A为集合B的__子集__，记作__A⊆B(或B⊇A)__；若A⊆B，且A≠B，则A B，我们就说A是B的真子集．(2)不含任何元素的集合叫做__空集__，记作__∅__，它是__任何一个集合的子集__，是任何一个__非空集合的真子集__，即∅⊆A，∅B(B≠∅)．3．集合的基本运算(1)并集：A∪B＝{x|x∈A__或__x∈B}；(2)交集：A∩B＝{x|x∈A__且__x∈B}；(3)补集：∁U A＝__{x|x∈U且x∉A}__．4．集合的运算性质(1)A∩B＝A⇔A⊆B，A∩A＝A，A∩∅＝∅；(2)A∪B＝A⇔A⊇B，A∪A＝A，A∪∅＝A；(3)A⊆B，B⊆C，则A⊆C；(4)∁U(A∩B)＝(∁U A)∪(∁U B)，∁U(A∪B)＝(∁U A)∩(∁U B)，A∩(∁U A)＝∅，A∪(∁U A)＝U，∁U(∁U A)＝A；(5)A⊆B，B⊆A，则A＝B.典例剖析【p2】考点1集合的基本概念例1(1)对集合{1，5，9，13，17}用描述法来表示，其中正确的是()A．{x|x是小于18的正奇数} B．{x|x＝4k＋1，k∈Z，且k<5}C ．{x |x ＝4t －3，t ∈N ，且t ≤5}D ．{x |x ＝4s －3，s ∈N *，且s ≤5}(2)已知集合A 是由0，m ，m 2－3m ＋2三个元素组成的，且2∈A ，则实数m 的值为( )A ．2B ．3C ．0或3D ．0或2或3(3)若集合A ＝{x |mx 2＋2x ＋m ＝0，m ∈R }中有且只有一个元素，则m 的取值集合是( )A ．{1}B ．{－1}C ．{0，1}D ．{－1，0，1}【点评】(1)用描述法表示集合，首先要搞清楚集合中代表元素的含义，再看元素的限制条件，明白集合的类型，是数集、点集，还是其他类型集合；(2)集合中元素的互异性常常容易忽略，求解问题时要特别注意．分类讨论的思想方法常用于解决集合问题． 考点2 集合间的基本关系例2(1)已知集合A ＝{x|y ＝ln (x ＋3)}，B ＝{x|x ≥2}，则下列结论正确的是( )A ．A ＝B B ．A ∩B ＝∅C ．A ⊆BD ．B ⊆A(2)若集合{a ，0，1}＝⎩⎨⎧⎭⎬⎫c ，1b ，－1，则a ＝______，b ＝______． (3)已知集合A ＝{x|x 2－3x －4≤0}，B ＝{x|x ≤a }，若A ∪B ＝B ，则实数a 的取值范围是( )A ．(4，＋∞)B ．[4，＋∞)C ．(－∞，4)D ．(－∞，4]【点评】已知两个集合间的关系求参数时，关键是将条件转化为元素或区间端点间的关系，进而转化为参数所满足的关系．常用数轴、Venn 图等来直观解决这类问题． 考点3 集合的基本运算例3(1)设集合A ＝{－1，0，1，2，3}，B ＝{x|x 2－3x ＜0}，则A ∩B ＝( )A ．{－1}B ．{1，2}C ．{1，2，3}D ．{0，－1，3}(2)已知全集U ＝R ，集合A ＝{x |x 2－2x －3>0}，则∁U A ＝________.(3)设全集U ＝{－2，－1，0，1，2}，集合A ＝{x |x 2－x －2＝0}，B ＝{0，2}，则B ∪(∁U A )＝( )A ．{0}B ．{－2，0，1，2}C ．{－1，0，2}D ．{－1，0，1，2}(4)设全集U 为实数集R ，集合A ＝{x |y ＝ln(3－2x )}，B ＝{y |(y －1)(y －3)≤0}，则图中阴影部分所表示的集合为( )A.()－∞，1∪⎣⎡⎭⎫32，＋∞B.⎣⎡⎭⎫1，32 C.[)3，＋∞ D.⎝⎛⎭⎫－∞，32∪[)3，＋∞ 【点评】(1)一般来讲，集合中的元素若是离散的，则用Venn 图表示；集合中的元素若是连续的实数，则用数轴表示，此时要注意端点的情况；(2)运算过程中要注意集合间的特殊关系的使用，灵活使用这些关系，会使运算简化．考点4 集合中的创新问题例4(1)定义一种集合运算A ⊗B ＝{x|x ∈(A ∪B )且x ∉(A ∩B )}，设M ＝{x||x|<2}，N ＝{x|x 2－4x ＋3<0}，则M ⊗N 用区间表示为________．(2)S (A )表示集合A 中所有元素的和，且A ⊆{}1，2，3，4，5，若S (A )能被3整除，则符合条件的非空集合A 的个数是( )A ．10B ．11C ．12D ．13【点评】解决以集合为背景的新定义问题，要抓住两点：(1)紧扣新定义．首先分析新定义的特点，把新定义所叙述的问题的本质弄清楚，并能够应用到具体的解题过程之中，这是破解新定义型集合问题难点的关键所在；(2)用好集合的性质．解题时要善于从试题中发现可以使用集合性质的一些因素，在关键之处用好集合的运算与性质．方 法 总 结 【p 3】1．集合中的元素的三个特征，特别是无序性和互异性在解题时经常用到．解题后要进行检验，要重视符号语言与文字语言之间的相互转化．2．对连续数集间的运算，借助数轴的直观性，进行合理转化；对已知连续数集间的关系，求其中参数的取值范围时，要注意单独考察等号能否取到．3．对离散的数集间的运算，或抽象集合间的运算，可借助Venn 图．这是数形结合思想的又一体现．4．解题中要明确集合中元素的特征，关注集合的代表元素(集合是点集、数集还是图形集)．对可以化简的集合要先化简再研究其关系运算．5．空集是任何集合的子集，是任何非空集合的真子集，时刻关注对空集的讨论，防止漏解．6．解题时注意区分两大关系：一是元素与集合的从属关系；二是集合与集合的包含关系．7．Venn图图示法和数轴图示法是进行集合交、并、补运算的常用方法，其中运用数轴图示法时要特别注意端点是实心还是空心．走进高考【p3】1．(2018·全国卷Ⅲ)集合A＝{x|x－1≥0}，B＝{0，1，2}，则A∩B＝()A．{0}B．{1}C．{1，2}D．{0，1，2}2．(2018·全国卷Ⅰ)已知集合A＝{x|x2－x－2>0}，则∁R A＝()A．{x|－1<x<2} B．{x|－1≤x≤2}C．{x|x<－1}∪{x|x>2} D．{x|x≤－1}∪{x|x≥2}3．(2018·全国卷Ⅱ)已知集合A＝{(x，y)|x2＋y2≤3，x∈Z，y∈Z}，则A中元素的个数为()A．9 B．8 C．5 D．4考点集训【p175】A组题1．集合{x∈N|x－3<2}用列举法表示是()A．{1，2，3，4} B．{1，2，3，4，5}C．{0，1，2，3，4，5} D．{0，1，2，3，4}2．下列各式：①1∈{0，1，2}；②∅⊆{0，1，2}；③{1}∈{0，1，2}；④{0，1，2}＝{2，0，1}，其中错误的个数是()A．1个B．2个C．3个D．4个3．设集合A＝{x|x2－4x＋3<0}，B＝{x|－1＜x＜3}，则()A．A＝B B．A⊇B C．A⊆B D．A∩B＝∅4．设全集U＝{－2，－1，0，1，2}，集合A＝{x|x2＋x－2＝0}，则∁U A＝()A．{－1，2} B．{－2，0，1} C．{－2，1} D．{－1，0，2}5．设全集U＝R，集合A＝{x|1<x<4}，集合B＝{x|2≤x<5}，则A∩(∁U B)＝()A．{x|1≤x<2} B．{x|1<x<2} C．{x|x<2} D．{x|x≥5}6．设全集U＝R，集合A＝{x|x－1≤0}，集合B＝{x|x2－x－6<0}，则下图中阴影部分表示的集合为()A．{x|x<3} B．{x|－3<x≤1} C．{x|x<2} D．{x|－2＜x≤1}7．设A＝{x|1＜x＜4}，B＝{x|x－a＞0}，若A⊆B，则a的取值范围是________．8．已知集合A＝{2，4}，B＝{a，a2＋3}，若A∩B＝{2}，则实数a的值为________．B组题1．设集合M＝{x|x≥4}，a＝11，则下列关系中正确的是()A．a∈M B．a∉M C．{a}∈M D．{a}∉M2．已知m，n∈R，集合A＝{2，log7m}，集合B＝{m，n}，若A∩B＝{0}，则m－n＝()A．1 B．2 C．4 D．83．设A，B是非空集合，定义A⊗B＝{x|x∈(A∪B)且x∉(A∩B)}，已知M＝{y|y＝－x2＋2x，0<x<2}，N＝{y|y＝2x－1，x>0}，则M⊗N＝______________．4．设集合A＝{x|x2＋4x＝0}，B＝{x|x2＋2(a＋1)x＋a2－1＝0}，若A∩B＝B，求实数a 的取值范围．。

第一章集合与常用逻辑用语第一节集合及其运算命题导航考试要点命题预测1.集合的含义与表示(1)了解集合的含义、元素与集合的属于关系.(2)能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.2.集合间的基本关系(1)理解集合之间包含与相等的含义,能识别给定集合的子集.(2)在具体情境中,了解全集与空集的含义.3.集合的基本运算(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集.(3)能使用韦恩(Venn)图表达集合的关系及运算.1.考向预测:(1)常与不等式、函数结合,考查集合的运算.(2)有时以新定义的形式考查集合的概念及关系.(3)与实际问题结合,考查集合的应用.2.学科素养:主要考查数学抽象、逻辑推理、数学运算的核心素养.1.元素与集合(1)集合中元素的特性:①确定性、互异性、无序性.(2)集合与元素的关系:若a属于集合A,记作②a∈A;若b不属于集合A,记作③b∉A.(3)集合的表示方法:④列举法、描述法、图示法.(4)常见数集及其符号表示:数集自然数集正整数集整数集有理数集实数集符号⑤N ⑥N*或N+⑦Z ⑧Q ⑨R2.集合间的基本关系文字语言符号语言记法集合间的基本关系子集集合A中任意一个元素都是集合B中的元素x∈A⇒x∈BA⊆B或B⑩⊇A真子集集合A是集合B的子集,并且B中至少有一个元素不属于AA⊆B,且∃x0∈B,x0∉AA⫋B或B⫌A相等集合A,B的元素完全相同A⊆B,B⊆A A=B空集不含任何元素的集合.空集是任何集合A的子集,是任何非空集合B的真子集∀x,x∉⌀,⌀⊆A,⌀⫋B(B≠⌀)⌀▶提醒(1)“⊆”与“⫋”的区别:A⊆B⇒A=B或A⫋B,若A⊆B和A⫋B同时成立,则A⫋B更准确.(2)⌀,{0}和{⌀}的区别,⌀是集合,不含有任何元素,{0}含有一个元素0;{⌀}含有一个元素⌀,且⌀∈{⌀}和⌀⊆{⌀}都正确.(3)在涉及集合之间的关系时,若未指明集合非空,则要考虑空集的可能性,如:若A⊆B,则要考虑A=⌀和A≠⌀两种情况.3.集合的基本运算集合的并集集合的交集集合的补集符号表示A∪B A∩B若全集为U,则集合A的补集为∁U A图形表示意义{x|x∈A或x∈B}{x|x∈A,且x∈B}{x|x∈U,且x∉A}4.集合的运算性质(1)并集的性质:A∪⌀=A;A∪A=A;A∪B=B∪A;A∪B=A⇔B⊆A;(2)交集的性质:A∩⌀=⌀;A∩A=A;A∩B=B∩A;A∩B=A⇔A⊆B;(3)补集的性质:A∪∁U A=U;A∩∁U A=⌀;∁U(∁U A)=A;∁U(A∪B)=∁U A∩∁U B;∁U(A∩B)=∁U A∪∁U B.知识拓展1.非常规性表示常用数集:如{x|x=2(n-1),n∈Z}为偶数集,{x|x=4n±1,n∈Z}为奇数集等.2.(1)一个集合的真子集必是其子集,一个集合的子集不一定是其真子集;(2)任何一个集合是它本身的子集;(3)对于集合A,B,C,若A⊆B,B⊆C,则A⊆C(真子集也满足).3.子集的个数:集合A中有n个元素,则集合A有2n个子集、(2n-1)个真子集、(2n-1)个非空子集、(2n-2)个非空真子集.1.判断正误(正确的打“√”,错误的打“✕”).(1){x|x≤1}={t|t≤1}.(√)(2){x|y=x2+1}={y|y=x2+1}={(x,y)|y=x2+1}.(✕)(3)含有n个元素的集合有(2n-1)个子集.(✕)(4)集合{x|x=x3}用列举法表示为{-1,1}.(✕)(5)若A∩B=A,则B⊆A.(✕)(6)若A={x|x=2k-1,k∈Z},B={x|x=2k+1,k∈Z},则集合A=B.(√)2.(2019课标全国Ⅰ,1,5分)已知集合M={x|-4<x<2},N={x|x2-x-6<0},则M∩N=()A.{x|-4<x<3}B.{x|-4<x<-2}C.{x|-2<x<2}D.{x|2<x<3}答案C3.已知集合A={0,1,x2-5x},若-4∈A,则实数x的值为.答案1或44.已知集合A={x|3≤x<7},B={x|2<x<10},则∁R(A∪B)=.答案{x|x≤2或x≥10}5.已知集合P={2,3,4,5,6},Q={3,4,5,7},若M=P∩Q,则M的子集的个数为. 答案8集合的基本概念典例1(1)设a,b∈R,若{1,a+b,a}={0,ba,b},则b-a=()A.1B.-1C.2D.-2(2)集合A={x|x2-7x<0,x∈N*},则B={y|6y∈N*,y∈A}中元素的个数为()A.1B.2C.3D.4答案(1)C (2)D方法技巧与集合中的元素有关的问题的求解策略(1)确定集合中的元素是什么,即集合是数集还是点集;(2)看这些元素满足什么限制条件;(3)根据限制条件列式求参数的值或确定集合中元素的个数.要注意检验集合中元素的互异性.1-1若集合A={x∈R|ax2-3x+2=0}中只有一个元素,则a=()A.92B.98C.0D.0或98答案 D 当a=0时,显然成立;当a≠0时,Δ=(-3)2-8a=0,即a=9.81-2已知集合A={m+2,2m2+m},若3∈A,则m的值为.答案-32解析因为3∈A,所以m+2=3或2m2+m=3.当m+2=3,即m=1时,2m2+m=3,此时集合A中有重复元素3,所以m=1不符合题意,舍去;当2m2+m=3时,或m=1(舍去),解得m=-32≠3符合题意.此时m+2=12所以m=-3.2集合间的基本关系典例2(1)已知集合A={x|x2-3x+2=0,x∈R},B={x|0<x<5,x∈N},则()A.B⊆AB.A=BC.A⫋BD.B⫋A(2)若集合A满足{a,b}⊆A⊆{a,b,c,d,e},则集合A的个数是()A.6B.7C.8D.9(3)已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B⊆A,则实数m的取值范围是.(4)集合A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0}.(i)若B是A的子集,则实数a的取值范围是;(ii)若A是B的子集,则实数a的取值范围是.答案(1)C (2)C (3)(-∞,3](4)(i)a≤-1或a=1;(ii)a=1解析 (1)由x 2-3x+2=0得x=1或x=2,∴A={1,2}.由题意知B={1,2,3,4},比较A,B 中的元素可知A ⫋B,故选C.(3)若B=⌀,则2m-1<m+1,所以m<2.若B ≠⌀,则{2m -1≥m +1,m +1≥-2,2m -1≤5,解得2≤m ≤3.综上可得,符合题意的实数m 的取值范围是(-∞,3].(4)由题意可得,A={0,-4}.(i)易知B ⊆A,∴B={0}或{-4}或⌀或{0,-4}.当B={0}或{-4}时,方程x 2+2(a+1)x+a 2-1=0有两个相等的实根,即[2(a+1)]2-4×(a 2-1)=0, ∴a=-1,此时B={0},满足题意.当B={0,-4}时,即x=0,-4是方程x 2+2(a+1)x+a 2-1=0的根,易得a=1. 当B=⌀时,即方程x 2+2(a+1)x+a 2-1=0无解, 则Δ<0,即[2(a+1)]2-4(a 2-1)<0,解得a<-1. 综上可得,a ≤-1或a=1. (ii)易知A ⊆B,A={0,-4},即0,-4是方程x 2+2(a+1)x+a 2-1=0的根, ∴{a 2-1=0,a 2-8a +7=0⇒a=1. ◆探究 (变条件)若将本例(3)中的“A={x|-2≤x ≤5}”改为“A={x|x<-2或x>5}”,求实数m 的取值范围.解析 当B=⌀时,有2m-1<m+1, ∴m<2,符合题意;当B ≠⌀时,有{m +1≤2m -1,m +1>5或{m +1≤2m -1,2m -1<-2, 解得{m ≥2,m >4或{m ≥2,m <-12, 即m>4.综上可知,实数m 的取值范围是(-∞,2)∪(4,+∞).方法技巧已知两个集合间的关系求参数,关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的关系,常用数轴、Venn 图等来直观地解决这类问题. 2-1 已知集合P={1,3},则满足P ∪Q={1,2,3,4}的集合Q 的个数是( )A.1 B .2 C.3 D.4 答案 D2-2 已知集合A={x|1≤x<5},B={x|-a<x ≤a+3},若B ⊆(A ∩B),则a 的取值范围是 . 答案 (-∞,-1]解析 因为B ⊆(A ∩B),所以B ⊆A. 当B=⌀时,满足B ⊆A,此时-a ≥a+3,即a ≤-32; 当B ≠⌀时,要使B ⊆A,则{-a <a +3,-a ≥1,a +3<5,解得-32<a ≤-1.综上可知,a 的取值范围是(-∞,-1].2-3 已知集合A={x|x 2=1},B={x|ax=1},若B 是A 的子集,则实数a 的取值集合为 . 答案 {0,1,-1}集合的基本运算典例3 (1)已知集合M={x|x -2x -3<0},N={x|2x -5x -2≤0},则M ∩N=( )A.[52,3) B .(2,52] C.[2,52] D.(52,3)A 、B 、I 均为非空集合,且满足A ⊆B ⊆I,则下列各式中正确的是( ) A.(∁I A)∪B=I B.(∁I A)∪(∁I B)=I C.A ∩(∁I B)=⌀D.(∁I A)∩(∁I B)=∁I B(3)已知集合A={x|y=√4-x 2},B={x|a ≤x ≤a+1},若A ∪B=A,则实数a 的取值范围是( ) A.(-∞,-3]∪[2,+∞) B.[-1,2]C.[-2,1] D .[2,+∞)答案 (1)B (2)ACD (3)C解析 (1)解不等式可得集合M=(2,3),集合N=(2,52], 所以M ∩N=(2,52].(2)如图,根据题意画出Venn 图,易知选ACD.方法技巧(1)离散型数集或抽象集合间的运算,常借用Venn 图求解.(2)集合中的元素若是连续的实数,常借助数轴求解,但要注意端点值能否取到. (3)根据集合的运算求参数,先把符号语言译成文字语言,然后适时应用数形结合求解. 3-1 若集合A={x|x 2+2x-8<0},B={x|5-m<x<2m-1}.若U=R ,A ∩∁U B=A,则实数m 的取值范围是 .答案 (-∞,3]解析 易知A={x|-4<x<2}.由A ∩∁U B=A,得A ⊆∁U B,则A ∩B=⌀,由数轴得5-m ≥2m-1或{2m -1≤-4,5-m <2m -1或{5-m ≥2,5-m <2m -1,解得m ≤3.集合中的新定义问题典例4 (1)定义集合的商集运算为AB ={x|x =m n,m ∈A,n ∈B},已知集合A={2,4,6},B={x|x =k2-1,k ∈A},则集合BA ∪B 中的元素的个数为( ) A.6 B .7 C.8 D .9(2)设A,B是两个非空集合,定义集合A-B={x|x∈A,且x∉B}.若A={x∈N|0≤x≤5},B={x|x2-7x+10<0},则A-B=()A.{0,1}B.{1,2}C.{0,1,2}D.{0,1,2,5}答案(1)B (2)D解析(1)由题意知,B={0,1,2},则BA ={0,12,14,16,1,13},则BA ∪B={0,12,14,16,1,13,2},共有7个元素.故选B.(2)∵A={x∈N|0≤x≤5}={0,1,2,3,4,5},B={x|x2-7x+10<0}={x|2<x<5},A-B={x|x∈A,且x∉B},∴A-B={0,1,2,5}.故选D.方法技巧解决集合中的新定义问题的方法解决以集合为背景的新定义问题,要抓住两点:(1)紧扣新定义.首先分析新定义的特点,把新定义所叙述的问题的本质弄清楚,并能够应用到具体的解题过程之中,这是破解新定义型集合问题难点的关键所在;(2)用好集合的性质.解题时要善于从题目中发现可以使用集合性质的一些因素,在关键之处用好集合的运算与性质.4-1设A是整数集的一个非空子集,对于k∈A,如果k-1∉A且k+1∉A,那么k是A的一个“单一元”,给定S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“单一元”的集合共有个.答案6解析符合题意的集合为{1,2,3},{2,3,4},{3,4,5},{4,5,6},{5,6,7},{6,7,8},共6个.1.若A={2,3,4},B={x|x=n·m,m,n∈A,m≠n},则集合B中的元素个数是()A.2B.3C.4D.5答案 B 由题意可知,当m=2时,n=3或4,此时x=6或8;当m=3时,n=2或4,此时x=6或12;当m=4时,n=2或3,此时x=8或12.所以B={6,8,12},故选B.2.已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为()A.77B.49C.45D.30答案 C 如图,集合A表示如图所示的所有圆点“”,集合B表示如图所示的所有圆点“”+所有圆点“”,则集合A⊕B显然是集合{(x,y)||x|≤3,|y|≤3,x,y∈Z}中除去四个点{(-3,-3),(-3,3),(3,-3),(3,3)}之外的所有整点(即横坐标与纵坐标都为整数的点),则集合A⊕B表示如图所示的所有圆点“”+所有圆点“”+所有圆点“”,共45个.故A⊕B中元素的个数为45.3.某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为.答案12解析设全集U为某班的30人,集合A为喜爱篮球运动的15人,集合B为喜爱乒乓球运动的10人,如图.设两项运动都喜爱的人数为x,则只喜爱篮球运动的有(15-x)人,只喜爱乒乓球运动的有(10-x)人,由此可得(15-x)+(10-x)+x+8=30,解得x=3.所以15-x=12,即所求人数为12.1.(2019课标全国Ⅲ,1,5分)已知集合A={-1,0,1,2},B={x|x2≤1},则A∩B=()A.{-1,0,1}B.{0,1}C.{-1,1}D.{0,1,2}答案A},B={x||x|<2},则A∩B=()2.已知集合A={x|y=x+1A.(-1,2)B.(0,2)C.(-2,0)D.(-2,-1)答案A的定义域为B,则A∩B=()3.设函数y=√4-x2的定义域为A,函数y=√1-xA.(1,2)B.(1,2]C.(-2,1)D.[-2,1)答案D4.已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为()A.1B.2C.3D.4答案B5.设集合A={x|-x2-x+2<0},B={x|2x-5>0},则集合A与B的关系是()A.B⊆AB.B⊇AC.B∈AD.A∈B}.答案 A 因为A={x|-x2-x+2<0}={x|x>1或x<-2},B={x|2x-5>0}={x|x>52在数轴上表示出集合A与集合B,如图所示,可知,B⊆A.6.已知集合A={x∈N|x<3},B={x|x=a-b,a∈A,b∈A},则A∩B=()A.{1,2}B.{-2,-1,1,2}C.{1}D.{0,1,2}答案D7.集合A={1,2,3,4},B={x|(x-1)(x-a)<0},若集合A∩B={2,3},则实数a的范围是()A.3<a<4B.3<a≤4C.3≤a<4D.a>3答案B8.设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=()A.{1,-3}B.{1,0}C.{1,3}D.{1,5}答案C9.设集合M={x|-12<x<12},N={x|x2≤x},则M∩N=.答案[0,12)10.若{3,4,m2-3m-1}∩{2m,-3}={-3},则m=.答案111.已知a∈R,b∈R,若{a,ln(b+1),1}={a2,a+b,0},则a2020+b2020=.答案1解析由已知得a≠0,所以ln(b+1)=0,所以b=0,于是a2=1,即a=1或a=-1,又根据集合中元素的互异性可知a=1应舍去,因此a=-1,故a2020+b2020=1.12.已知集合A={x|1≤x≤2},B={x|m≤x≤m+3}.(1)当m=2时,求A∪B;(2)若A⊆B,求实数m的取值范围.解析(1)当m=2时,B={x|2≤x≤5},∴A ∪B={x|1≤x ≤2}∪{x|2≤x ≤5}={x|1≤x ≤5}.(2)∵A ⊆B,∴{m ≤1,m +3≥2,解得-1≤m ≤1,∴实数m 的取值范围是[-1,1].13.已知集合A={x|x 2-3x+2=0},B={x|x 2-ax+a-1=0},若A ∪B=A,求实数a 的值.解析 依题意得A={x|x 2-3x+2=0}={1,2}.因为A ∪B=A,所以B ⊆A,所以集合B 可以为{1,2},{1},{2}或⌀.当B={1}时,有{Δ=a 2-4(a -1)=0,1-a +a -1=0,所以a=2,与题意相符;当B={2}时,有{Δ=a 2-4(a -1)=0,22-2a +a -1=0,无解; 当B=⌀,即方程x 2-ax+a-1=0无实数根时,Δ=a 2-4(a-1)<0=(a-2)2<0,无解;当B={1,2}时,有{Δ>0,a -1=1×2,a =1+2,所以a=3,与题意相符.综上,a=2或a=3.素养拓展R 2={(x,y)|x ∈R ,y ∈R |},M ⊆R 2,若∀P 0∈M,∃r>0,使得{P ∈R 2||PP 0|<r}⊆M,则称集合M 为“开集”.下列说法中正确的是( )A.集合{(x,y)|(x-1)2+(y-3)2<1}是开集B.集合{(x,y)|x ≥0,y>0}是开集C.开集在全集R 2上的补集仍然是开集D.两个开集的并集是开集答案AD 集合{(x,y)|(x-1)2+(y-3)2<1}表示以点(1,3)为圆心,1为半径的圆面(不含边界),取在该平面点集中的任一点(x0,y0),则该点到圆周上的点的最短距离为d,取r=d,满足“开集”的定义,故A正确;在x≥0,y>0的区域上任意取点(x0,y0),以任意正实数r为半径的圆面均不满足条件,故B错误;依题意可确定开集不含边界,所以开集在全集R2上的补集有边界,不是开集,故C错误;两个开集的并集满足开集的定义,故D正确.故选AD.15.当两个集合中的一个集合为另一个集合的子集时,称这两个集合构成“全食”,当两个集合有公共元素,但互不为对方子集时,称这两个集合构成“偏食”.对于集合A={-1,12,1},B={x|ax2=1,a≥0},若A与B构成“全食”或构成“偏食”,则a的取值集合为. 答案{0,1,4}解析当a=0时,B为空集,满足B⊆A,此时A与B构成“全食”;当a>0时,B={√a ,-√a},由题意知√a =1或√a=12,解得a=1或a=4.经检验,均符合要求,故a的取值集合为{0,1,4}.。