平行四边形的证明思路

证明平行四边形的步骤平行四边形证明是指根据给出的条件，证明一个四边形为平行四边形的过程。

下面我们将介绍一种基本的平行四边形证明方法。

这种方法分为以下几个步骤：第一步：根据给出的条件，将问题简化在做平行四边形证明题目时，首先我们需要根据给出的条件，将问题的难度降低，让问题变得更加容易证明。

我们可以通过以下几种方法来完成这一步骤：1. 根据图形的对称性，将重复的线段折叠在一起，从而得到简化的图形。

2. 如果一个四边形中有两条对角线互相平分，可以通过这两条对角线的交点来将四边形分成两个小的三角形，从而简化问题。

3. 如果问题中所涉及的线段或角度比较多，可以通过将图形平移或旋转来使它们两两相等，从而简化问题。

第二步：证明离义条件在进行平行四边形证明时，我们需要首先证明离义条件。

离义条件是指，如果一个四边形是平行四边形，那么它必须具备一些基本条件：1. 对边平行：这是平行四边形最基本的条件。

2. 对边相等：如果一个四边形的对边不相等，那么它不可能是平行四边形。

3. 同位角相等：任意一个平行四边形两个相邻的内角补角度必定互相相等。

我们可以通过以下几种方法来证明充要条件：1. 证明一个四边形的对边平行，可以通过角度关系或者线段长度关系来证明。

通过这些证明方法，我们可以验证一个四边形是否为平行四边形。

第四步：写出证明过程在完成以上三个步骤之后，我们需要将整个证明过程写出来，确保证明过程严谨完整。

在写证明过程时，我们需要注意以下几个问题：1. 表述清楚证明的目标：要明确证明的是一个四边形是否为平行四边形。

2. 排除其他可能性：在证明过程中，需要排除一些可能导致误判的因素，例如说，证明一个四边形不是矩形，不能以为它就是平行四边形。

3. 逻辑严密：证明过程中的推理步骤要严格，关键处要多加解释。

平行四边形证明方法平行四边形是几何学中常见的一种图形，其具有独特的性质和特点。

在证明平行四边形的相关问题时，我们需要掌握一些基本的证明方法和技巧。

本文将针对平行四边形的证明方法进行详细的介绍和讲解，希望能够帮助读者更好地理解和掌握平行四边形的证明方法。

首先，我们来介绍平行四边形的基本性质。

平行四边形是指具有两对对边分别平行的四边形，其性质包括对边相等、对角相等、对角线互相平分等。

在证明平行四边形的问题时，我们通常需要利用这些性质来进行推导和论证。

其次，证明平行四边形的方法有多种，其中比较常见的包括利用平行线性质、利用三角形全等性质、利用对角线性质等。

下面我们将分别介绍这些方法的具体应用。

首先是利用平行线性质来证明平行四边形。

当我们需要证明一个四边形是平行四边形时，可以通过观察其对边是否平行来进行推导。

如果能够找到一组平行线，使得四边形的对边分别被这组平行线所截，那么就可以利用平行线的性质来证明这个四边形是平行四边形。

其次是利用三角形全等性质来证明平行四边形。

在证明过程中，我们可以构造一些辅助线段或者角，将四边形分割成一些三角形，然后利用三角形的全等性质来进行推导。

通过证明四边形的某些部分是全等三角形，从而得出四边形是平行四边形的结论。

最后是利用对角线性质来证明平行四边形。

对于某些特殊的四边形，其对角线具有一些特殊的性质，我们可以通过观察对角线的长度、角度等特点，来进行证明。

例如，如果一个四边形的对角线互相平分，并且满足一定的条件，那么就可以得出这个四边形是平行四边形的结论。

总结一下，证明平行四边形的方法包括利用平行线性质、利用三角形全等性质、利用对角线性质等多种方式。

在实际应用中，我们需要根据具体的问题和条件来选择合适的证明方法，灵活运用各种几何知识和技巧，来解决平行四边形的相关问题。

希望通过本文的介绍，读者能够更加深入地理解和掌握平行四边形的证明方法，提高解题的能力和水平。

同时也希望读者能够在学习几何学的过程中，保持耐心和勇气，勇于探索和思考，不断提升自己的数学素养和解题能力。

平行四边形是指四条边都平行的四边形。

平行四边形的性质包括：
四条边都平行。

四个角都是直角。

对角线互相垂直，且长度互为相反数。

对角线的交点为四边形的中心。

对角线的中线均为平行四边形的中线。

对角线的中线的角度为45°。

判定定理：若一个四边形的对角线互相垂直，则这个四边形是平行四边形。

证明：由于对角线互相垂直，则对角线的交点为四边形的中心。

设四边形的边长分别为a、b、c、d，对角线长度分别为p、q。

由于对角线互为相反数，则有p=a+c，q=b+d。

所以四边形的周长为2(p+q)=2(a+b+c+d)。

因此，四边形的周长是定值。

由于四边形的四条边都平行，则四角都是直角。

所以，四边形是平行四边形。

因此，若一个四边形的对角线互相垂直，则这个四边形是平行四边形。

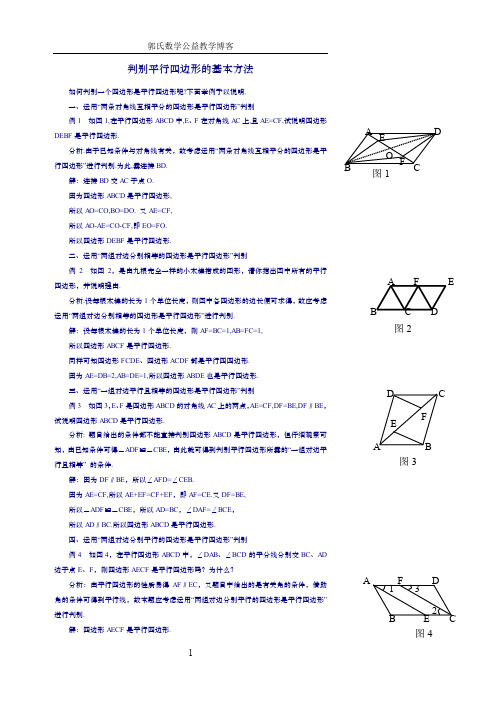
判别平行四边形的基本方法如何判别一个四边形是平行四边形呢?下面举例予以说明.一、运用“两条对角线互相平分的四边形是平行四边形”判别例1 如图1,在平行四边形ABCD中,E、F在对角线AC上,且AE=CF,试说明四边形DEBF是平行四边形.分析:由于已知条件与对角线有关，故考虑运用“两条对角线互相平分的四边形是平行四边形”进行判别.为此,需连接BD.解：连接BD交AC于点O.因为四边形ABCD是平行四边形,所以AO=CO,BO=DO. 又AE=CF,所以AO-AE=CO-CF,即EO=FO.所以四边形DEBF是平行四边形.二、运用“两组对边分别相等的四边形是平行四边形”判别例2 如图2，是由九根完全一样的小木棒搭成的图形，请你指出图中所有的平行四边形，并说明理由.分析:设每根木棒的长为1个单位长度，则图中各四边形的边长便可求得，故应考虑运用“两组对边分别相等的四边形是平行四边形”进行判别.解：设每根木棒的长为1个单位长度，则AF=BC=1,AB=FC=1,所以四边形ABCF是平行四边形.同样可知四边形FCDE、四边形ACDF都是平行四四边形.因为AE=DB=2,AB=DE=1,所以四边形ABDE也是平行四边形.三、运用“一组对边平行且相等的四边形是平行四边形”判别例3 如图3，E、F是四边形ABCD的对角线AC上的两点，AE=CF,DF=BE,DF∥BE，试说明四边形ABCD是平行四边形.分析: 题目给出的条件都不能直接判别四边形ABCD是平行四边形，但仔细观察可知，由已知条件可得△ADF≌△CBE，由此就可得到判别平行四边形所需的“一组对边平行且相等” 的条件.解：因为DF∥BE，所以∠AFD=∠CEB.因为AE=CF,所以AE+EF=CF+EF，即AF=CE.又DF=BE,所以△ADF≌△CBE，所以AD=BC，∠DAF=∠BCE，所以AD∥BC.所以四边形ABCD是平行四边形.四、运用“两组对边分别平行的四边形是平行四边形”判别例4 如图4，在平行四边形ABCD中，∠DAB、∠BCD的平分线分别交BC、AD 边于点E、F，则四边形AECF是平行四边形吗？为什么？分析：由平行四边形的性质易得AF∥EC，又题目中给出的是有关角的条件，借助角的条件可得到平行线，故本题应考虑运用“两组对边分别平行的四边形是平行四边形”进行判别.解：四边形AECF是平行四边形.图1图2AB C DEF图3AB CDEF图41 32理由：因为四边形ABCD 是平行四边形，所以AD ∥BC ，∠DAB =∠BCD ， 所以AF ∥EC .又因为∠1=21∠DAB ，∠2=21∠BCD ， 所以∠1=∠2.因为AD ∥BC ，所以∠2=∠3， 所以∠1=∠3，所以AE ∥CF . 所以四边形AECF 是平行四边形.判定平行四边形的五种方法平行四边形的判定方法有：（1）证两组对边分别平行；（2）证两组对边分别相等；（3）证一组对边平行且相等；（4）证对角线互相平分；（5）证两组对角分别相等。

平行四边形证明过程嘿，咱今儿来聊聊平行四边形的证明过程哈。

你说这平行四边形，就好像是几何世界里的一个特别存在。

你看哈，要证明一个四边形是平行四边形，那方法可多啦！就像是你有好多把钥匙能开同一把锁一样。

比如说，两组对边分别平行，这就好比两条平行线，它们永远不会相交，这不就说明这四边形的对边很有“个性”嘛，各自朝着自己的方向平行前进，那它就是平行四边形啦。

还有啊，两组对边分别相等，这就好像是四边形的两对边在比谁更长一样，结果发现它们长度一样，那也能说明它是平行四边形呀。

再说说一组对边平行且相等，这就像是一个人既有独特的技能，又有与之匹配的实力，那肯定很厉害呀，这四边形有这条件，那它就是平行四边形没跑啦。

对角线互相平分也能证明哦！这就好像是两条线在玩跷跷板，你这边下去我那边上来，配合得可好啦，那这四边形就是平行四边形呀。

你想想，要是一个四边形，它的边和边之间、线和线之间都这么有规律，这么“和谐”，那不就是平行四边形嘛。

咱证明平行四边形不就是找这些“线索”嘛。

就跟警察破案似的，找到关键证据就能确定啦。

你说要是碰到个四边形，你怎么看怎么觉得它就是平行四边形，可就是不知道从哪下手证明，那多着急呀！所以咱得把这些证明方法都牢记在心呀。

而且哦，这些证明方法之间也不是孤立的呀，有时候可以结合起来用呢。

就好像你做一件事，单靠一种方法可能有点费劲，但几种方法一起用，那不就轻松多啦。

咱学几何可不能死记硬背呀，得理解，得会用。

你得把这些图形都想象成活生生的东西在你眼前，它们在干嘛，它们有啥特点，这样才能更好地掌握嘛。

哎呀，平行四边形的证明过程真的很有意思呀，就看你能不能发现其中的奥秘啦！是不是很神奇呀？你要是能熟练掌握这些证明方法，那遇到平行四边形的问题就不怕啦，肯定能轻松搞定呀！所以呀，可得好好学，好好理解哦！别小瞧了这小小的平行四边形，它里面的学问可大着呢！。

证明四边形是平行四边形的条件四边形是几何学中的基本图形之一，它由四条线段组成，其特点是四个角均为直角或非直角。

而平行四边形则是四边形的一种特殊情况，它具有两对平行的边。

那么，如何判断一个四边形是平行四边形呢？下面将从不同的角度给出几个条件。

1. 对边平行条件：一个四边形是平行四边形的充分必要条件是它的对边是平行的。

也就是说，如果一个四边形的对边AB和CD平行，且边AB和边CD的长度相等，边AD和边BC的长度相等，那么这个四边形就是平行四边形。

2. 对角线平分条件：一个四边形是平行四边形的充分必要条件是它的对角线互相平分。

也就是说，如果一个四边形的对角线AC和BD 相交于点O，并且满足AO=CO，BO=DO，那么这个四边形就是平行四边形。

3. 两组对边相等条件：一个四边形是平行四边形的充分必要条件是它的两组对边相等。

也就是说，如果一个四边形的边AB和边CD相等，边AD和边BC相等，且边AB和边CD平行，边AD和边BC 平行，那么这个四边形就是平行四边形。

4. 对边夹角相等条件：一个四边形是平行四边形的充分必要条件是它的对边夹角相等。

也就是说，如果一个四边形的边AB和边CD平行，边AD和边BC平行，且∠BAD=∠CDA，∠ADC=∠BCD，那么这个四边形就是平行四边形。

通过以上四个条件，我们可以判断一个四边形是否为平行四边形。

同时，需要注意的是，这四个条件是充分必要条件，即满足任意一个条件的四边形都是平行四边形，而不满足这些条件的四边形则不是平行四边形。

通过以上的分析，我们可以看出，判断四边形是否为平行四边形的关键在于边的平行性和长度的相等性，以及角的相等性。

只有当这些条件同时满足时，我们才能确定一个四边形是平行四边形。

在几何学中，平行四边形是一个重要的概念，它具有许多特性和性质。

通过研究平行四边形，我们可以更深入地理解几何学的基本原理和定理。

同时，平行四边形也广泛应用于实际生活中，例如建筑设计、道路规划等领域。

平行四边形的证明方法平行四边形是初中数学中的一个重要概念，它具有独特的性质和特点。

在几何学中，我们经常需要证明某个四边形是平行四边形，这就需要用到一些具体的证明方法。

接下来，我们将介绍平行四边形的证明方法，希望能够帮助大家更好地理解和掌握这一知识点。

首先，我们来看一种常见的证明方法，利用平行线的性质。

假设我们需要证明四边形ABCD是平行四边形，我们可以先找到一条与AD平行的直线l，并且在直线l上找到一点E，使得AE与BC重合。

接下来，我们可以利用平行线的性质，通过证明∠BAD=∠BCD和∠ABD=∠ACD来得出结论，即四边形ABCD是平行四边形。

这种证明方法利用了平行线的性质，简洁明了，是常用的证明平行四边形的方法之一。

除了利用平行线的性质外，我们还可以利用平行四边形的性质进行证明。

平行四边形具有对角线互相平分的性质，即对角线互相平分。

因此，我们可以通过证明对角线互相平分来得出四边形是平行四边形的结论。

例如，我们可以证明对角线AC和BD互相平分，即AC和BD的交点O是对角线的中点，从而得出四边形ABCD是平行四边形的结论。

这种证明方法直接利用了平行四边形的性质，具有一定的普遍性和灵活性。

此外，我们还可以利用平行四边形的定义进行证明。

根据平行四边形的定义，四边形的对边是平行的，因此我们可以通过证明四边形的对边是平行的来得出结论。

例如，我们可以证明AB∥CD和AD∥BC，从而得出四边形ABCD是平行四边形的结论。

这种证明方法直接利用了平行四边形的定义，简洁明了，是常用的证明方法之一。

综上所述，我们可以利用多种方法来证明平行四边形。

无论是利用平行线的性质，还是利用平行四边形的性质或者是利用平行四边形的定义，都可以得出相应的结论。

在实际问题中，我们可以根据具体情况选择合适的证明方法，灵活运用，从而更好地理解和掌握平行四边形的知识点。

通过本文的介绍，相信大家对平行四边形的证明方法有了更深入的了解。

希望大家能够在学习和应用中灵活运用这些方法，提高自己的数学水平。

平行四边形常用的证明方法一利用平行四边形的相关定理证明1.(1)两组对边分别平行的四边形是平行四边形例题：已知在四边形ABCD中，∠A=∠C，∠B=∠D．求证：四边形ABCD是平行四边形证明：∵∠A=∠C，∠B=∠D，又∵∠A+∠C+∠B+∠D=3600，∴∠A+∠B=∠C+∠D=1800，∴AB∥CD，AD∥BC，∴四边形ABCD是平行四边形（2）两组对边分别相等的四边形是平行四边形例题：如图，□ABCD中，点E、F分别在边BC和AD上，且∠BAE=∠DCF．求证：四边形AECF是平行四边形证明：∵四边形ABCD是平行四边形，∴∠B=∠D，AB=CD，AD=BC,又∵∠BAE=∠DCF, ∴△BAE≌△DCF, ∴AE=CF,BE=DF, ∵AD=BC, ∴AF=EC, ∴四边形AECF是平行四边形（3）两组对角分别相等的四边形是平行四边形例题：如图，在□ABCD中，点E、F分别在CD、AB的延长线上，且AE=AD，CF=CB．求证：四边形AFCE是平行四边形证明：∵四边形ABCD是平行四边形，∴∠ADC=∠ABC，∠BAD=∠DCB，∴∠ADE=∠CBF,∴AE=AD,CF=CB,∴∠EAD=∠ADE,∠CBF=∠FCB，∵∠ADC=∠ABC，∴∠EAD=∠BCF，∴∠EAD+∠BAD=∠BCF+∠DCB，即∠EAF=∠ECF，∵∠EAD=∠BCF，∠EAD=∠ADE,∠CBF=∠FCB，∴∠EAD=∠ADE=∠CBF=∠FCB，∴∠E=∠F，∴四边形AFCE是平行四边形（4）两条对角线互相平分的四边形是平行四边形例题：如图，□AECF的对角线交于点O，DB经过点O，分别与AE，CF交于B，D．求证：四边形ABCD是平行四边形证明：∵四边形AECF是平行四边形，∴AO=CO，∠FCA=∠CAE，∵∠DOC=∠AOB，∴△AOB≌△COD，∴DO=BO，∴四边形ABCD是平行四边形（5）一组对边平行且相等的四边形是平行四边形例题：如图，□ABCD中，AM=（2／3）AB，CN=（2／3）CD．求证：四边形AMCN是平行四形证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，∵AM=（2／3）AB，CN=（2／3）CD，∴AM∥CN，AM ＝CN，∴四边形AMCN是平行四形2.(1)有一个角是直角的平行四边形是矩形例题：如图，在△ABC中，AB=AC，D为BC中点，四边形ABDE是平行四边形，求证：四边形ADCE是矩形证明：∵AB=AC，D为BC中点，∴AD⊥BC，BD=DC，∵四边形ABDE是平行四边形，∴AE=BD，AE∥BD，∵A、D、C在一条直线上，∴AE=CD，AE∥CD，∴四边形ADCE是平行四边形，∵∠ADC=900，∴四边形ADCE是矩形(2)有三个角是直角的四边形是矩形例题：如图，BD，BE分别是∠ABC与它的邻补角∠ABP的平分线．AE⊥BE，AD⊥BD，E，D为垂足，求证：四边形AEBD是矩形证明：∵BD，BE分别是∠ABC与它的邻补角∠ABP的平分线，∴∠PBE=∠ABE=0.5∠ABP，∠ABD=∠DBC= 0.5∠ABC，∵∠ABP+∠ABC=900，∴∠ABE+∠ABD=∠PBE+∠DBC=0.5×1800，∴∠EBD=900，∵AE⊥BE，AD⊥BD，∴∠AEB=900，∠ADB=900，∴∠EBD=∠AEB=∠ADB=900，∴四边形AEBD是矩形,(3)对角线相等的平行四边形是矩形例题：如图，□ABCD的对角线AC、BD相交于点O，△OAB是等边三角形，求证：四边形ABCD是矩形证明：∵△OAB是等边三角形，∴OA=OB，∵四边形ABCD是平行四边形，∴OA=OC，OB=OD，∴AO=OB=OC=OD，∴AC=BD，∴四边形ABCD是矩形3.(1)有一组邻边相等的平行四边形是菱形例题：如图，在△ABC中，AB＝BC，D、E、F分别为BC、AC、AB边的中点。

平行四边形对角相等的证明
平行四边形是一种特殊的四边形，具有两对平行边和相对的两个角度相等的特点。

其中一个性质是，平行四边形的对角线互相平分。

也就是说，平行四边形的两条对角线相交于中心点，并且这个中心点同时也是两条对角线的中点。

证明如下：
假设ABCD是一平行四边形，AC和BD是它的对角线，E是AC的中点，F是BD的中点。

我们需要证明的是AE=EC和BF=FD。

首先，我们可以证明△ABE和△CDE是全等的。

因为AB和CD是平行的，所以角A和角C相等。

同样，角B和角D也相等。

因此，根据三角形全等的条件，我们可以得出△ABE和△CDE是全等的。

因此，AE=EC。

接下来，我们可以证明△ABF和△CDF是全等的。

同样地，由于AB和CD是平行的，所以角A和角C相等，角B和角D也相等。

因此，根据三角形全等的条件，我们可以得出△ABF和△CDF是全等的。

因此，BF=FD。

因为AE=EC和BF=FD，所以我们可以得出平行四边形ABCD的对角线AC和BD相互平分。

- 1 -。