全站仪测角精度分析1

徕卡TS60全站仪操作说明书2016年6月26日For Leica Captivate v1.3角度测量测角精度1Hz, V 0.5"(0.15mgon)原理测角方式绝对编码，连续，四重轴系补偿距离测量(棱镜)范围2棱镜（GPR1，GPH1P ）31.5m ～3500 m 测距精度单次2,5/连续2,50.6mm + 1ppm /3mm+1.5ppm 测量时间单次2,5/连续2,5典型2.4秒/典型0.15秒距离测量(长测程模式)范围2长测程模式2,4,512000m 距离测量(无棱镜)范围2无棱镜（任意表面）41.5米至>1000m 精度/测量时间单次（任意表面）2,4,5,62mm + 2ppm / 典型3s激光光斑大小50m 处8mm x 20mm 测距技术基于相位原理系统分析技术同轴红色可见光徕卡TS60超高精度全站仪技术参数1.标准差，依据ISO17123‐32.阴天，无雾霾，能见度40KM ，无热流闪烁3.1.5m 至2000m ，使用360度棱镜（GRZ4，GRZ122）4.测量目标处于阴影下，阴天，柯达灰白板（90％反射率）5.标准差，依据ISO17123‐46.距离>500m ：精度4mm+2ppm,测量时间典型6秒徕卡TS60超高精度全站仪技术参数驱动驱动方式压电陶瓷驱动技术不需任何齿轮，仪器损耗小，更经久耐用电能直接转换为机械能，不产生磁场也不会被磁场干扰。

在测量以及瞄准过程中镜头不会抖动，保证测量精度。

通过控制热量的产生以及消散从而保证TS60的最高测距精度转速转速180°（200gon ）/ s 倒镜时间2.9s 自动目标识别（ATR plus ）ATR 2模式及工作范围可自动找目标测量圆棱镜(GPR1,GPH1P)1500m 360°棱镜(GRZ4, GRZ122)1000m LOCK 2模式及工作范围适用于动态实时跟踪监测目标圆棱镜(GPR1,GPH1P)1000m 360°棱镜(GRZ4, GRZ122)1000m 精度1,2/测量时间ATRplus 测角精度（Hz ，V）0.5″(0.15mgon)测量时间(GPR1)典型3 –4s 超级搜索PS (Power Search)测程360°棱镜(GRZ4, GRZ122)300米搜索时间一般典型5秒徕卡TS60超高精度全站仪技术参数图像广角相机和望远镜相机传感器500万像素CMOS传感器视场(广角相机/望远镜相机)19.4°/1.5°帧频率高达20帧每秒导向光（EGL）工作范围/精度5‐150m/典型5cm，100m处综合数据自动对焦望远镜放大倍数/ 调焦范围30x / 1.7m至无穷远机载软件系统Captivate软件（含应用程序）接口RS232，USB,Bluetooth®,wlan处理器TI OMAP4430 1GHZ 双核ARM®CortexTM‐A9 MPCoreTM操作系统‐Windows EC7键盘和显示屏显示/ 键盘WVGA, 5英寸,彩色触摸屏, 双面/ 37键，带屏幕，键盘照明数据存储内存2G存储卡SD卡可配1G或8G/U盘徕卡TS60超高精度全站仪技术参数操作微动螺旋3个无限位微动螺旋，一个伺服对焦驱动，两个自动对焦按键，可进行单手或双手操作自定义键√智能电源管理内置电池(GEB242)可更换锂电池，具备直接给机身电池充电功能操作时间/ 电池容量7‐9h / 5.8Ah 重量包括电池7.7kg 环境指标工作温度‐20℃至+50℃(‐4°F 至+122°F)防尘/防水(IEC 60529)/防雨IP65 /MIL ‐STD ‐810G,方法506.5‐I防潮IP65 / 95%, 无冷凝目录一、操作面板/图标介绍二、测前准备三、设站定向四、测量五、放样六、数据批量导入导出七、GeoCOM联机测量设置八、仪器四重轴系误差检校九、其他设置1.开机：按住2 s 打开。

全站仪精度分析资料全全站仪数字测图在城市测量中的误差估计随着现代高新技术的发展与运用，促使测绘工作正从传统的测绘技术手段向现代数字测绘过渡，全站仪在现代测绘工作中的应用比例也越来越大。

因此，有必要对全站仪在使用过程中的误差产生及大小做分析。

全站仪是全站型电子速测仪的简称，它集电子经纬仪、光电测距仪和微电脑处理器于一体，因此，它也兼具经纬仪的测角误差和光电测距仪的测距误差性质。

本文分别对这两项误差在城市测量中的大小进行分析，然后综合两方面的影响对地面点的点位误差进行分析与估算。

最后单独分析全站仪的高程误差。

、全站仪测图点位中误差分析1、全站仪测角误差分析检验合格的全站仪水平角观测的误差来源主要有：①仪器本身的误差（系统误差）。

这种误差一般可采用适当的观测方法来消除或减低其影响，但在全站仪测图中对角度的观测都是半测回，因此，这里还是要考虑其对测角精度的影响。

分析仪器本身误差的主要依据是其厂家对仪器的标称精度，即野外一测回方向中误差M标，由误差传播定律知，野外一测回测角中误差M i测= M标，野外半测回测角中误差M半测= M i测=2M标。

②仪器对中误差对水平角精度的影响，仪器对中误差对水平角精度的影响在《测量学》教材中有很详细的分析其公式为M中=p X S AB/S 1S2其中e为偏心距，熟练的仪器操作人员在工作中的对中偏心距一般不会超过3mm，这里取e=3mm。

S i在这里取全站仪测图时的设站点（图根点）至后视方向是（另一通视图根点）之间的距离，S2取全站仪设站点至待测地面点之间的规范限制的最大距离。

由公式知，对中误差对水平角精度的影响与两目标之间的距离S AB成正比，即水平角在180时影响最大，在本文讨论中只考虑其最大影响。

③目标偏心误差对水平角测角的影响，《测量学》教材推导出的化式为m偏=p /2 XV（e i/S i）2+（e2/S 2）2，S i、S2的取法与对中误差中的取法相同，e i取仪器设站时照准后视方向的误差，此项误差一般不会超过5mm，取e i=5mm ，e2取全站仪在测图中的照准待测点的偏差。

全站仪三角高程测量方法及精度分析摘要：通过结合全站仪和跟踪杆，我们可以大大提升测量高程的准确性，并且随着应用频率的增加，这种方法也会受到越来越多的重视。

相比于传统的三角测量方法，新型的三角测量技术不仅可以克服其局限性，还能够大大降低误差，提升测量精度。

通过采用无需重复测量仪器和棱镜高度的方式，可以大大减轻外部作业的负担，并且提高测量的效率，这种方法在实际应用中表现出色。

关键词：全站仪；三角高程测量；测量方法；精度分析引言通过使用全站仪测量三角高程，我们可以建立一个三维坐标控制网。

这种方法包括对向观测法和中间观测法。

在进行对向观测时，我们通常会将大气折射系数视为一个常数，但是如果我们忽略了不同方向折射系数的差异性，那么我们就无法准确地评估整个系统的精度。

通过中间观测法，我们可以将折光系数作为一个方向变量来考虑大气折射误差对三角高程测量的影响。

因此，本文将详细介绍三角高程测量方法，并对它们的准确性进行比较分析。

1研究背景和现状高程测量是测量工作的重要组成部分，现代高程测量技术包括水准测量、三角测量和GPS高程测量。

然而，GPS 高程测量技术存在测量精度较低的问题，无法满足日常测量的需求。

此外，传统的三角测量技术，如全站仪测量，也存在一定的局限性，无法满足高程测量的需求。

通过使用全站仪进行三角测量，可以获得两点之间的垂直高度差，这种方法比传统的水平测量更加精确，而且由于没有受到地形的影响，可以更加迅速、准确地完成测量任务。

2全站仪的基本测量原理测量是一项重要的技术，它的主要目的是测量物体的位置、倾斜角、高差。

与传统的测量方式不同，全站仪可以快速、准确地完成测量，大大提高了测量效率，并有效地减少了测量结果的偏差。

全站仪望远镜具有独特的优势，它的核心技术就是其精准的视准轴、高精度的测距光波发射与接收光轴的同轴化，以及可靠的双轴自动倾斜补偿，使得它可以一次性完成所有的测量要素，并确保测量结果的准确性。

3全站仪三角高程测量方法特征分析以及研究进程3.1单向观测法使用全站仪三角高程测量单向观测法可以获得较高的水准测量精度，但是在进行测量之前，必须充分考虑地球曲率和大气折射带来的可能影响，这将会对测量结果产生重大影响。

全站仪角度测量实验报告1.实验目的本实验旨在通过使用全站仪进行角度测量，掌握全站仪的使用方法，了解全站仪在工程测量中的应用。

2.实验仪器和设备本次实验使用的仪器和设备有：全站仪、三脚架、反光棱镜等。

3.实验原理全站仪是一种多功能的测量仪器，能够同时进行水平角和垂直角的测量。

其原理是利用仪器内的光学和电子设备，对测量目标进行定位和角度测量，并通过数码显示屏显示测量结果。

4.实验步骤4.1设置全站仪首先，将全站仪放在平整的地面上，并调整三脚架的高度，使全站仪处于水平状态。

然后使用水平仪进行准确调平，确保仪器的测量精度。

4.2定位测量目标使用全站仪的目标对准功能，将仪器对准待测量的目标物。

在目标物上放置反光棱镜。

4.3进行测量打开全站仪的测量模式，将视线对准反光棱镜，并通过调节仪器的水平和垂直角，使视线精确定位在棱镜上。

然后按下测量按钮，记录仪器所显示的水平角和垂直角的数值。

4.4反复测量进行多次测量，计算出平均值，以提高测量的准确性。

5.实验结果根据实验步骤所得到的数据，进行数据处理和分析，并计算得到所需的角度测量结果。

6.实验误差分析7.实验结论通过本次实验，我们学习了全站仪的使用方法，并进行了角度测量实验。

通过对实验数据的处理和分析，获得了需要的测量结果。

同时，我们也认识到实际测量中存在的误差，并探讨了减小误差的方法。

总结而言，全站仪角度测量实验是一项基础的测量实验，能够帮助我们掌握全站仪的使用方法，并了解其在工程测量中的应用。

通过这次实验，我们不仅熟悉了全站仪的操作步骤，还加深了对测量误差的认识，提高了我们的实验能力和测量技术水平。

全站仪精度分析全站仪代替水准测量精度分析1．引言目前, 在水准测量中, 水准仪仍然是主要的使.用仪器, 但山丁仪器本身的原因, 其仅使用于平坦地区在地形较复杂地区使用水准仪进行水准测量, 测站数很多, 精度也很难保障。

随着电子技术的发展, 与全站仪的普及, 测距精度已人人提高。

全站仪己普遍用于控制测量、地形测量和上程测量中。

但是能否使用全站仪代替水准仪进行水准测量是广大测量所关心的问题, 本文结合全站仪三角高程测量的原理和方法, 并将其主要误差来源与水准仪进行对比分析, 进而分析其代替水准测量的可行性。

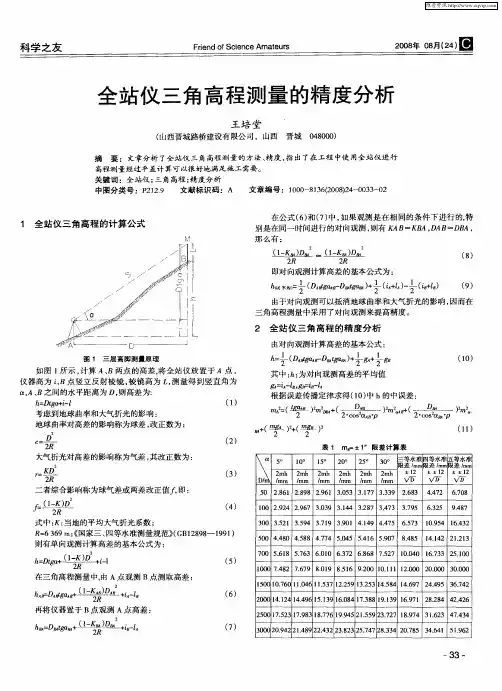
全站仪三角高程测量及其精度分析根据误差传播定律,得到(2) 式计算高差中误差为:则(3) 式可化简为如果取测角标准差mα= ±1″,测距标准差m S = ±(2 + 2 ×10 - 6 S ) mm ,仪器高和棱镜高量取中误差m g= ±110 mm ,则对应不同的竖直角α和倾斜距离S ,对向观测高差的中误差见表1 所示。

表1 对向观测高差中误差(单位:mm)从实验数据分析可看出:对向观测高差中误差随着竖直角及视线斜距的增大而增大。

对于短测距边长,仪器高和棱镜高量测误差是全站仪三角高程的主要误差。

若取二倍中误差作为三角高程极限误差,则对于测角中误差为±1″全站仪,对向观测法在测距边长大于100 m 情况下,其三角高程精度可以满足三等水准限差要求。

2 中间观测法不同方向的大气折光系数是有差异的,因而简单地进行对向观测加以抵消与实际的情况有出入。

为了提高三角高程观测精度,可采用中间观测法,即将全站仪置于A 和B 两点大致中间位置处,设S A 、S B 分别为测站与测点A 和B 之间的倾斜距离; D A 、D B 分别为测站与测点A 和B 之间的水平距离;αA 、αB 为全站仪照准棱镜中心的竖直角; i 为仪器高; v A 、v B 为棱镜高; R 为地球曲率半径。

全站仪的角度测量误差分析与校正引言：全站仪是一种重要的测量仪器，在土木工程、建筑施工等领域有着广泛的应用。

然而，由于各种因素的影响，全站仪在进行角度测量时可能存在一定的误差。

本文将从全站仪测量角度误差的原因和影响因素入手，探讨误差的分析和校正方法。

一、角度测量误差的原因1. 仪器误差：全站仪是由多个光学、电子和机械组件组成的复杂仪器，其中的各种误差会对角度测量结果产生影响。

例如，光学系统的非线性误差、仪器的刻度误差等。

2. 环境条件：大气压力、温度、湿度等环境条件的变化会引起光线折射的改变，从而导致角度测量误差。

此外，周围的振动、风力等也会对全站仪的测量稳定性产生影响。

3. 操作者技术：操作者的技术水平和经验对角度测量结果的准确性起着决定性的作用。

错误的操作、观测不精细等因素都会导致角度测量误差的产生。

二、角度测量误差的影响因素1. 近视效应：观察距离过远或目标太小会引起近视效应，使得观测者无法准确地对准目标，从而产生角度误差。

2. 仪器仰角：全站仪进行角度测量时，仰角的改变也会影响测量结果。

仰角过大或过小都会引起仪器的非正常工作，从而增加测量误差。

3. 仪器校准：仪器校准不准确会直接影响到角度测量的精度和准确性。

因此，定期对全站仪进行校准是保证角度测量准确性的关键。

三、角度测量误差的分析方法1. 数据分析：通过对测量数据进行统计分析，可以得到各个角度测量值的平均值、方差等指标。

根据分析结果，判断是否存在系统性的误差，并找出其产生的原因。

2. 观测重复性检验：该方法通过对同一目标进行多次观测，利用统计学方法判断观测者个体差和系统环境误差。

如果多次观测结果接近，则表明观测重复性较好；反之，则需要进一步分析原因。

3. 同一目标不同位置观测：通过在同一目标的不同位置进行观测，可以验证仪器的仰角误差和垂直轴误差。

若观测结果相差较大，则表明存在不可忽视的系统误差。

四、角度测量误差的校正方法1. 仪器校准：定期对全站仪进行校准是减小角度测量误差的关键。